Numerical Study on the Coupling Effect on a Retaining Structure of a Complex Deep Foundation Pit Group Excavation in a Soft-Soil Area
Abstract
1. Introduction
2. Project Overview
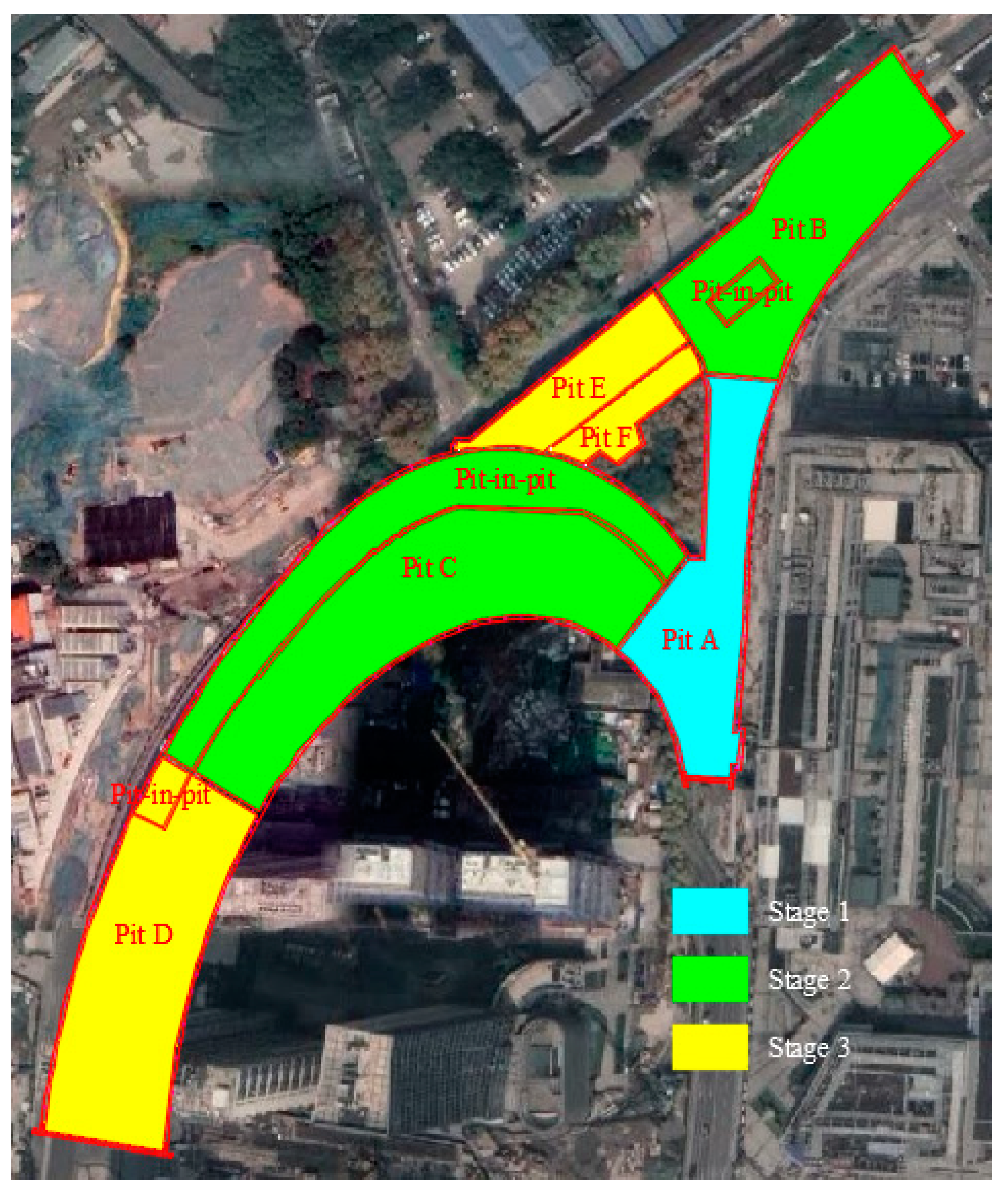
2.1. Project Description
2.2. Site Description
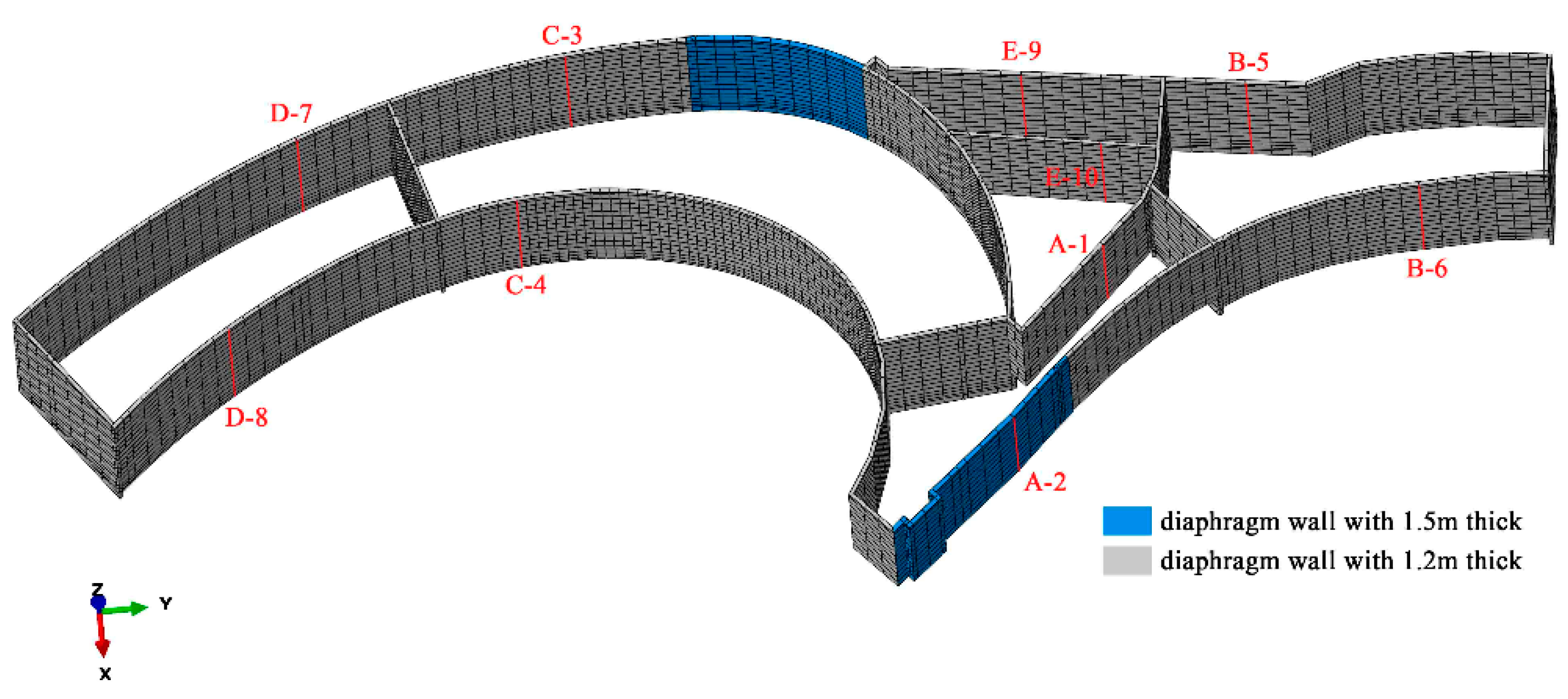
2.3. Retaining Structure and Construction Process
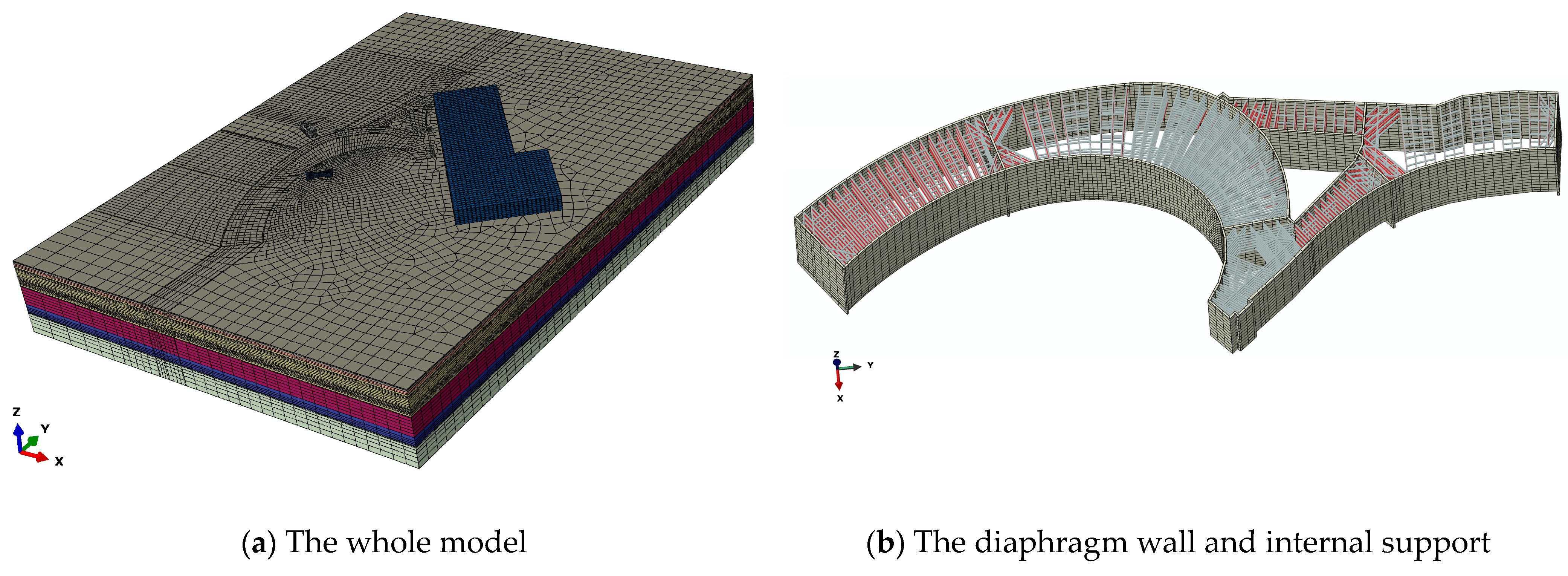
3. Numerical Model
3.1. Finite Element Model
3.2. Model Parameters
3.3. Construction Simulation
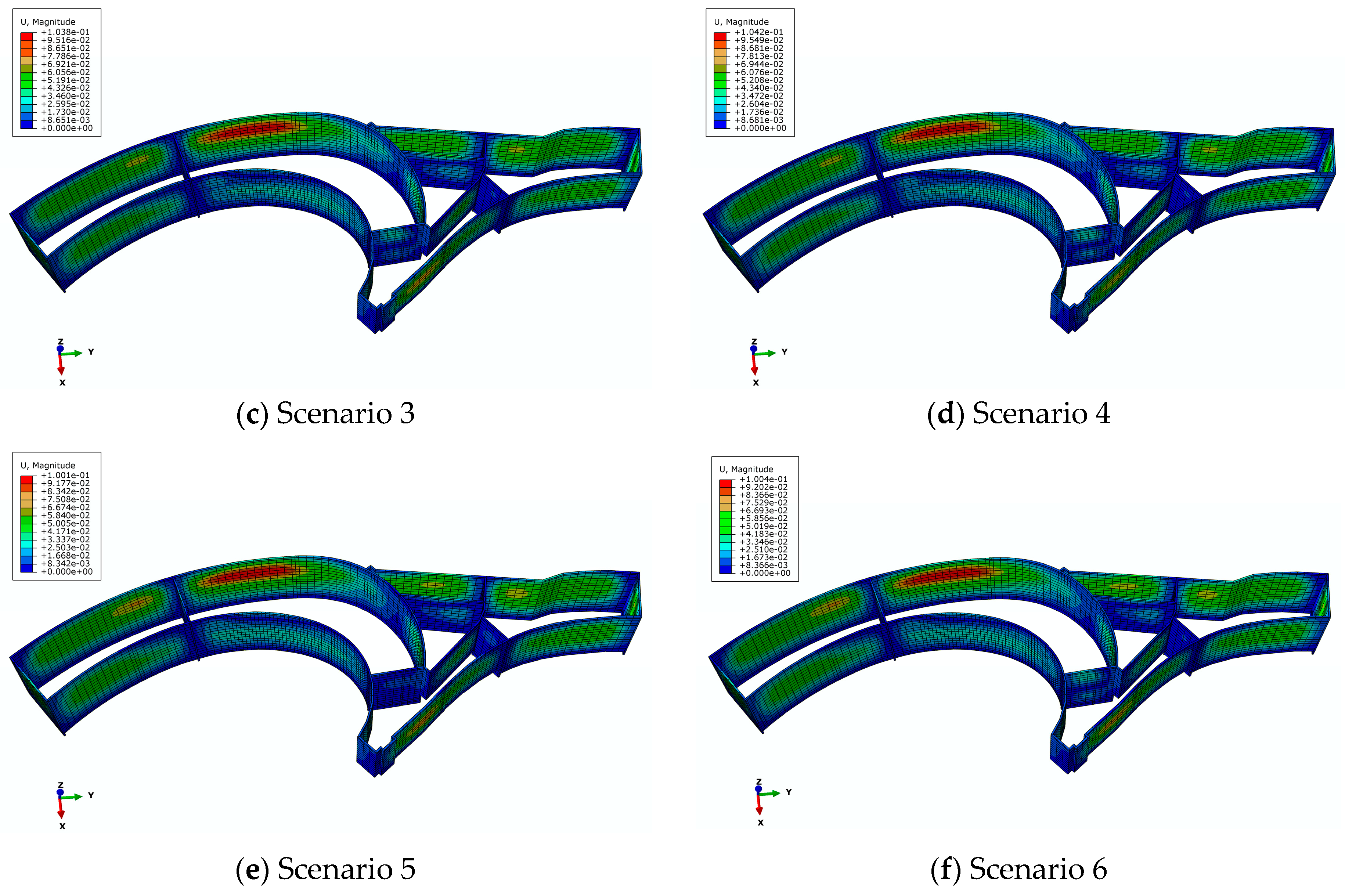
4. Results and Discussion
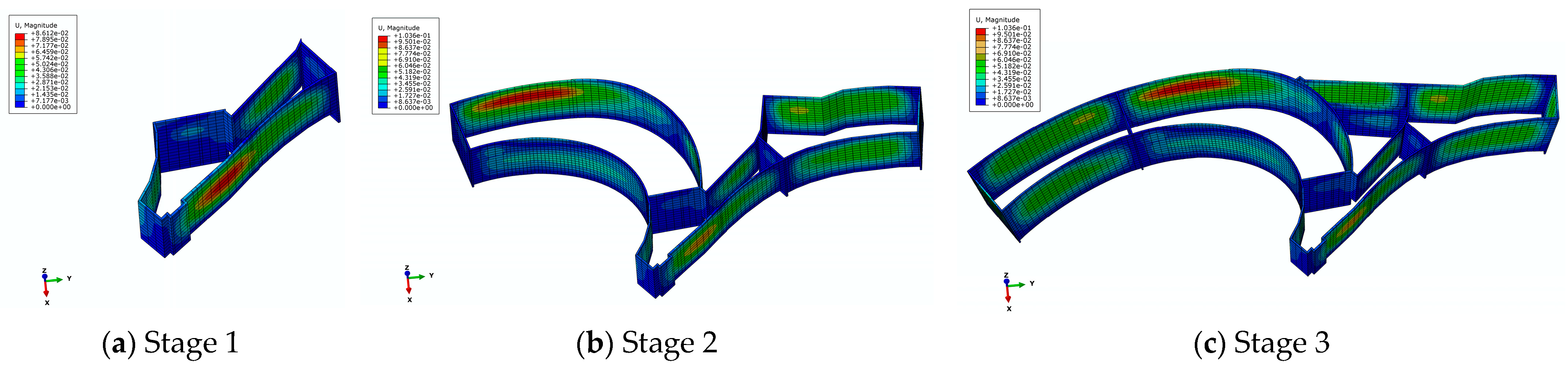
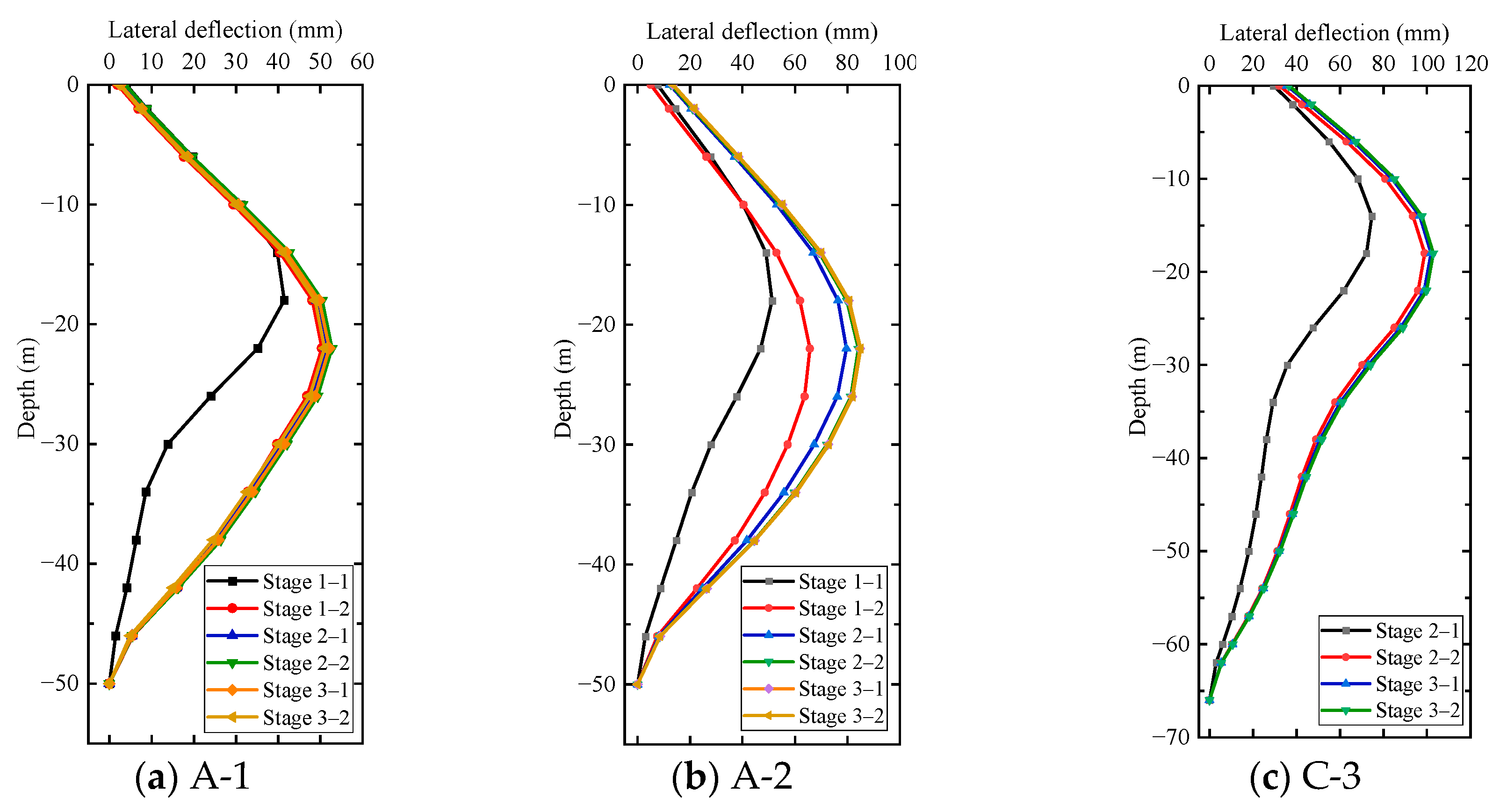
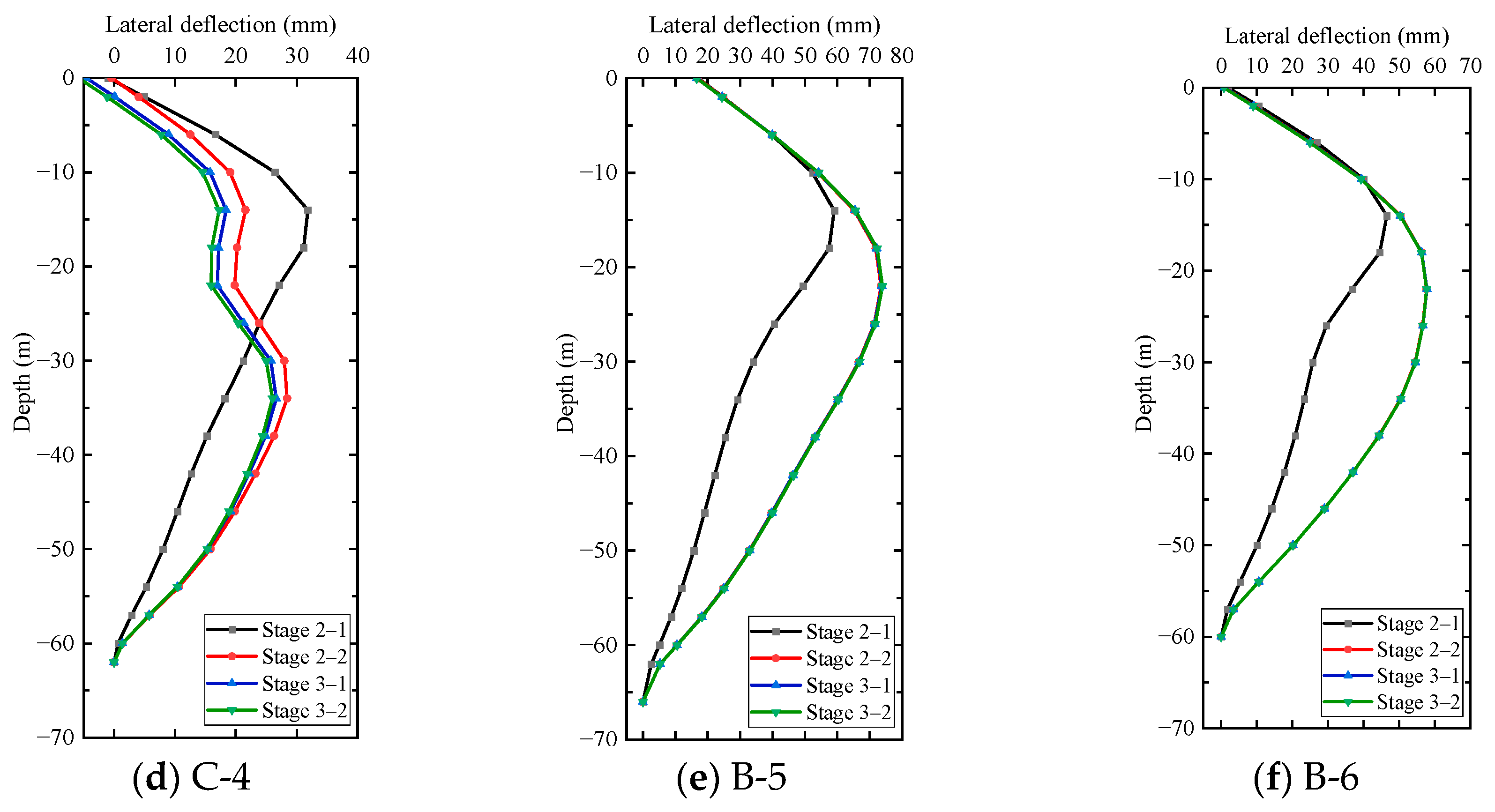
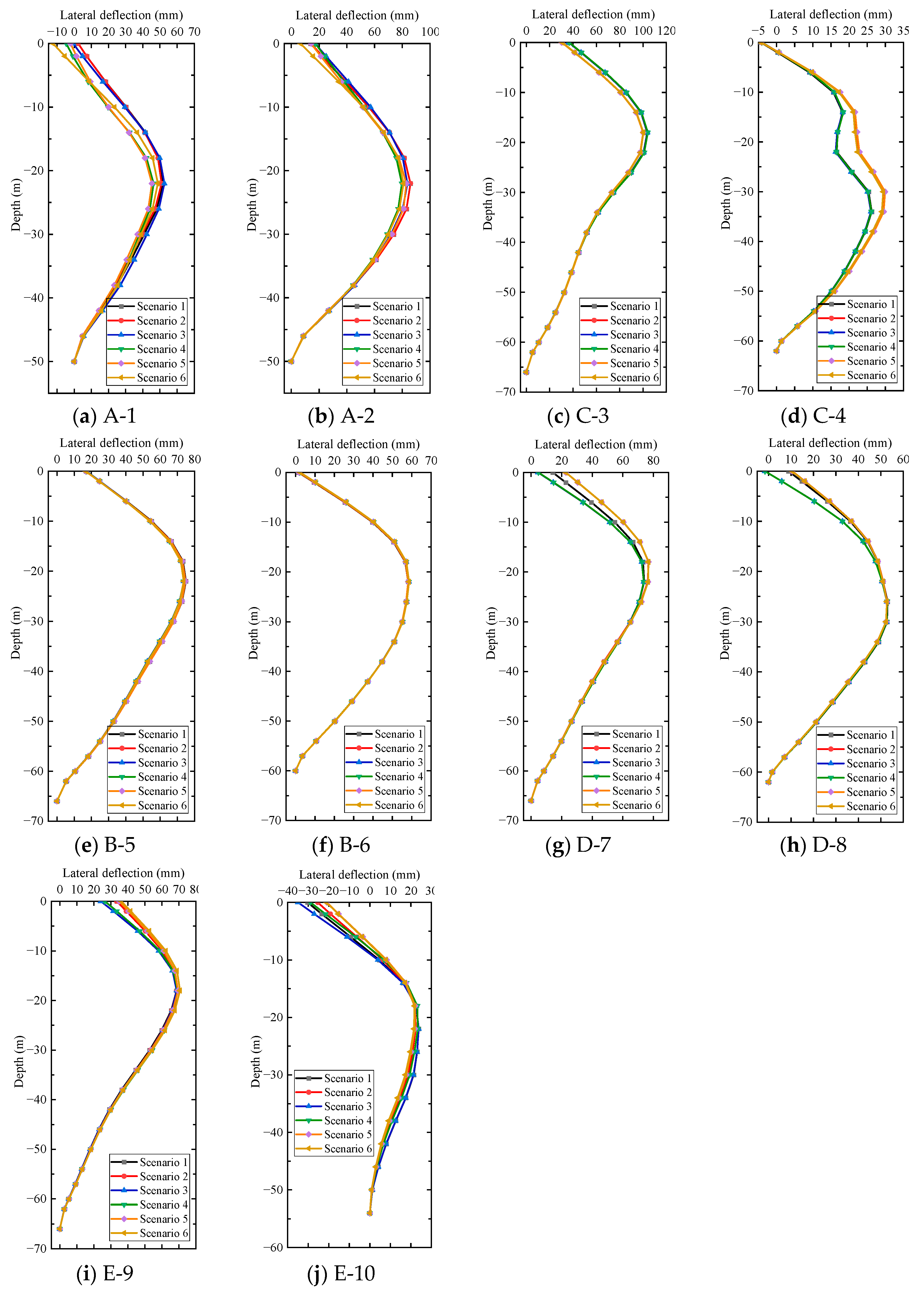
4.1. Lateral Wall Deflection
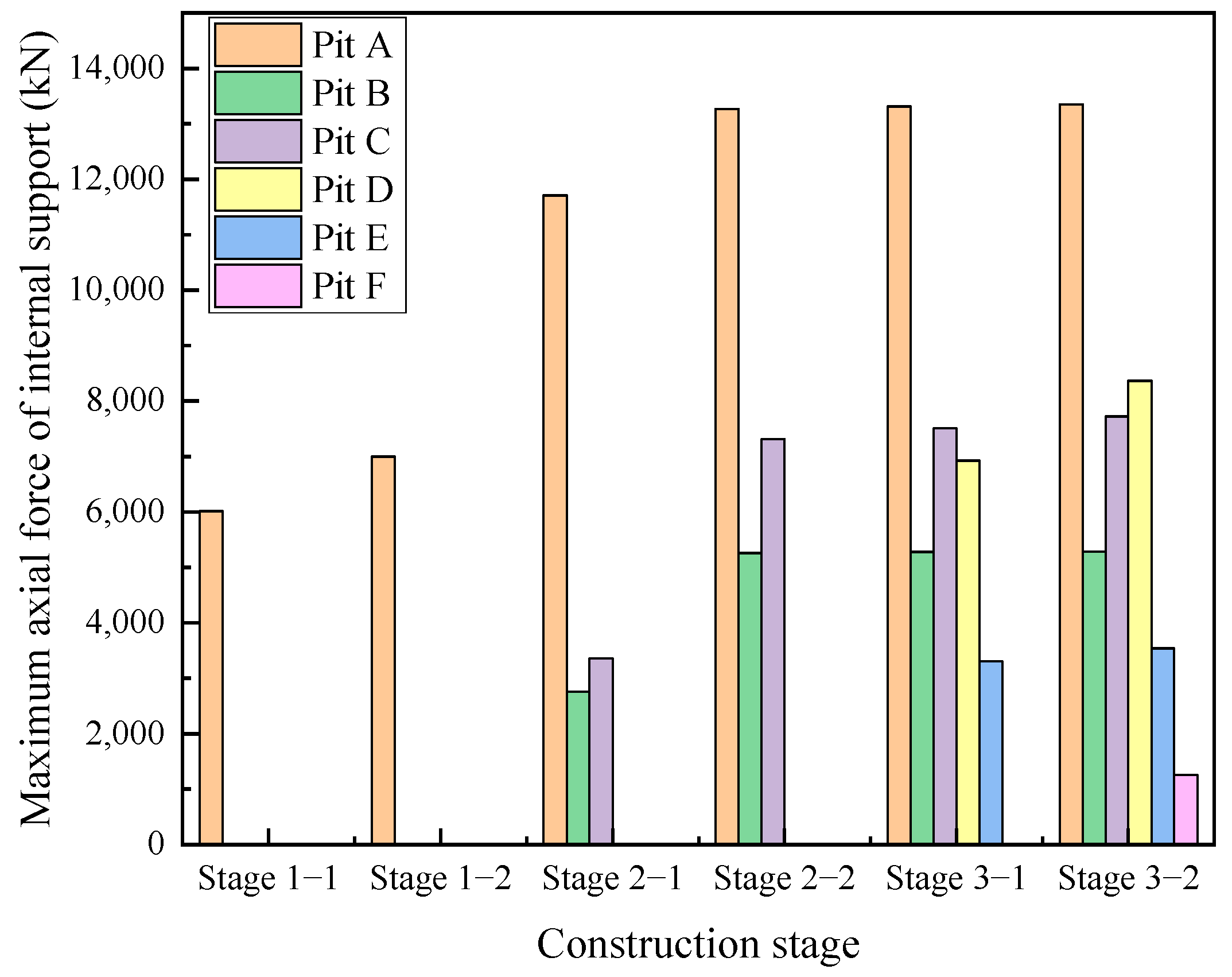
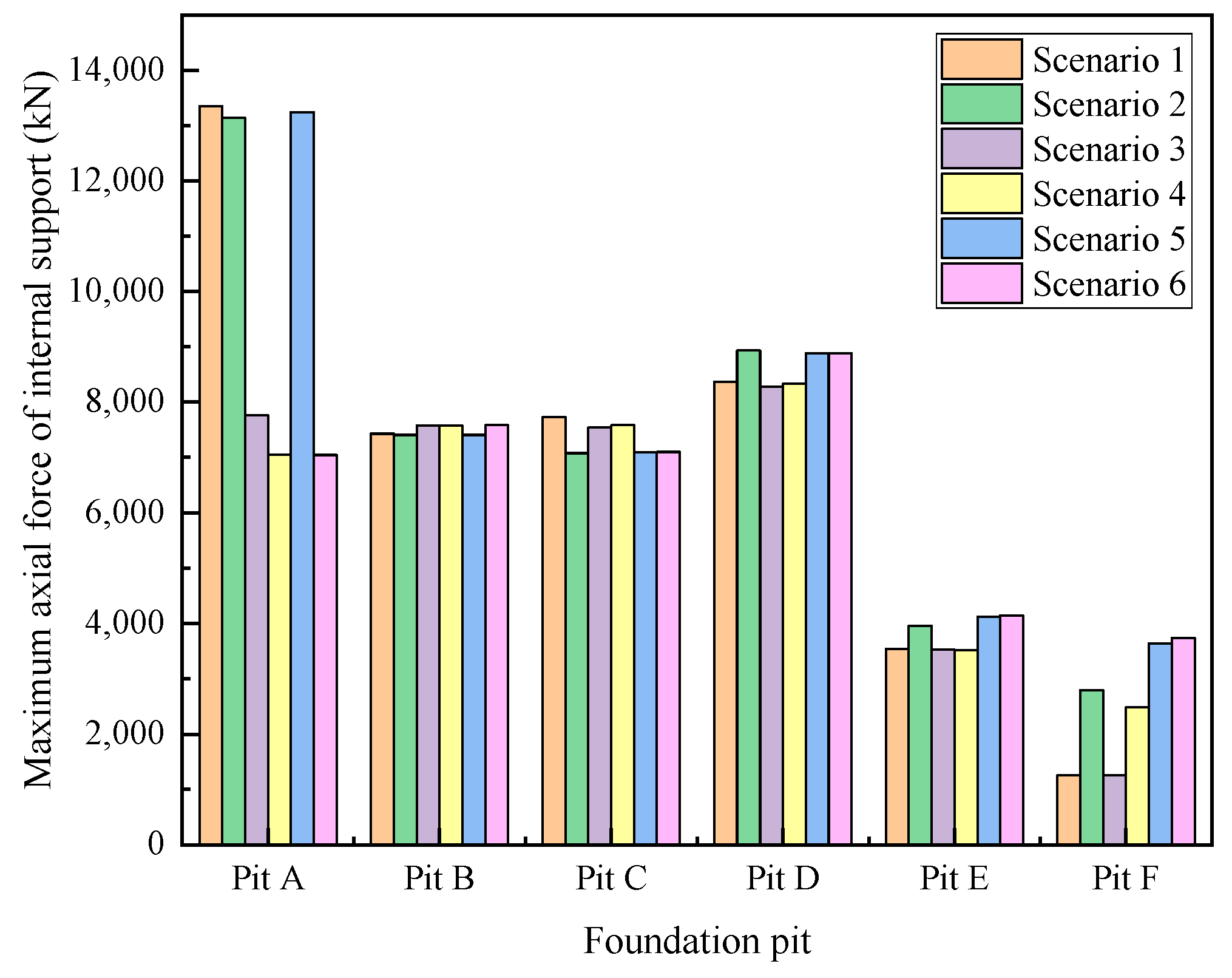
4.2. Internal Support Axial Force
5. Influence of Construction Sequence
5.1. Influence on Lateral Wall Deflection
5.2. Influence on Internal Support Axial Force
6. Conclusions
- In the original construction scenario (Scenario 1), the lateral deformation of the diaphragm walls at A-2 and C-4 showed the obvious coupling effect from the surrounding excavation, and the maximum change rates were 28.2% and 20.8%, respectively. The coupling effect on the lateral deformation of the diaphragm wall at A-1 and C-3 was not apparent, and the maximum change rates were 3.3% and 4%, respectively. However, the lateral deformation of the diaphragm wall at B-5 or B-6 was hardly affected by the excavation of other pits.
- In Scenario 1, the maximum axial force in Pit A was far greater than that in other pits, and it increased by 89.6% after the construction of Stage 2, indicating a strong coupling effect. In contrast, the construction of Stage 3 had little impact on the maximum axial force in Pit A and a certain degree of coupling effect on the maximum axial force in Pit C.
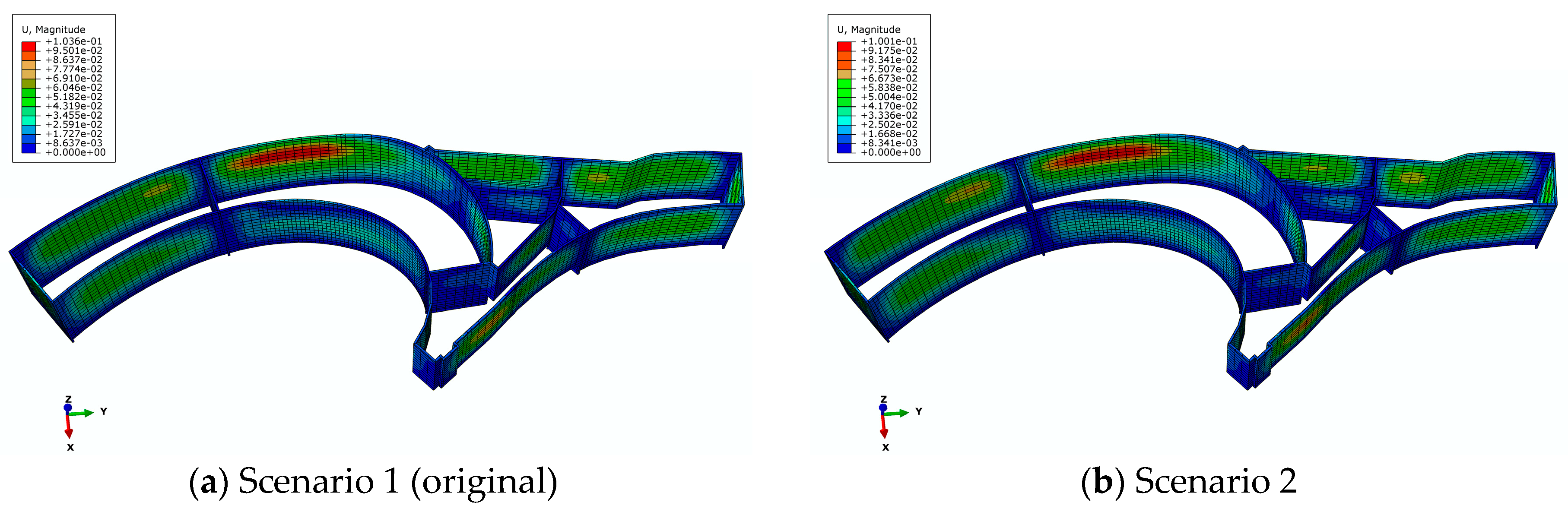
- After changing the construction sequence, the coupling effects on the lateral deformation of the diaphragm walls at A-1, A-2, C-4, and E-10 were obviously different. Among the six construction scenarios, the maximum change rates of maximum lateral deformation at the above positions were 15.9%, 7.5%, 15.4%, and 10.7%, respectively. However, the maximum change rates of maximum lateral deformation at other positions did not exceed 3%. The maximum change rates of the maximum axial force in Pit A and Pit F were 89.5% and 193.6%, respectively, and that in other pits was little affected by the construction sequence.
- The coupling effect of foundation pit group excavation on the lateral displacement of the diaphragm wall near the existing building was more significant, and the deformation development should be focused on. The constraint of the concrete cushion can effectively reduce the lateral displacement of the diaphragm wall. In addition, the maximum axial force of the support in the pit adjacent to the existing building was obviously affected by the coupling effect of the adjacent excavations.
- Due to the quantity and the irregular shape of the foundation pits in the foundation pit group, many different construction scenarios can be formulated. However, considering the impact of construction on traffic flow and the safety of the foundation pit group, the six scenarios studied in this paper are representative and reflect the coupling effects between each foundation pit during the construction of the foundation pit group, which can be used as a reference. The practical construction scheme must also be formulated by considering the on-site environment and various other factors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goh, A.T.; Zhang, F.; Zhang, W.; Chew, O.Y. Assessment of strut forces for braced excavation in clays from numerical analysis and field measurements. Comput. Geotech. 2017, 86, 141–149. [Google Scholar] [CrossRef]
- Liao, S.-M.; Wei, S.-F.; Shen, S.-L. Structural Responses of Existing Metro Stations to Adjacent Deep Excavations in Suzhou, China. J. Perform. Constr. Facil. 2016, 30, 04015089. [Google Scholar] [CrossRef]
- Liu, H.; Li, K.; Wang, J.; Cheng, C. Numerical Simulation of Deep Foundation Pit Construction under Complex Site Conditions. Adv. Civ. Eng. 2021, 2021, 6669466. [Google Scholar] [CrossRef]
- Shi, J.; Fu, Z.; Guo, W. Investigation of geometric effects on three-dimensional tunnel deformation mechanisms due to basement excavation. Comput. Geotech. 2019, 106, 108–116. [Google Scholar] [CrossRef]
- Shi, X.; Rong, C.; Cheng, H.; Cui, L.; Wang, B.; Sun, S. Analysis on Deformation and Stress Characteristics of a Multibraced Pit-in-Pit Excavation in a Subway Transfer Station. Adv. Civ. Eng. 2020, 2020, 8844461. [Google Scholar] [CrossRef]
- Wang, Z.-Z.; Goh, S.H.; Koh, C.G.; Smith, I.F. An efficient inverse analysis procedure for braced excavations considering three-dimensional effects. Comput. Geotech. 2019, 107, 150–162. [Google Scholar] [CrossRef]
- Chen, S.; Cui, J.; Liang, F. Case Study on the Deformation Coupling Effect of a Deep Foundation Pit Group in a Coastal Soft Soil Area. Appl. Sci. 2022, 12, 6205. [Google Scholar] [CrossRef]
- Guo, L.Q.; Cheng, Y.G. Consideration on Group Excavation Engineering. Appl. Mech. Mater. 2013, 256–259, 315–319. [Google Scholar] [CrossRef]
- Li, M.-G.; Zhang, Z.-J.; Chen, J.-J.; Wang, J.-H.; Xu, A.-J. Zoned and staged construction of an underground complex in Shanghai soft clay. Tunn. Undergr. Space Technol. 2017, 67, 187–200. [Google Scholar] [CrossRef]
- Wang, J.H.; Xu, Z.H.; Wang, W.D. Wall and Ground Movements due to Deep Excavations in Shanghai Soft Soils. J. Geotech. Geoenviron. Eng. 2010, 136, 985–994. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Yan, C.; Azzam, R. Numerical Evaluation of Isolation Walls in Modifying Excavation-Induced Dis-placement Field. Arab. J. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Chen, R.P.; Li, Z.C.; Chen, Y.M.; Ou, C.Y.; Hu, Q.; Rao, M. Failure Investigation at a Collapsed Deep Excavation in Very Sensitive Organic Soft Clay. J. Perform. Constr. Facil. 2015, 29, 04014078. [Google Scholar] [CrossRef]
- Blackburn, J.T.; Finno, R.J. Three-Dimensional Responses Observed in an Internally Braced Excavation in Soft Clay. J. Geotech. Geoenviron. Eng. 2007, 133, 1364–1373. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Y.; Azzam, R.; Yan, C. Performance of a top-down excavation in shanghai: Case study and numerical ex-ploration. Eur. J. Environ. Civ. Eng. 2021, 26, 7932–7957. [Google Scholar] [CrossRef]
- Huang, M.; Liu, X.-R.; Zhang, N.-Y.; Shen, Q.-W. Calculation of foundation pit deformation caused by deep excavation considering influence of loading and unloading. J. Central South Univ. 2017, 24, 2164–2171. [Google Scholar] [CrossRef]
- Tan, Y.; Zhu, H.; Peng, F.; Karlsrud, K.; Wei, B. Characterization of semi-top-down excavation for subway station in Shanghai soft ground. Tunn. Undergr. Space Technol. 2017, 68, 244–261. [Google Scholar] [CrossRef]
- Feng, T.; Liu, L.; Tong, T.; Zhou, M. Numerical study on lateral wall displacement of deep excavation supported by IPS earth retention system. Undergr. Space 2017, 2, 259–271. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q.; Dong, J.; Wang, J.; Wang, M. Comparative investigation on deformation monitoring and numerical simulation of the deepest excavation in Beijing. Bull. Eng. Geol. Environ. 2021, 80, 1233–1247. [Google Scholar] [CrossRef]
- Yang, J.; Kong, D. Deformation of deep and large foundation pit in soft soil of Fuzhou Subway. Arab. J. Geosci. 2020, 13, 36. [Google Scholar] [CrossRef]
- Dan, K.; Sahu, R.B. Estimation of Ground Movement and Wall Deflection in Braced Excavation by Minimum Potential Energy Approach. Int. J. Géoméch. 2018, 18, 04018068. [Google Scholar] [CrossRef]
- Zhou, N.; Vermeer, P.A.; Lou, R.; Tang, Y.; Jiang, S. Numerical simulation of deep foundation pit dewatering and optimization of controlling land subsidence. Eng. Geol. 2010, 114, 251–260. [Google Scholar] [CrossRef]
- Dong, Y.; Burd, H.J.; Houlsby, G.T. Finite element study of deep excavation construction processes. Soils Found. 2017, 57, 965–979. [Google Scholar] [CrossRef]
- Soomro, M.A.; Saand, A.; Mangi, N.; Mangnejo, D.A.; Karira, H.; Liu, K. Numerical modelling of effects of different multipropped excavation depths on adjacent single piles: Comparison between floating and end-bearing pile responses. Eur. J. Environ. Civ. Eng. 2021, 25, 2592–2622. [Google Scholar] [CrossRef]
| Soil/Rock | Thickness (m) | Unit Weight (kN/m3) | Compressive Modulus (MPa) | Poisson’s Ratio | Cohesion (kPa) | Friction Angle (°) | Permeability Coefficient (cm/s) |
|---|---|---|---|---|---|---|---|
| Miscellaneous fill | 3 | 1990 | 4.1 | 0.30 | 15 | 12 | 2 × 10–3 |
| Pain fill | 3 | 1790 | 3.77 | 0.35 | 19 | 16 | 2.5 × 10–5 |
| Mucky silty clay | 25 | 1760 | 3.57 | 0.30 | 10.6 | 18.2 | 5 × 10–6 |
| Clayey silt | 13 | 1770 | 4.2 | 0.35 | 10.8 | 19.8 | 4 × 10–6 |
| Fine silt sand | 11 | 1840 | 11.2 | 0.28 | 2.3 | 33.9 | 1.63 × 10–3 |
| Limestone | 25 | 2750 | - | 0.36 | 800 | 40 | - |
| Soil/Rock | Compression Index λ | Swelling Index κ | Critical State Parameter M | Initial Void Ratio e0 |
|---|---|---|---|---|
| Miscellaneous fill | 0.095 | 0.006 | 0.543 | 0.98 |
| Pain fill | 0.083 | 0.009 | 0.607 | 0.99 |
| Mucky silty clay | 0.127 | 0.008 | 0.673 | 1.06 |
| Clayey silt | 0.081 | 0.005 | 0.735 | 0.90 |
| Fine silt sand | 0.054 | 0.003 | 1.418 | 0.72 |
| Structure Type | Weight (kN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Diaphragm wall | 25 | 3.15 × 104 | 0.2 |
| Concrete support | 25 | 3.25 × 104 | 0.2 |
| Steel pipe support | 78 | 2.1 × 105 | 0.3 |
| Concrete cushion | 25 | 2.55 × 104 | 0.2 |
| Retaining pile (equivalent wall) | 16.36 | 1.54 × 104 | 0.2 |
| Calculation Step | Construction Stage | Construction Process |
|---|---|---|
| 0 | Initial stress equilibrium | |
| 1 | Construction of surrounding buildings | |
| 2 | Stage 1 | Construction of diaphragm walls |
| 3 | Dewatering (level 1) | |
| 4 | Excavation (level 1) | |
| 5 | Casting the struts (level 1) | |
| 6 | Dewatering (level 2) | |
| … | … | |
| 29 | Stage 2 | Construction of diaphragm walls |
| 30 | Dewatering (level 1) | |
| 31 | Excavation (level 1) | |
| 32 | Casting the struts (level 1) | |
| 33 | Dewatering (level 2) | |
| … | … | |
| 48 | Stage 3 | Construction of diaphragm walls |
| 49 | Dewatering (level 1) | |
| 50 | Excavation (level 1) | |
| 51 | Casting the struts (level 1) | |
| 52 | Dewatering (level 2) | |
| … | … |
| Construction Stage | Excavation Depth |
|---|---|
| Stage 1–1 | Pit A is excavated to −15 m. |
| Stage 1–2 | Pit A is excavated to −29 m. |
| Stage 2–1 | Pit B and Pit C are excavated to −15 m. |
| Stage 2–2 | Pit B is excavated to −22 m and pit-in-pit is excavated to −29 m. Pit C is excavated to −23.8 m and pit-in-pit is excavated to −27.7 m. |
| Stage 3–1 | Pit D and Pit E are excavated to −15 m. |
| Stage 3–2 | Pit D is excavated to −22 m. Pit E is excavated to −23 m. Pit F is excavated to −4.5 m. |
| Scenario No. | Construction Sequence | ||
|---|---|---|---|
| Stage 1 | Stage 2 | Stage 3 | |
| Scenario 1 (original) | Pit A | Pit B, Pit C | Pit D, Pit E, Pit F |
| Scenario 2 | Pit A | Pit D, Pit E, Pit F | Pit B, Pit C |
| Scenario 3 | Pit B, Pit C | Pit A | Pit D, Pit E, Pit F |
| Scenario 4 | Pit B, Pit C | Pit D, Pit E, Pit F | Pit A |
| Scenario 5 | Pit D, Pit E, Pit F | Pit A | Pit B, Pit C |
| Scenario 6 | Pit D, Pit E, Pit F | Pit B, Pit C | Pit A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, X.; Zhou, Q.; Xiao, Y.; Tong, L.; Yang, Q. Numerical Study on the Coupling Effect on a Retaining Structure of a Complex Deep Foundation Pit Group Excavation in a Soft-Soil Area. Appl. Sci. 2023, 13, 3263. https://doi.org/10.3390/app13053263
You X, Zhou Q, Xiao Y, Tong L, Yang Q. Numerical Study on the Coupling Effect on a Retaining Structure of a Complex Deep Foundation Pit Group Excavation in a Soft-Soil Area. Applied Sciences. 2023; 13(5):3263. https://doi.org/10.3390/app13053263
Chicago/Turabian StyleYou, Xinyu, Qiulong Zhou, Yu Xiao, Liyuan Tong, and Qiang Yang. 2023. "Numerical Study on the Coupling Effect on a Retaining Structure of a Complex Deep Foundation Pit Group Excavation in a Soft-Soil Area" Applied Sciences 13, no. 5: 3263. https://doi.org/10.3390/app13053263
APA StyleYou, X., Zhou, Q., Xiao, Y., Tong, L., & Yang, Q. (2023). Numerical Study on the Coupling Effect on a Retaining Structure of a Complex Deep Foundation Pit Group Excavation in a Soft-Soil Area. Applied Sciences, 13(5), 3263. https://doi.org/10.3390/app13053263






