Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm
Abstract
1. Introduction
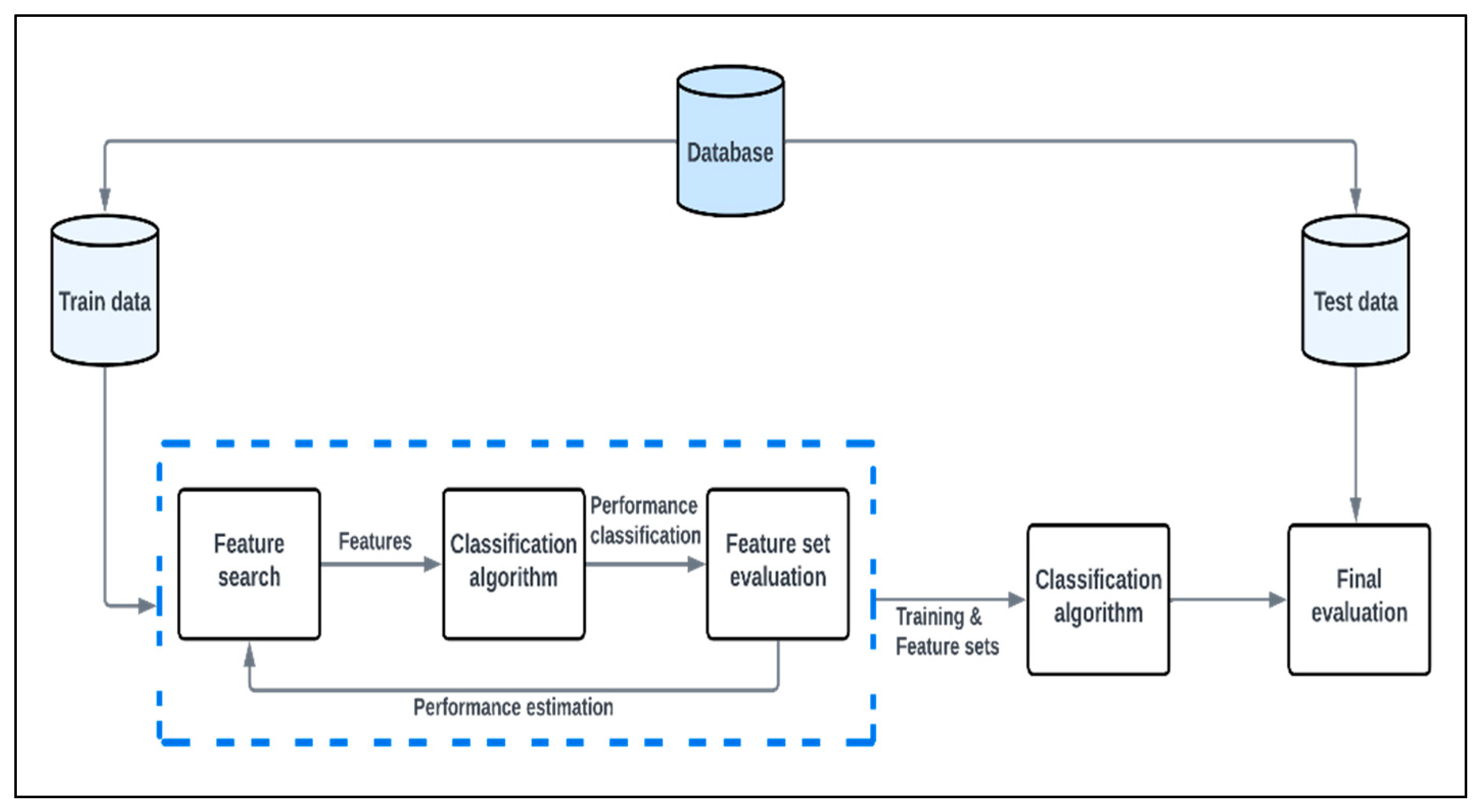
2. Methodology
2.1. Wrapper Method for Feature Selection
2.2. Fitness Function
2.3. Metaheuristics
2.3.1. Differential Evolution
| Algorithm 1: Differential evolution | ||
| Objective function Initialize population G = 0; Initialize all NP individuals WHILE | ||
| FOR to NP | ||
| GENERATE three individuals randomly based on the condition that MUTATION Form the donor vector using the formula: CROSSOVER The trial vector ui is developed either from the elements of the target vector xi or the elements of the donor vector vi as follows: | ||
| where ,, CR is the crossover rate, is random number generated for each and is random integer to ensure that in all cases EVALUATE if replace the individual with the trial vector | ||
| END | ||
| END | ||
2.3.2. Genetic Algorithm
| Algorithm 2: Genetic algorithm (roulette wheel) | |||
| Objective function Initialize population G = 0; Initialize all NP individuals WHILE Iterations < Maximum Iterations | |||
| FOR i ← 1 to NP | |||
| sum += fitness of this individual FOR all members of population probability = sum of probabilities + (fitness/sum) | |||
| sum of probabilities += probability | |||
| END number = random between 0 and 1 for all members of population if number > probability but less than next probability Iterations = Iterations + NP | |||
| END G = G + 1 | |||
| END | |||
| Algorithm 3: Genetic algorithm (tournament selection) | ||||
| Objective function Initialize population ; Initialize all individuals WHILE | ||||
| FOR | ||||
| WHILE need to generate more offspring | ||||
| IF then | ||||
| Refill: move all individuals from the temporary population to population | ||||
| END IF | ||||
| sampling individuals without replacement from population select the winner from the tournament move the sampled individuals into temporary population return the winner | ||||
| END | ||||
| END | ||||
| END | ||||
2.3.3. Particle Swarm Optimization
| Algorithm 4: Particle swarm optimization | |||
| Objective function Initialize population FOR | |||
| FOR | |||
| If then | |||
| END | |||
| FOR | |||
| IF THEN | |||
| ELSE IF THEN | |||
| IF THEN | |||
| IF THEN | |||
| END | |||
| END | |||
2.3.4. Flower Pollination Algorithm
- (a)
- A biotic process is global pollination and obeys Levy flights.
- (b)
- On the other hand, an abiotic process is local pollination.
- (c)
- Pollinators are the probabilities of reproduction.
- (d)
- Probability switches between local and global pollination.
| Algorithm 5: Flower pollination algorithm | |||
| Objective function Initialize population Find the best solution in the initial population Define a switch probability FOR | |||
| FOR | |||
| IF | |||
| Draw d-dimensional step vector L Global phase Equation (6) | |||
| ELSE | |||
| Draw in Equation (8) from a uniform distribution [0, 1] Local phase Equation (8) | |||
| END | |||
| Assess new solutions If new solutions > old solutions, update population | |||
| END current best solution | |||
| END | |||
2.3.5. Symbiotic Organism’s Search
| Algorithm 6: Symbiotic organisms search | |
| Objective function Initialize population FOR | |
| Mutual interaction phase Commensalism interaction phase Parasitic interaction phase current best solution | |
| END | |
2.3.6. Marine Predators’ Algorithm
| Algorithm 7: Marine predators algorithm | ||
| Objective function Initialize population Compute the fitness values, elite matrix and memory saving FOR t = 1: max generation | ||
| IF | ||
| ELSE IF | ||
The first half of the population is updated by The second half of the population is updated by | ||
| ELSE IF | ||
| END IF | ||
| Accomplish elite update and memory saving based on (where ) current best solution | ||
| END | ||
2.3.7. Manta Ray Foraging Optimization
| Algorithm 8: Manta ray foraging | |||
| Objective function Initialize population and maximum iterations Compute the fitness of each individual and obtain the best solutions FOR | |||
| IF THEN use cyclone foraging | |||
| IF THEN | |||
| ELSE | |||
| END IF | |||
| ELSE use chain foraging | |||
| END IF | |||
| Calculate the fitness of the individuals using | |||
| IF THEN | |||
| For somersault foraging | |||
| Calculate the fitness of the individuals using | |||
| IF THEN | |||
| END current best solution | |||
2.3.8. Weighted Superposition Attraction Algorithm
| Algorithm 9: Weighted superposition attraction algorithm | |
| Objective function ) Initialize population and maximum iterations Compute the fitness of each individual and obtain the best solutions FOR | |
| Ranking solutions by the fitness Determining the target point to move the simulated iteration towards it Evaluating the fitness value of the target Determination of the search direction for the solutions Each solution is moved toward its determined direction Update the fitness solutions for | |
| END current best solution | |
3. Results and Discussion
3.1. Dataset Description
3.2. Metaheuristic Parameters
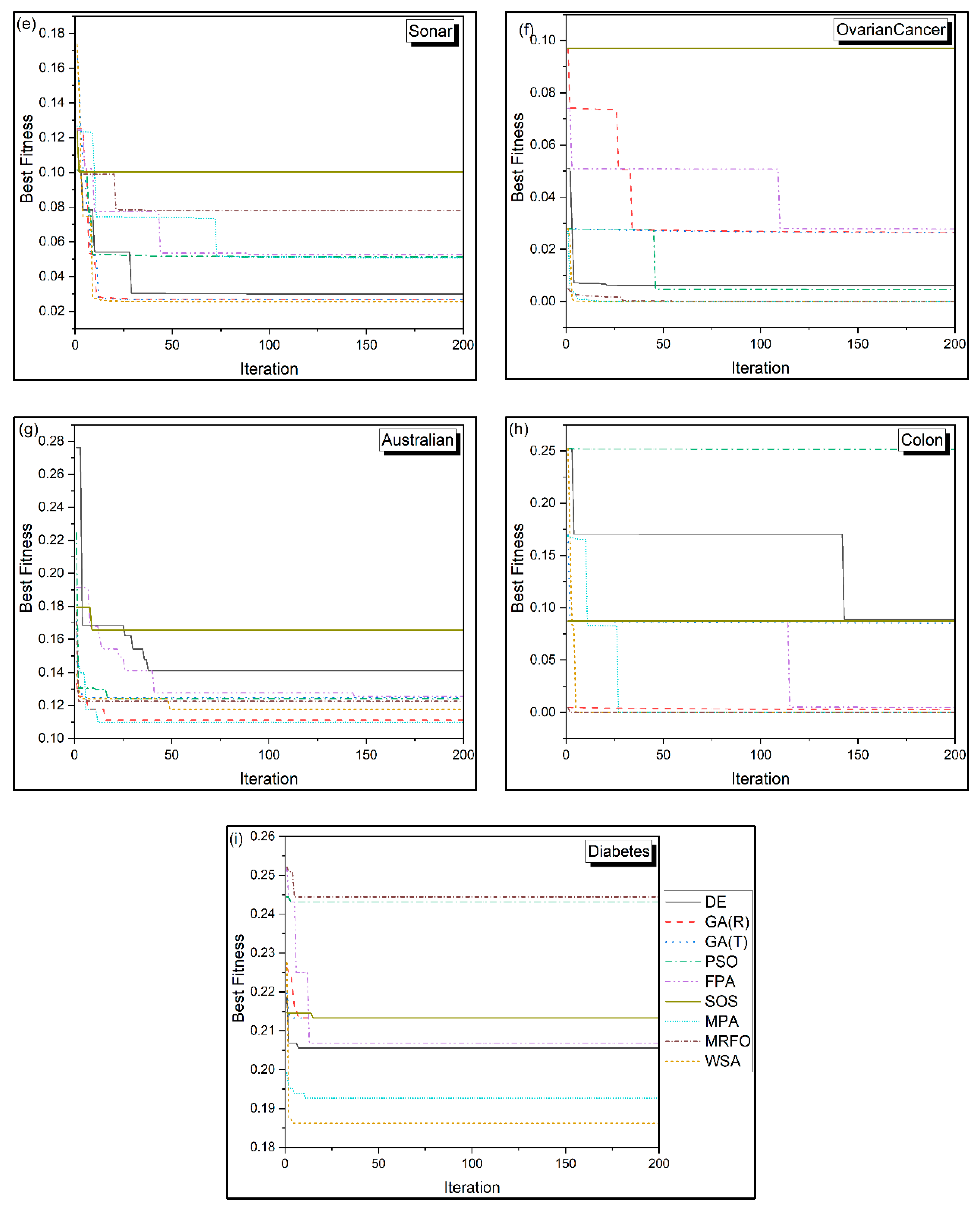
3.3. Performance of the Metaheuristic on the Real-World Datasets
3.4. Comparison with the State of the Art
4. Conclusions
- WSA > MPA > GA (T) > MRFO > GA (R) > FPA > PSO > DE > SOS is the order of the algorithms under consideration that provide the best fitness value. In contrast, while comparing these algorithms based on mean best fitness and standard deviation, WSA > MPA > MRFO > FPA > GA > GA > GA > GA > GA > DE > PSO > SOS is the order of their performance.
- The convergence of WSA and MPA is found to be superior to other algorithms.
- WSA > GA (T) > GA (R) > DE > MPA > MRFO > PSO > FPA > SOS is the ranking order of the algorithms with respect to the highest classification accuracy. On the other hand, in terms of mean best classification accuracy and standard deviation, WSA > MPA > MRFO > GA (T) > GA (R) > FPA > DE > PSO > SOS is the order of the algorithms.
- FPA and DE are noticed to be computationally faster than the other algorithms, and thus, based on the best computation time, the algorithms can be ranked as FPA > DE > WSA > PSO > MRFO > MPA > GA (T) > GA (R) > SOS. In terms of mean computational time and standard deviation, the ranking of these algorithms is FPA > DE > PSO > WSA > MRFO > MPA > GA (T) > GA (R) > SOS.
- With respect to the lowest number of features selected, the ranking is MPA > WSA > SOS > GA (T) > GA (R) > PSO > FPA > MRFO > DE, whereas for the mean and standard deviation of the number of features selected, the ranking is derived as SOS > MPA > GA (T) > GA (R) > WSA > PSO > FPA > DE > MRFO.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Too, J.; Mafarja, M.; Mirjalili, S. Spatial bound whale optimization algorithm: An efficient high-dimensional feature selection approach. Neural Comput. Appl. 2021, 33, 16229–16250. [Google Scholar] [CrossRef]
- Mukherjee, S.; Dutta, S.; Mitra, S.; Pati, S.K.; Ansari, F.; Baranwal, A. Ensemble Method of Feature Selection Using Filter and Wrapper Techniques with Evolutionary Learning. In Emerging Technologies in Data Mining and Information Security: Proceedings of IEMIS 2022; Springer: Berlin/Heidelberg, Germany, 2022; Volume 2, pp. 745–755. [Google Scholar]
- Liu, B.; Wei, Y.; Zhang, Y.; Yang, Q. Deep Neural Networks for High Dimension, Low Sample Size Data. In Proceedings of the International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2287–2293. [Google Scholar]
- Chen, C.; Weiss, S.T.; Liu, Y.-Y. Graph Convolutional Network-based Feature Selection for High-dimensional and Low-sample Size Data. arXiv 2022, arXiv:2211.14144. [Google Scholar]
- Constantinopoulos, C.; Titsias, M.K.; Likas, A. Bayesian feature and model selection for Gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1013–1018. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Wang, F.; Yang, L. Deep feature screening: Feature selection for ultra high-dimensional data via deep neural networks. arXiv 2022, arXiv:2204.01682. [Google Scholar]
- Yamada, M.; Jitkrittum, W.; Sigal, L.; Xing, E.P.; Sugiyama, M. High-dimensional feature selection by feature-wise kernelized lasso. Neural Comput. 2014, 26, 185–207. [Google Scholar] [CrossRef]
- Gui, N.; Ge, D.; Hu, Z. AFS: An attention-based mechanism for supervised feature selection. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 3705–3713. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Chen, J.; Stern, M.; Wainwright, M.J.; Jordan, M.I. Kernel feature selection via conditional covariance minimization. Adv. Neural Inf. Process. Syst. 2017, 30, 6949–6958. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Sastry, K.; Goldberg, D.; Kendall, G. Genetic algorithms. In Search Methodologies; Springer: Boston, MA, USA, 2005; pp. 97–125. [Google Scholar]
- Bansal, J.C. Particle swarm optimization. In Evolutionary and Swarm Intelligence Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; pp. 11–23. [Google Scholar]
- Singh, A.; Sharma, A.; Rajput, S.; Mondal, A.K.; Bose, A.; Ram, M. Parameter extraction of solar module using the sooty tern optimization algorithm. Electronics 2022, 11, 564. [Google Scholar] [CrossRef]
- Janaki, M.; Geethalakshmi, S.N. A Review of Swarm Intelligence-Based Feature Selection Methods and Its Application. In Soft Computing for Security Applications: Proceedings of ICSCS 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 435–447. [Google Scholar]
- Lee, C.-Y.; Hung, C.-H. Feature ranking and differential evolution for feature selection in brushless DC motor fault diagnosis. Symmetry 2021, 13, 1291. [Google Scholar] [CrossRef]
- Hancer, E.; Xue, B.; Zhang, M. Differential evolution for filter feature selection based on information theory and feature ranking. Knowl.-Based Syst. 2018, 140, 103–119. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.-W.; Gao, X.-Z.; Tian, T.; Sun, X.-Y. Binary differential evolution with self-learning for multi-objective feature selection. Inf. Sci. 2020, 507, 67–85. [Google Scholar] [CrossRef]
- Gokulnath, C.B.; Shantharajah, S.P. An optimized feature selection based on genetic approach and support vector machine for heart disease. Clust. Comput. 2019, 22, 14777–14787. [Google Scholar] [CrossRef]
- Sayed, S.; Nassef, M.; Badr, A.; Farag, I. A nested genetic algorithm for feature selection in high-dimensional cancer microarray datasets. Expert Syst. Appl. 2019, 121, 233–243. [Google Scholar] [CrossRef]
- Yu, X.; Aouari, A.; Mansour, R.F.; Su, S. A Hybrid Algorithm Based on PSO and GA for Feature Selection. J. Cybersecur. 2021, 3, 117. [Google Scholar]
- Rashid, M.; Singh, H.; Goyal, V. Efficient feature selection technique based on fast Fourier transform with PSO-GA for functional magnetic resonance imaging. In Proceedings of the 2nd International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 19–21 January 2021; pp. 238–242. [Google Scholar]
- Sakri, S.B.; Rashid, N.B.A.; Zain, Z.M. Particle swarm optimization feature selection for breast cancer recurrence prediction. IEEE Access 2018, 6, 29637–29647. [Google Scholar] [CrossRef]
- Almomani, O. A feature selection model for network intrusion detection system based on PSO, GWO, FFA and GA algorithms. Symmetry 2020, 12, 1046. [Google Scholar] [CrossRef]
- Sharkawy, R.M.; Ibrahim, K.; Salama, M.M.A.; Bartnikas, R. Particle swarm optimization feature selection for the classification of conducting particles in transformer oil. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1897–1907. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. Hybrid binary particle swarm optimization and flower pollination algorithm based on rough set approach for feature selection problem. In Nature-Inspired Computation in Data Mining and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2020; pp. 249–273. [Google Scholar]
- Majidpour, H.; Soleimanian Gharehchopogh, F. An improved flower pollination algorithm with AdaBoost algorithm for feature selection in text documents classification. J. Adv. Comput. Res. 2018, 9, 29–40. [Google Scholar]
- Yousri, D.; Abd Elaziz, M.; Oliva, D.; Abraham, A.; Alotaibi, M.A.; Hossain, M.A. Fractional-order comprehensive learning marine predators algorithm for global optimization and feature selection. Knowl. -Based Syst. 2022, 235, 107603. [Google Scholar] [CrossRef]
- Sahlol, A.T.; Yousri, D.; Ewees, A.A.; Al-Qaness, M.A.A.; Damasevicius, R.; Elaziz, M.A. COVID-19 image classification using deep features and fractional-order marine predators algorithm. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Abd Elminaam, D.S.; Nabil, A.; Ibraheem, S.A.; Houssein, E.H. An efficient marine predators algorithm for feature selection. IEEE Access 2021, 9, 60136–60153. [Google Scholar] [CrossRef]
- Hassan, I.H.; Mohammed, A.; Masama, M.A.; Ali, Y.S.; Abdulrahim, A. An Improved Binary Manta Ray Foraging Optimization Algorithm based feature selection and Random Forest Classifier for Network Intrusion Detection. Intell. Syst. Appl. 2022, 16, 200114. [Google Scholar] [CrossRef]
- Ghosh, K.K.; Guha, R.; Bera, S.K.; Kumar, N.; Sarkar, R. S-Shaped versus V-shaped transfer functions for binary Manta ray foraging optimization in feature selection problem. Neural Comput. Appl. 2021, 33, 11027–11041. [Google Scholar] [CrossRef]
- Mohmmadzadeh, H.; Gharehchopogh, F.S. An efficient binary chaotic symbiotic organisms search algorithm approaches for feature selection problems. J. Supercomput. 2021, 77, 9102–9144. [Google Scholar] [CrossRef]
- Han, C.; Zhou, G.; Zhou, Y. Binary symbiotic organism search algorithm for feature selection and analysis. IEEE Access 2019, 7, 166833–166859. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Ozsoydan, F.B.; Senol, M.E. Weighted superposition attraction algorithm for binary optimization problems. Oper. Res. 2020, 20, 2555–2581. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Şenol, M.E. Weighted superposition attraction algorithm for combinatorial optimization. Expert Syst. Appl. 2019, 138, 112792. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Ozsoydan, F.B. Dynamic optimization in binary search spaces via weighted superposition attraction algorithm. Expert Syst. Appl. 2018, 96, 157–174. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Gölcük, İ.; Özsoydan, F.B. Improving fuzzy c-means clustering via quantum-enhanced weighted superposition attraction algorithm. Hacet. J. Math. Stat. 2018, 48, 859–882. [Google Scholar]
- Adil, B.; Cengiz, B. Optimal design of truss structures using weighted superposition attraction algorithm. Eng. Comput. 2020, 36, 965–979. [Google Scholar] [CrossRef]
- Too, J.; Liang, G.; Chen, H. Memory-Based Harris hawk optimization with learning agents: A feature selection approach. Eng. Comput. 2022, 38 (Suppl. 5), 4457–4478. [Google Scholar] [CrossRef]
- Fang, Y.; Li, J. A Review of Tournament Selection in Genetic Programming. In International Symposium on Intelligence Computation and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 181–192. [Google Scholar]
- Du, K.-L.; Swamy, M.N.S. Particle swarm optimization. In Search and Optimization by Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 153–173. [Google Scholar]
- Singh, A.; Sharma, A.; Rajput, S.; Bose, A.; Hu, X. An investigation on hybrid particle swarm optimization algorithms for parameter optimization of PV cells. Electronics 2022, 11, 909. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Yang, X.-S. Flower pollination algorithm for global optimization. In International Conference on Unconventional Computing and Natural Computation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Ezugwu, A.E.; Prayogo, D. Symbiotic organisms search algorithm: Theory, recent advances and applications. Expert Syst. Appl. 2019, 119, 184–209. [Google Scholar] [CrossRef]
- Abdullahi, M.; Ngadi, M.A.; Dishing, S.I.; Abdulhamid, S.M.; Usman, M.J. A survey of symbiotic organisms search algorithms and applications. Neural Comput. Appl. 2020, 32, 547–566. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D. Symbiotic organisms search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Jangir, P.; Buch, H.; Mirjalili, S.; Manoharan, P. MOMPA: Multi-objective marine predator algorithm for solving multi-objective optimization problems. Evol. Intell. 2023, 16, 169–195. [Google Scholar] [CrossRef]
- Al-Qaness, M.A.A.; Ewees, A.A.; Fan, H.; Abualigah, L.; Abd Elaziz, M. Marine predators algorithm for forecasting confirmed cases of COVID-19 in Italy, USA, Iran and Korea. Int. J. Environ. Res. Public Health 2020, 17, 3520. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Houssein, E.H.; Emam, M.M.; Ali, A.A. Improved manta ray foraging optimization for multi-level thresholding using COVID-19 CT images. Neural Comput. Appl. 2021, 33, 16899–16919. [Google Scholar] [CrossRef]
- Tang, A.; Zhou, H.; Han, T.; Xie, L. A modified manta ray foraging optimization for global optimization problems. IEEE Access 2021, 9, 128702–128721. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Akpinar, Ş. Weighted Superposition Attraction (WSA): A swarm intelligence algorithm for optimization problems—Part 1: Unconstrained optimization. Appl. Soft Comput. 2017, 56, 520–540. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Akpinar, Ş. Weighted Superposition Attraction (WSA): A swarm intelligence algorithm for optimization problems—Part 2: Constrained optimization. Appl. Soft Comput. 2015, 37, 396–415. [Google Scholar] [CrossRef]
- Conrads, T.P.; Fusaro, V.A.; Ross, S.; Johann, D.; Rajapakse, V.; Hitt, B.A.; Steinberg, S.M.; Kohn, E.C.; Fishman, D.A.; Whitely, G.; et al. High-Resolution Serum Proteomic Features for Ovarian Cancer Detection. Endocr. -Relat. Cancer 2004, 11, 163–178. [Google Scholar] [CrossRef] [PubMed]
- Alon, U.; Barkai, N.; Notterman, D.A.; Gish, K.; Ybarra, S.; Mack, D.; Levine, A.J. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Cell Biol. 1999, 96, 6745–6750. [Google Scholar] [CrossRef]
- Feshki, M.G.; Shijani, O.S. Improving the heart disease diagnosis by evolutionary algorithm of PSO and Feed Forward Neural Network. In Proceedings of the 2016 Artificial Intelligence and Robotics (IRANOPEN), Qazvin, Iran, 9 April 2016; pp. 48–53. [Google Scholar]
- Chicco, D.; Jurman, G. Machine learning can predict survival of patients with heart failure from serum creatinine and ejection fraction alone. BMC Med. Inform. Decis. Mak. 2020, 20, 16. [Google Scholar] [CrossRef]
- Amin, M.S.; Chiam, Y.K.; Varathan, K.D. Identification of significant features and data mining techniques in predicting heart disease. Telemat. Inform. 2019, 36, 82–93. [Google Scholar] [CrossRef]
- Pouriyeh, S.; Vahid, S.; Sannino, G.; De Pietro, G.; Arabnia, H.; Gutierrez, J. A comprehensive investigation and comparison of machine learning techniques in the domain of heart disease. In Proceedings of the IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 204–207. [Google Scholar]
- Maji, S.; Arora, S. Decision tree algorithms for prediction of heart disease. In Proceedings of the Information and Communication Technology for Competitive Strategies: In Proceedings of the Third International Conference on ICTCS, Amman, Jordan, 11–13 October 2017; pp. 447–454. [Google Scholar]
- Reddy, G.T.; Reddy, M.P.K.; Lakshmanna, K.; Rajput, D.S.; Kaluri, R.; Srivastava, G. Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis. Evol. Intell. 2020, 13, 185–196. [Google Scholar] [CrossRef]

| Dataset | Instances | Features | Source |
|---|---|---|---|
| Heart | 303 | 13 | https://archive.ics.uci.edu/ml/datasets/heart+Disease (accessed on 1 February 2023) |
| Ionosphere | 351 | 34 | https://archive.ics.uci.edu/ml/datasets/ionosphere (accessed on 1 February 2023) |
| German | 1000 | 24 | http://www.liacc.up.pt/ML/old/statlog/datasets.html (accessed on 1 February 2023) |
| Breast | 699 | 9 | https://archive.ics.uci.edu/ml/datasets/breast+cancer+wisconsin+(diagnostic) (accessed on 1 February 2023) |
| Sonar | 208 | 60 | https://archive.ics.uci.edu/ml/datasets/Connectionist+Bench+(Sonar,+Mines+vs.+Rocks) (accessed on 1 February 2023) |
| Ovarian | 216 | 4000 | Conrads et al. [57] |
| Australian | 690 | 14 | https://archive.ics.uci.edu/ml/datasets/statlog+(australian+credit+approval) (accessed on 1 February 2023) |
| Colon | 62 | 2000 | Alon et al. [58] |
| Diabetes | 768 | 8 | https://archive.ics.uci.edu/ml/datasets/diabetes (accessed on 1 February 2023) |
| Algorithm | Parameter | Value |
|---|---|---|
| Common parameters | K | 5 |
| Iteration limit | 200 | |
| Search agents | 30 | |
| Independent runs | 20 | |
| Validation data | 20% | |
| DE | Crossover rate | 0.9 |
| Constant factor | 0.5 | |
| GA (R) | Crossover rate | 0.8 |
| Mutation rate | 0.01 | |
| GA (T) | Crossover rate | 0.8 |
| Mutation rate | 0.01 | |
| Tournament size | 3 | |
| PSO | 2 | |
| 2 | ||
| 0.9 | ||
| FPA | Levy component | 1.5 |
| Switch probability | 0.8 | |
| MPA | Levy component | 1.5 |
| Constant | 0.5 | |
| Fish aggregating devices effect | 0.2 | |
| MRFO | Somersault factor | 2 |
| WSA | 0.8 | |
| 0.001 | ||
| 0.75 | ||
| Step length | 0.035 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 0.06908 | 0.08635 | 0.08481 | 0.05258 | 0.08635 | 0.15312 | 0.10131 | 0.08558 | 0.08481 |
| Ionosphere | 0.06245 | 0.04478 | 0.05951 | 0.03123 | 0.01591 | 0.10194 | 0.02946 | 0.02976 | 0.01503 |
| German | 0.20920 | 0.18320 | 0.18153 | 0.18940 | 0.19847 | 0.23187 | 0.19268 | 0.20217 | 0.16793 |
| Breast | 0.01157 | 0.01046 | 0.00667 | 0.01046 | 0.01869 | 0.01046 | 0.01157 | 0.01647 | 0.01157 |
| Sonar | 0.00433 | 0.00183 | 0.00267 | 0.00250 | 0.00283 | 0.00500 | 0.00100 | 0.00183 | 0.00100 |
| Ovarian | 0.00566 | 0.00324 | 0.00455 | 0.00451 | 0.00346 | 0.00486 | 0.00001 | 0.00011 | 0.00001 |
| Australian | 0.08966 | 0.09612 | 0.08106 | 0.10975 | 0.08823 | 0.16354 | 0.10975 | 0.08894 | 0.09683 |
| Colon | 0.00489 | 0.00263 | 0.00242 | 0.08677 | 0.00456 | 0.08721 | 0.00001 | 0.00001 | 0.00001 |
| Diabetes | 0.20559 | 0.20684 | 0.20559 | 0.22250 | 0.19515 | 0.21331 | 0.19265 | 0.19912 | 0.18618 |
| Average rank | 6.39 | 4.78 | 4.11 | 5.39 | 5.17 | 8.11 | 4.06 | 4.39 | 2.61 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 0.11 (0.04) | 0.14 (0.04) | 0.13 (0.03) | 0.13 (0.05) | 0.14 (0.06) | 0.21 (0.05) | 0.13 (0.03) | 0.11 (0.04) | 0.1 (0.01) |
| Ionosphere | 0.11 (0.04) | 0.06 (0.02) | 0.07 (0.02) | 0.08 (0.03) | 0.06 (0.04) | 0.11 (0.01) | 0.04 (0.01) | 0.06 (0.03) | 0.03 (0.01) |
| German | 0.22 (0.01) | 0.21 (0.02) | 0.22 (0.03) | 0.21 (0.02) | 0.21 (0.01) | 0.24 (0.01) | 0.2 (0.01) | 0.21 (0.01) | 0.2 (0.02) |
| Breast | 0.02 (0.01) | 0.03 (0.01) | 0.02 (0.01) | 0.02 (0) | 0.03 (0.01) | 0.02 (0.01) | 0.02 (0.01) | 0.02 (0.01) | 0.02 (0.01) |
| Sonar | 0.02 (0.02) | 0.04 (0.03) | 0.04 (0.04) | 0.04 (0.02) | 0.02 (0.01) | 0.11 (0.09) | 0.02 (0.02) | 0.05 (0.04) | 0.01 (0.01) |
| Ovarian | 0.02 (0.01) | 0.02 (0.01) | 0.03 (0.02) | 0.02 (0.02) | 0.02 (0.01) | 0.05 (0.03) | 0 (0) | 0 (0) | 0 (0) |
| Australian | 0.12 (0.02) | 0.11 (0.01) | 0.12 (0.03) | 0.13 (0.02) | 0.11 (0.02) | 0.2 (0.05) | 0.12 (0.01) | 0.11 (0.01) | 0.11 (0.01) |
| Colon | 0.14 (0.11) | 0.05 (0.05) | 0.05 (0.05) | 0.17 (0.06) | 0.07 (0.07) | 0.12 (0.05) | 0 (0) | 0.02 (0.04) | 0 (0) |
| Diabetes | 0.23 (0.02) | 0.23 (0.02) | 0.22 (0.01) | 0.24 (0.01) | 0.21 (0.02) | 0.25 (0.04) | 0.22 (0.02) | 0.23 (0.02) | 0.22 (0.02) |
| Av. Rank (mean) | 5.61 | 5.00 | 5.44 | 6.33 | 5.11 | 8.56 | 3.00 | 4.33 | 1.61 |
| Av. Rank (SD) | 5.89 | 5.44 | 5.56 | 5.44 | 5.00 | 6.44 | 2.67 | 5.22 | 3.33 |
| Combined av. rank | 5.75 | 5.22 | 5.50 | 5.89 | 5.06 | 7.50 | 2.83 | 4.78 | 2.47 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 0.9333 | 0.9167 | 0.9167 | 0.9500 | 0.9167 | 0.8500 | 0.9000 | 0.9167 | 0.9167 |
| Ionosphere | 0.9429 | 0.9857 | 0.9571 | 0.9714 | 0.9429 | 0.9000 | 0.9714 | 0.9714 | 0.9857 |
| German | 0.7950 | 0.8200 | 0.8200 | 0.8150 | 0.8050 | 0.7700 | 0.8100 | 0.8000 | 0.8350 |
| Breast | 0.9928 | 0.9928 | 1.0000 | 0.9928 | 0.9856 | 0.9928 | 0.9928 | 0.9856 | 0.9928 |
| Sonar | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9512 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Ovarian | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Australian | 0.9130 | 0.9058 | 0.9203 | 0.8913 | 0.9130 | 0.8406 | 0.8913 | 0.9130 | 0.9058 |
| Colon | 1.0000 | 1.0000 | 1.0000 | 0.9167 | 1.0000 | 0.9167 | 1.0000 | 1.0000 | 1.0000 |
| Diabetes | 0.7974 | 0.7974 | 0.7974 | 0.7778 | 0.8105 | 0.7909 | 0.8105 | 0.8039 | 0.8170 |
| Average rank | 4.94 | 4.28 | 3.89 | 5.33 | 5.61 | 7.39 | 5.00 | 5.00 | 3.56 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 0.89 (0.04) | 0.87 (0.04) | 0.87 (0.03) | 0.87 (0.05) | 0.86 (0.06) | 0.79 (0.05) | 0.88 (0.03) | 0.89 (0.04) | 0.9 (0.01) |
| Ionosphere | 0.9 (0.04) | 0.94 (0.04) | 0.95 (0.02) | 0.92 (0.03) | 0.91 (0.03) | 0.9 (0.01) | 0.96 (0.01) | 0.94 (0.03) | 0.97 (0.01) |
| German | 0.79 (0.01) | 0.8 (0.02) | 0.79 (0.03) | 0.79 (0.02) | 0.79 (0.01) | 0.76 (0.01) | 0.8 (0.01) | 0.79 (0.01) | 0.81 (0.02) |
| Breast | 0.99 (0.01) | 0.98 (0.01) | 0.99 (0.01) | 0.99 (0) | 0.98 (0.01) | 0.98 (0.01) | 0.99 (0.01) | 0.98 (0.01) | 0.99 (0.01) |
| Sonar | 0.98 (0.02) | 0.98 (0.01) | 0.97 (0.03) | 0.97 (0.02) | 0.94 (0.02) | 0.89 (0.09) | 0.99 (0.02) | 0.96 (0.04) | 0.99 (0.01) |
| Ovarian | 0.99 (0.01) | 0.98 (0.01) | 0.99 (0.01) | 0.99 (0.02) | 0.99 (0.01) | 0.95 (0.03) | 1 (0) | 1 (0) | 1 (0) |
| Australian | 0.89 (0.02) | 0.89 (0.01) | 0.88 (0.03) | 0.87 (0.02) | 0.89 (0.02) | 0.8 (0.05) | 0.88 (0.01) | 0.89 (0.01) | 0.89 (0.01) |
| Colon | 0.87 (0.11) | 0.95 (0.05) | 0.95 (0.05) | 0.83 (0.06) | 0.93 (0.07) | 0.88 (0.05) | 1 (0) | 0.98 (0.04) | 1 (0) |
| Diabetes | 0.77 (0.02) | 0.77 (0.02) | 0.78 (0.01) | 0.76 (0.01) | 0.79 (0.02) | 0.75 (0.04) | 0.79 (0.02) | 0.77 (0.02) | 0.79 (0.02) |
| Av. Rank (mean) | 5.33 | 5.44 | 5.00 | 6.17 | 5.61 | 8.44 | 3.11 | 4.28 | 1.61 |
| Av. Rank (SD) | 5.94 | 5.17 | 5.06 | 5.61 | 5.56 | 6.67 | 2.83 | 4.89 | 3.28 |
| Combined av. rank | 5.64 | 5.31 | 5.03 | 5.89 | 5.58 | 7.56 | 2.97 | 4.58 | 2.44 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 37.3069 | 58.4510 | 59.3564 | 36.9822 | 37.2579 | 125.6186 | 71.1589 | 66.0726 | 35.9040 |
| Ionosphere | 4.8874 | 14.3396 | 14.8998 | 9.2014 | 4.9101 | 18.4415 | 9.8246 | 8.2109 | 5.4902 |
| German | 41.4371 | 126.0874 | 150.9288 | 94.9779 | 46.2631 | 171.6129 | 87.2630 | 75.1673 | 45.2955 |
| Breast | 42.1620 | 64.1089 | 65.3039 | 42.1937 | 37.8479 | 137.6404 | 74.1079 | 62.2471 | 45.1631 |
| Sonar | 32.8366 | 56.9434 | 54.5112 | 32.6148 | 32.5553 | 129.3449 | 65.7633 | 56.0746 | 34.6354 |
| Ovarian | 126.6548 | 137.8998 | 137.5729 | 122.3213 | 103.2913 | 155.3433 | 85.1104 | 83.8790 | 169.3444 |
| Australian | 38.4591 | 61.5668 | 62.1789 | 38.4547 | 38.7062 | 139.0013 | 77.3190 | 53.8778 | 37.9527 |
| Colon | 38.3924 | 56.6966 | 56.6441 | 47.9606 | 37.6771 | 109.1697 | 67.4664 | 53.6178 | 42.1641 |
| Diabetes | 86.3755 | 133.5861 | 130.1496 | 81.9149 | 78.9590 | 324.7326 | 73.3953 | 62.7816 | 39.9376 |
| Average rank | 3.00 | 6.67 | 6.67 | 3.67 | 2.44 | 8.89 | 6.22 | 4.33 | 3.11 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 37.67 (0.62) | 60.41 (2.35) | 62.8 (5.57) | 37.34 (0.23) | 41.35 (5.03) | 130.76 (4.1) | 74.69 (2.17) | 68.33 (1.93) | 38.59 (2.44) |
| Ionosphere | 4.97 (0.11) | 15.37 (0.9) | 15.85 (0.63) | 9.4 (0.2) | 5.05 (0.1) | 19.48 (0.81) | 10.29 (0.36) | 8.71 (0.32) | 5.62 (0.1) |
| German | 63.37 (29.87) | 138.45 (10.19) | 154.66 (5.76) | 96.22 (1.04) | 46.88 (0.71) | 183.47 (11.72) | 89.79 (2.52) | 78.52 (2.36) | 46.01 (0.92) |
| Breast | 43.33 (0.96) | 69.46 (6.36) | 67.98 (3.03) | 43.26 (0.93) | 38.24 (0.27) | 142.41 (4.31) | 76.91 (1.78) | 64.25 (2.11) | 48 (2.63) |
| Sonar | 32.96 (0.1) | 58.05 (1.22) | 55.76 (1.05) | 33.3 (1.2) | 32.63 (0.11) | 132.15 (1.64) | 66.85 (0.87) | 56.81 (0.58) | 34.78 (0.25) |
| Ovarian | 131.01 (3.26) | 142.65 (3.87) | 138.86 (1.46) | 123.76 (1.4) | 103.8 (0.42) | 168.66 (9.57) | 90.99 (7.2) | 91.38 (7.58) | 217.57 (82.28) |
| Australian | 39.88 (1.03) | 62.9 (1.76) | 62.87 (0.6) | 39.64 (1.79) | 40.54 (2.29) | 147.99 (7.3) | 78.32 (0.81) | 68.75 (9.5) | 39.71 (2.51) |
| Colon | 39.07 (0.59) | 57.78 (1.11) | 57.14 (0.43) | 48.27 (0.18) | 37.8 (0.09) | 121.52 (8.99) | 67.78 (0.21) | 55.4 (1.89) | 42.31 (0.22) |
| Diabetes | 88.07 (2.02) | 139.5 (4.17) | 138.37 (7.08) | 86.84 (3.4) | 83.91 (3.36) | 334.15 (7.5) | 75.12 (1.27) | 64.34 (1.14) | 40.15 (0.34) |
| Av. Rank (mean) | 3.00 | 6.78 | 6.33 | 3.44 | 2.44 | 8.89 | 6.11 | 4.67 | 3.33 |
| Av. Rank (SD) | 3.89 | 6.78 | 5.78 | 3.56 | 3.00 | 8.22 | 4.22 | 5.22 | 4.33 |
| Combined av. rank | 3.44 | 6.78 | 6.06 | 3.50 | 2.72 | 8.56 | 5.17 | 4.94 | 3.83 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 3 |
| Ionosphere | 12 | 6 | 7 | 10 | 11 | 2 | 3 | 10 | 3 |
| German | 12 | 9 | 8 | 11 | 9 | 7 | 6 | 10 | 7 |
| Breast | 2 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 2 |
| Sonar | 26 | 10 | 10 | 12 | 19 | 6 | 6 | 23 | 9 |
| Ovarian | 2014 | 1326 | 1294 | 1805 | 1888 | 2 | 5 | 1944 | 44 |
| Australian | 3 | 1 | 1 | 3 | 3 | 4 | 2 | 7 | 1 |
| Colon | 951 | 526 | 484 | 791 | 912 | 1 | 1 | 942 | 2 |
| Diabetes | 4 | 3 | 3 | 2 | 3 | 4 | 3 | 4 | 2 |
| Average rank | 7.78 | 4.67 | 4.39 | 5.72 | 6.28 | 3.89 | 2.67 | 6.89 | 2.72 |
| Dataset | DE | GA (R) | GA (T) | PSO | FPA | SOS | MPA | MRFO | WSA |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 4.4 (0.55) | 4 (1.41) | 4.6 (1.14) | 4.6 (1.34) | 5 (1.58) | 3.2 (0.45) | 4 (1.22) | 4 (1.58) | 4.6 (1.14) |
| Ionosphere | 15.4 (3.58) | 9.8 (2.39) | 9.4 (1.95) | 10.4 (0.55) | 14.4 (3.97) | 3.6 (1.14) | 4.2 (1.3) | 17.6 (5.03) | 5.2 (1.79) |
| German | 14.6 (2.3) | 11.8 (2.68) | 9 (0.71) | 12.8 (1.64) | 11 (2.35) | 10.8 (2.59) | 9 (2.35) | 14.6 (3.21) | 11.4 (3.05) |
| Breast | 4.4 (1.52) | 3.6 (1.34) | 4.8 (1.3) | 5 (1.41) | 4.4 (1.14) | 4.2 (0.84) | 4.4 (1.67) | 4.4 (1.52) | 3.4 (1.52) |
| Sonar | 33.2 (4.21) | 14.8 (3.11) | 14.4 (6.23) | 16.6 (3.36) | 21.8 (2.77) | 7 (1.41) | 10.8 (4.32) | 31 (5.79) | 16 (10.42) |
| Ovarian | 2443.2 (324.56) | 1374.2 (39.86) | 1325 (24.9) | 1846.4 (30.06) | 1924.4 (23) | 5.4 (3.58) | 6.4 (1.67) | 2010.8 (91.38) | 97.6 (56.42) |
| Australian | 4.8 (1.48) | 3.4 (1.52) | 3.4 (1.52) | 3.6 (0.89) | 4.2 (0.84) | 5 (1.22) | 3.8 (1.3) | 9.4 (1.82) | 3.8 (1.64) |
| Colon | 1061 (134.75) | 543 (18.32) | 499.6 (12.1) | 836.8 (28.25) | 936.8 (17.66) | 2.2 (1.3) | 1.6 (0.55) | 970.4 (21.38) | 3.8 (3.03) |
| Diabetes | 4.4 (0.89) | 4.2 (0.84) | 4.2 (0.84) | 3.6 (1.52) | 4.4 (1.14) | 4.2 (0.45) | 4.4 (1.14) | 4.4 (0.55) | 3.2 (1.1) |
| Av. Rank (mean) | 7.61 | 3.94 | 4.11 | 5.78 | 6.67 | 2.67 | 3.22 | 7.39 | 3.61 |
| Av. Rank (SD) | 5.78 | 5.44 | 4.28 | 4.67 | 4.61 | 2.11 | 4.56 | 7.39 | 6.17 |
| Combined av. rank | 6.69 | 4.69 | 4.19 | 5.22 | 5.64 | 2.39 | 3.89 | 7.39 | 4.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganesh, N.; Shankar, R.; Čep, R.; Chakraborty, S.; Kalita, K. Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm. Appl. Sci. 2023, 13, 3223. https://doi.org/10.3390/app13053223
Ganesh N, Shankar R, Čep R, Chakraborty S, Kalita K. Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm. Applied Sciences. 2023; 13(5):3223. https://doi.org/10.3390/app13053223
Chicago/Turabian StyleGanesh, Narayanan, Rajendran Shankar, Robert Čep, Shankar Chakraborty, and Kanak Kalita. 2023. "Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm" Applied Sciences 13, no. 5: 3223. https://doi.org/10.3390/app13053223
APA StyleGanesh, N., Shankar, R., Čep, R., Chakraborty, S., & Kalita, K. (2023). Efficient Feature Selection Using Weighted Superposition Attraction Optimization Algorithm. Applied Sciences, 13(5), 3223. https://doi.org/10.3390/app13053223








