Numerical Simulation and Experimental Verification of Wind Field Reconstruction Based on PCA and QR Pivoting

Abstract

Short-term wind forecasting is critical for the dispatch, controllability and stability of a power grid. As a challenging but indispensable work, short-term wind forecasting has attracted considerable attention from researchers. In this paper, Principal Component Analysis (PCA) is applied to Computational Fluid Dynamics (CFD) calculation results for feature extraction and then combined with sparse sensing to achieve the rapid reconstruction of a three-dimensional wind speed field and pressure field. Before reconstruction, the relationship between the reconstruction error and the noise level, and a number of the basis vectors is systematically studied. In the simulation, the wind shear effect is introduced into the inlet boundary condition, and the reconstruction errors of the uniform inlet are 0.21% and 6.46%, respectively, while the maximum reconstruction errors including the wind shear effect are 1.21% and 6.41%, respectively, which verifies the feasibility of applying a PCA-based reconstruction algorithm to a 3D wind field reconstruction. In addition, to solve the time-consuming problem of most optimization algorithms based on a brute-force combinatorial search, an innovative optimization algorithm based on the QR pivoting is investigated to determine the sparse sensor placements. Simulation results show that when the number of sensors is equal to the number of basis vectors, the error of random placement is even 20 times of the optimal placement, which illustrates that QR pivoting is a powerful optimization algorithm. Finally, a wind tunnel experiment of velocity field reconstruction is performed, to verify the practicability of the optimized method based on QR pivoting, and the results indicate that a reasonably high accuracy 3D wind field can be obtained with only 10 sensors (the error of most points is less than 5% and the minimum error is only 0.74%). In general, the proposed algorithm incorporating PCA, sparse sensing and QR pivoting can quickly reconstruct the 3D velocity and pressure fields with reduced measurement costs, which is of great significance for the development of short-term wind forecasting methods.

1. Introduction

With the acceleration of the development of modern industry, and the increasing utilization of resources, resource scarcity has become an urgent problem to be solved. Wind energy, as a clean renewable energy, is considered to be one of the alternatives to conventional fuel power generation. According to the “Global Wind Report 2022” from the Global Wind Energy Council, the global wind industry had its second-best year in 2021, with almost 94 GW of capacity added globally, trailing behind 2020’s record growth by only 1.8% [1]. Although wind power has great benefits in saving energy and protecting the environment, it also has some inherent defects. For example, wind energy is vulnerable to the instability and intermittence of random wind, which affects the stability of the power grid and reliability of power system operation. An effective way to overcome these difficulties is to vigorously develop short-term wind forecasting to reduce the uncertainty of wind power.

Wind speed forecasting is the key to a wind power system and plays an important role in the control and operation decisions of wind turbines, and to date various reliable and efficient forecasting methods have been developed, which can be roughly divided into two categories: physical model [2,3,4] and statistical model [5,6,7]. The physical method is mainly based on the large-scale weather forecasting system developed by meteorologists. According to multiple groups of meteorological data (such as temperature, humidity, air density, wind direction, etc.) and the surrounding environment of a wind power plant, such as surface roughness, obstacles, etc., the physical model is comprehensively analyzed and the prediction results are derived [8]. For example, Al-Yahyai et al. [9] proposed a nested ensemble NWP model for wind resource assessment, which provides information on the uncertainties of the NWP model as well as probability information compared to the current single NWP. In practice, the traditional physical method has some limitations, such as how researchers need to know a variety of physical properties, and substantial time is needed to collect the information. Extensive use of computational fluid dynamics (CFD) in wind field simulation provides a powerful means for wind forecasting [10]. However, sophisticated grids are required when the terrain is complex, which is often time-consuming and cannot achieve real-time wind speed prediction, hence it is more suitable for long-term wind forecasting [11].

The technical route for statistical model prediction is to use historical datasets to explore the relationship between input variables and output wind power. For example, Jiang et al. [7] proposed a novel hybrid forecasting system consisting of an effective denoising technique and a fuzzy time series method optimized by a multi-objective differential evolution algorithm to improve the forecasting accuracy and stability. Significantly, as an effective and promising tool, deep learning is expert in extracting inherent non-linear and high-order invariant features in data and has been applied in various fields [12]. For example, Qureshi et al. [13] developed a novel short-term wind forecasting method based on the concepts of learning ability and transfer learning of integrated technology in a deep neural network. It is undeniable that statistical methods play an important role in short-term wind forecasting. However, the accuracy of statistical models is essentially dependent on historical data, hence they are powerless in the event of dramatic changes in weather conditions.

In general, the previous short-term wind forecasting methods focus on point prediction and are vulnerable to the historical data. Although CFD-based physical model prediction can obtain a large amount of wind field information, it is time consuming and cannot achieve real-time prediction. Therefore, it is of practical value to develop a new approach based on real-time meteorological data to obtain wind field information quickly and accurately, which needs to solve the problems of the statistical model’s susceptibility to weather conditions and the time-consuming nature of physical modeling.

In order to solve the above problems, the feature extraction method can be applied to the CFD wind field calculation results with reference to the numerical reconstruction method in the field of aerodynamics [14,15,16], which creatively connects wind reconstruction to wind forecasting. The combination of wind reconstruction and wind forecasting is based on the following assumptions: Because wind farms are generally much smaller than wind fields, the speed distribution in wind farms is related to the wind speed beyond a certain distance (e.g., at the boundary of the wind field), which implies that there is a time buffer from the boundary to the wind farm. Therefore, in this period, the velocity of each point in the wind farm can be reconstructed rapidly using the measured values at the boundary, and the time spent in calculating the reconstruction represents the time scale in the ultra-short-term prediction. The main feature extraction methods used in aerodynamics are Principal Component Analysis (PCA) [17] and Proper Orthogonal Decomposition (POD) [18]. However, both feature extraction methods are applied to 2D flow field reconstruction, and the research on 3D flow field reconstruction is relatively scarce. Moreover, in wind field reconstruction, there are abundant studies on velocity field reconstruction, but few on pressure field reconstruction.

In addition, the placement of limited sensors is the key factor affecting the reconstruction results, hence optimizing sensor placement to improve reconstruction results may be critically enabling. In recent years, several studies of optimal sensor placement have been undertaken [19,20,21]. For example, Willcox [16] presented an optimization algorithm based on a minimum condition number theory to determine the sensor placement. Significantly, most optimization methods are generally based on a brute-force combinatorial search with greedy algorithms, which is characterized by its ability to determine the optimal position effectively, but its disadvantage is also very prominent, i.e., it is very time-consuming, and the combinatorial search does not scale well to a large 3D wind field.

Based on the above issues, this paper focuses on three aspects: (1) verify the feasibility of a PCA algorithm in 3D wind field reconstruction; (2) explore the feasibility of a 3D pressure field reconstruction in a large wind field; and (3) attempt to develop an optimal placement algorithm based on a mathematical matrix operation, which is different from a greedy algorithm, to solve the time-consuming problem while ensuring the accuracy of the reconstruction. For these proposals, sparse sensing and QR pivoting are employed in the reconstruction. Sparse sensing is expert in reconstructing complete signals from a small measurement subset, and QR pivoting is applied in the optimization process [22]. The reconstruction calculation is divided into two parts: First, the combination of PCA and sparse sensing is synergistic, in which the PCA is employed to extract features from CFD simulation results. Combining the extracted features with sparse measurements, the 3D velocity field and pressure field distribution can be obtained by using the developed inverse process algorithm. In addition, QR pivoting and the reconstruction algorithm are combined to determine the optimal sparse sensor placements. A simulation and an experiment are carried out to demonstrate that drastic reductions of sensors and improved reconstruction accuracy can be achieved using the proposed optimized algorithm.

In general, the key contribution of the innovative approach can be reflected in two aspects: First, the combination of PCA, CFD results and sparse sensing can creatively utilize rapid wind field reconstruction to achieve short-term wind forecasting, addressing the instability of the statistical model and large computational load of CFD calculation. Second, unlike a traditional brute-force combinatorial search, the proposed optimization algorithm is developed by QR pivoting and PCA, which bring a significant improvement of the reconstruction accuracy and the associated speedup of optimized sensing. In the wind power industry, this innovative approach can be used in a variety of situations; where sensors come at a high cost, or when ultra-short reconstruction time is required, the reduction in the number of sensors can be significant.

2. Reconstruction Method Based on PCA and Sparse Sensing

Principal Component Analysis, abbreviated as PCA, is one of the most commonly used dimension reduction methods [23], which is called Proper Orthogonal Decomposition (POD) in mechanical engineering [24], Karhunen–Loeve (K-L) transformation in signal processing [25] and Hotelling transformation in image analysis [26].

The core technical route of PCA is to express the high-dimensional vector $x_i\in {ℝ}^m$ as a linear combination of multiple basis vectors φ_k.

$$x_i={\displaystyle \sum _{k=1}^p{\alpha }_k{\phi }_k}$$

(1)

The basis vector φ_k and reconstruction coefficient α_k can be obtained by Singular Value Decomposition (SVD). Given a snapshot matrix containing multiple state vectors $\mathrm{X}=\left[x_1,x_2,\dots ,x_n\right]$, $\mathrm{X}\in {ℝ}^{m\times n}$, the singular value decomposition of matrix X yields:

$$\mathrm{X}=\Psi \Sigma {\Phi }^T$$

(2)

where Ψ and Φ are left and right singular vectors of matrix X, respectively, $\Psi \in {ℝ}^{m\times n}$, $\Phi \in {ℝ}^{n\times n}$, $\Sigma \in {ℝ}^{n\times m}$. All elements of matrix Σ are zero except those on the diagonal, and the diagonal elements are called singular values. When only the first p eigenvalues are taken, it is called truncated-PCA.

$$\mathrm{X}\approx \tilde{\mathrm{X}}={\Psi }_p{\Sigma }_p{\Phi }_p^T$$

(3)

The reconstruction coefficient vector α can be obtained by minimizing the error between X and $\tilde{\mathrm{X}}$:

$$\alpha ={\Psi }_p^{T}x$$

(4)

Inspired by the truncated-PCA, the extracted features can be used to represent high-dimensional data, making it possible to reconstruct an unknown state with limited measurements in a wind field. Based on Equation (3), supposing there is a matrix of wind velocity $V=\{v_1,v_2,\dots ,v_i,\dots ,v_N\}$ ($V\in {ℝ}^{n\times N}$), which can be decomposed by SVD:

$$V=\Psi \Sigma {\Phi }^T$$

(5)

From Equation (1), PCA basis vectors can express high-dimensional states v as linear combinations of φ_k that define a low-dimensional embedding space.

$$v={\displaystyle \sum _{k=1}^p{\alpha }_k{\phi }_k}$$

(6)

The sparse sensing is introduced to solve a, supposing only r ($r\ll n$) measurements are available, which enables the combination of sparse sensor placement and Equation (6) to determine the sparse variable y ($y\in {ℝ}^r$).

$$y=Mv=M{\displaystyle \sum _{k=1}^p{\alpha }_k{\phi }_k}=Ma\Psi$$

(7)

where the measurement matrix $M\in {ℝ}^{r\times n}$ represents measurement locations of v. Point measurements require that the measurement matrix M can be structured in the following way:

$$M={\left[e_{\lambda 1} e_{\lambda 2}\cdots e_{\lambda r}\right]}^T$$

(8)

where e_j are the canonical basis vectors for ${ℝ}^n$ with a unit entry at index j and zeros elsewhere. The form of M can be shown as follows:

$$M=\left[\begin{array}{cccccccccc}1& 0& \cdots & 0& & & & & \cdots & 0\\ 0& \cdots & 0& 0& 1& \cdots & & & \cdots & 0\\ 0& \cdots & 1& 0& \cdots & 0& & 0& \cdots & 0\\ ⋮& 0& & & \cdots & 0& 1& 0& \cdots & ⋮\\ 0& \cdots & & 1& \cdots & 0& 0& 0& \cdots & 0\end{array}\right]$$

(9)

This linear system converts the solution of the unknown state v into the determination of the reconstruction coefficient a with the Moore–Penrose pseudoinverse. Subsequently, the reconstruction of v is obtained using:

$$\widehat{v}=a\Psi , \mathrm{where} a=\{\begin{array}{c}{\Theta }^{-1}y={\left(M\Psi \right)}^{-1}y, r=p\hfill \\ {\Theta }^{†}y={\left(M\Psi \right)}^{†}y, r>p \hfill \end{array}$$

(10)

The accuracy of reconstruction results is measured by relative reconstruction error:

$$RE=\frac{{\Vert v-\widehat{v}\Vert }_1}{{\Vert v\Vert }_1}\times 100\%$$

(11)

3. Preliminaries

In this paper, the validity of the reconstruction method and optimization algorithm will be verified by a CFD simulation and a wind tunnel experiment. Therefore, the preliminaries before the reconstruction calculation will be described in this section, mainly including the construction of a geometric model for the simulated wind field, the construction of an experimental wind tunnel model and the construction of a snapshot matrix.

3.1. Construction of the Simulated Wind Tunnel Model

Before the simulation validation of the reconstruction method, a wind tunnel model is constructed, which combines two hemispheres and a sinusoidal rotation model for complex terrain, as shown in Figure 1. The length, width and height of the model are 4, 3 and 1 m, respectively. The inlet velocity is set to be perpendicular to the X-Z plane and evenly distributed along the x-axis. The incident angle is defined as the angle between the velocity and the positive x-half axis. In addition, the specific dimensions of the complex terrain composed of three obstacles are shown in Figure 2. Significantly, the wind tunnel model designed in this section will be used in the CFD calculation below, and its size is the same as the wind tunnel described in the next section.

3.2. Construction of an Experimental Wind Tunnel Model

In this paper, an experimental wind tunnel model is constructed to demonstrate the feasibility of the reconstruction algorithm and its optimal placement. The obstacle models in the experiment are a combination of two hemispheres and a sinusoidal rotation model with the same size as the simulated geometric model. The wind tunnel experimental equipment is shown in Figure 3.

A schematic diagram of the wind tunnel is shown in Figure 4, which includes the side view and top view of the measurement area. The length, width and height of the test section are 4, 3 and 1 m, respectively. To change the inlet wind speed, four regulating baffles are installed in the variable section. As shown in Figure 4b, eighty-one measuring locations are evenly distributed in the 1 × 1 m area; the anemometers can be fixed at the different heights of these locations to obtain the real-time wind speed.

In order to compare the CFD calculated values with the experimental measurements in Section 5, it is necessary to obtain the characteristics of the inlet wind speed distribution in advance. Firstly, the inlet with a width of 3000 mm is equally divided into 30 parts along the X direction, and 29 sensors are placed to measure the inlet wind speed. Next, four heights along the z-axis, including 200 mm, 400 mm, 600 mm and 800 mm, are selected, and the sensors are inserted in turn. Finally, after the fan is stabilized, a total of 116 speed values are obtained for each point.

Based on the velocity values of 116 measuring points, the distribution characteristics of wind speed at the entrance of the experimental section is shown in Figure 5. From Figure 5, the inlet wind speed has two characteristics: (1) the speed near the center is large and stable whereas the speed near the wall is small; (2) the wind speed increases with the measuring position, probably due to the effect of wind shear. Therefore, based on the wind speed distribution characteristics described above, database information with wind shear effect and turbulence intensity of a certain value need to be added in the construction of a wind speed database.

3.3. Construction of Snapshot Matrix

In preparation for reconstruction, the establishment of an accurate snapshot matrix is critical. In the present paper, the 3D wind field to be measured is expressed by five stacked planes. Several boundary conditions are designed, and a series of speed and relative pressure distributions are calculated by CFD, which are combined into a matrix database. The continuity equation and the momentum equation are mainly used in the calculation process. In this study, wind flow is considered to be stable under a constant temperature. Thus the time term in the continuity equation can be ignored.

Continuity equation:

$$\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}+\frac{\partial (\rho w)}{\partial z}=0$$

(12)

Momentum equation:

$$\{\begin{array}{l}\rho (u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z})=\rho F_x+\frac{\partial p_{xx}}{\partial x}+\frac{\partial p_{xy}}{\partial y}+\frac{\partial p_{xz}}{\partial z}\\ \rho (u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z})=\rho F_y+\frac{\partial p_{yx}}{\partial x}+\frac{\partial p_{yy}}{\partial y}+\frac{\partial p_{yz}}{\partial z}\\ \rho (u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z})=\rho F_z+\frac{\partial p_{zx}}{\partial x}+\frac{\partial p_{zy}}{\partial y}+\frac{\partial p_{zz}}{\partial z}\end{array}$$

(13)

where ρ is density; u, v and w represent the velocity of the x, y and z directions, respectively; p is pressure; and ρF is the unit mass force.

Based on the above equations, 28 boundary conditions are designed by changing the entrance speed and incident angle. Among them, the inlet velocity changes from 1 to 31 m/s with an interval of 5 m/s, and the incident angles are 30°, 70°, 110° and 150°. Notably the inlet velocity is uniformly distributed along the horizontal and vertical directions. Both databases containing 28 wind speed and relative pressure distributions can be represented by V, $V\in {ℝ}^{n\times N}$, where n stands for the number of sampling points; N is the number of boundary conditions. In the simulation, 2500 sampling points are selected for each plane, and the dimension of the snapshot matrix is 12,500 × 28; the following reconstruction calculation is based on this matrix.

However, considering that the real airflow around the wind farm is much more complex, especially the effect of wind shear on the wind speed distribution, the atmospheric turbulence inflow of stable vertical wind shear using the Normal Wind Profile model is introduced. The inlet speed can determined by the wind profile power law [27]:

$$V=V_r{\left(\frac{z}{z_r}\right)}^{\alpha }$$

(14)

where V(m/s) is the wind speed at height z (m), and V_r is the known wind speed at a reference height z_r. The exponent (α) is an empirical coefficient, approximately 1/7, or 0.143 [27]. Furthermore, z_r in the construction of the database is taken at 0.8 m. The wind velocities at z_r change from 1 to 31 m/s with an interval of 5 m/s, and the incident angles are 30°, 70°, 110° and 150°. The turbulence intensity and viscosity ratio are set to 5% and 10%, respectively.

ANSYS ICEM is employed to generate the hexahedral structured mesh and boundary layer. The mesh is encrypted around the boundary, and “o-block” is performed near the three geometric models. A total of 16 boundary layers are set around the hemisphere model with a grid spacing of 1.16 cm, and 20 boundary layers are set around the sinusoidal model with a grid spacing of 1.44 cm. The hexahedral structured mesh and boundary layer for the wind tunnel is shown in Figure 6. After the structured grid division is completed, the y+ of the hemispherical model and the sinusoidal model are calculated, with the y+ values of the hemispherical model varying from 2.41 to 84.62 and the sinusoidal model varying from 4.88 to 74.63. The calculation result of y+ proves the rationality of grid division and lays the foundation for the following fluent calculation.

ANSYS Fluent is used to generate the velocity and relative pressure distributions to construct the database. The solution parameters of Fluent are set as follows: The ‘Pressure-Based’ method and ‘Steady’ are selected as the Solver. For the boundary conditions, the type of inlet is selected as ‘velocity-inlet’ and the outlet is set as ‘pressure-outlet’. In the inlet, the turbulence intensity is 5% and viscosity ratio is 10%. Standard K-ε is chosen as the viscous model because of its advantages such as low calculation demand, strong calculation stability and fast convergence speed. The Solution Method and Gradient are chosen as ‘SIMPLE’ and ‘Least Squares Cell Based’, respectively; the Momentum and Turbulent Kinetic Energy is selected as ‘Second-Order Upwind’, and the convergence residual is set to 1 × 10⁻⁵.

Finally, the mesh independency test is carried out, where 2,628,578 cells are considered as the standard. Four groups of dense to sparse cells are designed for comparison: 986,523, 415,243 and 195,489. The 12,500 velocity values of five planes calculated from 2,628,578 cells are used as the criterion, and then the results of the other three groups are compared with this criterion. Finally the relative error is obtained by using Equation (11). The relative errors compared to 2,628,578 cells are shown in

Table 1. Mesh independence test.

Mesh Number	Relative Error (%)
986,523	0.12
415,243	0.22
195,489	0.58

. It is obvious that when the number of cells reaches approximately 400,000, the relative error decreases to approximately 0.2%, which can be considered to be within the acceptable range considering the calculation cost. Consequently, 415,243 cells are chosen for the following calculation.

4. Numerical Results of the Proposed Reconstruction Method

4.1. Presentation of Reconstruction Results of Velocity Field and Pressure Field

In what follows, five stacking planes with heights of 0.22, 0.25, 0.30, 0.35 and 0.4 m and dimensions of 1 × 1 m are selected to represent the 3D wind field. The 3D velocity field and relative pressure field corresponding to the boundary condition of 90 °, 15 m/s is selected to validate the performance of the reconstruction algorithm. A series of parameters, such as the number of basis vectors, the number of sensors and the measurement noise need to be considered. In the simulation, the measurement noise γ is defined by Gaussian noise:

$$\gamma \sim N\left(0,{\sigma }^2\right)$$

(15)

Here, $\sigma$ is the standard deviation and N is the normal distribution function related to ${\sigma }^2$; the noise level is defined by $\sigma$:

$$Noise\_level=\sigma \times 100\%$$

(16)

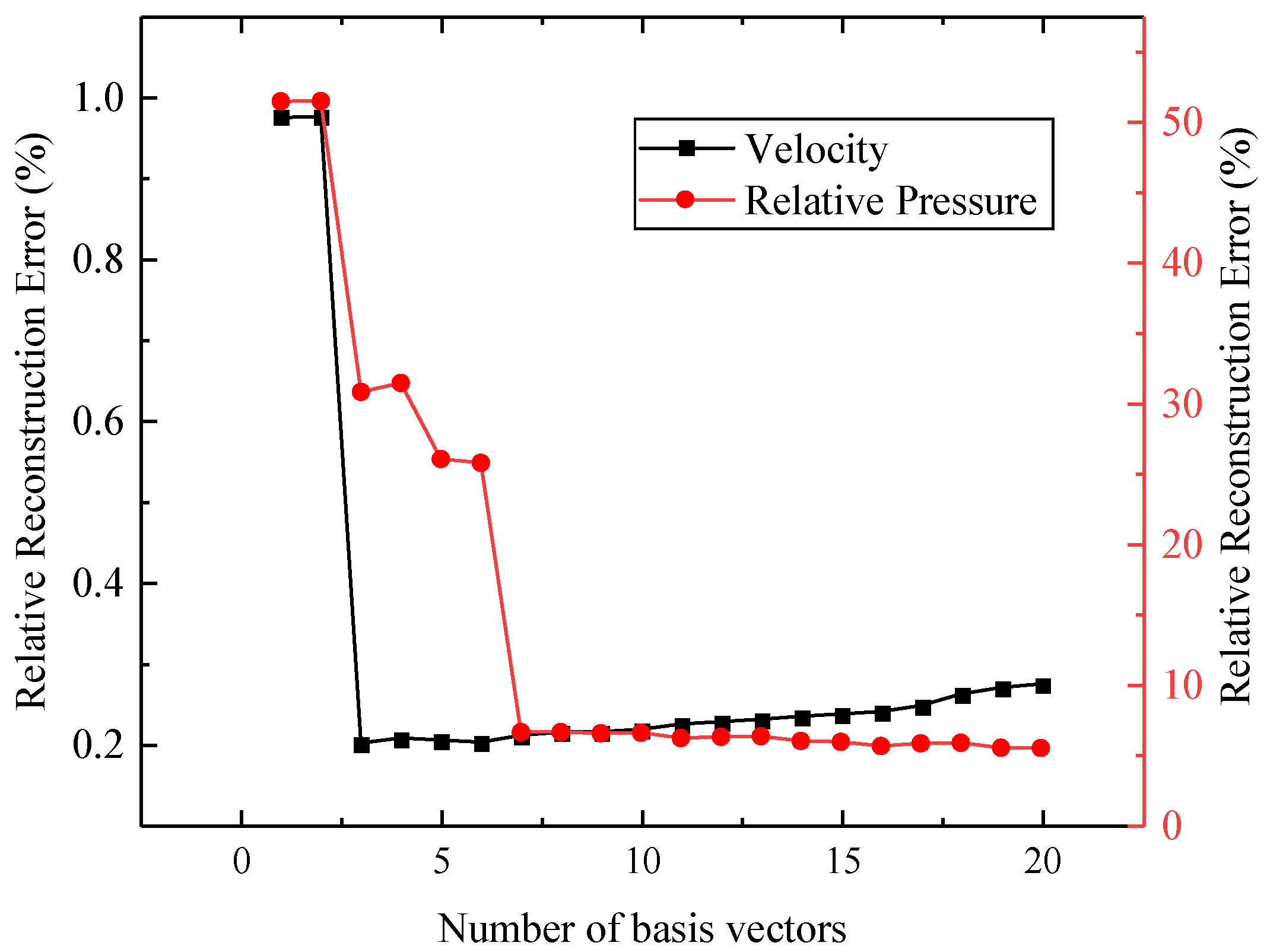
However it can be seen from Equation (10) that the selection of the number of basis vectors is crucial for reconstruction calculation. Before reconstruction, the joint effect of the number of basis vectors and the measurement noise on the reconstruction error will be explored to determine the number of basis vectors. First, the number of sensors and the noise level are determined to be 100 (only 1% of total data) and 10%, respectively, and then the number of basis vectors is increased from 1 to 20 to obtain the reconstruction error curve. To ensure accurate results, 1000 calculations for each reconstruction are performed to obtain the average value. The calculation results are shown in Figure 7.

Figure 7 is a double y-axis diagram, from which it could be found that the reconstruction error of relative pressure is nearly ten times higher than that of velocity. This is because the distribution of relative pressure is characterized by the fact that most of the pressure values are very small (close to 0), and the pressure gradient is very large.

In addition, the reconstruction error of the velocity field is not monotonically reduced, whereas the reconstruction error of the pressure field shows a steady downward trend. This reflects the reconstruction characteristics of velocity and pressure fields: First, the feature extraction of the velocity field is more accurate, which allows better reconstruction results with fewer basis vectors. However, this may lead to an increase in the sensitivity of reconstruction accuracy to noise level, i.e., when the number of basis vectors continues to increase, the reconstruction accuracy will decrease instead. Correspondingly, when feature extraction is more accurate, an excessive increase of the number of basis vectors will result in reconstruction errors being more sensitive to noise level.

To verify the accuracy of PCA feature extraction, an energy proportion $t\in (0,1]$ is specified to represent the importance of eigenvectors. If n eigenvalues are ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$, then t is defined as follows:

$$t_i=\frac{{\lambda }_i}{{\displaystyle \sum _{i=1}^n{\lambda }_i}}$$

(17)

Figure 8 shows the “energy proportion” of each eigenvalue in the velocity database and the pressure database. It can be seen from Figure 8 that the energy of the eigenvalue decreases rapidly in both databases; the first six and eight basis eigenvalues account for 99.9% “energy” of the total system in the velocity database and the pressure database, respectively, which is sufficient to represent the basis vectors.

Finally, by exploring the influence of different noise levels and the number of basis vectors on the reconstruction error, the optimal number of basis vectors is determined for reconstruction calculation. This section increases the noise level from 1% to 30% with an interval of 1%. Referring to Figure 7 and Figure 8, the number of eigenvectors of the velocity field is set to 2, 4, 6, 8 and 10, and the number of eigenvectors of the pressure field is set to 8, 9, 10, 11 and 12. With a fixed number of sensors and arrangement, the corresponding reconstruction error results are shown in Figure 9 and Figure 10.

The combined effect of eigenvectors and noise levels on reconstruction errors can be visually seen from the two preceding figures. By comparing the results of velocity and pressure fields, the following conclusions can be drawn:

Firstly, for velocity field reconstruction, when the number of eigenvectors is two, the error changes most smoothly with the increase of the noise level, although the reconstruction error is the largest. This indicates that the error is less sensitive to noise when the number of eigenvectors is small. As the eigenvector increases, the error is significantly affected by the noise level. These two features show that the increase of the eigenvector is beneficial to the improvement of the reconstruction error, but the excessive increase will make the error more sensitive to noise. Therefore, referring to Figure 7, Figure 8 and Figure 9, the number of basis vectors used for velocity field reconstruction is determined to be six.

Secondly, for pressure field reconstruction, the trend of error with an increasing number of basis vectors is different from that of a velocity field. As the number of basis vectors increases, the reconstruction errors increase monotonically, which indicates that for databases with large data gradients, the reconstruction accuracy is more susceptible to measurement errors. In this case, the selection of the number of basis vectors should comprehensively consider the accuracy of feature extraction and the impact of the noise level. Therefore, referring to Figure 7, Figure 8 and Figure 10, the number of basis vectors used for pressure field reconstruction is determined to be eight.

After determining the number of basis vectors, the reconstruction results of the velocity and pressure fields with the inlet boundary condition of 90°, 15 m/s are obtained in this section. Figure 11 shows the position of five planes, i.e., the 3D velocity field to be reconstructed. Figure 12 and Figure 13 show the simulated and reconstructed velocity nephograms, which show that the reconstructed velocity distribution is reasonably similar to the real distribution, and the relative error is only 0.21%. Figure 14 and Figure 15 show the simulated and reconstructed relative pressure nephograms, and the relative error is 6.46%. Figure 15 shows that the low-pressure area is mainly distributed around obstacles, where the velocity is relatively high, which is corresponding to the velocity distribution characteristics in Figure 13, indicating that the reconstructed pressure can accurately restore the real distribution characteristics. The minimal reconstruction error (0.21%) reflects the efficiency of this method in velocity field reconstruction. Meanwhile the relatively high pressure field reconstruction error (6.46%) seems to indicate that the method is not effective for the reconstruction of data with a large gradient. Significantly, the boundary condition of 90°, 15 m/s is not contained in the snapshot matrix, while the reconstruction results are satisfactory, which further validates the feasibility of the proposed reconstruction algorithm based on sparse sensors. Therefore, the following conclusions can be obtained after simulation: for the velocity field, the proposed method can accurately reconstruct the velocity distribution, whereas for the pressure field, the pressure distribution characteristics can be basically restored by using the proposed method.

4.2. Influence of Sensor Number and Placement on Reconstruction Performance

In the previous section, the selection of the number of basis vectors is discussed from two aspects: reconstruction accuracy and noise effect. For the velocity field, the increase of the eigenvector is beneficial to the improvement of the reconstruction error, but the excessive increase will make the error more sensitive to noise, so the number of basis vectors is determined as six. However, for the pressure field, the reconstruction accuracy is more susceptible to measurement errors due to the large data gradient. Hence, the selection of the number of basis vectors should comprehensively consider the accuracy of feature extraction and the impact of noise level, and finally, the number of basis vectors is determined as eight. After determining the number of base vectors, the factors that affect the accuracy of reconstruction need to be further explored. By observing Equation (10), M is the key factor affecting the solution of reconstruction coefficient a, and the number and location of sensors determine M. Thus the effect of the number and placement of sensors on the accuracy of reconstruction will be further discussed in this section.

In this section, four groups of sensors with the same number (100 sensors) but different placement are determined. To ensure the credibility of the analysis, the number of basis vectors and the noise level are the same as those in the previous section. Figure 16 shows the relative reconstruction errors corresponding to four sensor placements of the velocity field and the relative pressure field. As one would expect, the error and reconstruction are improved as more samples are taken. Moreover, the sensor arrangement has a significant impact on the reconstruction results when the number of sensors is less than 20, especially for the pressure field; the error difference can even reach 20 times. This indicates that when fewer sensors are available, the reconstruction accuracy depends critically on the arrangement of the sensors.

For brevity in the following discussion, Θ and its inversion are denoted by ${\mathrm{K}}_{\lambda }={\Theta }^T\Theta ({\mathrm{K}}_{\lambda }=\Theta \mathrm{if} r=p)$. To show the convergence of the random sampling, in addition to RE, another error metric is considered: the condition number of the matrix K_λ for a given measurement matrix M, which can be used to represent the stability of a linear equation:

$$\Phi ({\mathrm{K}}_{\lambda })=\Vert {\mathrm{K}}_{\lambda }\Vert \Vert {\mathrm{K}}_{\lambda }^{-1}\Vert =\frac{{\sigma }_{\max }}{{\sigma }_{\min }}$$

(18)

where the ${\sigma }_{\max }$ and ${\sigma }_{\min }$ represent the maximum and minimum singular values, respectively. Generally, the smaller the condition number of the matrix, the more stable the linear system is. Thus, it can be said that large condition numbers suggest poor reconstruction, whereas values that tend towards unity should perform well. Based on the two metrics, i.e., RE and Φ(K_λ), the variation of both metrics is studied in detail with 1 to 20 sensors. Given our random sampling strategy, the results that follow will be statistical in nature, computing averages and variances for batches of randomly selected sampling.

Figure 17 and Figure 18 depict the average over 1000 trials of the logarithm of RE, log(RE + 1) (unity is added to avoid negative numbers) and the logarithm of the condition number of K_λ, log[Φ(K_λ)]. From Figure 17 and Figure 18, three conclusions can be drawn: First, the relative error and condition number are largest and the most unstable when the number of sensors is less than the number of basis vectors. Second, the variance of the 1000 trails, depicted by the red bars is also quite large, suggesting that the reconstruction performance for fewer sensors is highly sensitive to their placement. Third, the error and condition number both perform better as sensors increase, and the trends of both are similar, which supports the hypothesis that the condition number can be used to evaluate the performance of the sparse measurements.

In particular, as shown in Figure 17 and Figure 18, there is a large variance in the distribution of the Φ(K_λ) and RE for six sensors in the velocity field and eight sensors in the pressure field. Specifically, the relative errors and condition number can change by orders of magnitude with the same sensors, but simply placed in different locations. From both figures, it can be seen that fewer sensors can produce both exceptional results and extremely poor performance depending upon the sensor locations, which illustrates that extremely high variability can be generated in reconstruction using random and sparse measurements.

Thus, the sparse sensor placement is critical for accurate 3D wind field reconstruction, which suggests that developing a principled way to determine optimal sensor placement is of great importance.

4.3. Reconstruction Results Considering Wind Shear Effect

Considering that the real airflow around the wind farm is much more complex, the final section of this chapter will show the wind farm reconstruction results containing the inlet wind shear effect to enrich the application scope of the proposed reconstruction method. In Section 3.3, based on Equation (14), a wind field database containing wind shear effects has been obtained. To verify the accuracy of wind field reconstruction under different wind shear conditions, three inlet boundary conditions are set in this section for verification, as shown in

Table 2. Three inlet boundary conditions containing different wind shear effects.

Inlet Boundary Conditions	Wind Speed (m/s) at zr	Incident Angle	zr (m)	Exponent (α)
1	5	50°	0.8	0.143
2	10	90°	0.8	0.2
3	15	130°	0.7	0.2

:

In this section, the number of basis vectors, the noise level and the number of sensors are set the same as in Section 4.1. The reconstruction errors of the velocity field and the pressure field under three boundary conditions are summarized in

Table 3. Reconstruction errors (%) of velocity and pressure fields under three different wind shear effects.

Inlet Boundary Conditions	Reconstruction Error of Velocity Field	Reconstruction Error of Pressure Field
1	0.51	5.48
2	1.14	6.28
3	1.21	6.41

. It is worth noting that the third boundary condition is to assume that the wind shear exponent (α), reference height (z_r), inlet velocity at z_r and incident angle are not in the prepared database, i.e., the inlet boundary condition is completely unknown. The reconstruction calculation under this condition is of great significance to verify the feasibility of applying this method to the complex airflow around the real wind field. The following conclusions can be drawn from the analysis of errors in the table: (1) Compared with the uniform entrance boundary, the reconstruction error under the boundary condition considering the wind shear effect is significantly larger. (2) The reconstruction errors under the second and third boundary conditions indicate that relatively satisfactory results can still be obtained with limited sensors under complex and unknown inlet boundary conditions. (3) Interestingly, the reconstruction error of the pressure field is smaller than that of uniform wind speed, probably because the pressure field distribution database built considering the wind shear effect is closer to the actual pressure field distribution, which also indicates the importance of database construction in the reconstruction calculation.

In general, based on the uniform inlet wind speed and the inlet wind speed condition considering wind shear effect, the proposed method is employed to verify the reconstruction under various unknown inlet conditions, and the factors that may affect the reconstruction accuracy are analyzed. The reconstruction results verify the feasibility of the proposed algorithm in a real and complex wind field environment. Sensor location optimization in wind field reconstruction with different inlet boundary conditions will be addressed in the next chapter.

5. Optimal Sensor Placement and Validation Results Based on QR Pivoting

5.1. Criterions for Optimal Sensor Placement

The optimal sensor placements are those that minimize the relative errors. From Equation (10), the problem of optimal placement of sensors is transformed into seeking rows of $\Psi$ which optimally condition the inversion of the matrix Θ. Therefore, the condition number of the linear system can be improved by optimizing the spectral content of K using its determinant, trace, or spectral radius. Based on the criterion of spectral radius, the smallest singular value of K_λ can be maximized by ${\mathrm{K}}_{\lambda }^{-1}$.

$${\lambda }^{\ast }=\underset{\lambda ,\left|\lambda \right|=r}{\arg \min }{\Vert {\mathrm{K}}_{\lambda }^{-1}\Vert }_2=\underset{\lambda ,\left|\lambda \right|=r}{\arg \max }{\sigma }_{\min }\left({\mathrm{K}}_{\lambda }\right)$$

(19)

Likewise, the criteria of optimizing the trace or determinant of its eigenvalue or singular value spectrum are as follows:

$${\lambda }^{\ast }=\underset{\lambda ,\left|\lambda \right|=r}{\arg \max \mathrm{tr}}\left({\mathrm{K}}_{\lambda ,\left|\lambda \right|=r}\right)=\underset{\lambda }{\arg \max }{\displaystyle \sum _i{\lambda }_i}\left({\mathrm{K}}_{\lambda }\right)$$

(20)

$${\lambda }^{\ast }=\underset{\lambda ,\left|\lambda \right|=r}{\arg \max \left|\det {\mathrm{K}}_{\lambda }\right|}=\underset{\lambda ,\left|\lambda \right|=r}{\arg \max }\prod _i{\sigma }_i({\mathrm{K}}_{\lambda })$$

(21)

However, if the above criteria are used for optimization, a combinatorial search over $\left(\begin{array}{c}n\\ r\end{array}\right)$ is required, which is a brute-force search containing all possible sensor configurations and is hence computationally intractable. Recently, with the development of EIMs (Empirical Interpolation Methods), the study of Q-DEIMs has attracted the most attention, where “Q” stands for QR pivoting [28,29,30], which provides an optimal sampling method for nonlinear interpolation reconstruction in ROMs (Reduced-Order Models). Based on QR factorization and column pivoting of ${\Psi }^T$ by the Q-DEIM method, an approximate greedy algorithm is proposed.

5.2. QR Pivoting for Sparse Sensor Placement

Inspired by Q-DEIM, the key to achieve the optimal placement of oversampling is to apply the QR factorization with column pivoting to the basis vectors. QR pivoting was proposed by Businger and Golub in the 1960s to solve the least-squares problems [31], which has found utility in various measurement applications [32,33,34].

The QR pivoting decomposes a matrix $A\in {ℝ}^{m\times n}$ into a unitary matrix Q, an upper-triangular matrix R and a column permutation matrix C, i.e., $A{C}^T=QR$. QR factorization provides an approximate greedy method consistent with Equation (21), which can achieve the submatrix volume maximization to maximize the determinant. QR factorization increases the volume of the submatrix by choosing a new pivot column with the largest 2-norm and then subtracting its orthogonal projection onto the pivot column.

Therefore QR pivoting determines r optimal sensor locations based on the tailored basis vectors when the number of basis vectors equals to r.

$${\Psi }_r^T{C}^T=QR$$

(22)

Furthermore, the oversampled case, i.e., r > p, may be solved by pivoted QR factorization of $\Psi {\Psi }_{}^T$, where the pivots are selected from an expensive QR factorization of an n × n matrix.

$$(\Psi {\Psi }_{}^T)C^T=QR$$

(23)

Based on the optimization method presented in this section, the capability of QR factorization to control the condition number is also validated in the following sections. Essentially the sparse sensor placement is similar to the concepts of the variable and feature selection in machine learning. Moreover, this sensor (feature) selection technique can be extended to data-driven classification, which has additionally been employed in the field of signal processing to sample and estimate signals of graphs efficiently.

5.3. Simulated Reconstruction Results of the Proposed Optimal Sensor Placement

As shown in the preceding section, we have completed simulation verification of the proposed reconstruction algorithm, proving its efficiency and stability in 3D reconstruction performance. Moreover the ability of the proposed method in reconstruction performance depends critically on the placement of the sensor locations. Thus it is essential to develop an algorithm to determine the optimal sensor placement.

An overarching goal of optimal sensor placement is choosing the fewest n sensors for reconstruction and inherently involves a tradeoff between the number of sensors and reconstruction accuracy. In what follows, the reconstruction performance based on QR pivoting is evaluated in three aspects: reconstructed nephograms, comparison of relative reconstruction errors and the condition number of K_λ. In this section, the number of optimized sensors for velocity field reconstruction and pressure field reconstruction is respectively set as 6, 10 and 8, 15 with reference to Figure 12 and Figure 13. In addition, the noise level is 10%; the boundary condition with 90°, 15 m/s and boundary condition 3 in Table 2 are selected for discussion. For ease of representation, the two boundary conditions are named Boundary Condition 1 and Boundary Condition 2, respectively. After optimizing calculation, it is found that the optimal locations of the sensors obtained by QR pivoting are unique for the determined database, which means that only the optimal locations of 10 and 15 sensors need to be determined, so only the location of 10 sensors in the velocity field and the location of 15 sensors in the pressure field need to be shown in this section.

Figure 19, Figure 20, Figure 21 and Figure 22 show the reconstructed nephograms of the velocity and pressure fields with sensor locations (red and black dots) using QR pivoting, which indicate that using limited sensors can still accurately reconstruct a wind field if the placement is reasonable. As can be seen from these figures, the optimized sensor locations are located on the first plane (0.22 m), so in order to more accurately observe the sensor locations, the nephograms of the first plane and the measurement points distribution are plotted separately, as shown in Figure 23, Figure 24, Figure 25 and Figure 26. Overall, two features of the optimized sensor distribution can be drawn from the nephograms: (1) the optimal locations are entirely distributed on the 0.22 m plane, where the velocity, pressure and their gradient are the largest; (2) most sensors are located near the sinusoidal model, where the gradients of velocity and pressure are relatively large. Both features seem to indicate that better reconstruction results can be obtained by placing the sensor in areas with large gradients of velocity and pressure, where reconstruction errors are also typically larger.

Given the new error metric, i.e., the matrix condition number presented in Section 4.2, the performance of QR pivoting in reducing the condition number will be further evaluated in this section.

Table 4. Logarithm of condition number of K_λ and relative reconstruction errors (%) of random placement and QR pivoting in velocity field (Boundary Condition 1).

Error Metric	6 Sensors		10 Sensors
	QR	Random	QR	Random
log[Φ(Kλ)]	1.47	3.15	1.38	1.62
RE	1.23	24.15	0.66	0.80

,

Table 5. Logarithm of condition number of K_λ and relative reconstruction errors (%) of random placement and QR pivoting in pressure field (Boundary Condition 1).

Error Metric	8 Sensors		15 Sensors
	QR	Random	QR	Random
log[Φ(Kλ)]	2.37	3.61	1.35	1.71
RE	12.06	101.46	7.25	10.65

,

Table 6. Logarithm of condition number of K_λ and relative reconstruction errors (%) of random placement and QR pivoting in velocity field (Boundary Condition 2).

Error Metric	6 Sensors		10 Sensors
	QR	Random	QR	Random
log[Φ(Kλ)]	2.36	2.84	2.52	2.76
RE	1.63	12.06	1.55	4.21

and

Table 7. Logarithm of condition number of K_λ and relative reconstruction errors (%) of random placement and QR pivoting in pressure field (Boundary Condition 2).

Error Metric	8 Sensors		15 Sensors
	QR	Random	QR	Random
log[Φ(Kλ)]	2.63	3.40	1.04	2.11
RE	15.38	83.05	6.99	18.16

show the condition number and the relative reconstruction error of two placements in the velocity field and the pressure field with two boundary conditions. The following conclusions can be drawn from these tables: (a) The reconstruction error and condition number can be significantly reduced when the number of sensors is greater than the number of basis vectors. This is because once the sensors exceed the number of basis vectors, the solution of the linear equation can be converted into an oversampling problem. (b) When the number of sensors is equal to the number of basis vectors, the error of random placement is even 20 times of the optimal placement, which illustrates that QR pivoting is a powerful optimization algorithm and can significantly improve the reconstruction results. (c) Compared with the optimization results under the two boundary conditions, although the reconstruction error is large under complex boundary conditions the QR pivoting can effectively reduce the reconstruction error, which proves the feasibility of the optimization method applied in real and complex wind fields.

In this section, we demonstrate that using the QR pivoting sensing on a tailored basis typically achieves more accurate wind field reconstruction than random measurements, facilitating a reduction in the number of sensors. Reducing the number of sensors may be critically enabling when an individual sensor is expensive or difficult to place.

5.4. Experimental Results of the Proposed Optimal Sensor Placement

As described in Section 3.2, an experimental wind tunnel model is constructed to demonstrate the feasibility of the reconstruction algorithm and its optimal placement. Due to the limited experimental conditions and the importance of obtaining the velocity field in a wind farm for wind power forecasting, only the reconstruction results of the velocity field are validated in this section.

The measurement is divided into four groups: 10 QR pivoting-based sensors; 10 randomly placed sensors; 15 randomly placed sensors; and 10 verification locations. Randomly placed sensors are used for comparison, and measurements at 10 verification locations are taken as reference values for error calculations. The steps of experimental data acquisition are as follows:

(1)

Calibrate the anemometers and insert them in the appropriate locations.

(2)

Turn on the fan and adjust it to the appropriate operating frequency.

(3)

After the fan works for 5 min, collect the data continuously for 10 min.

(4)

Calculate the average wind speed of each anemometer.

(5)

Repeat the above steps until all data acquisition is completed.

In this experiment, the number of basis vectors is 3 and the fan frequency is set to 25 Hz. The reconstructed nephograms and sensor placements are shown in Figure 27. The nephograms can accurately show the wind speed distribution characteristics, which verifies the reliability of the PCA-based reconstruction algorithm in practice. In addition, the relative reconstruction errors for the three sensor placements are shown in

Table 8. Relative reconstruction errors (%) for three sensor distributions.

Sensor Distribution	Relative Reconstruction Error (%)
QR Pivoting	5.04
10 random sensors	7.89
15 random sensors	6.83

. It is obvious that the optimal placement based on QR pivoting can achieve a more accurate reconstruction than random placement, no matter whether the number of random sensors is 10 or 15. This validates that in practical applications, QR pivoting can effectively reduce the number of sensors required while ensuring the reconstruction accuracy.

Similar to the error analyses in Section 4.2 and 4.3, the experimental results will be discussed from three aspects: number of basis vectors; number of sensors; and errors of ten verification points. First, the effect of the basis vectors on the experiment is explored, which is also the validation of the conclusions in Section 4.2. Since the measurement error is generally large and unavoidable in the experiment, given the conclusion of Section 4.2, i.e., the reconstruction error with more basis vectors is sensitive to the noise, the number of basis vectors are determined as two, three, four and five, respectively. Figure 28 shows the reconstruction errors with a different number of basis vectors. Compared with 10 sensors, 15 sensors can significantly reduce errors, but it is still higher than the QR pivoting-based placement. In addition, the reconstruction error of the QR pivoting-based placement has an upward trend with the increase of 4-mode dimension, which supports the conclusion in Section 4.2.

Next we will explore the effect of sensor increments on reconstruction errors in our experiments. When the number of basis vectors is taken to three, the reconstruction errors with different sensors are shown in Figure 29. It is obvious that when the sensors exceed three, the error decreases significantly, which supports the conclusion in Section 4.2, i.e., once the sensors exceed the number of basis vectors, the solution of the linear equation can be converted into an oversampling problem. Significantly, even if the number of anemometers randomly arranged reaches 15, the reconstruction error is still higher than that of 10 anemometers optimally arranged based on QR pivoting. Therefore the ability of optimal placement based on QR pivoting to effectively reduce the number of required sensors has been experimentally verified.

In addition, to visualize the differences between the CFD results and the wind tunnel results (containing the reconstruction results and the measurements), we counted the measurements of ten verification points, the CFD results, the reconstruction results and the error of each point in

Table 9. Measured value (m/s), CFD value (m/s), reconstructed value (m/s) and error (%) of each location.

Location	Verification Points	CFD	Error	QR Pivoting	Error	Random 10	Error	Random 15	Error
1	7.07	7.24	2.33	7.28	3.03	7.82	10.64	7.57	7.01
2	6.81	8.28	21.63	6.73	1.14	6.99	2.61	7.09	4.15
3	7.89	8.45	7.03	7.37	6.65	8.02	1.63	7.74	2.01
4	6.62	7.09	7.13	7.12	7.59	7.58	14.60	7.47	12.87
5	7.15	8.05	12.64	7.10	0.74	7.57	5.81	7.46	4.35
6	7.30	8.61	17.95	7.40	1.30	7.84	7.37	7.65	4.81
7	7.13	7.69	7.82	7.00	1.94	7.31	2.52	7.36	3.24
8	6.94	7.59	9.42	7.27	4.87	7.76	11.83	7.60	9.52
9	8.54	8.08	5.40	7.08	17.14	7.54	11.77	7.46	12.68
10	6.94	7.09	2.10	7.18	3.42	7.67	10.46	7.46	7.47

. Notably the CFD calculation results are based on the inlet velocity profile fitted by 116 measurements in Section 3.2. The difference between the velocity values of each group is clear. Firstly, there is only one point in the QR-pivoting group with a relative error exceeding 10%, and the remaining errors are almost lower than 5% (the minimum error is only 0.74%). Secondly, the reconstruction error obtained by two groups of randomly arranged sensors is generally large and unstable, especially when ten sensors are employed. Finally, the average relative error between the CFD simulation values and the ten verification points is 9.35%, which seems to have no advantages over the reconstruction method. However, considering the measurement error of the sensor and the fitting error of the inlet wind speed, although the final calculation result is not as accurate as that of the reconstruction, the CFD calculation does not require the support of the wind field database, which saves the time of offline database construction and is more suitable for application without sufficient wind field data. In general, Table 9 strongly demonstrates that the proposed optimized reconstruction algorithm incorporating QR pivoting has a higher practical value than CFD in velocity field reconstruction with sufficient wind data.

6. Conclusions

In the present paper, based on PCA and QR decomposition, a 3D field reconstruction method combining optimal sensor placement is proposed, which can accurately reconstruct the 3D velocity field and pressure field with limited sensor data. A PCA-based reconstruction algorithm can quickly and accurately obtain 3D velocity and pressure distribution, while QR pivoting is efficient in greatly reducing the number of sensors and improving the prediction accuracy. A simulation and an experiment were performed to verify the practicability of the algorithms. The major findings are as follows:

(1)

In the simulation, the reconstruction errors of the uniform inlet are 0.21% and 6.46%, respectively, while the maximum reconstruction errors including wind shear effect are 1.21% and 6.41%, respectively, which indicates that the reconstruction algorithm based on PCA and sparse sensing can accurately and quickly obtain the distribution characteristics of the velocity and pressure of a 3D wind field.

(2)

The effects of the number of basis vectors, measurement noise, number of sensors and placement on the reconstruction results were systematically investigated. The results show that an excessive increase of the number of basis vectors will result in reconstruction errors being more sensitive to noise level.

(3)

Reconstruction accuracy can be significantly influenced by the arrangement of sensors when sensor costs are restricted (e.g., less than 20), especially for the pressure field, where the difference between the maximum and minimum reconstruction errors is even 20 times.

(4)

Matrix QR pivoting was integrated into the reconstruction algorithm to determine the optimal sensor placement, and its performance was validated by the simulation. The results indicate that QR pivoting-based sensor placement can achieve better reconstruction performance than random measurements, which reduces costs associated with the purchase, placement and maintenance of sensors.

(5)

Optimized sensor placement characteristics indicate that better reconstruction results can be obtained by placing the sensor in areas with large gradients of velocity and pressure, where reconstruction errors are also typically larger.

(6)

A wind tunnel experiment of velocity field reconstruction was performed to verify the practicability of the optimized reconstruction method based on QR pivoting, and the results indicate that a reasonably high accuracy 3D wind field can be obtained with only 10 sensors (the error of most points is less than 5% and the minimum error is only 0.74%).

In this work, we have demonstrated the practical implementation of an algorithm combining PCA and QR pivoting on a 3D wind field by a simulation and a wind tunnel experiment. It is worth noting that there is no all-purpose strategy for the optimal sensor placement of a high-dimensional system, whereas the optimization algorithm described in this paper is particularly favorable, as it is fast, simple to implement and has the potential to be an effective approach for short-term wind forecasting. Admittedly, although wind shear effect is introduced in this paper, the real wind environment is often more complex. Therefore, the application of this method in a real wind field still faces the following unresolved issues: the applicability verification of the reconstruction method under complex terrain conditions and how to ensure the reconstruction efficiency in the case of a large dimension database caused by complex terrain, which are the directions of future research.