Featured Application
Magnetic anomaly detection and geomagnetic navigation.
Abstract
Under dynamic conditions, when the measured magnetic field is projected onto the sensitive axis of the fluxgate magnetometer, it will show strong dynamic characteristics, resulting in errors or delayed interpretation of the measured physical process. Considering the dynamic characteristics of the three-axis fluxgate magnetometer, this paper proposes a series dynamic compensator based on system identification to carry out system identification and modeling of the dynamic characteristics of the three-axis fluxgate magnetometer and proposes a system parameter calculating method based on hybrid optimization of the genetic algorithm and the simulated annealing algorithm (GA-SA). With these methods, not only can the parameter optimization process effectively avoid falling into the local optimal, but they can also greatly improve the search efficiency and shorten the time of solving the optimal solution. Thus, the full-space search ability of the algorithm is improved, and the accuracy of the dynamic magnetic measurements is improved to the maximum extent. The simulation results of the step signal show that the response time is reduced to 18.22% of the pre-compensation time. The standard signal test results of the step signal and sinusoidal signal, respectively, show that the response time of the step signal is reduced to 5.5% and, in the 0.01–10 Hz frequency band, the maximum attenuation decreases from 0.24% to 0.10%, and the phase difference is less than −0.5°. Moreover, the experimental results of the geomagnetic dynamic measurements show that the dynamic compensated data are mostly close to the real geomagnetic field values. In addition, the standard deviation errors are reduced from 95.30/277.35/108.51 nT to 3.41/2.36/2.75 nT in three geomagnetic vector components. The results of this work show the ability of dynamic measurement accuracy improvement of fluxgate magnetometers and are useful for geomagnetic dynamic measurement and related applications.
1. Introduction
Dynamic magnetic measurement can be applied to geological structure analysis, resource exploration, magnetic anomaly detection, geomagnetic navigation, and other fields and is usually realized by attaching to a mobile carrier [1,2,3]. The three-axis fluxgate magnetometer is the main sensor for mobile magnetic measurement. Its measurement accuracy is key for magnetic measurement and its applications. The error of the magnetometer consists of static measurement error and dynamic measurement error. The existing error calibration and compensation methods for the three-axis fluxgate magnetometer are all established for static measurement errors [4,5,6,7], including scale factor error, zero bias error, and nonorthogonal error, etc. For static magnetic measurement, the measured magnetic signal is in a relatively stable state and can be considered as an approximately time-invariant “static signal”. Moreover, the existing static compensation methods can realize error correction and complete restoration of the real signal well [8].
However, when the fluxgate magnetometer is in the mobile measurement state, the magnetic field input induced by its sensitive axis changes dynamically with time. Due to the limitation of the magnetometer’s sensitive materials, magnetic core structure, signal conditioning circuit, and other reasons [9,10,11], the wording frequency band of the magnetometer has a certain range and cannot completely cover all the frequency components in the dynamic input magnetic field, resulting in dynamic measurement error. A dynamic error is a function of time and varies with the frequency of the input signal, which cannot be corrected by traditional static compensation methods and reduced by the dynamic compensation method. At present, dynamic compensation methods are mainly aimed at pressure sensors, temperature sensors, and acceleration sensors, while dynamic error compensation for fluxgate magnetometers is still in a blank [8,12,13,14,15,16].
To solve this problem, a series dynamic compensator based on system identification is constructed in this paper, and a hybrid optimization method of the genetic algorithm (GA)-simulated annealing algorithm (SA) is proposed to solve the model parameter optimization problem of the dynamic compensator [17,18,19]. The hybrid optimization method cannot only expand the search scope effectively and improve the search efficiency, but also can avoid the problem that the genetic algorithm easily falls into the local optimum. Finally, the dynamic compensator model is established through the parameters determined by the hybrid optimization algorithm, and the dynamic error compensation of the fluxgate magnetometer is realized.
2. Materials and Methods
2.1. Construction of the Dynamic Compensator for the Fluxgate Magnetometer
2.1.1. System Identification for the Fluxgate Magnetometer
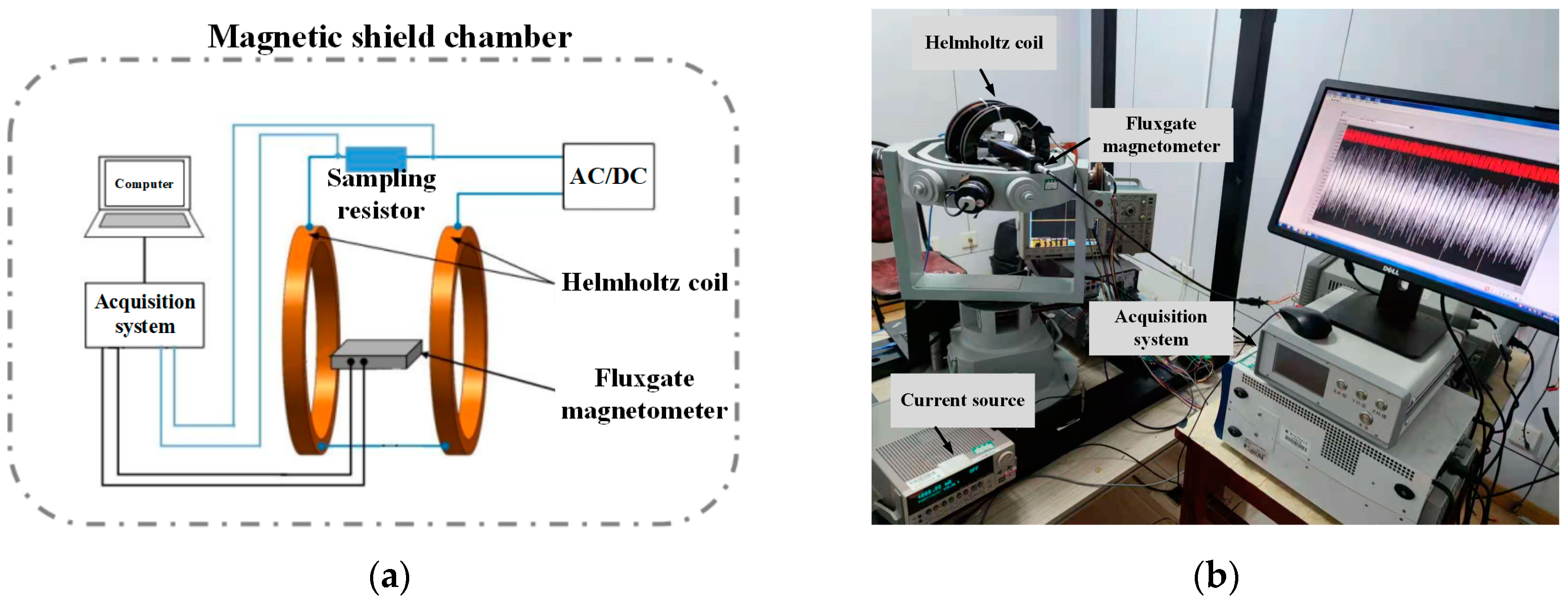
The dynamic characteristics of the fluxgate magnetometer are tested, and its model order is determined first. The sketch diagram of the test system and the photo of the real system with the experimental apparatus is shown in Figure 1. The test system mainly consists of two parts: a magnetic field generation module (excitation signal) and a signal acquisition module (excitation and response signal acquisition). The whole system is located in the magnetic shield chamber, which can effectively reduce the influence of magnetic noise such as the geomagnetic field and environmental electromagnetic interference on the dynamic characteristics of the magnetic sensor test. The magnetic field-generating module is mainly composed of a Helmholtz coil, an AC-DC current source, and a precision resistor. By applying AC-DC current to the coil through the AC-DC current source, an alternating/constant magnetic field can be generated inside the coil as the measured signal, namely, the input signal of the magnetic sensor. The signal acquisition module is mainly composed of a PXIe acquisition card, which is responsible for collecting the voltage at both ends of the precision sampling resistor and the output voltage of the magnetic sensor. By precisely sampling the voltage at both ends of the resistor, the current flowing through the coil can be calculated, and the magnetic field generated by the coil can be obtained. Similarly, by collecting the output voltage of the magnetic sensor, the output magnetic field of the magnetic sensor can be calculated according to the conversion coefficient of the magnetic sensor.
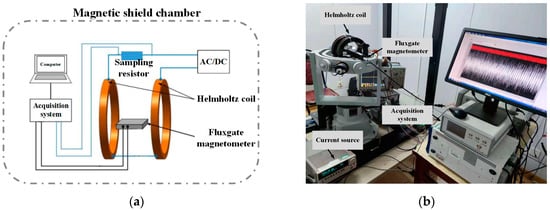
Figure 1.
Dynamic characteristic test system for the magnetometer: (a) sketch diagram of the system; (b) photo of the real system with experimental apparatus.
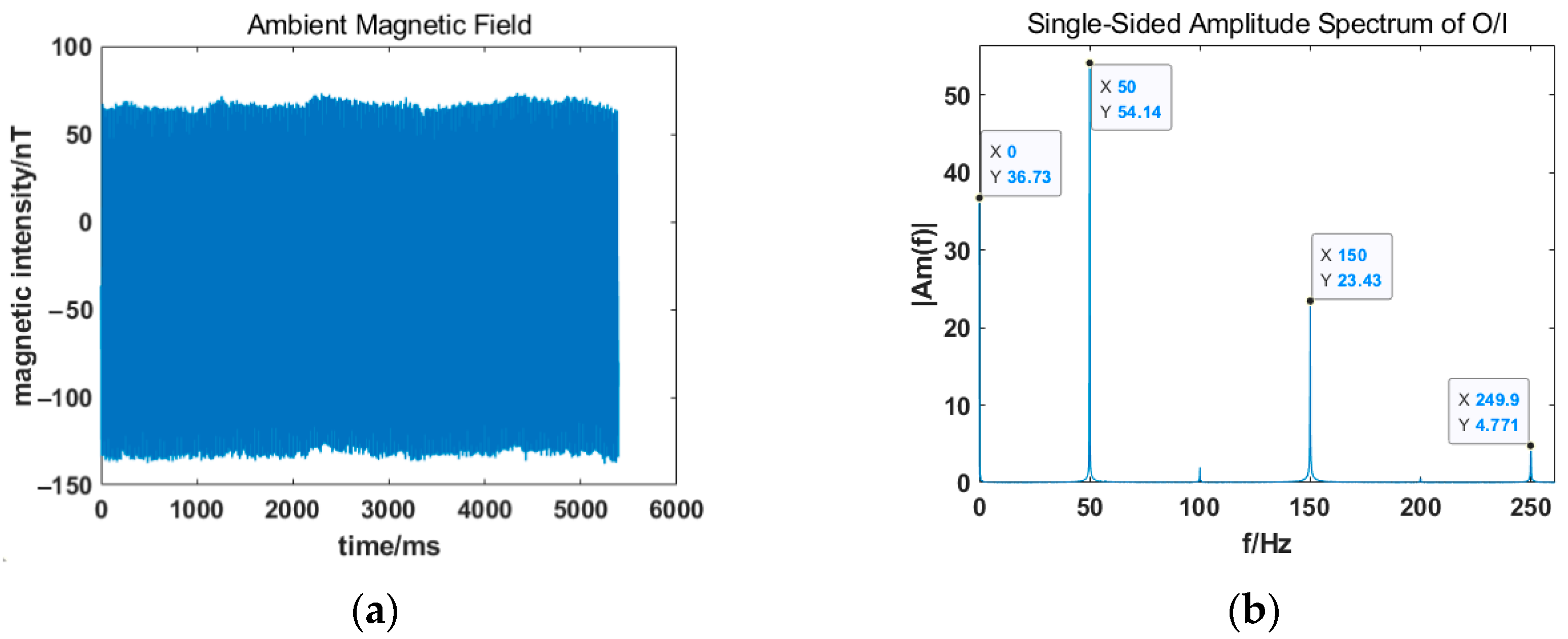
Before the dynamic response test and further compensation for magnetometer, the ambient magnetic field of the magnetic shield chamber must be measured [20], and magnetic noise influence must be reduced. Based on the closure of the shield chamber, the magnetometer is placed in the unenergized coil. The magnetic noise in the chamber is tested and the results obtained are shown in Figure 2.
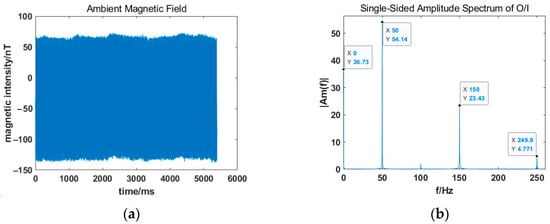
Figure 2.
Ambient magnetic field of the magnetic shield chamber: (a) time domain diagram; (b) single-sided amplitude spectrogram.
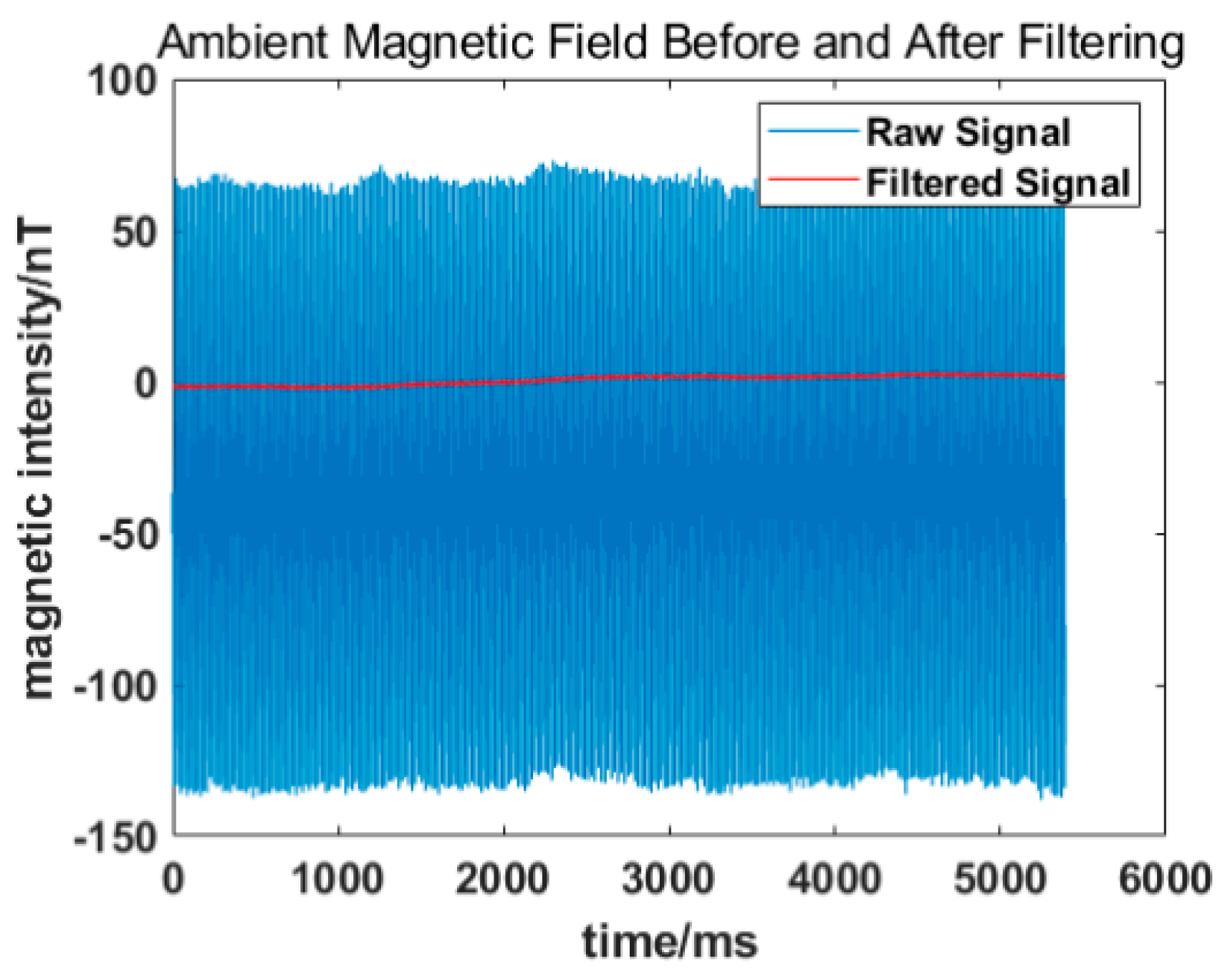
It can be seen from the time and frequency domain diagram that the average magnetic bias of the environment is −36.73 nT, and the peak-to-peak value is 215.29 nT. In addition, there are also three main interference signals of 50/150/250 Hz in the chamber which should be filtered. Therefore, a Butterworth low-pass filter is utilized to filter out the noise in the frequency band above 50 Hz and eliminate the alternating magnetic field interference in the ambient magnetic field. Furthermore, the signal is translated according to the DC magnetic field bias. The filtered ambient magnetic field of the chamber is shown in Figure 3, and the comparison of the ambient magnetic field before/after filtering is shown in Table 1.
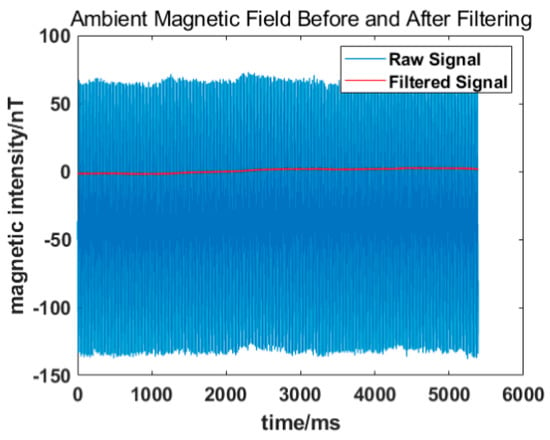
Figure 3.
Ambient magnetic field of the shield chamber before/after filtering.

Table 1.
Comparison of the ambient magnetic field before/after filtering.
From the comparison results, it can be seen that the ambient magnetic noise has been significantly reduced after the low-pass filter so that further tests and experiments for system identification can be carried out with higher precision.
The frequency characteristic curve of the magnetometer can be obtained by changing the frequency of the magnetic field while keeping the amplitude of the magnetic field unchanged [21]. In order to obtain the response signals of the magnetometer under magnetic fields of different frequencies, the current output frequency of the current source is gradually increased from 0.01 Hz of the lower frequency to 240 Hz of the higher frequency. Thus, magnetic fields of different frequencies are generated in the coil as the input magnetic field of the magnetometer.
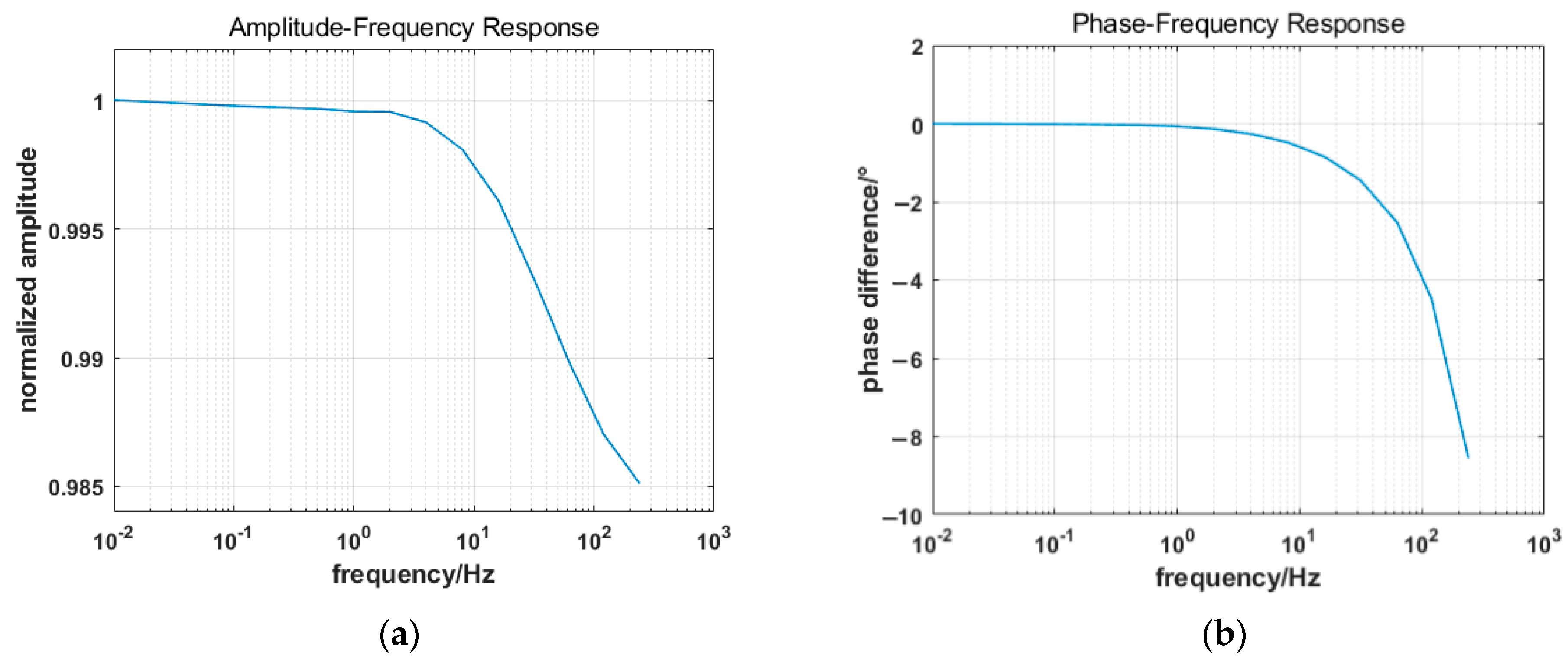
The amplitude–frequency characteristic curve and phase–frequency characteristic curve of the magnetometer are drawn according to the test results, as shown in Figure 4.
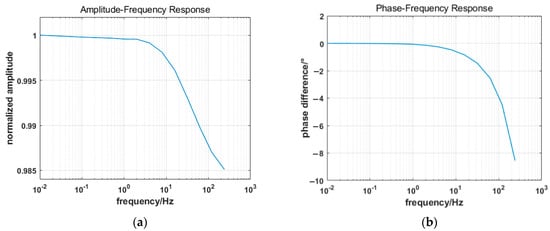
Figure 4.
Amplitude–frequency and phase–frequency characteristic curves of the fluxgate magnetometer: (a) amplitude–frequency characteristic curve; (b) phase–frequency characteristic curve.
It can be seen from Figure 4 that when the input magnetic field frequency increases, the output amplitude of the magnetometer decreases continuously, the amplitude attenuation becomes more and more serious, and the dynamic measurement error increases continuously. The time delay and phase difference between the output and input signals of the magnetometer are also increasing. In the test frequency band (0.01~240 Hz), the amplitude attenuation of the magnetometer is from 2% to 1.49%, which represents a 10–745 nT measurement error in the geomagnetic background field (average of 50,000 nT). Moreover, the maximum phase difference is −8.5508°. In Figure 4, the amplitude/phase–frequency characteristic curves of the magnetometer are consistent with the amplitude/phase–frequency characteristic curves of the first-order sensor [20]. Thus, the input and output data of the system are utilized to model the fluxgate magnetometer based on the system identification method.
The equivalent transfer function of the first-order sensor system is expressed as [12]:
In Equation (1), is the system time constant.
Equation (1) needs to be converted into a difference equation since the data of the sampling system are discrete. The transfer function in the S-domain is converted to a discrete function in the Z-domain by bilinear Z-transformation, and then, the difference equation is obtained:
In Equation (2), k is the time of the discrete system, and T is the sampling period of the discrete system. y(k) and x(k) represent the output and input signals at the time k, respectively.
Thus, the system model of the magnetometer is established and provides input signals as the previous step of the dynamic compensator.
2.1.2. Principle and Modeling of Dynamic Compensation
The dynamic characteristic compensation of the fluxgate magnetometer is to connect a dynamic characteristic compensation linked to the output end of the current sensor system. Thus, a new compensation synthesis system is formed with the current system. The goal of compensation is to reduce the dynamic error between the output of the whole compensation synthesis system and the measured signal so as to improve the dynamic characteristics of the fluxgate magnetometer. The dynamic characteristic compensation principle of the fluxgate magnetometer is shown in Figure 5.

Figure 5.
Dynamic characteristic compensation principle of the fluxgate magnetometer.
Where, x(t) is the measured signal, namely, the input signal of the fluxgate magnetometer, and y(t) is the output signal of it. After dynamic compensation, the output signal y(t) of the fluxgate sensor is u(t). The dynamic compensation link expands the working frequency band of the magnetometer, which reduces the amplitude attenuation and phase difference in the magnetometer to the measured signal. Finally, the output signal u(t) through the magnetometer and the dynamic compensation link is closer to the measured signal x(t).
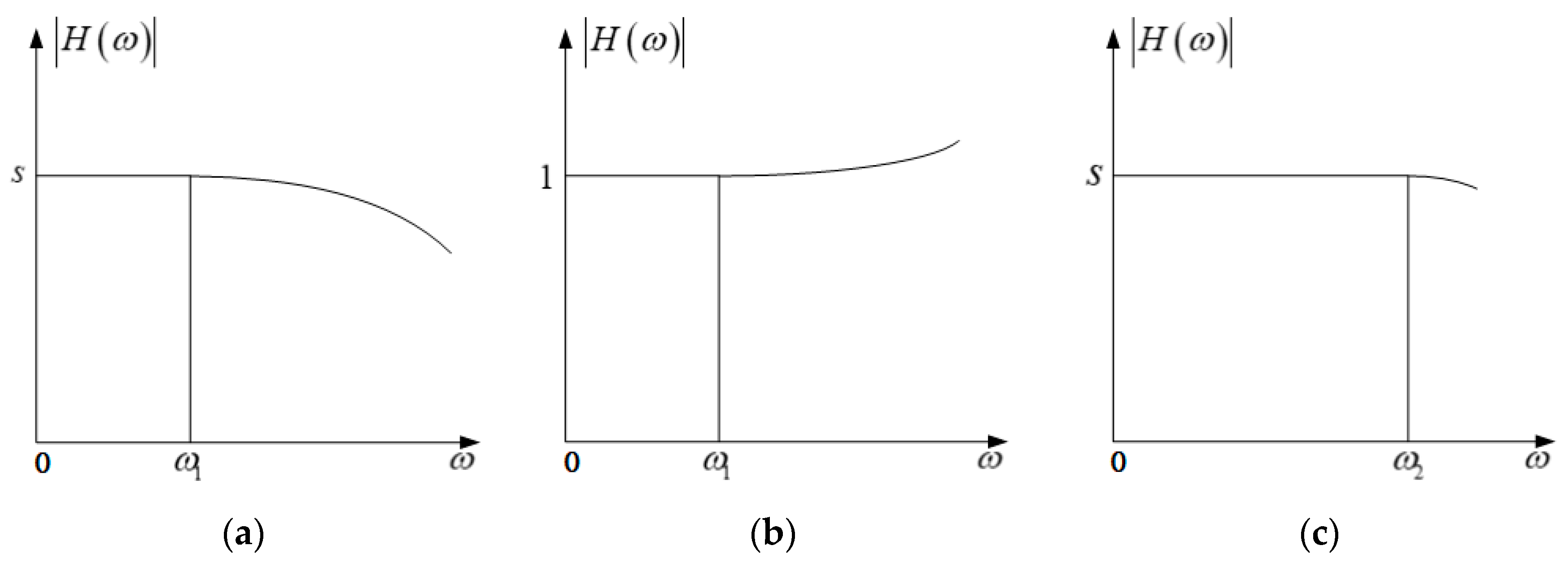
The amplitude–frequency response curve of the magnetometer system before and after dynamic compensation is shown in Figure 6. Before compensation, the effective working frequency band of the magnetometer is ω1. Through a series dynamic compensation link, the effective working frequency band of the compensation synthesis system is extended to ω2 so that the components in a larger frequency range of the measured signal can be collected, and the dynamic distortion of the output signal can be reduced.
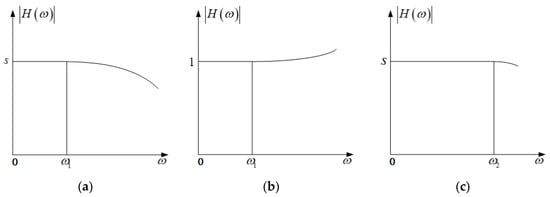
Figure 6.
Diagram of amplitude–frequency characteristic curves before and after dynamic compensation: (a) magnetometer; (b) compensation link; (c) after compensation.
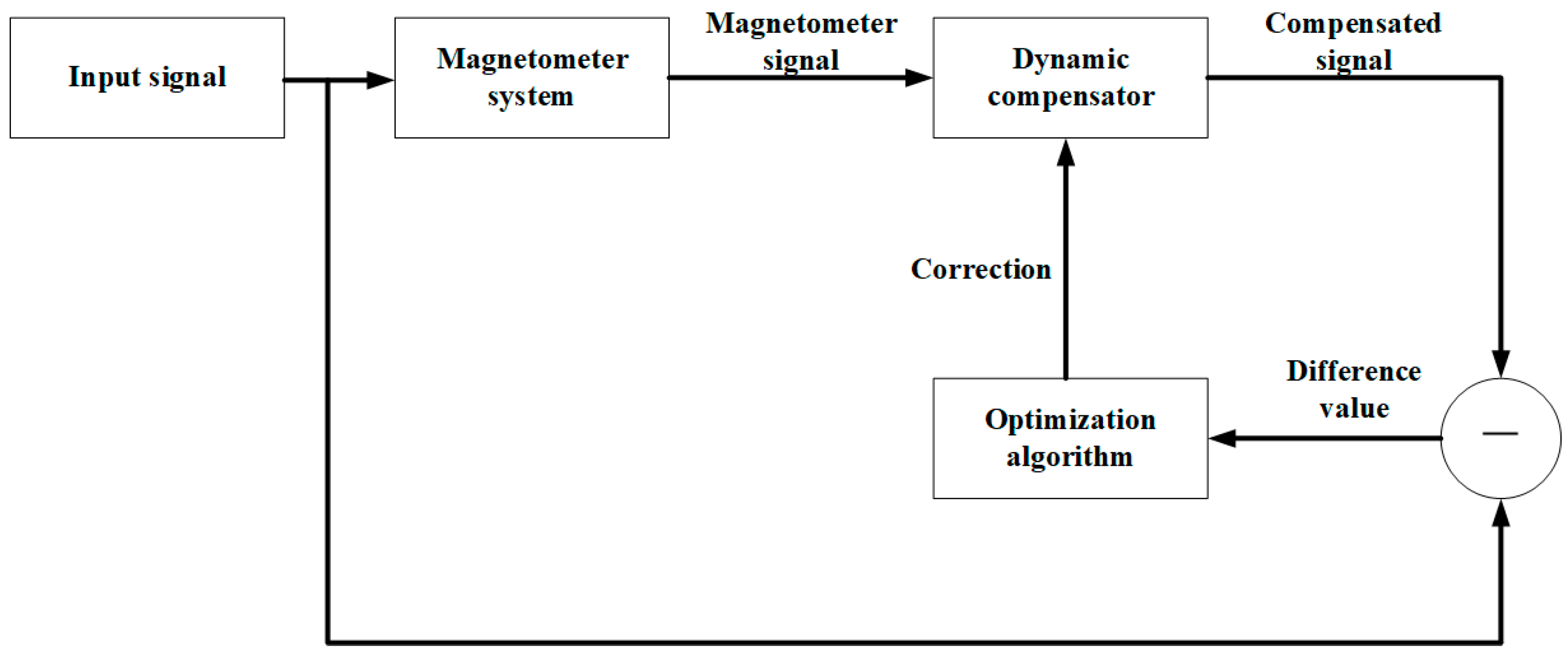
Considering that the factors and mechanisms affecting the dynamic characteristics of the magnetic sensor are complex, this paper selects system identification and modeling methods to solve the parameters of the dynamic compensator. The dynamic response of the sensor is taken as the input of the dynamic compensator, and the measured signal is taken as the output of the dynamic compensator. The parameters of the dynamic compensator are solved by the optimization algorithm to realize the modeling of the dynamic compensator. The basic schematic diagram is shown in Figure 7.
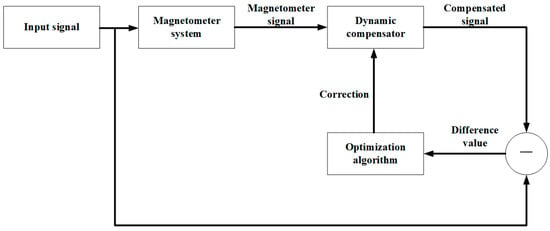
Figure 7.
The basic principle of the dynamic compensation solution.
In a sampling signal system, the dynamic characteristics of a discrete linear system can be described by the following difference equation [22]:
where u(k) represents the output of the dynamic compensator at time k, and u(k − i) represents the output of the dynamic compensator at time k − i. Similarly, y(k) and y(k − j), respectively, represent the input of the dynamic compensator at times k and k − j, that is, the output of the magnetometer at the corresponding time. m and n represent the order, and e(k) represents noise. The output of a dynamic compensator depends not only on its input sequence, but also on the historical sequence of its output.
Convert Equation (3) to a vector form:
where A = [−a1, −a2, … −am, b0, b1, … bn] is the coefficient vector; Uk = [u(k − 1), …, u(k − m), y(k), …, y(k − n)]T contains the output and input sequences of the dynamic compensator; and e(k) is noise.
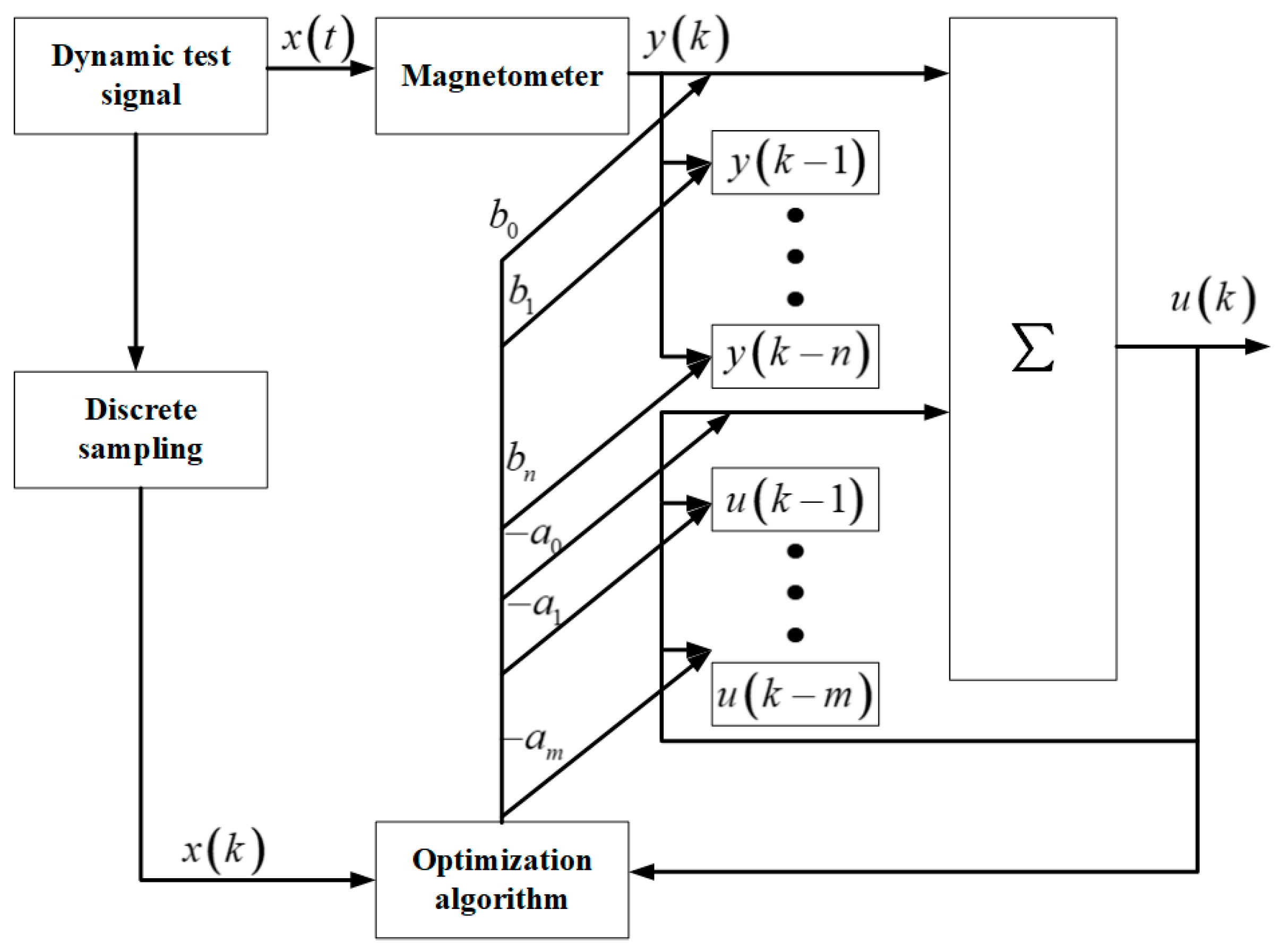
The designed block diagram of the compensator is shown in Figure 8.
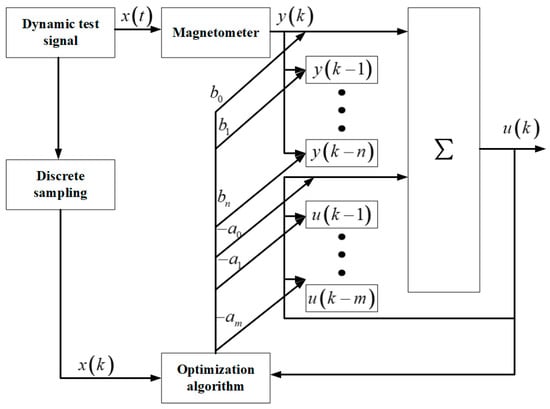
Figure 8.
Block diagram of the dynamic compensator.
The dynamic test signal x(t) is measured by the magnetometer output signal y(k), which is also used as the input of the dynamic compensator. After dynamic compensation by the dynamic compensator, the output is u(k). The dynamic test signal x(k) is x(t) after discrete sampling. The purpose of the dynamic compensator is to continuously optimize u(k) through an optimization algorithm and gradually approximate the dynamic test signal x(k) after discrete sampling. Finally, the output data after compensation is infinitely close to the input dynamic test signal of the magnetometer to realize the non-distortion reproduction of the input signal of the magnetometer to the maximum extent. This requires the minimum difference between the output u(k) of the dynamic compensator and the input signal x(k) of the magnetometer, that is, the minimum value of the objective function shown in Equation (5).
where N is the number of signals in the dynamic test signal sequence.
Thus, the design of the dynamic compensator of the magnetometer is transformed into an optimization problem of the objective function. Parameter A in Equation (4) is solved by an optimization algorithm to minimize the objective function shown in Equation (5), that is, to complete the design of the dynamic compensator of the magnetometer.
2.2. GA-SA Hybrid Optimization Algorithm
GA is an optimization algorithm established by Professor Holland of the University of Michigan and influenced by Darwinian evolution [23,24]. By simulating the process of biological heredity, biological individuals can be selected and eliminated according to the rule of “survival of the fittest” in biological heredity. Finally, the best individual is obtained. However, in the process of population evolution, variation is only a small probability event. The population has limited ability to explore new solution space, which can easily to fall into the local optimal and be unable to obtain the global optimal solution.
SA is an optimization algorithm proposed by Professor Kirkpatrick with reference to the Metropolis criterion, based on the recognition of the similarities of combinatorial optimization and solid annealing [25]. The simulated annealing algorithm simulates the annealing process of a solid substance in physics and randomly searches for the global optimal solution of the objective function in the solution space by combining probabilistic jump characteristics. However, in order to obtain the optimal solution to the problem, a relatively high initial temperature is generally set during initialization, and a relatively slow cooling rate and a relatively low-end temperature are set during de-warming, resulting in a long execution time of the algorithm. Moreover, the simulated annealing algorithm keeps only one possible solution in the iterative process, which creates a lack of historical information storage and fault tolerance.
Considering the respective problems of the above two algorithms, this paper combines the two algorithms for hybrid optimization and proposes the hybrid optimization strategy of the genetic algorithm-simulated annealing algorithm (GA-SA): the defect of GA falling into the local optimum can be avoided by utilizing the probabilistic jump of SA, which changes time and tends to zero in the search process. In the evolutionary process of GA, the population is large and diverse, and the cross mutation can further increase the diversity of the population and solve the shortcomings of the SA iterative process of lack of historical information and fault tolerance [24,25]. Finally, the full-space search capability of the hybrid algorithm can be improved to ensure that the output solution is globally optimal to the greatest extent.
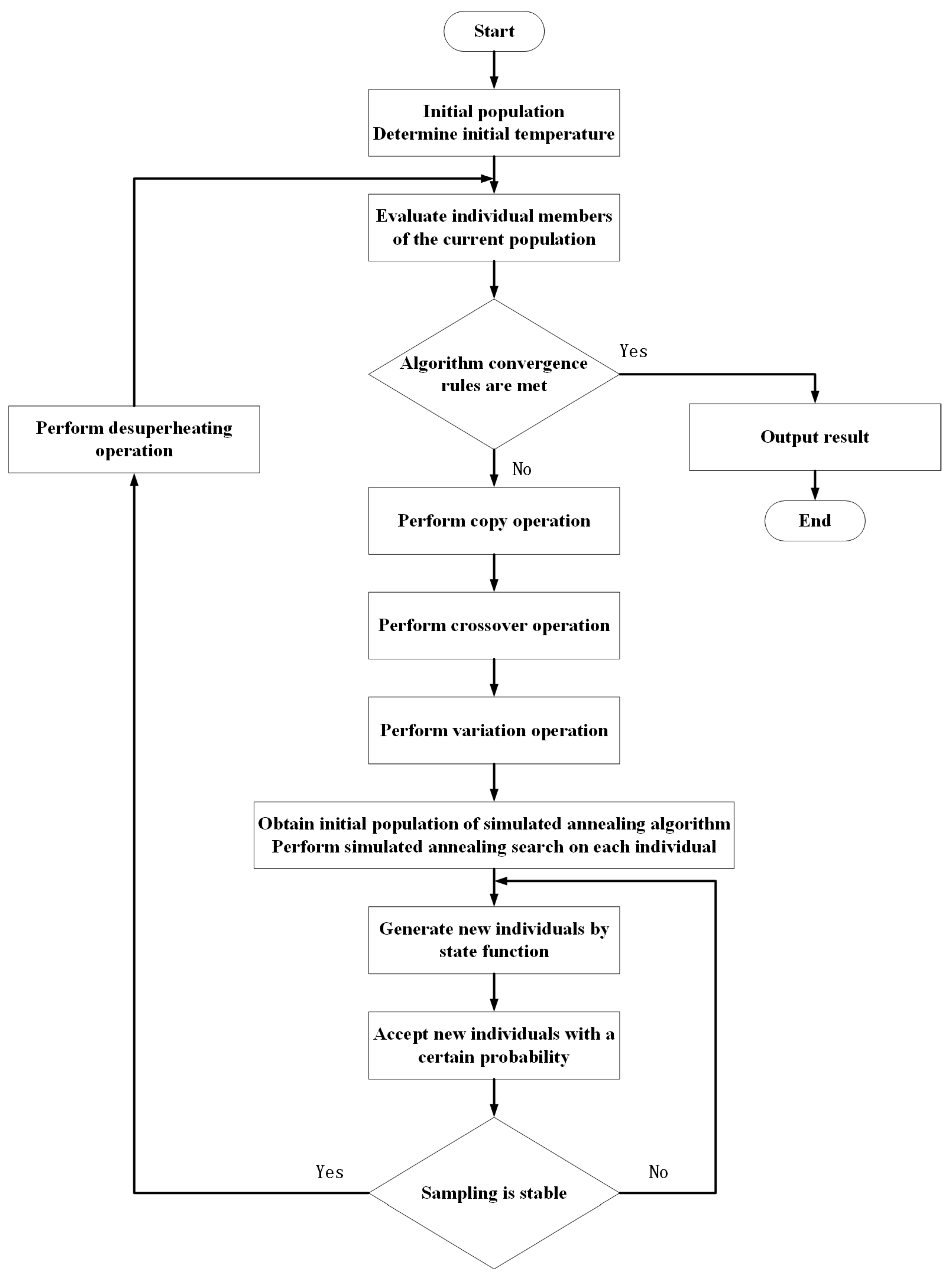
Therefore, the objective function in Equation (5) is taken as the fitness function of the GA-SA algorithm and is iteratively updated to solve parameters in the dynamic compensator. The algorithm flow is shown in Figure 9.
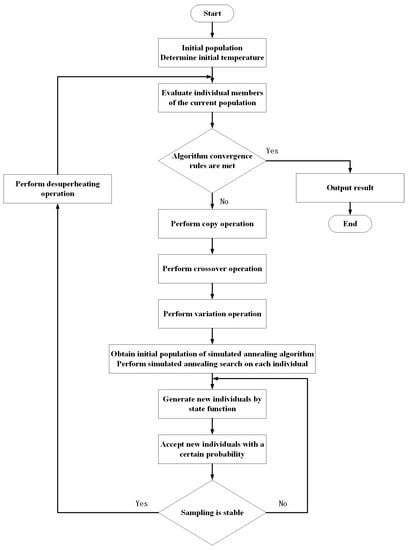
Figure 9.
Flowchart of the GA-SA hybrid optimization algorithm.
The specific steps of the algorithm are as follows:
- Initialization: the simulation process of biological evolution.
For this problem, each feasible solution (Parameter Ai) is represented as an individual, and different individuals constitute the population, which is the set of feasible solutions for the current problem, expressed as:
where n represents the population size, namely, the number of individuals in the population. According to experience, in the initialization process, set the population size n = 100; that is, generate 100 possible solutions randomly (Parameter A, where the value range is [−10, 10]). Generate the initial population and set the crossover probability pc = 0.7, the variation probability pm = 0.05, the initial temperature T0 = 100 °C, the maximum number of iterations tmax = 5000, the threshold value th = 0.001, and the annealing temperature attenuation parameter α = 0.85.
- 2.
- Calculation of the fitness function:
Equation (5) is utilized to calculate the fitness function of each Ai in the population, and the optimal fitness of individuals in the population is obtained.
- 3.
- Determine whether convergence criteria are met:
Determine if the optimal fitness is less than the threshold th or the number of iterations reaches the maximum number tmax. If ‘Yes’, output the result. If ‘No’, keep the algorithm proceeding.
- 4.
- Perform replication, crossover, and variation operations on individuals. Generate the next generation population.
(1) Replication: The purpose of replication is to retain excellent individuals in the evolutionary process of the population so that the population converges in the direction of the optimal solution. The gambling wheel selection method not only ensures that excellent individuals have a greater probability of being selected, but also allows individuals with poor fitness to have a chance of being selected so as to maintain the diversity of the population. The specific implementation is as follows:
First, the probability function pi of each Ai is calculated according to the fitness function.
In this way, each individual Ai forms a unit interval of length 1 according to the probability function pi, and the interval length represented by each individual Ai is equal to its probability function pi, generating random numbers r between [0, 1]. According to the interval where the random number is located, the individuals represented by the interval are selected to be copied and retained by the next generation. If the random number r is satisfied with , select individual Ai to copy into the next generation population.
(2) Crossover: The purpose of crossover is to pass the good genes in the population to the next generation and generate a new generation of individuals through information exchange to maintain the diversity of the population. In order to avoid excessive damage to excellent individuals caused by the crossing process, the single-point crossing method with the weakest strength is selected as the crossing method, which is implemented as follows:
The individual is encoded in binary to generate a binary string. In a crossover operation, a number pair (i,j), i, j∈[1, n] in the range of the population size is randomly generated. That is, the binary strings of individuals Ai and Aj are selected for crossover operation; then, an integer m within the length range of the binary string is randomly generated, and the mth point in the binary string is selected as the intersection point. Finally, a random number r′∈ [0, 1] is generated for comparison with the crossover probability pc. If the random number r′ is less than the crossover probability pc, the crossover will be carried out, and the coding bits after the crossover point of the two individuals will be exchanged to generate the next generation of individuals. If the random number r′ is greater than the crossover probability pc, no crossover is performed. For example, when m = 4, the change in binary strings Ci and Cj of individuals Ai and Aj is shown in Equation (8).
where and represent the binary strings of the kth generation of individuals Ai and Aj. and represent the binary strings of the k + 1th generation of individuals Ai and Aj.
(3) Variation: The purpose of variation is to maintain the diversity of the solution set, and the process is basically the same as crossover. In a variation operation, a number i∈[1, n] within the range of the population size is randomly generated; that is, a binary string of individual Ai is selected for variation operation. Then, randomly generate an integer m in the binary string length range. The mth point in the binary coding string is selected as the variation point. Finally, generate a random number r″∈[0, 1], and compare it with the variation probability pm. If r″ is less than the pm, the variation point is inversely calculated. On the contrary, there is no variation. For example, when m = 7, the change process of the binary coded string Ci of individual Ai is shown in Equation (8).
and represent the binary strings of the kth generation and k + 1th generation of individual Ai.
- 5.
- Simulated annealing searches are performed on each individual of the population.
- Take the first individual A1 in the population as an example:
- (1)
- Generate individual new states: where y is a zero random number with a bilateral symmetric distribution, and UB and LB are the upper and lower bounds of the solution range. For the current difference equation coefficients, take −10 and 10, respectively.
- (2)
- If , accept the new state of the individual, namely, . Otherwise, deny updating the new state.
- (3)
- Determine whether the Metropolis criterion is met. If ‘Yes’, go to Step 6. Otherwise, repeat Step 5.
- 6.
- Annealing:
, set k = k + 1
- 7.
- Repeat Step 2 and Step 3 until the algorithm convergence rules are met and the current result is outputted.
3. Simulation and Signal Test
In order to verify the effect of the dynamic compensator proposed in the previous section based on the GA-SA algorithm for the hybrid optimization solution, a simulation and an experiment were carried out, respectively.
3.1. Simulation Results and Discussion
In Section 2, the dynamic characteristics of the fluxgate magnetometer were tested, and the system was determined to be a first-order model. The first-order transfer function is obtained by identifying the test data through the Simulink system, and the difference equation of the magnetometer system is determined according to Equation (2):
The dynamic response of the magnetometer is set as the input of the dynamic compensator, and the measured signal is set as the target output of the dynamic compensator. The parameters of the dynamic compensator are solved by the optimization algorithm so as to realize the solution of the dynamic compensator. Since the step signal contains relatively rich frequency components, the step response signal of the magnetometer is selected as the input of the dynamic compensator, and then, the parameters of the dynamic compensator are solved. In this way, the problem that the dynamic compensator obtained by selecting the dynamic response signal of a single frequency as the input is only compensated for the signal of a single frequency is avoided.
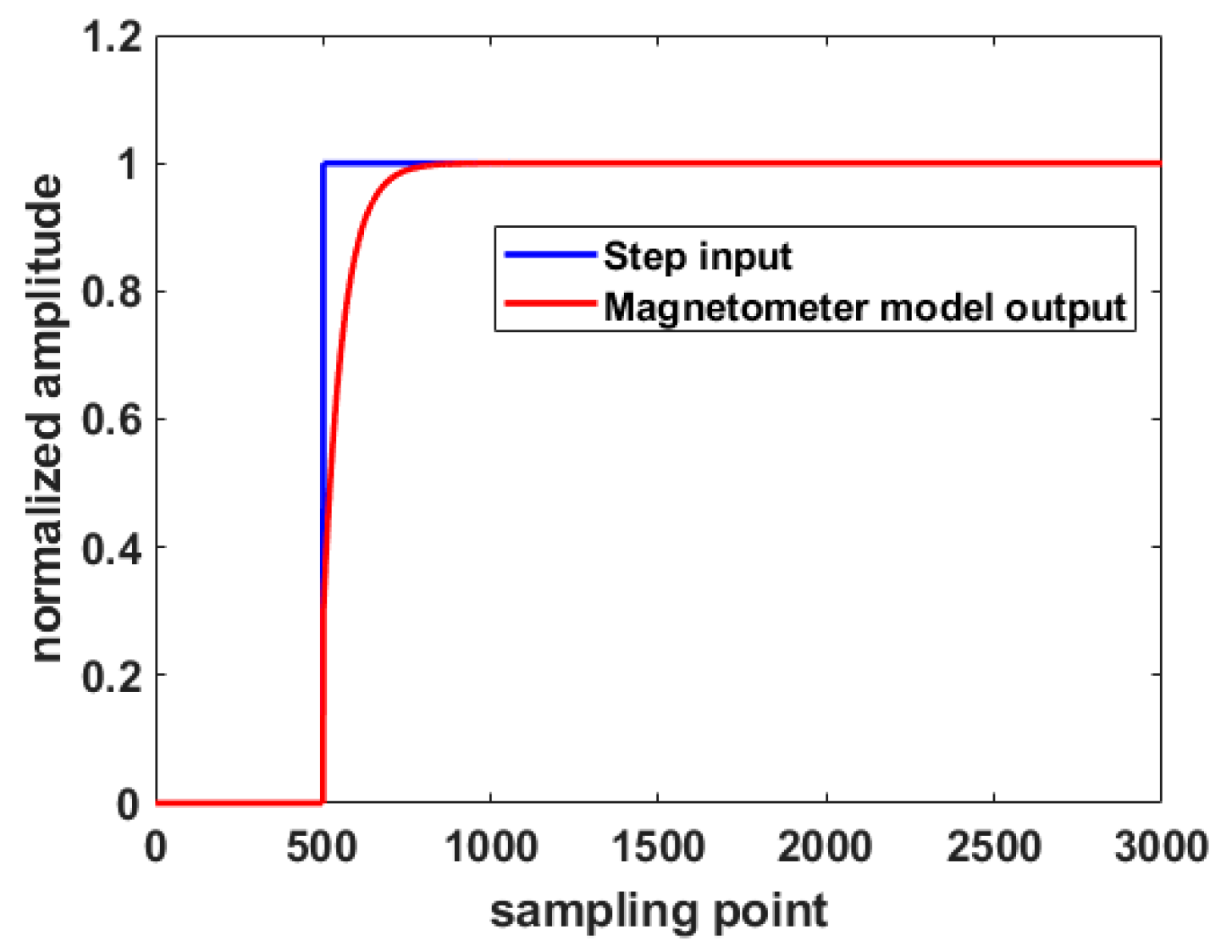
In Simulink, the input signal of the magnetic sensor is set as a step signal with an amplitude of 1. The input signal generates a step at 25 ms, and the simulation time is 150 ms. The step response curve of the magnetometer model is shown in Figure 10. The response time is 10.70 ms. It means that the output of magnetometer model reaches 98% of the steady-state value after 10.70 ms after the step of the input signal, which has a certain lag.
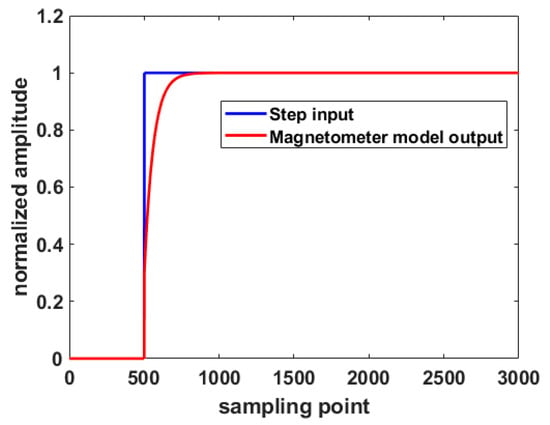
Figure 10.
Step response curve of the magnetic sensor model.
3.1.1. Comparison of Compensation Effects of Different Order Dynamic Compensators
In order to explore the relationship between the order of the dynamic compensator and the dynamic compensation effect, the dynamic compensator is set to different orders, respectively, the GA-SA algorithm is utilized to calculate the parameters of the dynamic compensator, and the compensation effects of the dynamic compensator for different orders are compared. The results are shown in Figure 11 and Table 2.
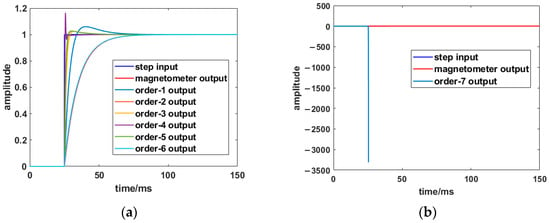
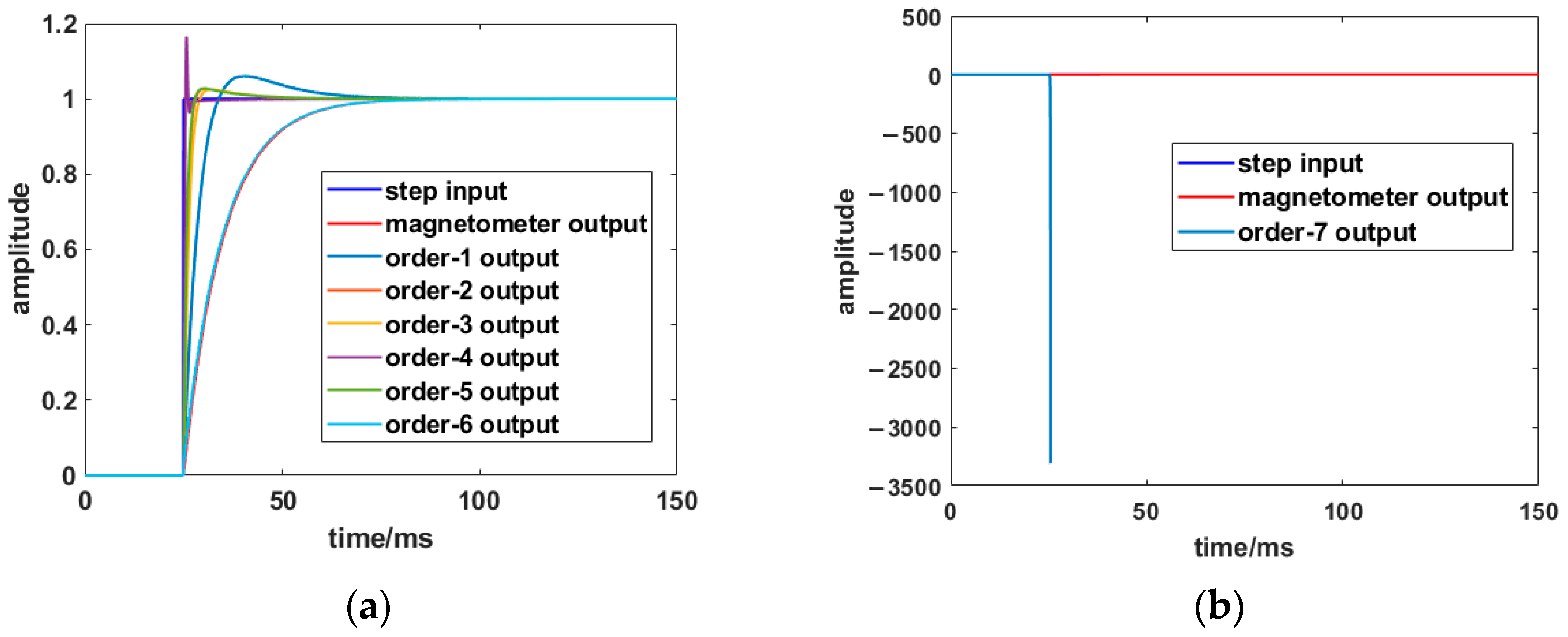
Figure 11.
Dynamic compensator compensation results for different orders: (a) order 1 to 6; (b) order 7.

Table 2.
Dynamic compensator’s performance for different orders.
It can be seen that the second-order dynamic compensator can shorten the response time from 10.70 ms to 1.95 ms, and no high overshoot is introduced, which is only 0.17%. The response time could also be reduced by the third-order dynamic compensator, but 32.39% overshoot is generated as well. Subsequently, with the increase in the order, the performance of the compensator deteriorates and completely diverges at the 7th order. Thus, the second-order compensator improves the response time and overshoot, and the output dynamic error after compensation is minimal.
3.1.2. Comparison of Compensation Effects of the Optimization Algorithm
In order to illustrate the improvement of the dynamic performance of the magnetometer by the hybrid optimization algorithm of GA-SA, GA, and SA, these three algorithms are, respectively, utilized to calculate parameters of the second-order dynamic compensator. Taking the step response of the magnetometer model as the input of the dynamic compensator and the step input as the ideal output of the dynamic compensator, different equations of the dynamic compensator can be obtained as follows:
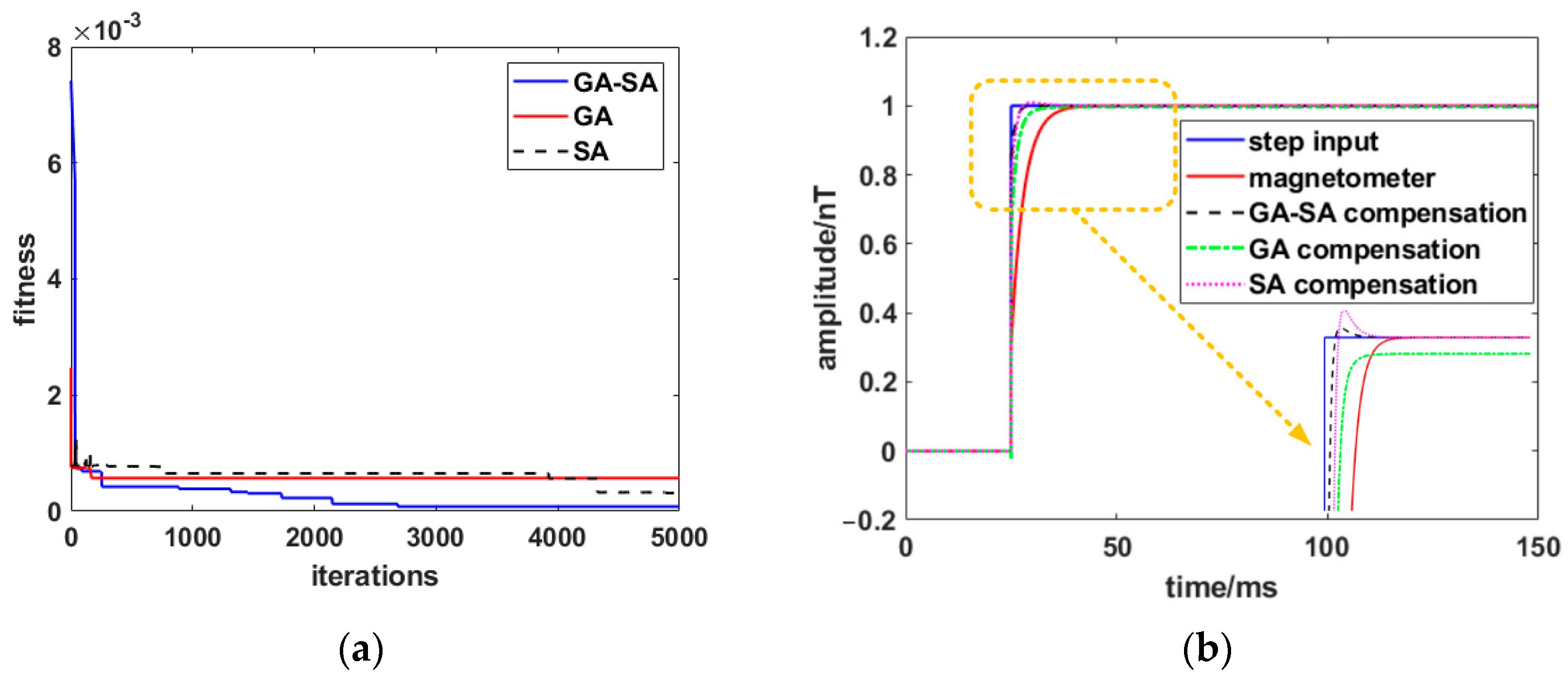
The simulation and comparison results are shown in Figure 12. As shown in Figure 12a, the fitness of the GA algorithm converges after 300 iterations, and the final fitness is higher than that of the SA and GA-SA algorithms. It falls into the local optimum too early and fails to obtain the global optimal solution, which is the shortcoming of the GA algorithm. The fitness of the SA algorithm converges slowly in the late stage and does not change in some iterations of 1000–4000, resulting in low efficiency and a long algorithm execution time. The GA-SA algorithm overcomes the problems of the above two algorithms. In the iterative process, it converges fast, has the lowest fitness and obtains the global optimal solution. As shown in Figure 12b, the GA-SA algorithm has the lowest fitness, so the output compensated by the GA-SA algorithm follows the step input the fastest, minimizing the dynamic error. The specific evaluation indicators are shown in Table 3.
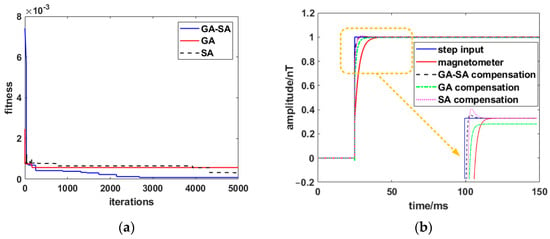
Figure 12.
GA, SA, and GA-SA algorithm simulation comparison: (a) fitness convergence curve; (b) compensated response curve.

Table 3.
GA, SA, and GA-SA algorithm performance comparison.
3.2. Standard Signal Test Results and Discussion
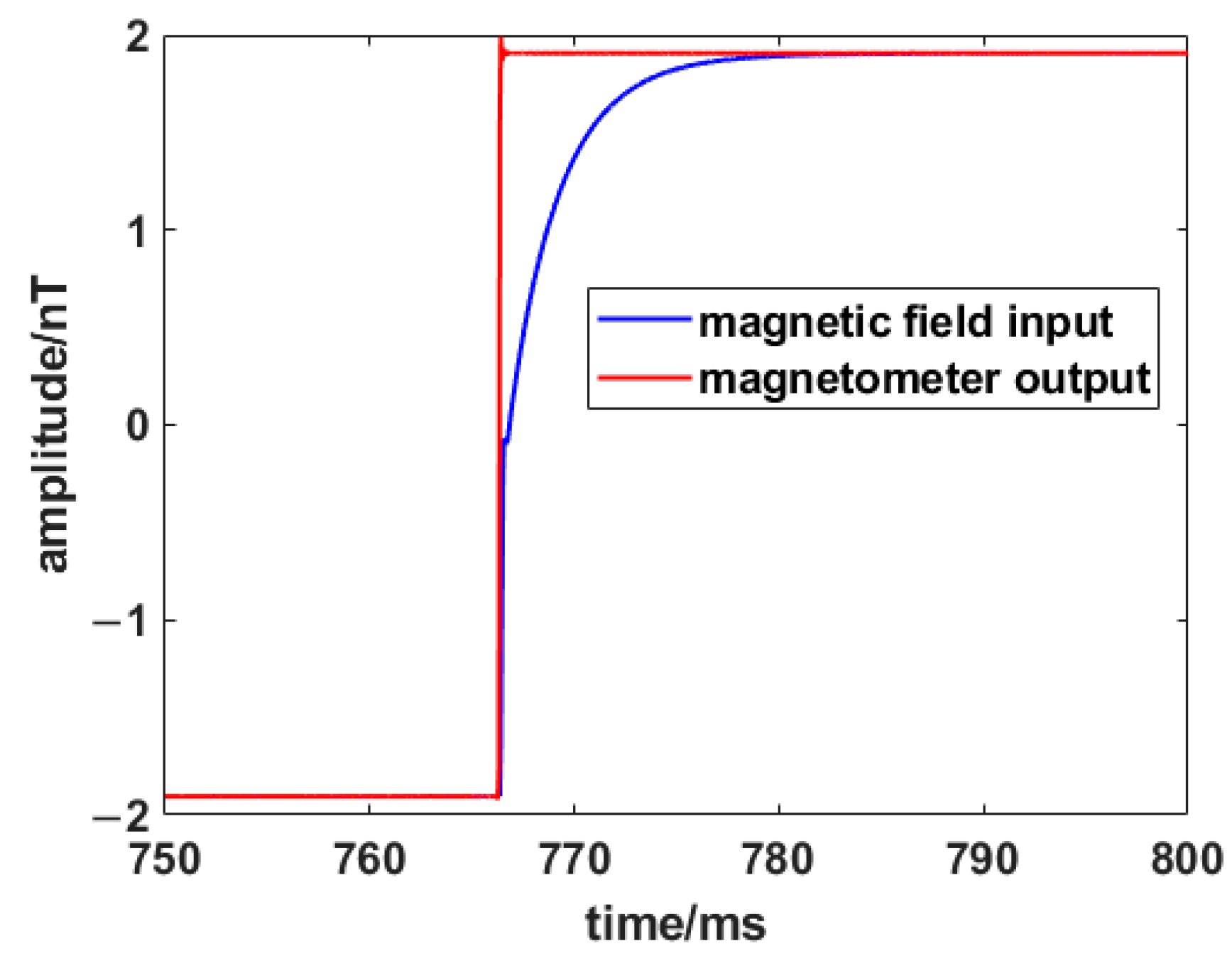
In order to further verify the actual effect of the dynamic compensator, the magnetometer dynamic characteristic test system set up in Figure 1 is utilized to sample test signals, and the parameters of the dynamic compensator are calculated for the fluxgate magnetometer used in this paper. The signal selected during the parameter calculation of the dynamic compensator is a rising edge of the square wave signal, as shown in Figure 13.
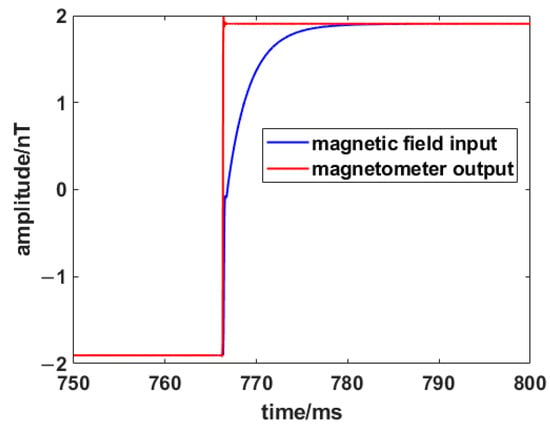
Figure 13.
Magnetometer input and output of the rising edge of the square wave.
3.2.1. Verification of the Step Magnetic Field Compensation Effect
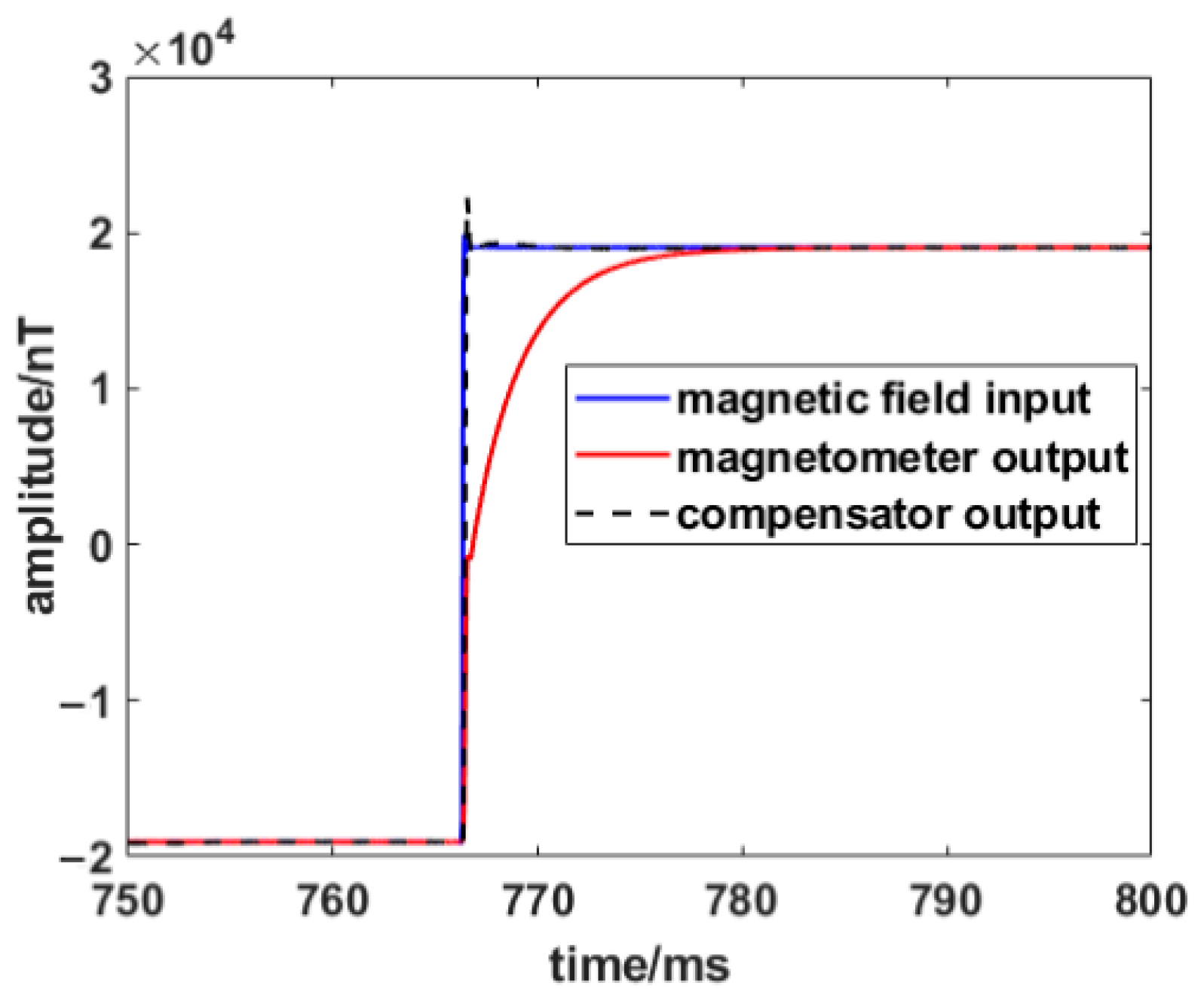
The dynamic compensator obtained from Equation (10) is utilized to compensate for the rising edge signal. The output signal after the dynamic compensator is shown in Figure 14. The time domain dynamic performance index of the magnetometer before and after the dynamic compensator is shown in Table 4.
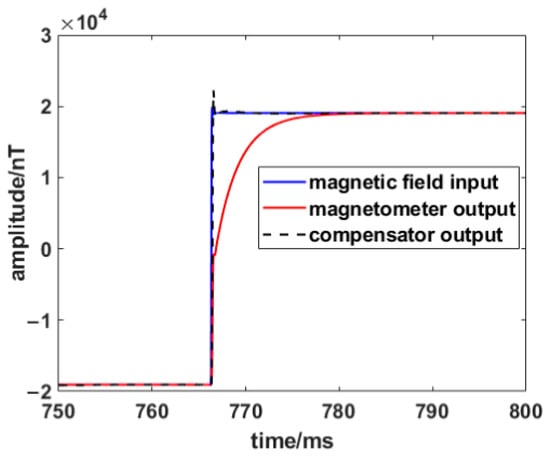
Figure 14.
Output of the fluxgate magnetometer after dynamic compensation.

Table 4.
Dynamic performance index of the magnetometer before/after dynamic compensation.
As shown in Figure 14 and Table 4, the response time is shortened from 10.91 ms to 0.63 ms (calculated by 2% steady-state error), and the response time is shortened to 5.5% of that before dynamic compensation. Although there is a small overshoot in the step, the compensated waveform is basically consistent with the input signal. In addition, the error of the compensator output is much less than the magnetometer output, which is from 22932.55 nT to 231.74 nT. It shows that the output signal can quickly follow the changes in the input magnetic field under the step response signal excitation, which is a typical system identification and compensation of the excitation signal. Since the step signal contains all the frequency components, the fast response result to the step input signal can prove the validity of the dynamic compensation method.
3.2.2. Verification of Different Frequency Sinusoidal Magnetic Field Compensation Effects
In order to further verify the compensation effect of the dynamic compensator on sinusoidal input magnetic fields with different frequencies, sinusoidal magnetic field signals with different frequencies are used as input signals of the magnetometer and the output signal of the magnetometer after the dynamic compensator is collected. A Fourier transform is performed on the output data of the magnetic sensor after the dynamic compensation, amplitude, and phase are extracted, and the amplitude is normalized. The amplitude–frequency and phase–frequency response curves of the magnetometer after dynamic compensation are obtained, as shown in Figure 15.
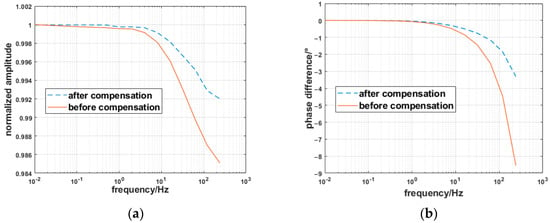
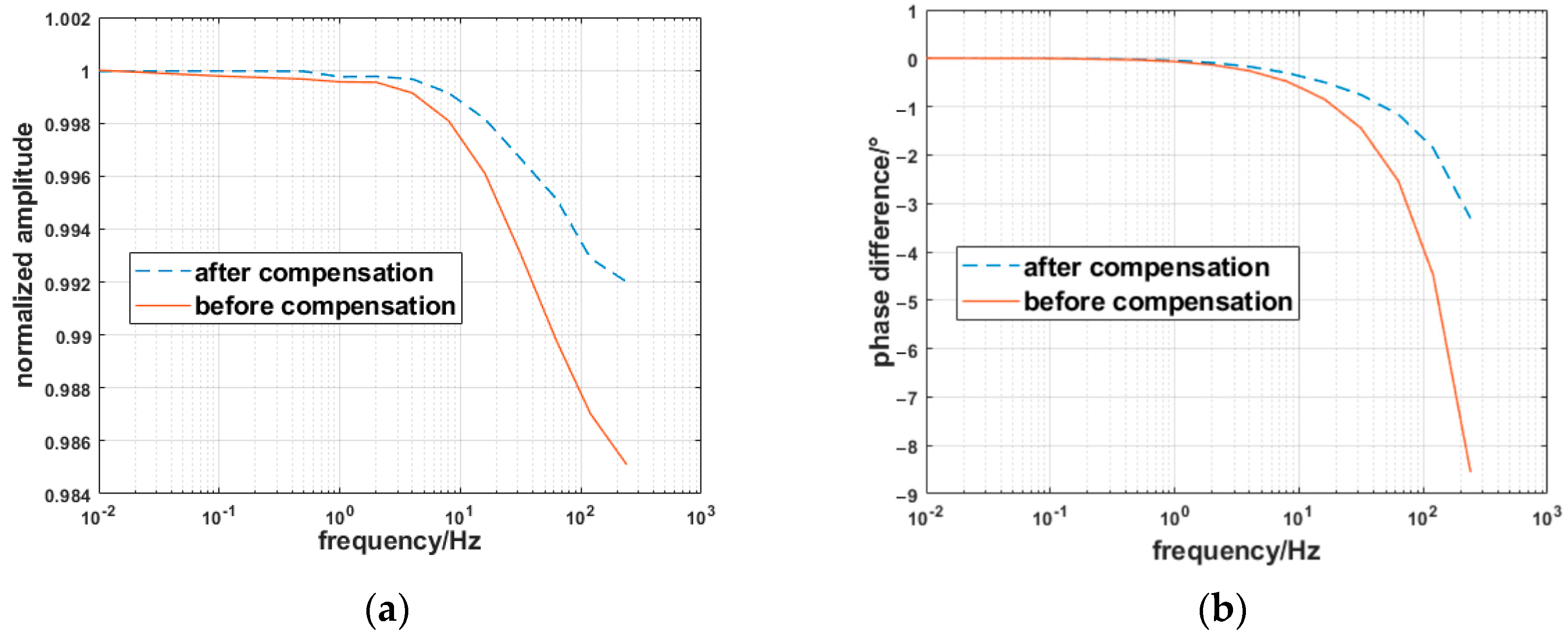
Figure 15.
Amplitude/phase–frequency response curves of the fluxgate magnetometer before/after dynamic compensation: (a) amplitude–frequency curves; (b) phase–frequency curves.
Figure 15 shows that, after dynamic compensation, the amplitude–frequency characteristic curve remains flat in the low-frequency range (0.01–4 Hz), the attenuation of amplitude is reduced based on the original, and the normalized amplitude is close to 1, consistent with the input amplitude. In the higher frequency band (4–240 Hz), the dynamic compensator plays a more obvious role in reducing the amplitude attenuation, which is a great improvement compared with before dynamic compensation, so its dynamic error will also decrease accordingly. The amplitude–frequency response improvement ratio is from 0.02% to 0.69%, which represents measurement accuracy improvements of 10–345 nT in the geomagnetic background field (average of 50,000 nT). Furthermore, the dynamic compensator improves the phase frequency characteristics of the magnetic sensor more obviously; the phase difference is reduced to less than half of the original, the time delay between the output and input signals is reduced, and the input magnetic field signal can be quickly responded to the change.
On the whole, the dynamic compensator improves the amplitude–frequency and phase–frequency response characteristics of the magnetometer, reduces the amplitude attenuation and phase delay of the magnetometer to the input signal to some extent, and achieves the effect of reducing the dynamic error.
4. Experiment and Discussion
In order to verify the effectiveness of the proposed method, a dynamic geomagnetic measurement experiment was carried out in an outdoor field with a stable geomagnetic environment. In the experiment, the magnetometer and inertial navigation system are combined to form a strap-down measuring system, which is mounted on the truss for dynamic measurement. Through the standard deviation of the geomagnetic vector dynamic measurement value and its comparison with the static measurement calibration value, the measurement accuracy and the effectiveness of the compensation method are verified. The procedure of the experiment is: (1) geomagnetic measurement system establishment; (2) geomagnetic field calibration; (3) dynamic measurement and compensation; and (4) compensated geomagnetic measurement value assessment.
4.1. Experimental Equipment and System
The designed strap-down geomagnetic vector measurement system is shown in Figure 16, and the installation details of the internal instruments are shown in Figure 16b.

Figure 16.
Strap-down geomagnetic dynamic measurement system: (a) overall system appearance; (b) internal system composition.
The system enclosure is made of nonmagnetic material (aluminum alloy). The internal system consists of a high-precision fluxgate magnetometer, a high-precision inertial navigation system, and a data acquisition terminal, which are respectively used to provide geomagnetic three-component measurement values, a high-precision strap-down system attitude angle and data information fusion acquisition, and packaged output.
During the experiment, the designed system slides back and forth on a designed truss, which is shown in Figure 17. The truss is 3 m × 1.5 m and is made of nonmagnetic material as well. The 1 mm eccentric wheel of the trolley on the truss is designed to make the dynamic characteristic of the measurement signal more significant.

Figure 17.
The designed experiment system and truss.
4.2. Experiment Process
4.2.1. Calibration of the Geomagnetic Background Field
As shown in Figure 18, the geomagnetic total field of the experiment area is calibrated by a proton magnetometer first, which is 48,845.53 nT. The single point stability of the geomagnetic field in this area is better than 1 nT, and the gradient is less than 2 nT, which ensures that this area is suitable for carrying out geomagnetic vector measurement experiments.

Figure 18.
The calibration of the geomagnetic field.
It is measured that the magnetic field stability of this area is reliable. Therefore, in order to obtain the calibration value of the geomagnetic vector in this area, static vector sampling is carried out in the front, middle, and back sections of the truss, respectively, to obtain three groups of geomagnetic vector measurement values, and the mean value is taken as the calibration value of the geomagnetic vector. The calibration vectors’ values are shown in Table 5. Bx is the north component of the geomagnetic field; By is the east component of the geomagnetic field; Bz is the vertical component of the geomagnetic field.

Table 5.
Geomagnetic vectors’ calibration values.
4.2.2. Geomagnetic Dynamic Measurement
After the measurement of the geomagnetic calibration value of the experiment area, the geomagnetic dynamic measurement is carried out by repeated sliding 10 times on the truss. During the dynamic measurement, the data acquisition terminal collects the sample data in real time and sends it to the upper computer for compensation and display. The real-time curve measurement by the upper computer is shown in Figure 19.
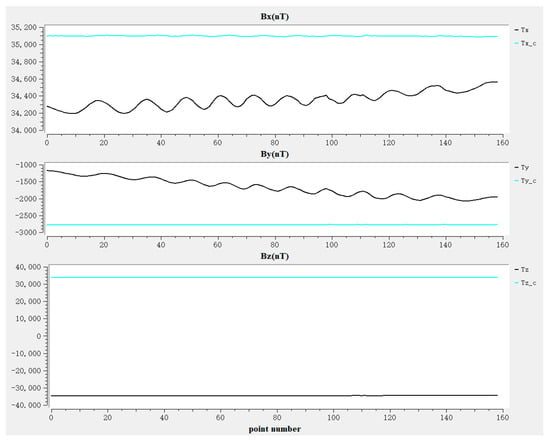
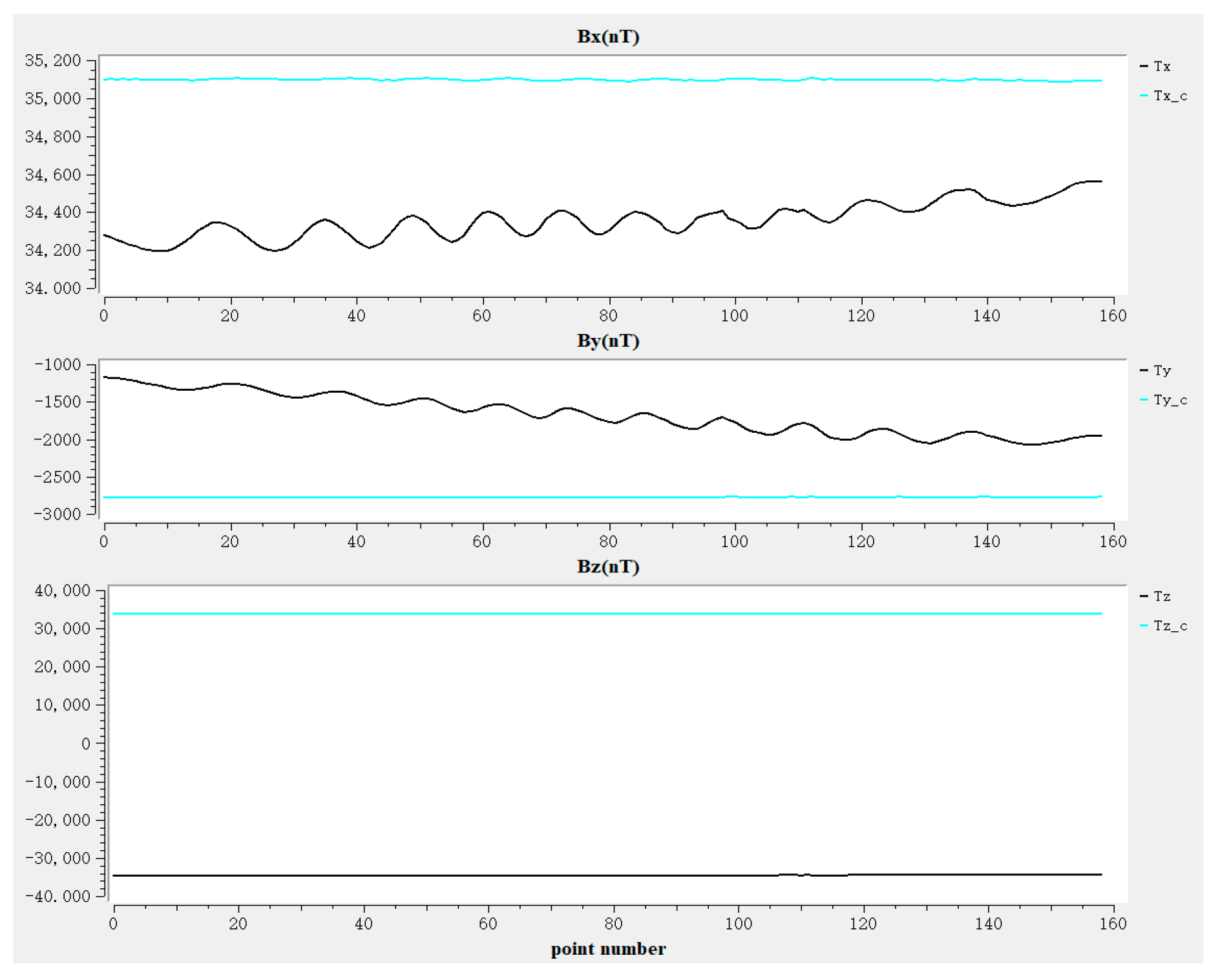
Figure 19.
Real-time curve display on the upper computer.
The black curve represents the measured data before compensation, and the indigo curve shows the dynamic compensated curve. The effect of dynamic compensation can be preliminarily seen from the comparison of the two curves in Figure 19. Further comparison and analysis are carried out in the next section.
4.3. Result and Discussion
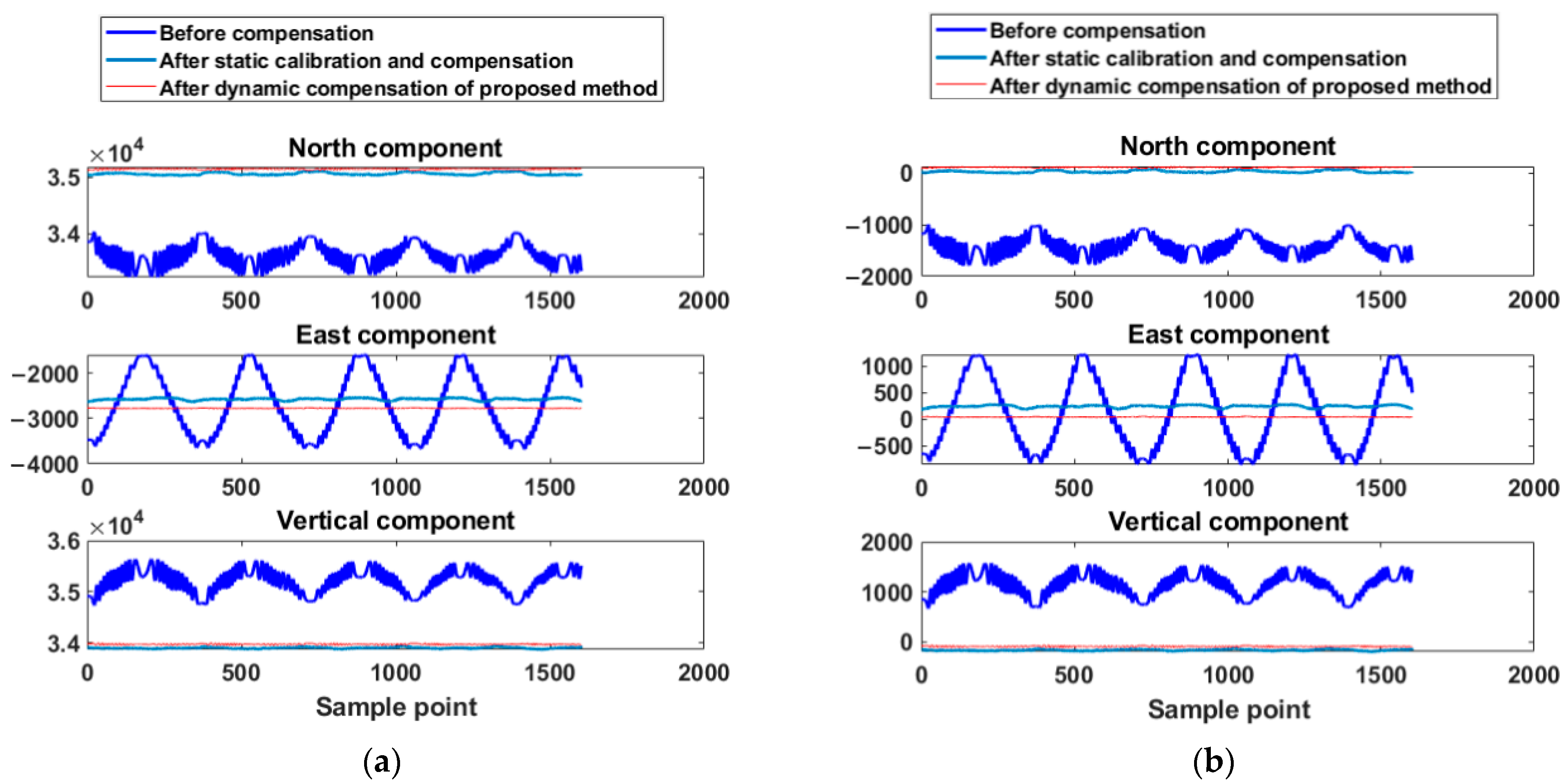
After sliding the dynamic measurement 10 times, the measurement data are processed by static correction and the proposed GA-SA dynamic compensation method, respectively. The results of the raw data and compensated data by the two methods are shown in Figure 20a. To further verify the accuracy, the pre-calibrated geomagnetic field values are subtracted from the data in Figure 20a and are shown in Figure 20b. During the compensation process, the vertical component is converted from the east-north-up coordinate system to the north-east-down coordinate system, so the raw data of the vertical component is multiplied by −1 to facilitate comparison.
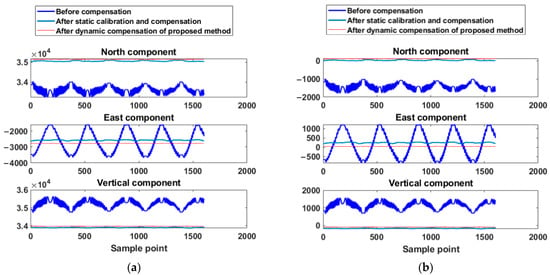
Figure 20.
Dynamic measurement and static/dynamic compensation results: (a) results of raw data; (b) results of data subtracting the calibration value.
The comparison of the average standard deviations of the 10-time measurements is shown in Table 6. Bx is the north component of the geomagnetic field; By is the east component of the geomagnetic field; Bz is the vertical component of the geomagnetic field.

Table 6.
Comparison of the mean standard deviations of 10-time measurements.
It is clear from the comparison results of Figure 20 that the measurement stability of the dynamic compensation data by the proposed method is much better than raw data and static compensation data. Meanwhile, it is clear from Figure 20b that the accuracy of the dynamic compensation data is best since it is almost entirely close to zero after subtracting the field calibration. Furthermore, in Table 6, the mean standard deviations of the north/east/vertical components decrease from 95.30/277.35/108.51 nT to 3.41/2.36/2.75 nT. The comparison of the mean standard deviations of 10-time measurements shows the accuracy and stability of the proposed method. Thus, the results and comparison of the geomagnetic measurement experiment verify the effectiveness of the proposed method in a practical application.
5. Conclusions
In this paper, the principle of dynamic error compensation of the fluxgate magnetometer was introduced first. The dynamic error compensation of the magnetometer was realized by the series dynamic compensator behind the magnetometer. A parameter-calculating method of the dynamic compensator based on the hybrid optimization strategy of the GA-SA algorithm was proposed. Finally, simulation and experimental verification were carried out.
First, the compensation effect of different compensator orders under the input of a step signal was analyzed by simulation, and it was confirmed that the compensation effect is best when the compensator order is second order. The comparison of the three algorithms shows that the GA-SA compensation is the closest to the simulation input signal; the overshot after compensation was 50% of the GA and 17% of the SA, and the response time was 18.22% of that before compensation and 46.43% and 92.86% of the GA and SA.
Second, the signal test results of the step signal input show that the step response time was reduced to 5.5% of that before dynamic compensation.
Further, sinusoidal signal input and tests with different frequencies were carried out. The amplitude–frequency and phase–frequency characteristic curves show that the attenuation of the maximum value of the magnetic sensor decreased from 0.24% to 0.10% in the 0.01–10 Hz frequency band after dynamic compensation, and the phase difference was less than −0.5°.
At last, the geomagnetic measurement results show that the dynamic measurement results, after being compensated by the proposed method, reduced the standard deviation error from 95.30/277.35/108.51 nT to 3.41/2.36/2.75 nT in three geomagnetic vector components. Moreover, the dynamic compensated results are mostly close to the real calibrated geomagnetic field values, which verifies the effectiveness and accuracy of the proposed dynamic compensation method.
To sum up, the accuracy and convergence of the proposed algorithm were proved by a simulation and an experiment. Moreover, dynamic compensation had certain compensation effects on the magnetometer in this paper, which improved the dynamic magnetic measurement performance and its application capabilities.
Author Contributions
Conceptualization, Z.C. and Q.Z.; methodology, Z.C.; software, Z.W.; validation, M.P.; formal analysis, Z.L.; investigation, D.C.; resources, Y.X.; data curation, Z.C. and Z.W.; writing—original draft preparation, Z.C.; writing—review and editing, D.C. and Q.Z.; visualization, Z.C. and Z.W.; supervision, Q.Z.; project administration, M.P.; funding acquisition, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hunan Province under Project 2021JJ40687.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting this study’s findings are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Z.; Liu, Z.; Zhang, Q.; Chen, D.; Pan, M.; Hu, J.; Xu, Y.; Wang, Z.; Wang, Z. An Improved Geomagnetic Navigation Method Based on Two-Component Gradient Weighting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3213779. [Google Scholar] [CrossRef]
- Liu, Z.; Pang, H.; Pan, M.; Wan, C. Calibration and Compensation of Geomagnetic Vector Measurement System and Improvement of Magnetic Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2016, 13, 2519026. [Google Scholar] [CrossRef]
- Du, A.M.; Zhang, Y.; Li, H.Y.; Qiao, D.H.; Yi, Z.; Zhang, T.L.; Ge, Y.S.; Luo, H.; Zhao, L.; Sun, S.Q.; et al. The Chinese mars rover fluxgate magnetometers. Space Sci. Rev. 2020, 216, 1–15. [Google Scholar] [CrossRef]
- Sheinker, A.; Frumkis, L.; Ginzburg, B.; Salomonski, N.; Kaplan, B.-Z. Magnetic Anomaly Detection Using a Three-Axis Magnetometer. IEEE Trans. Magn. 2009, 45, 160–167. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Q.; Pan, M.; Shan, Q.; Geng, Y.; Guan, F.; Chen, D.; Tian, W. Distortion Magnetic Field Compensation of Geomagnetic Vector Measurement System Using a 3-D Helmholtz Coil. IEEE Geosci. Remote Sens. Lett. 2016, 14, 48–51. [Google Scholar] [CrossRef]
- Pang, H. Error Analysis and Calibration/Compensation Method of Portable Geomagnetic Vector Measurement System. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2015. [Google Scholar]
- Ninness, B.M. Stochastic and Deterministic Modeling. Ph.D. Thesis, Dept. of Electrical Engineering, University of Newcastle, Newcastle, Australia, 1993. [Google Scholar]
- Ljung, L. System Identification; Birkhäuser: Boston, MA, USA, 1998. [Google Scholar]
- Chen, S. Research on Performance Enhancement of Residence Time Difference Fluxgate Sensors Based on the Dynamic Hysteresis Model. Ph.D. Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Yu, H.; Feng, S.; Li-Hua, W. Synchronous correction of two three-axis magnetometers using FLANN. Sens. Actuators A Phys. 2012, 179, 312–318. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Lai, K.L.; Harman, R.R. Real-Time Attitude-Independent Three-Axis Magnetometer Calibration. Am. Inst. Aeronaut. Astronaut. 2005, 28, 115–120. [Google Scholar] [CrossRef]
- Altintas, Y.; Park, S.S. Dynamic compensation of spindle-integrated force sensors. CIRP Ann. 2004, 53, 305–308. [Google Scholar] [CrossRef]
- Ralf, Z.; Rolf, I. Nonlinear time constant estimation and dynamic compensation of temperature sensors. Control. Eng. Pract. 2010, 18, 300–310. [Google Scholar]
- Yu, D.; Liu, F.; Lai, P.-Y.; Wu, A. Nonlinear Dynamic Compensation of Sensors Using Inverse-Model-Based Neural Network. IEEE Trans. Instrum. Meas. 2008, 57, 2364–2376. [Google Scholar] [CrossRef]
- Xin, L. Identification of Nonlinear Systems with non-Ideal Process Data. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Marconato, A.; Hu, M.; Boni, A.; Petri, D. Dynamic Compensation of Nonlinear Sensors by a Learning-From-Examples Approach. IEEE Trans. Instrum. Meas. 2008, 57, 1689–1694. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A.; Powell, J.D. Feedback Control of Dynamic Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H.; Ding, J.J. Signals and Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Wu, D.; Huang, S.; Zhao, W.; Xin, J. Infrared thermometer sensor dynamic error compensation using Hammerstein neural network. Sens. Actuators A Phys. 2009, 149, 152–158. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Narendra, K.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef]
- Chongz, F.; Dey, X. Process Identification; Tsinghua University Publishing House Co., Ltd.: Beijing, China, 1988. [Google Scholar]
- Schoen, M.P.; Hoover, R.C.; Chinvorarat, S.; Schoen, G.M. System identification and robust controller design using genetic algorithms for flexible space structures. J. Dyn. Syst. Meas. Control. 2009, 131, 304–314. [Google Scholar] [CrossRef]
- Li, M.Q.; Kou, J.; Lin, D.; Li, S.Q. Basic Theory and applicAtion of Genetic Algorithm; The Publishing of Science: Beijing, China, 2002. [Google Scholar]
- Pang, F. The Principle of Simulated Annealing Algorithm and Its Application in Optimization Problems. Ph.D. Thesis, Jilin University, Changchun, China, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).