Dispersion Curve Interpolation Based on Kriging Method
Abstract
1. Introduction
2. Data
- Data preprocessing including demeaning, detrending and filtering (0.08–2 Hz);
- Cut continuous waveforms into one day’s length;
- Time domain normalization and frequency domain spectrum whitening, which eliminates the influence of seismic activity;
- Cross-correlate the waveforms of each station pair;
- Drop the Noise Cross-correlation Functions with signal-to-noise ratio [32] less than 2;
- Extract dispersion curves with FTAN [33];
- Inverse the dispersion curves.
3. Methods
3.1. Kriging and Dispersion Curves
3.2. Procedure of Applying Kriging to Dispersion Curves
3.3. Application in the Changbai Volcano
4. Results
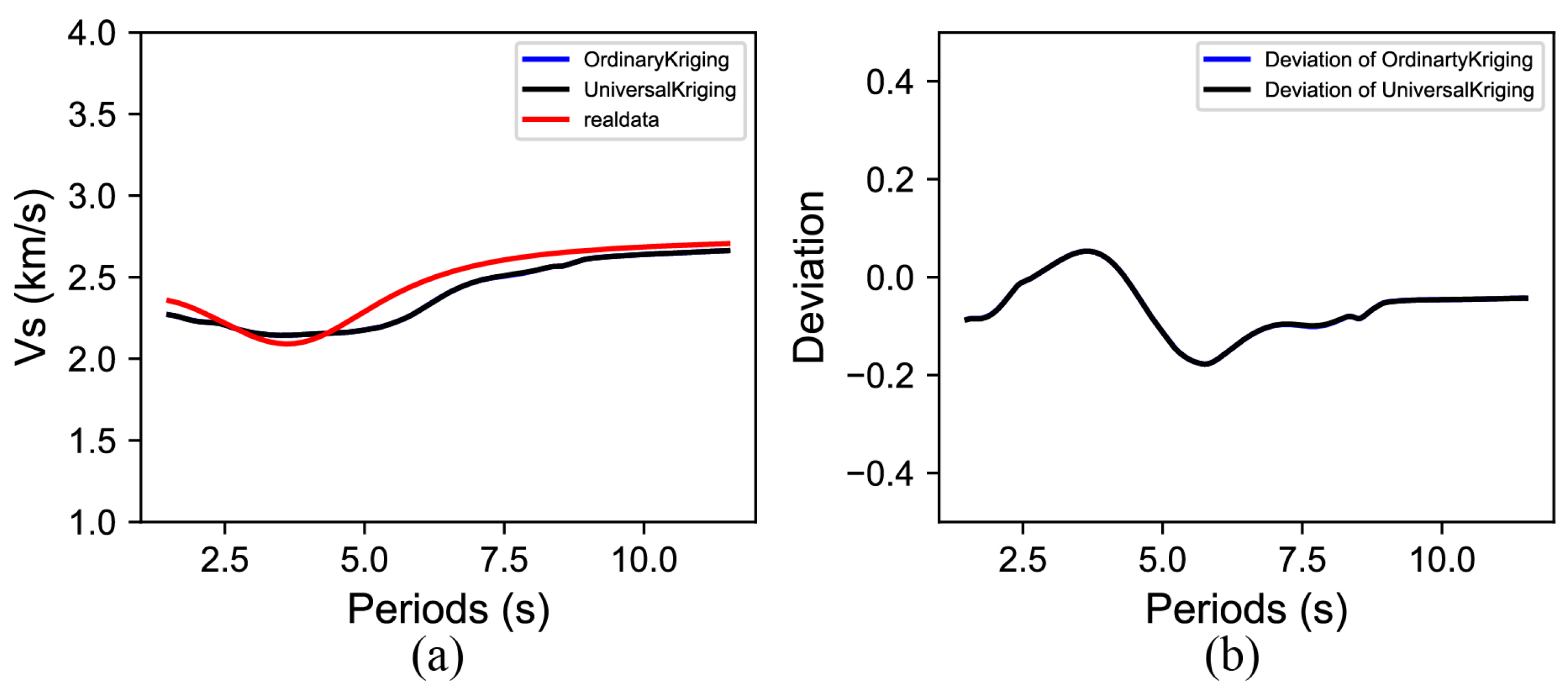
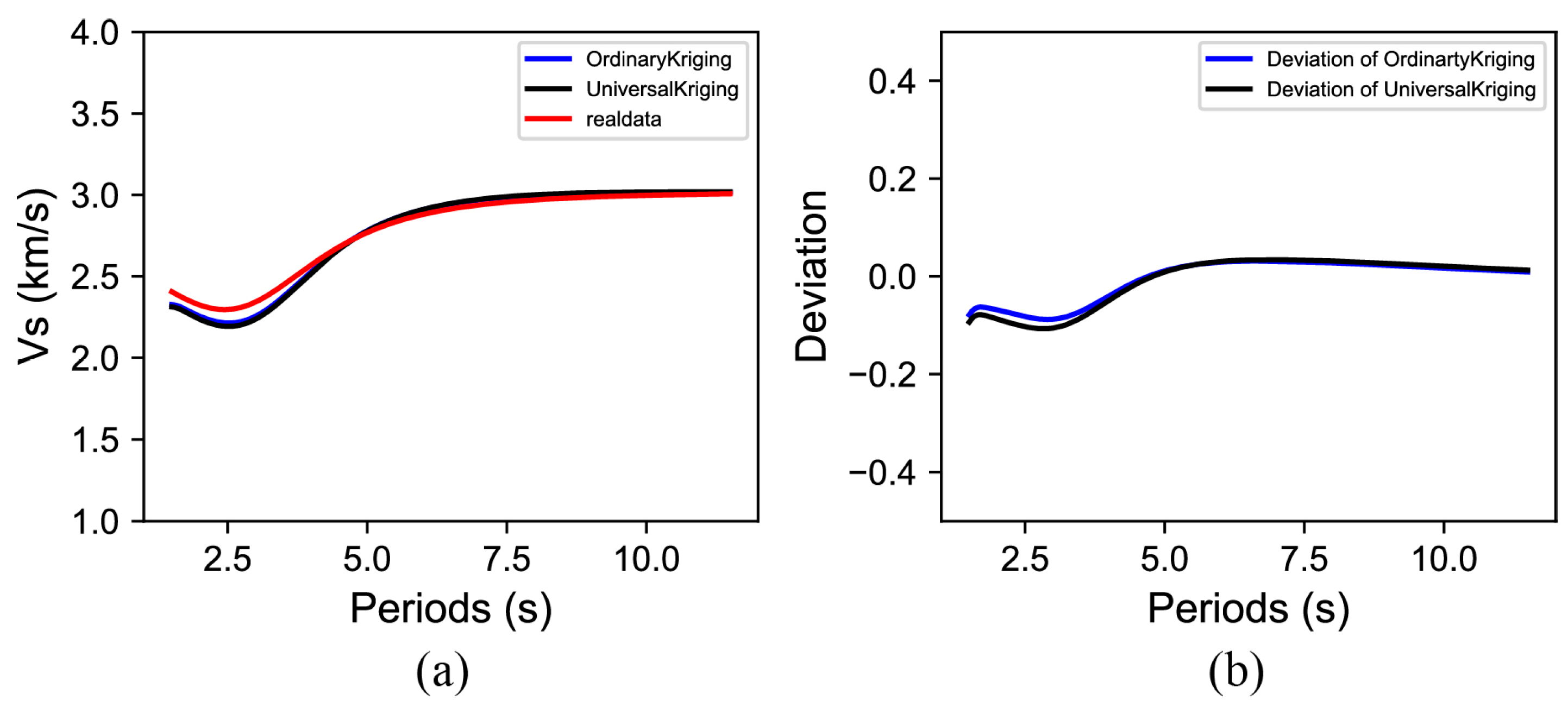
4.1. Test Results
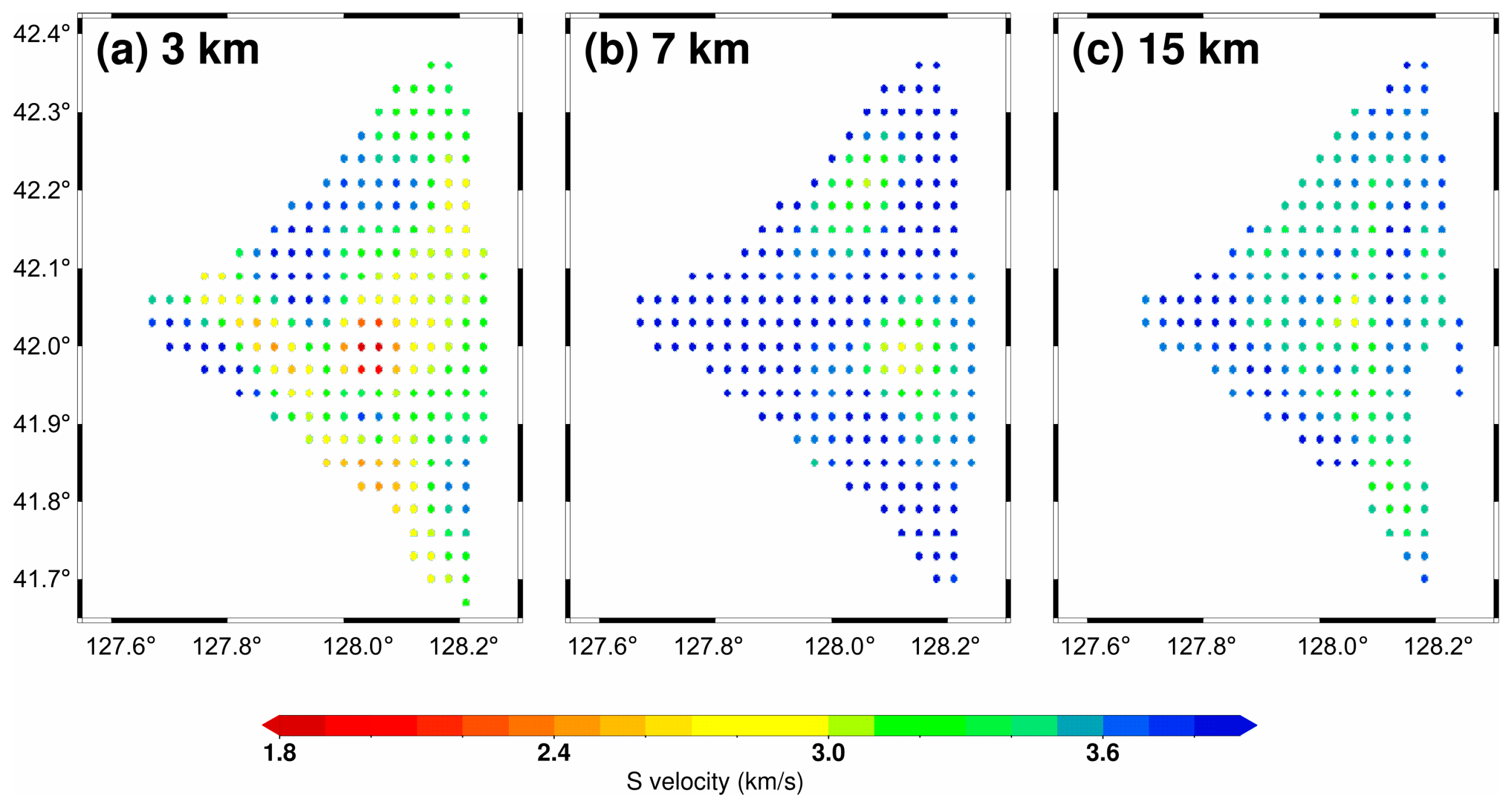
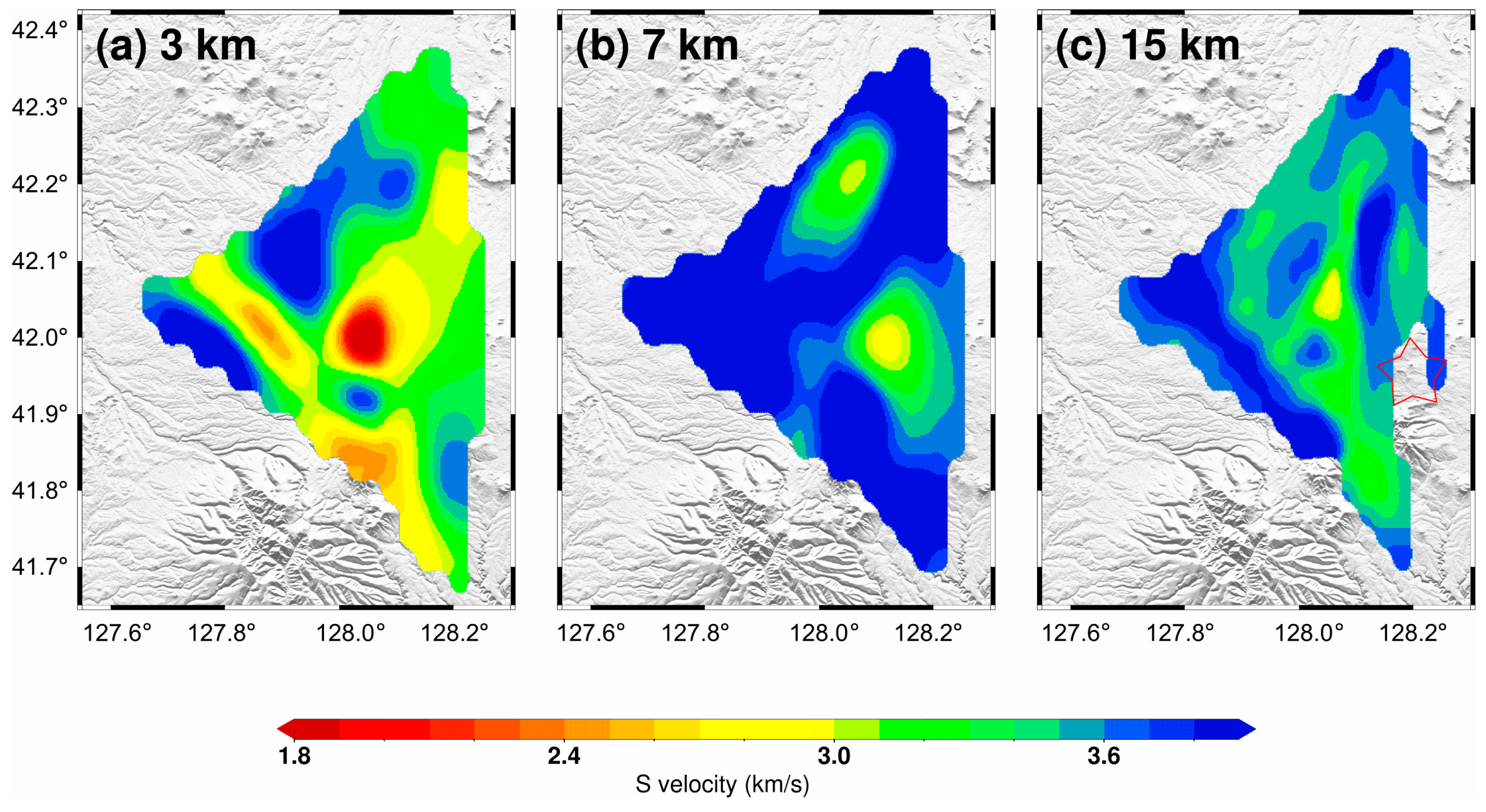
4.2. Results for the Changbai Volcano
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Period (s) | Method | Variogram | R–Square |
|---|---|---|---|
| 2 | Ordinary Kriging | linear | −0.17239 |
| gaussian | 0.32272 | ||
| spherical | 0.04819 | ||
| Universal Kriging | linear | −0.20511 | |
| gaussian | −54.0814 | ||
| spherical | 0.19007 | ||
| 4 | Ordinary Kriging | linear | 0.22706 |
| gaussian | 0.24714 | ||
| spherical | 0.44061 | ||
| Universal Kriging | linear | −0.13863 | |
| gaussian | −0.07201 | ||
| spherical | 0.48276 | ||
| 6 | Ordinary Kriging | linear | 0.21364 |
| gaussian | 0.28400 | ||
| spherical | 0.35176 | ||
| Universal Kriging | linear | −0.24132 | |
| gaussian | −0.13955 | ||
| spherical | 0.28400 | ||
| 8 | Ordinary Kriging | linear | −0.01302 |
| gaussian | 0.22846 | ||
| spherical | 0.27741 | ||
| Universal Kriging | linear | −0.63261 | |
| gaussian | −363.477 | ||
| spherical | 0.27772 | ||
| 10 | Ordinary Kriging | linear | −0.34288 |
| gaussian | 0.32577 | ||
| spherical | 0.14228 | ||
| Universal Kriging | linear | −0.90197 | |
| gaussian | −655.004 | ||
| spherical | 0.20754 |
| 185° | 230° | 265° | 300° | |
|---|---|---|---|---|
| 10,000 m | 0.140 | 0.140 | 0.139 | 0.145 |
| 15,000 m | 0.075 | 0.075 | 0.076 | 0.0797 |
| 20,000 m | 0.079 | 0.079 | 0.080 | 0.0830 |
| 30,000 m | 0.093 | 0.093 | 0.095 | 0.1000 |












References
- Hutapea, F.L.; Tsuji, T.; Ikeda, T. Real-time crustal monitoring system of Japanese Islands based on spatio-temporal seismic velocity variation. Earth Planets Space 2020, 72, 19. [Google Scholar] [CrossRef]
- Li, L.; Revesz, P. Interpolation methods for spatio-temporal geographic data. Comput. Environ. Urban Syst. 2004, 28, 201–227. [Google Scholar] [CrossRef]
- Antonić, O.; Križan, J.; Marki, A.; Bukovec, D. Spatio-temporal interpolation of climatic variables over large region of complex terrain using neural networks. Ecol. Model. 2001, 138, 255–263. [Google Scholar] [CrossRef]
- Kilibarda, M.; Tadić, M.P.; Hengl, T.; Luković, J.; Bajat, B. Global geographic and feature space coverage of temperature data in the context of spatio-temporal interpolation. Spat. Stat. 2015, 14, 22–38. [Google Scholar] [CrossRef]
- Li, S.; Griffith, D.A.; Shu, H. Temperature prediction based on a space-time regression-kriging model. J. Appl. Stat. 2020, 47, 1168–1190. [Google Scholar] [CrossRef]
- Bezyk, Y.; Sówka, I.; Górka, M.; Blachowski, J. Gis-based approach to spatio-temporal interpolation of atmospheric co2 concentrations in limited monitoring dataset. Atmosphere 2021, 12, 384. [Google Scholar] [CrossRef]
- Revesz, P. Spatiotemporal Interpolation Algorithms. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Boston, MA, USA, 2009; pp. 2736–2739. [Google Scholar]
- Shapiro, N.M.; Campillo, M.; Stehly, L.; Ritzwoller, M.H. High-Resolution Surface-Wave Tomography from Ambient Seismic Noise. Science 2005, 307, 1615–1618. [Google Scholar] [CrossRef]
- Lin, F.-C.; Ritzwoller, M.H.; Townend, J.; Bannister, S.; Savage, M.K. Ambient noise Rayleigh wave tomography of New Zealand. Geophys. J. Int. 2007, 170, 649–666. [Google Scholar] [CrossRef]
- Yang, Y.; Ritzwoller, M.H.; Levshin, A.L.; Shapiro, N.M. Ambient noise Rayleigh wave tomography across Europe. Geophys. J. Int. 2007, 168, 259–274. [Google Scholar] [CrossRef]
- Shen, W.; Ritzwoller, M.H.; Kang, D.; Kim, Y.; Lin, F.-C.; Ning, J.; Wang, W.; Zheng, Y.; Zhou, L. A seismic reference model for the crust and uppermost mantle beneath China from surface wave dispersion. Geophys. J. Int. 2016, 206, 954–979. [Google Scholar] [CrossRef]
- Zhu, H.; Tian, Y.; Zhao, D.; Li, H.; Liu, C. Seismic Structure of the Changbai Intraplate Volcano in NE China From Joint Inversion of Ambient Noise and Receiver Functions. J. Geophys. Res. Solid Earth 2019, 124, 4984–5002. [Google Scholar] [CrossRef]
- Li, Z.; Ni, S.; Zhang, B.; Bao, F.; Zhang, S.; Deng, Y.; Yuen, D.A. Shallow magma chamber under the Wudalianchi Volcanic Field unveiled by seismic imaging with dense array. Geophys. Res. Lett. 2016, 43, 4954–4961. [Google Scholar] [CrossRef]
- Levshin, A.L.; Ritzwoller, M.H. Automated Detection, Extraction, and Measurement of Regional Surface Waves. Pure Appl. Geophys. 2001, 158, 1531–1545. [Google Scholar] [CrossRef]
- Natale, M.; Nunziata, C.; Panza, G.F. Average shear wave velocity models of the crustal structure at Mt. Vesuvius. Phys. Earth Planet. Int. 2005, 152, 7–21. [Google Scholar] [CrossRef]
- Wang, J.; Wu, G.; Chen, X. Frequency-Bessel Transform Method for Effective Imaging of Higher-Mode Rayleigh Dispersion Curves from Ambient Seismic Noise Data. J. Geophys. Res. Solid Earth 2019, 124, 3708–3723. [Google Scholar] [CrossRef]
- Wu, G.-X.; Pan, L.; Wang, J.-N.; Chen, X. Shear Velocity Inversion Using Multimodal Dispersion Curves from Ambient Seismic Noise Data of USArray Transportable Array. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018213. [Google Scholar] [CrossRef]
- Li, H.; Tian, Y.; Zhao, D.; Kumar, R.; Li, H.; Yan, D.; Liu, C. Shear-wave tomography of the Changbai volcanic area in NE China derived from ambient noise and seismic surface waves. J. Asian Earth Sci. 2022; in press. [Google Scholar] [CrossRef]
- Fang, H.; Yao, H.; Zhang, H.; Huang, Y.-C.; van der Hilst, R.D. Direct inversion of surface wave dispersion for three-dimensional shallow crustal structure based on ray tracing: Methodology and application. Geophys. J. Int. 2015, 201, 1251–1263. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Wang, Y.; Zu, S. The Interpolation of Sparse Geophysical Data. Surv. Geophys. 2019, 40, 73–105. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y.; Liu, C.; Zheng, Z.; Cui, Y. Seismic data interpolation using deeply supervised U-Net++ with natural seismic training sets. Geophys. Prospect. 2023, 71, 227–244. [Google Scholar] [CrossRef]
- Garabito, G. Prestack seismic data interpolation and enhancement with common-reflection-surface–based migration and demigration. Geophys. Prospect. 2021, 69, 913–925. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Pereira, P.E.C.; Rabelo, M.N.; Ribeiro, C.C.; Diniz-Pinto, H.S. Geological modeling by an indicator kriging approach applied to a limestone deposit in Indiara city—Goiás. REM—Int. Eng. J. 2017, 70, 331–337. [Google Scholar] [CrossRef]
- Journel, A.G.; Alabert, F.G. New method for reservoir mapping. J. Pet. Technol. 1990, 42, 212–218. [Google Scholar] [CrossRef]
- Kumar, V. Optimal contour mapping of groundwater levels using universal kriging—A case study. Hydrol. Sci. J. 2007, 52, 1038–1050. [Google Scholar] [CrossRef]
- Kaur, L.; Rishi, M.S. Integrated geospatial, geostatistical, and remote-sensing approach to estimate groundwater level in north-western India. Environ. Earth Sci. 2018, 77, 786. [Google Scholar] [CrossRef]
- Chica-Olmo, M.; Luque-Espinar, J.A. Applications of the local estimation of the probability distribution function in environmental sciences by kriging methods. Inverse Probl. 2002, 18, 25–36. [Google Scholar] [CrossRef]
- Kurtulus, T.; Kurtulus, B.; Avsar, O.; Avsar, U. Evaluating the thermal stratification of Koycegiz Lake (SW Turkey) using in-situ and remote sensing observations. J. Afr. Earth Sci. 2019, 158, 103559. [Google Scholar] [CrossRef]
- Bensen, G.D.; Ritzwoller, M.H.; Barmin, M.P.; Levshin, A.L.; Lin, F.; Moschetti, M.P.; Shapiro, N.M.; Yang, Y. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophys. J. Int. 2007, 169, 1239–1260. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, Y.; Xu, Y.; Xu, H.; Zhao, K.; Wang, K. On the limitations of interstation distances in ambient noise tomography. Geophys. J. Int. 2015, 201, 652–661. [Google Scholar] [CrossRef]
- Eric, N.N.; Charles, T.T.; Alain-Pierre, K.T. Frequency Time Analysis (FTAN) and Moment Tensor Inversion Solutions from Short Period Surface Waves in Cameroon (Central Africa). Open J. Geol. 2014, 4, 33–43. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Wakefield, J. Statistical Analysis of Environmental Space-Time Processes edited by N. D. Le and J. V. Zidek. Biometrics 2007, 63, 624–625. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
- Jin, C.; Yang, W.H.; Luo, D.G.; Liu, J.P. Comparative analysis of extracting methods of surface wave dispersion curves. Prog. Geophys. 2016, 31, 2735–2742. (In Chinese) [Google Scholar] [CrossRef]





| Period (s) | Method | the Best Variogram |
|---|---|---|
| 2 | Ordinary Kriging | Gaussian |
| Universal Kriging | Spherical | |
| 4 | Ordinary Kriging | Spherical |
| Universal Kriging | Spherical | |
| 6 | Ordinary Kriging | Spherical |
| Universal Kriging | Spherical | |
| 8 | Ordinary Kriging | Spherical |
| Universal Kriging | Spherical | |
| 10 | Ordinary Kriging | Gaussian |
| Universal Kriging | Spherical |
| Parameter | |
|---|---|
| Method | Universal Kriging |
| Variogram | Spherical |
| Distance | 15,000 (m) |
| Angle | 265 (°) |
| Depth (km) | Original | Interpolating | Expansion Multiple |
|---|---|---|---|
| 1 | 225 | 479 | 2.129 |
| 2 | 240 | 479 | 1.996 |
| 3 | 239 | 479 | 2.004 |
| 4 | 243 | 479 | 1.971 |
| 5 | 245 | 479 | 1.971 |
| 7 | 234 | 479 | 1.955 |
| 10 | 235 | 479 | 2.038 |
| 12 | 218 | 479 | 2.197 |
| 15 | 198 | 479 | 2.419 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Tian, Y.; Zhao, P. Dispersion Curve Interpolation Based on Kriging Method. Appl. Sci. 2023, 13, 2557. https://doi.org/10.3390/app13042557
Zhang H, Tian Y, Zhao P. Dispersion Curve Interpolation Based on Kriging Method. Applied Sciences. 2023; 13(4):2557. https://doi.org/10.3390/app13042557
Chicago/Turabian StyleZhang, Han, You Tian, and Pengfei Zhao. 2023. "Dispersion Curve Interpolation Based on Kriging Method" Applied Sciences 13, no. 4: 2557. https://doi.org/10.3390/app13042557
APA StyleZhang, H., Tian, Y., & Zhao, P. (2023). Dispersion Curve Interpolation Based on Kriging Method. Applied Sciences, 13(4), 2557. https://doi.org/10.3390/app13042557





