Abstract
The purpose of this paper is to present applications and design elements of scale models of the carbody of railway vehicles integrated in experimental laboratory systems to verify the effectiveness of the methods to reduce vertical bending vibration of the carbody. In the first part of the paper, some applications of such experimental systems are presented, which include different scale models of the railway vehicle carbody. In the second part of the paper, the structure and dimensioning elements of a new demonstrative experimental system, specially designed by the authors of the present paper for testing the functionality of an original method of reducing the vertical bending vibrations of the carbody of railway vehicles, are presented. This method is based on an innovative approach that involves the use of a passive system consisting of two bars rigidly mounted on the longitudinal beams of the carbody underframe, having the role of opposing the bending of the carbody. The main element of the demonstrative experimental system is the scale model of the vehicle carbody, reduced to a beam, on which the two bars, called anti-bending bars, are mounted. For the dimensioning of the experimental model of the carbody and the anti-bending bars, original methodologies are developed in which several conditions are involved. In the case of the dimensioning of the experimental model of the carbody, the conditions refer to the convenient adoption of the scaling factor of the dimensions of the real carbody from the perspective of the practical realization of the experimental model of the carbody, ensuring the buckling stability of the demonstrative experimental system, achieving natural frequency of the vertical bending of the real carbody and avoiding the interference of the bounce vibration with the vertical bending vibration of the demonstrative experimental model of the carbody. The dimensions of the anti-bending bars are established from the condition that the vertical bending frequency of the experimental model of the carbody is outside the range of sensitivity of the human body to vertical vibration. Additionally, the natural frequency of the vertical bending vibration of the anti-bending bars must be chosen to avoid interference with the vertical bending vibration of the experimental model of the carbody. The effectiveness of the anti-bending bars in reducing the vertical bending vibration of the experimental model of the carbody is investigated with the help of numerical simulation results developed based on an original theoretical model of the experimental model of the carbody with anti-bending bars.
1. Introduction
Weight reduction is a basic criterion for the design of railway vehicles in order for them to reach high speeds with the lowest possible energy consumption. By reducing the weight of railway vehicles, vibrations transmitted through the ground and manufacturing costs are also reduced. In addition, the demand of transport service providers to maximize the use of axle loads, which are limited, requires the railway industry to adopt lightweight carbody designs [1,2].
Reducing the carbody weight involves using lighter materials and changing the mechanical structure. This implicitly leads to a decrease in the structural rigidity of the carbody, respectively, to a decrease in eigenfrequencies. The flexibility of the carbody increases the lighter it is, which favours the excitation of structural vibrations of the carbody. The structural vibrations affect the ride comfort, the vehicle’s dynamic performance and shorten its life as a result of fatigue stresses [3].
Although the structural vibrations of the carbody are particularly complex, with numerous global and local forms, the first carbody mode of vertical bending has the greatest influence on ride comfort [4]. The eigenfrequency of the first mode of vertical bending of the carbody is usually found in the frequency interval 6 Hz–12 Hz, an interval in which the human body has a greater sensitivity to vertical vibrations [5,6,7]. Ride comfort worsens especially in the middle of the carbody, and, in some situations, there may even be repositioning of the critical points from the point in terms of ride comfort from the extremities of the carbody to its middle [8].
The topic of structural vibrations of flexible carbody has become a topic of interest for researchers around the world, the influence of these vibrations on the dynamic behaviour of the railway vehicle being analysed in several studies [1,3,9,10,11,12,13]. Additionally, the problem of reducing or controlling structural vibrations in order to improve ride comfort has been the subject of numerous research. These researches are based on passive, semi-active and active concepts, and can be grouped according to the following approach: concepts that as their purpose to isolate vibrations and aim to reduce the transmission of excitation to the carbody through the suspension [14,15,16,17,18,19,20,21,22,23,24,25], and concepts that as their purpose the damping of the carbody vibrations [26,27,28,29,30,31,32,33,34,35,36] and which aim to reduce the amplitude of the structural vibrations of the carbody [37,38]. In general, this research uses results obtained through numerical simulations, the numerical simulation applications being developed based on mechanical models of the vehicle-track system obtained through the simplified representation of the real system. There are few cases in which the validation of the concepts or the effectiveness of the proposed methods for reducing the flexible vibration modes of the carbody of the railway vehicles are validated by the results of the experimental research carried out on special test vehicles in the laboratory (Figure 1) [22,34] or on the line (Figure 2) [35].

Figure 1.
The Shinkansen type test vehicle [22,34].

Figure 2.
The commuter type test vehicle [35].
A separate category of research is dedicated to the possibilities of reducing the flexible vibrations of the carbody of the high-speed electrical multiple units (EMU). Compared to trains with centralized power, EMU use distributed power technology. Distributed power involves mounting several power equipment under the chassis of the carbody, such as traction transformer, traction converter, and air compressor. In addition to the power equipment, other functional systems and equipment are also mounted under the carbody underframe, such as the braking unit, the waste collection unit, etc.
Although EMU have been in operation for years, such as the TGV (Train à Grande Vitesse) in France, the ICE (Inter-City Express) in Germany, the Shinkansen in Japan and the CRH (China Railways High-Speed) in China, the identification of the best solution regarding the suspension of the equipment in order to lower the level of carbody vibration and to improve the ride comfort is still the subject of many studies [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. Two conventional passive methods are frequently used to reduce the vibrations of the flexible carbody of EMU, one based on the vibration isolation theory and the other on the dynamic vibration absorber theory. The active vibration reduction methods can also be added to these, but they are not applicable due to the high cost of implementation and maintenance [59]. Although several studies based on experimental research have been identified on this topic [40,42,43,44,45,47,48,51,52,53,54], their number is relatively small compared to the large number of published papers.
Carrying out experimental research in the laboratory on special test vehicles requires a large investment of time and a considerable financial effort for the development of complex stands equipped with specialized systems and equipment for simulating real traffic conditions and measuring, controlling, and acquiring data. Thus, it can be explained that the small number of studies in which the vibration reduction methods of flexible carbody of railway vehicles are investigated based on both numerical simulation results and experimental results.
A less expensive alternative to experimental research on full-scale test vehicles is laboratory research on experimental systems that have as their main structure the scale model of the vehicle carbody [60,61,62,63,64,65,66,67,68,69,70,71,72,73]. Such systems have been used to verify the results of some methods of passive or active damping of flexible vibrations of the carbody of the railway vehicles [60,61,62,63,64,65,66,67,68,72,73], in the experimental study of a method of increasing the structural damping of the light carbody of the high-speed trains [67], or in evaluating the influence of some elements of the vehicle on the flexible vibrations of the carbody [74]. Section 2 of the paper describes these experimental systems, which include different scale models (1:5, 1:6, 1:10; 1:12; 1:24.5) of the vehicle carbody.
Section 3 of the paper presents the structure and dimensioning elements of a new demonstrative experimental system, specially designed by the authors of the present paper for experimental testing the functionality of an original method of reducing vertical bending vibration of the carbody of the railway vehicles. This method, proposed by one of the authors of this paper, relies on an innovative approach that implies the use of a passive system [29]. This system consists of two bars, hereafter referred to as anti-bending bars, which are rigidly mounted on the longitudinal beams of the carbody underframe. When the carbody bends, the anti-bending bars act as elastic elements developing at the clamping ends two opposing longitudinal forces that act below the neutral axis of the carbody and create two bending moments which oppose the bending of the carbody. The couples corresponding to these forces limit the rotation of the cross-sections of the carbody caused by vertical bending vibration. The advantage of the method being proposed consists in the fact that the anti-bending bars parameters are determined from the requirement to achieve a frequency of the first vertical bending mode of the carbody, advantageous from the ride comfort. In other words, the eigenfrequency of the carbody vertical bending can be increased and taken out of the frequency interval of sensitivity to vertical vibrations of the human body. Additionally, the proposed method has the advantage that it involves the use of a simple mechanical system, which does not require high manufacturing, implementation, and maintenance costs.
The main element of the demonstrative experimental system is the scale model of the vehicle carbody, reduced to a beam, on which the anti-bending bars are mounted. For the vibration study of the experimental model of the vehicle carbody, it is represented by an original theoretical model developed based on the Euler–Bernoulli beam theory. This theory is widely used in the railway field to model the vehicle carbody [13,29,37], wheelset [75], or rail [76,77]. To determine the dimensions of the experimental model of the carbody, the dimensions of the real carbody of a passenger vehicle are taken as a starting point and the following original criteria are introduced: the convenient adoption of the scaling factor of the dimensions of the real carbody from the point of view of the practical realization of the experimental model of the carbody, ensuring the buckling stability of the demonstrative experimental system, achieving the natural frequency of the vertical bending of the real carbody, and avoiding the interference of the bounce vibration with the vertical bending vibration of the experimental model of the carbody. As shown above, achieving a vertical bending frequency of the experimental model of the carbody with anti-bending bars, convenient from the point of view of ride comfort, is the main condition underlying the dimensioning of the anti-bending bars. Added to this is the condition that the vertical bending vibration of the anti-bending bar do not interfere with the vertical bending vibrations of the experimental model of the carbody.
At the end of Section 3, the results of the numerical simulations on the frequency response function of the acceleration of the experimental model of the carbody without/with anti-bending bars are presented. Based on these results, the effectiveness of the anti-bending bars in reducing the vertical bending vibrations of the experimental model of the carbody is analysed for different constructive dimensions of the anti-bending bars.
The theoretical results presented show that there are premises for the next stage of the research, namely the experimental verification of the functionality of the method of reducing vertical bending vibrations of the railway vehicle carbody with the help of the anti-bending bar system, using the experimental model of the carbody integrated in the special demonstrative experimental system conceived.
The original elements of the paper can be found in Section 3 and consist mainly of: the conception of a new demonstrative experimental system dedicated to testing in the laboratory the effectiveness of the method of reducing vertical bending vibrations of the carbody of railway vehicles with the help of the system consisting of two anti-bending bars; development of the theoretical model of the experimental model of the carbody with anti-bending bars; development of methodologies for dimensioning the experimental model of the carbody and the anti-bending bars; analysis of the effectiveness of the anti-bending bars in reducing the vertical bending vibrations of the experimental carbody model and increasing the resonance frequency of the vertical bending vibrations based on numerical simulations.
2. Applications of Scale Models in Experimental Research on the Reducing of Vertical Vibrations of the Railway Vehicle Carbody
In the last 20 years, several methods have been developed to reduce the vertical vibration of the carbody of the railway vehicles with impact on ride comfort. Exploring the specialized literature on this topic, we identified several experimental studies carried out on scale models that confirmed the effectiveness of some passive or active methods of damping the vibrations of the railway vehicle carbody or have validated solutions to optimize the constructive elements of the vehicle that lead to the minimization of the flexible vibrations of the carbody. A series of studies belong to teams of Japanese researchers, whose research focused both on the possibilities of passively reducing the vibration of the railway vehicle carbody using piezoelectric elements [60,61,62,63,64] or stack type piezoelectric transducers [65], or on the active control of the vibrations of the railway vehicle carbody with piezoelectric actuators [66]. A recent study by a team of researchers from Spain aims to experimentally analyse a passive method for increasing the structural damping of light carbody of high-speed trains to improve ride comfort [67]. Other works contain detailed descriptions of experimental systems specially designed to be used in the investigation of methods of reducing structural vibrations of the railway vehicle carbody [68,69,70,71,72,73]. The longitudinal interaction between carbody and bogie through the traction rod can influence the bending vibrations of the vehicle carbody, an aspect studied in the research focused on the effect of the flexural and twisting modes on the ride quality index of the high-speed Shinkansen railway vehicle carbody. In this context, a scale model of the vehicle was constructed to validate the numerical results [74].
In the following, a general description of these experimental systems is presented, which include scale models of the railway vehicle carbody.
Takigami et al. used piezoelectric elements in a passive method to improve ride comfort by reducing vertical bending vibrations of the railway vehicle carbody [60,61,62,63,64]. The principle of the method is based on the property of piezoelectric elements to transform the mechanical energy of vibrations into electrical energy, which was then dissipated in a shunt circuit. Two types of shunt circuits were investigated, both designed to be used in conditions of high amplitude vibrations. For the damping of a single mode of vibration, the shunt circuit consisted of an inductor and a resistor in series, tuned for a single frequency (single-mode shunt circuit). To reduce two modes of vibration, the resistor and inductor connected in series were connected in parallel with a capacitor in series with another resistor and inductor, thus obtaining two electrical resonances (two-mode shunt circuit). The piezoelectric elements were attached to the side beams (four on each beam) of a 1:5 scale model of the carbody of a Shinkansen vehicle (Figure 3). This model had the length of 4.9 m, the width of 0.67 m, the height of 0.6 m, and the mass of 292 kg. The scale model of the carbody rested on air springs at four points corresponding to the suspension positions of a real vehicle. An electrodynamic shaker was used to generate vertical vibrations, which was mounted at one end of the scale model of the carbody. The excitation force was measured with a load cell mounted between the rod of the electrodynamic shaker and the the scale model of the carbody. To measure the vibrations of the scale model of the carbody, accelerometers were mounted on its surface.

Figure 3.
Scale model of a Shinkansen vehicle [60,63,64].
Kamada et al. have proposed new control method of the vibrations of the railway vehicle carbody through damping shunts, based on stack-type piezoelectric devices [65]. For this purpose, two types of shunt circuits were analysed, respectively, an LR-LRC shunt circuit and a negative capacitance shunt circuit. Effectiveness and robustness of the shunt damping systems were investigated experimentally with a 1:6 scale model of the carbody a Shinkansen vehicle. The carbody was reduced to a beam made of aluminium, having the natural frequencies of the first five modes of vibration very close to those of the carbody of the Shinkansen vehicle. The beam had a length of 4 m and a rectangular section with the width of 0.55 m and the height of 0.025 m. The mass of the beam was 150.15 kg. The beam was supported by two air springs and is excited with the help of an electro-magnetic shaker positioned at one end of it. The excitation force was measured with the force cell mounted between the electro-magnetic shaker and the beam, and the vibrations of the beam were measured with the three accelerometers mounted in its middle and at the two ends.
The main structure of the experimental system presented above, namely the 1:6 scale model of the Shinkansen vehicle carbody reduced to an aluminium beam, supported on two air springs, was also used by Kamada et al. [65,66] to investigate the effectiveness of an active carbody vibration control method. This method is based on the combined use of piezoelectric actuators and linear actuators. Linear actuators were used to reduce rigid vibration modes (first and second vibration modes) and piezoelectric actuators to reduce flexible vibration modes (third, fourth, and fifth vibration modes).
The method proposed by Melero et al. [67] involves increasing the structural damping of light carbody of high-speed trains using the viscoelastic patches (through Constrained Layer Damping—CLD). The research methodology is based on experimental modal analysis of scaled aluminium beam corresponding to a portion of the floor of a light rail vehicle (see Figure 4) to which different CLDconfigurations were added. To identify the CLD configuration that provided the highest absolute and specific modal damping, several solutions were compared regarding the type of constraint layer (uniform or honeycomb), viscoelastic layer thickness, location, covered area, and continuity between patches. The scale model corresponding to a portion of the floor of the railway vehicle shown in Figure 4 consisted of two webs having a width of 130 mm and a length of 5078 mm. These dimensions were chosen so that the stiffness per unit width of the scale model is the same as that of the railway vehicle floor.

Figure 4.
The scaled aluminium beam; mounting supports detail [67].
Figure 5 shows different types of CLD patches used. Type A represents the beam without CLD, and types B and C were constructed by attaching a rigid aluminium sheet (uniform or honeycomb) to a layer of viscoelastic polymer. The constraint layer used for type B corresponded to an aluminum sheet with a length of 2500 mm, a width of 125 mm and a thickness of 6 mm. For type C, a honeycomb with a thickness of 20 mm was used, made of aluminum foil with a thickness of 0.08 mm, having a hexagonal cell with a size of 6.4 mm. The honeycomb was sandwiched between two aluminum sheets of different thicknesses, the thicker one being the furthest from the aluminum beam. For types B and C, two different thicknesses were used for the viscoelastic polymer layer, 1 mm, and 2 mm, respectively. Twelve different cases of partial treatment of the aluminium beam with CLD were thus obtained, which were evaluated experimentally. These cases are represented schematically in Figure 6.

Figure 5.
Types of scaled beams: (a) without CLD; (b) with CLD patch with uniform constraining layer; (c) with CLD patch with honeycomb constraining layer [67].
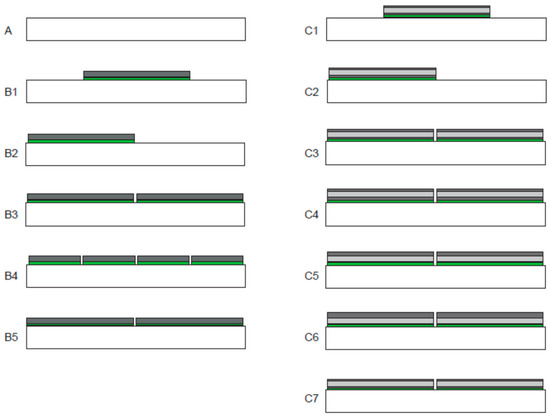
Figure 6.
CLD configurations analysed experimentally [67].
In a research project developed by a team in Japan, an experimental system was built that includes a 1:12 scale model of the Maglev vehicle carbody [68,69]. This experimental system, named MAGMOX (Figure 7), was designed to study different methods of reducing vehicle vibration. The carbody was made of aluminium and thus designed to be flexible enough to be used for bending vibration studies. At each end, the carbody was supported by helical springs on a bogie. Coil springs shaped the vehicle’s secondary suspension.
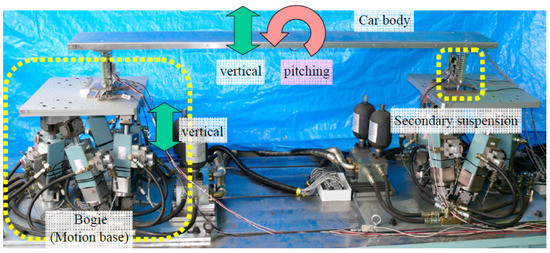
Figure 7.
Configuration of the MAGMOX experimental system [68,69].
The vehicle carbody was specially designed to have the natural frequency of the first vertical bending mode below 50 Hz, which is the maximum vibration frequency that can be generated by the motion base. Two carbodies were built, one with the natural frequency of the first vertical bending mode of 45 Hz and the other with the frequency of 50 Hz. The length (2 m) and width (0.25 m) of both types of carbodies were equivalent to about 1/12 the length and width of a full-scale vehicle. The heights of the two types of carbodies were reduced to 30 mm and 35 mm, respectively, because it was necessary to minimize the second-order cross-sectional moment. Each bogie was represented by a hydraulically powered movement base, having 6 degrees of freedom, respectively, three translations—vertical, lateral, and longitudinal, and three rotations—yaw, pitch, and roll. The secondary structure of the suspension has been designed to allow vertical translation and pitching rotation of the carbody and, at the same time, to limit lateral, rolling and yawing motions. In the four corners of the carbody, linear motors were mounted, which had the role of actuator for controlling the vibrations of the secondary suspension.
In a study by a team of Austrian researchers, a test bench set up for flexible carbody of light rail vehicles is described [70,71]. The test bench was built to be used in the investigation of active methods of suppressing structural vibrations of the vehicle carbody [72,73]. It consisted of a modular test stand, the 1:10 scale vehicle carbody structure and all components used for actuation and measurement (Figure 8).

Figure 8.
Overview of the test bench [70].
In the present case, the carbody model was made of aluminium sheet, glued with a structural metal adhesive. It is specified that this stand allowed the testing of any lightweight flexible structure between 1 and 2.5 m in length and approximately 0.4 m in width. The vehicle carbody was elastically suspended by means of 4 coil springs supported by a structure with adjustable height. This construction allowed connection with the shaker which was mounted on an individual concrete foundation for vibration isolation. The shaker was placed inside a steel frame that allowed different mounting positions in relation to the structure. Using this framework, vertical and horizontal excitations could be applied to both the top and bottom of the carbody structure.
For the evaluation of the numerical results regarding the effect of the traction rod on the flexible vibrations of the railway vehicle carbody in the paper [74], an experimental test rig based on a scaled model of a Shinkansen high-speed railway vehicle was constructed. The main structure of the test rig was the 1:24.5 scale model of the Shinkansen vehicle carbody reduced to a flexible beam, supported at the two ends on four coil springs that represent the secondary suspension. The primary suspension of each bogie also consisted of four coil springs. Two piezotronics modal shakers were used to excite the two bogies of the vehicle.
3. Demonstrative Experimental System for Testing the Functionality of a New Method of Reducing Vertical Bending Vibration of the Railway Vehicle Carbody
3.1. Theoretical Concept of the Method
The method of reducing the vertical bending vibration of the carbody of railway vehicles is based on the concept that a passive system can be used to limit the rotation of the cross-sections of the carbody to oppose the bending of the carbody. This system is represented by two anti-bending bars, which are rigidly mounted to the longitudinal beams of the carbody underframe. The effectiveness of using anti-bending bars in terms of reducing carbody bending vibration and improving the ride comfort of the vehicle was investigated using the results obtained through numerical simulations. Numerical simulation applications were developed based on a rigid–flexible-coupled railway vehicle model [29]. The model of the railway vehicle with anti-bending bars, mounted on either side of the carbody, is presented in Figure 9. The carbody was modeled by a free–free equivalent beam, of Euler–Bernoulli type, and the bogies and axles were considered as rigid bodies. It was considered that the vehicle is running at constant speed on a perfectly rigid track. The vertical irregularities of the track impose the vertical displacements η1...4 in the axles.
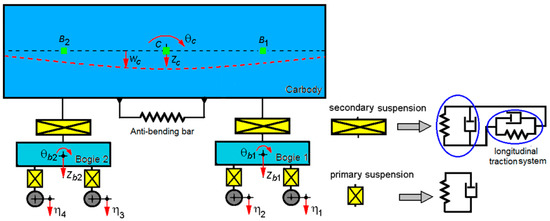
Figure 9.
The rigid-flexible coupled model of the railway vehicle [29].
The vertical vibration modes of the carbody relevant from the point of view of ride comfort were considered, namely the rigid vibration modes—bounce, zc, and pitch, θc, and the first carbody vertical bending, wc. In the case of bogies, the rigid vibration modes were considered, respectively, the bounce zb1,2 and pitch θb1,2.
The secondary suspension afferent to a bogie was modeled via two Kelvin–Voigt systems, where one was for the representation of the vertical suspension of the vehicle and the other one was used to model the traction longitudinal system between the carbody and the bogie. Each vertical primary suspension corresponding to an axis was modeled by a Kelvin–Voigt system. The anti-bending bars were represented by two elastic elements.
The influence of the bars longitudinal and bending vibrations was neglected. The main constructive parameters of the anti-bending bars, namely its length and diameter, were determined by imposing two conditions. The first referred to reaching a certain bending frequency of the carbody equipped with anti-bending bars, convenient from the perspective of the ride comfort. By the second condition, it was necessary that the bending frequency of the anti-bending bars be high enough compared to the bending frequency of the carbody, so as to avoid the interference between the bending vibrations of the anti-bending bars and the ones of the carbody.
The influence of the anti-bending bars upon the dynamic response of the carbody was examined based on the results of numerical simulations regarding the frequency response functions of the vehicle. Figure 10 features the power spectral density (PSD) of the carbody vertical acceleration weighted according to UIC 513 and EN 12,299 [78,79] to account for human sensitivity to vertical vibrations. The PSD was calculated in three reference points of the carbody, relevant for ride comfort (see Figure 9)—in the center of the carbody (point C) and above the two bogies (points B1 and B2).
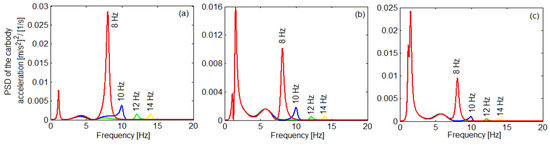
Figure 10.
Effect of the anti-bending bars upon the carbody dynamic response at velocity of 270 km/h: (a) at the carbody centre; (b) above the front bogie, and (c) above the rear bogie [29].
In the case of the carbody without anti-bending bars, the spectrum of the vertical acceleration power density was dominated in the centre of the carbody by the bending vibrations having the frequency of 8 Hz. Due to the anti-bending bars, the peaks of the acceleration power spectral density decreased near the bending frequency of the carbody. As appropriate, these peaks were then found at 10 Hz, 12 Hz and 14 Hz, respectively. The introduction of anti-bending bars had the effect of reducing the level of vibrations due to bending of the carbody and above the bogies. It should be noted, however, that the vibration level of the carbody due to bending decreased significantly after increasing the bending frequency from 8 Hz to 12 Hz. Further increasing the bending frequency of the carbody to 14 Hz did not introduce any noticeable changes.
The effect of the anti-bending bars on ride comfort (evaluated via the ride comfort index [78,79]) at the reference points located in the centre of the carbody and above the two bogies is shown in Figure 11. A more important improvement in ride comfort was noticeable in the centre of the carbody, especially at high velocities. For example, at velocity of 270 km/h, the comfort index for the carbody without anti-bending bars was 2.68. At the bending frequency of the carbody at 12 Hz, the ride comfort index was reduced to 1.19, and at 14 Hz, the comfort index dropped to 1.06. It is worth noting that for carbody bending frequencies higher than 12 Hz, a significant improvement in ride comfort was no longer obtained. The ride comfort was also slightly increased above the bogies where, by increasing the bending frequency of the carbody to 14 Hz due to the anti-bending bar, at a velocity of 270 km/h, the comfort index drops from 2.11 to 1.67—above the front bogie, respectively to 2.25 to 1.85—above the rear bogie.
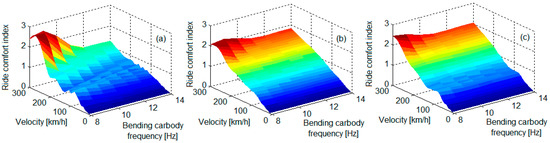
Figure 11.
Influence of the anti-bending bars upon ride comfort: (a) at the carbody centre; (b) above the front bogie, and (c) above the rear bogie [29].
3.2. Structure of the Demonstrative Experimental System for Laboratory Testing of the Method’s Functionality
Demonstrative experimental system for testing the functionality of the method of reducing vertical bending vibrations of the carbody of the railway vehicles based on a system consisting of two anti-bending bars is schematically represented in Figure 12.
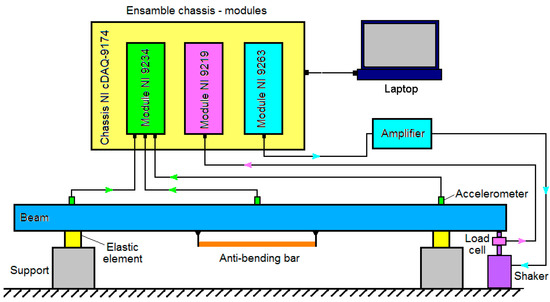
Figure 12.
Scheme of the demonstrative experimental system.
The main element of the demonstrative experimental system was the scale model of the vehicle carbody, which was reduced to an aluminium beam, with the bending eigenfrequency close to the bending eigenfrequency of the real carbody. On either side of the carbody scale model, the anti-bending bars were attached.
The carbody experimental model was supported on rubber elements (suspension elastic elements). The excitation force was generated with an electro-dynamic vibration generator (shaker) and measured by a load cell located between the shaker and the carbody experimental model. The vibrations measurement of the carbody experimental model was obtained with the accelerometers mounted on its middle and against the support points on the elastic elements.
The demonstrative experimental system integrated more specialized components, meant for the acquisition and processing of the experimental data (the acceleration of the carbody model and the excitation force) or for generating the command signals of the shaker, controlled via dedicated software applications. It is about the ensemble comprising the NI cDAQ-9174 type chassis and three modules with specialized functions—the NI 9234 module for acquiring and synthesis of the data flow from the three accelerometers type 4514 Brüel and Kjær, the NI 9263 module for generation the command signals of the shaker type of LDS V201 and the NI 9219 module meant for the measurements of voltage and current with applications in the resistive electric tensometry. This ensemble together with the three accelerometers, the shaker and the amplifier formed the measurement and control chain of the demonstrative experimental system. This was connected to a laptop.
3.3. Theoretical Model of the Experimental Model of the Carbody with Anti-Bending Bars
Experimental model of the vehicle carbody (Figure 13) could be assimilated to a uniform free–free Euler–Bernoulli beam of length lc, with rectangular cross-section of width b and height h (Figure 14).
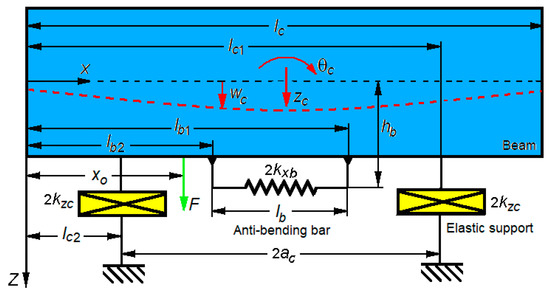
Figure 13.
Theoretical model of the experimental model of the carbody with anti-bending bars.
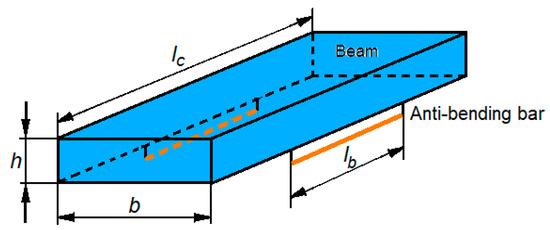
Figure 14.
Dimensions of the experimental model of the carbody with anti-bending bars.
The mass of the experimental model of the carbody was Mc = ρbhlc, where ρ is the density of the material, and the mass of the beam per unit length is mc = Mc/lc. The bending stiffness of the beam is EcIc, where Ec is the longitudinal modulus of elasticity, and Ic is the moment of inertia of the cross-section of the beam. Additionally, the loss factor due to structural damping was introduced, denoted by ηc. Anti-bending bars of length lb were fixed rigidly to the lower part of the experimental model of the carbody, at the distances lb1,2 = (lc ± lb)/2 from the origin of the reference system (XOZ), respectively, at the distance hb from the neutral axis of the experimental model of the carbody.
The anti-bending bars were stressed in tension–compression, and each introduced a longitudinal stiffness given by the relation
where Eb is the longitudinal modulus of the bar material, and Db is the diameter of the cross-section of bar.
The experimental model of the carbody was laid on four elastic supports that modeled the suspension elements of the vehicle carbody, of stiffness kzc and loss factor ηzc. The longitudinal base of the elastic supports was 2ac, and the distances lc1,2 = lc/2 ± ac fixed the support points of the experimental carbody model on the elastic supports.
The main vibration modes of the experimental model of the carbody were bounce, pitch, and the first vertical bending mode. The vertical displacement of a section of the experimental carbody model at x distance from the origin of the reference system, wc(x, t), was the result of the superposition of the three modes of vibration,
where zc is the displacement of the experimental model due to the bounce, θc is the pitch angle, and Tc is the time-coordinate of the first vertical bending mode; Xc is the eigenfunction associated to the vertical bending mode
with
which verifies the characteristic equation
where ωvb is the angular frequency of the vertical bending of the experimental model of the carbody without anti-bending bars.
Vertical harmonic force F(t) = Focosωt, of amplitude Fo and angular frequency ω, acts upon the experimental model of the carbody at the distance xo from the origin of the reference system.
Equation of motion of the experimental model of the carbody with anti-bending bars was obtained using the Euler–Bernoulli beam theory, of the form
where δ(.) is Dirac delta function, Fzci are the forces in the elastic supports, and Fxbi are the forces developed by the anti-bending bars, due to the rotation of the cross-sections where the bars were fixed to the carbody,
Applying the modal analysis method [80] and retaining the first three modes of vibration Equation (2), equations of motion of the experimental model of the carbody result:
where Jc is the mass moment of inertia about the lateral axis of symmetry and, kmc and Mmc are the modal stiffness and modal mass of the experimental model of the carbody,
The following notations were adopted:
Equations of motion (9)–(11) became:
where .
It was observed that the bounce vibration was coupled with the vertical bending vibration (see Equations (15) and (17)), meanwhile the pitch vibration was independent (Equation (16)).
3.4. Dimensioning the Experimental Model of the Carbody
To determine the dimensions of the experimental model of the carbody, the dimensions of the actual carbody of a passenger coach were used. For example, Table 1 shows the main dimensions of the passenger coach series 21–90, also known as AVA 200.

Table 1.
The main dimensions of the carbody of the AVA 200 passenger coach [81].
The dimensions of the experimental carbody model were determined based on the condition of achieving the natural frequency of the first vertical bending mode of the real carbody. This frequency was determined experimentally and according to the specialized literature, for long and light carbody of passenger coaches, it was located in the range of 8–12 Hz, depending on the vehicle configuration [1,34,45,47,65].
As shown above, the first vertical bending mode was coupled to the bounce vibration and, to calculate the natural frequencies of the two coupled vibration modes of the experimental carbody model, the following homogeneous equations of motion derived from Equations (15) and (17) were considered
Harmonic solutions were imposed
where Zco and Tco are the amplitudes of the bounce and vertical bending vibrations.
Differential equations set (18) and (19) became
resulting in the condition
Solving biquadratic equation, the natural frequencies of the bounce and vertical bending coupled vibrations of the experimental model of the carbody with anti-bending bars were obtained,
where the natural frequencies of the bounce and bending uncoupled vibrations appeared:
- –
- bounce,
- –
- vertical bending,and the following notationswhere ε is calculated with Equation (13) for lc1 and lc2 corresponding to the wheelbase 2ac obtained by scaling the passenger coach wheelbase.
Taking kxb = 0 (fxb = 0), the natural frequencies of the experimental model of the carbody without anti-bending bars result
The natural frequency of the bounce vibration of the railway vehicle was set for comfort reasons around 1 Hz, a value much lower than the natural frequency of the vertical bending vibration, which practically ensured the decoupling of the two types of vibrations. On the other hand, the natural bounce frequency of 1 Hz required the static deflection of the suspension to be approx. 0.25 m [82]. This static deflection value was far too large to be achieved with the demonstrative experimental system. It was noticed that the large static deflection of the elastic supports corresponded to a small stiffness of the elastic supports, which could be obtained by increasing the length and/or reducing their section. In this case, buckling stability problems of the demonstrative experimental system may arise. Considering the above two aspects, the bounce vibration frequency was adopted to a sufficiently high value, to ensure the stability of the experimental model and avoid the interference of the bounce vibration with the vertical bending vibration.
By conveniently choosing the frequencies f(b_vb)1 and fb, the vertical bending natural frequency of the experimental carbody model was obtained with the relation
Knowing the dimensions and material characteristics of the carbody experimental model, the vertical bending natural frequency could be calculated with the relation
where βlc = 4.7300407449 is the smallest nonzero solution to the characteristic Equation (5).
Equation (31) shows that the natural frequency of vertical bending increased directly proportional to the height of the experimental model of the carbody h, decreased with the square of the length lc and did not depend on the width of the experimental model b.
To determine the dimensions of the experimental model of the carbody, it was necessary to know the correlation between the length of the model lc, the natural frequency of the vertical bending fvb and the height of the model h. It followed from Equation (31)
The length of the experimental carbody model was obtained by conveniently adopting the scaling factor of the actual passenger coach carbody length. Accepting the scaling factor 1:10, for the carbody of the AVA 200 passenger coach, lc = 2.6 m was obtained.
By scaling 1:10 of the carbody width of the AVA 200 passenger coach, b = 0.28 m results. However, considering that the natural frequency of the vertical bending of the experimental carbody model did not depend on the model width (see. Equation (31)), b = 0.4 m was adopted to improve the stability of the carbody model on elastic supports.
Further on, considering fb = 30 Hz and f(b_vb)1 = 8 Hz, the frequency fvb of 10.92 Hz results from Equation (29). According to the relation (32), for fvb = 10.92 Hz, Ec = 0.7·1011 N/m2 and ρ = 2.7·103 kg/m3 (aluminium model), h = 0.013 m was obtained by rounding.
With all dimensions set, the mass of the experimental carbody model without anti-bending bars results, Mc = 36.058 kg.
The stiffness of the elastic supports of the demonstrative experimental model was established from the condition of achieving the natural frequency of the bounce vibration fb = 30 Hz, with the relation
Table 2 centralizes the main parameters and material characteristics of the experimental model of the carbody without anti-bending bars established in this section. Table 3 shows the natural frequencies of the experimental carbody model without anti-bending bars.

Table 2.
Characteristics of the experimental model of the carbody.

Table 3.
Natural frequencies of the experimental model of the carbody.
3.5. Dimensioning of Anti-Bending Bars
The main constructive parameters of the anti-bending bar, namely its length and diameter, were established from the condition of achieving a certain vertical bending frequency of the experimental model of the carbody with anti-bending bars,, convenient from the point of view of ride comfort.
Taking in Equation (24)
results first
and then the stiffness of the anti-bending bar was obtained from Equation (27)
By appropriately choosing the vertical bending frequency of the experimental carbody model with anti-bending bars () and the length of the anti-bending bar (lb), the cross-section area (Sb) of the anti-bending bar could be calculated using the relation (1)
where Eb is the longitudinal modulus of the anti-bending bar.
To avoid the interference between the structural vibration of the anti-bending bar and that of the experimental model of the carbody, it was necessary to ensure the condition that the vertical bending frequency of the anti-bending bar was sufficiently high in relation to the vertical bending frequency of the experimental model of the carbody. Considering the anti-buckling bar as a Euler-Bernoulli beam embedded in the fasteners of the experimental carbody model, the first vertical bending frequency of the anti-bending bar was given by the relation
where Ib is the cross-section inertia moment of the anti-bending bar, ρb its density, and α = 4,7300407449.
Requiring that the frequency of the anti-bending bar be at least one octave from the natural frequency of the experimental model of the carbody with anti-bending bars (), the maximum length of the anti-bending bar was obtained in the form of a nonlinear equation
which ca be solved via the simple iteration method.
Knowing lbmax, the minimum section of the anti-bending bar was further determined,
and its diameter Dbmin = 2(Sbmin/π)1/2.
For reasons of effectiveness of the stiffening of the experimental model of the carbody with the help of the anti-bending bars, it was envisaged that they will be made of steel (Eb = 2.1·1011 N/m2 and ρb = 7.850·103 kg/m3).
Figure 15 shows the maximum length of anti-bending bars, and Figure 16 shows their minimum diameter for the vertical bending frequency of the experimental carbody model with anti-bending bars between 12 and 18 Hz. It was specified that the lower limit of the frequency range had been set so that it is outside the range of sensitivity of the human body to vertical vibrations. Calculations were performed for hb = 40 mm. It was observed that both the maximum length of the anti-bending bars and their minimum diameter increased approximately linearly as a function of , but the increase was more pronounced in the case of the minimum diameter of the anti-bending bars. For example, the maximum length of the anti-bending bars increased according to the natural frequency of the experimental model of the carbody with anti-bending bars from 900 mm, at Hz, to 1006 mm for Hz, respectively, 11.78%. The increase in the minimum diameter of the anti-bending bars was 89%, respectively, from approx. 4.19 mm to 7.92 mm.
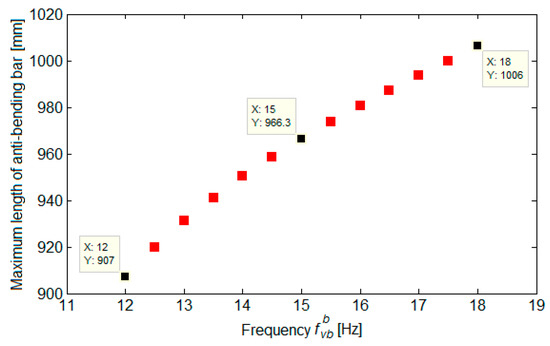
Figure 15.
Maximum length of the anti-bending bars.
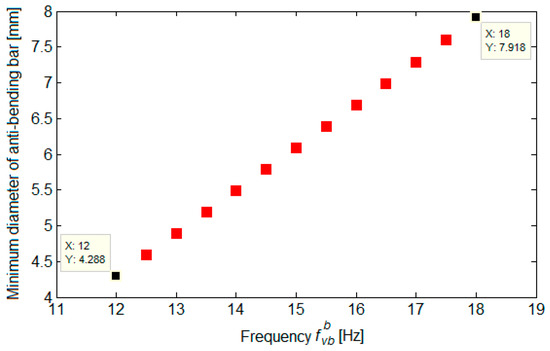
Figure 16.
Minimum diameter of the anti-bending bars.
It was also noted that the natural frequency of the vertical bending of the experimental carbody model could be brought outside the range of sensitivity of the human organism to vertical vibrations for anti-bending bars with a maximum length of 907 mm and a diameter greater than 4.288 mm.
Sizing of the anti-bending bars could be done starting from a certain imposed frequency of vertical bending of the experimental model of the carbody with anti-bending bars, convenient from the point of view of ride comfort, and conveniently choosing the length of the bars. Applying the algorithm presented above, the value of the diameter of the bar was obtained, the value of which was then rounded to a whole number for practical reasons. Finally, the natural frequency of the vertical bending of the experimental model of the carbody with anti-bending bars was calculated and it was verified that it was not significantly different from the one imposed initially. For example, if the length of anti-bending bars lb = 900 mm was imposed and adopted (value which is less than the limit of 966.3 mm, according to Figure 15), then Db = 6.22 mm results. Rounding to Db = 6 mm, a deviation of approx. 2.34% in relation to the imposed frequency was obtained.
To experimentally test the effectiveness of the method of reducing the vertical bending vibrations of the experimental carbody model with the help of anti-bending bars, several constructive variants of the anti-bending bars could be adopted. For instance, the solution of anti-bending bars of fixed length, lb = 900 mm, but with different diameters could be adopted. Table 4 shows the values of the natural frequencies of the vertical bending of the experimental model of the carbody with anti-bending bars that could be obtained for bars with a diameter between 5 and 8 mm, mounted at hb = 40 mm.

Table 4.
Frequency of the experimental model of the carbody with anti-bending bars as a function of the minimum diameter of the anti-bending bars.
3.6. Calculation of the Frequency Response Functions of the Experimental Carbody Model
For the calculation of the frequency response functions of the acceleration of the experimental model of the carbody with anti-bending bars under the action of the harmonic force F(t) = Focos(ωt), the following complex quantities were associated with the real ones:
where ,,, are complex amplitudes.
Hysteretic damping specific to the rubber element was introduced
and hysteretic damping of the experimental carbody model and anti-bending bars
where hc and hb were the corresponding loss factors.
Equations of motion (15)–(17) became
The solutions of these equations of motion were of the form:
With the relations (48)–(50), the frequency response functions of the acceleration of the experimental model of the carbody with anti-bending bars corresponding to the three vibration modes could be calculated
The amplitude of vibration of the experimental model of the carbody at some section x was given by the relation
and the acceleration amplitude of the experimental model of the carbody was
The acceleration frequency response function of the experimental model of the carbody was calculated with the relation
in which the contributions of the three modes of vibration could be identified,
The first term represented the contribution of bounce vibration, the second term is due to pitch vibration, and the third term came from the vertical bending of the experimental model of the carbody.
After processing, Equation (54) was brought to the form:
For the calculation of the frequency response function of the acceleration in the middle of the experimental model of the carbody, x = lc/2 iwa considered, and above the elastic supports, x = lc1,2.
3.7. Results of the Numerical Simulations
In this section, the results of the numerical simulations on the frequency response function of the acceleration of the experimental model of the carbody without/with anti-bending bars are presented. Based on these results, the effectiveness of the anti-bending bars in reducing the vertical bending vibration of the experimental model of the carbody is analysed. The numerical simulation parameters of the experimental model of the carbody without anti-bending bars are those presented in Table 2. The following loss factors are also considered: ηzc = 0.12—for elastic rubber elements and ηc = ηb = 0.01—for the experimental model of the carbody and anti-bending bars.
Figure 17 shows the component of the frequency response function of the acceleration of the experimental model of the carbody corresponding to the vertical bending, highlighted in Equation (55) as , calculated in the middle of the experimental model of the carbody (diagram a) and above the elastic supports (diagram b). The results were obtained for anti-bending bars of length 900 mm, positioned at hb = 40 mm from the neutral axis of the experimental model of the carbody, and four diameter values, namely 5 mm, 6 mm, 7 mm and 8 mm.
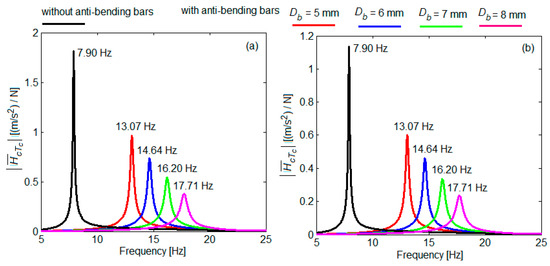
Figure 17.
Component of the acceleration response function of the experimental model of the carbody corresponding to the vertical bending: (a) at middle; (b) above elastic supports.
To verify the effectiveness of the anti-bending bars, the acceleration response function component of the experimental model of the carbody without anti-bending bars was also represented on the diagrams, calculated with the relation
It was noted the increase in the resonance frequency of the vertical bending of the experimental model of the carbody when the diameter of the anti-bending bars increased, results that are consistent with the observations are presented in Figure 16.
The increase in the resonance frequency of the vertical bending of the experimental model of the carbody was the result of the stiffening of the system because of the increase in the rigidity of the anti-bending bars when their diameter increased. The effectiveness of the anti-bending bars in reducing the vertical bending vibrations of the experimental model of the carbody was highlighted both in the middle of the experimental model of the carbody and above the elastic supports. By introducing the anti-bending bars, a significant reduction in the peaks of the response function of the acceleration corresponding to the vertical bending was obtained at the vertical bending frequency of the experimental model of the carbody. The reduction became more important as the diameter of the anti-bending bars increased. For example, for bars with a diameter of 5 mm, the reduction in the peak of the response function was 47% and reached 79% for bars with a diameter of 8 mm.
It should be noted that the vertical bending vibration were more pronounced in the middle of the experimental model of the carbody than above the elastic supports. For example, for the experimental model of the carbody without anti-bending bars, at the resonance frequency of 7.90 Hz, the response function had the value of 1.817 (m/s2)/N in the middle of the experimental model, which was about 60% higher than above elastic supports where the value is 1.137 (m/s2)/N.
Figure 18 shows five curves corresponding to the maximum of the acceleration frequency response function (Equation (56)), calculated along the experimental model of the carbody, in the frequency range 5–20 Hz, the range in which the vertical bending frequencies of the experimental model of the carbody without/with anti-bending bars were found. Anti-bending bars with the length of 900 mm were considered, mounted at hb = 40 mm and with the same four diameter values of the anti-bending bars as in the previous example. For the calculation of the frequency response function of the acceleration of the experimental model of the carbody without anti-bending bars, the relation (56) was used, adapted to this situation:
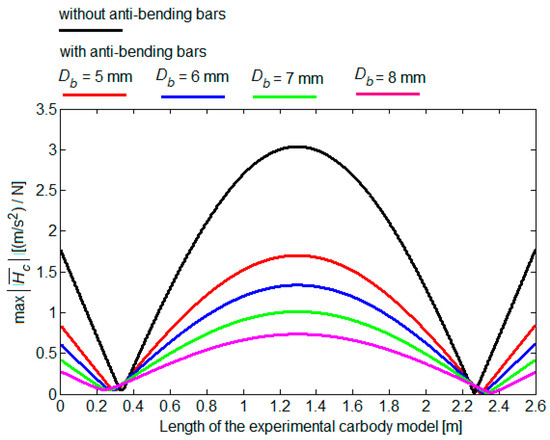
Figure 18.
Maximum of the acceleration frequency response function along the experimental carbody model.
All five curves of the maximum of the acceleration frequency response function have the same shape: they recorded a maximum in the middle of the experimental model of the carbody, decreased continuously to the points corresponding to the two nodes of the vertical bending, then increased continuously towards the two ends of the experimental model of the carbody. These results show that the effect of the anti-bending bars in reducing vertical bending vibrations was manifested along the entire length of the experimental model of the carbody, but the greatest effectiveness was recorded in the middle of the experimental model of the carbody, where vertical bending had an important contribution, as shown above (see Figure 17). It was again noted that the effectiveness of the anti-bending bars increased as their diameter increased. For example, in the middle of the experimental model of the carbody without anti-bending bars the acceleration frequency response function was 3.037 (m/s2)/N and decreased to 1.702 (m/s2)/N in the case of the experimental model of the carbody with anti-bending bars with the diameter of 5 mm. For anti-bending bars with the diameter of 8 mm, the decrease was more important, reaching up to 0.735 (m/s2)/N.
Diagrams in Figure 19 show the frequency response functions of the acceleration of the experimental model of the carbody without anti-bending bars, respectively, with anti-bending bars of length 900 mm and different diameters, mounted both at the distance hb = 40 mm and at the distance hb = 50 mm. The presented results show that the increase in resonance frequencies of vertical bending was not only influenced by the diameter of the bar, but also by the distance hb. As can be seen, for the same diameter of the anti-bending bars, the resonance frequency of the vertical bending of the experimental model of the carbody increased as the distance hb was higher, and this can be explained by the increase in the bending moment of the longitudinal force in the anti-bending bars.
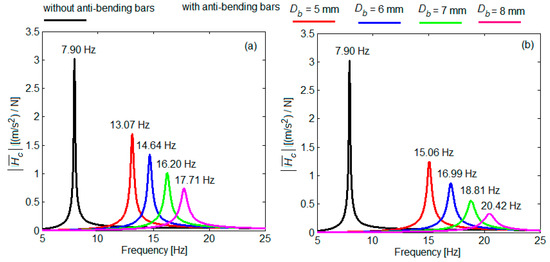
Figure 19.
Influence of the diameter of the anti-bending bars in correlation with the distance hb on the frequency response function of the acceleration in the middle of the experimental mode of the carbody: (a) hb = 40 mm; (b) hb = 50 mm.
Figure 20 shows the acceleration frequency response functions of the experimental model of the carbody without/with anti-bending bars of 6 mm diameter and four length values, respectively, 600 mm, 700 mm, 800 mm and 900 mm. For the distance hb, two values were considered, 40 mm and 50 mm. On the one hand, it was also observed here that increasing hb had the effect of increasing the vertical bending frequency of the experimental model of the carbody by at least 2 Hz. On the other hand, a slight increase in the frequency of vertical bending of the experimental model of the carbody was observed when increasing the length of the anti-bending bar. For example, according to diagram (a), the vertical bending frequency increased from 13.30 Hz for lb = 600 mm to 14.64 Hz for lb = 900 mm. This result seems to be paradoxical, since when increasing the length of the anti-bending bars, their longitudinal stiffness decreased (Equation (1)), which led to the reduction in the vertical bending frequency of the experimental model of the carbody. Analysing the relation (24), with the help of which the vertical bending frequency of the experimental model of the carbody with anti-bending bars was calculated, it was observed that the bar length intervened through both stiffness of the anti-bending bars kxb and parameter ψ = dXc(lb1)/dx.
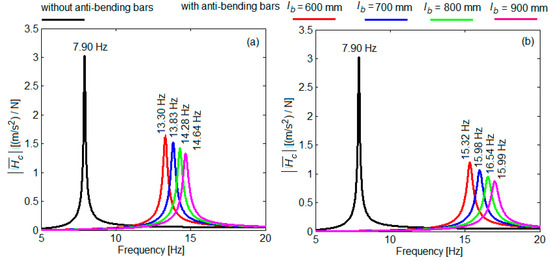
Figure 20.
Influence of the length of the anti-bending bars in correlation with the distance hb on the frequency response function of the acceleration in the middle of the experimental model of the carbody: (a) hb = 40 mm; (b) hb = 50 mm.
The combined effect of the two quantities, kxb and ψ, on the vertical bending frequency is shown in Figure 21, for four values of the diameter of the anti-bending bars. Regardless of the diameter of the anti-bending bars, the vertical bending frequency curves of the experimental model of the carbody showed a maximum of 1565 mm. For smaller values of the length of the bars, the effect of the parameter ψ was dominant and the vertical bending frequency increased as the bars were longer. At larger lengths, the influence of the bar length was manifested mainly through the stiffness of the anti-bending bars and for this reason the vertical bending frequency decreased when the bars are longer.
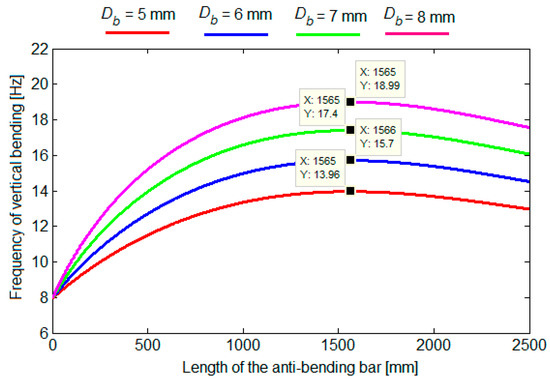
Figure 21.
Influence of the length of the anti-bending bars on the vertical bending frequency of the experimental model of the carbody.
4. Conclusions
In the first part of the paper, applications of the experimental laboratory systems used for validation of the concepts or the effectiveness of the proposed methods for reducing the flexible vibration modes of the carbody of the railway vehicles are presented.
The second part of the paper is dedicated to the presentation of a new demonstrative experimental system specially designed by the authors of the present paper for testing the functionality of an original method of reducing vertical bending vibration of the carbody of the railway vehicles based on a passive system consisting of two anti-bending bars.
The main element of the experimental demonstrative system is the scale model of the vehicle carbody, assimilated to a beam, to which the two anti-bending bars can be attached. The methodology for dimensioning the experimental model of the carbody and the anti-bending bars is original and is based on several conditions introduced: ensuring the buckling stability of the demonstrative experimental system, achieving the natural frequency of the vertical bending of the real carbody without anti-bending-bars, achieving the vertical bending frequency of the experimental model of the carbody with anti-bending bars outside the range of sensitivity of the human body to vertical vibration, avoidance of the interference of the bounce vibration with the vertical bending vibration of the demonstrative experimental model of the carbody and of the interference of the vertical bending vibration of the anti-bending bars with the vertical bending vibration of the experimental model of the carbody.
The effectiveness of the anti-bending bars from the perspective of increasing the natural frequency of vertical bending vibrations, and from the perspective of reducing the level of vertical bending vibrations of the experimental carbody model is investigated based on the results of numerical simulations. These highlight that the increase in the natural frequency of the vertical bending of the experimental carbody model is more pronounced when the diameter of the anti-bending bars and the distance at which the anti-bending bars are mounted in relation to the neutral axis of the experimental carbody model increases and less sensitive to the increase in the length of the bars anti-bending. The effect of the anti-bending bars in reducing the vertical bending vibrations is manifested along the entire length of the carbody model, but the greatest effectiveness is recorded in the middle of the carbody model, where the vertical bending has an important contribution. The effect of the anti-bending bars in the vibration reducing is more important the larger their diameter or if the distance from the longitudinal axis of the anti-bending bar to the neutral axis of the experimental carbody model increases.
These favourable theoretical results regarding the functionality and efficiency of the method of reducing vertical bending vibrations of the experimental model of the carbody with the help of the anti-bending bar system create the premises for research development and the transition to the next stage, namely the experimental verification of the functionality of the method.
Author Contributions
Conceptualization, M.D. and T.M.; methodology, T.M and M.D.; software, T.M.; validation, M.D. and T.M.; formal analysis, M.D., T.M. and I.I.A.; investigation, T.M. and M.D.; resources, M.D. and I.I.A.; writing—original draft, M.D. and T.M.; writing—review and editing, M.D. and T.M; project administration, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Ministry of Research, Innovation and Digitization, CCCDI—UEFISCDI, project number PN-III-P2-2.1-PED-2021-0319, within PNCDI III”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Tomioka, T.; Takigami, T.; Suzuki, Y. Numerical analysis of three-dimensional flexural vibration of railway vehicle car body. Veh. Syst. Dyn. 2006, 44, 272–285. [Google Scholar] [CrossRef]
- Huang, C.; Zeng, J.; Luo, G.; Shi, H. Numerical and experimental studies on the car body flexible vibration reduction due to the effect of car body-mounted equipment. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 103–120. [Google Scholar] [CrossRef]
- Yang, G.; Wang, C.; Xiang, F.; Xiao, S. Effect of train carbody’s parameters on vertical bending stiffness performance. Chin. J. Mech. Eng. 2016, 29, 1120–1126. [Google Scholar] [CrossRef]
- Diana, G.; Cheli, F.; Collina, A.; Corradi, R.; Melzi, S. The development of a numerical model for railway vehicles comfort assessment through comparison with experimental measurements. Veh. Syst. Dyn. 2002, 38, 165–183. [Google Scholar] [CrossRef]
- Fu, B.; Bruni, S. An examination of alternative schemes for active and semi-active control of vertical car-body vibration to improve ride comfort. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 386–405. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, B.K.; Thompson, C. A comparison study of ride comfort indices between Sperling’s method and EN 12299. Int. J.Rail Transp. 2019, 7, 279–296. [Google Scholar] [CrossRef]
- Orvanäs, A. Methods for Reducing Vertical Carbody Vibrations of a Rail Vehicle. In Report in Railway Technology Stockholm; KTH Engineering Sciences Department of Aeronautical and Vehicle Engineering, Division of Rail Vehicles: Stockholm, Sweden, 2010. [Google Scholar]
- Dumitriu, M. On the critical points of vertical vibration in a railway vehicle. Arch. Mech. Eng. 2014, 61, 115–140. [Google Scholar] [CrossRef]
- Dumitriu, M.; Dihoru, I.I. Influence of bending vibration on the vertical vibration behaviour of railway vehicles carbody. Appl. Sci. 2021, 11, 8502. [Google Scholar] [CrossRef]
- Bokaeian, V.; Rezvani, M.A.; Arcos, R. The coupled effects of bending and torsional flexural modes of a high-speed train car body on its vertical ride quality. Proc. Inst. Mech. Part K J. Multi-Body Dyn. 2019, 233, 979–993. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, C. Influences of carbody vertical flexibility on ride comfort of railway vehicles. Arch. Mech. Eng. 2017, 64, 119–238. [Google Scholar] [CrossRef]
- Hui, C.; Weihua, Z.; Bingrong, M. Vertical vibration analysis of the flexible carbody of high speed train. Int. J. Veh. Struct. Syst. 2015, 7, 55–60. [Google Scholar]
- Zhou, J.; Goodall, R.; Ren, L.; Zhang, H. Influences of car body vertical flexibility on ride quality of passenger railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 461–471. [Google Scholar] [CrossRef]
- Palomares, E.; Morales, A.L.; Nieto, A.J.; Chicharro, J.M.; Pintado, P. Comfort improvement in railway vehicles via optimal control of adaptive pneumatic suspensions. Veh. Syst. Dyn. 2022, 60, 1702–1721. [Google Scholar] [CrossRef]
- Lewis, T.D.; Jiang, J.Z.; Neild, S.A.; Gong, C.; Iwnicki, S.D. Using an inerter-based suspension to improve both passenger comfort and track wear in railway vehicles. Veh. Syst. Dyn. 2020, 58, 472–493. [Google Scholar] [CrossRef]
- Sugahara, Y.; Kojima, T. Suppression of vertical vibration in railway vehicle carbodies through control of damping force in primary suspension: Presentation of results from running tests with meter-gauge car on a secondary line. WIT Trans. Built Environ. 2018, 181, 329–337. [Google Scholar]
- Zheng, X.; Zolotas, A.C.; Goodall, R.M. Combining active structural damping and active suspension control in flexible bodied railway vehicles. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 8938–8944. [Google Scholar]
- Dumitriu, M. Influence of the suspension damping on ride comfort of passenger railway vehicles. UPB Sci. Bull. Ser. D Mech. Eng. 2012, 74, 75–90. [Google Scholar]
- Sugahara, Y.; Watanabe, N.; Takigami, T.; Koganei, R. Development of primary suspension damping control system for suppressing vertical bending vibration of railway vehicle car body. In Proceedings of the 9th World Congress on Railway (WCRR 2011), Lille, France, 22–26 May 2011; p. 115148008. [Google Scholar]
- Sugahara, Y.; Watanabe, N.; Takigami, T.; Koganei, R. Vertical vibration suppression system for railway vehicles based on primary suspension damping control—system development and vehicle running test results. Q. Rep. RTRI 2011, 52, 13–19. [Google Scholar] [CrossRef]
- Sugahara, Y.; Kazato, A.; Koganei, R.; Sampei, M.; Nakaura, S. Suppression of vertical bending and rigid-body-mode vibration in railway vehicle car body by primary and secondary suspension control: Results of simulations and running tests using Shinkansen vehicle. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 517–531. [Google Scholar] [CrossRef]
- Sugahara, Y.; Takigami, T.; Kazato, A.; Koganei, R.; Sampei, M. Suppression of vertical vibration in railway vehicles by damping force control of primary suspension using an LQG controller. J. Syst. Des. Dyn. 2008, 2, 251–262. [Google Scholar] [CrossRef]
- Sugahara, Y.; Takigami, T.; Sampei, M. Suppressing vertical vibration in railway vehicles through primary suspension damping force control. J. Syst. Des. Dyn. 2007, 1, 224–235. [Google Scholar] [CrossRef]
- Wu, P.; Zeng, J.; Dai, H. Dynamic response analysis of railway passenger car with flexible carbody model based on semi-active suspensions. Veh. Syst. Dyn. 2004, 41, 774–783. [Google Scholar]
- Foo, E.; Goodall, R.M. Active suspension control of flexible bodied railway vehicles using electro-hydraulic and electromagnetic actuators. Control Eng. Pract. 2000, 8, 507–518. [Google Scholar] [CrossRef]
- Gong, D.; Wang, K.; Duan, Y.; Zhou, J. Car body floor vibration of high-speed railway vehicles and its reduction. J. Low Freq. Noise Vibr. Act. Control 2020, 39, 925–938. [Google Scholar] [CrossRef]
- Dumitriu, M. Study on improving the ride comfort in railway vehicles using anti-bending dampers. Appl. Mech. Mater. 2018, 880, 207–212. [Google Scholar] [CrossRef]
- Graa, M. Modeling and control for vertical rail vehicle dynamic vibration with comfort evaluation. Int. J. Math. Model. Methods Appl. Sci. 2017, 11, 240–245. [Google Scholar]
- Dumitriu, M. A new approach to reducing the carbody vertical bending vibration of railway vehicles. Veh. Syst. Dyn. 2017, 55, 1787–1806. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.; Sun, W. Passive control of railway vehicle car body flexural vibration by means of under frame dampers. J. Mech. Sci. Technol. 2017, 31, 555–564. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.; Sun, W.; Sun, Y.; Xia, Z. Method of multi-mode vibration control for the carbody of high-speed electric multiple unit trains. J. Sound Vib. 2017, 409, 94–111. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.S.; Sun, W.J. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber. J. Vib. Control 2013, 19, 649–657. [Google Scholar] [CrossRef]
- Tomioka, T. Reduction of car body elastic vibration using high-damping elastic supports for under-floor equipment. Railw. Technol. Avalanche 2012, 41, 245–270. [Google Scholar]
- Tomioka, T.; Takigami, T. Reduction of bending vibration in railway vehicle carbodies using carbody–bogie dynamic interaction. Veh. Syst. Dyn. 2010, 48, 467–486. [Google Scholar] [CrossRef]
- Takigami, T.; Tomioka, T. Bending vibration suppression of railway vehicle carbody with piezoelectric elements (Experimental results of excitation tests with a commuter car). J. Mech. Syst. Transp. Logist. 2008, 1, 111–121. [Google Scholar] [CrossRef]
- Schandl, G.; Lugner, P.; Benatzky, C.; Kozek, M.; Stribersk, M. Comfort enhancement by an active vibration reduction system for a flexible railway car body. Veh. Syst. Dyn. 2007, 45, 835–847. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, C. Approaches for reducing structural vibration of the carbody railway vehicles. In Proceedings of the MATEC Web of Conferences—21st Innovative Manufacturing Engineering & Energy International Conference—IManE&E, 2017, Iași, Romania, 24–26 May 2017; Volume 112, p. 07006. [Google Scholar]
- Skachkova, A.; Trifonova, V.; Zaytseva, A.; Samoshkin, S. Methods of suppression of elastic oscillations of bodies of passenger railcars. Transp. Res. Procedia. 2021, 54, 522–529. [Google Scholar] [CrossRef]
- Dumitriu, M. Numerical study on the influence of suspended equipments on the ride comfort in high speed railway vehicles. Sci. Iran. 2020, 27, 1897–1915. [Google Scholar] [CrossRef]
- Dumitriu, M. Numerical analysis on the influence of suspended equipment on the ride comfort in railway vehicles. Arch. Mech. Eng. 2018, 65, 477–496. [Google Scholar]
- Huang, C.; Zeng, J. Suppression of the flexible carbody resonance due to bogie instability by using a DVA suspended on the bogie frame. Veh. Syst. Dyn. 2022, 60, 3051–3070. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, J.; Gong, D.; You, T.; Che, J. Research on multi-point connection of under-chassis equipment suspension system in high-speed trains. AIP Adv. 2021, 11, 125315. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, J.; Wu, Y.; Zhu, B. Study on semi-active suspension applied on carbody underneath suspended system of high-speed railway vehicle. J. Vib. Control 2020, 26, 671–679. [Google Scholar] [CrossRef]
- Guo, J.; Shi, H.; Li, F.; Wu, P. Field measurements of vibration on the car body-suspended equipment for high-speed rail vehicles. Shock Vib. 2020, 2020, 6041543. [Google Scholar] [CrossRef]
- Guo, J.; Shi, H.; Luo, R.; Wu, P. Parametric analysis of the car body suspended equipment for railway vehicles vibration reduction. IEEE Access 2019, 7, 88116–88125. [Google Scholar] [CrossRef]
- Zhu, T.; Lei, C.; Xiao, S.; Yu, J.P. Suspension stiffness selecting method of elastic suspension equipment under vehicle. J. Traffic Transp. Eng. 2018, 18, 111–118. [Google Scholar]
- Sun, W.; Zhou, J.; Gong, D.; You, T. Analysis of modal frequency optimization of railway vehicle car body. Adv. Mech. Eng. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.; Sun, W. Influence of under-chassis-suspended equipment on high-speed EMU trains and the design of suspension parameters. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1790–1802. [Google Scholar] [CrossRef]
- Shi, H.; Wu, P. Flexible vibration analysis for car body of high-speed EMU. J. Mech. Sci. Technol. 2016, 30, 55–66. [Google Scholar] [CrossRef]
- Dumitriu, M. Influence of suspended equipment on the carbody vertical vibration behavior of high-speed railway vehicles. Arch. Mech. Eng. 2016, 63, 145–162. [Google Scholar] [CrossRef]
- Aida, K.Y.; Tomioka, T.; Takigami, T. Reduction of carbody flexural vibration by the high-damping elastic support of under-floor equipment. Q. Rep. RTRI 2015, 56, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Zeng, J.; Wang, Q. Identifying the relationship between suspension parameters of underframe equipment and carbody modal frequency. J. Mod. Transp. 2014, 22, 206–213. [Google Scholar] [CrossRef]
- Shi, H.; Luo, R.; Wu, P. Influence of equipment excitation on flexible carbody vibration of EMU. J. Mod. Transp. 2014, 22, 95–205. [Google Scholar] [CrossRef]
- Shi, H.L.; Luo, R.; Wu, P.B. Application of DVA theory in vibration reduction of carbody with suspended equipment for high-speed EMU. Sci. China Technol. Sci. 2014, 57, 1425–1438. [Google Scholar] [CrossRef]
- Shi, H.L.; Luo, R.; Wu, P.B.; Zeng, J. Suspension parameters designing of equipment for electric multiple units based on dynamic vibration absorber theory. J. Mech. Eng. 2014, 50, 155–161. [Google Scholar] [CrossRef]
- Shi, H.L.; Wu, P.B.; Luo, R. Coupled vibration characteristics of flexible car body and equipment of EMU. J. Southwest JiaoTong Univ. 2014, 49, 693–699. [Google Scholar]
- Wu, H.C.; Wu, P.B.; Zeng, J. Influence of equipment under car on carbody vibration. J. Traffic Transp. Eng. 2012, 12, 50–56. [Google Scholar]
- Sun, V.; Gong, D.; Zhou, J.; Zhao, Y. Influences of suspended equipment under car body on highspeed train ride quality. Procedia Eng. 2011, 16, 812–817. [Google Scholar] [CrossRef]
- Sun, Y.; Gong, D.; Zhou, J. Study on vibration reduction design of suspended equipment of high speed railway vehicles. J. Phys. 2016, 744, 012212. [Google Scholar] [CrossRef]
- Hansson, J.; Takano, M.; Takigami, T.; Tomioka, T.; Suzuki, Y. Vibration suppression of railway car body with piezoelectric elements (A study by using a scale model). JSME Int. J. Ser. C 2004, 47, 451–456. [Google Scholar]
- Takigami, T.; Tomioka, T. Vibration suppression of scale model of railway carbody with piezoelectric elements (a study focused on designing shunt circuits). In Proceedings of the 12th SPIE International Symposium Smart Structures and Materials, San Diego, CA, USA, 17 May 2005; Volume 5760, pp. 329–340. [Google Scholar]
- Takigami, T. Investigation into suppressing the bending vibration of railway vehicle carbody with piezoelectric elements. Railw. Technol. Avalanche 2005, 9, 54–60. [Google Scholar]
- Takigami, T.; Tomioka, T. Investigation to suppress bending vibration of railway vehicle carbodies using piezoelectric elements. Q. Rep. RTRI 2005, 46, 225–230. [Google Scholar] [CrossRef]
- Takigami, T.; Tomioka, T.; Hansson, J. Vibration suppression of railway vehicle carbody with piezoelectric elements (A study by using a scale model of Shinkansen). J. Adv. Mech. Des. Syst. Manuf. 2007, 1, 649–660. [Google Scholar] [CrossRef]
- Kamada, T.; Kiuchi, R.; Nagai, M. Suppression of railway vehicle vibration by shunt damping using stack type piezoelectric transducers. Veh. Syst. Dyn. 2008, 46, 561–570. [Google Scholar] [CrossRef]
- Kamada, T.; Hiraizumi, T.; Nagai, M. Active vibration suppression of lightweight railway vehicle body by combined use of piezoelectric actuators and linear actuators. Veh. Syst. Dyn. 2010, 48, 73–87. [Google Scholar] [CrossRef]
- Melero, M.; Nieto, A.J.; Morales, A.L.; Palomares, E.; Chicharro, J.M.; Ramiro, C.; Pintado, P. Experimental analysis of constrained layer damping structures for vibration isolation in lightweight railway vehicles. Appl. Sci. 2022, 12, 8220. [Google Scholar] [CrossRef]
- Suzuki, E.; Watanabe, K.; Hoshino, H.; Yonezu, T.; Nagai, M. A study of Maglev vehicle dynamics using a reduced-scale vehicle model experiment apparatus. In Proceedings of the International Symposium on Speed-up, Safety and Service Technology for Railway and Maglev Systems (STECH’09), Niigata, Japan, 16–19 June 2009; p. 355984. [Google Scholar]
- Suzuki, E.; Watanabe, K.; Hoshino, H.; Yonezu, T.; Nagai, M. A study of Maglev vehicle dynamics using a reduced-scale vehicle model experiment apparatus. J. Mech. Syst. Transp. Logist. 2010, 3, 196–205. [Google Scholar] [CrossRef]
- Kozek, M.; Bilik, C.; Benatzky, C. A PC-based flexible solution for virtual instrumentation of a multi-purpose test bed. Int. J. Online Biomed. Eng. Eng. 2006, 2, 1–5. [Google Scholar]
- Popprath, S.; Benatzky, C.; Bilik, C.; Kozek, M.; Stribersky, A.; Wassermann, J. Experimental modal analysis of a scaled car body for metro vehicles. In Proceedings of the 13th International Congress on Sound and Vibration, Vienna, Austria, 2–6 July 2006. [Google Scholar]
- Kozek, M.; Benatzky, C.; Schirrer, A.; Stribersky, A. Vibration damping of a flexible car body structure using piezo-stack actuators. In Proceedings of the 17th World Congress the International Federation of Automatic Control, Seoul, Republic of Korea, 6–11 July 2008. [Google Scholar]
- Schirrer, A.; Kozek, M.; Schöftner, J. MIMO Vibration control for a flexible rail car body: Design and experimental validation. In Vibration Analysis and Control—New Trends and Development; Carbajal, F.B., Ed.; InTech: London, UK, 2011; pp. 309–336. [Google Scholar]
- Bokaeian, V.; Rezvani, M.A.; Arcos, R. A numerical and scaled experimental study on ride comfort enhancement of high-speed rail vehicle through optimizing traction rod stiffness. J. Vib. Control 2021, 27, 2548–2563. [Google Scholar] [CrossRef]
- Mazilu, T.; Gheți, M.A. On the bending vibration of a train driving wheelset. In Proceedings of the IOP Conference Series: Materials Science and Engineering, 2019, ModTech International Conference—Modern Technologies in Industrial Engineering, Iași, Romania, 19–22 June 2019; Volume 591, p. 012059. [Google Scholar]
- Mazilu, T.; Răcănel, I.R.; Ghindea, C.L.; Cruciat, R.L.; Leu, M.C. Rail joint model based on the Euler-Bernoulli beam theory. Rom. J. Transp. Infrastruct. 2019, 8, 16–29. [Google Scholar] [CrossRef]
- Mazilu, T. The dynamics of an infinite uniform Euler-Bernoulli beam on bilinear viscoelastic foundation under moving loads. Procedia Eng. 2017, 199, 2561–2566. [Google Scholar] [CrossRef]
- UIC 513R; Guidelines for Evaluating Passenger Comfort in Relation to Vibration in Railway Vehicles. International Union of Railways: Paris, France, 1994.
- EN 12299; Railway Applications. Ride Comfort for Passengers. Measurement and Evaluation. British Standard: London, UK, 1999.
- Meirovitch, L. Elements of Vibration Analysis; McGraw-Hill International Edition: New York, NUY, USA, 1986; pp. 235–238. [Google Scholar]
- ROMARC SA. Available online: https://romarc.ro/2019/04/04/vagon-salon-ava-200/ (accessed on 11 February 2023).
- Sebeşan, I.; Dumitriu, M.; Tudorache, C. Contributions to the study of the elastic constants for suspensions used on high-speed steering bogies. Mech. Transp. Commun. 2009, 3, 30–34. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).