Abstract
We report the start-to-end modeling of our accelerator lattice design employing a laser-assisted bunch compression (LABC) scheme in an X-ray free electron laser (XFEL), using the proposed Matter-Radiation Interactions in Extremes (MaRIE) XFEL parameters. The accelerator lattice utilized a two-stage bunch compression scheme, with the first bunch compressor performing a conventional bulk compression enhancing the beam current from 20 A to 500 A, at 750 MeV. The second bunch compression was achieved by modulating the beam immediately downstream of the first bunch compressor by a laser with 1- wavelength in a laser modulator, accelerating the beam to the final energy of 12 GeV, and compressing the individual 1- periods of the modulated beam into a sequence of microbunches with 3-kA current spikes by the second bunch compressor. The LABC architecture presented had been developed based on the scheme of enhanced self-amplified spontaneous emission (ESASE), but operated in a disparate regime of parameters. Enabled by the novel technology of the cryogenic normal conducting radiofrequency photoinjector, we investigated an electron beam with ultra-low emittance at the starting point of the lattice design. Our work aimed at mitigating the well-known beam instabilities to preserve the beam emittance and suppress the energy spread growth.
1. Introduction
An X-ray free electron laser (XFEL) is a light source that generates high brightness coherent X-ray pulses [1]. XFEL facilities, such as the Linac Coherent Light Source (LCLS) at the SLAC National Accelerator Laboratory, have found multidisciplinary applications in the scientific research fields of material science, biology, chemistry and physics [2,3]. At Los Alamos National Laboratory (LANL), scientists have been investigating XFEL as a candidate technology for the Matter-Radiation Interactions in Extremes (MaRIE) initiative [4,5], with the goal of eventually achieving the Dynamic Mesoscale Material Science Capability (DMMSC) [6]. The MaRIE XFEL requires 42 keV X-ray photon energy, photons per pulse and fractional spectral bandwidth [5].
The major challenges facing the endeavor of pursuing an XFEL with lower electron beam emittance as well as lower energy spread in order to meet the MaRIE XFEL requirements include coherent synchrotron radiation (CSR) effects [7,8,9,10] and microbunching instability (MBI) [11,12,13]. The undulator resistive wall wakes (URWW) [14,15,16] degrade the electron beam lasing performance in the X-ray undulator.
In an effort to alleviate the above-mentioned negative effects commonly found in XFEL beamline designs that routinely use bulk compression schemes and to realize the conditions for MaRIE, an XFEL scheme using the approach of a laser-assisted bunch compression (LABC) was developed [17,18,19], based on the scheme of enhanced self-amplified spontaneous emission (ESASE). As a general concept, an LABC scheme utilizes the integration of linear laser optics and dispersive beamline elements to achieve electron bunch compression [20], shaping the input bulk electron beam into a train of compressed periodic microbunches with a high peak current. One type of well-established LABC architecture is the combination of a laser modulator (LM) and a downstream chicane bunch compressor (BC), which was first proposed to implement enhanced self-amplified spontaneous emission (ESASE) for XFEL [21,22,23]. The original motivation of the ESASE method was to maximize the microbunch peak current, so as relieve the demanding requirement on the electron beam emittance for achieving gain length reduction. Inspired by the pioneering ESASE concept, our accelerator lattice design discussed in this paper used an LABC scheme with a laser modulator and a downstream chicane bunch compressor, as well; however, the goal of our design was different, and the parameter regime was more advanced. We prioritized the reduction of the beam instabilities, mentioned above, by investigating an electron beam with ultra-low emittance produced by a well-developed cryogenic normal conducting radiofrequency (RF) photoinjector [24,25,26,27] at the very starting point of the accelerator lattice. The ultra-low emittance was preserved until the end of the beamline, where the beam also presented a small energy spread. The practicality of the novel cryogenic normal conducting RF photoinjectors has been revolutionary in the field of XFEL instrumentation. It immediately eliminated the necessity of maximizing the beam current in order to overcome the difficulty of achieving a short gain length due to the otherwise comparatively large beam emittance, as in the original description of ESASE [21,22,23]. Meanwhile, this novel photoinjector technology made it possible to explore the unprecedented LABC parameter space, leading to potentially improved XFEL performance as presented in this paper. Moreover, we used fine manipulation of the microbunch longitudinal phase space to carefully overcompress the microbunch so as to achieve a greater utilization rate of the beam charge than that in the previously reported ESASE design [17,21] and to realize higher quality X-ray lasing. For narrative convenience and terminology consistency with prior studies [17,18], we use LABC to refer to our beamline design developed from the ESASE scheme.
In our accelerator design for MaRIE XFEL using an LABC scheme, the first stage of the electron bunch compression employed the bulk compression method as is the case in the conventional scheme using a chicane bunch compressor. For the second stage of the bunch compression, our scheme used an LABC method, which was accomplished in two steps [17,18,19]. In the first step, the beam was modulated by a laser modulator downstream of the first bunch compressor; in the second step, a C-chicane bunch compressor converted the energy modulation formed in the beam by the laser modulator into a longitudinal electron density modulation, creating periodic, high current spikes with intervals equal to the laser wavelength. It was the electrons residing inside the high current spikes that participated in the effective X-ray lasing in the undulator. The two steps of our LABC method were not necessarily occurring at the same beam energy. Because the bunch compressor following the laser modulator entailed only a small value, it could be located downstream of the last linac section with the beam at the final lasing energy [17].
Architecture compactness was also pursued in the design of the MaRIE XFEL while using an LABC scheme. Compact XFEL was demonstrated with the SPring-8 Angstrom Compact free electron LAser (SACLA) [28] and at the SwissFEL XFEL facility [29,30], assisted with high-gradient C-band normal conducting linac structures. Recent progress in the application of a laser wakefield accelerator in the demonstration of free electron lasing has provided an alternative approach for achieving compact XFEL [31]. In our accelerator lattice design, the linac sections were assumed to be built with cryogenic copper RF high-gradient accelerator cavities [32,33], which significantly shortened the length of the linac sections, enabling an overall compact XFEL architecture. Joint experimental research by UCLA and SLAC found that at X-band, cryogenic cooled copper accelerator structures could outperform the room temperature structures in terms of achieving a significantly higher accelerating gradient at the same breakdown rate. While the C-band cryogenic copper RF high gradient accelerator technology was still under development [19,27,34], we assumed here that each accelerator cell in the C-band linac sections was already capable of achieving an accelerating gradient of up to 120.0 MV/m.
The simulations in the work reported in this paper were performed entirely using Elegant code [35], assisted by in-house Python [36] scripts.
The content of this paper is arranged as follows. An overview of the accelerator lattice configuration, including the major specifications, is provided in Section 2. The overview addresses the beamline elements in the order of the geometry, from the electron bunch entering the first section of the linac at the starting point to the beam entering the X-ray undulator at the end. Section 3 through Section 5 elaborates on the designs of the beamline elements by their different categories, in the order of the laser modulator, the bunch compressors, and the linac sections, respectively. A final beam analysis at the entrance of the X-ray undulator is presented in Section 6, followed by the conclusions in Section 7.
2. Accelerator Lattice Overview
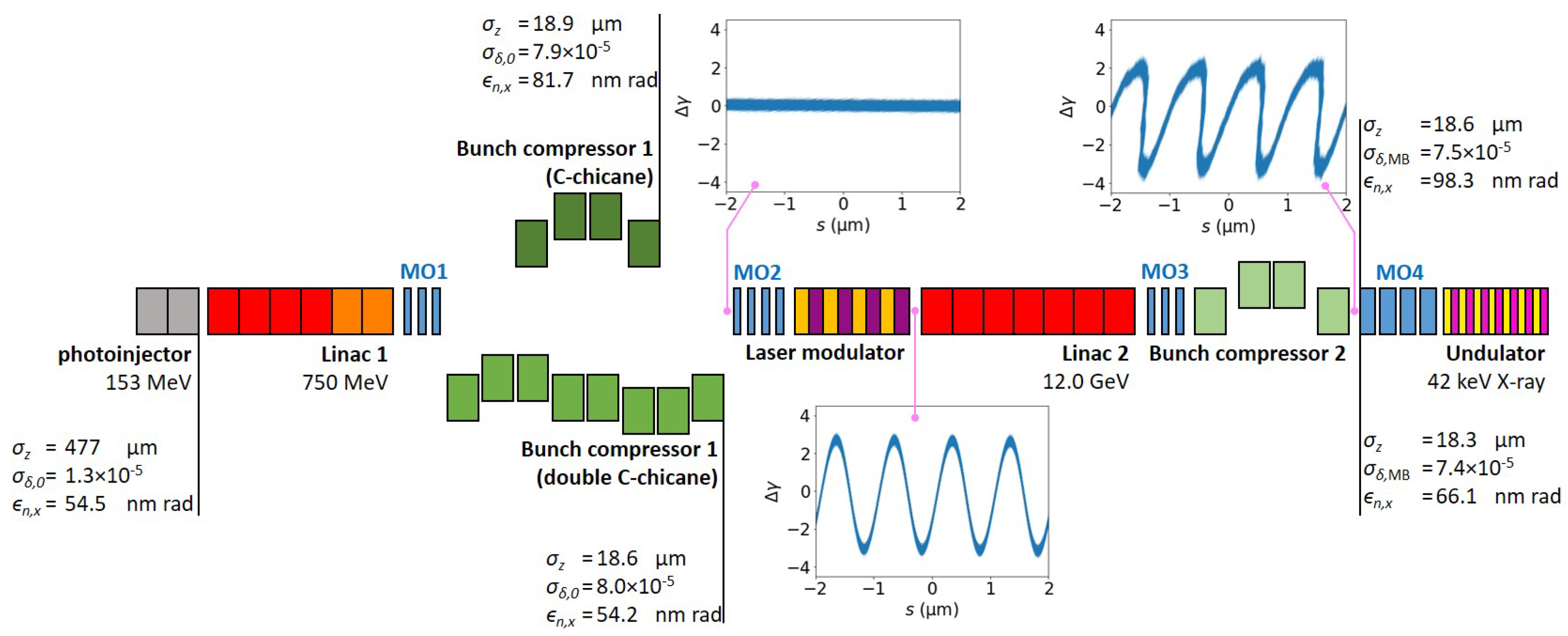
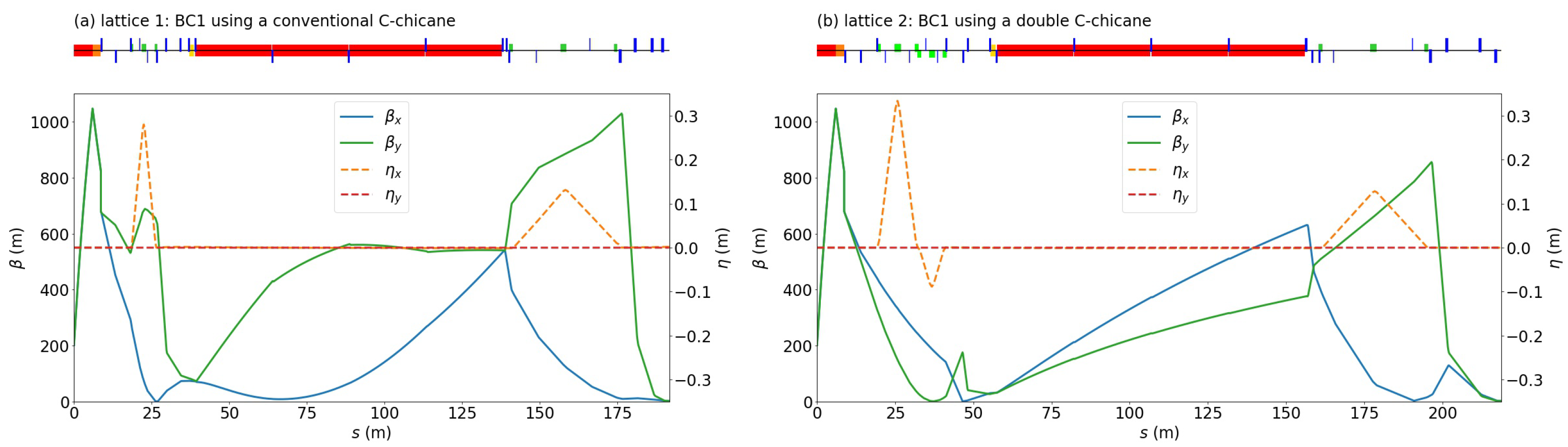
The accelerator lattice discussed was located between the exit of the photoinjector and the entrance of the X-ray undulator. The schematic of the accelerator lattice is shown in Figure 1. In this paper, we discuss two sets of accelerator lattice footprint designs, each with a distinct configuration of the first bunch compressor (BC1). The first set of accelerator lattice (referred to as “lattice 1”, hereafter) used a conventional C-chicane of four bending magnets as its BC1, and the second set (referred to as “lattice 2”, hereafter) used a double C-chicane as its BC1. The evolution of the Twiss parameters along the beamlines of both lattice 1 and 2 are shown in Figure 2 a and b, respectively. The total length of lattice 1 was 192 m and for lattice 2, 219 m. The greater length of lattice 2 was primarily contributed by the longer double C-chicane in its BC1. In the -function plots in Figure 2, the -function values of several intermediate sections reach around 1000 m, and these seemingly enormous values were due to the increase in the transverse beam size with the ultra-low emittance preserved. In all the Elegant simulations, we used a beam file of 29.9 million macroparticles, with a total electron beam charge of 100 pC.
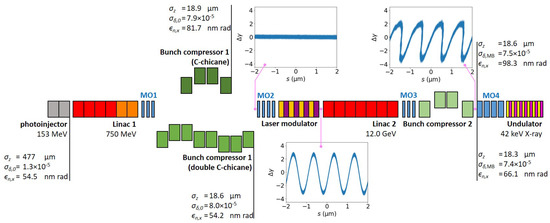
Figure 1.
Schematic of the proposed MaRIE XFEL accelerator lattice using an LABC scheme for the second stage of the bunch compression. The two different configurations of the first bunch compressor (BC1) are shown. The evolution of the beam properties in lattice 1 using a conventional C-chicane as BC1 is shown at the top, and for lattice 2, which uses a double C-chicane as its BC1, is shown at the bottom. The evolution of the energy modulation, given in the variation of the Lorentz factor, is shown at the exits of BC1, the laser modulator (LM), and the second bunch compressor (BC2), explaining the development of the sequence of the high current spikes to be used for lasing in the X-ray undulator at the end of the lattice. In the figure, the instances of the matching optics (MO) are also shown.
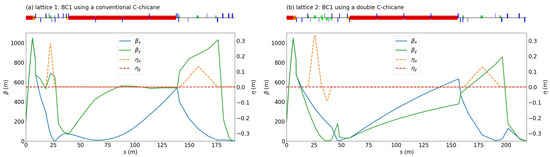
Figure 2.
The evolution of the Twiss parameters, along the beamline for (a) lattice 1 using a conventional C-chicane as BC1 and (b) lattice 2 using a double C-chicane as BC1. An overview of the lattice elements is provided at the top of the respective plot. Note that the profiles of the -functions in lattice 2 inside the section of L2 appeared unaffected by the quadrupoles because only a small focusing strength was needed in this case.
The electron beam entered the first section of the linac (L1) at an energy of 153 MeV, with a beam current of 20 A. The L1 comprised two sections: the 5.699 GHz (C-band) accelerator and the 17.098 GHz (Ku-band) linearizer. The combination of the accelerator and the linearizer created an energy chirp in the beam in the longitudinal direction for the bunch compression in the BC1 downstream. The L1 accelerator section performed the off-crest acceleration of the beam to create a longitudinal variation of the beam energy, and the higher harmonic L1 linearizer section finalized the shaping of the chirp. At the exit of the L1, the mean energy of the beam reached 750 MeV.
The first bunch compressor compressed the electron bunch with a compression ratio of 25, enhancing the beam current from 20 A to 500 A. As shown in Figure 1, two different configurations of BC1 were investigated. The BC1 design using a conventional C-chicane as in lattice 1 had advantages, such as its intrinsic simplicity and a comparatively short length, but the beam at the bunch compressor exit had a non-trivial and non-uniform horizontal momentum shift along the beam due to the CSR effects. In comparison, the BC1 configuration using a double C-chicane, as in lattice 2, showed merits in outputting a beam with little horizontal momentum shift and a smaller horizontal emittance [37,38,39], though the total length of the bunch compressor was greater.
After the first stage of the bunch compression, the electron beam was modulated by a laser beam in a laser modulator. The laser modulator applied energy modulation within the beam by coupling to the horizontal motion of the electrons inside the undulator. The laser modulator had 10 undulator periods, and the laser wavelength used was 1 . The laser modulation of the beam could be described by the energy modulation contrast ratio, defined as the ratio of the energy variation to the uncorrelated energy spread . The energy modulation contrast ratio varied sinusoidally along the beam, and its amplitude was referred to as the modulation amplitude, symbolized by A as in Equation (1) [17,21].
The modulation amplitude A was used to evaluate the strength of the laser modulation. Although the energy modulation could be preserved as the beam traverses the entire lattice, the uncorrelated energy spread of the beam changed notably. At the position of the laser modulator, we used a laser power of 3.4 GW to generate a modulation amplitude at . Downstream of the laser modulator, various effects could cause the uncorrelated energy spread to increase, e.g., the incoherent synchrotron radiation (ISR) in the second bunch compressor (BC2), so the effective modulation parameter A of the entire LABC architecture would be less than .
The modulated electron beam was accelerated to 12.0 GeV by the second section of the linac (L2). L2 also operated at 5.699 GHz. The off-crest acceleration and the short-range wakefield in the RF cavities evened out the chirp in the beam over the entire L2 acceleration section. The energy modulation by the upstream LM was preserved after the acceleration by L2.
The second bunch compressor reached a compression ratio of 6, compressing each 1- period of the modulated electron beam into a current spike with a peak current at 3.0 kA. The entire electron bunch presented no macroscopic chirp; however, BC2 utilized the energy differential within each 1- period of the modulated beam and converted it into the longitudinal electron density modulation, forming the microbunches (MB) with high current spikes. The normalized dispersive strength of BC2 was defined in Equation (2) [17], where the transfer matrix element of BC2 is used, and is the wave number of the laser used in the LM upstream.
The modulation parameter A and the compression parameter B are the core parameters of an LABC architecture because they determine the longitudinal phase space distribution of the beam [17,40]. The ideal parameter set of A and B for our LABC configuration was obtained by minimizing A while varying B in order to achieve the desired microbunch current profile, or the microbunched electron beam longitudinal phase space distribution, unique to our design of LABC [17]. Parameter A was minimized because a smaller A value led to a lower laser power required and a reduced energy spread within each individual microbunch, constituting a current spike. Instead of maximizing the microbunch peak current by pursuing a prominently spiky current profile for each microbunch, as in the configuration for ESASE, our configuration discreetly overcompressed the laser-modulated electron beam for the purpose of forming a comparatively broad flat top at a reduced current level of 3.0 kA at the central section of the current distribution of each microbunch. This particular microbunch current profile had two advantages. First, this special operating point of the LABC method allowed a greater portion of the entire electron beam charge to participate in the X-ray lasing in the undulator at the end of the beamline [17]. Second, because the length of each microbunch was enhanced in this design, the X-ray lasing performance was less prone to the slippage effect, as compared to ESASE.
Matching optics (MO) using quadrupoles with a length of 0.15 m were used upstream of the BC1 (MO1, triplet) and the LM (MO2, quadruplet) over the entire L2 section (five quadrupoles, equally spaced) and upstream of the BC2 (MO3, triplet), but downstream of BC2 (MO4). The MO4 in our design was a quadruplet that consisted of four (4) 0.45 m-long quadrupoles. Two factors led to this special configuration of the MO4. First, there was a very demanding requirement for the MO4 as it was supposed to shape and transport the electron beam to the X-ray undulator at the end of the beamline over a relatively short distance, where the beam was focused down in order to attain a horizontal and a vertical rms size of around 2.5 , with a minimized magnitude of the -functions. Second, we limited the magnetic field gradient in all quadrupoles to below 20 T/m.
3. Laser Modulator
The laser modulator was implemented by a planar undulator and a high-power laser co-propagating with the electron beam. The laser modulator was 1.5 m long with 10 undulator periods. The laser wavelength was 1 , and the laser power used was 3.4 GW, with a pulse length of 1.2 ps (4 mJ). The parameters regarding the undulator and the laser beam used in the laser modulator are listed in Table 1, where we abided by the notations used in the references [17,40,41].

Table 1.
Design parameters of the laser modulator.
The reasons that led to the determination of the laser wavelength being 1 were as follows. On the one hand, we pursued a laser wavelength as small as possible. As mentioned in Section 2, the LABC parameters A and B determined the distribution of the longitudinal phase space of the electron beam. For a determined LABC compression parameter B that included a given uncorrelated fractional energy spread, as indicated in Equation (2), a greater laser wave number , i.e., a smaller laser wavelength , enabled the usage of a smaller value for the second bunch compressor, which was beneficial in suppressing the gain of MBI [13]. On the other hand, there was a lower limit for the value of the laser wavelength. As mentioned above, it was the microbunches formed inside the electron beam that would participate in the X-ray lasing. Meanwhile, we assume that the X-ray photons stemmed from the center of the electron microbunches. As a result, the half-width at the half-maximum (HWHM) of the microbunches () in the electron beam had to be large enough to cover the X-ray radiation coherence length [42,43] for the slippage considered, so that the radiation coherence was assured for the entire X-ray lasing duration in the undulator. This criterion was acquired by Equation (3).
On condition that the desired LABC beam current profile was attained, a smaller laser wavelength would lead to a smaller value of . Equation (3) thus set the lower limit for the laser wavelength to be used. We defined the microbunches by the sections of the electron beam that contributed to a beam current above 2.0 kA, resulting in a microbunch HWHM of nm from the simulation results, where 1- laser wavelength was presumed. In the MaRIE XFEL, a reasonable estimate of 3000 undulator periods resulted in an X-ray coherence length of nm, and thus the relationship in Equation (3) was satisfied. Therefore, our selection of a laser wavelength of 1 was appropriate and justified.
In the discussion above, we defined the lower limit of the microbunch beam current as 2.0 kA. As compared to the beam current level of 3.0 kA, 2.0-kA beam current resulted in a 30% longer gain length, according to our Ming-Xie parameterization analysis [44] (see Section 6.3 for basic undulator parameters). Moreover, the X-ray lasing power per unit charge for 2.0-kA beam current was 40% lower than that in the case of the 3.0-kA beam current. Therefore, the beam portion with a beam current below 2.0 kA had a significantly smaller contribution to the X-ray photon generation. In addition, we noted that the 2.0-kA lower limit of the microbunch beam current led to a microbunch HWHM sufficient for accommodating the slippage effect during the X-ray lasing process.
The choice of the 2.0-mm laser waist size was made with the purpose of guaranteeing a homogeneous laser field strength that the electron beam witnessed on a certain transverse plane, with a reasonable laser power. It was not optimized for the best laser modulation efficiency with the electron beam parameters provided. A carefully optimized laser configuration by 3D laser-electron matching analysis with an effectively smaller Rayleigh length should be able to reduce the laser power required by the laser modulation of the electron beam by a significant amount.
According to Table 1, the Rayleigh length of the laser beam was much greater than the total length of the laser modulator. For the entire interaction duration between the electron beam and the laser beam, the transverse rms electron beam sizes were below 100 , i.e., below 5% of the 2.0-mm laser beam waist size. In addition, the 1.2-ps laser pulse length was much longer than the electron beam rms duration of fs. As a result, the laser fields that the electron beam witnessed were close to those of a linearly polarized plane wave, and the absolute energy modulation distribution within the beam was estimated using Equation (4) [40,41].
where is a constant with the same dimension as that of power, which is defined as GW with kA. The maximal energy modulation estimated by Equation (4) was , while the calculation using Elegant was 2.74. The 20% discrepancy between Equation (4) and the Elegant result was due to the imperfect assumption of the laser field profile as a plane wave with a constant amplitude in space as well as neglecting the slippage effect. The simple form of Equation (4) could be used to roughly estimate the laser peak power required to achieve the desired energy modulation, which was to be refined and determined by the Elegant simulations.
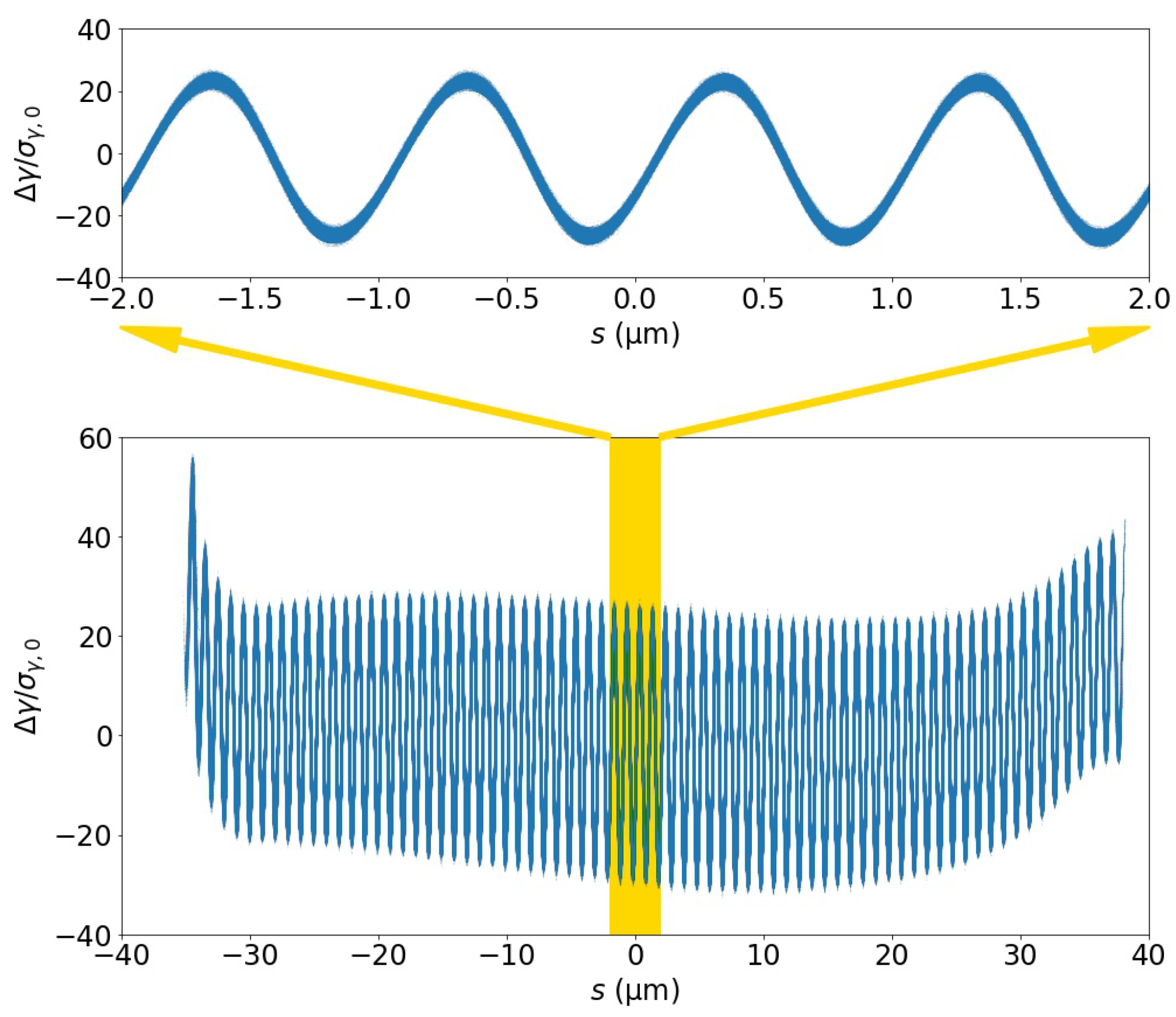
To describe the effectiveness of the energy modulation, the energy modulation contrast ratio for the beam downstream of the laser modulator in lattice 1 is shown in Figure 3. The modulation amplitude was achieved at , with the uncorrelated energy spread before the beam entered the laser modulator. After laser modulation, the uncorrelated energy spread of the beam increased to 0.118. This increase in the uncorrelated energy spread could have been due to the differential of the laser electric field strength in the horizontal direction, resulting in slightly inconsistent beam horizontal momentum modulations at different horizontal coordinates. In addition, the uncompensated transverse dynamics induced by the laser modulation could have been a contributor, as well. Note that this modulation amplitude was different from the LABC modulation parameter A of the entire accelerator architecture, which was discussed (at BC2 exit) in Section 4.2.2.
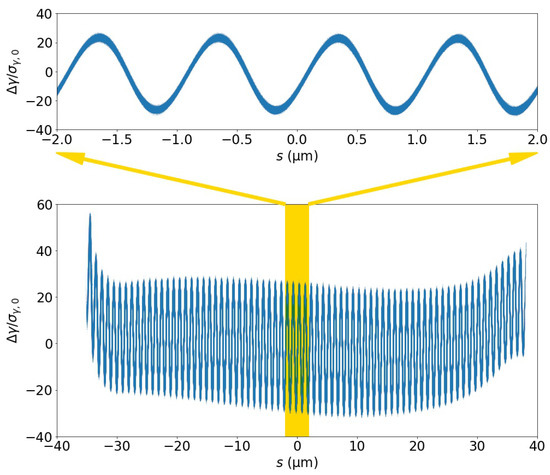
Figure 3.
Energy modulation contrast ratio of the entire beam downstream of the laser modulator. The central section of the plot that is shaded in yellow is expanded and provided at the top, showing the details of the electron beam energy modulation.
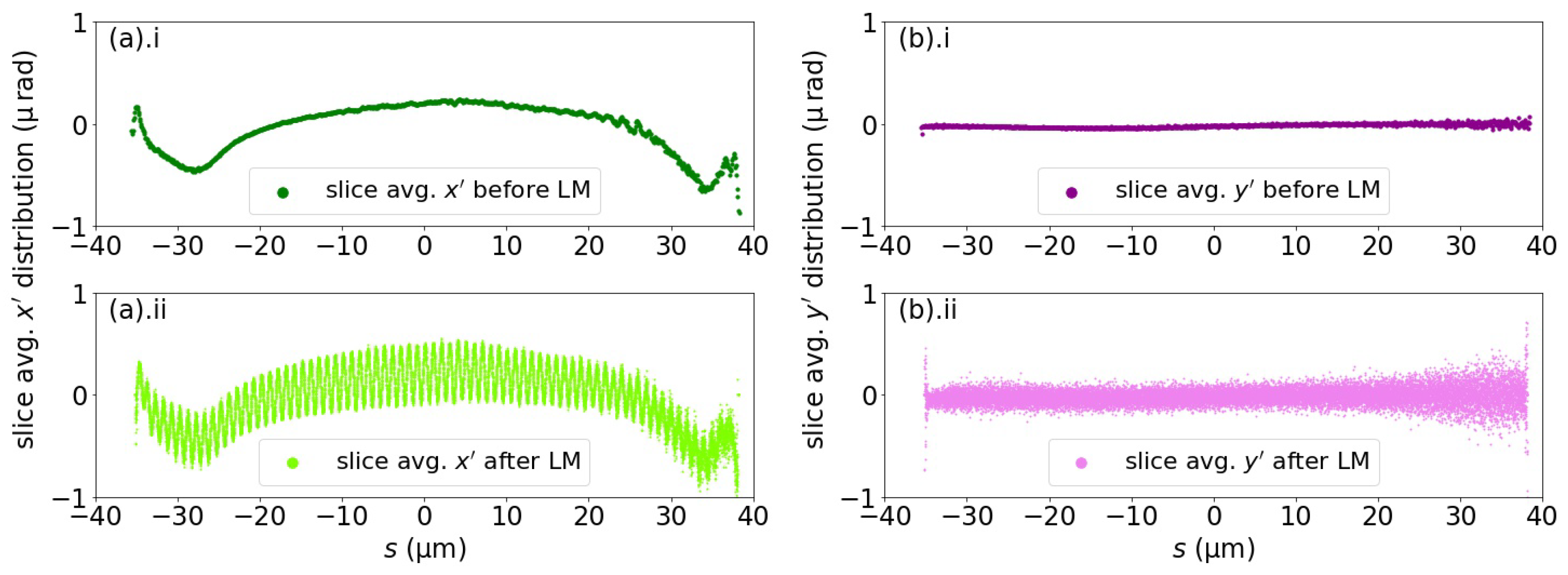
In addition, because the energy modulation was achieved by the horizontal electric field coupling with the electron undulator motion, the horizontal momentum of the electron beam was also modulated by the laser, as shown in Figure 4, where the electron beam in lattice 1 was used as an example. The electron beam was longitudinally sliced into 20,000 equally sized slices, and the average horizontal (, Figure 4a) as well as the average vertical (, Figure 4b) momentum of each slice, before and after the laser modulation, was evaluated. The vertical momentum along the beam was slightly perturbed in an uncorrelated manner; the longitudinal distribution of the horizontal momentum along the beam was modulated by the laser, with a modulation amplitude of around .
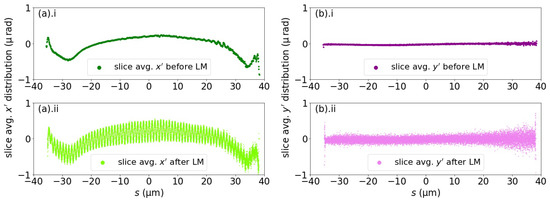
Figure 4.
The (a) horizontal () and (b) vertical () transverse momentum along the beam. (a).i and (b).i show the transverse momentum distribution before the laser modulation. (a).ii and (b).ii show the transverse momentum distribution after the laser modulation. Downstream of the laser modulator, the vertical momentum is slightly perturbed in an uncorrelated manner, but clear modulation is seen on the profile of the horizontal momentum.
Note that the undulator used in the laser modulator could also be implemented with an optimized tapering of the undulator parameter. Undulator tapering enabled the match between the electron beam and the laser beam to be finely tuned. It was also possible that the tapering could lead to a reduced average magnetic field in the undulator, mitigating the overall dispersive effect, which reduced the increase in the uncorrelated energy spread of the electron beam.
4. Bunch Compressors
In this section, we first discuss the two different schemes of the first bunch compressor in lattices 1 and 2, and then we discuss the second bunch compressor.
In the Elegant simulations of the bunch compressors, the particle tracking inside the dipoles took into consideration both the coherent and the incoherent synchrotron radiation. CSR calculations were included for the drift spaces within the chicanes as well as those upstream and downstream of the chicanes.
4.1. First Bunch Compressor
The first stage of the bunch compression occurred at a beam energy of 750 MeV, downstream of the first linac section, L1. The Twiss parameters, along with other beam properties at the L1 exit, are listed in Table 2. Note that the energy chirp of the beam formed for the first stage of the bunch compression is represented by the energy chirp coefficient .

Table 2.
Twiss parameters and other beam properties at L1 exit. Beam energy 750 MeV.
BC1 achieved a compression ratio of 25, increasing the beam current from 20 A to 500 A. A triplet using quadrupoles 0.15 m in length (MO1 in Figure 1) was used between the L1 exit and BC1, so the beam emittance increase due to CSR was minimized.
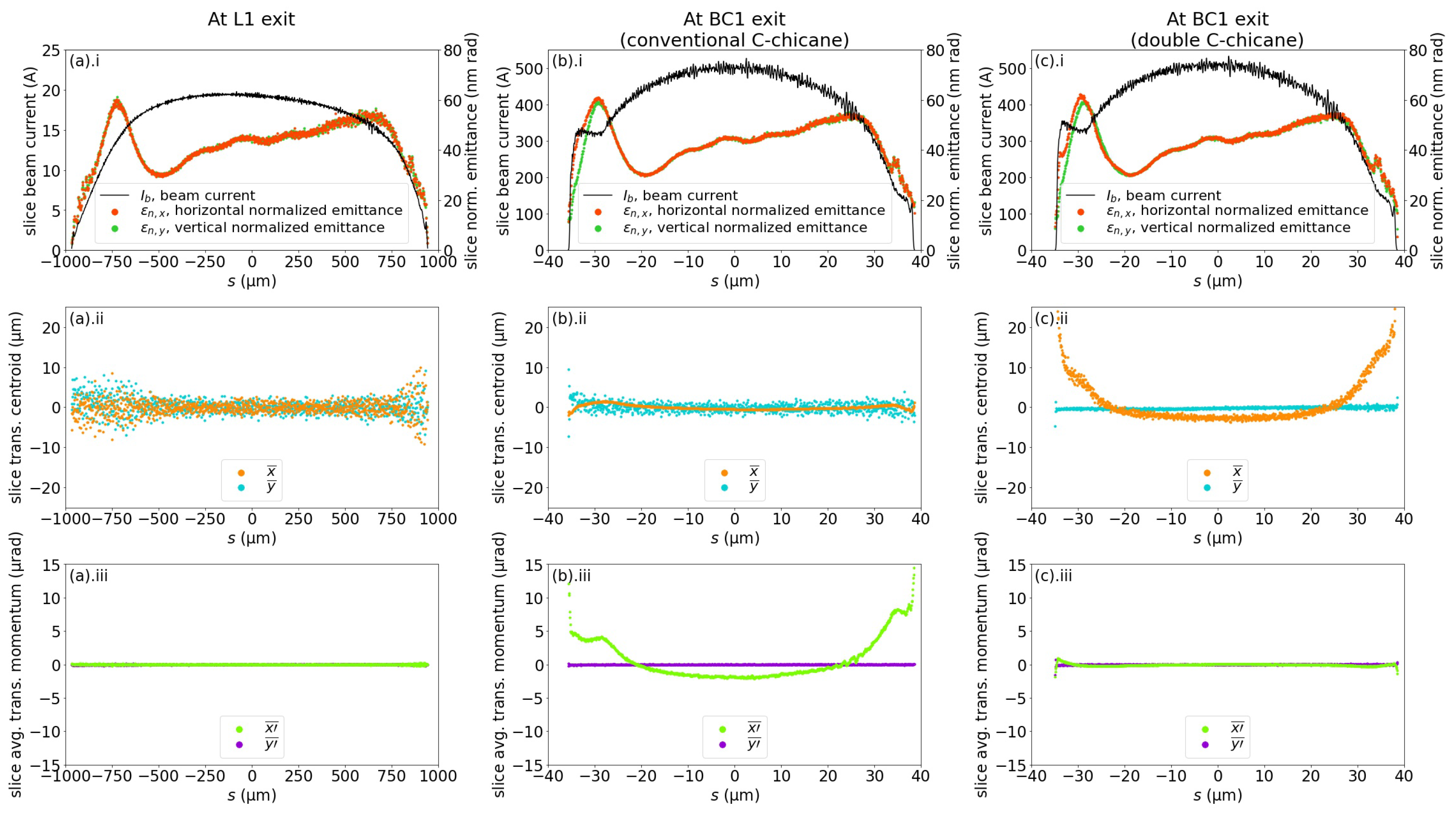
The BC1 scheme using a conventional C-chicane, as in lattice 1, or a double C-chicane, as in lattice 2, are introduced individually in the following paragraphs, with a discussion comparing the performance of the two different BC1 configurations afterwards. For narrative convenience, the performances of both configurations of BC1 are provided in Figure 5, before the exposition of the details of the designs. In Figure 5, at the exit of L1 (Figure 5a) and at the exit of the BC1s of both configurations (Figure 5b,c), the beam is partitioned longitudinally into 1000 slices of equal length; for each slice, the analyses of the beam current, normalized emittances, transverse centroids, and average transverse momentum shifts are shown.
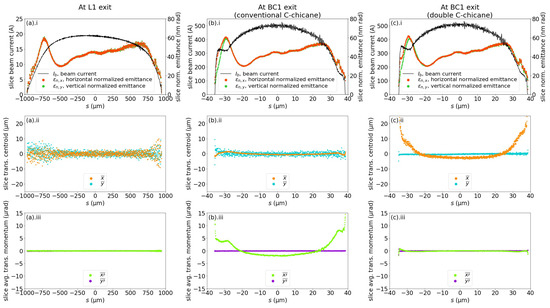
Figure 5.
Performance comparison of BC1 configurations in a conventional C-chicane (lattice 1) and a double C-chicane (lattice 2). The electron beam is divided into 1000 slices (a) at the exit of L1, (b) at the exit of BC1 using a conventional C-chicane, and (c) at the exit of BC1 using a double C-chicane. (a).i, (b).i, and (c).i show the normalized emittances and the currents of each slice along the beam; (a).ii, (b).ii, and (c).ii show the distributions of the transverse centroids; (a).iii, (b).iii, and (c).iii show the distributions of the average transverse momentum shifts.
4.1.1. BC1 Using a Conventional C-Chicane
The design of the conventional C-chicane of four bending magnets is very straightforward, as used in lattice 1. The design parameters are shown in Table 3. Two weak quadrupoles, 0.05 m in length, were used to reduce the dispersion functions at the end of the bunch compressor, and they were inserted between the first and the second, as well as between the third and the fourth, bending magnets. The magnetic field gradients of all weak quadrupoles concerned in this paper were limited to below 5 T/m.

Table 3.
BC1 conventional C-chicane design parameters.
Due to the CSR effect and the dispersion caused by the quadrupoles interacting with a beam with an energy chirp, the projected horizontal normalized emittances at the end of the bunch compressor increased to 81.7 nm rad while the projected vertical normalized emittance was unchanged, at 65.8 nm rad.
The performance of the BC1 using a conventional C-chicane is shown in Figure 5b.i–iii. The central section of the output beam carried a current of 500 A while the beam emittance of each slice was preserved. The comparison between Figure 5a.iii and b.iii indicated that CSR exerted transverse kicks on the beam as it traversed the bending magnets of BC1. However, the comparison between Figure 5a.ii and b.ii showed that there was little change to the beam transverse centroid shift profile as the beam transited from the L1 exit to the BC1 exit.
4.1.2. BC1 Using a Double C-Chicane
The double C-chicane version of BC1 consisted of two C-chicanes (hereafter referred to as C-1 and C-2), with the the offset of the central dipoles in the respective C-chicanes oriented in opposite directions, as illustrated in Figure 1. This was the BC1 configuration used in lattice 2. The purpose of investigating a double C-chicane configuration for BC1 was to have the electron beam present a minimal horizontal momentum shift profile along the beam as it exited BC1, which was likely to be achievable from the horizontal kicks related to the CSR effects of the individual C-chicanes canceling each other [45]. Minimized transverse momentum shift profile would result in a reduced transverse motion of the beam, which was favored for the beam acceleration in L2. In order to reduce the dispersion functions, two weak quadrupoles with 0.05 m lengths were used in each C-chicane and inserted between the two central and the two side bending magnets.
In order to perform the optimization of the double C-chicane configuration of BC1 and to reduce the complexity of the optimization by limiting the number of variants involved, the length and the magnetic field of the dipoles in C-1 were set as constants, at m and T. The compression ratio of C-1, the length of the dipoles in C-2, and the magnetic field of the dipoles in C-2 were used as the variables. Therefore, the optimization was carried out as a 3D parameter scan. The Elegant optimizer was used for each individual 3D parameter scan, with the optimization goal set to minimize the transverse projected emittances of the beam by using the MO1 triplet quadrupole strengths and the two inner drift space lengths as the optimizer variables. When each optimizer scan finished, the resulting beam was divided into 1000 equal-length slices in the longitudinal direction, and the current-weighted standard deviation of the slice-average horizontal kick of all the slices, symbolized as , was calculated. In other words, the transverse projected emittances were minimized in each 3D parameter scan as the first step, and the value of was calculated afterwards based on the optimizer results. The goal of the described 3D parameter scan was set to search for the minimum value of .
As an example, a 2D contour plot is provided in Figure 6, showing the calculated value of varying according to the C-1 compression ratio and to the C-2 bending magnet dipole length , in a C-2 dipole magnetic field of T. In the figure, the white marker is placed at the position of the minimum value of with m and a C-1 compression ratio of 7.50. This 2D scan was performed for each value investigated, with the corresponding minimal value of recorded, constituting a 3D parameter scan.
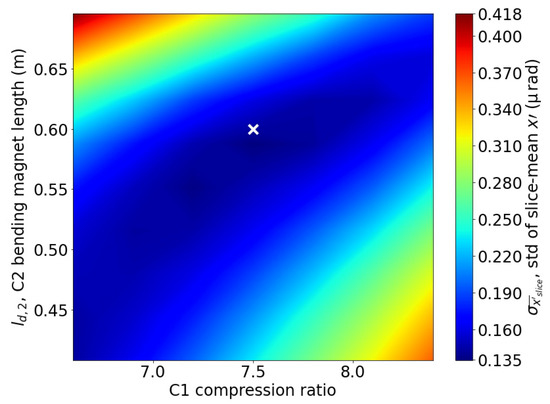
Figure 6.
Contour plot of the value of , the current-weighted standard deviation of the slice-average horizontal kick of all the beam slices, varying according to C-1 compression ratio and C-2 bending magnet length at T. The white marker is placed at the minimum of on the contour plot. A 2D scan was performed for each value, constituting a 3D parameter scan.
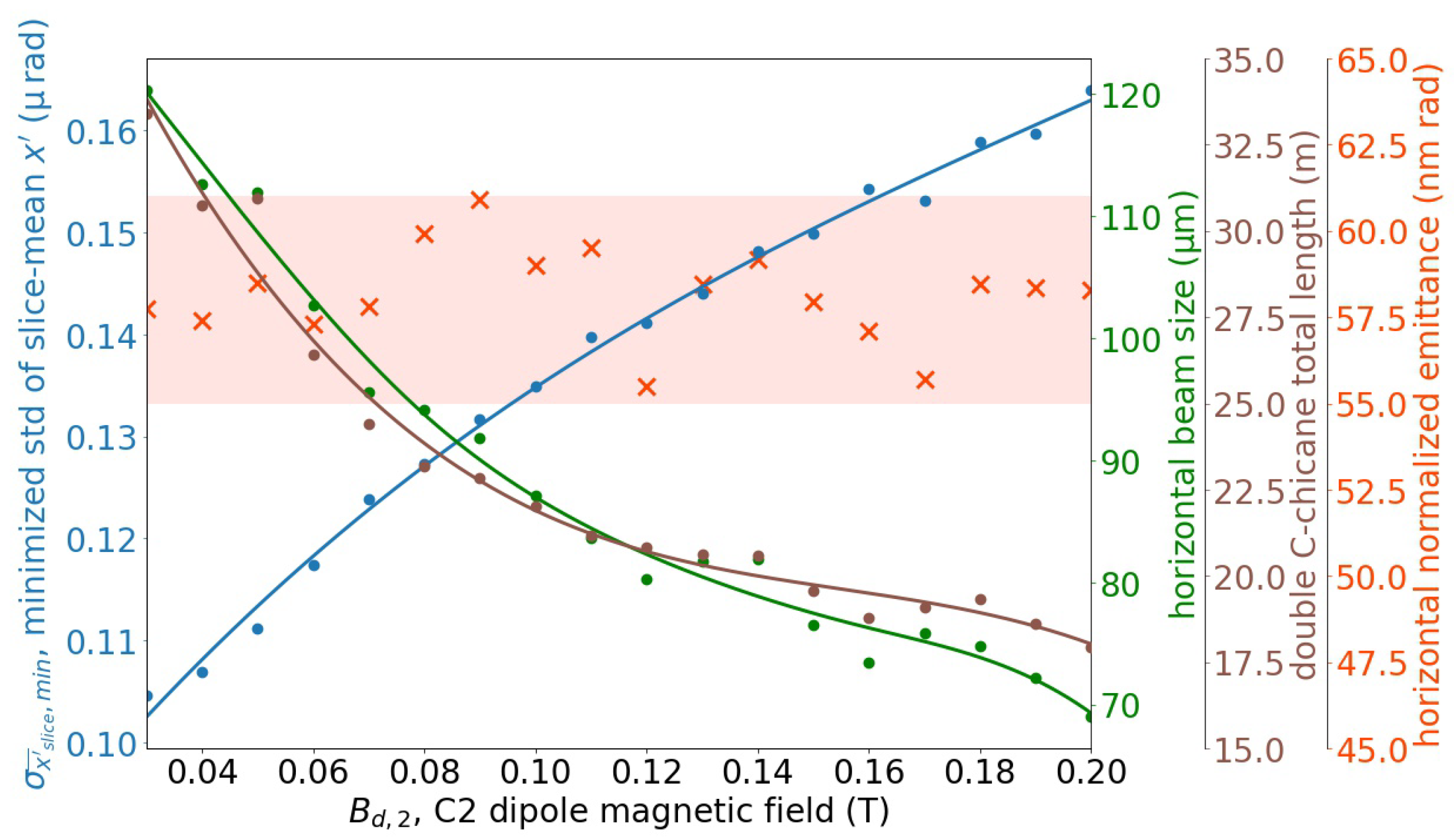
A summary plot of the entire 3D parameter scan is shown in Figure 7. The value of increased monotonically with the increase in , and no global minimum of could be identified. Therefore, the determination of the double C-chicane design parameters needed to take into account additional factors, e.g., the electron beam properties at the bunch compressor exit and the lattice’s total length. A shorter lattice length is always preferred, and it should be noted that the greater the beam size is at BC1 exit, the more difficult it is to attain a short matching optics MO2 (Figure 1) to transform the properties of the beam to those in favor of the laser modulation in LM as well as the acceleration in L2. In Figure 7, the double C-chicane total length and the horizontal beam size decreased monotonically as increased. In addition, the minimized normalized projected horizontal beam emittance obtained for the range of used in the simulations had no apparent correlation with the variation of , and the values of the minimized projected horizontal normalized emittance were within the range of 55–61 nm rad. In the end, the value of the dipole field in the second C-chicane was determined to be T. This value of the C-2 dipole field allowed the double C-chicane to have a reasonable total length in the beamline, and it also allowed the electron beam to present an appropriate horizontal beam size at the exit of the double C-chicane. The finalized design parameters of the BC1 configuration using a double C-chicane are shown in Table 4.
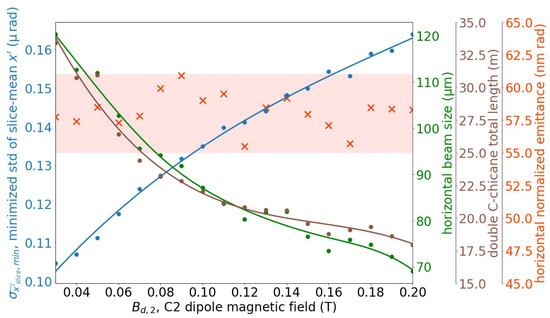
Figure 7.
Summary plot of the entire 3D parameter scan for the optimization of BC1 using a double C-chicane scheme. The minimum value of the current-weighted standard deviation of the slice-average horizontal kick of all 1000 slices of the beam (blue), the horizontal beam size (green) as well as the projected horizontal normalized emittance (red) at the double C-chicane BC1 exit, and the total length of the double C-chicane BC1 lattice (brown) were calculated for each value of the C-2 dipole magnetic field used in the parameter scan, and the results were plotted.

Table 4.
BC1 double C-chicane design parameters.
At the exit of the double C-chicane, the normalized projected horizontal and vertical beam emittances were 54.2 and 69.9 nm rad. The performance of the BC1 using a double C-chicane is shown in Figure 5c.i–iii. The central section of the output beam presented a current of 500 A while the beam emittance of each slice was preserved. The comparison between Figure 5a.ii and c.ii showed that the integration of the horizontal CSR kick throughout the two C-chicanes resulted in accumulated horizontal beam centroid shifts at the head and the tail of the beam. There was a net shift of the horizontal centroid at the central section as well, but the variation of this net shift value was very small. The comparison between Figure 5a.iii and c.iii showed that the horizontal momentum shift, caused by CSR throughout the electron beam at the double C-chicane exit, was negligible, except for the mild perturbations visible at the very head and tail sections.
4.1.3. BC1 Comparison of Designs
As compared to the double C-chicane configuration, the conventional C-chicane version of BC1 occupied less space and should involve fewer complications when tuning its parameters for use in practical applications.
The projected horizontal normalized emittance of the beam at the exit of the double C-chicane was significantly smaller than at the exit of the conventional C-chicane.
The conventional C-chicane did not induce notable horizontal centroid shifts in the beam (Figure 5b.ii), while the double C-chicane induced up to approximately 20 horizontal centroid shifts at the head and the tail of the beam (Figure 5c.ii).
The CSR effect of the conventional C-chicane resulted in a horizontal kick with a magnitude of about 2 at the center of the beam (Figure 5b.iii), as compared to the double C-chicane, where, due to the cancellation of the CSR horizontal kicks in the individual C-chicanes with opposite orientations, there was a negligible horizontal kick along the beam (Figure 5c.iii) at the BC1 exit.
4.2. Second Bunch Compressor
The second stage of the bunch compression occurred at a beam energy of 12 GeV and downstream of the second section of the linac, L2. The second bunch compressor used a configuration of a conventional C-chicane of four bending magnets. The Twiss parameters and other beam properties at the L2 exit are listed in Table 5. For the discussion of BC2 in this section, we used lattice 1 as an example, with the electron beam modeled through BC1 as a conventional C-chicane.

Table 5.
Twiss parameters and other beam properties at L2 exit, as in lattice 1. Beam energy 12 GeV.
At the L2 exit, the short-range wakefield and the off-crest acceleration of L2 eliminated the correlated energy chirp over the entire acceleration distance. In Table 5, the discrepancy between the uncorrelated and correlated energy spreads was due to the energy modulation imposed by the laser modulator.
4.2.1. BC2 Mechanism, Design, and Performance
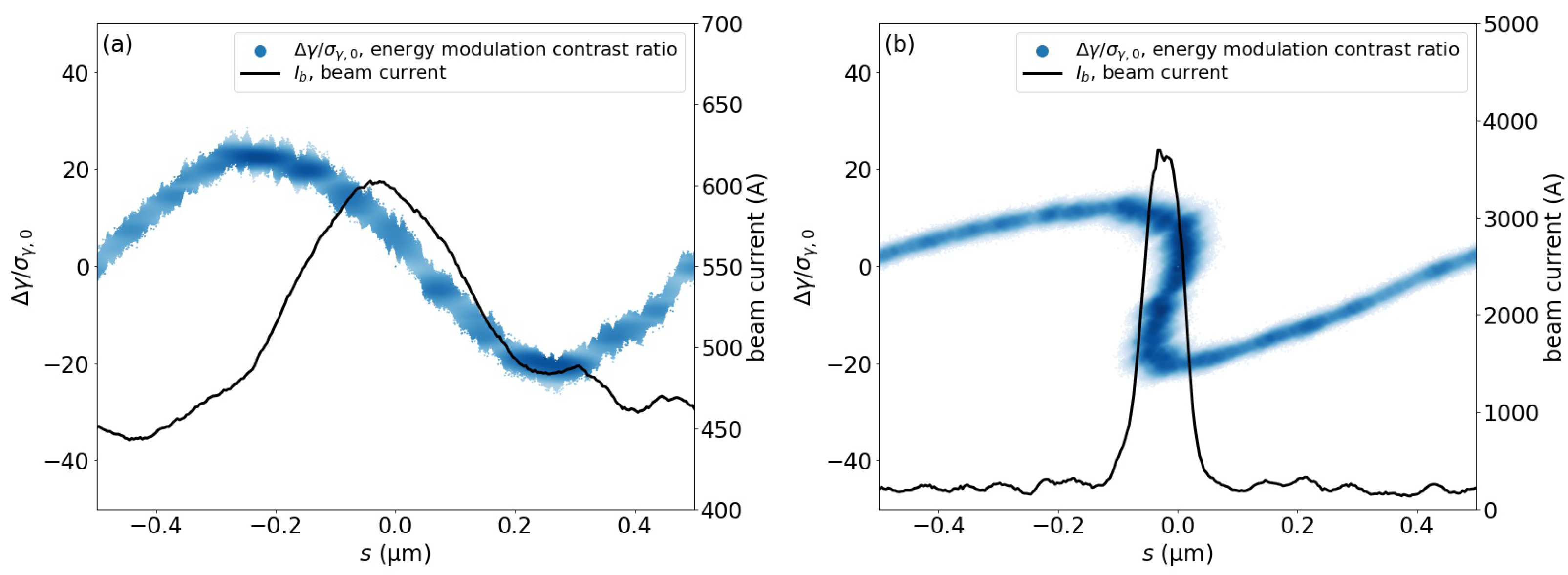
Figure 8 illustrates the bunch compression mechanism of BC2. As stated above, BC1 performed a bulk compression of the beam. BC2, however, considered the incoming electron beam as a sequence of modulated beam sections with a period equal to the laser wavelength (1 ) of the laser modulator (Figure 8a); BC2 compressed each individual modulated period utilizing the energy differential within that laser wavelength, converting it to the longitudinal electron density modulation (Figure 8b) and shaping the beam current into a sequence of 3-kA current spikes. In addition, the modulation amplitude decreased at the BC2 exit, as compared to the results at the L2 exit, and this was due to the uncorrelated energy spread of the beam increasing from , at L2 exit, to 0.170, at BC2 exit, by the ISR effect in BC2.
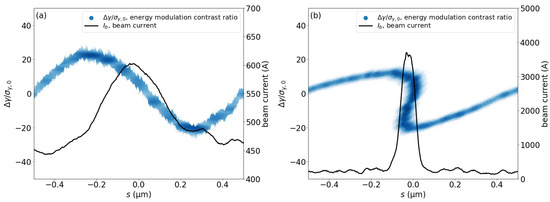
Figure 8.
Longitudinal phase space of the electron beam plotted in the form of the energy modulation contrast ratio vs. the relative longitudinal coordinate, and beam current plotted within one laser wavelength (1 ), (a) before and (b) after the bunch compression by BC2. Within each energy modulation period by the laser modulator, BC2 converts the energy modulation into the longitudinal electron density modulation, enhancing the average beam current of 500 A prior to BC2 to a current spike of 3 kA downstream of BC2. Note that the modulation amplitude after BC2 decreased due to the increase in the uncorrelated energy spread by the ISR effect in BC2.
The major advantage of performing the second stage of the bunch compression by enhancing the peak current in each modulation period created by laser modulation, instead of simply by conventional bulk compression, was that the absolute value of of BC2 could be greatly reduced. A smaller reduced the energy spread increase caused by MBI. Meanwhile, however, as shown in Figure 8b, the beam current did not decrease to zero between the spikes. As a result, a portion of the charge in the beam could not participate in the X-ray lasing of the undulator.
The compression ratio of BC2 was 6, as measured by the ratio of the downstream current spike peak of 3 kA to the upstream average beam current of 500 A. A triplet using quadrupoles, 0.15 m in length (MO3 in Figure 1), was used between the L2 exit and BC2, so the emittance dilution due to CSR in BC2 was minimized. Two 0.05 m long weak quadrupoles were used between the first and the second bending magnets as well as between the third and the fourth bending magnets, to reduce the dispersion functions. The design parameters of BC2 are shown in Table 6.

Table 6.
BC2 design parameters.
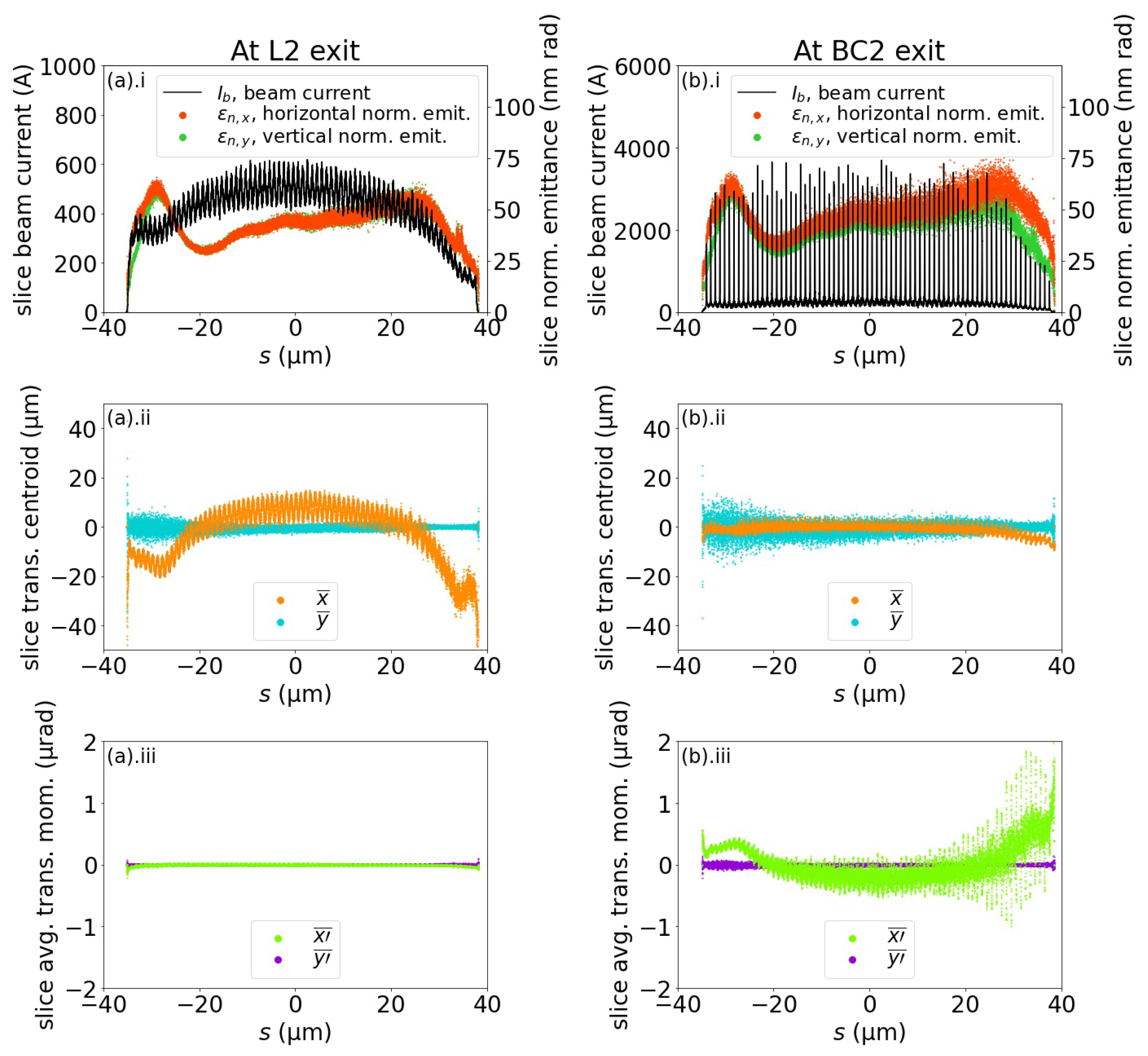
Downstream of BC2, the projected horizontal normalized emittance of the beam increased to 98.3 nm rad, likely due to CSR, while the vertical normalized emittance remained unchanged at 86.8 nm rad. The slice analysis of the beam divided the beam into 20,000 slices of equal lengths, and the results are provided in Figure 9. When comparing Figure 9a.i and b.i, we noted that the periodic 3 kA current spikes were formed in the beam. The portion of the charge in the beam, where the current was above 2.0 kA, was calculated as 38.8%. There was also a slight overall increase in the horizontal normalized emittance per slice downstream of BC2. The reduced horizontal centroid shift at the head and the tail of the beam are shown in Figure 9b.ii. When compared to Figure 9a.ii, the difference was due to the reduced horizontal rms beam size. As shown in Figure 9b.iii, the beam presented a greater variation in the distribution of the slice-average horizontal momentum downstream of BC2, and this was likely caused by a combined effect of both the coherent and the incoherent synchrotron radiation.
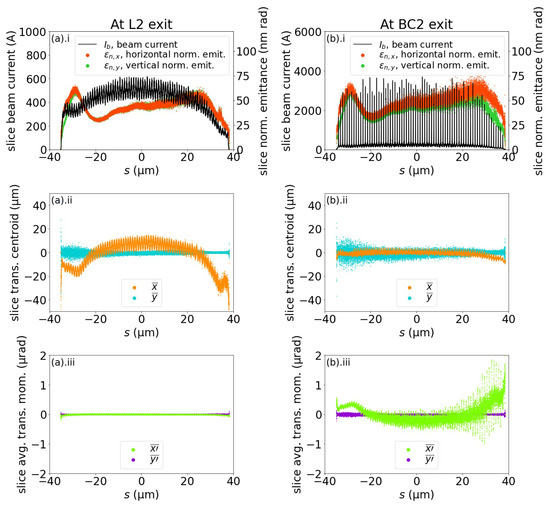
Figure 9.
Performance of BC2 in lattice 1, where the electron beam had previously been compressed by BC1 of a conventional C-chicane configuration. The electron beam is divided into 20,000 slices at (a) L2 exit and (b) BC2 exit. (a).i and (b).i show the normalized emittances and the currents of each slice along the beam; (a).ii and (b).ii show the distributions of the transverse centroids; and (a).iii and (b).iii the distributions of the average transverse momentum shifts.
4.2.2. Determination of LABC Parameters
The LABC modulation parameter A and the compression parameter B were calculated using the uncorrelated energy spread of the electron beam at BC2 exit , which was remarkably larger than that at BC1 exit used for the calculation of the laser modulator modulation amplitude (Table 1). According to Equations (1) and (2), the LABC parameters of lattice 1 were calculated to be and .
The theoretical prediction in [17] indicated that the ideal LABC operating point for MaRIE XFEL was represented by LABC parameters of and for a compression ratio of in BC2. The difference between the theoretical prediction and the Elegant simulation results should be considered according to two aspects. First, the LABC beam current profile feature was characterized by the product of A and B, as the bunching factor in [40] suggested, which was provided by Equation (5).
The product of A and B from the Elegant simulation results was 21% greater than the theoretical prediction. Second, A and B from the Elegant simulation results deviated from the theoretical prediction also in terms of their individual numerical values.
To clarify the reasons for this discrepancy, we should note that the theoretical prediction used an ideal formalism [40] that assumed the BC2 bunch compression capability would not be affected by the uncorrelated energy spread of the beam. In reality, the compression ratio achieved was consistently below the prediction by the ideal theory, i.e., the effective B value was below that provided in Equation (2). With the uncorrelated energy spread considered in the realistic bunch compression in BC2, a smaller effective B value, as compared to that derived from the Elegant simulations using Equation (2), was likely to result in the product of A and B being consistent with the critical condition of our desired LABC beam current profile feature.
5. Linac Sections
The linac acceleration of the beam began at the exit of the photoinjector. The photoinjector followed a TOPGUN design [24,25,26], and the simulations for the beam profile were performed using the General Particle Tracer (GPT) [46]. The electron beam Twiss parameters and other properties are provided in Table 7.

Table 7.
Twiss parameters and other beam properties at the photoinjector exit. Beam energy 153 MeV.
The linac sections accounted for the majority of the beamline design footprint. In the Elegant simulations, the longitudinal space charge (LSC) effect was calculated for the entire length of the first and second sections of the linac.
5.1. First Linac Section
There were two goals for the first linac section: to accelerate the electron beam to an energy of 750 MeV and to prepare the longitudinal energy chirp inside the beam for the downstream bunch compression by BC1. To achieve these goals, L1 was divided into two sections. The first section was the 5.699 GHz linear accelerator, and the second section was the linearizer operating at 17.098 GHz (3 times the operating frequency of the linear accelerator section).
The linear accelerator section boosted the electron beam energy by off-crest acceleration at a phase of 76.33 degrees from 153 MeV at the photoinjector exit to 851 MeV, over a distance of 6.00 m. The accelerator cavities were assumed to operate at an accelerating gradient of 120.0 MV/m. The evolution of the longitudinal energy distribution within the beam over the linear accelerator section is shown in Figure 10a, at the photoinjector exit, and extends to Figure 10b, at the end of the linear accelerator section.
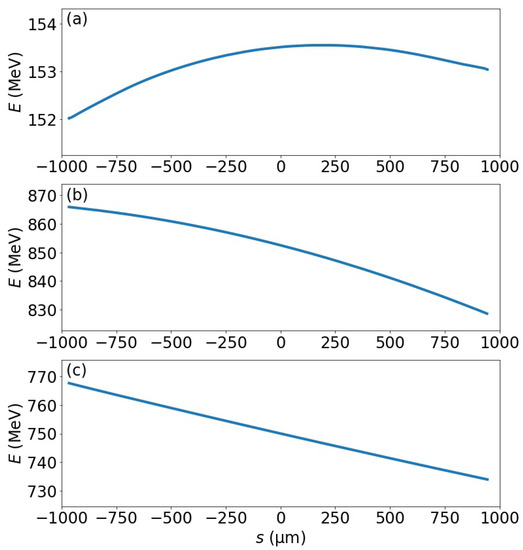
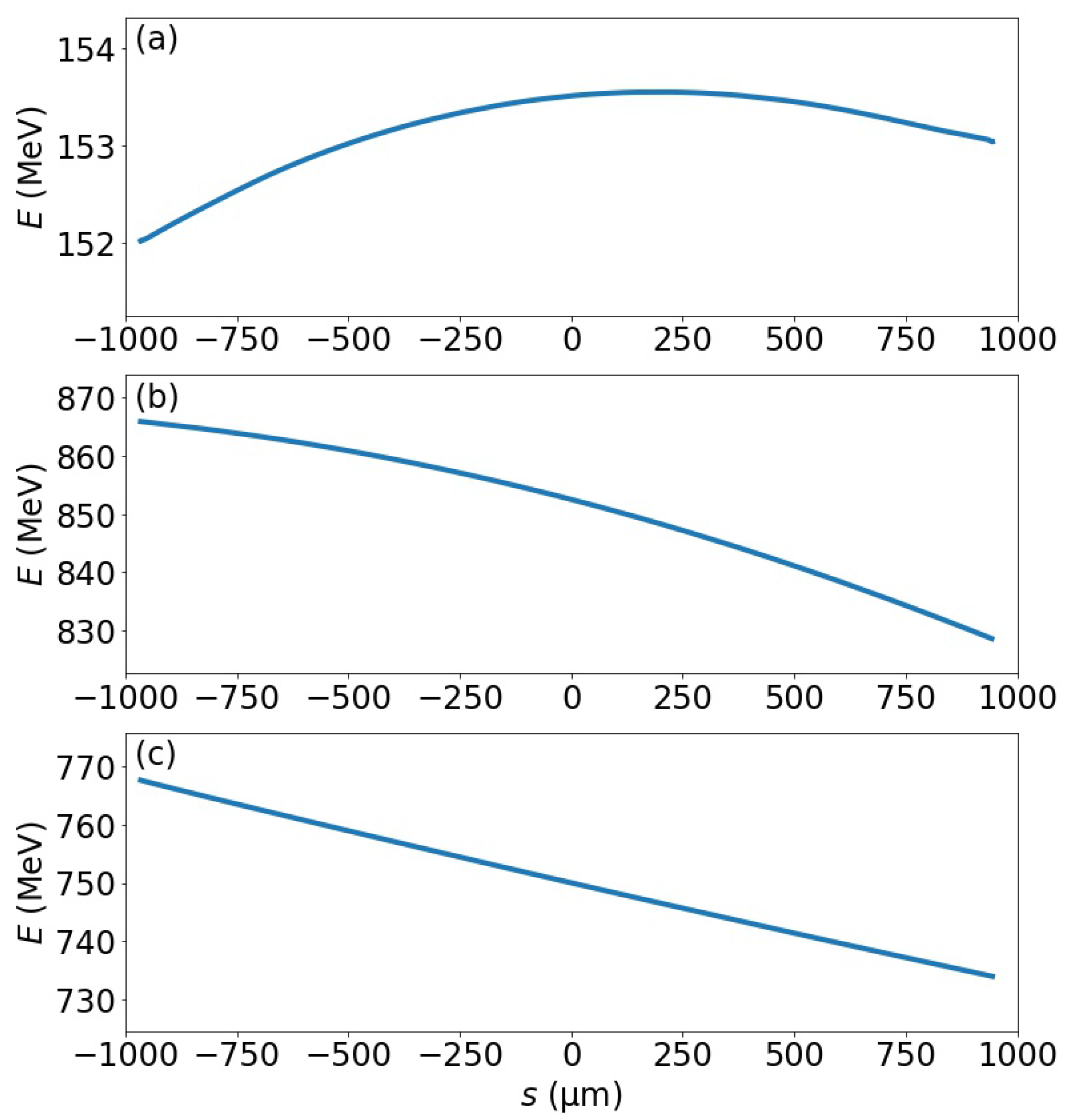
Figure 10.
The evolution of the longitudinal energy distribution within the beam from (a) the photoinjector exit, (b) at the end of the linear accelerator section, and (c) at the end of the linearizer section. The final form of the longitudinal energy distribution within the beam is the chirp that is used in BC1.
The linearizer section operated at a decelerating phase of −92.64 degrees, and the beam energy was reduced from 851 MeV to 750 MeV at the exit of L1, over a distance of 2.68 m. The magnitude of the accelerating gradient of the linearizer was 38.1 MV/m. The function of the linearizer was to rectify the shape of the longitudinal energy chirp, increasing the linearity in the relationship between the energy and the relative longitudinal coordinate of the electrons in the beam. The finalized chirp is shown in Figure 10c, where the curve exhibited a very prominent linearity. However, the second order variation still remained in the chirp profile to cancel the nonlinear effect in BC1.
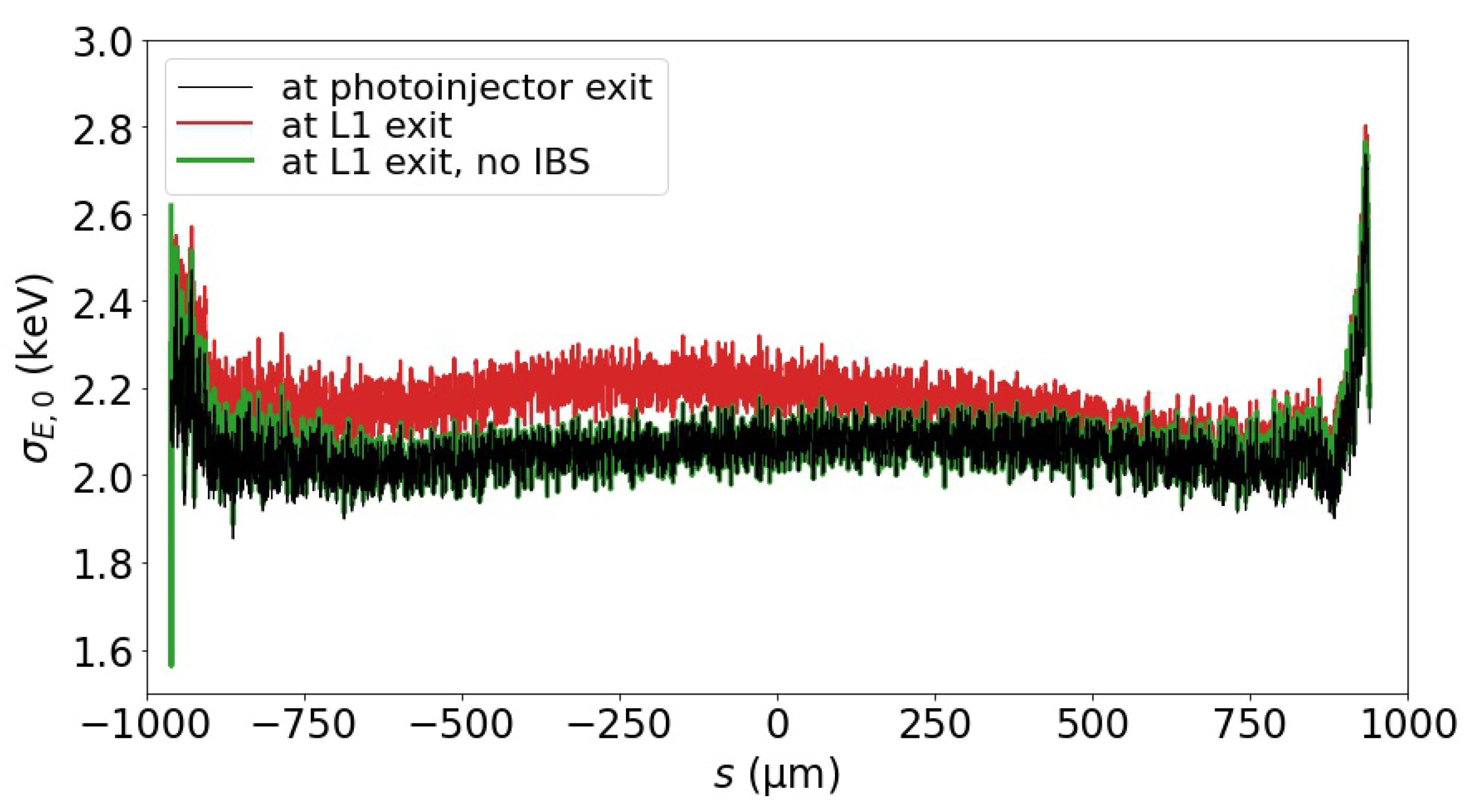
Figure 11 shows the increase in the uncorrelated energy spread along the beam, as it traverses L1. At the photoinjector exit, the uncorrelated energy spread was below 2.1 keV. By the end of L1, the uncorrelated energy spread grew, in general, by approximately 0.2 keV, with the intra-beam scattering (IBS) considered in the Elegant simulation. As also shown in Figure 11, if IBS was excluded from the simulation, the change of the uncorrelated energy spread was trivial. Therefore, other factors, e.g., the longitudinal space charge force, had negligible influence on the uncorrelated energy spread in L1.
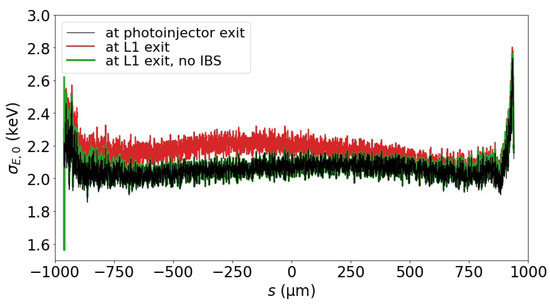
Figure 11.
Illustration of the uncorrelated energy spread distribution along the beam, plotted for the beam at the photoinjector exit; at the L1 exit with IBS calculation included in the Elegant simulation; and at the L1 exit, without considering IBS.
The horizontal and vertical normalized emittances increased from 54.4 nm rad at the photoinjector exit (Table 7) to 65.9 nm rad at the L1 exit (Table 2). This was due to the chromatic RF focusing by the linac cavities and was a correlated effect, which could be compensated for by the instances of the matching optics downstream.
5.2. Second Linac Section
There were two goals set for the second linac section: to accelerate the electron beam to 12 GeV and to remove the longitudinal energy chirp by the off-crest acceleration and the short-range wakefield.
L2 also operated at a frequency of 5.699 GHz and an accelerating gradient of 120.0 MV/m, at a phase of 103.00 degrees and with a total structure length of 97.94 m. Five quadrupoles, 0.15 m long and equally spaced from the start to the end of L2, were used to maintain the desired beam properties throughout the L2 acceleration. L2 constituted the major real estate cost of the entire MaRIE XFEL facility, as currently configured.
6. Beam Analysis at X-ray Undulator Entrance
In this section, we first discuss the Elegant simulation results of the properties of the electron beam prior to the X-ray lasing in the undulator, and then we discuss the beam instability mitigation achieved in our entire beamline design. The preliminary results of the X-ray generation simulations in Genesis [47] are also introduced.
6.1. Beam Properties
The last matching optics (MO4 in Figure 1) downstream of BC2 shaped and transported the beam for the final input into the X-ray undulator. The designed horizontal and vertical rms beam sizes at this position were approximately 2.5 , with a minimal magnitude of -functions. This beam size had been determined as a preliminary selection for the X-ray lasing investigations according to the Ming-Xie parameterization method [44], which indicated that an average -function smaller than 2 m at the entrance of the undulator was essential for yielding X-ray pulses with a sufficient number of photons to meet the MaRIE requirement. Because it was the microbunched portion of the electron beam that participated in X-ray lasing, the energy spread calculation considered only the sections inside the beam where the current was above 2.0 kA. We present the simulation results of the electron beam at the X-ray undulator entrance of lattice 1 (Table 8, Figure 12a.i–f.i) and lattice 2 (Table 9, Figure 12a.ii–f.ii).

Table 8.
Lattice 1 electron beam Twiss parameters and other properties at X-ray undulator entrance. Beam energy 12 GeV.
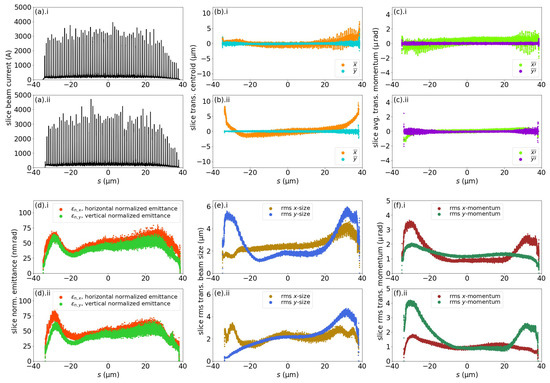
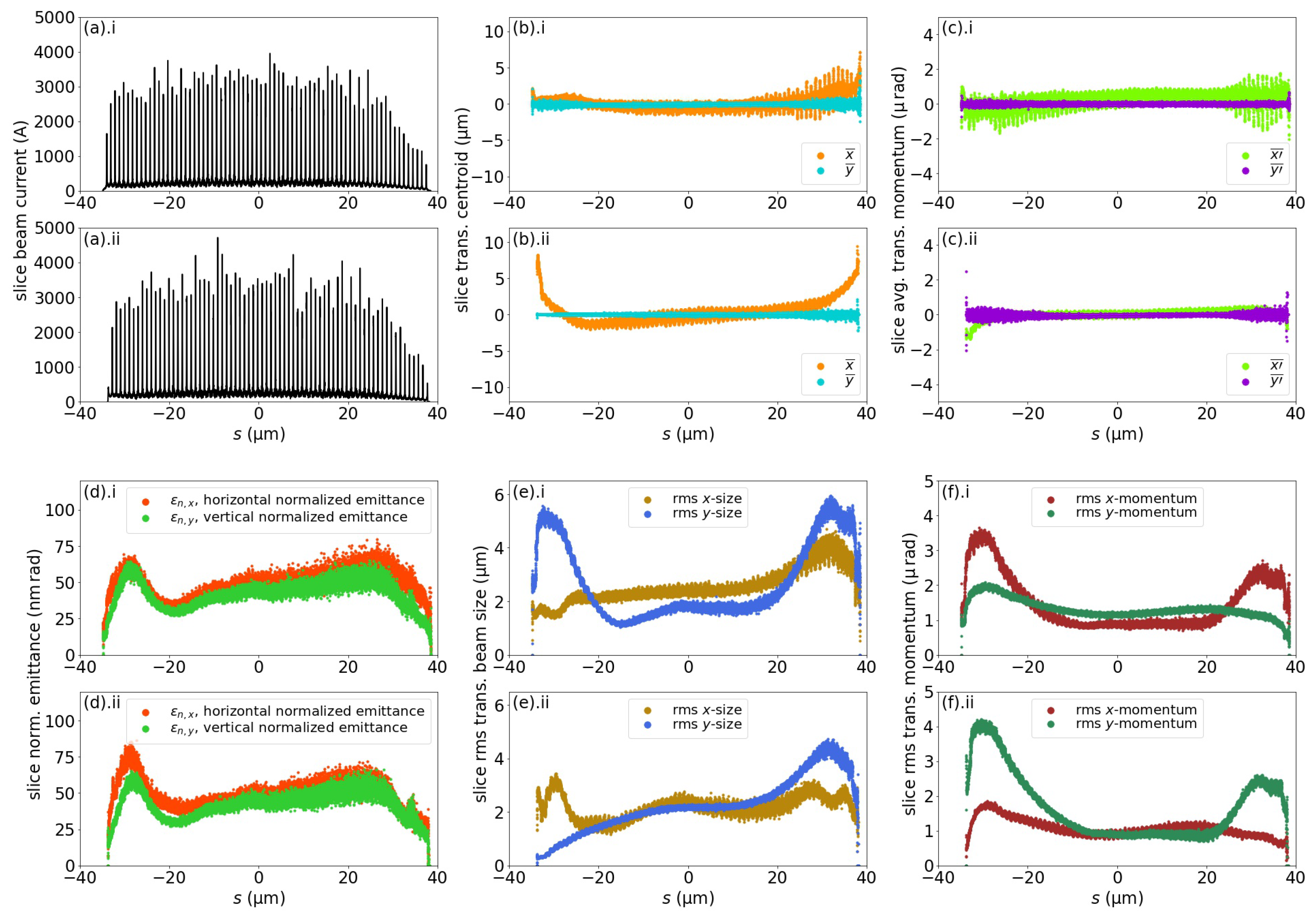
Figure 12.
Comparison of the longitudinal distributions of the electron beam properties at the entrance of the X-ray undulator, after the beam traversed lattice 1 (a.i–f.i) and lattice 2 (a.ii–f.ii). The beams are divided into 20,000 slices with equal lengths, and the beam properties per slice are shown for (a) beam currents, (b) transverse centroid shifts, (c) transverse average momentum shifts, (d) normalized transverse emittances, (e) rms transverse beam sizes, and (f) rms transverse beam momentum profiles.

Table 9.
Lattice 2 electron beam Twiss parameters and other properties at X-ray undulator entrance. Beam energy 12 GeV.
Microbunches carrying a current spike at 3.0 kA were formed in the beam for both lattices 1 and 2 (Figure 12a). The beam in lattice 1 had a comparatively more consistent transverse centroid distribution than the beam in lattice 2, the head and tail sections of which had notable horizontal centroid shifts acquired via BC1 bunch compression using a double C-chicane (Figure 12b). The beam in lattice 1 had a horizontal average momentum shift variation between −2 and 2 , as compared to the negligible horizontal average momentum shift variation in the beam in lattice 2, except for the mild perturbations in the head and tail sections (Figure 12c). Figure 12d shows that both the beams in lattices 1 and 2 has their slice emittances preserved after traversing the lattices. The beam in lattice 2 has a comparatively more consistent profile of transverse rms sizes along the beam, while the beam in lattice 1 has greater vertical rms sizes at the head and tail sections (Figure 12e). Finally, the central sections of the electron beams from both lattices 1 and 2 exhibited a steady value of approximately 1 for the horizontal and vertical rms momentum.
The Twiss parameters and the other properties of the beam at the entrance of the X-ray undulator, as shown here, have not ultimately been optimized for X-ray lasing performance in the undulator; therefore, the simulation results shown in this section serve as a nominal example of the beam preparation achieved by the end of the accelerator lattice. Prior research [17] indicated a projected horizontal normalized emittance of 200 nm rad and an uncorrelated fractional energy spread within the current spikes below in order for the MaRIE XFEL, when using the LABC method, to meet the requirements for X-ray lasing performance. In comparison, the beam properties provided in Table 8 and Table 9 for both lattice 1 and 2 easily met these requirements.
6.2. Achieved Mitigation of Beam Instabilities
It was important to emphasize that in the XFEL architecture using the LABC method shown in this work, the desired beam properties at the X-ray undulator entrance were acquired without the application of a laser heater [48], which is typically applied for the purpose of MBI suppression by intentionally increasing the uncorrelated energy spread downstream of the photoinjector. In our accelerator lattice design, the uncorrelated energy spread of the electron beam was consistently maintained at a very low level. The energy spread increase caused by MBI was successfully constrained by using the small magnitude of the of the second bunch compressor, and by placing the second bunch compressor at the end of the electron beam acceleration.
A comparison of the URWW effect on the electron beam, processed with our LABC (in lattice 1) method and with the conventional bulk compression method for BC2, is shown in Figure 13. BC2 for the bulk compression of the beam was implemented at 2.5 GeV, producing a peak beam current of 3.0 kA, and the beam was fully de-chirped by the end of the ensuing third section of the linac (L3) to the final beam energy of 12 GeV. This bulk compression was developed in order to compare the URWW effect, and it was not a beamline that had been substantially optimized. The URWW calculations were performed using in-house Python scripts that had been composed based on the analytical theories in [14], assuming that the electron beam properties remained constant while the electron beam traveled though the undulator. The calculations included 3000 undulator periods, with individual undulator periods of 18.6 mm.
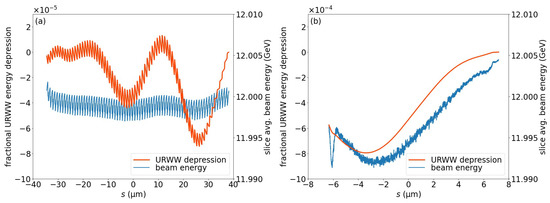
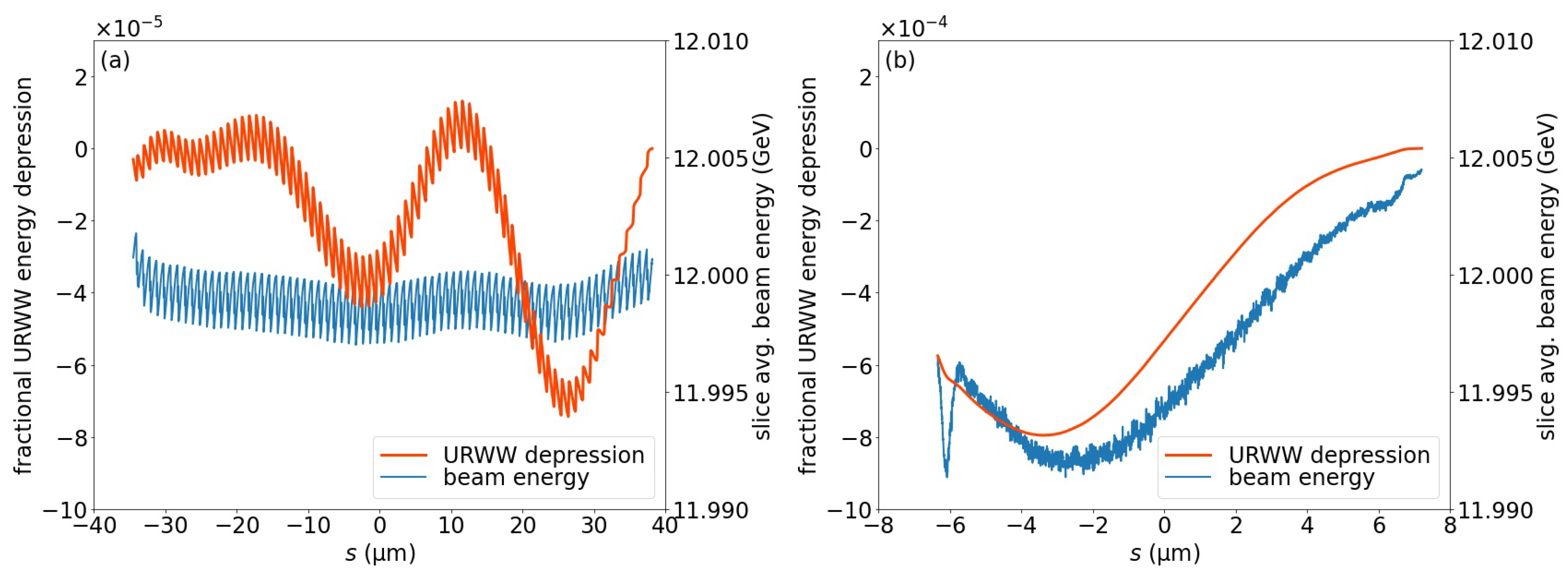
Figure 13.
Comparison of the URWW effect on the electron beam (a) from lattice 1, processed with our LABC method and (b) with the conventional bulk compression method. In each plot, the distributions of the fractional URWW beam energy depression and of the predicted depressed beam energy distribution within the beam are provided. Note that the head of the beam is to the right of the plot.
The electron beam vacuum chamber was assumed to be made of copper with an inner radius of 3 mm and with the alternating current (AC) conductivity parameter [14] set as . As Figure 13 shows, the fractional energy depression by URWW is one order of magnitude smaller in our LABC method, as compared to the bulk compression method. The physical mechanism that led to a significantly smaller URWW effect (when using the LABC method) was that the total beam length of an LABC electron bunch was much longer than the length of the bulk compression bunch, as shown in the comparison of the abscissa scales in Figure 13. When using the LABC method, the bunch compression of BC2 did not shorten the total length of the electron beam. The longer beam length caused the longitudinal resistive-wall wakefield inside the LABC bunch to be much weaker than that of the bulk compression beam [14,17]. After the imprint of the URWW effect on the beam energy distribution, the average fractional energy spread in the individual LABC microbunches was increased to , and the total fractional energy spread of all microbunches as an ensemble was . Therefore, the URWW degradation of the microbunch properties of the LABC beam was minimal. In comparison, after applying the URWW energy depression, the central section of the bulk compression beam that produced a fractional energy spread less than constituted 44% of the entire beam charge, which was similar to the portion of the LABC beam charge in the microbunches that participated in the X-ray lasing. However, the charge portion of the central section of the bulk compression beam that contributed to a fractional energy spread, up to , was only 19%. As a result, the LABC method was favorable in terms of achieving a better performance and reducing the negative effects of URWW.
In Table 8 and Table 9,when using our LABC method, the portion of the beam charge that participated in the X-ray lasing in the undulator was around 40%. This was smaller than the X-ray lasing beam charge portion typical in XFEL architecture using exclusively bulk beam compression schemes. Nonetheless, with the presentation of the capabilities of mitigating the beam instabilities, of preserving the ultra-low beam emittance, and of producing a beam with very low energy spread, the proposed XFEL architecture using an LABC method provides a competitive alternative to the conventional XFEL architecture. In addition, due to the overcompression of the microbunch in our LABC configuration, the lasing portion of the beam charge, as shown in Table 8 and Table 9, was greater than in the ESASE scenario [17], where the microbunch current spike profile was much sharper.
6.3. Preliminary X-ray Lasing Calculation
Preliminary time-independent GENESIS simulations were performed using only the electron beam slices contributing to a beam current above 2 kA, as in lattice 1. The uniform undulator period was set at 18.6 mm, with an undulator parameter of 1.22. A FODO-type quadrupole arrangement was used to focus the beam for the entire length of the undulator. The length and strength of the quadrupoles, together with the length of the undulator segments, were used as variables in order to determine the maximal saturation lasing power. Because these preliminary simulations were not time dependent, the electron beam properties were not able to evolve over the course of the undulator.
The simulations demonstrated 42 keV photon energy X-ray lasing with more than photons per pulse. A refined undulator design, e.g., with carefully engineered tapering, would be sufficient to enhance the X-ray photon generation for the MaRIE requirement of photons per pulse. However, the beam properties resulted in an estimated fractional X-ray spectral bandwidth of , which was greater than the MaRIE requirement. This relatively large bandwidth was caused by the extremely small transverse beam size that had been employed to minimize the gain length and create margins for the design of the undulator beam focusing.
In order to reduce the X-ray spectral bandwidth, a revised MO4 in lattice 1 was then tested to focus the electron beam at the entrance of the undulator with a horizontal and vertical rms beam size of 25 . In this scenario, the estimated fractional spectral bandwidth of the X-ray pulse was reduced to , satisfying the MaRIE requirement but increasing the saturation length. The time-independent GENESIS simulation for this scenario showed little degradation of the 42-keV photon production efficiency, and the results indicated that the number of photons generated per pulse was still .
Extensive X-ray lasing simulations have been planned for the next step of our MaRIE XFEL research using the proposed LABC approach.
7. Conclusions
Footprint designs of the accelerator lattices for MaRIE X-ray free electron lasers (XFELs) that utilized a specific set of parameters for laser-assisted bunch compression (LABC) have been presented in this paper, with two different configurations of the first bunch compressor. The accelerator lattices were able to transport and process the electron beam from the photoinjector exit to the entrance of the X-ray undulator. The properties of the electron beam met the MaRIE requirements for X-ray lasing. The presented LABC method was based on and shares the same architecture with the ESASE scheme, but the design goals and the operating parameters, including the microbunch phase space manipulation, were more advanced.
The presented LABC approach was achievable in our simulations by using a laser modulator in the form of a magnet undulator, downstream of the first bunch compressor at 750 MeV, in which the electron beam was modulated by a 3.4-GW 1- wavelength laser, and the second bunch compressor, with a smaller magnitude of the value, after the acceleration of the electron beam to a final energy of 12 GeV.
The LABC accelerator lattices shown in this work demonstrated the suppression of both MBI and URWW. The emittance dilution and the electron beam profile deformation caused by the CSR effects were reduced to a satisfactory level by a longer overall beam length, which was intrinsic to the LABC method, by the optimized matching optics, and specially in lattice 2, by the carefully designed double C-chicane in BC1.
Two configurations of the first bunch compressor were investigated. The conventional C-chicane configuration had a streamlined design with a much shorter length; it also led to a better alignment of the horizontal centroid distribution of the beam at the entrance of the X-ray undulator. The double C-chicane configuration occupied more space and added to the complication of the lattice, but it enabled the electron beam to have minimal transverse momentum shifts throughout the beam and to have a much smaller projected horizontal emittance as the beam exited the first bunch compressor. This comparatively smaller projected horizontal emittance was also noted at the entrance of the X-ray undulator, where the beam exhibits trivial horizontal momentum shifts along the length.
This study showed that the MaRIE XFEL accelerator lattice could be established at a length of approximately 200 m, promoting the feasibility of hosting XFEL facilities at a smaller scale, e.g., on university campuses, as opposed to only being available at national laboratories.
Author Contributions
Conceptualization, B.E.C., P.M.A. and Q.R.M.; methodology, P.M.A. and H.X.; formal analysis, P.M.A., Q.R.M. and H.X.; investigation, H.X., L.D.D. and R.R.R.; writing—original draft preparation, H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. Department of Energy through the Laboratory Directed Research and Development program of the Los Alamos National Laboratory, under project number 20200287ER.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McNeil, B.; Thompson, N. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814–821. [Google Scholar] [CrossRef]
- Bostedt, C.; Boutet, S.; Fritz, D.; Huang, Z.; Lee, H.; Lemke, H.; Robert, A.; Schlotter, W.; Turner, J.; Williams, G. Linac coherent light source: The first five years. Rev. Mod. Phys. 2016, 88, 015007. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Frontiers of Materials Research: A Decadal Survey; National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- Lewellen, J.; Bishofberger, K.; Carlsten, B.; Duffy, L.; Krawczyk, F.; Marksteiner, Q.; Nguyen, D.; Russell, S.; Sheffield, R.; Yampolsky, N. Status of the MaRIE X-FEL accelerator design. In Proceedings of the IPAC2015, Richmond, VA, USA, 3–8 May 2015; pp. 3–8. [Google Scholar]
- Sheffield, R.; Barnes, C.; Tapia, J. Matter-Radiation Interactions in Extremes (MaRIE): Project Overview; Technical Report LA-UR-17-27562; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2017.
- Bohon, J.; Ortega, A.; O’Toole, J.; Sheffield, R.; Barnes, C. A survey of current and emerging experimental requirements for dynamic mesoscale materials science at user facilities. Aip Conf. Proc. 2020, 2272, 060003. [Google Scholar]
- Nodvick, J.; Saxon, D. Suppression of coherent radiation by electrons in a synchrotron. Phys. Rev. 1954, 96, 180. [Google Scholar] [CrossRef]
- Carlsten, B.; Raubenheimer, T. Emittance growth of bunched beams in bends. Phys. Rev. E 1995, 51, 1453. [Google Scholar] [CrossRef] [PubMed]
- Bane, K.; Decker, F.J.; Ding, Y.; Dowell, D.; Emma, P.; Frisch, J.; Huang, Z.; Iverson, R.; Limborg-Deprey, C.; Loos, H.; et al. Measurements and modeling of coherent synchrotron radiation and its impact on the Linac Coherent Light Source electron beam. Phys. Rev. ST Accel. Beams 2009, 12, 030704. [Google Scholar] [CrossRef]
- Ryne, R.; Mitchell, C.; Qiang, J.; Carlsten, B.; Yampolsky, N. Large scale simulation of synchrotron radiation using a Lienard-Wiechert approach. In Proceedings of the IPAC 2012, New Orleans, LA, USA, 20–25 May 2012; Volume 46, p. TUPPP036. [Google Scholar]
- Huang, Z.; Borland, M.; Emma, P.; Wu, J.; Limborg, C.; Stupakov, G.; Welch, J. Suppression of microbunching instability in the linac coherent light source. Phys. Rev. ST Accel. Beams 2004, 7, 074401. [Google Scholar] [CrossRef]
- Saldin, E.; Schneidmiller, E.; Yurkov, M. Longitudinal space charge-driven microbunching instability in the TESLA Test Facility linac. Nucl. Instrum. Meth. A 2004, 528, 355–359. [Google Scholar] [CrossRef]
- Borland, M. Modeling of the microbunching instability. Phys. Rev. ST Accel. Beams 2008, 11, 030701. [Google Scholar] [CrossRef]
- Bane, K.; Sands, M. The Short-Range Resistive Wall Wakefields. AIP Conf. Proc. 1996, 367, 131–149. [Google Scholar]
- Al-Khateeb, A.; Boine-Frankenheim, O.; Hofmann, I.; Rumolo, G. Analytical calculation of the longitudinal space charge and resistive wall impedances in a smooth cylindrical pipe. Phys. Rev. E 2001, 63, 026503. [Google Scholar] [CrossRef] [PubMed]
- Bane, K.; Stupakov, G. Resistive Wall Wakefield in the LCLS Undulator Beam Pipe; Technical report; SLAC National Accelerator Lab.: Menlo Park, CA, USA, 2004. [Google Scholar]
- Carlsten, B.; Anisimov, P.; Barnes, C.; Marksteiner, Q.; Robles, R.; Yampolsky, N. High-brightness beam technology development for a future dynamic mesoscale materials science capability. Instruments 2019, 3, 52. [Google Scholar] [CrossRef]
- Anisimov, P. Laser Assisted Bunch Compression for High Energy X-ray Free Electron Lasers; Technical Report LA-UR-19-28673; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2019.
- Rosenzweig, J.; Majernik, N.; Robles, R.; Andonian, G.; Camacho, O.; Fukasawa, A.; Kogar, A.; Lawler, G.; Miao, J.; Musumeci, P.; et al. An ultra-compact X-ray free-electron laser. New J. Phys. 2020, 22, 093067. [Google Scholar] [CrossRef]
- Perosa, G.; Mitri, S.D. Matrix model for collective phenomena in electron beam’s longitudinal phase space. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef]
- Zholents, A. Method of an enhanced self-amplified spontaneous emission for X-ray free electron lasers. Phys. Rev. ST Accel. Beams 2005, 8, 040701. [Google Scholar] [CrossRef]
- Duris, J.; MacArthur, J.; Glownia, J.; Li, S.; Vetter, S.; Miahnahri, A.; Coffee, R.; Hering, P.; Fry, A.; Welch, M.; et al. Controllable X-ray pulse trains from enhanced self-amplified spontaneous emission. Phys. Rev. Lett. 2021, 126, 104802. [Google Scholar] [CrossRef] [PubMed]
- Zholents, A.; Fawley, W.; Emma, P.; Huang, Z.; Stupakov, G.; Reiche, S. Current-Enhanced SASE Using an Optical Laser and Its Application to the LCLS; Technical report; Lawrence Berkeley National Lab.: Berkeley, CA, USA, 2004.
- Rosenzweig, J.; Cahill, A.; Carlsten, B.; Castorina, G.; Croia, M.; Emma, C.; Fukusawa, A.; Spataro, B.; Alesini, D.; Dolgashev, V.; et al. Ultra-high brightness electron beams from very-high field cryogenic radiofrequency photocathode sources. Nucl. Instrum. Meth. A 2018, 909, 224–228. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Cahill, A.; Dolgashev, V.; Emma, C.; Fukasawa, A.; Li, R.; Limborg, C.; Maxson, J.; Musumeci, P.; Nause, A.; et al. Next generation high brightness electron beams from ultrahigh field cryogenic rf photocathode sources. Phys. Rev. Accel. Beams 2019, 22, 023403. [Google Scholar] [CrossRef]
- Robles, R.; Camacho, O.; Fukasawa, A.; Majernik, N.; Rosenzweig, J. Versatile, high brightness, cryogenic photoinjector electron source. Phys. Rev. Accel. Beams 2021, 24, 063401. [Google Scholar] [CrossRef]
- Simakov, E.; Alexander, A.; Gorelov, D.; Hall, T.; Middendorf, M.; Rai, D.; Tajima, T.; Zuboraj, M. Update on the Status of C-Band Research and Facilities at LANL. In Proceedings of the NAPAC 2022, Albuquerque, NM, USA, 6–12 August 2022. [Google Scholar]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Milne, C.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray free electron laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Prat, E.; Ferrari, E.; Calvi, M.; Ganter, R.; Reiche, S.; Schmidt, T. Demonstration of a compact X-ray free-electron laser using the optical klystron effect. Appl. Phys. Lett. 2021, 119, 151102. [Google Scholar] [CrossRef]
- Wang, W.; Feng, K.; Ke, L.; Yu, C.; Xu, Y.; Qi, R.; Chen, Y.; Qin, Z.; Zhang, Z.; Fang, M.; et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator. Nature 2021, 595, 516–520. [Google Scholar] [CrossRef] [PubMed]
- Cahill, A.; Rosenzweig, J.; Dolgashev, V.; Li, Z.; Tantawi, S.; Weathersby, S. rf losses in a high gradient cryogenic copper cavity. Phys. Rev. Accel. Beams 2018, 21, 061301. [Google Scholar] [CrossRef]
- Cahill, A.; Rosenzweig, J.; Dolgashev, V.; Tantawi, S.; Weathersby, S. High gradient experiments with X-band cryogenic copper accelerating cavities. Phys. Rev. Accel. Beams 2018, 21, 102002. [Google Scholar] [CrossRef]
- Simakov, E. New Accelerator Capabilities with the High-Gradient C-Band; Technical Report LA-UR-21-30757; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2021.
- Borland, M. Elegant: A flexible SDDS-Compliant Code for Accelerator Simulation; Technical Report LS-287; Argonne National Lab.: Lemont, IL, USA, 2000.
- van Rossum, G.; Drake, F. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Stulle, F.; Adelmann, A.; Pedrozzi, M. Designing a bunch compressor chicane for a multi-TeV linear collider. Phys. Rev. ST Accel. Beams 2007, 10, 031001. [Google Scholar] [CrossRef]
- Mitri, S.D.; Cornacchia, M.; Spampinati, S. Cancellation of coherent synchrotron radiation kicks with optics balance. Phys. Rev. Lett. 2013, 110, 014801. [Google Scholar] [CrossRef]
- Jing, Y.; Hao, Y.; Litvinenko, V. Compensating effect of the coherent synchrotron radiation in bunch compressors. Phys. Rev. ST Accel. Beams 2013, 16, 060704. [Google Scholar] [CrossRef]
- Hemsing, E.; Stupakov, G.; Xiang, D.; Zholents, A. Beam by design: Laser manipulation of electrons in modern accelerators. Rev. Mod. Phys. 2014, 86, 897–941. [Google Scholar] [CrossRef]
- Zholents, A.; Zolotorev, M. Attosecond X-ray pulses produced by ultra short transverse slicing via laser electron beam interaction. New J. Phys. 2008, 10, 025005. [Google Scholar] [CrossRef]
- McNeil, B.; Thompson, N.; Dunning, D. Transform-limited X-ray pulse generation from a high-brightness self-amplified spontaneous-emission free-electron laser. Phys. Rev. Lett. 2013, 110, 134802. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J. 5. Coherence of optical waves. In Statistical Optics; John Wiley & Sons Inc.: New York, NY, USA, 2000; pp. 157–236. [Google Scholar]
- Xie, M. Design optimization for an X-ray free electron laser driven by SLAC linac. In Proceedings of the Particle Accelerator Conference, Dallas, TX, USA, 1–5 May 1995; Volume 1, pp. 183–185. [Google Scholar]
- Xu, H.; Duffy, L.; Marksteiner, Q.; Anisimov, P. Comparison study on first bunch compressor schemes by conventional and double C-chicane for MaRIE XFEL. In Proceedings of the NAPAC 2022, Albuquerque, NM, USA, 6–12 August 2022. [Google Scholar]
- Loos, M.D.; der Geer, S.V. General Particle Tracer: A new 3D code for accelerator and beamline design. In Proceedings of the 5th European Particle Accelerator Conference, Sitges, Barcelona, Spain, 10–14 June 1996; p. 1241. [Google Scholar]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Meth. A 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Huang, Z.; Brachmann, A.; Decker, F.J.; Ding, Y.; Dowell, D.; Emma, P.; Frisch, J.; Gilevich, S.; Hays, G.; Hering, P.; et al. Measurements of the linac coherent light source laser heater and its impact on the X-ray free-electron laser performance. Phys. Rev. ST Accel. Beams 2010, 13, 020703. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).