Bridge Health Monitoring Using Proper Orthogonal Decomposition and Transfer Learning
Abstract
:Featured Application
Abstract
1. Introduction
2. TL-Based Damage Identification
2.1. SVD for Damage Detection
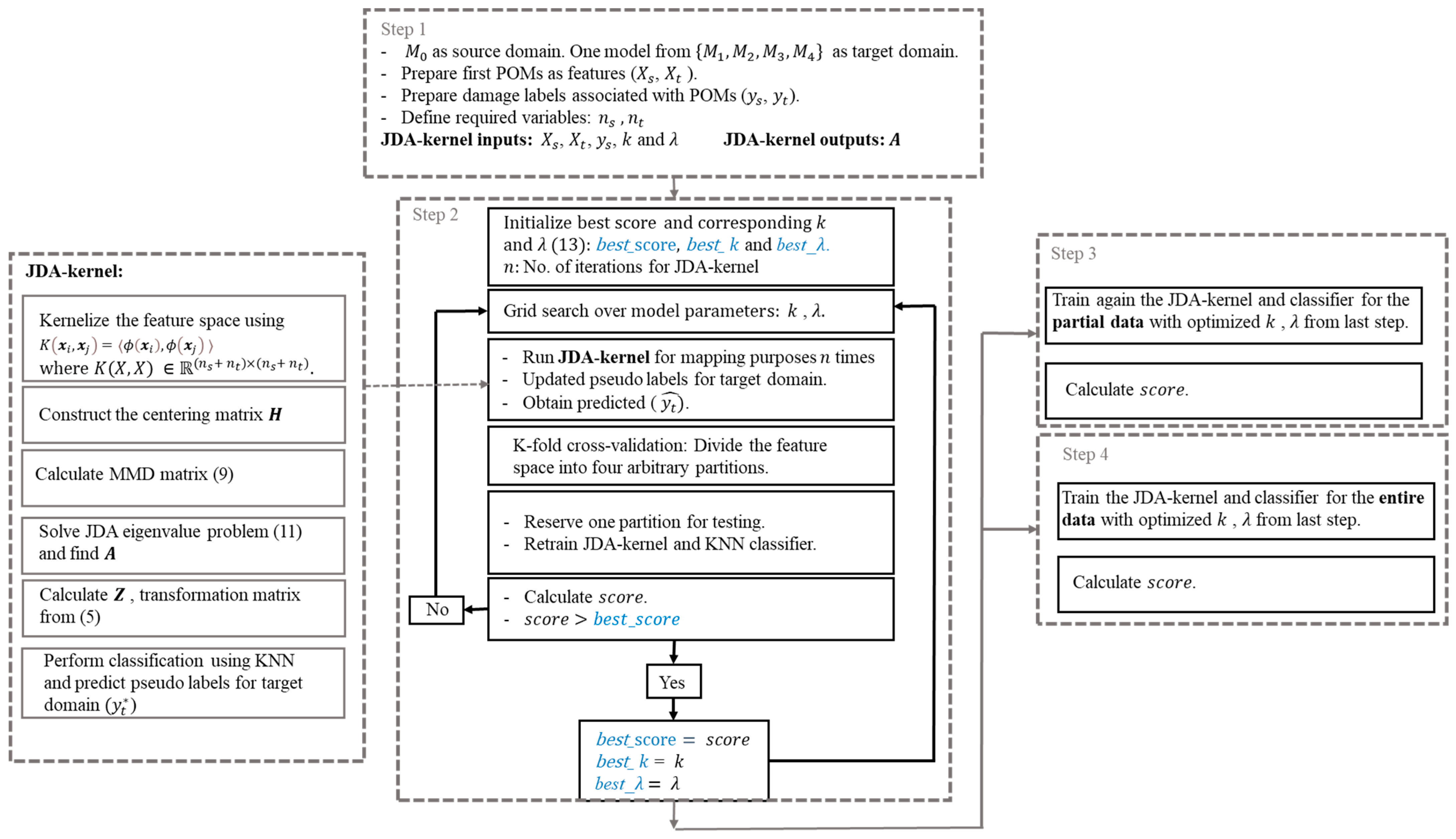
2.2. TL Using JDA–kernel
3. Validating TL for Bridge Damage Detection Using Simulated Experiments
3.1. Railway Bridge Study
3.2. FE Modeling
3.3. Simulated Experiments
3.4. POMs
4. TL Using Coupled POD and JDA–kernel
5. Results and Discussion
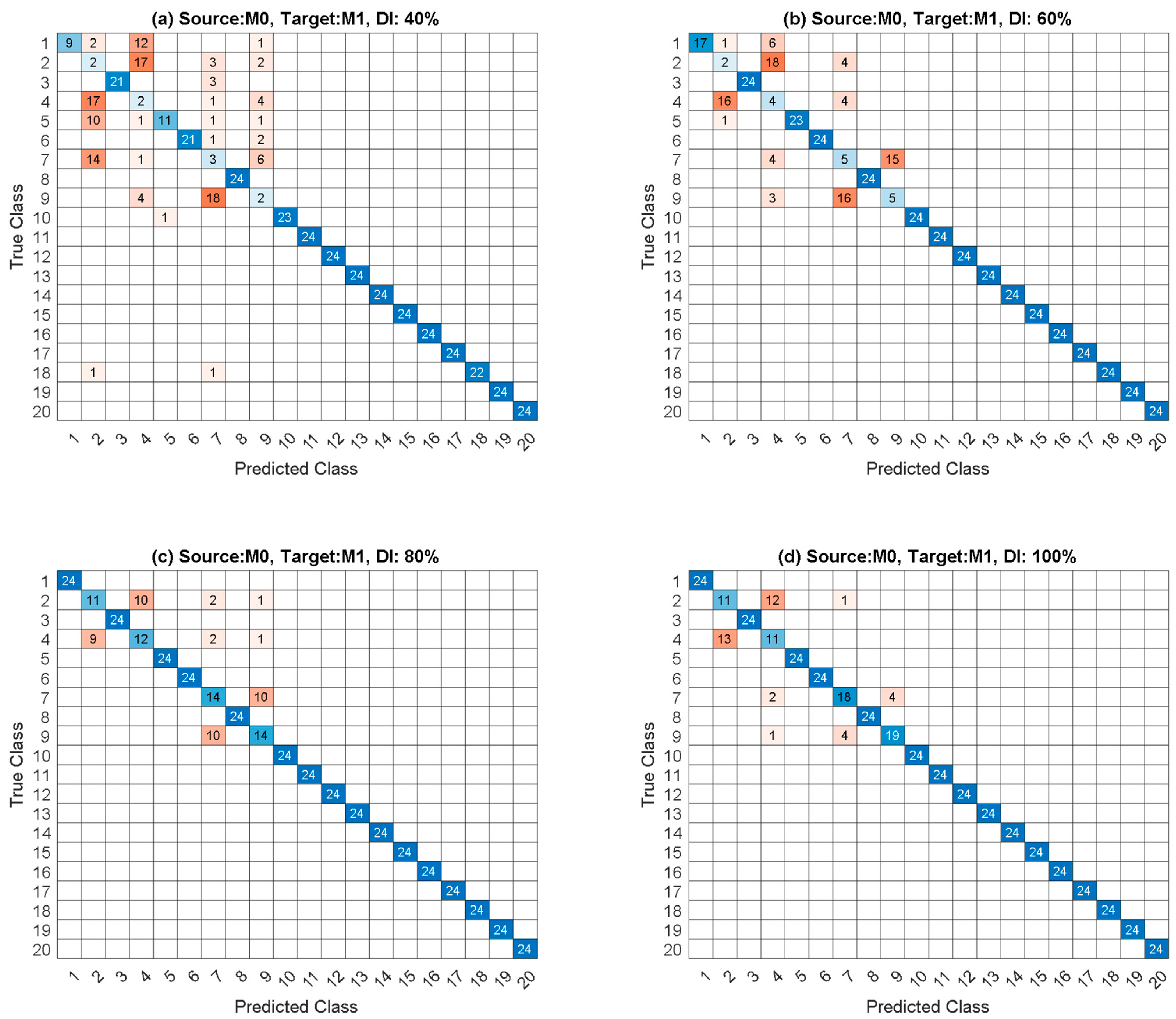
5.1. Scenario 1: DI Known, DL Unknown
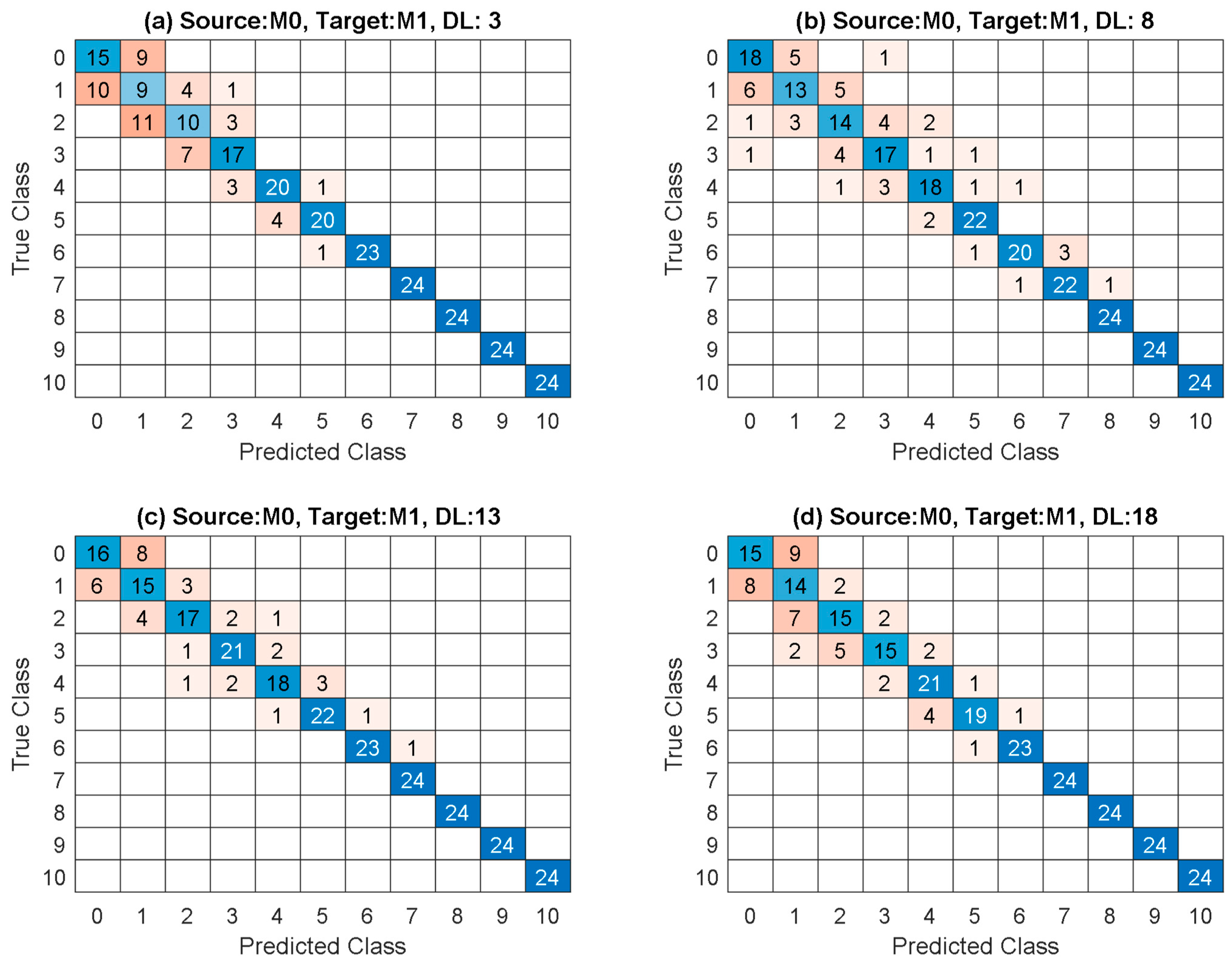
5.2. Scenario 2: DL Known, DI Unknown
5.3. Scenario 3: DL and DI Unknown
6. Conclusions
- TL successfully identified DL labels for each target model. Label identification was less accurate at locations with similar POMs.
- TL was shown to be an effective method for identifying the DIs for the bridge and MUs that were studied. As expected, TL method accuracy improved at larger DIs.
- Live load position influenced TL method effectiveness, with more effective DI identification occurring in close proximity to loaded tracks.
- The JDA–kernel TL significantly improved damage identification when compared against KNN.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Ruotolo, R.; Surace, C. Using SVD to detect damage in structures with different operational conditions. J. Sound Vib. 1999, 226, 425–439. [Google Scholar] [CrossRef]
- Gardner, P.; Liu, X.; Worden, K. On the application of domain adaptation in structural health monitoring. Mech. Syst. Signal Process. 2020, 138, 106550. [Google Scholar] [CrossRef]
- Worden, K.; Manson, G. The application of machine learning to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 365, 515–537. [Google Scholar] [CrossRef] [PubMed]
- Figueiredo, E.; Santos, A. Machine Learning Algorithms for Damage Detection. In Vibration-Based Techniques for Damage Detection and Localization in Engineering Structures; World Scientific: Singapore, 2017; Volume 10, pp. 1–39. [Google Scholar] [CrossRef]
- Worden, K.; Tomlinson, G.R. Nonlinearity in experimental modal analysis. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2001, 359, 113–130. [Google Scholar] [CrossRef]
- Juang, J.-N.; Pappa, R.S. Effects of noise on modal parameters identified by the Eigensystem Realization Algorithm. J. Guid. Control. Dyn. 1986, 9, 294–303. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Obrien, E.; Quirke, P.; Bowe, C. Railway Track Monitoring Using Train Measurements: An Experimental Case Study. Appl. Sci. 2019, 9, 4859. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.G.; Rxnnquist, A.; Navik, P.; Liu, Z.D. Contact Wire Irregularity Stochastics and Effect on High-speed Railway Pantograph-Catenary Interactions. IEEE Trans. Instrum. Meas. 2020, 69, 8196–8206. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bellino, A.; Fasana, A.; Garibaldi, L.; Marchesiello, S. PCA-based detection of damage in time-varying systems. Mech. Syst. Signal Process. 2010, 24, 2250–2260. [Google Scholar] [CrossRef]
- Galvanetto, U.; Violaris, G. Numerical investigation of a new damage detection method based on proper orthogonal decomposition. Mech. Syst. Signal Process. 2007, 21, 1346–1361. [Google Scholar] [CrossRef]
- Shane, C.; Jha, R. Proper orthogonal decomposition based algorithm for detecting damage location and severity in composite beams. Mech. Syst. Signal Process. 2011, 25, 1062–1072. [Google Scholar] [CrossRef]
- Azam, S.E.; Rageh, A.; Linzell, D. Damage detection in structural systems utilizing artificial neural networks and proper orthogonal decomposition. Struct. Control Health Monit. 2018, 26, e2288. [Google Scholar] [CrossRef]
- Ardani, S.; Akintunde, E.; Linzell, D.; Azam, S.E. Application of proper orthogonal decomposition to bridge damage detection-field investigations. In Bridge Safety, Maintenance, Management, Life-Cycle, Resilience and Sustainability; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Xu, H.; Humar, J. Damage Detection in a Girder Bridge by Artificial Neural Network Technique. Comput. Civ. Infrastruct. Eng. 2006, 21, 450–464. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Khaji, N.; Moharrami, H.; Bahreininejad, A. Damage detection of truss bridge joints using Artificial Neural Networks. Expert Syst. Appl. 2008, 35, 1122–1131. [Google Scholar] [CrossRef]
- Gu, J.; Gul, M.; Wu, X. Damage detection under varying temperature using artificial neural networks. Struct. Control Health Monit. 2017, 24, e1998. [Google Scholar] [CrossRef]
- Bakhary, N.; Hao, H.; Deeks, A.J. Damage detection using artificial neural network with consideration of uncertainties. Eng. Struct. 2007, 29, 2806–2815. [Google Scholar] [CrossRef]
- Astroza, R.; Alessandri, A. Effects of model uncertainty in nonlinear structural finite element model updating by numerical simulation of building structures. Struct. Control Health Monit. 2018, 26, e2297. [Google Scholar] [CrossRef]
- Lee, J.J.; Yi, J.H.; Yun, C.B.; Jung, H.Y. Neural networks-based damage detection for bridges considering errors in baseline finite element models. J. Sound Vib. 2005, 280, 555–578. [Google Scholar] [CrossRef]
- Rageh, A.; Azam, S.E.; Linzell, D.G. Steel railway bridge fatigue damage detection using numerical models and machine learning: Mitigating influence of modeling uncertainty. Int. J. Fatigue 2019, 134, 105458. [Google Scholar] [CrossRef]
- Gardner, P.; Bull, L.; Gosliga, J.; Dervilis, N.; Worden, K. Foundations of population-based SHM, Part III: Heterogeneous populations—Mapping and transfer. Mech. Syst. Signal Process. 2020, 149, 107142. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359 . [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Networks 2010, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer Feature Learning with Joint Distribution Adaptation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 2200–2207. Available online: https://openaccess.thecvf.com/content_iccv_2013/html/Long_Transfer_Feature_Learning_2013_ICCV_paper.html (accessed on 3 September 2021).
- Long, M.; Wang, J.; Ding, G.; Pan, S.J.; Yu, P.S. Adaptation Regularization: A General Framework for Transfer Learning. IEEE Trans. Knowl. Data Eng. 2013, 26, 1076–1089. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C.; Guo, B. Transfer-learning guided Bayesian model updating for damage identification considering modeling uncertainty. Mech. Syst. Signal Process. 2021, 166, 108426. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, X.; Liu, Y. Distribution adaptation deep transfer learning method for cross-structure health monitoring using guided waves. Struct. Health Monit. 2021, 21, 853–871. [Google Scholar] [CrossRef]
- Yan, W.-J.; Chronopoulos, D.; Yuen, K.-V.; Zhu, Y.-C. Structural anomaly detection based on probabilistic distance measures of transmissibility function and statistical threshold selection scheme. Mech. Syst. Signal Process. 2021, 162, 108009. [Google Scholar] [CrossRef]
- Mei, L.F.; Yan, W.J.; Yuen, K.V.; Beer, M. Structural novelty detection with Laplace asymptotic expansion of the Bhattacharyya distance of transmissibility and Bayesian resampling scheme|Elsevier Enhanced Reader. J. Sound Vibratio 2022, 540, 117277. [Google Scholar] [CrossRef]
- Bull, L.; Gardner, P.; Gosliga, J.; Rogers, T.; Dervilis, N.; Cross, E.; Papatheou, E.; Maguire, A.; Campos, C.; Worden, K. Foundations of population-based SHM, Part I: Homogeneous populations and forms. Mech. Syst. Signal Process. 2020, 148, 107141. [Google Scholar] [CrossRef]
- Klema, V.; Laub, A. The singular value decomposition: Its computation and some applications. IEEE Trans. Autom. Control 1980, 25, 164–176. [Google Scholar] [CrossRef]
- Rageh, A. Optimized Health Monitoring Plans for a Steel, Double-Track Railway Bridge. Civil and Environmental Engineering Theses, Dissertations, and Student Research. May 2018. Available online: https://digitalcommons.unl.edu/civilengdiss/122 (accessed on 3 September 2021).
- CSI. SAP2000 V-8. Integrated Finite Element Analysis and Design of Structures Basic Analysis Reference Manual; Computers and Structures Inc.: Berkeley, CA, USA, 2002. [Google Scholar]
- Moler, C.B. Numerical Computing with Matlab; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2004. [Google Scholar] [CrossRef]
- Al-Emrani, M. Fatigue Performance of Stringer-to-Floor-Beam Connections in Riveted Railway Bridges. J. Bridg. Eng. 2005, 10, 179–185. [Google Scholar] [CrossRef]
- Al-Emrani, M.; Åkesson, B.; Kliger, R. Overlooked Secondary Effects in Open-Deck Truss Bridges. Struct. Eng. Int. 2004, 14, 307–312. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–133. [Google Scholar] [CrossRef]
- John, G.H. Cross-Validated C4.5: Using Error Estimation for Automatic Parameter Selection. Training 1994, 3, 4. [Google Scholar]





| Model | Assignment | Normalized Rotational Spring Coefficient |
|---|---|---|
| Uniform increase +80% in | 1.80 | |
| Uniform increase +80% in , estimated with | 1.80 | |
| Uniform decrease −50% in | 0.5 | |
| Random, ±50% in | Between 0.53 and 1.45 | |
| Random, ±25% in | Between 0.76 and 1.25 | |
| Random, ±100% in | Between 0.23 and 1.92 |
| Target Model | Accuracy, Cross-Validation (%) | Accuracy, Entire Data (%) |
|---|---|---|
| 90 | 100 | |
| 88 | 89 | |
| 87 | 85 | |
| 87 | 94 |
| DI (%) | Accuracy, Test Data (%) | Accuracy, Entire Data (%) |
|---|---|---|
| 40 | 72 | 92 |
| 60 | 85 | 98 |
| 80 | 90 | 100 |
| 100 | 94 | 99 |
| Target Model | Accuracy, Test Data (%) | Accuracy, Entire Data (%) |
|---|---|---|
| 85 | 89 | |
| 92 | 84 | |
| 90 | 93 | |
| 90 | 87 |
| DL | Accuracy, Test Data (%) | Accuracy, Entire Data (%) |
|---|---|---|
| 3 | 82 | 81 |
| 8 | 81 | 88 |
| 13 | 88 | 93 |
| 18 | 85 | 89 |
| Target Model | Accuracy, KNN, without Applying TL (%) | Accuracy, JDA–kernel, Test Data (%) | Accuracy, JDA–kernel, Entire Data (%) | KNN without TL, Runtime (s) | JDA–kernel, Runtime (s) |
|---|---|---|---|---|---|
| 35 | 79 | 86 | 0.3 | 1464 | |
| 12 | 77 | 76 | 0.3 | 1420 | |
| 18 | 80 | 75 | 0.3 | 1442 | |
| 12 | 75 | 73 | 0.3 | 1445 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ardani, S.; Eftekhar Azam, S.; Linzell, D.G. Bridge Health Monitoring Using Proper Orthogonal Decomposition and Transfer Learning. Appl. Sci. 2023, 13, 1935. https://doi.org/10.3390/app13031935
Ardani S, Eftekhar Azam S, Linzell DG. Bridge Health Monitoring Using Proper Orthogonal Decomposition and Transfer Learning. Applied Sciences. 2023; 13(3):1935. https://doi.org/10.3390/app13031935
Chicago/Turabian StyleArdani, Samira, Saeed Eftekhar Azam, and Daniel G. Linzell. 2023. "Bridge Health Monitoring Using Proper Orthogonal Decomposition and Transfer Learning" Applied Sciences 13, no. 3: 1935. https://doi.org/10.3390/app13031935
APA StyleArdani, S., Eftekhar Azam, S., & Linzell, D. G. (2023). Bridge Health Monitoring Using Proper Orthogonal Decomposition and Transfer Learning. Applied Sciences, 13(3), 1935. https://doi.org/10.3390/app13031935







