Dimensional Error Compensation Based on Data-Driven Sliding Mode Terminal Iterative Learning Control for CNC Batch Grinding
Abstract
:1. Introduction
2. Grinding Protocol and Problem Formulation
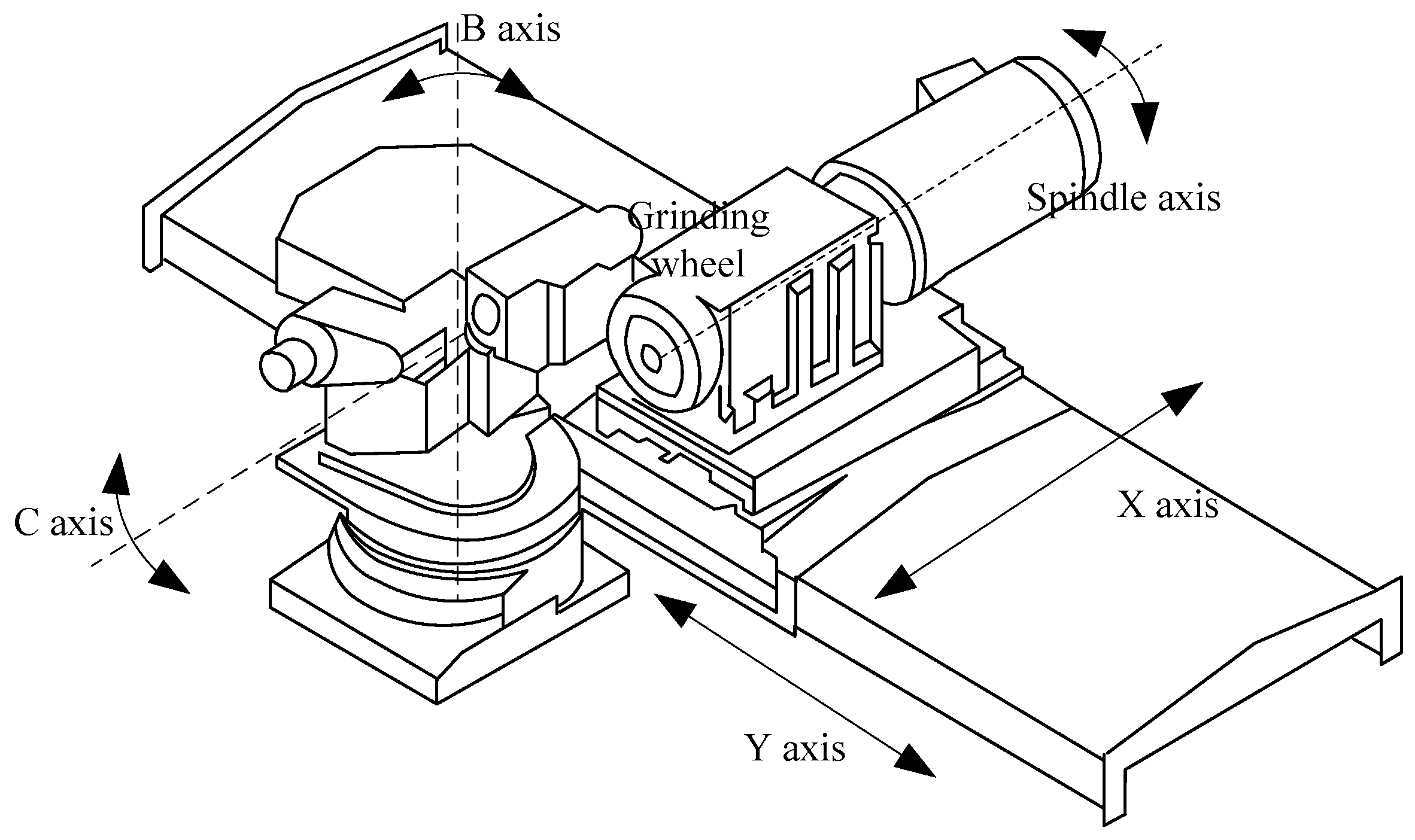
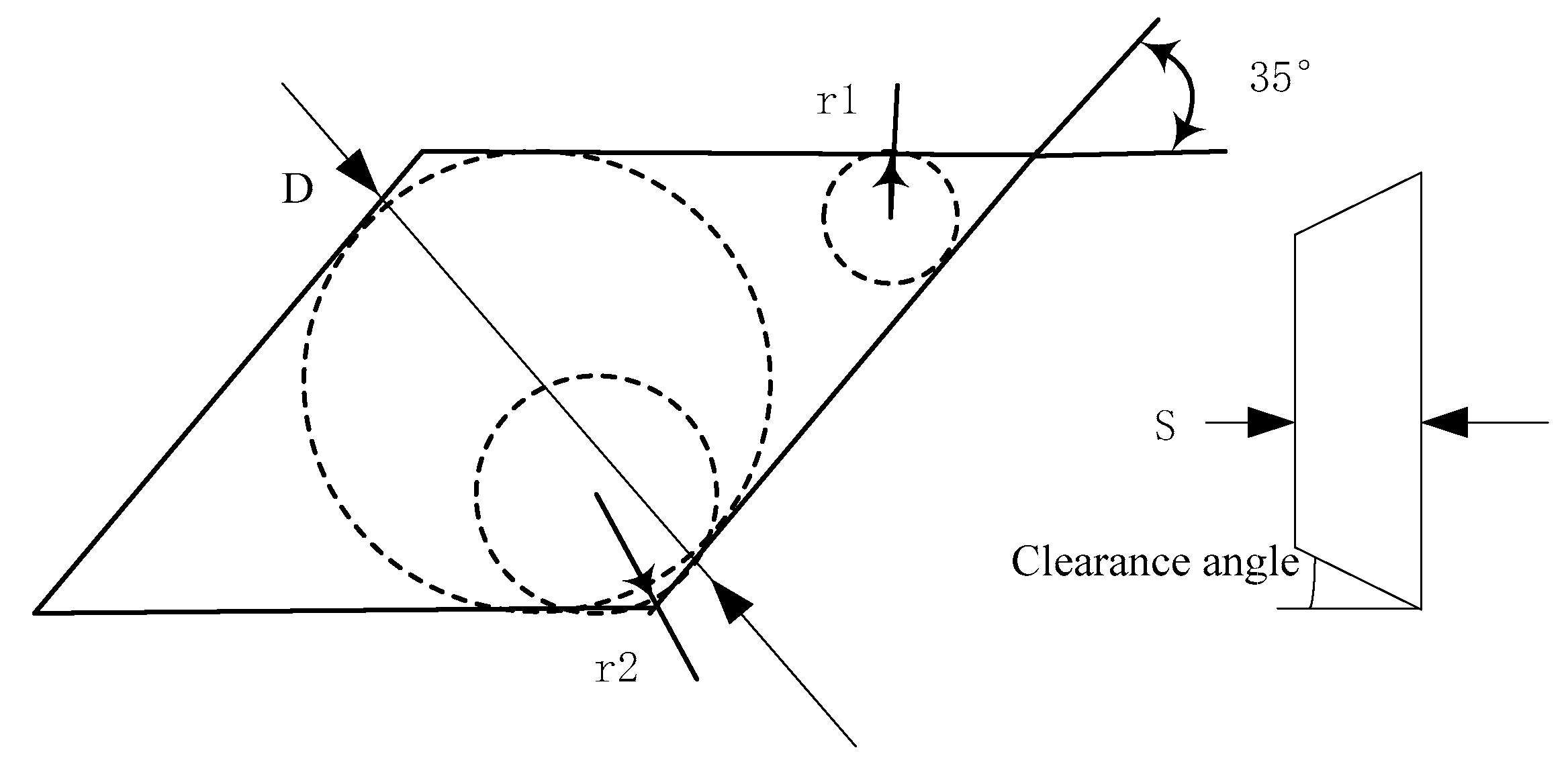
2.1. Grinding Model
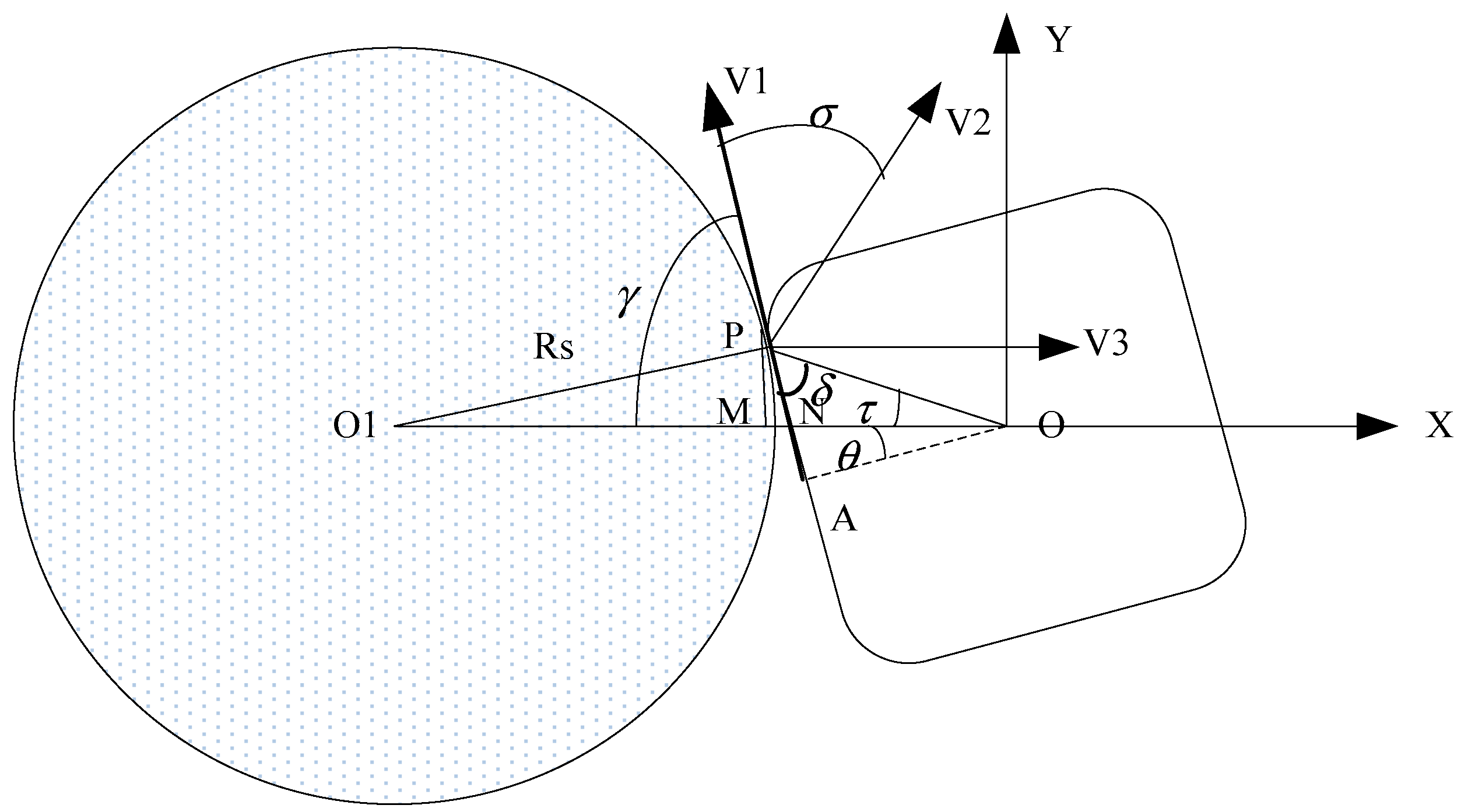
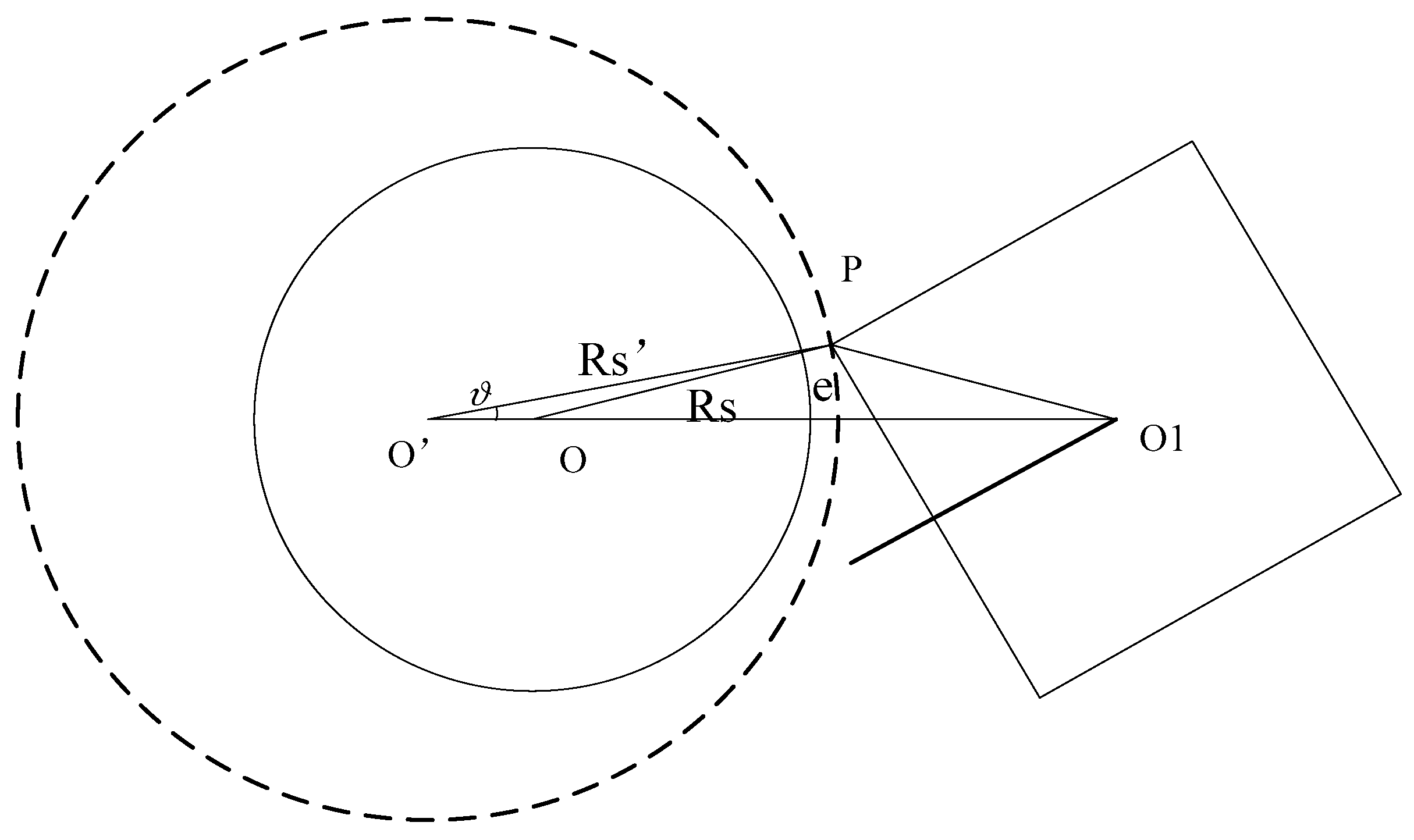
2.2. Dimensional Error Analysis
2.3. Problem Formulation
3. Sliding Mode Terminal Iterative Learning Compensation Method
- 1.
- Define as the terminal dimensional error of the workpiece, which is shown as Equation (15):Here, is the terminal dimension of the workpiece, which is measurable by laser sensor. is the desired dimension of the workpiece. If is within the accepted error limit , the error compensation is ignored; otherwise, the compensation is operated.Substituting Equation (13) into Equation (15) yields Equation (16). Equation (16) is transformed as follows:
- 2.
- Introduce an iteration-dependent slide surface function and an index function [26], which are two common functions in sliding mode control. The Equations are shown as follows:where , . They are weighting factors.Substituting Equation (16) and Equation (17) into Equation (18), the Equation (18) is transformed into Equation (19). The Equation (19) is shown as follows:In optimal conditions, the control input can be obtained in Equation (20), which is shown as follows:
- 3.
- In the upper part, the compensation control input is deduced, which is the function of the previous two-dimensional errors, the previous dimension, and the estimation parameter. In this part, the convergence analysis of the grinding system with the control input is derived.In combination with Equation (20) and Equation (13), in virtue of Equation (16), then Equation (21) can be deduced. It is shown as follows [26]:According to the above Equation (21), it is easy to derive the Equation (22),Therefore, for the sliding surface Equation (17), it can be derived Equation (23),Since , .Then =0. Since is bounded, is bounded. Therefore, the following Equation (24) can be derived.Therefore, the sliding surface will converge to 0.Substituting Equation (17) into Equation (24), =0. Then, Equation (25) can be deduced.Since , the following Equation (26) can be derived.Therefore, the terminal error will converge to 0.As mentioned above, the convergence analysis is made.
- 4.
- As it is mentioned in Section 2, the system input is constant of every cycle at an arbitrary sampling time for one batch and it is executed by X axis. The compensation is executed by the compensation module if it is necessary; the compensation input for the workpiece is computed as follows.
4. Simulation and Verification
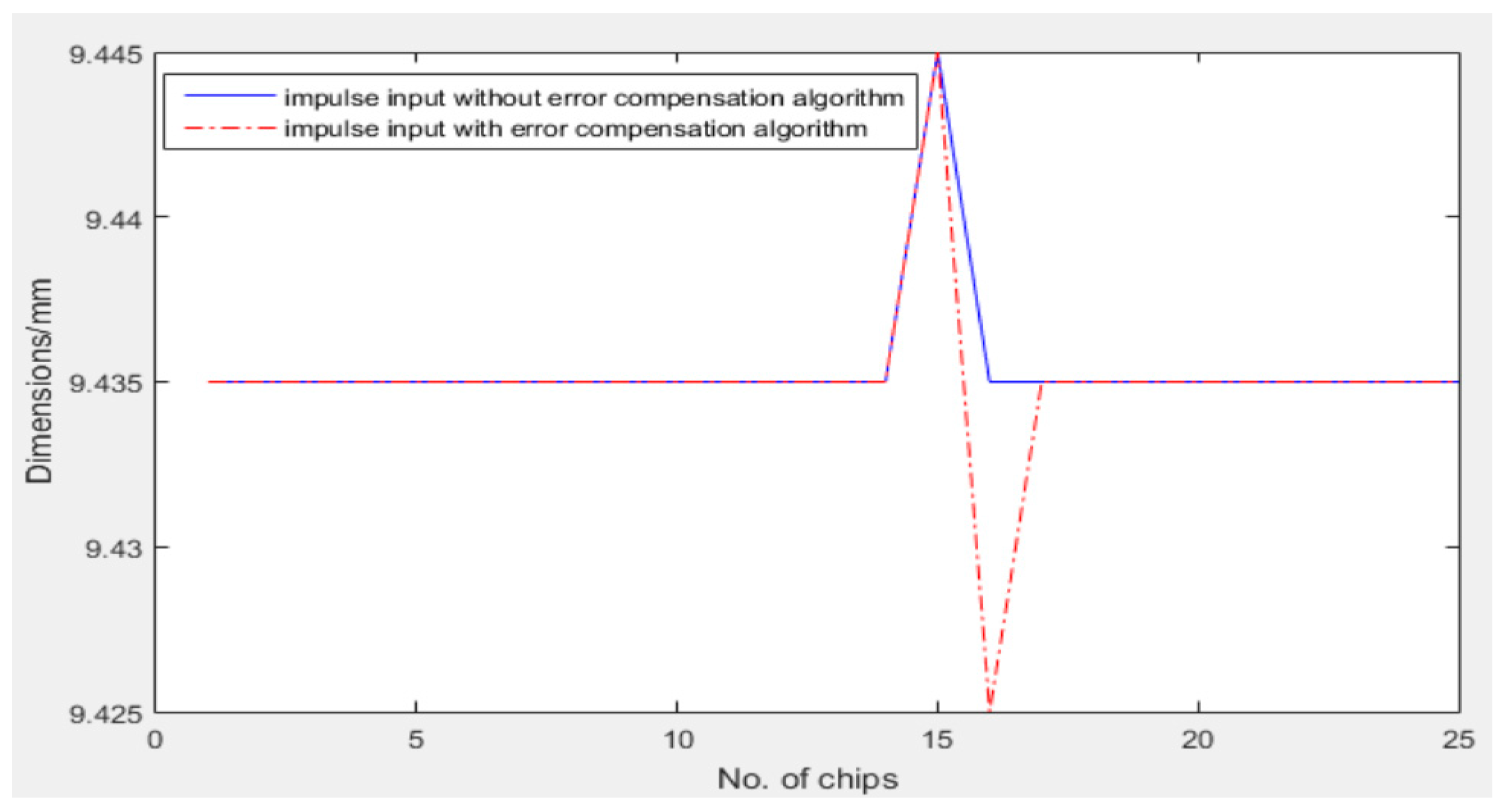
4.1. Simulation
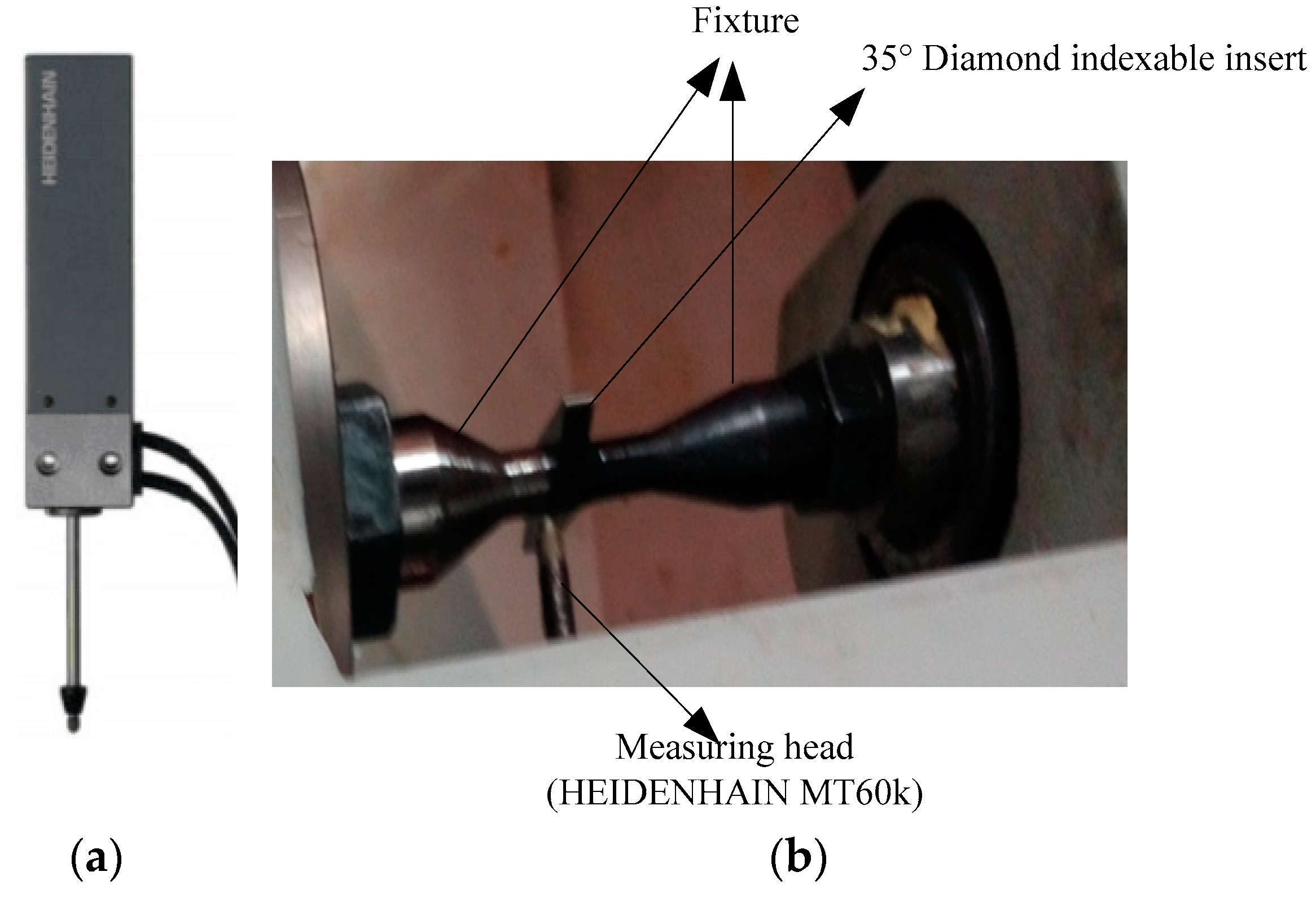
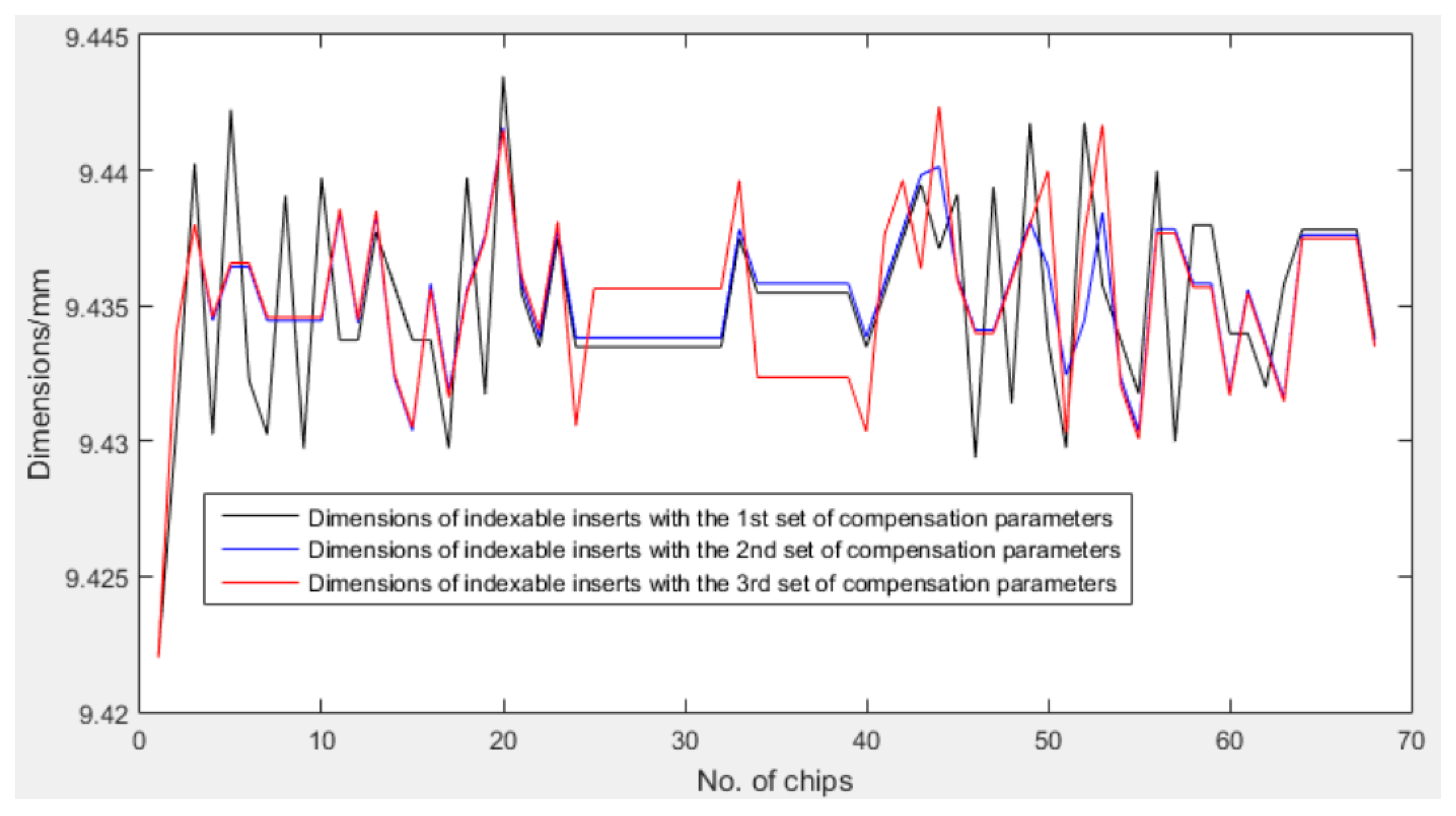
4.2. Experimental Investigation
5. Conclusions
- (1)
- Based on the theory of sliding mode terminal iterative learning control, the compensation method is presented. This method only needs to measure the terminal dimension using a touch probe, without using other sensors to detect all kinds of error sources. Moreover, there is no need of model information, which is data-driven;
- (2)
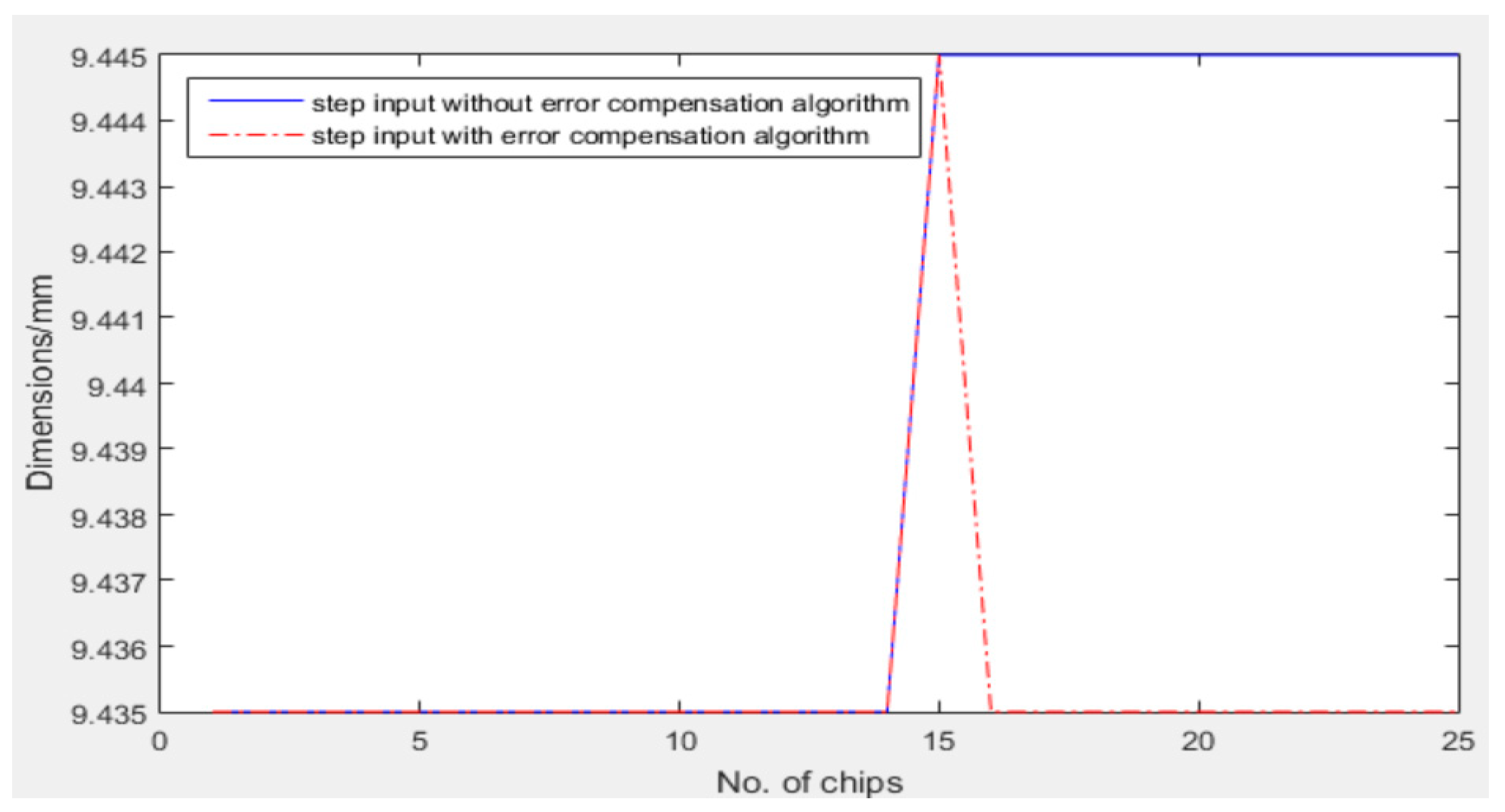
- Step and impulse input were introduced into the compensation module to simulate errors. Through many simulations, the values of compensation parameters were defined, and the simulation results showed that the compensation effectiveness was obvious;
- (3)
- In order to verify the compensation performance in an actual industrial environment, two groups of experiment were carried out on the machine tool. Based on the comparisons, the compensation parameters defined by simulation performed well and the performance effectiveness of this proposed compensation method was obvious. In the experiment, for 68 pieces of indexable inserts, the qualified rate increased from 48.5% to 95%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nojedeh, M.V.; Habibi, M.; Arezoo, B. Tool path accuracy enhancement through geometric error compensation. Int. J. Mach. Tools Manu. 2011, 51, 471–482. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Ziegert, J.C.; Canning, J.S.; Raul, Z. Case study: A comparison of error sources in high-speed milling. Prec. Eng. 2008, 32, 126–133. [Google Scholar] [CrossRef]
- Yin, S.H.; Ohmori, H.; Dai, Y.T.; Uehara, Y.; Chen, F.J.; Tang, H.N. ELID grinding characteristics of glass—Ceramic materials. Int. J. Mach. Tools Manu. 2009, 49, 333–338. [Google Scholar] [CrossRef]
- Khan, A.W.; Chen, W.Y. A methodology for systematic geometric error compensation in five-axis machine tools. Int. J. Adv. Manuf. Technol. 2011, 53, 615–628. [Google Scholar] [CrossRef]
- Li, J.; Xie, F.G.; Liu, X.J.; Li, W.D.; Zhu, S.W. Geometric error identification and compensation of linear axes based on a novel 13-line method. Int. J. Adv. Manuf. Technol. 2016, 87, 2269–2283. [Google Scholar] [CrossRef]
- Chen, J.; Lin, S.; Zhou, X.; Gu, T. A ballbar test for measurement and identification the comprehensive error of tilt table. Int. J. Mach. Tools Manu. 2016, 103, 1–12. [Google Scholar] [CrossRef]
- Wu, C.J.; Fan, J.W.; Wang, Q.H.; Pan, R.; Tang, Y.H.; Li, Z.S. Prediction and compensation of geometric error for translational axes in multi-axis machine tools. Int. J. Adv. Manuf. Technol. 2018, 95, 3413–3435. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Lan, S.; Ni, J.; Wu, W.; Lu, B. A review on spindle thermal error compensation in machine tools. Int. J. Mach. Tools Manu. 2015, 95, 25–38. [Google Scholar] [CrossRef]
- Wu, C.W.; Tang, C.H.; Chang, C.F.; Shao, Y.S. Thermal error compensation method for machine center. Int. J. Adv. Manuf. Technol. 2012, 59, 681–689. [Google Scholar] [CrossRef]
- Wang, H.T.; Wang, L.P.; Li, T.M.; Han, J. Thermal sensor selection for the thermal error modeling of machine tool based on the fuzzy clustering method. Int. J. Adv. Manuf. Technol. 2013, 69, 121–126. [Google Scholar] [CrossRef]
- Yang, J.; Shi, H.; Feng, B.; Zhao, L.; Ma, C.; Mei, X.S. Thermal error modeling and compensation for a high-speed motorized spindle. Int. J. Adv. Manuf. Technol. 2015, 77, 1005–1017. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Sun, M.J.; Wu, Y.L.; Zhu, T.J. Comprehensive thermal growth compensation method of spindle and servo axis error on a vertical drilling center. Int. J. Adv. Manuf. Technol. 2017, 88, 2507–2516. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Cai, L.G.; Cheng, Q.; Liu, Z.F.; Gu, P.H. A geometric error budget method to improve machining accuracy reliability of multi-axis machine tools. J. Intell. Manuf. 2019, 30, 495–519. [Google Scholar] [CrossRef]
- He, G.; Ma, W.; Yu, G.; Lang, A. Modeling and experimental validation of cutting forces in five-axis ball-end milling based on true tooth trajectory. Int. J. Adv. Manuf. Technol. 2015, 78, 189–197. [Google Scholar] [CrossRef]
- Ma, W.K.; He, G.Y.; Zhu, L.M.; Guo, L.Z. Tool deflection error compensation in five-axis ball-end milling of sculptured surface. Int. J. Adv. Manuf. Technol. 2016, 84, 1421–1430. [Google Scholar] [CrossRef]
- Manna, M.A.; Ramesh, R.; Poo, A.N. Error compensation in machine tools-a review part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manu. 2007, 40, 1235–1256. [Google Scholar]
- Chen, T.T.; Tian, X.C.; Yan, L. Intelligent dimensional error pre-compensation in CNC grinding using iterative learning approach. Int. J. Adv. Manuf. Technol. 2013, 67, 1825–1835. [Google Scholar] [CrossRef]
- Chen, T.T.; Tian, X.C. An intelligent self-learning method for dimensional error pre-compensation in CNC grinding. Int. J. Adv. Manuf. Technol. 2014, 75, 1349–1356. [Google Scholar] [CrossRef]
- Xu, J.X.; Chen, Y.Q.; Heng, L.T.; Yamamoto, S. Terminal iterative learning control with an application to RTPCVD thickness control. Automatic 1999, 35, 1535–1542. [Google Scholar] [CrossRef]
- Chi, R.H.; Liang, H.; Lin, N.; Zhang, R.K.; Huang, B. Constraint data driven optimal terminal ILC of end product quality for a class of I/O constrained batch processes. Can. J. Chem. Eng. 2018, 96, 215–222. [Google Scholar] [CrossRef]
- Knight, J.; Shirsavar, S.; Holderbaum, W. An improved reliability cuk based solar inverter with sliding mode control. IEEE Trans. Power Electron. 2017, 21, 1107–1115. [Google Scholar] [CrossRef]
- Li, S.; Du, H.; Yu, X. Discrete-time terminal sliding mode control systems based on Euler’s discretization. IEEE Trans. Autom. Control 2014, 59, 546–552. [Google Scholar] [CrossRef]
- Wang, W.H.; Hou, Z.S. New adaptive quasi-sliding mode control for nonlinear discrete-time systems. J. Syst. Eng. Electron. 2008, 19, 154–160. [Google Scholar]
- Hou, Z.S.; Jin, S.T. A novel data-driven control approach for a class of discrete-time nonlinear systems. IEEE T. Contr. Syst. T. 2011, 19, 1549–1558. [Google Scholar] [CrossRef]
- Chi, R.H.; Wang, D.W.; Hou, Z.S.; Jin, S.T. Data-driven optimal terminal iterative learning control. J. Process Control 2012, 22, 2026–2037. [Google Scholar] [CrossRef]
- Chi, R.H.; Wei, Y.C.; Wang, R.R. SMC-based data-driven terminal ILC for nonlinear discrete-time systems with unavailable intermediate measurements. In Proceedings of the 31st Chinese Control and Decision Conference, Nanchang, China, 3–5 June 2019. [Google Scholar]



| Parameters | Value |
|---|---|
| diamond wheel | resin bonded, mesh #220, concentration 100% |
| wheel diameter (mm) | 350 |
| wheel rotation (mm/s) | 18 |
| feed rate (mm/s) | 0.03–0.05 |
| no spark time(s) | 3 |
| coolant | water soluble |
| temperature of coolant (°C) | 12–13 |
| No. | Dimensions of the Group Workpieces without Compensation (mm) | Dimensions of the Group Workpieces with Compensation (mm) |
|---|---|---|
| 1 | 9.422 | 9.422 |
| 2 | 9.424 | 9.434 |
| 3 | 9.428 | 9.438 |
| 4 | 9.428 | 9.434 |
| 5 | 9.43 | 9.436 |
| 6 | 9.43 | 9.436 |
| 7 | 9.428 | 9.434 |
| 8 | 9.428 | 9.434 |
| 9 | 9.428 | 9.434 |
| 10 | 9.428 | 9.434 |
| 11 | 9.432 | 9.438 |
| 12 | 9.432 | 9.434 |
| 13 | 9.436 | 9.438 |
| 14 | 9.434 | 9.432 |
| 15 | 9.432 | 9.431 |
| 16 | 9.432 | 9.436 |
| 17 | 9.428 | 9.432 |
| 18 | 9.428 | 9.436 |
| 19 | 9.43 | 9.438 |
| 20 | 9.434 | 9.442 |
| 21 | 9.436 | 9.436 |
| 22 | 9.434 | 9.434 |
| 23 | 9.438 | 9.438 |
| 24 | 9.434 | 9.434 |
| 25 | 9.434 | 9.434 |
| 26 | 9.434 | 9.434 |
| 27 | 9.434 | 9.434 |
| 28 | 9.434 | 9.434 |
| 29 | 9.434 | 9.434 |
| 30 | 9.434 | 9.434 |
| 31 | 9.434 | 9.434 |
| 32 | 9.434 | 9.434 |
| 33 | 9.438 | 9.438 |
| 34 | 9.436 | 9.436 |
| 35 | 9.436 | 9.436 |
| 36 | 9.436 | 9.436 |
| 37 | 9.436 | 9.436 |
| 38 | 9.436 | 9.436 |
| 39 | 9.436 | 9.436 |
| 40 | 9.434 | 9.434 |
| 41 | 9.436 | 9.436 |
| 42 | 9.438 | 9.438 |
| 43 | 9.44 | 9.439 |
| 44 | 9.446 | 9.440 |
| 45 | 9.448 | 9.436 |
| 46 | 9.446 | 9.434 |
| 47 | 9.446 | 9.434 |
| 48 | 9.448 | 9.436 |
| 49 | 9.45 | 9.438 |
| 50 | 9.452 | 9.436 |
| 51 | 9.448 | 9.432 |
| 52 | 9.45 | 9.434 |
| 53 | 9.454 | 9.438 |
| 54 | 9.452 | 9.432 |
| 55 | 9.45 | 9.431 |
| 56 | 9.452 | 9.438 |
| 57 | 9.452 | 9.438 |
| 58 | 9.45 | 9.436 |
| 59 | 9.45 | 9.436 |
| 60 | 9.446 | 9.432 |
| 61 | 9.446 | 9.436 |
| 62 | 9.444 | 9.434 |
| 63 | 9.442 | 9.432 |
| 64 | 9.444 | 9.438 |
| 65 | 9.444 | 9.438 |
| 66 | 9.444 | 9.438 |
| 67 | 9.444 | 9.438 |
| 68 | 9.44 | 9.434 |
| Number of workpieces within the dimensional error tolerance 0.005 mm | 33 | 65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Tian, X. Dimensional Error Compensation Based on Data-Driven Sliding Mode Terminal Iterative Learning Control for CNC Batch Grinding. Appl. Sci. 2023, 13, 1822. https://doi.org/10.3390/app13031822
Chen T, Tian X. Dimensional Error Compensation Based on Data-Driven Sliding Mode Terminal Iterative Learning Control for CNC Batch Grinding. Applied Sciences. 2023; 13(3):1822. https://doi.org/10.3390/app13031822
Chicago/Turabian StyleChen, Tiantian, and Xincheng Tian. 2023. "Dimensional Error Compensation Based on Data-Driven Sliding Mode Terminal Iterative Learning Control for CNC Batch Grinding" Applied Sciences 13, no. 3: 1822. https://doi.org/10.3390/app13031822
APA StyleChen, T., & Tian, X. (2023). Dimensional Error Compensation Based on Data-Driven Sliding Mode Terminal Iterative Learning Control for CNC Batch Grinding. Applied Sciences, 13(3), 1822. https://doi.org/10.3390/app13031822





