Hilbert–Huang-Transform-Based Seismic Intensity Measures for Rocking Response Assessment
Abstract
1. Introduction
2. Methods
2.1. Intensity Measures
2.1.1. HHT-Based IMs
2.1.2. Conventional IMs
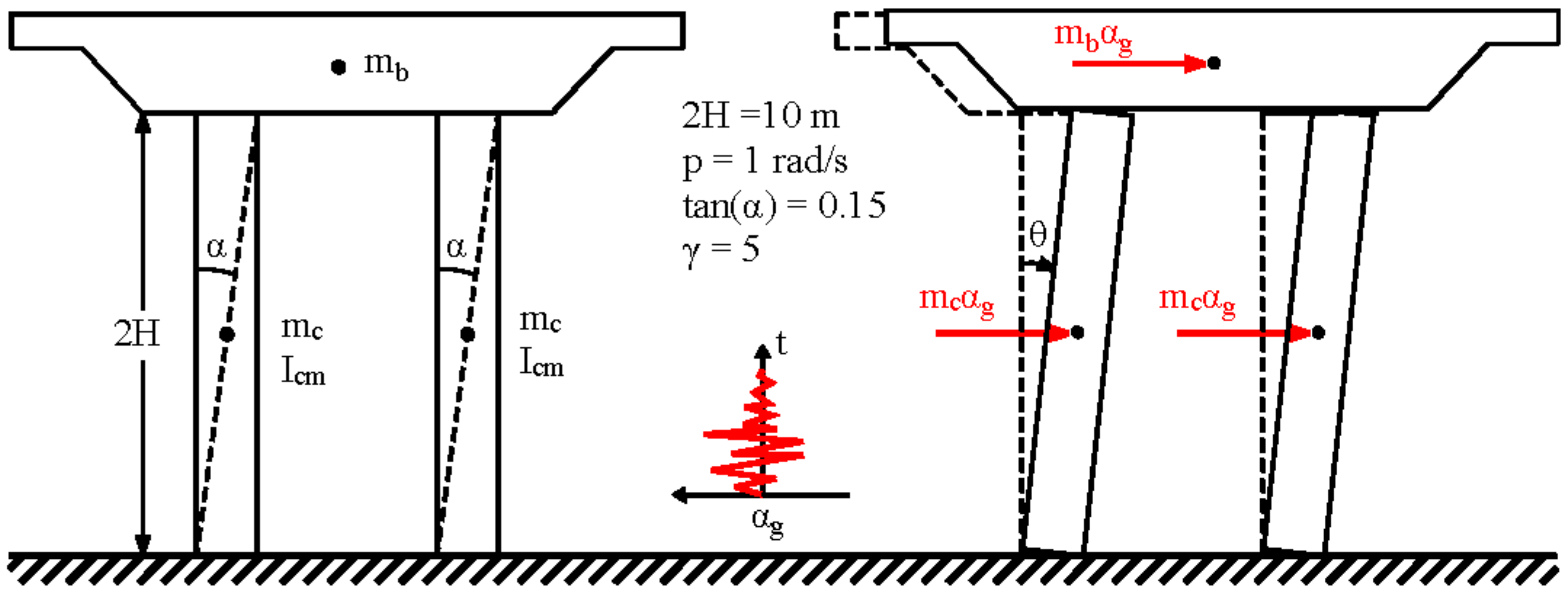
2.2. Dynamics of Rocking Frames
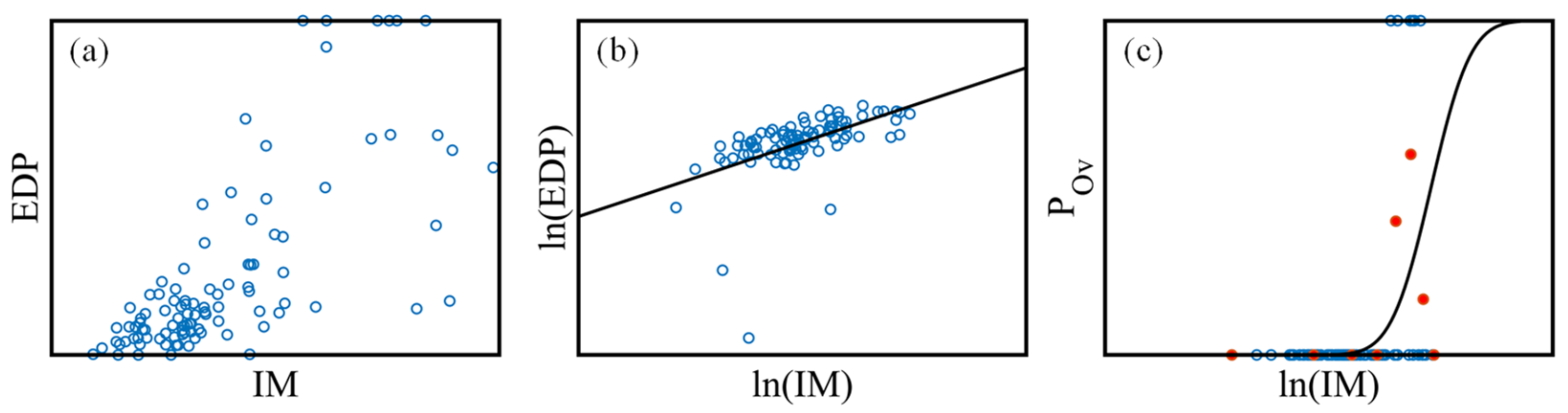
2.3. Fragility Analysis
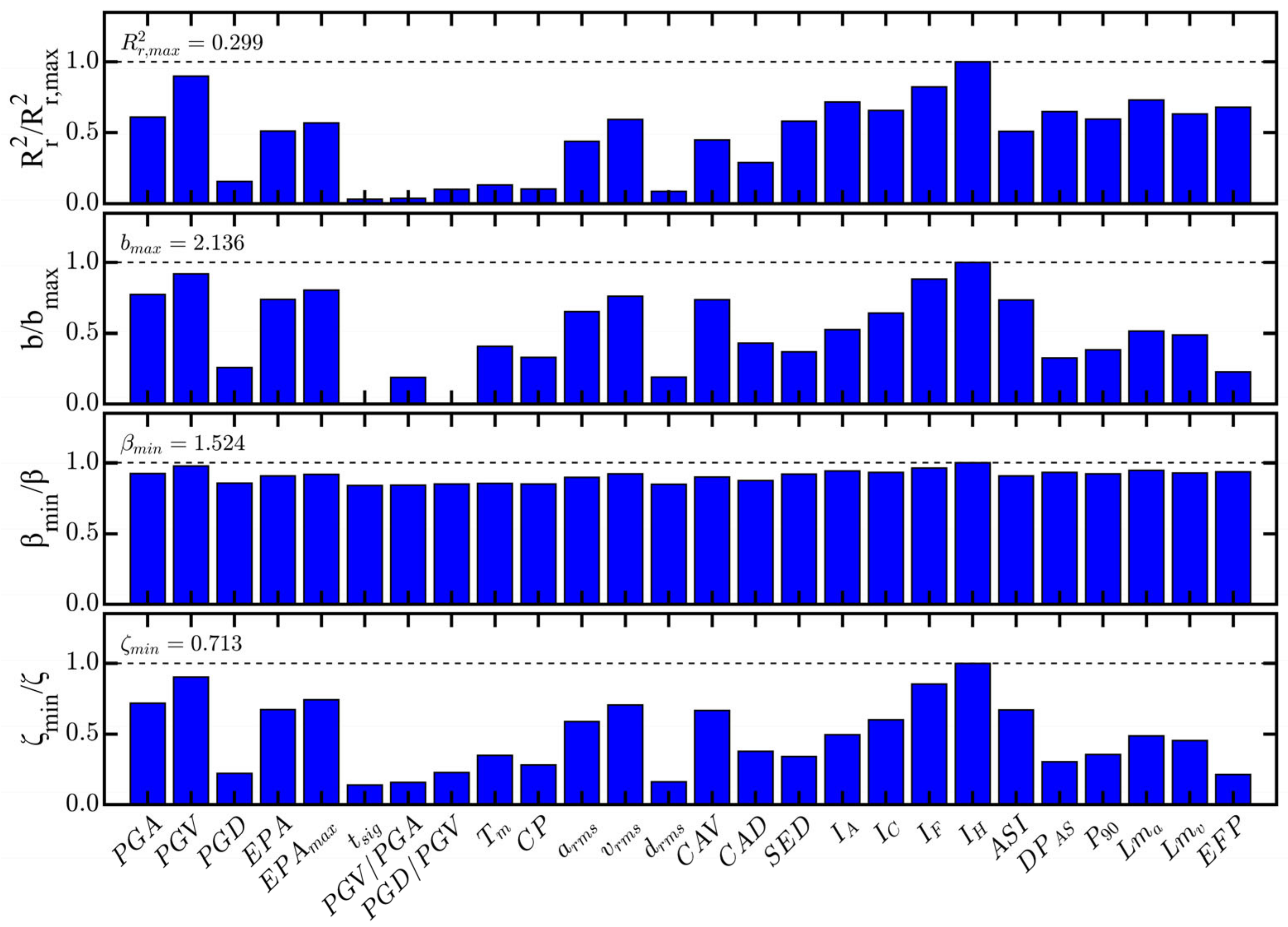
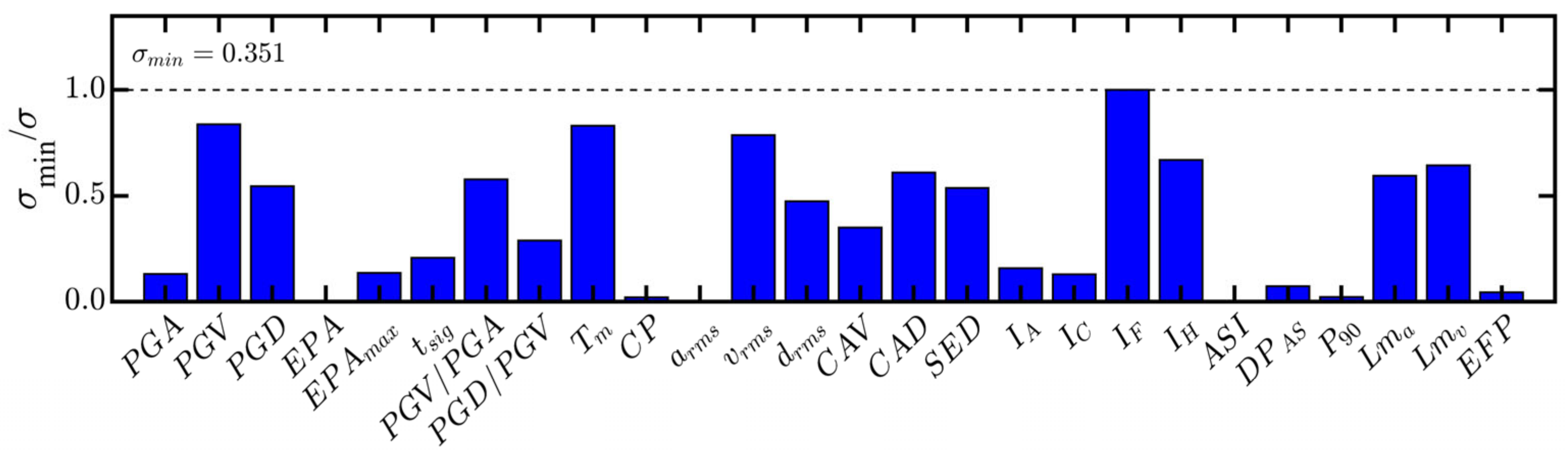
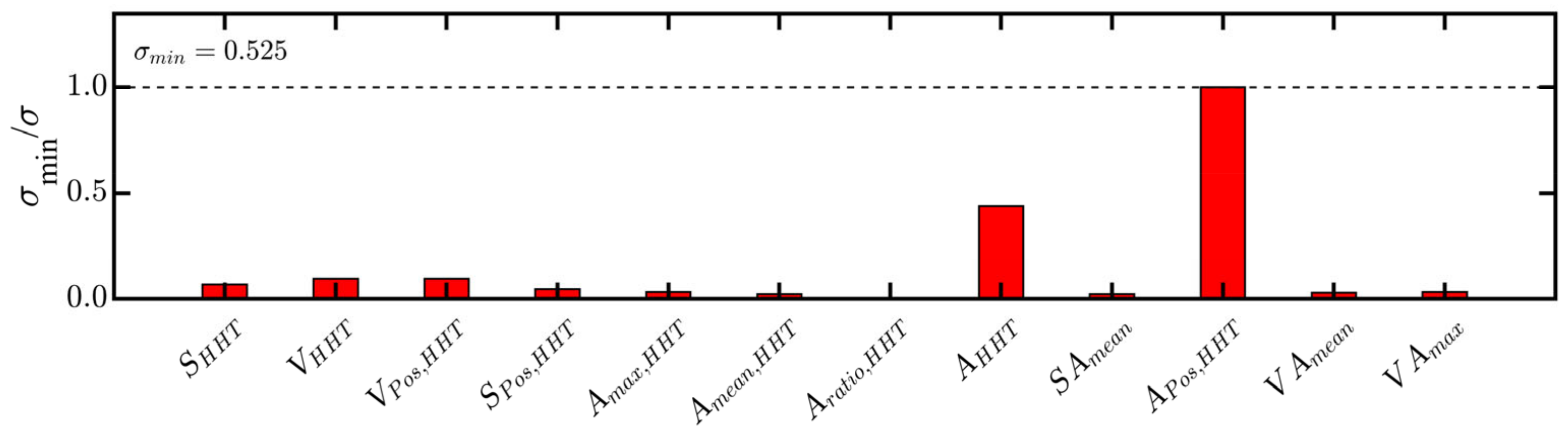
2.4. Optimal Intensity Measures
2.5. EDP-Limit States
2.6. Discriminant Analysis
3. Results
3.1. Fragility Analysis
3.2. Discriminant Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elnashai, A.S.; Di Sarno, L. Fundamentals of Earthquake Engineering; Wiley: New York, NY, USA, 2008; p. 347. [Google Scholar]
- Flenga, M.G.; Favvata, M.J. Fragility curves and probabilistic seismic demand models on the seismic assessment of RC frames subjected to structural pounding. Appl. Sci. 2021, 11, 8253. [Google Scholar] [CrossRef]
- Liu, R.; Palermo, A. Controlled rocking, dissipative controlled rocking and multi-hierarchical activation: Numerical analysis and experimental testing. In Proceedings of the 7th European Congress on Computational Methods In Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- Makris, N. A half-century of rocking isolation. Earthq. Struct. 2014, 7, 1187–1221. [Google Scholar] [CrossRef]
- Chatzikonstantinou, N.; Makarios, T.K.; Athanatopoulou, A. Integration Method for Response History Analysis of Single-Degree-of-Freedom Systems with Negative Stiffness. Buildings 2022, 12, 1214. [Google Scholar] [CrossRef]
- Housner, G.W. The behavior of inverted pendulum structures during earthquakes. Bull. Seismol. Soc. Am. 1963, 53, 403–417. [Google Scholar] [CrossRef]
- Oliveto, G.; Calio, I.; Greco, A. Large displacement behaviour of a structural model with foundation uplift under impulsive and earthquake excitations. Earthq. Eng. Struct. Dyn. 2003, 32, 369–393. [Google Scholar] [CrossRef]
- Acikgoz, S.; DeJong, M.J. The rocking response of large flexible structures to earthquakes. Bull. Earthq. Eng. 2014, 12, 875–908. [Google Scholar] [CrossRef]
- Vassiliou, M.F.; Truniger, R.; Stojadinović, B. An analytical model of a deformable cantilever structure rocking on a rigid surface: Development and verification. Earthq. Eng. Struct. Dyn. 2015, 44, 2775–2794. [Google Scholar] [CrossRef]
- Makris, N.; Vassiliou, M.F. Planar rocking response and stability analysis of an array of free-standing columns capped with a freely supported rigid beam. Earthq. Eng. Struct. Dyn. 2013, 42, 431–449. [Google Scholar] [CrossRef]
- Giouvanidis, A.I.; Dimitrakopoulos, E.G. Seismic performance of rocking frames with flag-shaped hysteretic behavior. J. Eng. Mech. 2017, 143, 04017008. [Google Scholar] [CrossRef]
- Makris, N.; Aghagholizadeh, M. The dynamics of an elastic structure coupled with a rocking wall. Earthq. Eng. Struct. Dyn. 2017, 46, 945–962. [Google Scholar] [CrossRef]
- Bachmann, J.A.; Vassiliou, M.F.; Stojadinović, B. Dynamics of rocking podium structures. Earthq. Eng. Struct. Dyn. 2017, 46, 2499–2517. [Google Scholar] [CrossRef]
- Bantilas, K.E.; Kavvadias, I.E.; Vasiliadis, L.K. Seismic response of elastic multidegree of freedom oscillators placed on the top of rocking storey. Earthq. Eng. Struct. Dyn. 2021, 50, 1315–1333. [Google Scholar] [CrossRef]
- Bantilas, K.E.; Kavvadias, I.E.; Vasiliadis, L.K. Analytical investigation of the seismic response of elastic oscillators placed on the top of rocking storey. Bull. Earthq. Eng. 2021, 19, 1249–1270. [Google Scholar] [CrossRef]
- Karam, G.; Mazen, T. Rocking blocks stability under critical pulses from near-fault earthquakes using a novel energy based approach. Appl. Sci. 2020, 10, 5924. [Google Scholar] [CrossRef]
- Li, S.; Tsang, H.H.; Lam, N. Seismic protection by rocking with superelastic tendon restraint. Earthq. Eng. Struct. Dyn. 2022, 51, 1718–1737. [Google Scholar] [CrossRef]
- Lagomarsino, S. Seismic assessment of rocking masonry structures. Bull. Earthq. Eng. 2015, 13, 97–128. [Google Scholar] [CrossRef]
- Buzov, A.; Radnić, J.; Grgić, N.; Baloević, G. Effect of the Drum Height on the Seismic Behaviour of a Free-Standing Multidrum Column. Adv. Mater. Sci. Eng. 2018, 2018, 5729068. [Google Scholar] [CrossRef]
- Stiros, S.C. Monumental articulated ancient Greek and Roman columns and temples and earthquakes: Archaeological, historical, and engineering approaches. J. Seismol. 2020, 24, 853–881. [Google Scholar] [CrossRef]
- Huang, B.; Günay, S.; Lu, W. Seismic assessment of freestanding ceramic vase with shaking table testing and performance-based earthquake engineering. J. Earthq. Eng. 2022, 26, 7956–7978. [Google Scholar] [CrossRef]
- Ko, K.W.; Ha, J.G.; Kim, D.S. Analytical evaluation and experimental validation on dynamic rocking behavior for shallow foundation considering structural response. Earthq. Eng. Eng. Vib. 2022, 21, 37–51. [Google Scholar] [CrossRef]
- He, X.; Unjoh, S. Development of rocking isolation bearing system (RIBS) to control excessive seismic responses of bridge structures. Earthq. Eng. Struct. Dyn. 2022, 51, 369–392. [Google Scholar] [CrossRef]
- Beck, J.L.; Skinner, R.I. The seismic response of a reinforced concrete bridge pier designed to step. Earthq. Eng. Struct. Dyn. 1973, 2, 343–358. [Google Scholar] [CrossRef]
- Sharpe, R.D.; Skinner, R.I. The seismic design of an industrial chimney with rocking base. Bull. N. Z. Natl. Soc. Earthq. Eng. 1983, 16, 98–106. [Google Scholar] [CrossRef]
- Wada, A.; Qu, Z.; Motoyui, S.; Sakata, H. Seismic retrofit of existing SRC frames using rocking walls and steel dampers. Front. Archit. Civ. Eng. China 2011, 5, 259. [Google Scholar] [CrossRef]
- Yim, C.S.; Chopra, A.K.; Penzien, J. Rocking response of rigid blocks to earthquakes. Earthq. Eng. Struct. Dyn. 1980, 8, 565–587. [Google Scholar] [CrossRef]
- Bachmann, J.A.; Strand, M.; Vassiliou, M.F.; Broccardo, M.; Stojadinović, B. Is rocking motion predictable? Earthq. Eng. Struct. Dyn. 2018, 47, 535–552. [Google Scholar] [CrossRef]
- Psycharis, I.N.; Fragiadakis, M.; Stefanou, I. Seismic reliability assessment of classical columns subjected to near-fault ground motions. Earthq. Eng. Struct. Dyn. 2013, 42, 2061–2079. [Google Scholar] [CrossRef]
- Bantilas, K.E.; Kavvadias, I.E.; Vasiliadis, L.K.; Elenas, A. Seismic fragility and intensity measure investigation for rocking podium structures under synthetic pulse-like excitations. Earthq. Eng. Struct. Dyn. 2021, 50, 3441–3459. [Google Scholar] [CrossRef]
- Kavvadias, I.E.; Vasiliadis, L.K.; Elenas, A. Seismic response parametric study of ancient rocking columns. Int. J. Archit. Herit. 2017, 11, 791–804. [Google Scholar] [CrossRef]
- Dimitrakopoulos, E.G.; Paraskeva, T.S. Dimensionless fragility curves for rocking response to near-fault excitations. Earthq. Eng. Struct. Dyn. 2015, 44, 2015–2033. [Google Scholar] [CrossRef]
- Solarino, F.; Giresini, L. Fragility curves and seismic demand hazard analysis of rocking walls restrained with elasto-plastic ties. Earthq. Eng. Struct. Dyn. 2021, 50, 3602–3622. [Google Scholar] [CrossRef]
- Liu, P.; Xue, W.; Pang, H.; Zhang, Y.M.; Chen, H.T.; Yang, W.G. Seismic overturning fragility analysis for freestanding building contents subjected to horizontal bidirectional floor motions. Soil Dyn. Earthq. Eng. 2020, 161, 107414. [Google Scholar] [CrossRef]
- Diamantopoulos, S.; Fragiadakis, M. Modeling, fragility and risk assessment of ancient freestanding columns and colonnades. Eng. Struct. 2023, 275, 115273. [Google Scholar] [CrossRef]
- Bakhtiary, E.; Gardoni, P. Probabilistic seismic demand model and fragility estimates for rocking symmetric blocks. Eng. Struct. 2016, 114, 25–34. [Google Scholar] [CrossRef]
- Pappas, A.; Sextos, A.; Da Porto, F.; Modena, C. Efficiency of alternative intensity measures for the seismic assessment of monolithic freestanding columns. Bull. Earthq. Eng. 2017, 15, 1635–1659. [Google Scholar] [CrossRef]
- Kavvadias, I.E.; Papachatzakis, G.A.; Bantilas, K.E.; Vasiliadis, L.K.; Elenas, A. Rocking spectrum intensity measures for seismic assessment of rocking rigid blocks. Soil Dyn. Earthq. Eng. 2017, 101, 116–124. [Google Scholar] [CrossRef]
- Giouvanidis, A.I.; Dimitrakopoulos, E.G. Rocking amplification and strong-motion duration. Earthq. Eng. Struct. Dyn. 2018, 47, 2094–2116. [Google Scholar] [CrossRef]
- Lachanas, C.G.; Vamvatsikos, D.; Dimitrakopoulos, E.G. Statistical property parameterization of simple rocking block response. Earthq. Eng. Struct. Dyn. 2022, 52, 394–414. [Google Scholar] [CrossRef]
- Sieber, M.; Vassiliou, M.F.; Anastasopoulos, I. Intensity measures, fragility analysis and dimensionality reduction of rocking under far-field ground motions. Earthq. Eng. Struct. Dyn. 2022, 51, 3639–3657. [Google Scholar] [CrossRef]
- Elenas, A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings. Soil Dyn. Earthq. Eng. 2000, 20, 93–100. [Google Scholar] [CrossRef]
- Elenas, A.; Meskouris, K. Correlation study between seismic acceleration parameters and damage indices of structures. Eng. Struct. 2001, 23, 698–704. [Google Scholar] [CrossRef]
- Alvanitopoulos, P.F.; Andreadis, I.; Elenas, A. Neuro-fuzzy techniques for the classification of earthquake damages in buildings. Measurement 2010, 43, 797–809. [Google Scholar] [CrossRef]
- Elenas, A. Seismic-Parameter-Based Statistical Procedure for the Approximate Assessment of Structural Damage. Math. Probl. Eng. 2014, 2014, 916820. [Google Scholar] [CrossRef]
- Elenas, A. Interdependency between seismic acceleration parameters and the behavior of structures. Soil Dyn. Earthq. Eng. 1997, 16, 317–322. [Google Scholar] [CrossRef]
- Kostinakis, K.; Athanatopoulou, A.; Morfidis, K. Correlation between ground motion intensity measures and seismic damage of 3D R/C buildings. Eng. Struct. 2015, 82, 151–167. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wang, Q.; Geng, P.; Chen, J.; He, C. Dynamic discrimination method of seismic damage in tunnel portal based on improved wavelet packet transform coupled with Hilbert-Huang transform. Mech. Syst. Signal Process. 2023, 188, 110023. [Google Scholar] [CrossRef]
- Tyrtaiou, M.; Elenas, A. Novel Hilbert spectrum-based seismic intensity parameters interrelated with structural damage. Earthq. Struct. 2019, 16, 197–208. [Google Scholar]
- Tyrtaiou, M.; Elenas, A. Seismic Damage Potential Described by Intensity Parameters Based on Hilbert-Huang Transform Analysis and Fundamental Frequency of Structures. Earthq. Struct. 2020, 18, 507–517. [Google Scholar]
- Tyrtaiou, M.; Elenas, A.; Andreadis, I.; Vasiliadis, L. Hilbert-Huang Transform-Based Seismic Intensity Parameters for Performance-Based Design of RC-Framed Structures. Buildings 2022, 12, 1301. [Google Scholar] [CrossRef]
- Alvanitopoulos, P.F.; Andreadis, I.; Elenas, A. Interdependence between damage indices and ground motion parameters based on Hilbert–Huang transform. Meas. Sci. Technol. 2019, 21, 025101. [Google Scholar] [CrossRef]
- Chen, G.; Yang, J.; Liu, Y.; Kitahara, T.; Beer, M. An energy-frequency parameter for earthquake ground motion intensity measure. Earthq. Eng. Struct. Dyn. 2022, 52, 271–284. [Google Scholar] [CrossRef]
- Cramer, D. Advanced Quantitative Data Analysis; McGraw-Hill Education: London, UK, 2003. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Meskouris, K. Structural Dynamics: Models, Methods, Examples; Ernst & Sohn: Berlin, Germany, 2000. [Google Scholar]
- ATC 3-06 Publication. Tentative Provisions for the Development of Seismic Regulations for Buildings; US Government Printing Office: Washington, DC, USA, 1978. [Google Scholar]
- Trifunac, M.D.; Brady, A.G. A study on the duration of strong earthquake ground motion. Bull. Seismol. Soc. Am. 1975, 65, 581–626. [Google Scholar]
- Rathje, E.M.; Abrahamson, N.A.; Bray, J.D. Simplified frequency content estimates of earthquake ground motions. J. Geotech. Geoenviron. Eng. 1998, 124, 150–159. [Google Scholar] [CrossRef]
- Housner, G.; Jennings, P.C. Generation of artificial earthquakes. J. Eng. Mech. Div. 1964, 90, 113–150. [Google Scholar] [CrossRef]
- Vanmarcke, E.H.; Lai, S.S.P. Strong-motion duration and RMS amplitude of earthquake records. Bull. Seismol. Soc. Am. 1980, 70, 1293–1307. [Google Scholar]
- Cabãnas, L.; Benito, B.; Herráiz, M. An approach to the measurement of the potential structural damage of earthquake ground motions. Earthq. Eng. Struct. Dyn. 1997, 26, 79–92. [Google Scholar] [CrossRef]
- Arias, A. A Measure of Earthquake Intensity; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Ang, A.H.S. Reliability bases for seismic safety assessment and design. In Proceedings of the 4th U.S. National Conference on Earthquake Engineering, Earthquake Engineering Research Institute, Palm Springs, CA, USA, 20–24 May 1990. [Google Scholar]
- Fajfar, P.; Vidic, T.; Fischinger, M. A measure of earthquake motion capacity to damage medium-period structures. Soil Dyn. Earthq. Eng. 1990, 9, 236–242. [Google Scholar] [CrossRef]
- Housner, G.W. Spectrum intensities of strong-motion earthquakes. In Symposium on Earthquakes and Blast Effects on Structures; Earthquake Engineering Research Institute: Los Angeles, CA, USA, 1952. [Google Scholar]
- Von Thun, J.; Roehm, L.; Scott, G.; Wilson, J. Earthquake ground motions for design and analysis of dams. In Earthquake Engineering and Soil Dynamics II–Recent Advances in Ground-Motion Evaluation; Geotechnical Special Publication; ASCE: New York, NY, USA, 1988. [Google Scholar]
- Araya, R.; Saragoni, G.R. Earthquake accelerogram destructiveness potential factor. In Proceedings of the 8th World Conference on Earthquake Engineering, EERI, San Francisco, CA, USA, 21–28 July 1984. [Google Scholar]
- Jennings, P.C. Engineering seismology. In Earthquakes: Observation, Theory and Interpretation; Kanamori, H., Boschi, E., Eds.; Italian Physical Society: Varenna, Italy, 1982; pp. 138–173. [Google Scholar]
- Dimitrakopoulos, E.G.; Kappos, A.J.; Makris, N. Dimensional analysis of yielding and pounding structures for records without distinct pulses. Soil Dyn. Earthq. Eng. 2009, 29, 1170–1180. [Google Scholar] [CrossRef]
- Giovenale, P.; Cornell, A.C.; Esteva, L. Comparing the adequacy of alternative ground motion intensity measures for the estimation of structural responses. Earthq. Eng. Struct. Dyn. 2004, 33, 951–979. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Shinozuka, M.; Feng, M.Q.; Kim, H.K.; Kim, S.H. Nonlinear static procedure for fragility curve development. J. Eng. Mech. 2000, 126, 1287–1295. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthq. Eng. Struct. Dyn. 2005, 34, 1193–1217. [Google Scholar] [CrossRef]
- Gehl, P.; Seyedi, D.M.; Douglas, J. Vector-valued fragility functions for seismic risk evaluation. Bull. Earthq. Eng. 2013, 11, 365–384. [Google Scholar] [CrossRef]
- Luco, N.; Cornell, C. Structure-specific scalar intensity measures for near-source and ordinary earthquake motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef]
- Padgett, J.E.; Nielson, B.G.; DesRoches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
- Pacific Earthquake Engineering Research Centre (PEER). Strong Motion Database. 2016. Available online: http://ngawest2.berkeley.edu/ (accessed on 12 November 2022).
- Duda, R.O.; Hart, P.E.; Stork, D.H. Pattern Classification, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]

| Category | Seismic Parameter | Description | |
|---|---|---|---|
| Amplitude-Based | PGA | Peak Ground Acceleration | [57] |
| PGV | Peak Ground Velocity | [57] | |
| PGD | Peak Ground Displacement | [57] | |
| EPA | Effective Peak Acceleration | [58] | |
| EPAmax | maximum EPA | [58] | |
| Duration-Based | tsig | Strong motion duration | [59] |
| Frequency-Based | PGV/PGA | Period parameter | [56] |
| PGD/PGV | Period parameter | [39] | |
| Tm | Mean Period | [60] | |
| CP | Central Period | [61] | |
| Energy-Based | arms | Acceleration’s Root Mean Square | [62] |
| vrms | Velocity’s Root Mean Square | [62] | |
| drms | Displacement’s Root Mean Square | [62] | |
| CAV | Cumulative Absolute Velocity | [63] | |
| CAD | Cumulative Absolute Displacement | [63] | |
| SED | Specific Energy Density | [57] | |
| IA | Arias Intensity | [64] | |
| IC | Characteristic Intensity | [65] | |
| IF | Fajfar–Vidic–Fischinger Intensity | [66] | |
| IH | Housner Intensity | [67] | |
| ASI | Acceleration Spectrum Intensity | [68] | |
| DPAS | Araya–Saragoni Destructiveness Potential | [69] | |
| P90 | Seismic Power of Jennings | [70] | |
| Lma | Characteristic length scale of acceleration | [71] | |
| Lmv | Characteristic length scale of velocity | [31] | |
| EFP | Energy–Frequency Parameter | [54] | |
| Limit State | |θmax|/α | Performance Level | Description |
|---|---|---|---|
| LS1 | 0.10 | Slight Rocking | Rocking initiation |
| LS2 | 0.50 | Moderate Rocking | Local damage due to impact |
| LS3 | ∞ | Rocking Overturn | Collapse |
| IMs | PSDM | MLE | |||||
|---|---|---|---|---|---|---|---|
| a | b1 | b2 | βD|IM | μ | σ | λ | |
| PGA—Tm | 0.58 | 2.28 | 1.87 | 1.49 | −0.06 | 0.19 | 0.49 |
| AHHT—PGD | 5.54 | 1.37 | 0.53 | 1.48 | −1.98 | 0.29 | 0.64 |
| AHHT—Tm | 5.21 | 1.38 | 0.92 | 1.48 | −1.14 | 0.22 | 0.40 |
| AHHT—PGV/PGA | 6.12 | 1.41 | 0.59 | 1.51 | −2.48 | 0.27 | 0.59 |
| AHHT—IF | 2.97 | 1.01 | 1.19 | 1.44 | 0.26 | 0.32 | 0.13 |
| Classes | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Description | 0 < θ/α ≤ 0.10 | 0.10 < θ/α ≤ 0.50 | 0.5 < θ/α ≤ 1 | θ/α > 1 |
| Set | Accuracy | Recall | Precision | F1 Score |
|---|---|---|---|---|
| Train | 0.96 (0.97) | 0.92 (0.96) | 0.95 (0.96) | 0.93 (0.96) |
| Test | 0.75 (0.85) | 0.75 (0.85) | 0.79 (0.85) | 0.76 (0.85) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bantilas, K.E.; Kavvadias, I.E.; Tyrtaiou, M.; Elenas, A. Hilbert–Huang-Transform-Based Seismic Intensity Measures for Rocking Response Assessment. Appl. Sci. 2023, 13, 1634. https://doi.org/10.3390/app13031634
Bantilas KE, Kavvadias IE, Tyrtaiou M, Elenas A. Hilbert–Huang-Transform-Based Seismic Intensity Measures for Rocking Response Assessment. Applied Sciences. 2023; 13(3):1634. https://doi.org/10.3390/app13031634
Chicago/Turabian StyleBantilas, Kosmas E., Ioannis E. Kavvadias, Magdalini Tyrtaiou, and Anaxagoras Elenas. 2023. "Hilbert–Huang-Transform-Based Seismic Intensity Measures for Rocking Response Assessment" Applied Sciences 13, no. 3: 1634. https://doi.org/10.3390/app13031634
APA StyleBantilas, K. E., Kavvadias, I. E., Tyrtaiou, M., & Elenas, A. (2023). Hilbert–Huang-Transform-Based Seismic Intensity Measures for Rocking Response Assessment. Applied Sciences, 13(3), 1634. https://doi.org/10.3390/app13031634






