1. Introduction
The robot operating system (ROS) offers a service-oriented solution for the development of distributed robotic systems. It enables the integration of open-source libraries and tools by standardizing the methodology of software design and the underlying communication layer [
1,
2].
Most robotic systems are classified as real-time and safety-critical. The predictable execution of the timing under real-time constraints is an important key design for such complex systems. ROS focuses on the fast and functional integration of different applications, while execution control and timing constraints are not adequately addressed by the middleware [
3]. Despite the effort in the new ROS-2 distribution to address the support of real-time and fault-tolerance mechanisms [
4], there is no clear definition of callback execution order within an executor and there is no control over the execution order between the different nodes. The precedence of execution and the dependencies between different nodes and callbacks cannot be clearly defined, and there are no mechanisms to define the real-time scheduling of running entities [
5].
Research on the end-to-end real-time analysis of ROS-2 embedded applications has started recently. Casini et al. [
6] proposed a pioneering analysis of end-to-end timing chains in ROS-2. Subsequently, several studies addressed the real-time behavior of the ROS-2 execution model and its performance and security capabilities [
3,
7]. New scheduling techniques were proposed to improve the conventional ROS-2 scheduler by proposing an alternate scheduler as in [
8] or keeping it unmodified as in [
9].
All these previous studies consider the number of callbacks and executors to be predefined and assume that the callbacks are already assigned to executors. They then propose solutions for the real-time scheduling of the application. To schedule an embedded application in ROS, we need to map callbacks to an executor in the context of which callbacks are executed on the processor. ROS does not impose any requirements on this step of configuration. The execution model is based on the processes that run the executors to receive messages and invoke callbacks [
4]. For large systems, manually setting up an execution order of callbacks inside the executor, as well as assigning priorities to executors, is always error-prone and difficult to predict. In critical safety systems, static memory allocation is crucial. In the initialization phase, the system designer determines the number of callbacks for the embedded application and the necessary dynamic memory to be allocated before the system execution. Then, the system designer maps the callbacks to the executors. The order of callbacks within an executor is important because it may affect the real-time execution and performance of the embedded system in real-time. During the configuration step, the system designer shall define the number of callbacks and their sequence within the executor.
The simplest approach is to bind each callback to one executor. However, mapping each callback to a dedicated executor leads to a lot of context switches and may lead to a deadline violation and significant OS overhead. Similarly, mapping all callbacks of a node to a single executor may leave the system unresponsive if the executor fails. In addition, the internal branching structure of such a process becomes complex to schedule. Having these two extremes in mind, finding a middle solution is an optimization goal. Our problem consists of finding a partitioning of the callbacks set that is schedulable with a minimum number of executors. The number of partitions to be explored for n callbacks is the Bell number [
10]. The Bell number is exponential with respect to the number of callbacks n and can be computed by the following recurrence relation:
For example, to search for a space of 500 callbacks, we obtain
. If we group callbacks that have identical periods, the search space can be reduced to
, where
is the Bell number of the set i of n callbacks with equal periods and m is the number of sets. However, this number remains exponential. Given the complexity of the problem, we need to use heuristics to reduce the search space. A simple heuristic is to regroup callbacks with the same period (or integer multiples) to be assigned to one executor. Several studies have considered the software clustering problem in the context of real-time systems. Common optimization goals are stack memory usage [
11,
12] using genetic algorithms and scheduling algorithms, core load balancing [
11], inter-communication overhead [
13,
14] using integer linear programming (ILP), data consistency using ILP and heuristic methods [
15], and deadline violation [
16,
17] using genetic algorithms and the greedy heuristic approach for system resource clustering. Other work proposes regrouping runnables with arbitrary periods on the same task using a greedy heuristic approach combined with linear cost function and schedulability test [
18,
19]. This approach may lead to a minimum number of executors needed to schedule overloaded systems while minimizing the stack memory usage and context switch overhead. This paper adopts this approach and adapts it to ROS-2 applications.
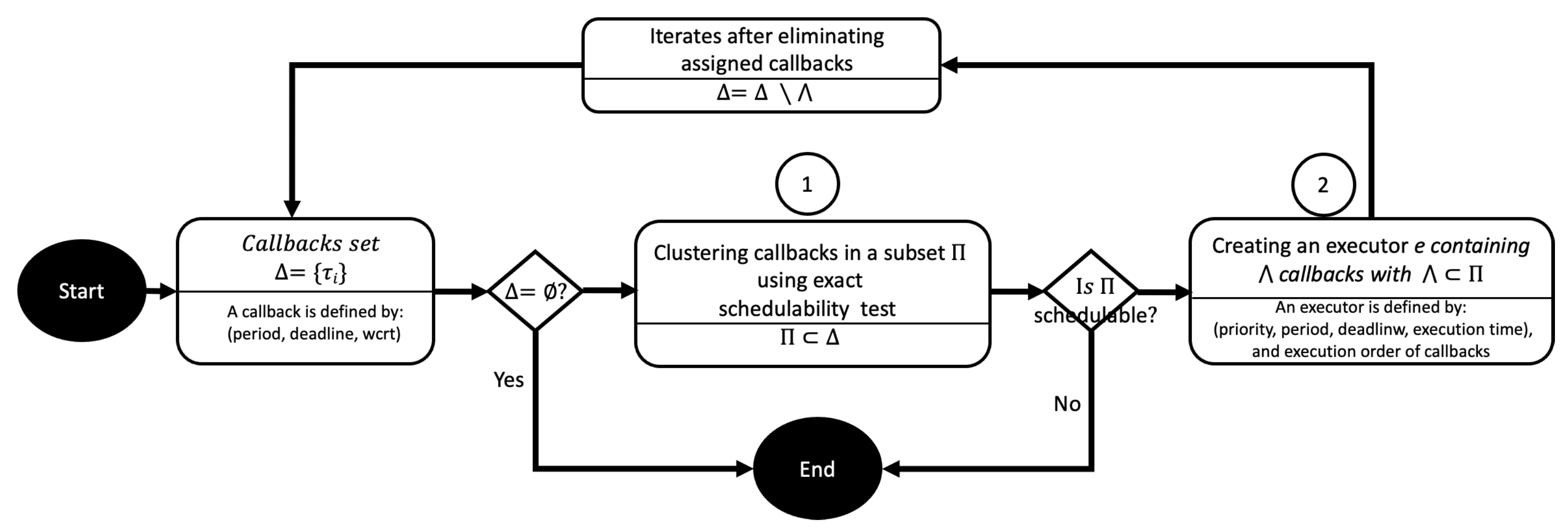
Contribution: This work adopts a greedy heuristic approach to quickly construct a correct solution to the mapping and resource configuration problem of the ROS embedded system. The heuristic itself is not the central work of this paper. The main contribution is the design of the cost function and the associated schedulability test, which efficiently reduce the clustering complexity. The proposed algorithm assigns a set of callbacks to the executors while preserving the schedulability of the real-time system and simultaneously determines the number of executors required to schedule a set of callbacks, the priority assignment of the executor, and the sequence of callbacks within an executor (
Figure 1).
First, the two-stage approach clusters callbacks using an exact schedulability test before building an executor with priority assignment. The results of this work are as follows:
A formal model to analyze the system.
A low-complexity heuristic algorithm to build executors from a set of callbacks.
A method to assign priority to executors and to define the order of execution of callbacks inside an executor.
Organization: This article is organized as follows:
Section 2 reviews the relevant related works.
Section 3 introduces the ROS-2 architecture, its main concepts, and the scheduling mechanisms. The formulation of the system model is provided in
Section 4.
Section 5 presents the new algorithm for real-time scheduling and resource mapping for ROS-2.
Section 6 discusses the results of the experiments obtained.
Section 7 concludes the work and identifies potential perspectives.
2. Related Works
Real-time scheduling and resource allocation have been widely addressed by the real-time systems community, such as [
20,
21,
22]. In the particular context of ROS embedded systems, most of the research work focuses on the integration of real-time scheduling capabilities into the conventional scheduler of the ROS core system [
6,
8,
23,
24]. The authors of [
6] have made a significant contribution to the field by proposing a formal model with analytical methods for the analysis of the end-to-end response time of ROS embedded systems. It is the first attempt to analyze the response time of ROS-2 processing chains. In subsequent work, [
24] gives a more detailed analysis of end-to-end paths with the assumption that a callback may belong to one chain. In [
8], the authors suggested an alternative ROS scheduler to reduce end-to-end latency. They consider both system scheduling techniques and the mapping functions of callbacks to executors for monocore and multicore systems. Their algorithm provides callback priority assignments to improve real-time predictability. However, the proposed solution assumes that the set of executors is defined a priori. The work in [
23] proposes a method to prioritize message transmission between ROS nodes with harmonic and non-harmonic periods. The results reveal a reduced response time and low variance between nodes.
Furthermore, several studies have evaluated ROS-2 performance using measurement-based approaches instead of analytical methods, such as [
3,
5]. They mainly conduct empirical performance measures to propose improvement directions. Security aspects are addressed by [
25,
26,
27,
28]. In [
27], the authors investigated the security plug-ins in ROS-2 to study its ability to mitigate multiple threats. The study considers the impact of both QoS and security on ROS-2 network performance using measurement-based results. In [
28], the authors use a probabilistic model checker to validate the real-time performance and reliability of ROS-2. Their method reduces the data loss rate and the response time of the system without considering real-time scheduling. In [
25], the authors propose an approach to integrate reliability and QoS services into ROS-2 using DDS middleware services. In [
26], Krichen et al. adopted a model-based security testing (MBST) approach to check the security of IoT applications in the context of smart cities. The proposed approach uses extended timed automata to model security and behavioral requirements, to design and generate security tests, and to execute and evaluate the security tests. The model-based nature of the proposed approach makes it applicable to other real-time systems such as ROS-2.
Other works take advantage of optimization methods to address the NP-hard problem of software resource allocation and configuration. These works adopted another perspective using optimization methods [
11,
12,
13,
19]. In [
11], Thomas Wilhelm et al. propose methods to optimize the mapping of runnables to tasks in multicore automotive control units. First, a constraint programming method is used to automate the generation of initial configurations while balancing core utilization. Second, an evolutionary algorithm is used to optimize the mapping of runnables to tasks. Task creation is conducted using a simple heuristic of mapping runnables with the same period (or integer multiple) to the same task. The optimization steps are performed in a serial manner, so the process may become stuck in local minima. In [
13], the authors address the problem of mapping tasks in multicore architecture using rate monotonic scheduling (RMS). The solution regroups tasks with the same period on the same core; then, a heuristic method is proposed to minimize the intercommunication overhead between the core and task response time. The authors of [
12] address the issues of AUTOSAR model design analysis to minimize memory stack utilization for mixed-criticality systems with preemptive threshold setting that addresses the design synthesis problem. In a prior work [
19], the authors developed a heuristic algorithm to configure task mapping for AUTOSAR-based embedded systems. The main goal is to optimize the operating system and task mapping to improve system performance. Their method constructs a set of tasks from a set of runnables with arbitrary periods while guaranteeing real-time requirements.
The problem of grouping/clustering has recently been addressed by several studies with an application to the planning of autonomous robot paths [
29,
30,
31]. Metaheuristic algorithms are proposed to find optimal collision-free paths between two points for mobile robots. The low complexity of the proposed methods and their efficiency of resource usage have been approved for large-scale and crowded farmlands. Metaheuristic algorithms are suitable for multimodal, multi-objective systems. However, for large systems with multiple objectives, these methods suffer from high time complexity and the local minima trap. Heuristic methods quickly provide a solution to a difficult optimization problem. For the particular resource optimization of this study, we opted for the heuristic method to solve a scheduling problem. Combining heuristic with metaheuristic methods to solve a holistic optimization problem seems to be promising for large-scale systems.
Table 1 summarizes related works by classifying them into three main classes: analytical, heuristic, and metaheuristic methods. The online/offline variable indicates that the developed method runs during a configuration step or at runtime. Some methods are integrated into the ROS-2 core scheduler (Built-in). The set of decision variables and cost objectives is listed for the optimization problem.
To the best of our knowledge, this is the first work that applies resource mapping and scheduling with arbitrary periods to construct and schedule a set of executors given a set of callbacks for an ROS embedded system.
3. Background of ROS-2 Architecture
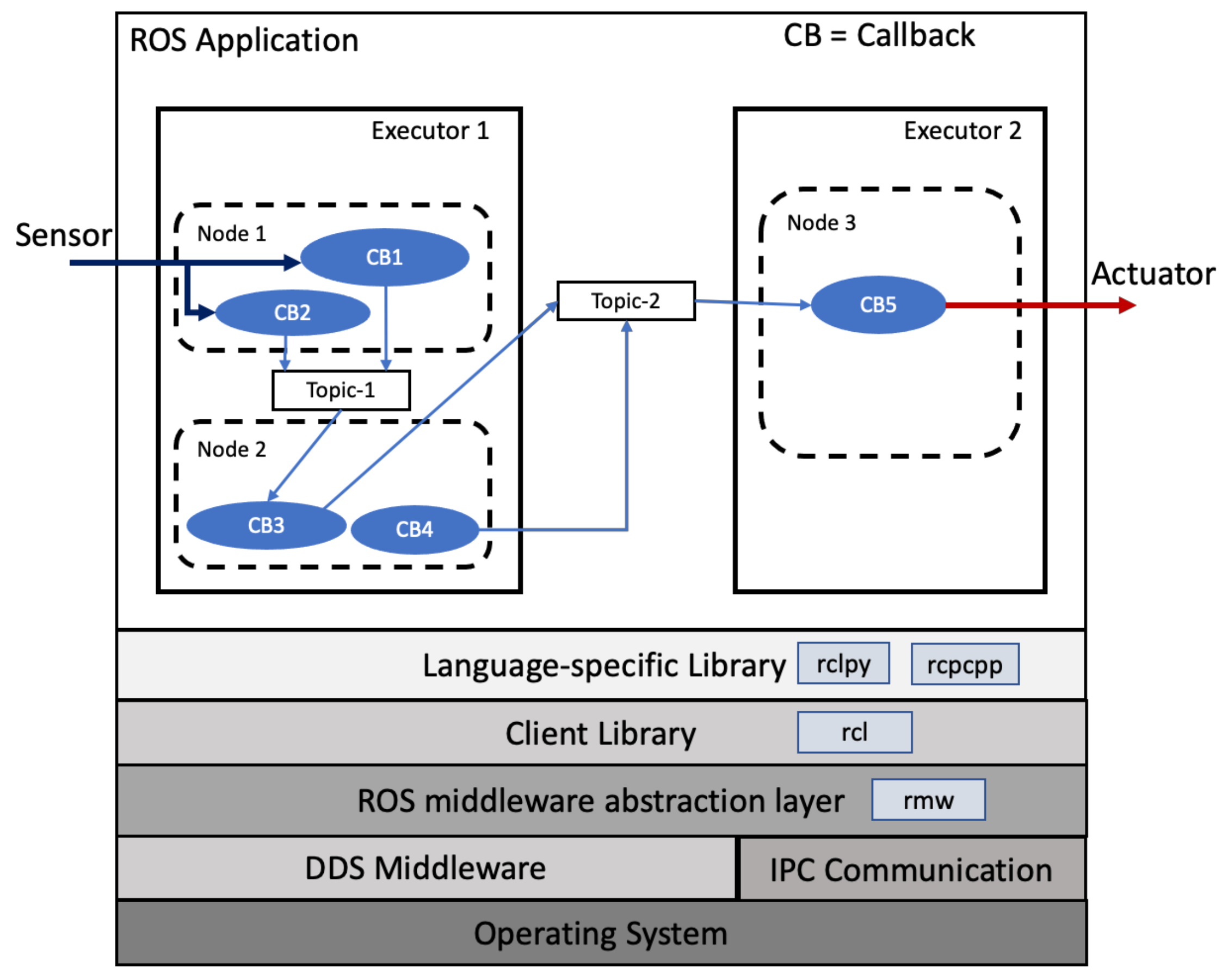
An embedded application in ROS consists of a set of interconnected nodes (
Figure 2). Each node contains one or more callbacks, which are the smallest pieces of code of the application. To ensure the consistent execution of programs written with different specific languages and different underlying platforms, a set of libraries provides the required abstraction at different layers. rmw is the middleware layer that ensures the interface between the data distribution service (dds) [
32] layer and the robot client library (rcl) layer. The rcl layer provides the abstraction of application programming interfaces (APIs) to the application to ensure consistent execution between the rmw layer and specific language client libraries such as Python (rclpy) and C++ (rcpcpp) [
33]. dds is a vendor-specific implementation of rmw that standardizes real-time communication between nodes.
The nodes communicate using a publisher/subscriber communication paradigm or a client/server communication paradigm. The publisher/subscriber communication paradigm is suitable for data flow streaming and sensor nodes, while the client/server communication paradigm is more suitable for synchronous remote procedural call and control nodes. Nodes use topics to communicate between publishers and subscribers, and use services to communicate between clients and servers. Topics and services are identified by a unique name, and one node can publish data on several topics and may also subscribe to several topics. A server may have multiple clients, but a client must have one server.
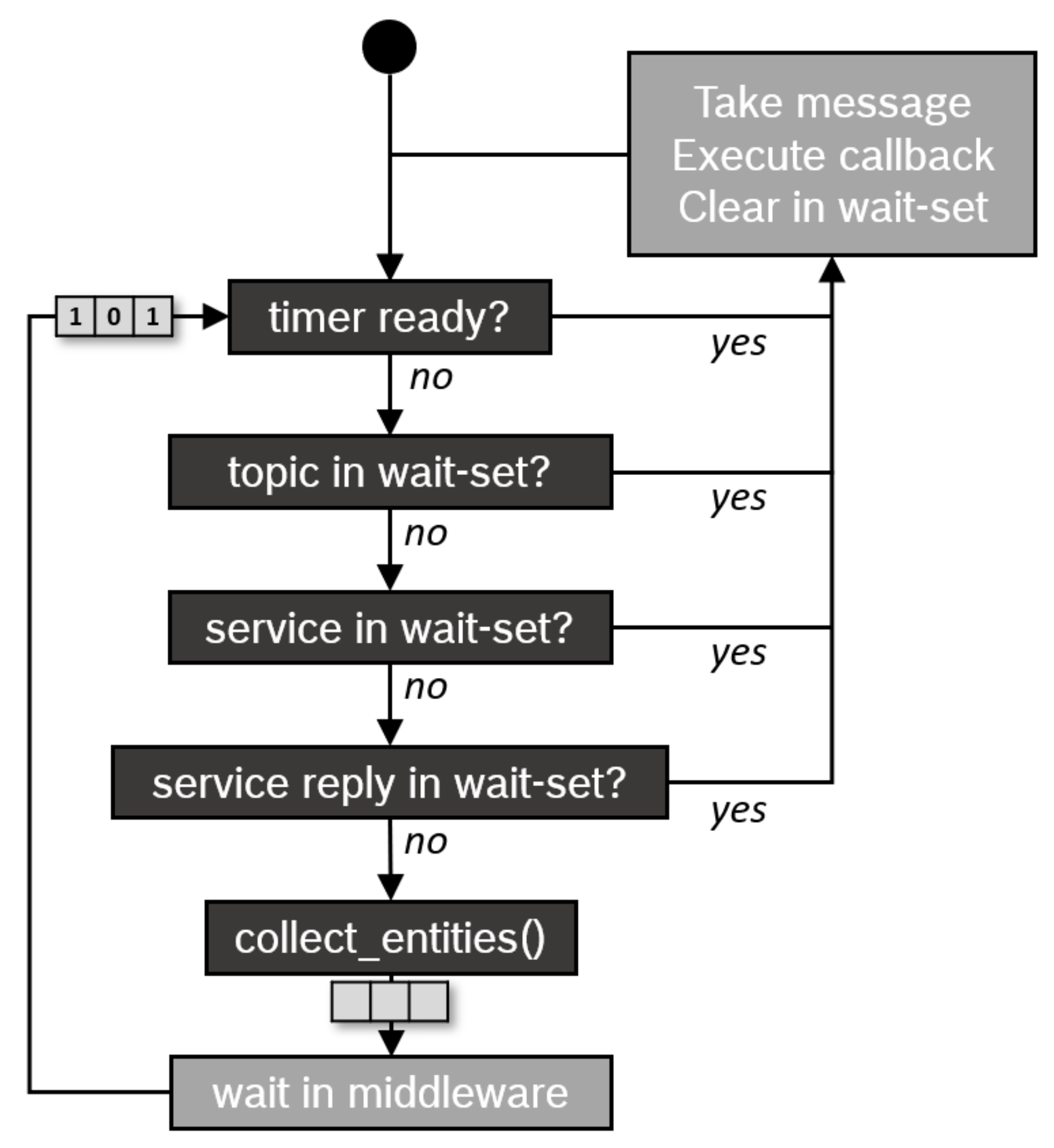
Scheduling in ROS-2
This section gives a brief description of the ROS scheduling mechanism and scheduling-related artifacts. The ROS scheduling model is implemented using executors. An executor selects pending callbacks from the ready list to be executed. Basically, two implementations are defined in ROS: a single executor and a multithreaded executor. In this study, we consider a single-threaded executor.
- Callback
This is the smallest executable code scheduled in ROS-2. ROS-2 defines five types of callbacks: timers that are time-triggered by system-level timers, subscribers that are triggered by the reception of new messages at a topic, services, and clients callbacks that are triggered by service requests and responses, respectively.
- Node
The node is the minimal self-contained unit of behavior. A node contains a set of callbacks organized by application programmers for the modularity and logical partitioning of functions. All callbacks from the same node are executed by the same executor.
- Executor
The executor reads the incoming messages from a ready list and executes, in a non-preemptive manner, the corresponding callback according to their type and activation instant in this order: timer callbacks first, then subscriber callbacks, service callbacks, and, finally, client callbacks, as illustrated in
Figure 3. Unlike common real-time priority-based scheduling algorithms, the executor does not always execute callbacks in their activation instances. Instead, the executor updates the ready status of non-timer callbacks in their respective queues when all queues are empty (called a polling point), and such a delayed update of callback readiness makes the priority assignment of non-timer callbacks ineffective and lets chains run in a round-robin-like manner.
Although the conventional scheduling semantic of ROS-2 does its job well for most applications, there are some limitations that are not compatible with safety-critical embedded systems, such as well-defined execution order, priority inversion, and the high and complex scheduling overhead in terms of CPU and memory usage.
4. System Model
We assume a periodic, fixed priority with constrained deadlines to represent real-time embedded systems. A steady-state system is considered, i.e. callbacks are defined at the initialization phase, and the configuration is still static during run-time since we consider safety-critical systems in the context of this work. The response time of a callback is the duration from the release instant to the completion of the job execution. Each callback must have a relative deadline. If the worst-case response time of the callback is shorter than or equal to its relative deadline, we say that the callback is schedulable. In the following, some useful definitions are given, which are used later in this article.
Definition 1 (GCD). The greatest common divisor (GCD) of two positive integers (a, b), denoted by GCD(a,b), is defined as the greatest positive number that is a common factor of both positive integers (a, b). Example: GCD(3,4) = 1.
Definition 2 (LCM). The least common multiple (LCM) of two positive integers (a, b), denoted by LCM(a,b), is defined as the smallest positive integer that is divisible by both a and b. Example: LCM(3,4) = 12.
Let us denote by
, a set of m callbacks
. A callback
is the smallest piece of code that runs in the context of an executor, denoted
. A callback
can be formalized as follows:
: The worst-case execution time (WCET).
: The callback period.
: The deadline for a callback.
: A positive integer that defines the order of callback execution within the executor.
Let us denote by
a set of n executors
. To model an executor, a multi-frame task model [
34] is adopted where the execution of an executor
consists of a sequence of
N frames characterized as follows:
: The executor deadline.
: The executor priority.
: The executor period.
: A vector of components. Each component represents the execution time of in frame j.
The execution time of the frame should be less than the executor period .
The period
of an executor
that contains m callbacks can be determined as the greatest common divisor (GCD) of the periods:
The frames of the executor
periodically repeat with a major cycle of
equal to the least common divisor (LCM) of the callback periods:
The number of frames can be determined by dividing the major cycle by the executor period as follows: .
Each execution time
of the
frame
is given by the following equation:
where the function
indicates that the
callback is present or not in the
frame as follows:
with
computes a location for callback
in frame s (
).
represents the repetition factor of
in
.
indicates the position of
.
Table 2 summarizes the main notation of the system model.
Hereafter, an example with the callbacks set ’{, , and }’ is assigned to one executor .
Table 3 illustrates an example of how to compute the parameters of the executor model, and
Figure 4 shows a visual representation of the executor and its callbacks.
5. Heuristic Scheduling Algorithm
We try to assign a callback from a set to a unique executor of a set . The problem consists of finding a feasible assignment using a minimal number of executors while meeting the timing requirements. The system is declared schedulable if and only if any executor of is schedulable and satisfies the deadline constraint.
To achieve this, we propose the following algorithm that assigns
n callbacks from
to
m executors of
(Algorithm 1).
| Algorithm 1: Assigning callbacks to executors. |
![Applsci 13 01532 i001 Applsci 13 01532 i001]() |
To establish the output list of executors , the algorithm invokes two other algorithms in its main loop. The first algorithm, ‘Assignment’ (Algorithm 2), establishes a subset of callbacks to be assigned to the same executor by starting from the lowest priority level (j = 1). In the case of not empty , a second algorithm, called ‘CreateExecutor’ (Algorithm 3), is called to define the subset of callbacks from to be assigned to the executor and determine its parameters. By iteration, the set of executors is constructed until all callbacks () are assigned to the executors. If, in any iteration, Algorithm 2 does not find a feasible subset , then the entire system is declared unschedulable. In the following, we detail Algorithms 2 and 3 used by the main Algorithm 1.
5.1. Algorithm 2: Assignment
This section details Algorithm 2, the objective of which is to identify a subset of callbacks that could be regrouped with one executor while satisfying real-time requirements.
Theorem 1. Suppose a set Δ of callbacks and an executor . There is a subset that can be assigned to the same executor if and only if each element of is schedulable when assigned a lower priority and other elementsΔ - are assigned higher priorities.
Proof. The proof can be obtained by contradiction. Let us suppose two callbacks and with and as deadlines, respectively. Suppose that the set of callbacks {, } is feasible with the lowest priority. Two distinct cases may appear: (1) has a higher priority than , or (2) has a higher priority than . The response times of and when assigned the lowest priority are identical for the two cases. This means that and must always complete the execution before the shortest deadline. Therefore, the set of callbacks , } can be assigned to an executor with a deadline D =. Consequently, if a set of callbacks is feasible when all callbacks are assigned the lowest priority, then this set can be assigned to only one executor. On the other hand, if {, } is not schedulable with the lowest priority, there is no priority assignment that allows scheduling callbacks. Therefore, if a set of callbacks can be assigned to one executor, each callback is feasible when assigned to the lowest priority. □
As stated in the above theorem, the subset
can be obtained if each callback of
satisfies the following equation:
is the worst-case response time of callback
when assigned the lowest priority and all callbacks are released at the same time (critical instant).
and
are, respectively, the period and the worst-case execution time for the
callback. This results in the longest response time to callback [
21]. As all callbacks have the same wcrt when assigned to the lowest priority,
can be simplified as:
and
R can be solved by the following recurrence relation:
where
. Equation (
11) surely converges if the processor utilization factor does not exceed 100%. The schedulability condition is given by the following condition:
where
is the deadline for the
callback.
The Algorithm 2 finds, from a set
, a subset of callbacks
that can be assigned to the same executor with a time complexity of
.
| Algorithm 2: Mapping feasibility test |
![Applsci 13 01532 i002 Applsci 13 01532 i002]() |
5.2. Algorithm 3: Executor Creation
This section presents the algorithm , whose objective is to select a subset of callbacks to be assigned to one executor and to determine its scheduling parameters.
The Algorithm 3 takes as input a set of callbacks and then determines as output a subset to be assigned to an executor e. The algorithm also defines the sequence order of callbacks within the executor and computes its timing parameters: vector of execution times , period T, and deadline D.
We say that there is a set of callbacks that can be assigned to the same executor if and only if:
- Condition 1:
- Condition 2:
- Condition 3:
Condition 3 is ensured by the feasibility test, which guarantees that R is less than or equal to the shortest callback deadline. Moreover, the executor deadline may be longer than its period, and consequently, buffering instances may occur for the execution of an executor. The number of buffered instances of an executor is bounded by . The first condition prevents the maximum buffering of an executor instance by creating subsets of callback periods.
To implement this, the bucket select algorithm (BSA) is used to divide
n callbacks into several buckets
using the divisibility test by prime numbers. The bucket select Algorithm 4 described in the following and illustrated by an example in
Figure 5 selects one bucket from n callbacks with a time complexity of
.
| Algorithm 3: CreateExecutor |
![Applsci 13 01532 i003 Applsci 13 01532 i003]() |
| Algorithm 4: Bucket select algorithm |
![Applsci 13 01532 i004 Applsci 13 01532 i004]() |
Let [K] be a list of first prime numbers. For each prime number (i = 1 to k), the algorithm regroups in a list (i = 1 to k) the callbacks whose periods can be divided by . Therefore, each bucket contains a subset of callback periods characterized by two timing parameters: , which corresponds to the GCD of the callback periods of the bucket , and , which is the minimum prime number, where is divisible by it. Finally, the algorithm returns the bucket with and the highest period value , denoted by .
To avoid overloading the executor, a sequencing of callbacks within the executor is necessary. For that, we adapt the lowest peak (LP) method developed in [
35]. The algorithm chooses the callback offset through a larger frame window
, which is equal to the LCM of the callback periods. The maximum execution time
must be less than or equal to the executor period
.
The Algorithm 3 creates an executor e from n callbacks with a time complexity of , where N is the frame number () and k is the number of prime numbers.
6. Experimental Results
This section presents and discusses the evaluation of the proposed algorithm. The evaluation is carried out in a uniprocessor case study with periodic and independent callbacks. The proposed solution is compared with three scheduling methods: RMS, GBFS, and greedy LL scheduling algorithms.
The rate monotonic scheduling (RMS) algorithm was introduced by Liu and Layland in 1973 [
21] and is considered a baseline for real-time scheduling. It is a preemptive fixed-priority scheduling algorithm suited for periodic independent and synchronous tasks. The priority of a task is inversely proportional to its period, i.e., the highest priority task will correspond to the task with the shortest period. The algorithm clusters n callbacks on m executors in two steps:
In the first step, callbacks that have the same periods are grouped in the same executor with a time complexity of ;
In the second step, a merge sort algorithm is used to define callback priority by assigning high priority to the shortest deadlines with a time complexity of .
In the following, a pseudocode of the RMS algorithm is given (Algorithm 5). The algorithm iterates to regroup elements of S that have the same period while satisfying a linear schedulability test (Schedule() function) defined in [
36] and considering the following assumptions:
Clustering two elements
and
in S
produces a new element with the following parameters:
,
, and
.
| Algorithm 5: Rate monotonic scheduling (RMS) algorithm. |
![Applsci 13 01532 i005 Applsci 13 01532 i005]() |
Note that the number of executors in this case is equal to at least the number of distinct periods in the set of callbacks. In industry, the system designer still uses the algorithm for embedded critical systems, as it guarantees upper bounds to the response time and is simple to implement. However, it is generally too conservative (pessimiste) for practical use and does not optimize the use of system resources [
37].
The GBFS algorithm developed by [
17] uses the greedy heuristic approach to gather the largest number of callbacks to the same executor. Priorities are assigned by deadline, i.e., the callbacks with the shortest deadline have the highest priority. The time complexity of the algorithm is of
, where n is the initial number of callbacks to be clustered (Algorithm 6).
| Algorithm 6: GBFS algorithm. |
![Applsci 13 01532 i006 Applsci 13 01532 i006]() |
For each clustering iteration, the algorithm uses a sufficient schedulability test and a cost function to select the best result in each clustering iteration (Equation (
13)).
The third algorithm used for comparison is the least loaded (LL) heuristic approach, used in [
18]. The approach applies a deadline test schedulability similar to the one used in this paper along with a heuristic approach of least load to design the cost function, and defines the sequencing order of callbacks inside the executor with a complexity of
).
6.1. Workload Generation
A set of callbacks is generated randomly using the UUnifast algorithm developed by [
22] in order to accurately assess the proposed solution in different execution scenarios. The algorithm splits the CPU usage factor
U into smaller usage factors
for
n callbacks. For each callback
, the deadline
is determined by the following equation:
where
generates values from a uniform distribution in the interval
with
. Using these equations, several sets of callbacks are randomly generated with a cardinality varying from 10 to 10,000. The callback period is chosen randomly in the range of [10, 275] ms and the deadline is set equal to the period.
6.2. Performance Metrics
The comparison study considers four performance metrics: success ratio, number of executors, execution time, and average response time.
- Success ratio:
Consider a set
composed of
N subsets of callbacks
, and
A as a scheduling algorithm. We say that
can be scheduled by the scheduling algorithm
A if all callbacks from
meet their deadlines, denoted by
, and if not, we denote it by
. As a result, the success rate
of the scheduling algorithm
A on
is defined by the following:
- Number of executors:
This metric represents the number of executors provided by the algorithm to schedule all callbacks while meeting real-time constraints. We try to minimize this metric.
- Runtime:
This metric measures the time it takes the algorithm to obtain a solution.
- Average response time:
Average response time is the time elapsed between the activation and completion of a callback. The following equation is defined to calculate the average response time rate
for a set of callbacks with cardinality
n:
6.3. Schedulability Test
Figure 6 shows the success ratio of all algorithms when varying callback deadlines. For each deadline interval
, we run all algorithms on sets of 1000 callbacks with a cardinality of 100 callbacks per set and a CPU utilization factor of
.
Figure 6 shows that the proposed algorithm significantly outperforms both the RMS and the GBFS algorithms in terms of the success ratio. We observe that the ratio decreases as the deadlines become shorter (stressed system). RMS algorithms quickly fail to schedule callbacks when the proposed algorithm continues to provide feasible solutions under tight deadlines. However, LL provides the same success ratio as the proposed algorithm, since it applies the same schedulability test.
6.4. Number of Executors
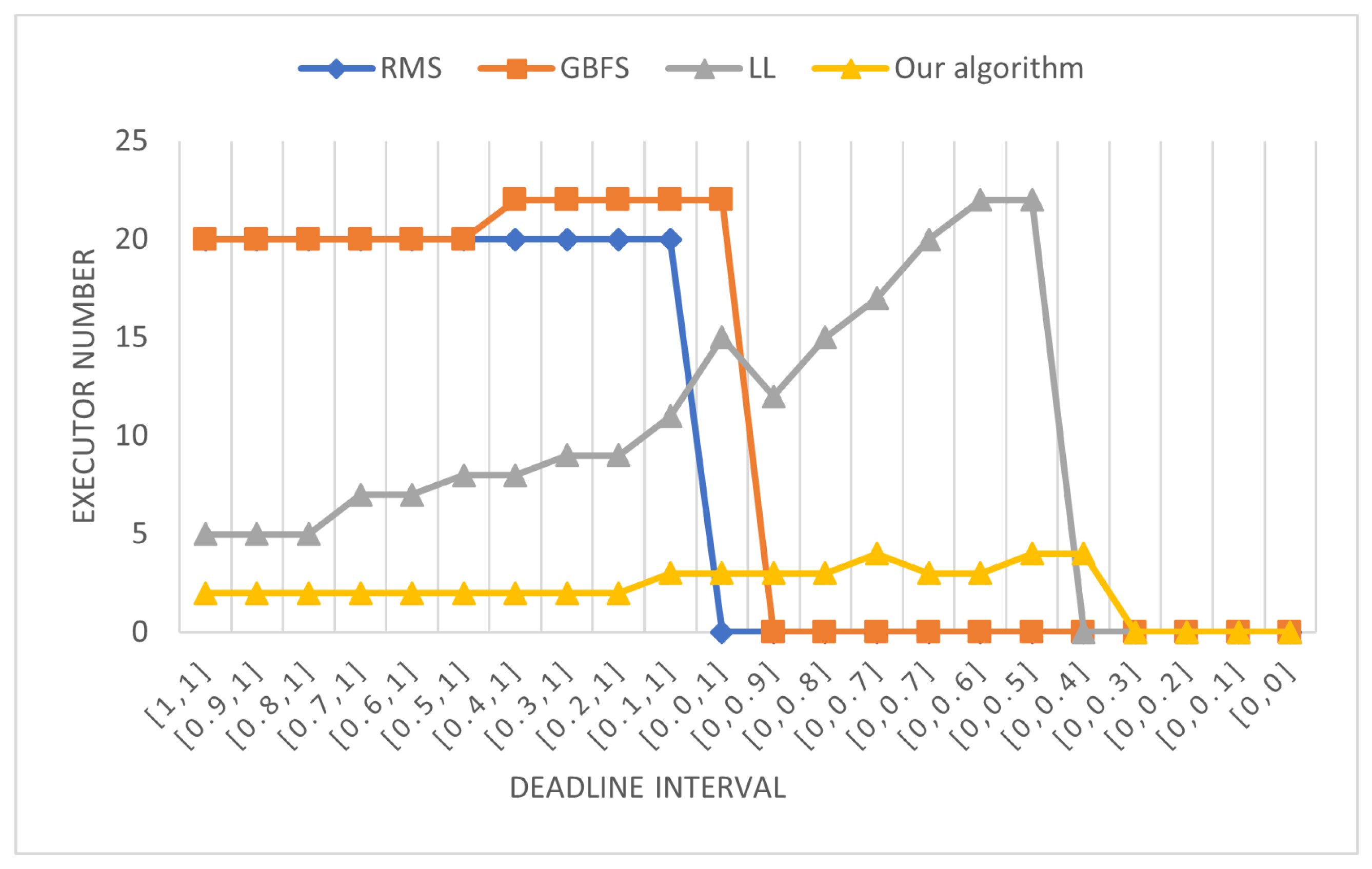
In this experiment, we compare the number of executors obtained by all algorithms. A utilization factor of is used and 10 callback sets are randomly generated with a cardinality of 100 and a deadline on request.
We then successively run all algorithms on all workloads and determine the maximum number of executors among the 10 sets of callbacks.
As shown in
Figure 7, the proposed algorithm outperforms RMS, LL, and GBFS in terms of the number of executors. For both RMS and GBFS, the algorithms try to regroup callbacks with the same period to the same executor, while LL regroups periods to the same executor. The proposed algorithm builds executors from callbacks with arbitrary periods. This leads to a minimal number of executors with low variance while guaranteeing system schedulability even in very stringent deadline situations. On the other hand, in RMS and GBFS, the variance is greater and the number of executors may be twice the number of distinct periods. This may have a major influence on the system stack memory. For example, suppose that all callbacks consume the same stack memory size of 512 bytes. The stack of an executor is the maximum size of all callbacks assigned to it. Therefore, the stack memory used to implement MPS for a deadline interval [0.2, 1] is 20 executors*512 bytes = 10 kb. However, in the proposed algorithm, it is only 2 executors*512 bytes = 1 kb.
Let us also note that the RMS and GBFS algorithms do not succeed in scheduling the system, since the deadline becomes tight where the proposed algorithm still finds a schedulable system.
6.5. Runtime Analysis Comparison (in ms)
Runtime analysis of algorithms is performed by running each algorithm on different sets of callbacks with a cardinality ranging from 1 to 1000. For each cardinality value, ten sets of callbacks are randomly generated with a deadline on request (i.e., the deadline is equal to the period), and a CPU utilization factor of . All algorithms are run successively on all callback sets, and the average execution time is computed for each. The runtime is obtained using a PC i7-2640-2.8 GHz and 8 GB of memory.
As shown in
Table 4, the GBFS algorithm quickly fails to find an acceptable solution (n/a) when the number of callbacks increases. However, the proposed algorithm outperforms RMS in finding a schedulable solution in a reasonable time. The lower time complexity of the algorithm proposed by
leads to a minimum runtime, compared to the RMS and LL algorithms that have a time complexity of
and
, respectively, and the GBFS algorithm that has a polynomial time complexity of
.
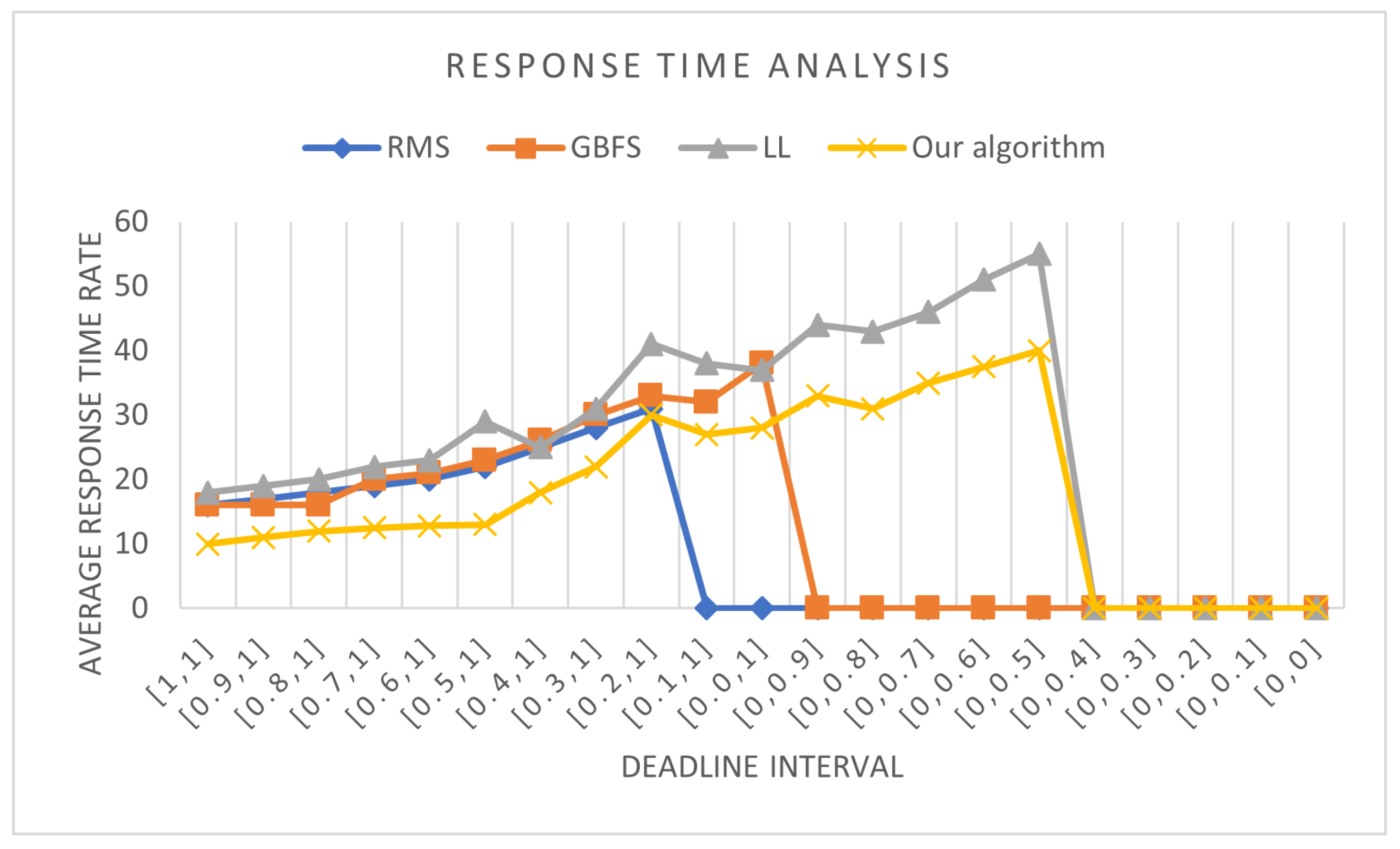
6.6. Response Time Analysis
This experiment considers 10 sets of callbacks. A set contains 100 callbacks randomly generated with a CPU utilization factor of .
For each deadline interval
, we run all algorithms on 10 sets of callbacks and determine the maximum average response time.
Figure 8 shows the average response time versus the deadline. The proposed algorithm finds a mapping of callbacks to executors that gives better response times than those obtained by other algorithms. This is due to the tuning of the callback sequencing and activation. However, the LL algorithm underperforms compared with the RMS and GBFS algorithms by causing the highest response times. Furthermore, we note that when the deadlines tighten after the interval [0.2, 1], both the LL and the proposed algorithm continue to be schedulable with a gradual increase in response time up to the interval [0, 0.5].
7. Limitations, Extensions, and Conclusions
This paper provides a new method to optimize the allocation and configuration of software resources for ROS embedded systems. The proposed solution builds a set of executors, maps callbacks to executors, assigns executor priority, and defines the execution sequencing of callbacks. The experimental results reported in this article demonstrate the efficiency of the new proposed algorithm in improving system scheduling and performance. For overloaded systems with tight deadlines, the proposed algorithm continues to provide a feasible solution while minimizing the number of executors to schedule the embedded application, whereas other algorithms do not find a solution.
The proposed solution is applied to critical embedded real-time systems with periodic executions. Formal analysis and optimization should be performed in the configuration phase and before system execution. The study considers a monocore system with a priority-driven scheduling policy. In extension to this study, future work should extend the system model to consider multicore architecture with resource dependencies. A trade-off between response time, stack memory usage, and data consistency should be considered. In addition, end-to-end system analysis can be performed by extending the model with the notion of end-to-end chains for distributed systems. Thus, the analysis considers dependencies among callbacks when computing the bound of end-to-end response time.