Rankine Active Earth Pressure of Unsaturated Filling under Earthquake
Abstract
:1. Introduction
2. Principals and Methods
2.1. Unified Shear Strength of Unsaturated Soil
2.2. Pseudo-static Analysis of Seismic Active Earth Pressure
2.2.1. Stress Analysis of The Rhombic Element
2.2.2. Intensity of Seismic Active Earth Pressure
2.2.3. Resultant Pressure and the Acting Position
3. Analyses and Results
3.1. Distribution of Seismic Active Earth Pressure
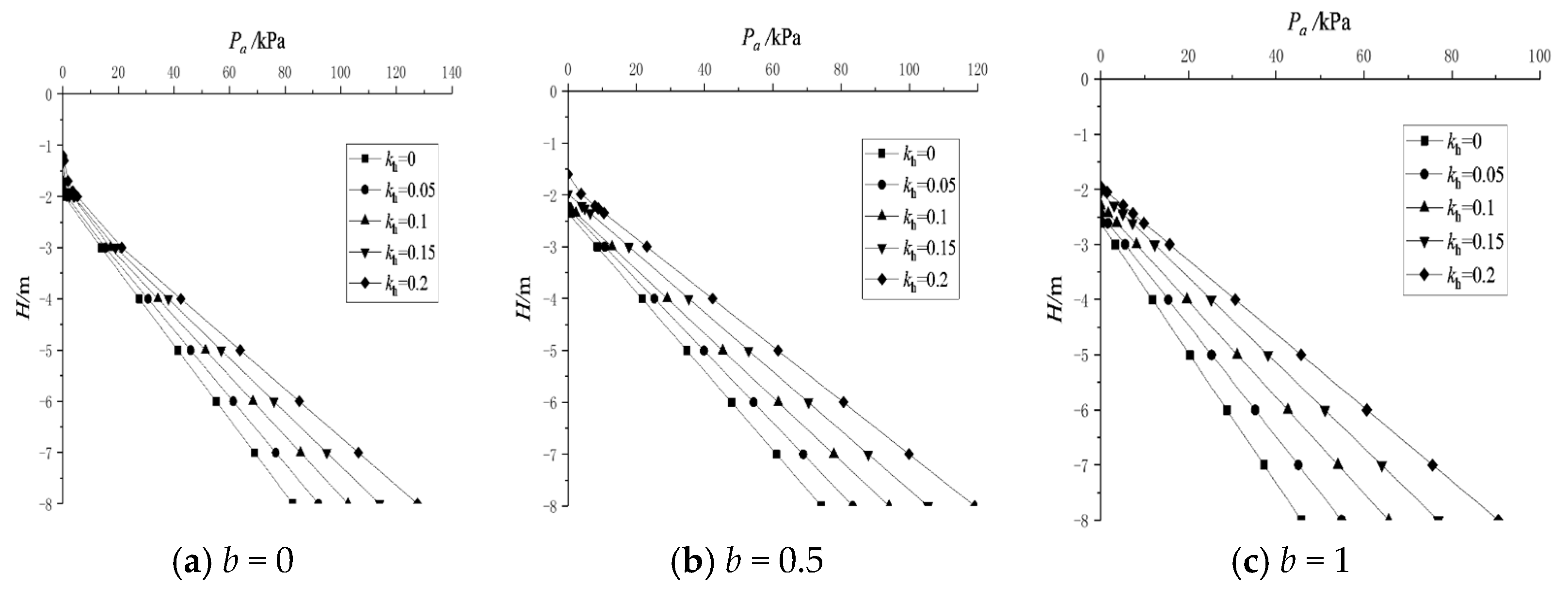
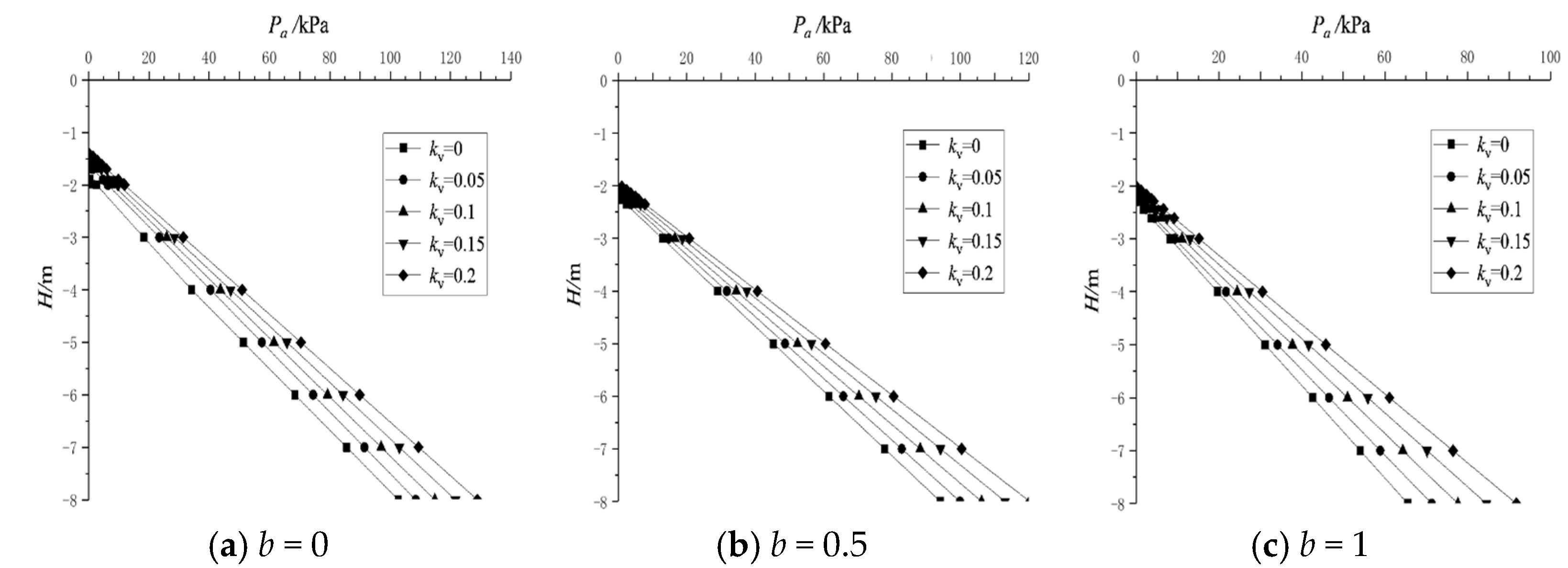
3.1.1. Effect of Seismic Coefficients
3.1.2. Effect of Unsaturation Parameters
3.2. Resultant Location of Seismic Active Earth Pressure
3.2.1. Effect of Seismic Coefficients
3.2.2. Effect of Unsaturation Parameters
3.3. Verification
3.3.1. Comparison with Classic Rankine Solution
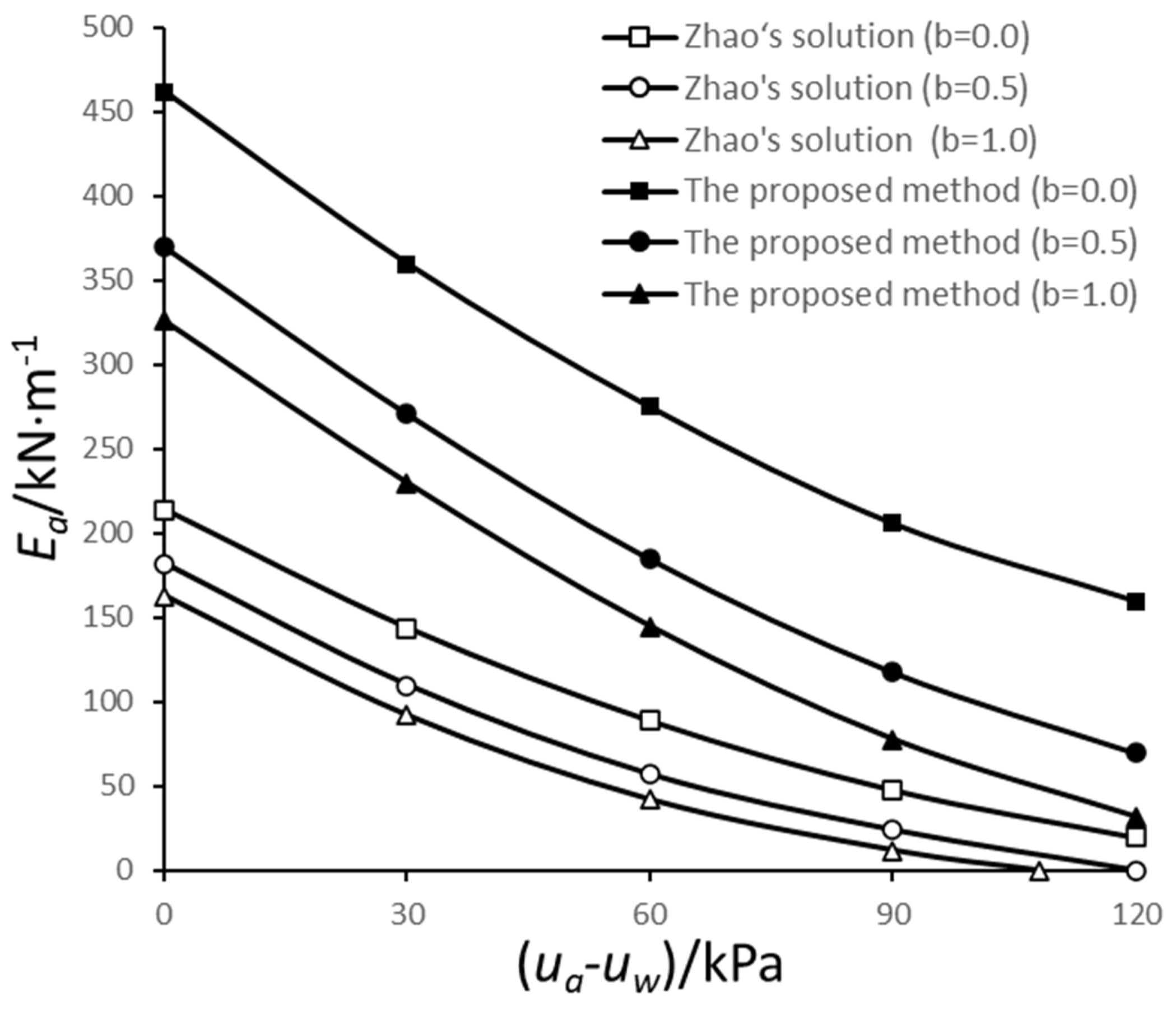
3.3.2. Comparison with Unsated Solution
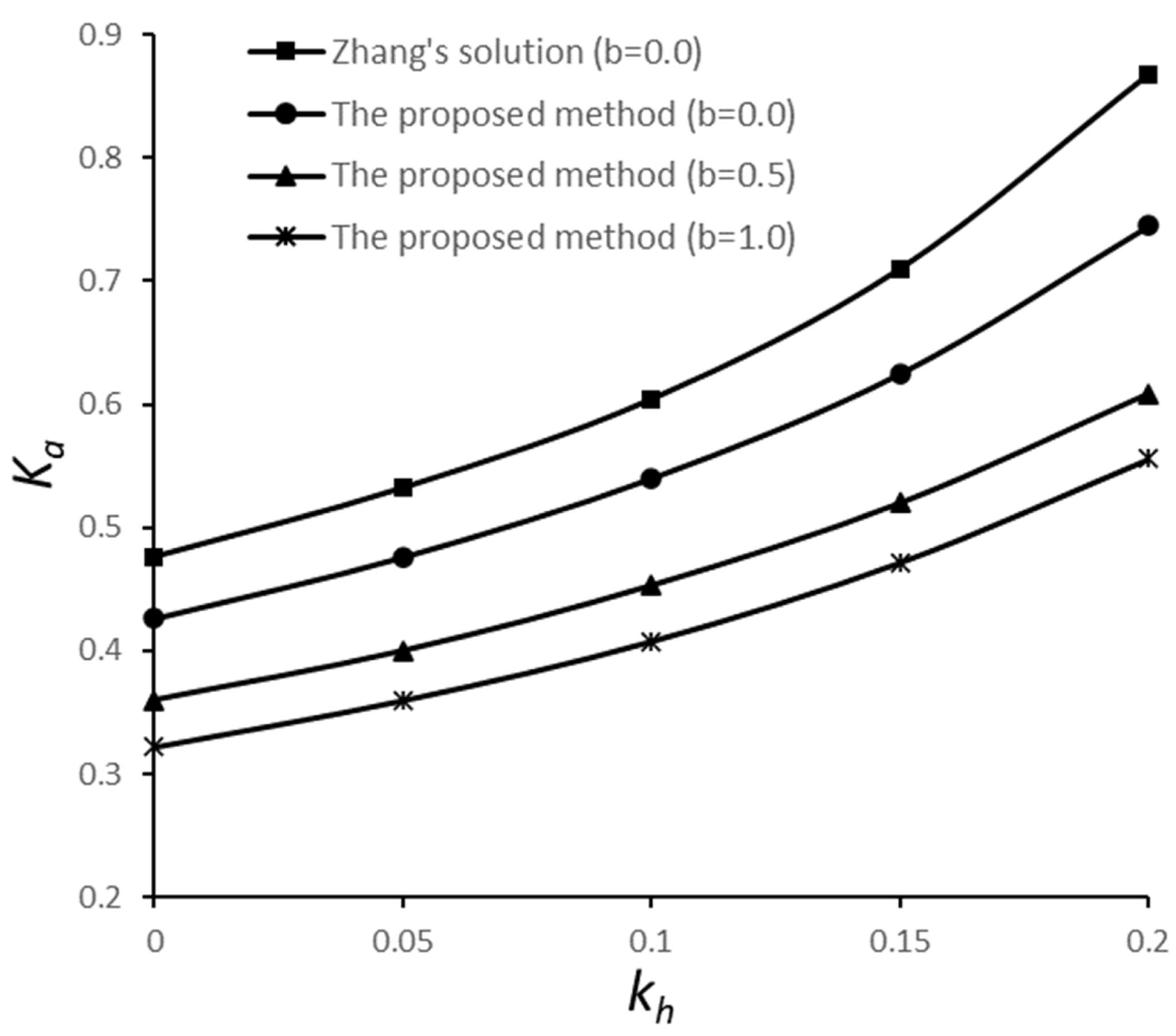
3.3.3. Comparison with Seismic Solution
4. Conclusions
- (1)
- By combining the shear strength model of unsaturated soil and the unified strength theory, the calculation model of seismic active earth pressure for unsaturated inclined backfill was deduced. The proposed method could be simplified to those in the previous literature under certain conditions. It extends the application range of the classic Rankine theory by taking earthquake, unsated soil, inclined rough wall back, non-horizontal backfill surface, and the intermediate principal stress into consideration.
- (2)
- As the seismic coefficients increase, the intensity of the Rankine active earth pressure will become larger. The earth pressure at 4 m depth with b = 0.5 and kv = 0 increased by 35% when kh increased from 0 to 0.1. With the decrease of the seismic coefficients or increase of the unified strength factor, the acting scope of Rankine active earth pressure moves downward slightly and the intensity reduces. The earth pressure at 4 m depth with kh = 0.1 and kv = 0.1 decreased by 44% when b increased from 0 to 1.
- (3)
- The horizontal seismic coefficient had a more significant effect on the resultant point location. For instance, in the case of kh = 0.1 and b = 1, the resultant point of earth pressure varied from 2.20 m to 2.31 m when kv increased from 0 to 0.2. Comparatively, for kv = 0.1 and b = 1, the resultant point moved from 2.08 m to 2.38 m when kh increased from 0 to 0.2. The intermediate principal stress caused a reduction of resultant acting height as well. In the case of (ua−uw) = 30 kPa and φb = 14°, the resultant point moved downwardly from 2.43 m to 2.02 m when the intermediate principal stress was taken fully into consideration.
- (4)
- As verification shows, the proposed model and algorithm are fit for seismic or unsaturated conditions. Owing to the scarce examples reported in the research subdivision, the validity of the proposed solution needs to be further examined by more examples. In any case, due to the consideration of the intermediate principal stress in the soil, the calculation result would be closer to the real solution theoretically. However, since it is difficult to determine an objective and accurate value for the unified strength factor (b), the solution is still a certain distance from engineering application, and more comparative research should be performed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| F and F′ | are yield functions under different stress conditions |
| σ | is the total normal stress |
| σ1, σ2 and σ3 | are the principal stresses and σ1 ≥ σ2 ≥ σ3 |
| ua and uw | are the pore air pressure and pore water pressure |
| σt and σc | are the tensile strength and compressive strength of the filling |
| τf | is the shear strength of unsaturated soil |
| c′ and φ′ | are the effective cohesion and effective friction angle of the saturated soil |
| φb | is the friction angle attributed by the matric suction |
| c′t and φ′t | are unified effective cohesion and unified effective friction angle |
| φbt | is the unified friction angle attributed by the matric suction |
| b | is the unified strength factor (0 ≤ b ≤ 1) |
| ctt | is the apparent cohesion |
| H | is the wall height |
| β | is the dip angle of backfill |
| δ | is the interface friction angle between the retaining wall and the backfill |
| α | is the inclination of wall back |
| kh and kv | are horizontal and vertical seismic coefficients |
| Ea | is the resultant force of the active earth pressure |
| pa | is the earth pressure intensity |
| Ka | is the active earth pressure coefficient |
| (σv−ua) and (σh−ua) | are the net normal stresses acting in different direction |
| d0a | is the gravitational distance from the resultant action position to the bottom |
| z0a | is the crack depth |
| η | is the seismic angle |
| γ | is the volumetric weight of the backfill |
References
- Hu, H.; Yang, M.; Lin, P.; Lin, X. Passive Earth Pressures on Retaining Walls for Pit-in-Pit Excavations. IEEE Access 2018, 7, 5918–5931. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Liu, X.X.; Wang, W.W. Calculation of nonlimit active earth pressure against rigid retaining wall rotating about base. Appl. Sci. 2022, 12, 9638. [Google Scholar] [CrossRef]
- Pufahl, D.E.; Fredlund, D.G.; Rahardjo, H. Lateral earth pressures in expansive clay soils. Can. Geotech. J. 1983, 5, 134–146. [Google Scholar] [CrossRef]
- Fu, D.; Yang, M.; Deng, B.; Gong, H. Estimation of active earth pressure for narrow unsaturated backfills considering soil arching effect and interlayer shear stress. Sustainability 2022, 14, 12699. [Google Scholar] [CrossRef]
- Ren, C.J.; Jia, H.B. The influence of Unsaturated Soil’s Characteristics on Rankine Earth Pressure. Sci. Technol. Eng. 2015, 15, 78–82. [Google Scholar]
- Yao, P.F.; Zhang, M.; Dai, R. Generic Rankine theory for unsaturated soils. J. Eng. Geol. 2004, 12, 285–291. [Google Scholar]
- Zhang, C.G.; Zhao, J.H.; Zhang, D.F. Nonlinearity of unsaturated soils strength and its influence on passive earth pressure. Journal of Guangxi University: Nat. Sci. Ed. 2012, 37, 797–802. [Google Scholar]
- Wang, D.J.; Tong, L.Y.; Qiu, Y.F. Rankine’s earth pressure analysis of unsaturated soil under condition of rainfall infiltration. Rock Soil Mech. 2013, 34, 3192–3194. [Google Scholar]
- Zhang, J.; Hu, R.L.; Yu, W.L. Sensitivity analysis of parameters of Rankine’s earth pressure with inclined surface considering intermediate principal stress. Chin. J. Geotech. Eng. 2010, 32, 1566–1572. [Google Scholar]
- Zhao, J.H.; Yin, J.; Zhang, C.G. Unified solutions of Rankine’s earth pressure of unsaturated soil under rainfall. J. Archit. Civ. Eng. 2016, 33, 1–6. [Google Scholar]
- Zhang, C.G.; Zhang, Q.H.; Zhao, J.H. Unified solutions of shear strength and earth pressure for unsaturated soils. Rock Soil Mech. 2010, 31, 1871–1876. [Google Scholar]
- Iskander, M.; Omidvar, M.; Elsherif, O. Conjugate stress approach for Rankine seismic active earth pressure in cohesionless soils. J. Geotech. Geoenviron. Eng. 2012, 139, 1205–1210. [Google Scholar] [CrossRef]
- Lin, Y.L.; Yang, G.L.; Zhao, L.H. Horizontal slices analysis method for seismic earth pressure calculation. Rock Soil Mech. 2010, 29, 2581–2591. [Google Scholar]
- Sun, Y. Unified solution of seismic active earth pressure and its distribution on a retaining wall. Rock Soil Mech. 2012, 33, 255–261. [Google Scholar]
- Zhang, G.X. New analysis method of seismic active earth pressure and its distribution on a retaining wall. Rock Soil Mech. 2014, 35, 335–339. [Google Scholar]
- Shi, Y.Q.; Xie, X.L.; Zhang, Q.K.; Jiang, H.; Peng, J.J.; Liao, X. Study on spectrum characteristics of dynamic earth pressure of loess landslides based on wavelet transform. Chin. J. Rock Mech. Eng. 2020, 39, 2570–2581. [Google Scholar]
- Liu, H.; Kong, D.Z.; Gan, W.S.; Wang, B.J. Seismic active earth pressure of limited backfill with curved slip surface considering intermediate principal stresses. Appl. Sci. 2022, 12, 169. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some aspects of effective stress in saturated soils. Geotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Fredlund, D.C.; Morgenstem, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.Z.; Hu, R.L. Analysis of seismic active earth pressure of backfill with infinite inclined surface behind non-vertical retaining wall. Rock Soil Mech. 2017, 38, 1069–1075. [Google Scholar]
- Zhao, J.H.; Liang, W.B.; Zhang, C.G. Unified solutions of Coulomb’s active earth pressure for unsaturated soils. Rock Soil Mech. 2013, 34, 609–615. [Google Scholar]



| H/m | (ua − uw)/kPa | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 30 | 60 | 90 | 120 | 0 | 30 | 60 | 90 | 120 | 0 | 30 | 60 | 90 | 120 | |
| b = 0 | b = 0.5 | b = 1 | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3.43 | 0 | 0 | 0 | 0 | 2.01 | 0 | 0 | 0 | 0 | 1.64 | 0 | 0 | 0 | 0 |
| 2 | 16.13 | 6.06 | 0 | 0 | 0 | 10.25 | 4.05 | 0 | 0 | 0 | 9.30 | 0 | 0 | 0 | 0 |
| 3 | 29.84 | 23.89 | 12.61 | 0 | 0 | 25.50 | 21.80 | 10.88 | 0 | 0 | 19.76 | 16.43 | 9.69 | 0 | 0 |
| 4 | 46.54 | 41.71 | 29.21 | 15.35 | 2.08 | 44.75 | 39.55 | 27.38 | 0 | 0 | 32.33 | 27.94 | 17.03 | 0 | 0 |
| 5 | 65.24 | 59.53 | 45.81 | 32.86 | 12.94 | 60.4 | 55.30 | 40.88 | 16.56 | 9.79 | 46.89 | 37.44 | 24.37 | 12.99 | 6.23 |
| 6 | 85.39 | 77.36 | 62.40 | 50.37 | 28.26 | 77.25 | 73.05 | 58.39 | 33.28 | 24.41 | 57.45 | 46.94 | 31.71 | 18.36 | 11.62 |
| 7 | 104.1 | 95.18 | 79.00 | 67.88 | 46.14 | 101.4 | 91.80 | 72.89 | 50.00 | 39.02 | 75.02 | 56.44 | 39.05 | 23.73 | 18.15 |
| 8 | 131.3 | 113.0 | 95.60 | 85.38 | 67.55 | 129.7 | 109.5 | 92.39 | 66.73 | 53.63 | 90.58 | 65.95 | 46.39 | 29.10 | 21.51 |
| H/m | φb/° | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 13 | 16 | 19 | 22 | 10 | 13 | 16 | 19 | 22 | 10 | 13 | 16 | 19 | 22 | |
| b = 0 | b = 0.5 | b = 1 | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 4.66 | 0 | 0 | 0 | 0 | 3.12 | 0 | 0 | 0 | 0 | 1.29 | 0 | 0 | 0 | 0 |
| 2 | 11.4 | 5.18 | 3.94 | 2.6 | 1.54 | 14.39 | 4.17 | 2.49 | 1.37 | 0.69 | 5.55 | 0 | 0 | 0 | 0 |
| 3 | 29.23 | 23.0 | 21.77 | 20.43 | 19.37 | 31.14 | 20.92 | 20.32 | 19.2 | 18.52 | 15.01 | 9.99 | 12.43 | 10.43 | 8.52 |
| 4 | 47.05 | 40.8 | 39.59 | 38.25 | 37.19 | 47.89 | 38.67 | 38.14 | 37.02 | 36.34 | 27.68 | 22.5 | 21.94 | 19.94 | 18.03 |
| 5 | 64.87 | 58.6 | 57.41 | 56.07 | 55.01 | 64.64 | 54.42 | 55.96 | 54.84 | 54.16 | 38.44 | 34.6 | 31.44 | 29.44 | 27.53 |
| 6 | 82.7 | 76.4 | 75.24 | 73.9 | 72.84 | 81.39 | 72.17 | 73.79 | 72.67 | 71.99 | 52.3 | 44.5 | 40.94 | 38.94 | 37.03 |
| 7 | 100.5 | 94.30 | 93.06 | 91.72 | 90.66 | 98.14 | 90.92 | 91.61 | 90.49 | 89.81 | 65.47 | 54.01 | 50.45 | 48.45 | 46.54 |
| 8 | 118.3 | 112.1 | 110.8 | 109.5 | 108.4 | 114.8 | 108.6 | 109.3 | 108.2 | 107.5 | 83.33 | 64.51 | 59.95 | 57.95 | 56.04 |
| kv | kh | d0a/m | kv | kh | d0a/m | ||||
|---|---|---|---|---|---|---|---|---|---|
| b = 0 | b = 0.5 | b = 1 | b = 0 | b = 0.5 | b = 1 | ||||
| 0 | 0.1 | 2.43 | 2.24 | 2.2 | 0.1 | 0 | 2.34 | 2.16 | 2.08 |
| 0.05 | 0.1 | 2.46 | 2.26 | 2.22 | 0.1 | 0.05 | 2.43 | 2.22 | 2.17 |
| 0.1 | 0.1 | 2.5 | 2.29 | 2.25 | 0.1 | 0.1 | 2.5 | 2.29 | 2.25 |
| 0.15 | 0.1 | 2.52 | 2.32 | 2.28 | 0.1 | 0.15 | 2.56 | 2.37 | 2.31 |
| 0.2 | 0.1 | 2.55 | 2.37 | 2.31 | 0.1 | 0.2 | 2.63 | 2.43 | 2.38 |
| (ua−uw)/kPa | φb/° | d0a/m | (ua − uw)/kPa | φb/° | d0a/m | ||||
|---|---|---|---|---|---|---|---|---|---|
| b = 0 | b = 0.5 | b = 1 | b = 0 | b = 0.5 | b = 1 | ||||
| 0 | 14 | 2.69 | 2.48 | 2.23 | 30 | 10 | 2.52 | 2.31 | 2.1 |
| 30 | 14 | 2.43 | 2.24 | 2.02 | 30 | 13 | 2.45 | 2.26 | 2.05 |
| 60 | 14 | 2.2 | 2.03 | 1.78 | 30 | 16 | 2.38 | 2.2 | 1.98 |
| 90 | 14 | 1.86 | 1.71 | 1.49 | 30 | 19 | 2.31 | 2.13 | 1.9 |
| 120 | 14 | 1.57 | 1.43 | 1.22 | 30 | 22 | 2.23 | 2.02 | 1.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.; Shen, H.; Li, W.; Wang, Y. Rankine Active Earth Pressure of Unsaturated Filling under Earthquake. Appl. Sci. 2023, 13, 1398. https://doi.org/10.3390/app13031398
Fang W, Shen H, Li W, Wang Y. Rankine Active Earth Pressure of Unsaturated Filling under Earthquake. Applied Sciences. 2023; 13(3):1398. https://doi.org/10.3390/app13031398
Chicago/Turabian StyleFang, Wei, Hongyu Shen, Wan Li, and Yiwei Wang. 2023. "Rankine Active Earth Pressure of Unsaturated Filling under Earthquake" Applied Sciences 13, no. 3: 1398. https://doi.org/10.3390/app13031398
APA StyleFang, W., Shen, H., Li, W., & Wang, Y. (2023). Rankine Active Earth Pressure of Unsaturated Filling under Earthquake. Applied Sciences, 13(3), 1398. https://doi.org/10.3390/app13031398








