1. Introduction
In mass-start bicycle racing, because cyclists travel at comparatively high speeds, the aerodynamic drag is a critical factor that influences the outcome of competitions [
1]. Therefore, cyclists form dense groups to avoid air resistance. A cyclist running behind another cyclist, called drafting, can reduce air resistance and save energy consumption; however, a cyclist running ahead as a leader receives more air resistance than those behind. Consequently, cooperative behavior, considered altruistic behavior, occurs among cyclists in a self-organizing manner, rotating and taking turns at the front. In contrast, cooperation and self-interested behavior are required to win a competition. A points race held in a cycling velodrome is a competition for accumulated points following the sprint laps held for every specified lap, in this case, every 10th lap. Here, there are several opportunities to receive points; hence, the groups of cyclists constantly switch between cooperative (altruistic) and non-cooperative (self-centered) behaviors and are repeatedly separated and recombined in the race [
2].
Many studies on the self-organization of group organisms have been conducted by analyzing groups of insects and animals, such as swarm flocks and herds [
3]. These organisms engage in behaviors advantageous for survival by forming groups to reduce energy consumption during movement and their predation probability. Mathematical models have been used to understand the formation of animal groups [
4,
5]. In contrast, other studies show that animal group collective dynamics are determined in part by an order parameter or collective variable representing the entire group’s state and control parameters that influence the state order. To understand these order and control parameters, studies have been conducted to identify animal group dynamics by quantifying the behaviors of individual animals within their collectives. For example, Ballerini et al. [
6] studied bird flocks and observed that individual birds exhibited anisotropic tendencies in the direction of their nearest neighbors relative to the motion of the entire flock. Cavagna et al. [
7] analyzed the velocity of each individual in large flocks of starlings and found a scale-free behavioral correlation between the average motion and the flock size. Thus, the system of groups has an order parameter or collective variable that represents the entire group’s state and control parameters that influence the state order. Trenchard and Perc reviewed collective behavior based on drafting in biological and non-biological systems [
8].
Helbing et al. [
9] verified a pedestrian crowd simulation that used a social force model with experimental data under various environments, such as bottlenecks and intersections in human crowds. Murakami et al. [
10] showed that lane formation was inhibited by the people whose attention was obstructed by the smartphone task and that mutual anticipation affected their self-organization. These studies suggest that variables represent the order of the human groups and are influenced by the control parameters.
Okumura, Yokoyama, and Yamamoto [
2] recorded points races that repeated separation and recombination, quantified the configuration of cyclists, and analyzed their state transitions using principal component analysis. The four states, including a dense group, stretched group, a divided group, and an escape group far from a single dense group, were defined in each quadrant on the plane with the first and second principal components. Most state transitions stayed in the same state and transitioned to the adjacent state. However, it is unclear what variables affect the state transition in bicycle racing and how separation and recombination occur.
Trenchard et al. [
11] analyzed mass-start bicycle races in the velodrome and identified the phase state of the cycling peloton, which is a group of cyclists, such as the high-density compact phase and low-density stretched phase. Trenchard et al. [
12] simulated a peloton applying experimental data in a points race and discussed the importance of cyclists’ maximal sustainable outputs (MSO) in terms of power output, the proportion of the current power output to cyclists’ MSOs in both the front and drafting positions, and how these factors affect peloton configurations. These factors are the principal control factors that determine peloton configurations. Trenchard [
13] refined the description of the stretched phase in terms of the mathematical model described by Trenchard et al. [
11,
12], that is, as occurring within the term of their PCR (peloton conversion ratio) equation. However, the dynamics of group separation and recombination in cycling races have not yet been analyzed in detail.
Studies of bird flocks have used the function of the velocity of individuals as a variable to represent the population order, such as the polarization of the group’s direction [
5]. During velodrome cycling competitions, the direction of travel is determined in one direction. Therefore, the velocity of the cyclist running at the head of each group may reasonably be the representing variable of the movement of each group; the velocity of the cyclist who leads the whole and, if there is an escape group, the velocity of the leading cyclist of the main group, which is the largest group, would be the representation of the group state. Additionally, the relative speed difference between the leading cyclist and the leading cyclist in the main group is also considered a promising candidate for a descriptive variable affecting the state transition in the cycling race. Furthermore, the time difference between the escape group and the main group is represented by the group state. In previous research, Trenchard et al. correlated the peloton phase to cyclists’ power output [
11]. The cyclists’ MSO in the leading position and drafting position were determinant variables of phase states and their transitions. However, since MSO is unknown information during the racing competition, and the external power to overcome air resistance is proportional to the cube of speed [
14], speed can be used as alternative information for MSO to describe the phase state and transition of bicycle racing. Therefore, we firstly hypothesize that the velocity of the leading cyclist, the velocity of the cyclist in the main group, their speed difference, and the time difference are the candidate descriptive variables for the state transition of groups in the cycling competition, wherein the groups separate and recombine.
Hysteresis often presents in the change in order based on self-organization [
15,
16]. Hysteresis is the dependence on the state of the system concerning history. In human movement, Kelso [
17] found that a phase transition from anti-phase to in-phase occurs in the movement coordination within an individual; however, an in-phase to anti-phase transition could not occur, suggesting hysteresis. Schmidt et al. [
18] also showed that hysteresis occurs during the coordination task of leg movements between two individuals sitting on each other, switching between two modes (in-phase and anti-phase synchronization). Aoi et al. [
19] verified the hysteresis in the phase transition of gait with four legs by using a robot. In the sports events, Yamamoto and Gohara [
20] showed a third-order sequence effect due to hysteresis in the continuously repeated switching of the forehand and backhand tennis strokes. Sørensen, Ingvaldsen, and Whiting [
21] also showed that hysteresis occurs in selecting fore-backhand strokes for table tennis. This hysteresis occurs as two discrete processes measured separately from each other. Besides these examples, hysteresis can occur as an asymmetry in one continuous dynamical process, for example, vehicle traffic hysteresis [
22].
Trenchard examined hysteresis in a peloton applying the definition in vehicle traffic [
23]. He identified three forms of hysteresis using flow analyses based on vehicle traffic research. Specifically, the second of the three was based on the observation of a points race resulting from rapid acceleration followed by periods of decreasing speeds and decreasing the number of cyclists over time. A phenomenon such as hysteresis can be observed in cycling competitions for the state transition; it is believed there is an asymmetry in the separation and recombination of the cycling group and dependence on history as two discrete processes. Okumura, Yokoyama, and Yamamoto [
2] quantified the cyclists’ global configuration in the points race, including the separated groups, and identified the group states using the principal component analysis results. It is unclear whether hysteresis occurs in the separation–recombining transition in the points race. Therefore, we secondly hypothesize the existence of a phenomenon such as a hysteresis in the separation and recombination of groups in cycling competition.
This study aimed to verify the hypothesis that the descriptive parameters related to the order change of group separation and recombination in the points race are the velocity of the leading cyclist, the velocity of the leader of the main group, the difference between their velocities, and their time difference. The study also verifies the hypothesis of whether group separation and recombination show asymmetric phenomena such as hysteresis.
4. Discussion
This study examined the descriptive parameter related to the global state transition of group separation and recombination and the hysteresis concerning the global state transitions.
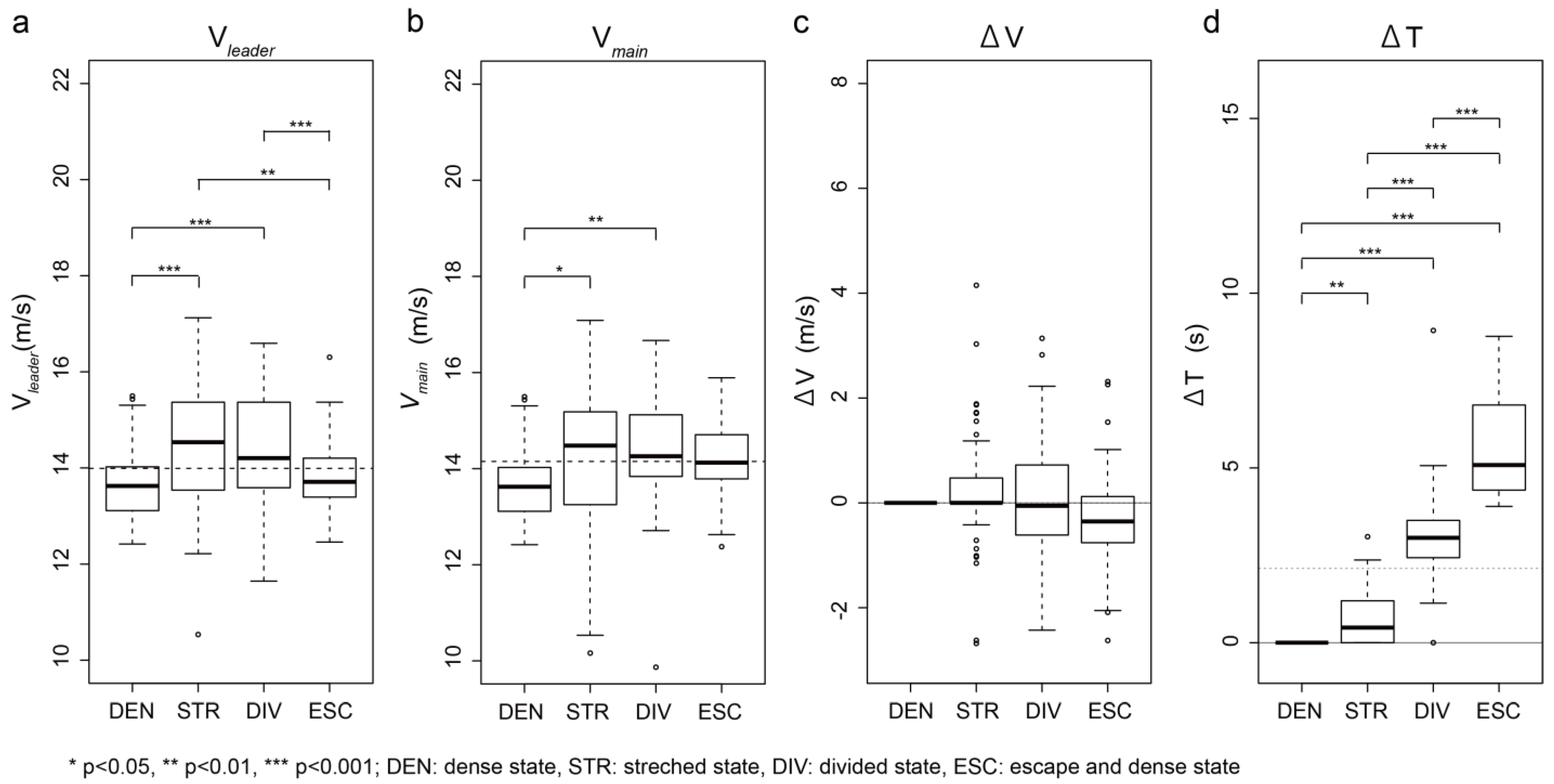
In the candidate descriptive parameters analysis in each global state, including the stretched and divided state, the speed of the leading cyclist (V
leader) was higher than in other states (
Figure 1a). The speed of a leading cyclist may be too high for the follower to sustain when approaching maximal sustainable output when the group stretches or separates. According to Trenchard et al. [
11], group separation in a cycling race occurs when a drafting or following cyclist cannot sustain the pace of the leading rider even by drafting. Therefore, group stretch and separation are a consequence of increases in competition speeds that approach cyclists’ maximal sustainable outputs. The time differences between the leader and the front of the main group (ΔT) became larger following the state transition from dense to stretched, divided, and escape and dense state. This suggests that time difference could be regarded as an order parameter corresponding to the global state transition defined by Okumura, Yokoyama, and Yamamoto [
2].
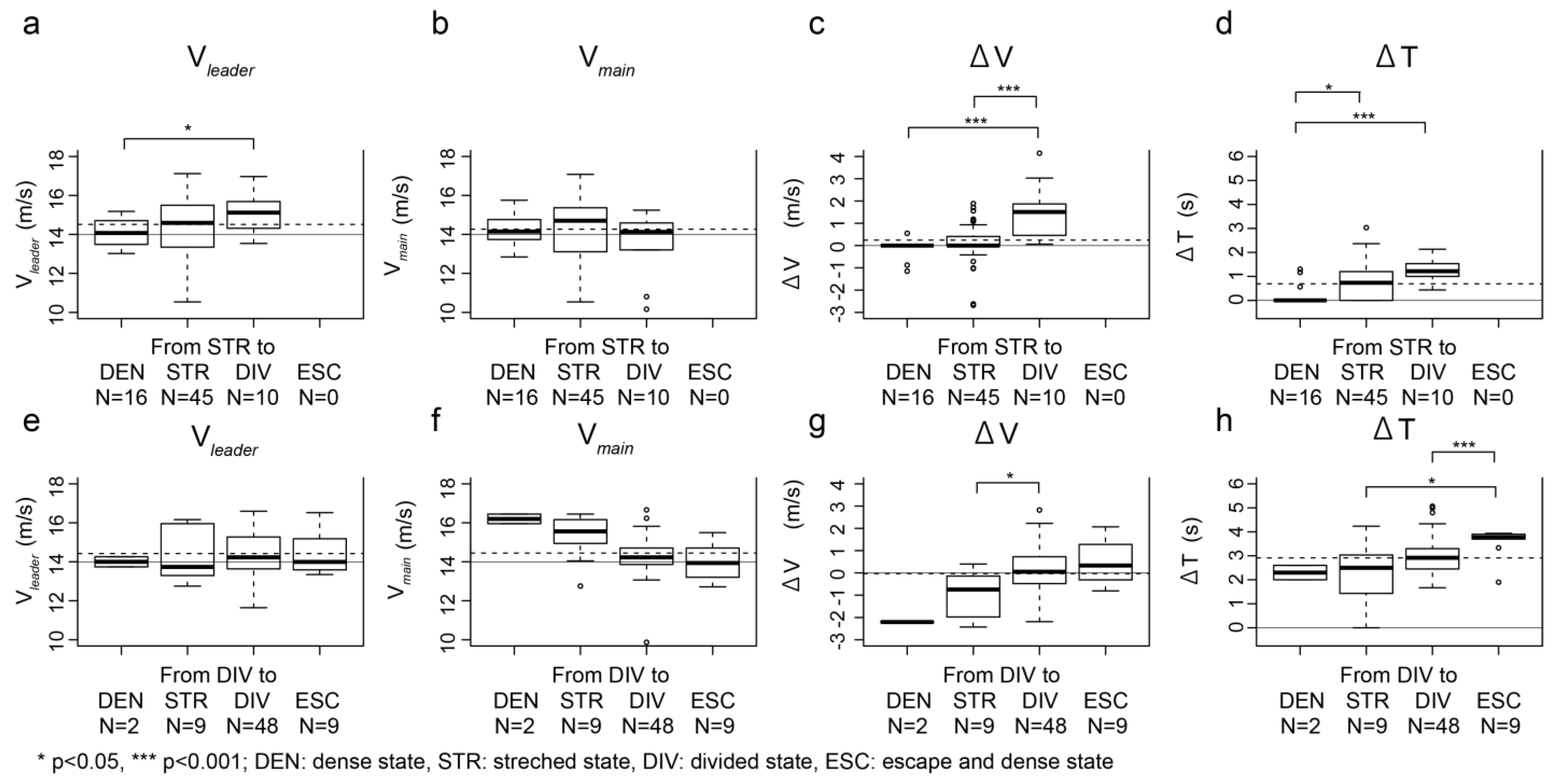
When focusing on the separation and recombination, there was a significant speed difference between the speed of the leading cyclist and the velocity of the front of the main group (ΔV); that is, there was a significant difference between the case where the state was maintained and the case where the group was separated from a stretched to divided state, or the group was recombined from a divided to stretched state (
Figure 2c,g). However, the speed of the leading cyclist did not significantly differ between the separation and recombination (
Figure 2a,e). The time difference between the speed of the leading cyclist and the velocity of the front of the main group was considered to have a relative relationship between the speed of the leader and the main group.
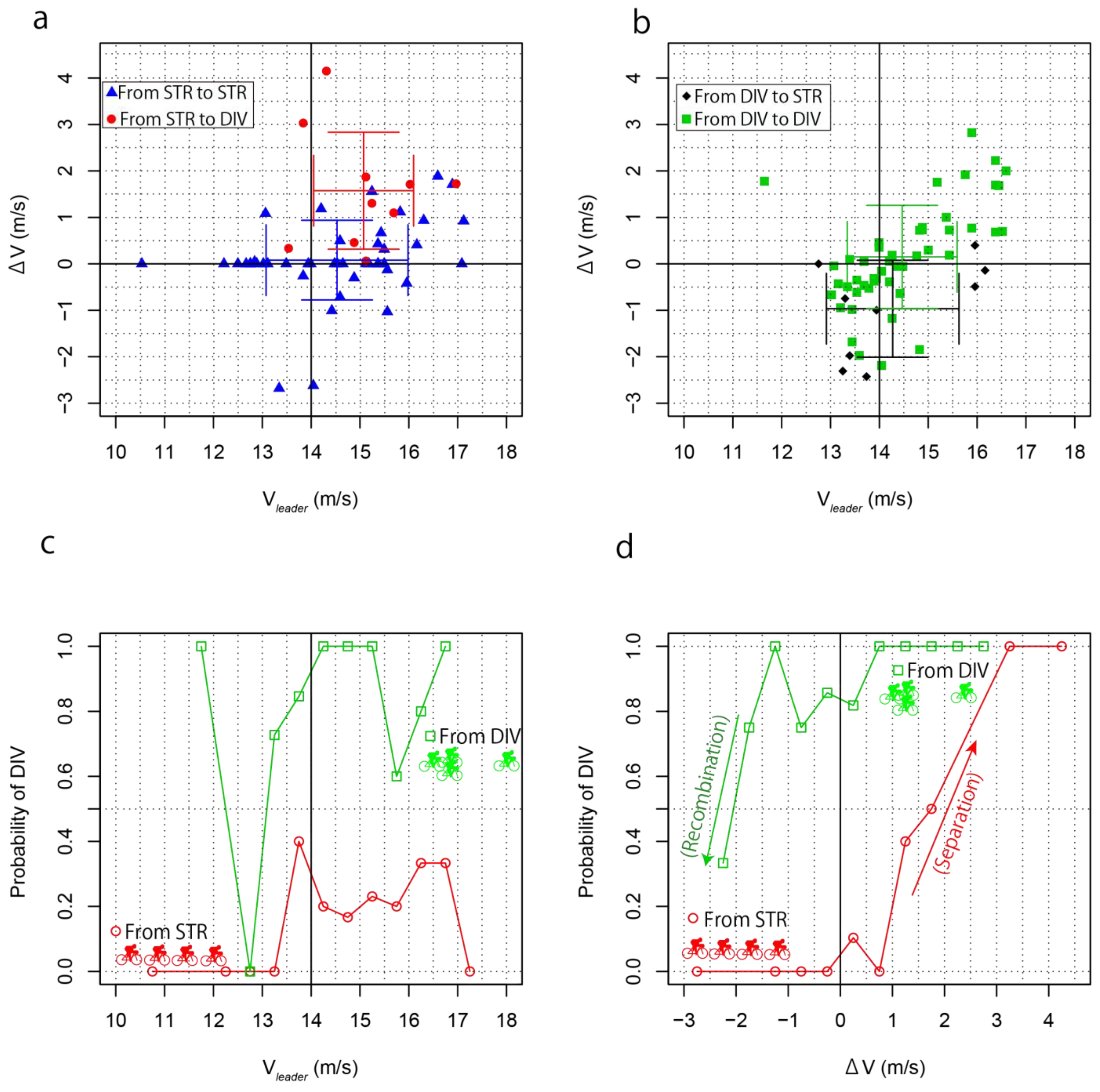
To examine the relationship between the speed of the leader and the main group, this study analyzed the speed of the leader and the speed difference between the leader and the main group when the group separated, the stretched group was maintained, the group rejoined, and the divided state was maintained. When the group was separated, the leader’s velocity tended to be higher, and the speed difference was positive; that is, the leader tended to be faster than the main group compared to when the group remained stretched and was not divided. This suggests that for the group to be separated, it is necessary to make a difference in velocity and increase the velocity. When speeds are low relative to cyclists’ maximal speed capabilities, it is challenging for cyclists to “attack” and escape from the group because chasing cyclists have abundant energy to chase the attacker and to reduce any separations generated by the attacking cyclist. Accelerating to 14 m/s or more and escaping from the group requires a further speed difference of 1.0 m/s or more; that is, to escape from a pack, an attacking cyclist needs to attain speeds at least 1.0 m/s more than the followers. However, our observation was of an elite-level men’s velodrome race; hence, this may be applicable only to narrow circumstances. Trenchard [
13] introduced a random acceleration parameter (RAP) in the range of 0.0–2.0 m/s to the simulation of a cycling competition. RAP is a random acceleration added to the velocity of each agent, which was incorporated into a general algorithm based on a simulation of a flock of birds [
11] to better reproduce a cycling competition. In Trenchard’s simulation, RAP simulated cyclists’ adjustments in speed to generate passing between cyclists at comparatively low speeds, but RAP was not high enough to cause separations in the peloton. This suggests that the leader’s velocity and the speed difference between the leader and the main group were critically important to descriptive parameters for the separation and the recombination, partially supporting the first hypothesis.
Regarding the second hypothesis, we could find hysteresis in the separation and recombination state transitions. Trenchard did not account for group divisions for analysis of peloton hysteresis [
22]; however, our observation supports his observation. For instance, there was a rapid acceleration at about lap 9.5 up to lap 10, in which the peloton achieves a stretched state; this is followed by a gradual deceleration from laps 10 to 13, and all the while, the peloton remains in the stretched state (
Supporting Figure S1). This confirms the hysteresis identified by Trenchard involving asymmetric acceleration and deceleration epochs [
22]. The group separation was caused by the acceleration of the leading cyclist and the resulting increase in the speed difference from the main group, and the recombination of the groups was caused by the pursuit of the main group at speed faster than the leader. However, even though these variables were the same value, the separation and recombination of groups did not always occur (
Supporting Figure S1); that is, the state of the group was not uniquely determined by the speed difference between the leader and the main group, and the influence of the speed difference for separation or recombination depended on the group state at that time. This suggests that the group separation and recombination in a points race occur by different mechanisms. There are differences in cyclists’ conditions between a lap near the beginning of the race when cyclists are fresh and a lap halfway through the race when the cyclists may be starting to fatigue. This factor can affect hysteresis. For example, the transition from stretched state to divided state in LAP18.5 occurred in half a lap due to the velocity difference (>0) between the leader and the main group. In contrast, in the recombination in LAP60, the interval between the groups was shortened due to the speed difference (<0) between the leader and the main group; the interval between the groups was so vast that the divided state continued for one lap, and subsequently, the transition to the stretched state occurred (
Supporting Figure S2). This was related to the sprint lap of earning points, and the transition of the state of the group occurred depending on the group state at that time, and the group state is a combination of self-organized dynamics and top-down constraints due to competition rules [
25].
5. Conclusions
The group separation results from self-interested behavior in an attempt to score points in the second half of the tenth lap. The group recombination results from the termination of selfish non-cooperative behavior after earning points and the resumption of altruistic, cooperative behavior in the first half of ten laps. Considering conserving energy consumption, it is not necessary for the leader to have an extended time gap with the main group, and the large main group behind would also be recovering while conserving energy consumption. This suggests that the time gap required to sustain group separation is dependent upon relative fatigue between leading and following riders. To manage such time differences, cyclists must develop tactical skills and sufficient fitness to optimize their energy expenditures throughout a range of rapidly changing competitive circumstances. These suggest that the cyclists need the ability to choose an appropriate speed and distance from other cyclists depending on the situation, for example, remaining distance, remaining laps for the sprints, or the critical moment for success or not.
Since this study analyzed only one points race, future research needs to include the analysis of additional races in order to confirm our results. The accuracy of measuring speed is also one of the limitations of our study. We calculated the speed based on the time it took to complete the 125 m half lap. However, as the cyclist moves left and right and climbs the bank, the distance traveled changes. For more precise speed measurement, an instrument such as a speedometer should be used to measure. Furthermore, because cyclists are required to make instantaneous judgments, new methods for collecting all movements in such races need to be developed.