Simulation of Elastic Wave Propagation Based on Meshless Generalized Finite Difference Method with Uniform Random Nodes and Damping Boundary Condition

Abstract

When the grid-based finite difference (FD) method is used for elastic wavefield forward modeling, it is inevitable that the grid divisions will be inconsistent with the actual velocity interface, resulting in problems related to the stepped grid diffraction and inaccurate travel time of reflected waves. The generalized finite difference method (GFDM), which is based on the Taylor series expansion and weighted least square fitting, solves these problems. The partial derivative of the unknown parameters in the differential equation is represented by the linear combination of the function values of adjacent nodes. In this study, the Poisson disk node generation algorithm and the centroid Voronoi node adjustment algorithm were combined to obtain an even and random node distribution. The generated nodes fit the internal boundary more accurately for model discretization, without the presence of diffracted waves caused by the stepped grid. To avoid the instability caused by the introduction of boundary conditions, a Cerjan damping boundary condition was proposed for boundary reflection processing. The test results generated by the different models showed that the generalized finite difference method can effectively solve the problems related to inaccurate travel time of reflection waves and stepped grid diffraction.

1. Introduction

Elastic wave numerical simulation is an important means by which to study the law of seismic wave propagation within the ground, and it plays a vital role in the whole process of seismic exploration, including data acquisition, processing, and interpretation. Many numerical simulation methods, including the finite element [1,2], finite difference [3,4,5], spectral element [6], and pseudo spectral [7] methods have been successfully applied to elastic wave forward modeling. The staggered grid finite difference method (SGFD) is widely used in the forward modeling of elastic wave equations owing to its high calculation efficiency, high accuracy, and convenient implementation process. However, there are two problems with SGFD. One is that the fixed grid step may discretize the interface to the wrong depth, resulting in an inaccurate travel time for the reflected waves. The second is that a stepped interface will appear when the undulating interface is discretized with a regular grid, which will generate false diffracted waves. To eliminate grid diffraction, many scholars have carried out extensive research, including using variable grid algorithms [8], vertical grid mapping based on coordinate transformation [9], body fitted grids [10], and other methods. These methods effectively suppress stepped diffraction to a certain extent, but they also have problems. For example, the variable mesh algorithm essentially uses a smaller mesh step size to discretize the undulating interface, so it cannot fundamentally eliminate the stepped diffraction; the difference method based on coordinate transformation requires a corresponding transformation of the wave equation; and the implementation process is relatively complex.

In recent years, the meshless method, which avoids mesh generation, discretizes the solution area into a series of independent nodes and constructs approximate functions on these discrete nodes to obtain linear equations [11]. Since the nodes change flexibly with the velocity model, the meshless method can effectively avoid grid diffraction [12]. The generalized finite difference method is a meshless method with a simple principle, flexible node arrangement, and high calculation accuracy, and it has been widely used to solve a variety of mathematical and engineering problems [13,14,15]. Jensen (1972) first used the Taylor series expansion of several adjacent nodes around a center point, based on a distance function, to solve differential equations [16]. Later, Benito et al. (2001) developed the explicit formula of the generalized finite difference method [17]. Based on the Taylor series expansion and weighted least square fitting, the partial derivative of the unknown quantity in the differential equation is expressed as a linear combination of the function values of several adjacent nodes. Thus, the basic theory of the generalized finite difference method was formed. Since then, many scholars have improved the theory of this method and its implementation technology. For example, Benito and Ureña systematically analyzed various factors that affect the accuracy of the GFDM calculations, such as node generation [18,19], star of nodes shape [20], and weight function [17], and they pointed out that as the discretization (cloud of nodes) becomes more regular, the results obtained become more stable [21].

Ureña et al. (2011) first applied the generalized finite difference method to the forward modeling of elastic wave equations, and proposed an adaptive method to minimize the effect of the irregularity of node distributions on dispersion [22]; on this basis, Ureña et al. (2012) discussed the dispersion and stability of elastic wave forward modeling using the generalized finite difference method under regular and irregular node conditions [23]. Benito et al. (2013) further studied the generalized finite difference method for solving the problem of determining seismic wave propagation in homogeneous isotropic media [24]. Benito et al. (2015) discussed the influence of node settings on simulation accuracy using circular hole models with Dirichlet uniform boundary conditions and square hole model scatterers with free boundary conditions [25]. Benito et al. (2017) applied the generalized finite difference method (GFDM) to solve the problem of elastic wave propagation, and analyzed the influence of the type of node clouds (regular and irregular) on discretization [17]. Salete et al. (2017) put forward a generalized finite difference scheme to solve the two-dimensional seismic wave propagation problem with a perfectly matched layer absorption boundary, and discussed the stability of PML. They also pointed out that the stability condition at the boundary of PML is stricter than that in the internal computational domain [26].

In this study, the elastic wave equation was solved using the meshless generalized finite difference method. This method first discretizes the solution area into a series of independent nodes, and then constructs an approximate function for these discrete nodes based on the Taylor series expansion and weighted least squares fitting. Finally, it solves the linear system to obtain an approximate solution for the boundary value of the elastic wave equation. An algorithm combining the Poisson disk node generation algorithm and the centroid Voronoi node adjustment algorithm is suggested to improve the stability of the node “star”. The Cerjan damping boundary condition is introduced to avoid the instability caused by the absorbing boundary conditions. In some worked examples, the GFDM is compared with SGFD, and analytical solutions based on homogeneous, horizontal layered, undulating interface, and fault models are also tested.

2. Methodology

2.1. Elastic Wave Equation

The two-dimensional elastic wave equation can be expressed as:

$$\{\begin{array}{l}\rho \frac{{\partial }^2{u}_x}{\partial t^2}=\left(\lambda +2\mu \right)\frac{{\partial }^2{u}_x}{\partial x^2}+\left(\lambda +\mu \right)\frac{{\partial }^2{u}_z}{\partial x\partial z}+\mu \frac{{\partial }^2{u}_x}{{\partial }^{2}z}+f_x\\ \rho \frac{{\partial }^2{u}_z}{\partial t^2}=\mu \frac{{\partial }^2{u}_z}{\partial x^2}+\left(\lambda +\mu \right)\frac{{\partial }^2{u}_x}{\partial x\partial z}+\left(\lambda +2\mu \right)\frac{{\partial }^2{u}_z}{\partial z^2}+f_z\end{array}$$

(1)

where $t$ is the time, $\rho$ is the density of the medium, $\lambda$ and $\mu$ are Lame constants, $\lambda =\rho \left(v_p^2-2v_s^2\right)$, $\mu =\rho v_s^2$, $v_p$, and $v_s$ are the velocities of compressional and shear waves, $u_x$ and $u_z$ represent displacement in the $x$ and $z$ directions, and $f_x$ and $f_z$ represent source terms in the $x$ and $z$ directions.

2.2. Central Difference for Time Partial Derivative Approximation

The displacement at time $t+\Delta t$ and $t-\Delta t$ can be expanded at time $t$ via the Taylor series:

$$u(t+\Delta t)=u(t)+\Delta t\frac{\partial u(t)}{\partial t}+\frac{{\left(\Delta t\right)}^2}{2!}\frac{{\partial }^{2}u(t)}{\partial t^2}+\frac{{\left(\Delta t\right)}^3}{3!}\frac{{\partial }^{3}u(t)}{\partial t^3}+\dots$$

(2)

$$u(t-\Delta t)=u(t)-\Delta t\frac{\partial u(t)}{\partial t}+\frac{{\left(\Delta t\right)}^2}{2!}\frac{{\partial }^{2}u(t)}{\partial t^2}-\frac{{\left(\Delta t\right)}^3}{3!}\frac{{\partial }^{3}u(t)}{\partial t^3}+\dots$$

(3)

Truncating the 2M-order obtains the central difference expression:

$$u(t+\Delta t)=2u(t)-u(t-\Delta t)+2{\displaystyle \sum _{m=1}^M\frac{\Delta t^{2m}}{2m!}}\frac{{\partial }^{2m}u(t)}{\partial t^{2m}}+O\left(\Delta t^M\right)$$

(4)

When $M=1$, then:

$$u(t+\Delta t)=2u(t)-u(t-\Delta t)+\Delta t^2\frac{{\partial }^{2}u(t)}{\partial t^2}+O\left(\Delta t^2\right)$$

(5)

The time partial derivatives ${\partial }^2{u}_x\left(t\right)/\partial t^2$ and ${\partial }^2{u}_z\left(t\right)/\partial t^2$ in Equation (1) can be converted using Equation (5) into the following form:

$$\{\begin{array}{l}{u}_x\left(t+\Delta t\right)=2u_x\left(t\right)-u_x\left(t-\Delta t\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+\Delta t^2\left[\frac{\lambda +2\mu }{\rho }\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{\mu }{\rho }\frac{{\partial }^2{u}_x}{{\partial }^{2}z}+\frac{\lambda +\mu }{\rho }\frac{{\partial }^2{u}_z}{\partial x\partial z}\right]+f_x\left(t+\Delta t\right)\\ u_z\left(t+\Delta t\right)=2u_z\left(t\right)-u_z\left(t-\Delta t\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+\Delta t^2\left[\frac{\lambda +2\mu }{\rho }\frac{{\partial }^2{u}_z}{\partial x^2}+\frac{\mu }{\rho }\frac{{\partial }^2{u}_z}{{\partial }^{2}z}+\frac{\lambda +\mu }{\rho }\frac{{\partial }^2{u}_x}{\partial x\partial z}\right]+f_z\left(t+\Delta t\right)\end{array}$$

(6)

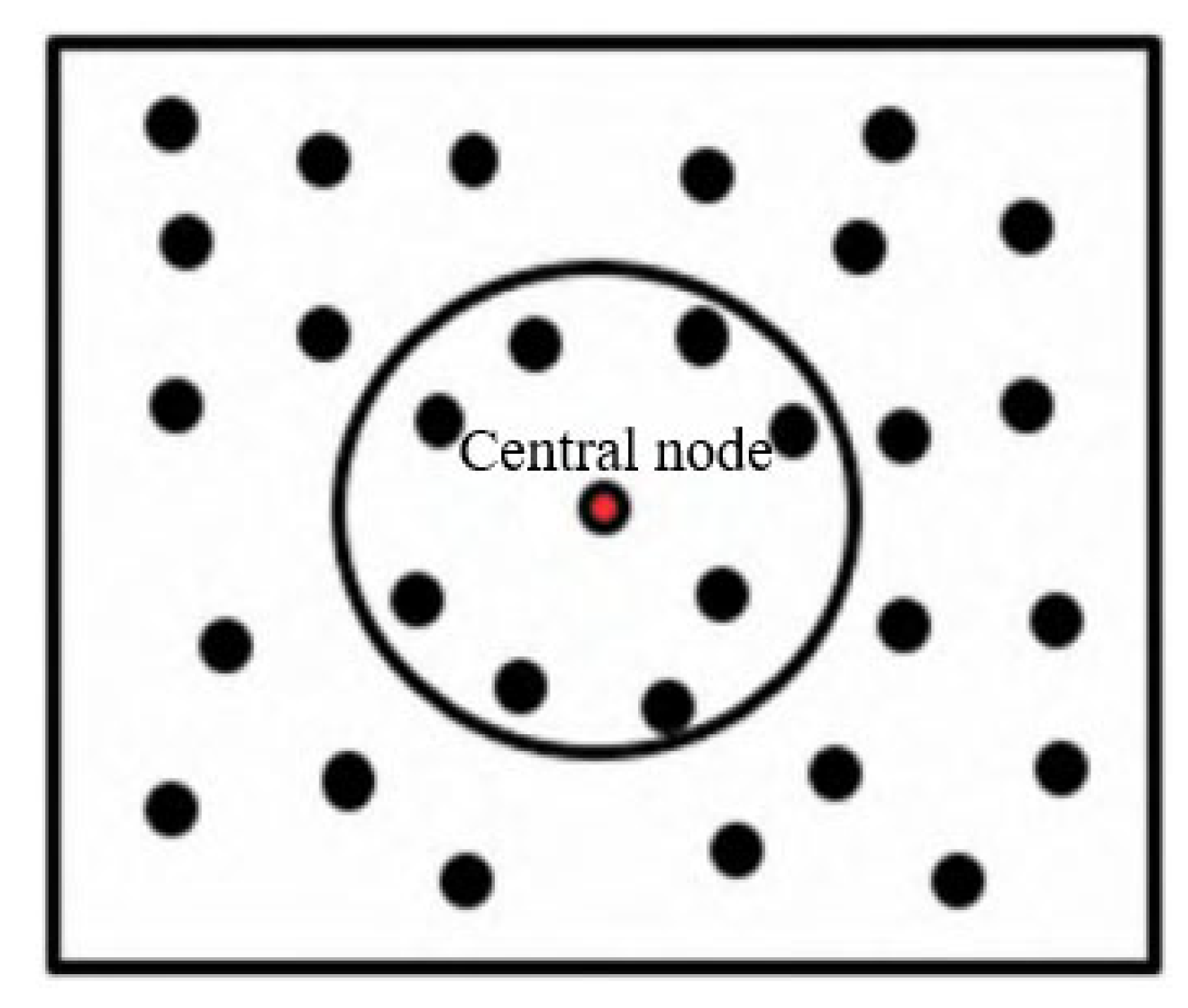
2.3. GFDM for Spatial Partial Derivative Approximation

In the GFDM, through utilizing the Taylor series expansion and weighted least squares fitting, the derivatives of unknown variables can be approximated by a linear combination of function values of some neighboring nodes, which are located inside a star. First, a regular or irregular cloud of points is generated in the computation domain and along the boundary. For a given node $i$, which is denoted as a central node, the $m$ nearest nodes surrounding the node $i$ will be found. The concept of the star refers to a group of established nodes in relation to the central node, as shown in the black circle in Figure 1. Each node is assigned an associated star.

If $u_0$ is the function value at the central node $x_0$ of the star and $u_i\left(i=1,2,\cdots ,m\right)$ is the function value at one of the rest of the nodes, then the Taylor series expansion around the central node can be expressed in the following form:

$$u_i=u_0+h_i\frac{\partial u_0}{\partial x}+l_i\frac{\partial u_0}{\partial z}+\frac{h_i^2}{2}\frac{{\partial }^2{u}_0}{\partial x^2}+\frac{l_i^2}{2}\frac{{\partial }^2{u}_0}{\partial z^2}+h_i{l}_i\frac{{\partial }^2{u}_0}{\partial x\partial z}+\cdots$$

(7)

where the coefficients $h_i=x_i-x_0$, $l_i=z_i-z_0$, and $\left(x_0,z_0\right)$ are the coordinates of the central node, and $\left(x_i,z_i\right)$ are the coordinates of the node $i$ in the star. By truncating the Taylor series with the second derivative, the residual function $B\left(u\right)$ can be defined by the following equation:

$$B{\left(u\right)}_{2^{nd}}={{\displaystyle \sum _{i=1}^m\left[\left(u_0-u_i+h_i\frac{\partial u_0}{\partial x}+l_i\frac{\partial u_0}{\partial z}+\frac{h_i^2}{2}\frac{{\partial }^2{u}_0}{\partial x^2}+\frac{l_i^2}{2}\frac{{\partial }^2{u}_0}{\partial z^2}+h_i{l}_i\frac{{\partial }^2{u}_0}{\partial x\partial z}\right)w_i\right]}}^2$$

(8)

By truncating the Taylor series with the fourth derivative, the residual function $B\left(u\right)$ can be defined by the following:

$$\begin{array}{c}B{\left(u\right)}_{4^{th}}={\displaystyle \sum _{i=1}^m[(u_0-u_i+h_i\frac{\partial u_0}{\partial x}+l_i\frac{\partial u_0}{\partial z}+\frac{h_i^2}{2}\frac{{\partial }^2{u}_0}{\partial x^2}+\frac{l_i^2}{2}\frac{{\partial }^2{u}_0}{\partial z^2}+h_i{l}_i\frac{{\partial }^2{u}_0}{\partial x\partial z}}\\ +\frac{h_i^3}{6}\frac{{\partial }^3{u}_0}{\partial x^3}+\frac{l_i^3}{6}\frac{{\partial }^3{u}_0}{\partial z^3}+\frac{h_i^2{l}_i}{2}\frac{{\partial }^3{u}_0}{\partial x^2\partial z}+\frac{h_i{l}_i^2}{2}\frac{{\partial }^3{u}_0}{\partial x\partial z^2}+\frac{h_i^4}{24}\frac{{\partial }^4{u}_0}{\partial x^4}+\frac{l_i^4}{24}\frac{{\partial }^4{u}_0}{\partial z^4}\\ {+\frac{h_i^3{l}_i}{6}\frac{{\partial }^4{u}_0}{\partial x^3\partial z}+\frac{h_i{l}_i^3}{6}\frac{{\partial }^4{u}_0}{\partial x\partial z^3}+\frac{h_i^2{l}_i^2}{4}\frac{{\partial }^4{u}_0}{\partial x^2\partial z^2})w_i]}^2\end{array}$$

(9)

In Equations (8) and (9), $w_i=w\left(h_i,l_i\right)$ represents the distance weight function of the star. In all the examples considered in this paper, the weighting function was chosen as per [27]:

$$w_i=\{\begin{array}{ll}1-6{\left(\frac{d_i}{d_{\max }}\right)}^2+8{\left(\frac{d_i}{d_{\max }}\right)}^3-3{\left(\frac{d_i}{d_{\max }}\right)}^4,& d_i\le d_{\max }\\ 0,& d_i>d_{\max }\end{array}$$

(10)

where $d_i$ denotes the distance between nodes $\left(x_i,z_i\right)$ and $\left(x_0,z_0\right)$, and $d_{\max }$ is the distance between the central node and the farthest node in the star. Let the following terms be defined:

$$D_u=\left[\frac{\partial u_0}{\partial x},\frac{\partial u_0}{\partial z},\frac{{\partial }^2{u}_0}{\partial x^2},\frac{{\partial }^2{u}_0}{\partial z^2},\frac{{\partial }^2{u}_0}{\partial x\partial z},\cdots \right]$$

(11)

$$p_i=\left\{h_i,l_i,\frac{h_i^2}{2},\frac{l_i^2}{2},h_i{l}_i,\cdots \right\},i=1,2,\cdots ,m$$

(12)

$$P_{}=\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_m\end{array}\right]=\left[\begin{array}{cccc}{h}_1& l_1& \cdots & h_1{l}_1\\ h_2& l_2& \cdots & h_2{l}_2\\ ⋮& ⋮& \ddots & ⋮\\ h_m& l_m& \ddots & h_m{l}_m\end{array}\begin{array}{c}\cdots \\ \cdots \\ \cdots \\ \cdots \end{array}\right]$$

(13)

The residual function defined in Equations (8) and (9) can be expressed in matrix form:

$$B\left(u\right)={\left(P{D}_u+u_0-u\right)}^{T}W\left(P{D}_u+u_0-u\right)$$

(14)

where $u={\left[u_1,u_2,\cdots ,u_m\right]}^T$, $u_0={\left[u_0,u_0,\cdots ,u_0\right]}^T$, and $W=diag\left(w_1^2,w_2^2,\cdots ,w_m^2\right)$.

To minimize the residual function $B\left(u\right)$ with respect to the unknown derivatives at the central point $\left(x_0,z_0\right)$:

$$\frac{\partial B\left(u\right)}{\partial D_u}=0$$

(15)

yields the following linear equation system,

$$A{D}_u=b$$

(16)

and

$$A=P^{T}WP$$

(17)

$$b=P^{T}W\left(u-u_0\right)$$

(18)

According to Equations (16)–(18), the partial derivative vector $D_u$ can be expressed as:

$$D_u=A^{-1}b=A^{-1}{P}^{T}W\left(u-u_0\right)=-a{u}_0+{\displaystyle \sum _{i=1}^m{a}_i{u}_i}$$

(19)

where $a={\displaystyle \sum _{i=1}^m{a}_i}$, $a={\left[a_1,a_2,a_3,a_4,a_5\right]}^T$, and ${\displaystyle \sum _{i=1}^m{a}_i}={\left[{\displaystyle \sum _{i=1}^m{a}_{1i}},{\displaystyle \sum _{i=1}^m{a}_{2i}},{\displaystyle \sum _{i=1}^m{a}_{3i}},{\displaystyle \sum _{i=1}^m{a}_{4i}},{\displaystyle \sum _{i=1}^m{a}_{5i}}\right]}^T$. Expanding the partial derivative vector $D_u$, we can obtain:

$$\{\begin{array}{l}\frac{\partial u_0}{\partial x}=-a_1{u}_0+{\displaystyle \sum _{i=1}^m{a}_{1i}{u}_i}\\ \frac{\partial u_0}{\partial z}=-a_2{u}_0+{\displaystyle \sum _{i=1}^m{a}_{2i}{u}_i}\\ \frac{{\partial }^2{u}_0}{\partial x^2}=-a_3{u}_0+{\displaystyle \sum _{i=1}^m{a}_{3i}{u}_i}\\ \frac{{\partial }^2{u}_0}{\partial z^2}=-a_4{u}_0+{\displaystyle \sum _{i=1}^m{a}_{4i}{u}_i}\\ \frac{{\partial }^2{u}_0}{\partial x\partial z}=-a_5{u}_0+{\displaystyle \sum _{i=1}^m{a}_{5i}{u}_i}\end{array}$$

(20)

Substituting Equation (20) into the Equation (6), the discrete formula for solving the elastic wave equation can be obtained:

$$\{\begin{array}{l}{u}_{x,0}^{n+1}=2u_{x,0}^n-u_{x,0}^{n-1}+\Delta t^2[\frac{\lambda +2\mu }{\rho }\left(-a_3{u}_{x,0}^n+{\displaystyle \sum _{i=1}^m{a}_{3i}{u}_{x,i}^n}\right)\\ \hspace{1em}\hspace{1em}+\frac{\lambda +\mu }{\rho }\left(-a_5{u}_{z,0}^n+{\displaystyle \sum _{i=1}^m{a}_{5i}{u}_{z,i}^n}\right)+\frac{\mu }{\rho }\left(-a_4{u}_{x,0}^n+{\displaystyle \sum _{i=1}^m{a}_{4i}{u}_{x,i}^n}\right)]+f_x^{n+1}\\ u_{z,0}^{n+1}=2u_{z,0}^n-u_{z,0}^{n-1}+\Delta t^2[\frac{\lambda +2\mu }{\rho }\left(-a_4{u}_{z,0}^n+{\displaystyle \sum _{i=1}^m{a}_{4i}{u}_{z,i}^n}\right)\\ \hspace{1em}\hspace{1em}+\frac{\lambda +\mu }{\rho }\left(-a_5{u}_{x,0}^n+{\displaystyle \sum _{i=1}^m{a}_{5i}{u}_{x,i}^n}\right)+\frac{\mu }{\rho }\left(-a_3{u}_{z,0}^n+{\displaystyle \sum _{i=1}^m{a}_{3i}{u}_{z,i}^n}\right)]+f_z^{n+1}\end{array}$$

(21)

For the stability analysis, the aim is to construct a harmonic decomposition of the approximated solution at the grid points at a given time level (n). The amplification factor must be less than or equal to one in order to determine the stability limit. This has been studied by [23] and the condition for the stability of the star has been established as:

$$\Delta t\le \sqrt{\frac{4}{\left(v_p^2+v_s^2\right)\left(\left|a_3\right|+\left|a_4\right|\right)+\left(v_p^2-v_s^2\right)\sqrt{{\left(a_3-a_4\right)}^2+4a_5^2}}}$$

(22)

where $v_p$ and $v_s$ are the velocity of compressional and shear waves, respectively.

2.4. Node Generation Algorithm

Benito et al. (2017) pointed out that when the discretization (cloud of nodes) becomes more regular, the obtained results become more logical [21]. Furthermore, to avoid the diffraction caused by the difference between the node and the interface positions, it is necessary to adjust the node position at the inner part of the interface and the boundary, so that the nodes are located at the interface and the boundary. In this study, we proposed an algorithm combining the Poisson disk node generation algorithm and the centroid Voronoi adjustment algorithm, to obtain a reasonable node distribution according to the velocity model.

(1)

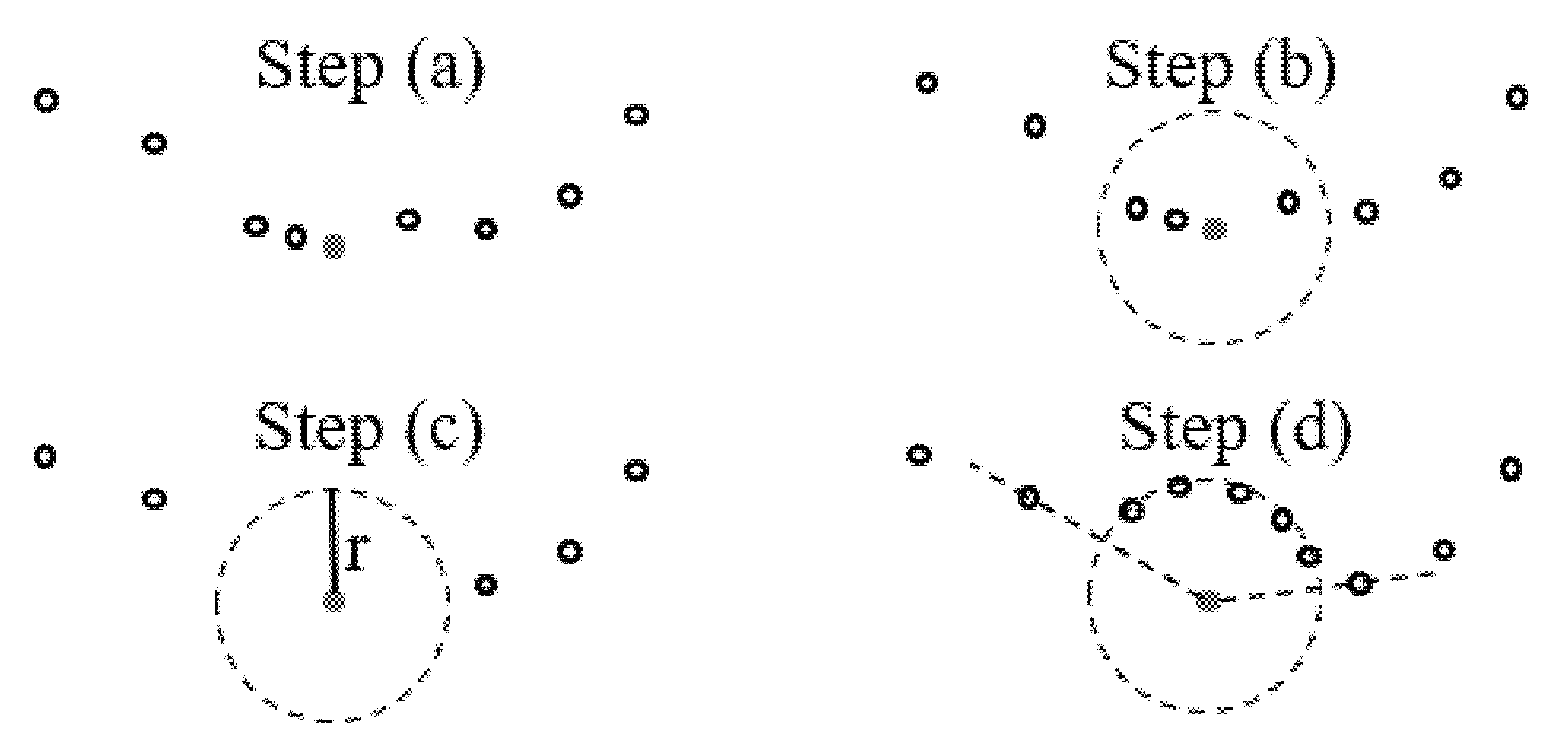
Randomly Distributed Node Generation

The Poisson disk node generation algorithm proposed by Fornberg et al. (2015) was used [28]. In the two-dimensional case, the calculation steps for the random node generation algorithm (Figure 2) are as follows:

(a)

Set the horizontal positions (potential dot positions, PDPs) of the initial nodes, and randomly set the vertical coordinates;

(b)

Out of all the current PDPs, find the PDP closest to the bottom of the model, and classify this PDP as the determined dot position (DDP). The newly determined DDP is at the center of the circle, and the discrete distance set by the position model parameters is the radius (noting the radius is a function of velocity [29]);

(c)

No other center may appear inside the circle, so all PDPs except the DDP within the circle are removed;

(d)

Determine the two PDPs closest to the DDP at the circle center, make a circle through these two PDPs with the DDP as the center, and select multiple (we used five) new PDPs at equal angles on the arc between the two DDPs;

(e)

Then, select the PDP closest to the bottom (excluding the cycled PDP and adding a new PDP) and repeat steps (b)–(d) until the cycle for all points in the calculation area is completed. At this point, uniformly and randomly distributed node coordinates will have been obtained in the computing area.

(2)

Node Adjustment

To adjust the nodes, overlay the random nodes obtained in the previous step with the interface and boundary nodes, and discard the nodes within a half radius of any boundary node, as shown in Figure 3b. After the redundant nodes are discarded, the nodes at the internal interface and the boundary will be unevenly distributed. Therefore, we propose a node adjustment algorithm based on the centroid Voronoi structure. This algorithm divides Voronoi polygons into multiple polygonal regions formed by the boundary and interfaces, and uses the centroid point of the Voronoi polygon as the new node location. Since the distribution of the nodes before adjustment is relatively uniform, only 10–15 iterations are needed to evenly distribute the nodes near the interface. This method has good stability and can obtain a more uniform node distribution, however, since the conventional Voronoi polygon division is borderless, the Voronoi polygon division requires computing the intersection of the Voronoi diagram and the irregular boundary, which leads to a high computation cost. To solve this problem, GPU was used to accelerate the Voronoi polygon division and the adjustment of the centroid points in the irregular boundary area.

The algorithm takes the internal node and boundary node coordinates as its inputs, and its main steps are as follows:

(a)

Calculate the coordinates of the $k$ points closest to each node, and connect the node and the $k$ points into a line segment Voronoi unit (see Figure 3);

(b)

Calculate the intersection between each Voronoi element and the boundary polygon, and trim the Voronoi diagram (see Figure 3);

(c)

The centroid of the Voronoi element is calculated and used as the new node position;

(d)

Repeat the above three steps 10–15 times to get the final node distribution.

Figure 4 shows the node generation steps for the two-layer simple model. It can be seen from the figure that the algorithm first generates variable density nodes through Poisson disks in the boundary region (Figure 4a). Then, the nodes that are too close to the interface nodes are deleted, and nodes with an uneven distribution at the boundary are obtained (Figure 4c). Finally, variable density internal nodes, and a uniform distribution of boundary nodes, are obtained through the centroid Voronoi adjustment algorithm (Figure 4d). The figure shows not only that the final node distribution is accurately arranged at the interface location, but also that the overall nodes layout is evenly distributed across the different regions.

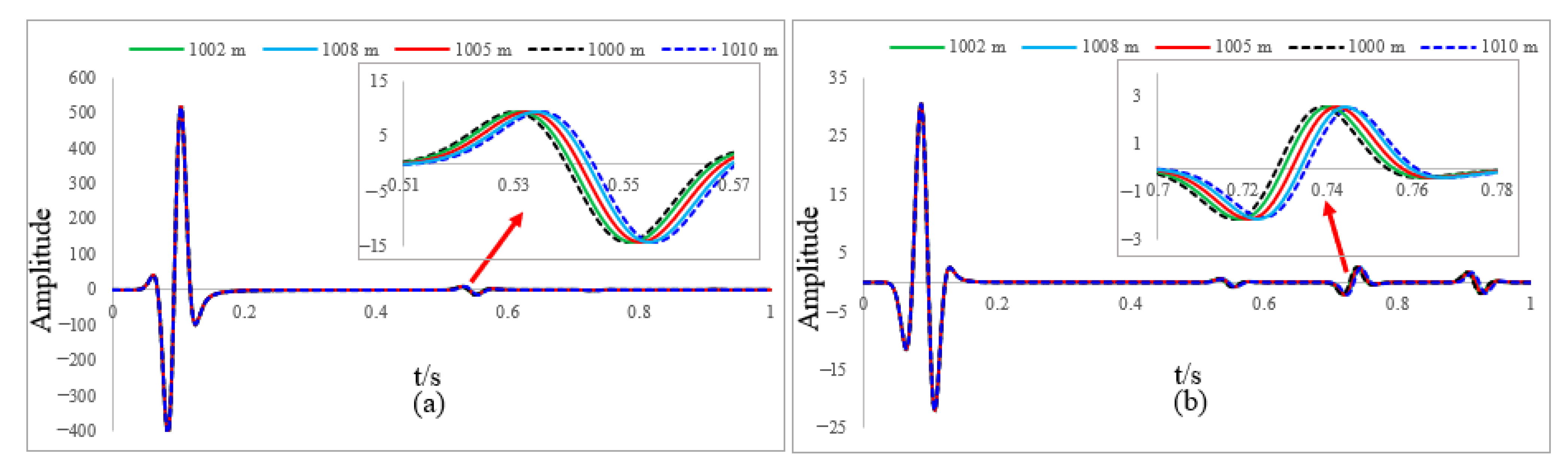
2.5. Boundary Condition

In practice, the seismic wave propagates in the underground infinite medium after being excited. When the elastic wave equation is used for seismic wave numerical simulation, it is difficult to simulate the infinite medium, so it is necessary to control the size of the model within a certain range to generate an artificial boundary. If the artificial boundary is not treated with a numerical method, the elastic wave will be reflected when it propagates to the boundary, and will interfere with the wavefield inside the model. For the generalized finite difference method in the time domain, the damping attenuation boundary condition does not involve the problem of stability. By selecting appropriate attenuation parameters, a good absorption effect can be achieved.

The damping factor proposed by Cerjan [31] is as follows:

$$damp=\exp \left[-{\alpha }^2{\left(I-i\right)}^2\right]$$

(23)

where $I$ is the grid number of the attenuation boundary thickness, $i=1,2,\cdots ,I$, and $\alpha$ is the absorption coefficient. It can be seen from the formula that the selection of the absorption coefficient and the thickness of the attenuation boundary directly influence the absorption effect. The generalized finite difference method discretizes the model into nodes instead of into grids, so $I$ represents the thickness of the attenuation boundary divided by the exclusion radius, $r$; and $i$ represents the distance between the node and the inner boundary of the attenuation layer divided by the exclusion radius, $r$. The parameters used in this study were referenced to those used by to Li (2014) [32]. Figure 5 compares the wave field before and after adding the attenuation boundary. When there is no attenuation boundary, the energy of the wave field is covered by the boundary reflection. After adding 45 layers of attenuation boundary, the boundary reflection can be effectively absorbed.

2.6. Source Term

The source term in Equation (1) is the product of the seismic wavelet and the source spatial position function:

$$f\left(x,z;t\right)=s(t)\phi (x,z)$$

(24)

where $s\left(t\right)$ is the seismic wavelet function, and $\phi \left(x,z\right)$ represents the impulse function. Ricker wavelet [33] and Gaussian pulse functions are used in this paper:

$$s(t)=\left[1-2{\pi }^2{f}_m{}^2{\left(t-t_0\right)}^2\right]\exp \left[-{\pi }^2{f}_m{}^2{\left(t-t_0\right)}^2\right]$$

(25)

where f_m is the dominant frequency of the wavelet, and $t_0$ is the delay time Moreover:

$$\phi (x,z)=e^{-\left[{\left(x-x_0\right)}^2+{\left(z-z_0\right)}^2\right]}$$

(26)

where $\left(x_0,z_0\right)$ is the source position.

3. Examples

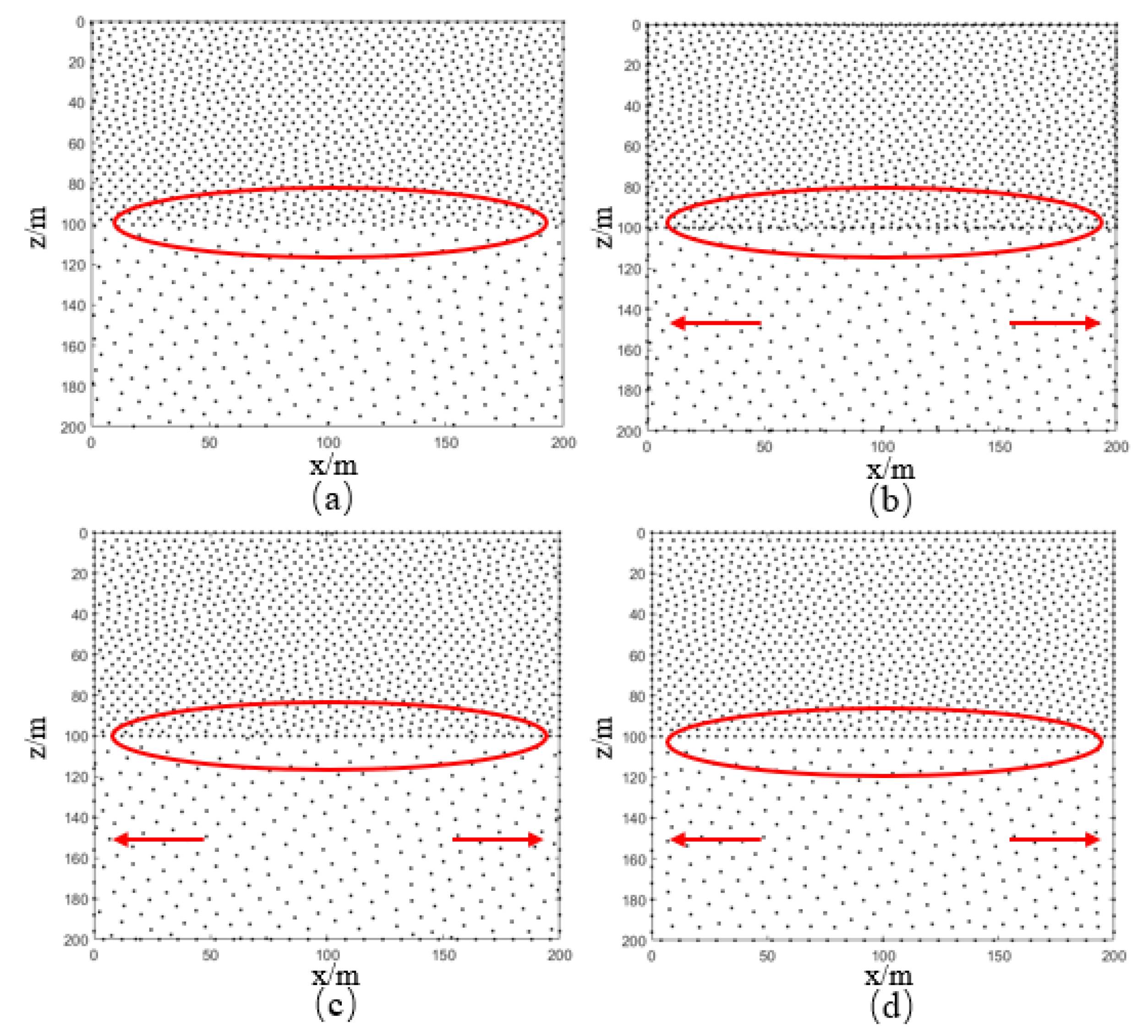
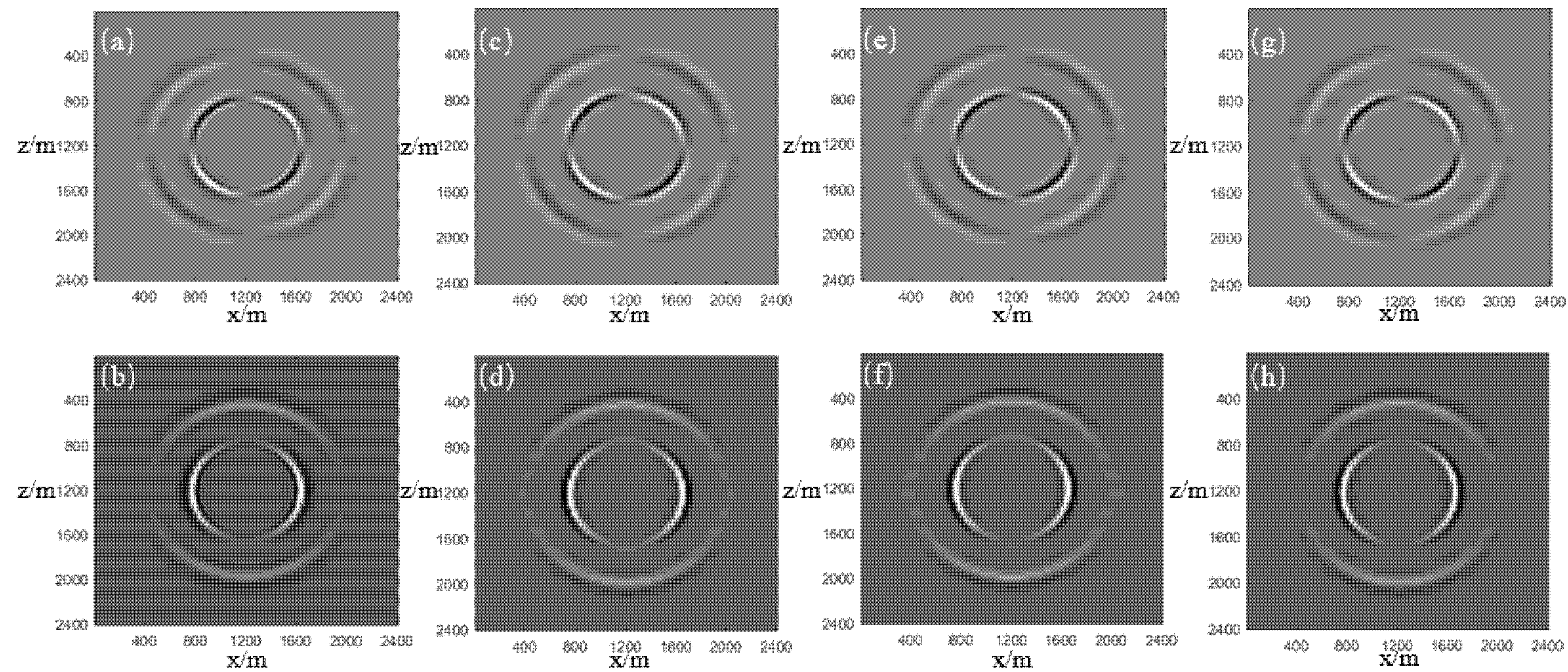
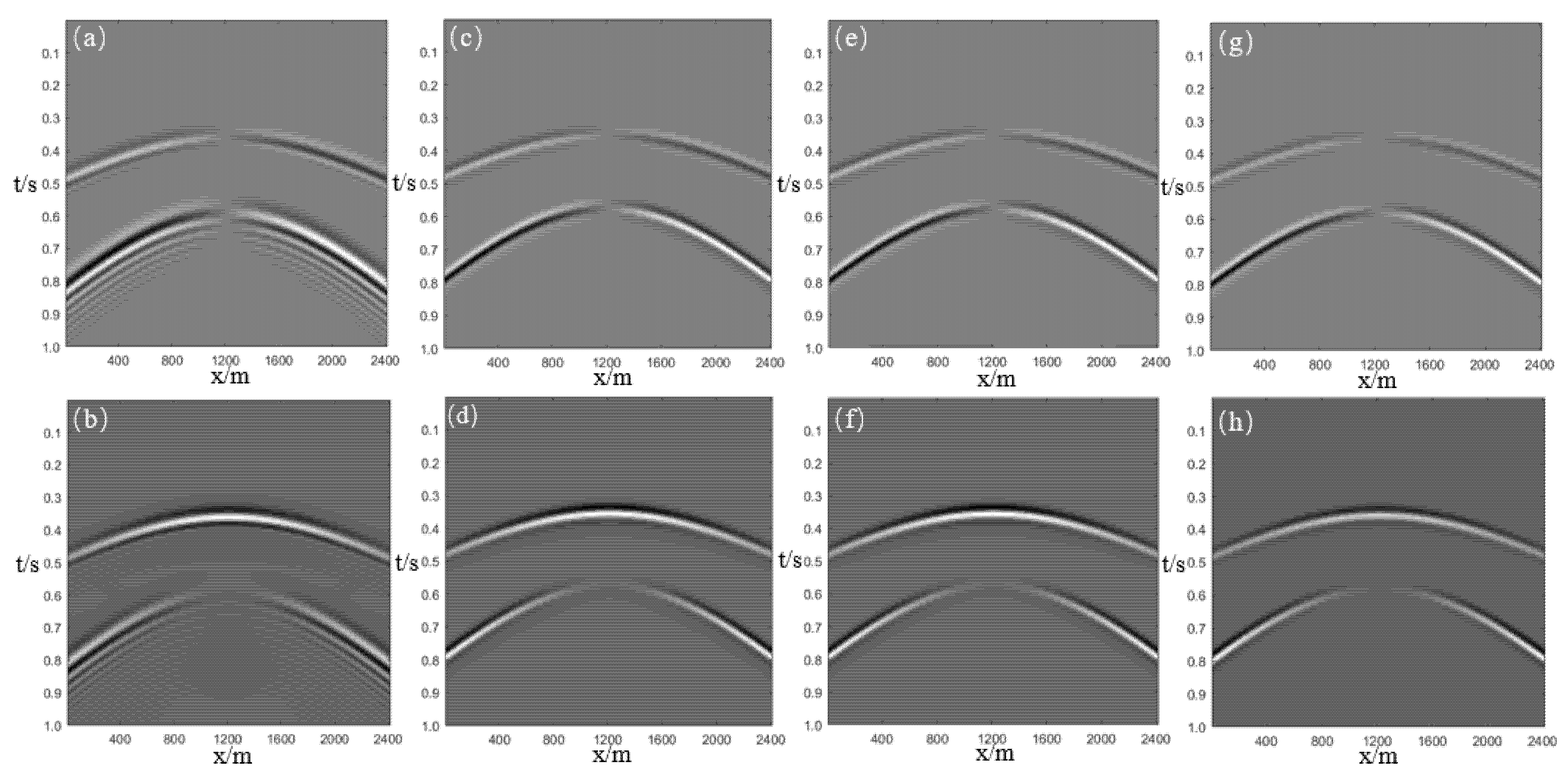
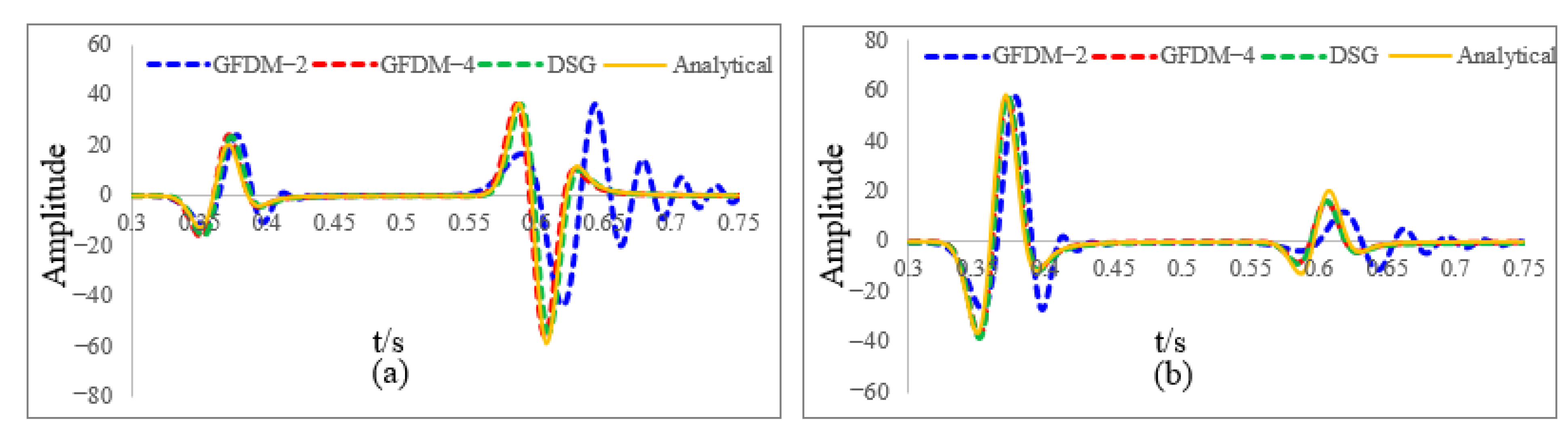
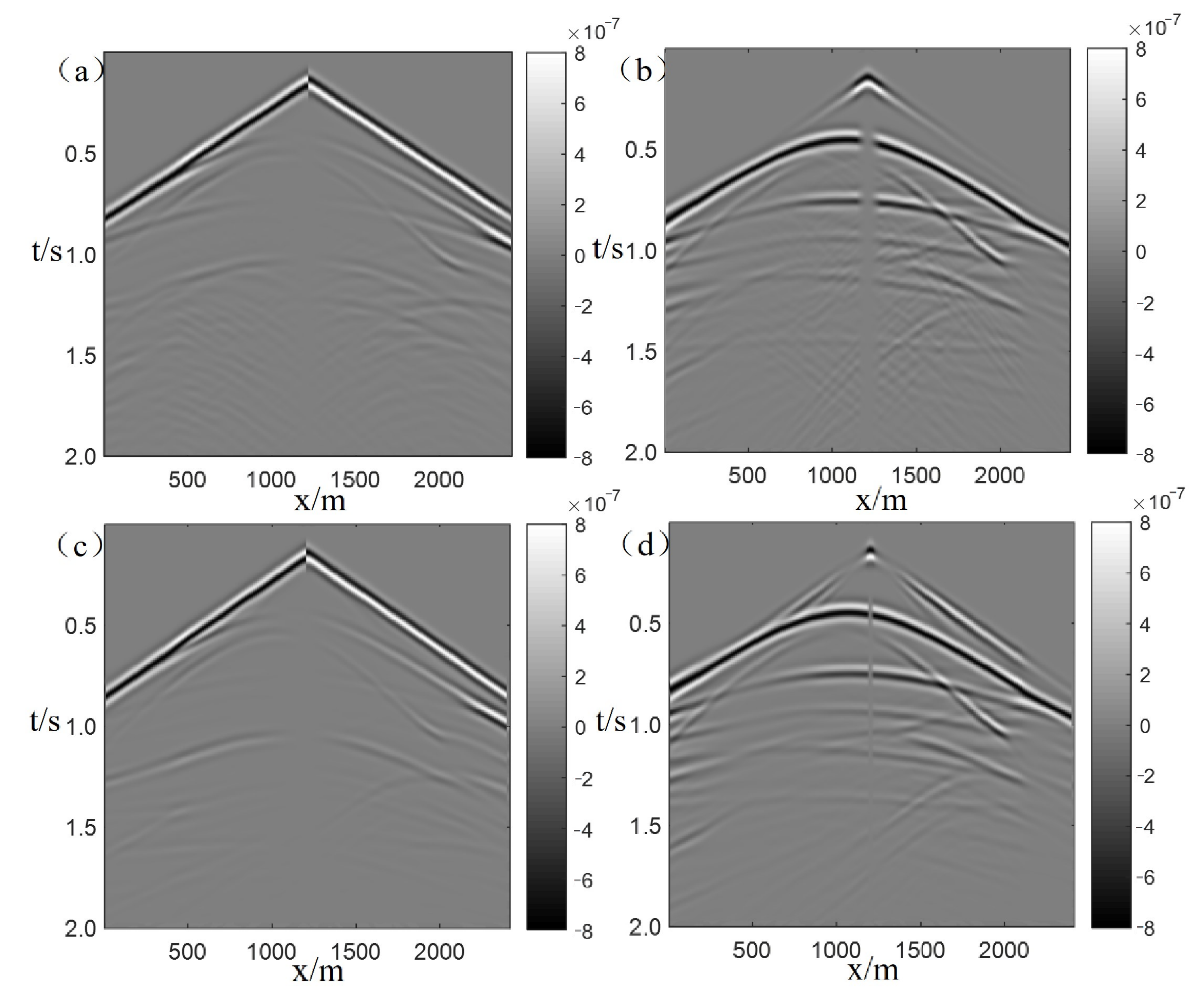
3.1. Homogeneous Model

To verify the correctness of the generalized finite difference method for solving the elastic wave equation, a two-dimensional homogeneous medium model was set (2400 m × 2400 m), with a P-wave velocity of 4000 m/s, an S-wave velocity of 2300 m/s and a density of 2000 kg/m³. The dominant frequency of the Ricker wavelet was 20 Hz, and the source was located at the center of the model. For comparison, all sources were loaded onto the vertical component of the displacement. The generalized finite difference method was compared with both the analytical solution and the staggered grid finite difference method (SGFD). The node distribution was consistent with the rectangular grid of the staggered grid finite difference method, and the spacing of the grid (nodes) was 10 m.

To ensure the stability of the simulation, the time step was set at 0.5 ms, and the total computation time at 1.0 s. The forward modeling was performed using a 2nd-order precision 13 points GFDM, a 4th-order precision 21 nodes GFDM, and an 8th-order staggered grid finite difference method. Figure 6 shows a comparison of the 400 ms wavefield obtained by the different methods. The wavefront obtained by the GFDM is consistent with the analytical solution, which proves the correctness of the GFDM. The dispersion energy of the shear wave can be seen in Figure 6a,b, which was obtained through the 2nd-order 13 points GFDM. The results obtained using the 4th-order 21 nodes GFDM are almost the same as those obtained from the SGFD method, without any visible dispersion. This shows that improving the difference order can achieve a high calculation accuracy. In further comparing the shot records (Figure 7), the same conclusion can be drawn. In extracting the 80th trace from the shot record for comparison (Figure 8), little difference can be seen between the 4th-order GFDM results and the analytical solution, and the overall calculation accuracy is almost equivalent to that of the SGFD method. Therefore, it can be concluded that the time domain GFDM for elastic wave simulation is correct and effective.

3.2. Two-Layer Model

When SGFD methodology is used for elastic wave simulation, the grid step is determined. If the interface is located at an integral multiple of the step, the grid can accurately describe the interface; otherwise, it will cause an inaccuracy in the travel time of the reflected wave. The GFDM can directly set the nodes at the interface, therefore it can accurately describe the changes in the interface and can obtain more accurate travel time simulation results. A two-layer horizontal model (2000 m × 2000 m) was designed to show the advantages of the GFDM over the SGFD model. The P-velocity, S-velocity, and density of the upper layer of the model were 4000 m/s, 2300 m/s, and 2.4 g/cm³, respectively, and those of the lower layer were 6000 m/s, 3500 m/s, and 2.6 g/cm³, respectively. The simulation time step was set at 0.5 ms, and the total computation time at 1.0 s. The source was located at (1000 m, 0 m), and the dominant frequency of the Ricker wavelet was 20 Hz. When the model is discretized, the SGFD model adopted a fixed grid step of 10 m. Therefore, only when the interface was located at an integral multiple of 10 (for example, when the interface was located at 1000 m), can the grid points accurately describe the interface. However, when the interface is located between 1000 m and 1010 m, the results obtained by SGFD are the same, and the travel time of the reflected wave will not change. When the 4th-order 21 nodes GFDM was used, the proposed node generation algorithm was applied to discretize the model, using a node radius of 10 m for the first layer, and 12 m for the second layer. The coordinates of the nodes change along with the real interface position, so more accurate travel time information of the reflected wave can be obtained. When the interfaces were located at 1002 m, 1005 m, and 1008 m, respectively, the GFDM and SGFD results obtained are shown in Figure 9. The black and blue dotted lines represent the seismic records obtained by SGFD when the interface depth was set as 1000 m and 1010 m, respectively. The green, red, and blue solid lines correspond to seismic records obtained by GFDM when the interfaces were located at 1002m, 1005 m, and 1008 m, respectively. Comparing the reflected wave information for the two algorithms, the SGFD can only obtain the exact record time of interfaces located at 1000m and 1010 m—when the interface depths are 1002 m, 1005 m, and 1008 m, the record time will never change. In contrast, for the GFDM results, the record time shifts with the interface depth, which is more consistent with reality compared to the SGFD results. This shows that the GFDM can accurately describe the changes in the interface, and can obtain more accurate travel time simulation results.

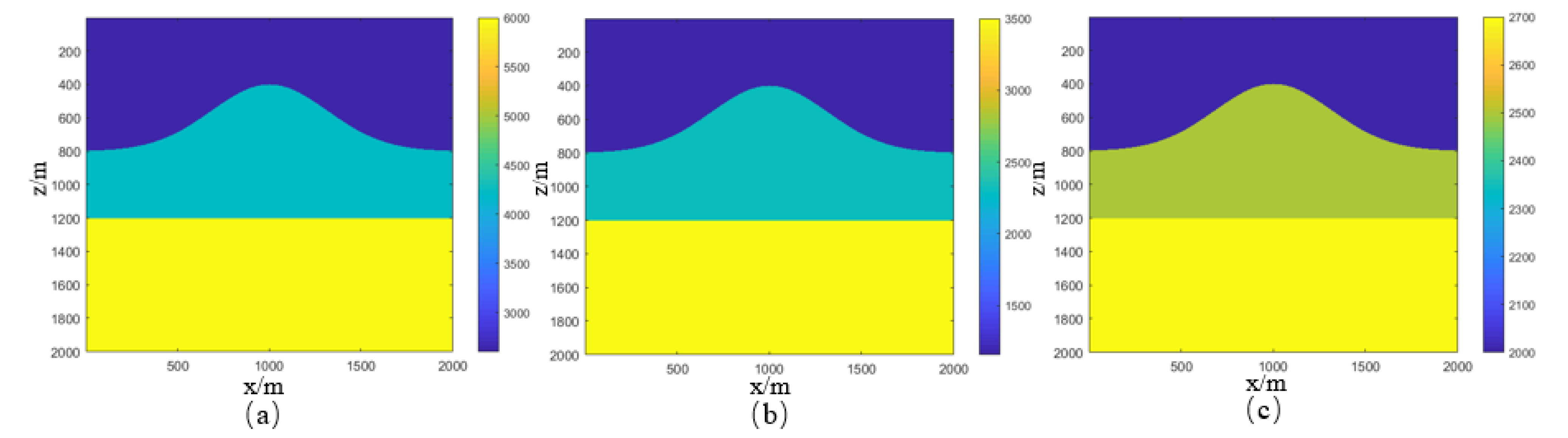
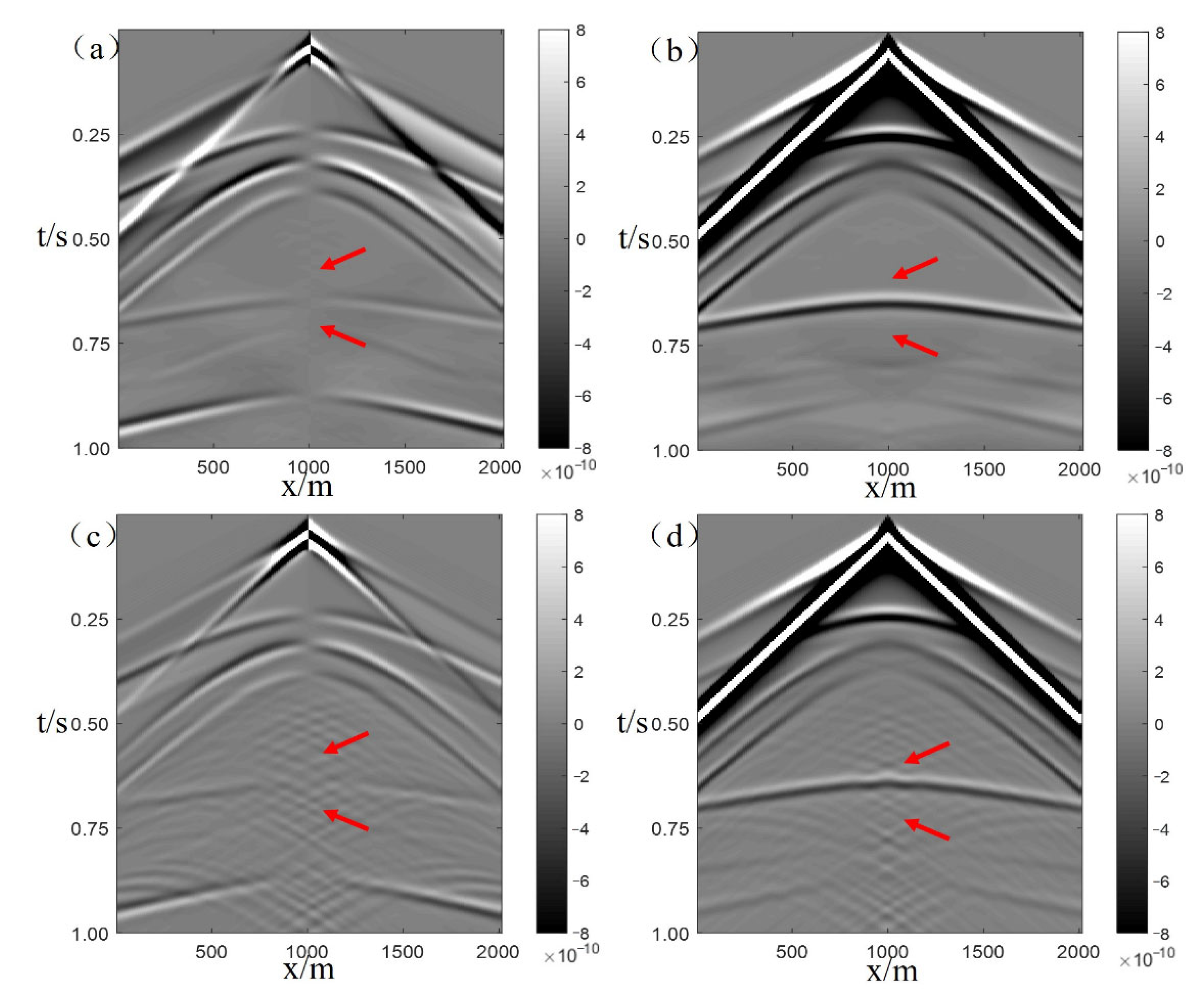
3.3. Undulating Interface Model

The SGFD model will cause false diffraction due to the stepped grid when dealing with undulating interfaces. These diffraction waves will affect the accuracy of elastic wave modeling. The GFDM can simulate an elastic wave based on nodes adapting to the change of an undulating interface, so there will be no stepped grid diffraction. When the undulating interface model, as shown in Figure 10, was used, the velocity and density of the upper layer of the model were 4000 m/s, 2300 m/s, and 2.4 g/cm³, respectively, those of the middle layer were 5000 m/s, 2800 m/s, and 2.5 g/cm³, and those of the lower layer were 6000 m/s, 3500 m/s, 2.6 g/cm³. The time sampling interval was 0.5 ms, and the total computation time was 1.0 s. The source was located at (1000 m, 0 m), and the dominant frequency of the Ricker wavelet was 20 Hz. When the 4th-order 21 nodes GFDM was used, the proposed node generation algorithm was applied to discretize the model, with the node radius at 10 m, 12 m, and 15 m for the first, second, and third layers, respectively. For comparison, the SGFD model was used based on regular grids with a grid spacing of 10 m. The local grid distribution of the SGFD model is shown in Figure 11a, in which the stepped grid can be seen clearly, while the local node distribution of the GFDM is shown in Figure 11b, in which the nodes are directly and accurately distributed on the interface. It can be seen from the seismic records depicted in Figure 12a,b that there are a lot of diffracted waves behind the primary reflected wave when modeled by SGFD, while diffraction waves are practically non-existent in the GFDM record (Figure 12c,d). The results demonstrate that the forward modeling using GFDM avoids the effect of stepped grid diffraction, and is suitable for the forward modeling of a formation with undulating interfaces.

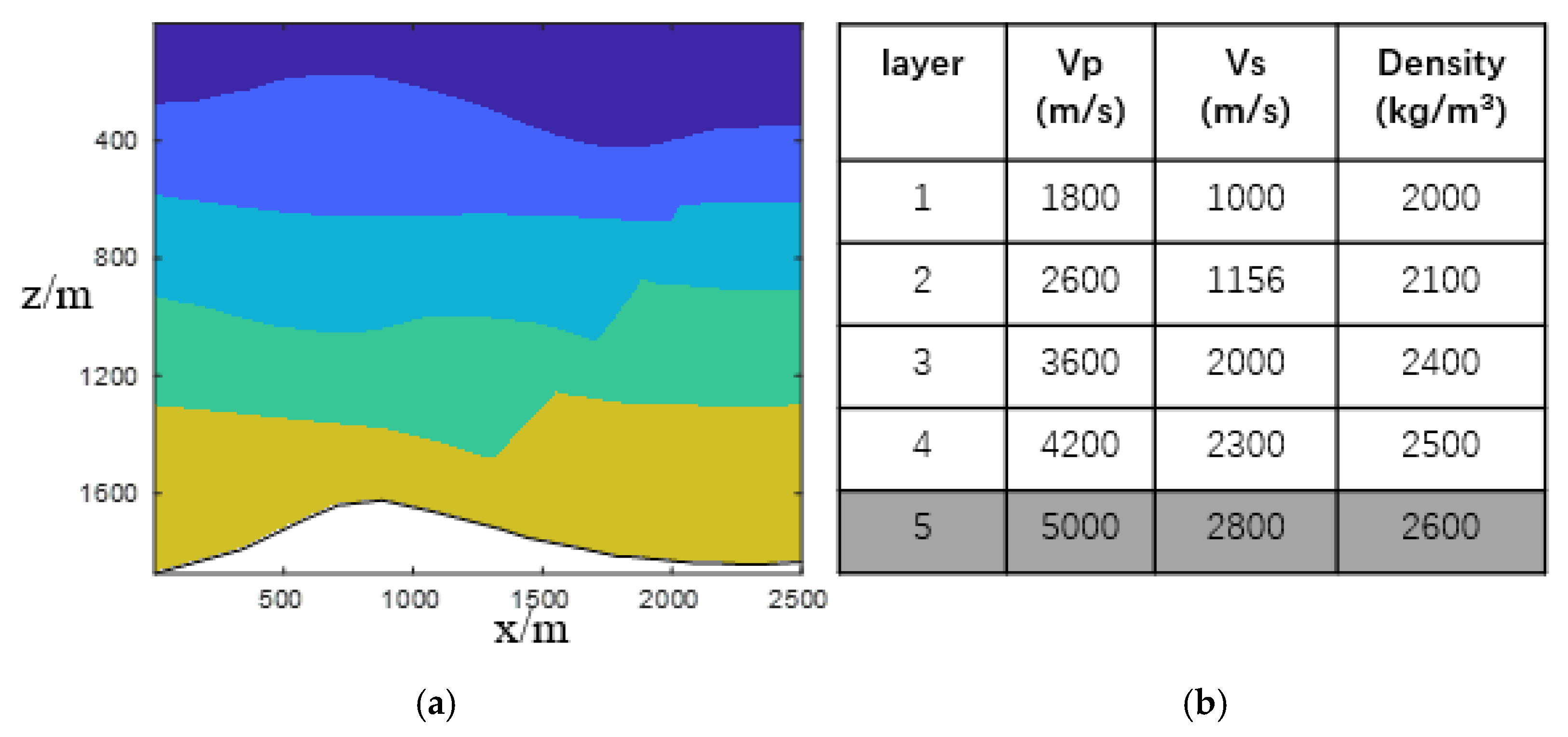
3.4. Fault Model

Fault zones are closely related to the genesis of many fossil deposits. Therefore, a model with igneous rock (model parameters in gray) and fault zones, as shown in Figure 13, was designed with an irregular boundary for elastic wave numerical simulation. The time sampling interval was 0.5 ms, and the total computation time was 2.0 s. The source was located at (1200 m, 10 m), and the dominant frequency of the Ricker wavelet was 10 Hz. When the 4th-order 21 nodes GFDM was used, the proposed node generation algorithm was applied to discretize the model. For comparison, the SGFD model was used based on regular grids with a grid spacing of 10 m and with the irregular boundary extended to a rectangular boundary. It can be seen from the seismic records obtained using the two different methods that the direct and reflected wave events are essentially the same, but it is noted that there were a number of scattered waves behind the reflection wave in the SGFD records (Figure 14a,b), while there are almost no scattered waves in the GFDM records (Figure 14c,d). This shows that the method used in this study is suitable for application to such complex models without any sharp lateral changes. Moreover, the GFDM method does not require an extension of the irregular boundary to a rectangular boundary, as it can calculate the wavefield by directly setting nodes on the irregular boundary.

4. Conclusions

In this study, the time partial derivative of the elastic wave equation was discretized using the central difference scheme, and the spatial partial derivative was discretized using a meshless GFDM. When realizing the elastic wave numerical simulation via the GFDM in the time domain, the Poisson disk node generation algorithm and the centroid Voronoi node adjustment algorithm were combined to obtain an even and random distribution of nodes, and the Cerjan damping boundary condition was introduced. Through numerical calculation, the following understandings and conclusions were obtained:

(a)

The GFDM is a meshless numerical calculation method based on scattered node approximation; it overcomes the dependence of traditional methods on grids, and can lay nodes in the simulation area in a flexible manner;

(b)

When using the GFDM for forward modeling, the nodes can be rendered consistent with the real velocity interface by generating a suitable distribution of nodes, so that the velocity interface can be accurately depicted, avoiding the situation where the grid and velocity interface cannot be aligned in the conventional finite difference forward modeling; thus eliminating the diffraction problems due to a stepped grid, and the record time error caused by an inaccurate description of the interface position;

(c)

One of the main problems in the GFDM forward modeling is in how to best discretize the model. The node discretization scheme used in this study is applicable to a model with gentle changes in lateral velocity. For models with sharp changes in lateral velocity, the simulation stability will be affected, so it would be necessary to explore a more stable and applicable node discretization scheme;

(d)

The 2nd-order GFDM has high computational efficiency, but low accuracy. The 4th-order GFDM is unstable when using a “star” composed of fewer points (for example, 13 points), therefore it can only use a “star” composed of more calculation nodes (21 nodes were used in this study), causing the calculation efficiency to be greatly reduced. To improve computing efficiency, high-performance computing can be considered to enable better efficiency;

(e)

Compared with SGFD, the GFDM requires some preprocessing before forward modeling can be applied, including calculation of the node distribution and the difference stencil, which makes GFDM more complicated in practical application.