Large Field-Size Elliptic Curve Processor for Area-Constrained Applications
Abstract
1. Introduction
1.1. Related Work
1.2. Research Gap
1.3. Contributions
- We have presented an area-optimized hardware accelerator of a large field-size elliptic curve point multiplication processor over binary and fields. The design details are described in Section 3.
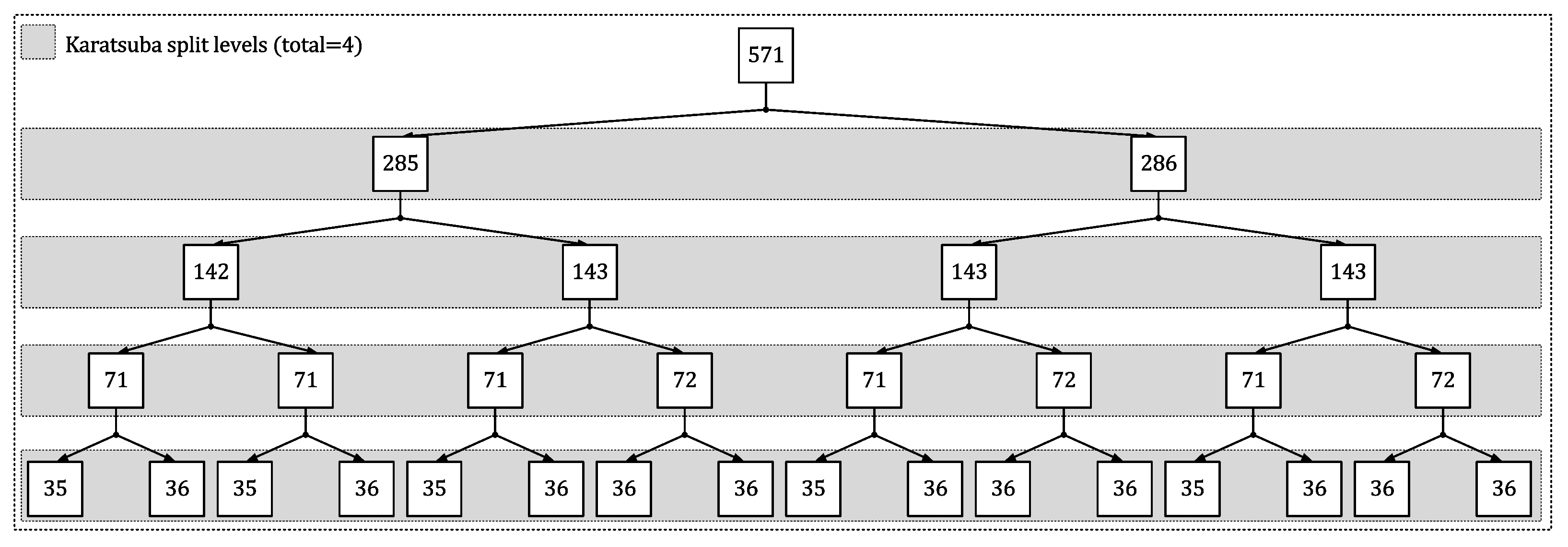
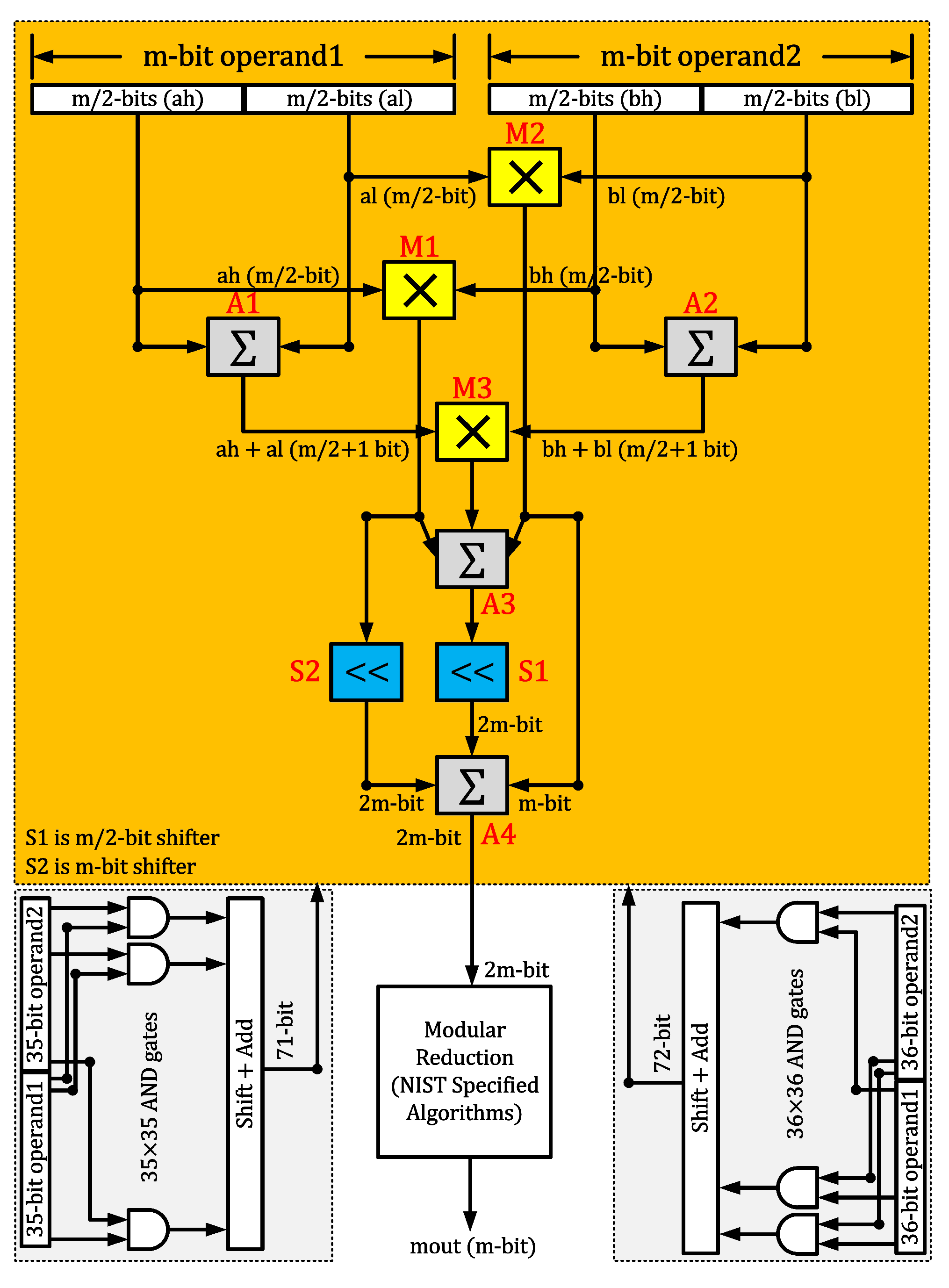
- Towards the area reduction, we have first proposed a hybrid polynomial multiplier architecture for efficient polynomial multiplications. Subsequently, we have utilized the proposed polynomial multiplier to operate modular square and addition chains of the Itoh-Tsujii algorithm [27] for modular inverse computation. A hybrid approach in our polynomial multiplier design is achieved in two steps: (i) 4-level polynomial splits for multiplying large polynomial operands using a general Karatsuba multiplier and (ii) traditional schoolbook multiplication for smaller polynomial multiplications of length 35 and 36 bits. The details of the hybrid approach are presented in Section 3.3.
- An efficient finite-state-machine (FSM) based controller is implemented to provide read/write operations from/to utilized memory block. Moreover, the implemented FSM (also) generates the corresponding control signals for the routing networks (i.e., multiplexer(s) and demultiplexer(s)). We have provided the relevant details in Section 3.4.
2. ECC Background
| Algorithm 1: Montgomery PM Algorithm [17,26] |
| Input: with , Output:

|
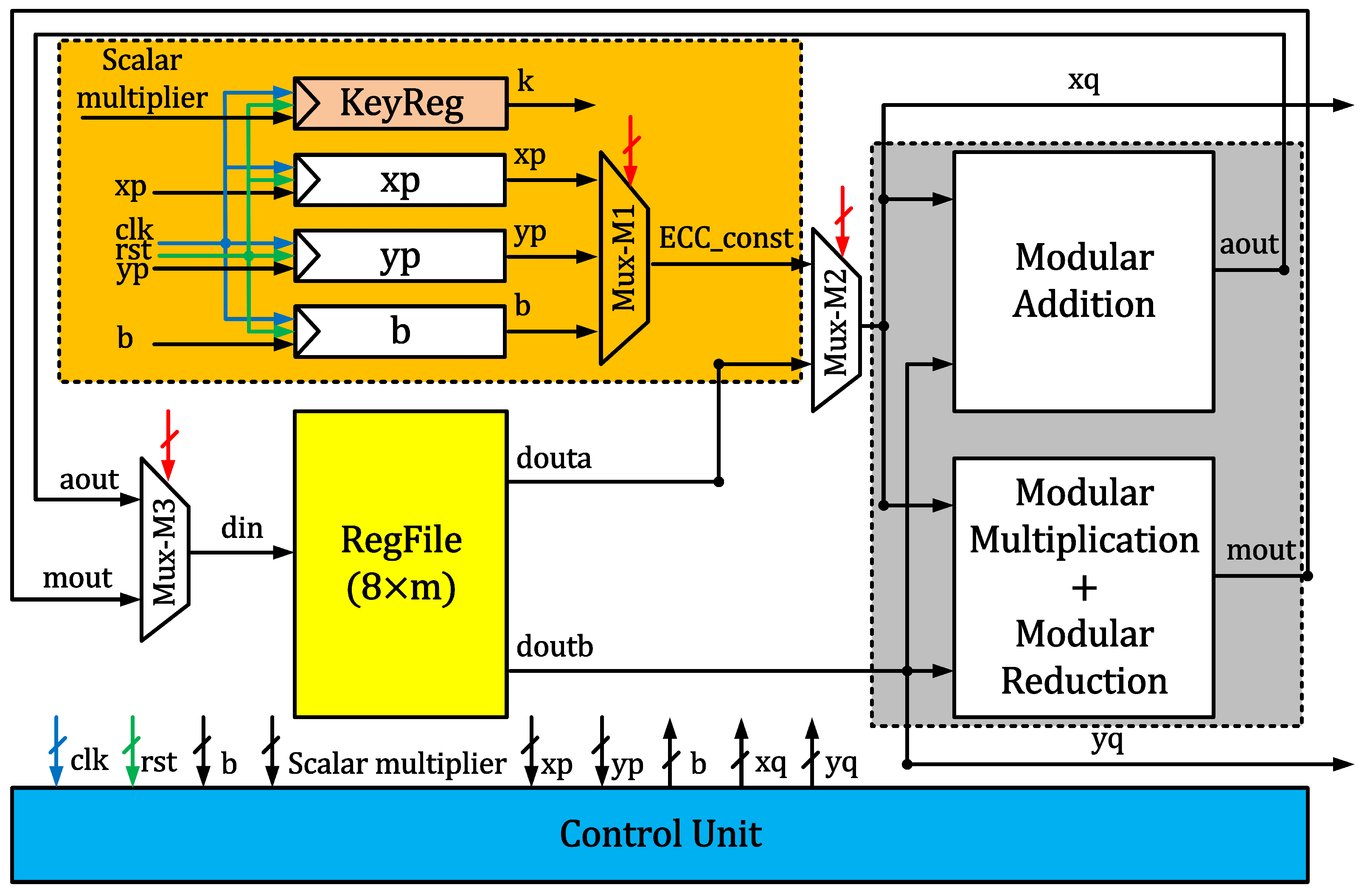
3. Proposed Crypto Processor Architecture
3.1. Data Buffers
3.2. RegFile
3.3. Arithmetic Unit
Proposed Hybrid Karatsuba Modular Multiplier
| Algorithm 2: NIST reduction over [14] |
Input: Polynomial, with -bit length Output: Polynomial, with m-bit length
|
| Algorithm 3: NIST reduction over [14] |
Input: Polynomial, with -bit length Output: Polynomial, with m-bit length
|
3.4. Control Unit and Clock Cycles Calculation
4. Implementation Results and Performance Comparison
4.1. Results
4.2. Comparison to State of the Art
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Proceedings of the Advances in Cryptology—CRYPTO’85 Proceedings; Williams, H.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 417–426. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Sinha Roy, S.; Basso, A. High-speed Instruction-set Coprocessor for Lattice-based Key Encapsulation Mechanism: Saber in Hardware. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 443–466. [Google Scholar] [CrossRef]
- Imran, M.; Almeida, F.; Raik, J.; Basso, A.; Roy, S.S.; Pagliarini, S. Design Space Exploration of SABER in 65 nm ASIC. In Proceedings of the 5th Workshop on Attacks and Solutions in Hardware Security, Virtual Event, 19 November 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 85–90. [Google Scholar] [CrossRef]
- NIST. PQC Standardization Process: Announcing Four Candidates to be Standardized, Plus Fourth Round Candidates. Available online: https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4 (accessed on 11 August 2022).
- Kumar, K.A.; Krishna, A.V.N.; Chatrapati, K.S. New secure routing protocol with elliptic curve cryptography for military heterogeneous wireless sensor networks. J. Inf. Optim. Sci. 2017, 38, 341–365. [Google Scholar] [CrossRef]
- Gulen, U.; Baktir, S. Elliptic Curve Cryptography for Wireless Sensor Networks Using the Number Theoretic Transform. Sensors 2020, 20, 1507. [Google Scholar] [CrossRef] [PubMed]
- Noori, D.; Shakeri, H.; Niazi, T.M. Scalable, efficient, and secure RFID with elliptic curve cryptosystem for Internet of Things in healthcare environment. EURASIP J. Inf. Secur. 2020, 2020, 13. [Google Scholar] [CrossRef]
- Calderoni, L.; Maio, D. Lightweight Security Settings in RFID Technology for Smart Agri-Food Certification. In Proceedings of the 2020 IEEE International Conference on Smart Computing (SMARTCOMP), Bologna, Italy, 22–25 June 2020; pp. 226–231. [Google Scholar] [CrossRef]
- Singh, R.; Miglani, S. Efficient and secure message transfer in VANET. In Proceedings of the 2016 International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016; Volume 2, pp. 1–5. [Google Scholar] [CrossRef]
- Chavhan, S.; Doriya, R. Secured Map Building using Elliptic Curve Integrated Encryption Scheme and Kerberos for Cloud-based Robots. In Proceedings of the 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 11–13 March 2020; pp. 157–164. [Google Scholar] [CrossRef]
- Malina, L.; Dzurenda, P.; Ricci, S.; Hajny, J.; Srivastava, G.; Matulevičius, R.; Affia, A.A.O.; Laurent, M.; Sultan, N.H.; Tang, Q. Post-Quantum Era Privacy Protection for Intelligent Infrastructures. IEEE Access 2021, 9, 36038–36077. [Google Scholar] [CrossRef]
- NIST. Recommended Elliptic Curves for Federal Government Use (1999). Available online: https://csrc.nist.gov/csrc/media/publications/fips/186/2/archive/2000-01-27/documents/fips186-2.pdf (accessed on 5 January 2023).
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2004; pp. 1–311. Available online: https://link.springer.com/book/10.1007/b97644 (accessed on 5 January 2023).
- Li, L.; Li, S. High-Performance Pipelined Architecture of Point Multiplication on Koblitz Curves. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1723–1727. [Google Scholar] [CrossRef]
- Li, J.; Wang, W.; Zhang, J.; Luo, Y.; Ren, S. Innovative Dual-Binary-Field Architecture for Point Multiplication of Elliptic Curve Cryptography. IEEE Access 2021, 9, 12405–12419. [Google Scholar] [CrossRef]
- Khan, Z.U.A.; Benaissa, M. Throughput/Area-efficient ECC Processor Using Montgomery Point Multiplication on FPGA. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 1078–1082. [Google Scholar] [CrossRef]
- Imran, M.; Pagliarini, S.; Rashid, M. An Area Aware Accelerator for Elliptic Curve Point Multiplication. In Proceedings of the 2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Zhao, X.; Li, B.; Zhang, L.; Wang, Y.; Zhang, Y.; Chen, R. FPGA Implementation of High-Efficiency ECC Point Multiplication Circuit. Electronics 2021, 10, 1252. [Google Scholar] [CrossRef]
- Islam, M.M.; Hossain, M.S.; Hasan, M.K.; Shahjalal, M.; Jang, Y.M. Design and Implementation of High-Performance ECC Processor with Unified Point Addition on Twisted Edwards Curve. Sensors 2020, 20, 5148. [Google Scholar] [CrossRef]
- Islam, M.M.; Hossain, M.S.; Hasan, M.K.; Shahjalal, M.; Jang, Y. FPGA Implementation of High-Speed Area-Efficient Processor for Elliptic Curve Point Multiplication Over Prime Field. IEEE Access 2019, 7, 178811–178826. [Google Scholar] [CrossRef]
- Lara-Nino, C.A.; Diaz-Perez, A.; Morales-Sandoval, M. Lightweight elliptic curve cryptography accelerator for internet of things applications. Ad Hoc Netw. 2020, 103, 102159. [Google Scholar] [CrossRef]
- Sajid, A.; Rashid, M.; Imran, M.; Jafri, A.R. A Low-Complexity Edward-Curve Point Multiplication Architecture. Electronics 2021, 10, 1080. [Google Scholar] [CrossRef]
- Rashid, M.; Imran, M.; Jafri, A.R.; Mehmood, Z. A 4-Stage Pipelined Architecture for Point Multiplication of Binary Huff Curves. J. Circuits Syst. Comput. 2020, 29, 2050179. [Google Scholar] [CrossRef]
- Rashid, M.; Imran, M.; Kashif, M.; Sajid, A. An Optimized Architecture for Binary Huff Curves With Improved Security. IEEE Access 2021, 9, 88498–88511. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Jafri, A.R.; Kashif, M. Throughput/area optimised pipelined architecture for elliptic curve crypto processor. IET Comput. Digit. Tech. 2019, 13, 361–368. [Google Scholar] [CrossRef]
- Itoh, T.; Tsujii, S. A fast algorithm for computing multiplicative inverses in GF (2m) using normal bases. Inf. Comput. 1988, 78, 171–177. [Google Scholar] [CrossRef]
- Rashid, M.; Imran, M.; Jafri, A.R.; Al-Somani, T.F. Flexible Architectures for Cryptographic Algorithms — A Systematic Literature Review. J. Circuits, Syst. Comput. 2019, 28, 1930003. [Google Scholar] [CrossRef]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Open-source Library of Large Integer Polynomial Multipliers. In Proceedings of the 2021 24th International Symposium on Design and Diagnostics of Electronic Circuits & Systems (DDECS), Vienna, Austria, 7–9 April 2021; pp. 145–150. [Google Scholar] [CrossRef]
- Mehrabi, M.A.; Doche, C. Low-Cost, Low-Power FPGA Implementation of ED25519 and CURVE25519 Point Multiplication. Information 2019, 10, 285. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M. Architectural review of polynomial bases finite field multipliers over GF(2m). In Proceedings of the 2017 International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; pp. 331–336. [Google Scholar] [CrossRef]
| Inst | Point Addition () | Inst | Point Double () |
|---|---|---|---|
| m | Slices | LUTs | FFs | Clock Cycles | Freq (MHz) | Latency (s) | Thrpt | FoM |
|---|---|---|---|---|---|---|---|---|
| 409 | 4439 | 12,568 | 4129 | 13,903 | 357 | 38.94 | 25.68 kbps | 5.78 |
| 571 | 5683 | 14,356 | 5961 | 20,551 | 317 | 64.82 | 15.42 kbps | 1.07 |
| m | Area (m) | Clock Cycles | Freq (MHz) | Latency (s) | Thrpt | FoM |
|---|---|---|---|---|---|---|
| 409 | 30,561 | 13,903 | 1800 | 7.72 | 129.53 kbps | 4238.40 |
| 571 | 36,857 | 20,551 | 1450 | 14.17 | 70.57 kbps | 1914.69 |
| Ref/Year | m | Device | Slices | LUTs | CCs | Freq (MHz) | Latency (s) |
|---|---|---|---|---|---|---|---|
| Implementations of Weierstrass model of ECC | |||||||
| [15]/2018 | 409 | Virtex 7 | 12,290 | NA | NA | NA | 9.50 |
| [17]/2015 | 409 | Virtex 7 | 6888 | 20,881 | NA | 316 | 32.72 |
| [19]/2021 | 409 | Virtex 6 | NA | 116,241 | 5784 | 135 | 41.36 |
| [15]/2018 | 571 | Virtex 7 | 20,291 | NA | NA | NA | 18.51 |
| [17]/2015 | 571 | Virtex 7 | 12,965 | 38,547 | NA | 250 | 57.61 |
| [19]/2021 | 571 | Virtex 6 | NA | 116,241 | 7628 | 135 | 56.50 |
| [16]/2021 | 571 | Virtex 7 | NA | 80,970 | NA | 274 | 12.55 |
| Implementations of Edward model of ECC | |||||||
| [20]/2020 | 256 | Virtex 6 | 6600 | NA | NA | 93 | 2130 |
| [21]/2019 | 256 | Virtex 7 | 8873 | NA | 262,650 | 178 | 1480 |
| [22]/2020 | 233 | Virtex 6 | 1245 | 3878 | NA | 107 | 6720 |
| [23]/2021 | 233 | Virtex 7 | 2662 | 24,727 | 3244 | 179 | 18.10 |
| [30]/2019 | CURVE25519 | ZYNQ 7000 | NA | 12.95k | NA | 137 | 280.64 |
| Implementations of Huff model of ECC | |||||||
| [25]/2021 | 233 | Virtex 7 | 7123 | NA | 15,495 | 188 | 82.4 |
| [24]/2020 | 233 | Virtex 7 | 7017 | NA | 13,057 | 434 | 30.08 |
| This work | 409 | Virtex 6 | 6439 | 14,578 | 13,903 | 210 | 66.20 |
| This work | 571 | Virtex 6 | 7237 | 16,856 | 20,551 | 170 | 120.88 |
| This work | 409 | Virtex 7 | 4596 | 12,845 | 13,903 | 349 | 39.83 |
| This work | 571 | Virtex 7 | 5797 | 14,687 | 20,551 | 311 | 66.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, M.; Sonbul, O.S.; Zia, M.Y.I.; Kafi, N.; Sinky, M.H.; Arif, M. Large Field-Size Elliptic Curve Processor for Area-Constrained Applications. Appl. Sci. 2023, 13, 1240. https://doi.org/10.3390/app13031240
Rashid M, Sonbul OS, Zia MYI, Kafi N, Sinky MH, Arif M. Large Field-Size Elliptic Curve Processor for Area-Constrained Applications. Applied Sciences. 2023; 13(3):1240. https://doi.org/10.3390/app13031240
Chicago/Turabian StyleRashid, Muhammad, Omar S. Sonbul, Muhammad Yousuf Irfan Zia, Nadeem Kafi, Mohammed H. Sinky, and Muhammad Arif. 2023. "Large Field-Size Elliptic Curve Processor for Area-Constrained Applications" Applied Sciences 13, no. 3: 1240. https://doi.org/10.3390/app13031240
APA StyleRashid, M., Sonbul, O. S., Zia, M. Y. I., Kafi, N., Sinky, M. H., & Arif, M. (2023). Large Field-Size Elliptic Curve Processor for Area-Constrained Applications. Applied Sciences, 13(3), 1240. https://doi.org/10.3390/app13031240









