Integer Ambiguity Parameter Identification for Fast Satellite Positioning and Navigation Based on LAMBDA-GWO with Tikhonov Regularization

Abstract

Satellite positioning is one of the main navigation technologies in unmanned aerial vehicles (UAVs), the accuracy of which has an important impact on the safety, stability, and flexibility of UAVs. The parameters of integer ambiguity are important factors affecting the accuracy of satellite positioning. However, the accuracy of the integer ambiguity cannot be guaranteed when only a few epoch data can be obtained in the fast positioning such that the identification matrix of the integer ambiguity parameters is seriously ill-conditioned and the information of position deviation is enlarged. In this paper, an error checking and correcting strategy is proposed, where a Least-square Ambiguity Decorrelation Adjustment-Grey Wolf Optimization (LAMBDA-GWO) Method combined with the Tikhonov regularization method is developed to improve the accuracy of integer ambiguity for fast satellite positioning. More specifically, the LAMBDA-GWO is first used to search the integer ambiguity parameters. To reduce the ill-condition of the integer ambiguity parameter identification matrix, the Tikhonov regularization method is introduced to regularize the identification matrix such that a reliable integer ambiguity floating-point solution can be obtained. Furthermore, the correctness of the integer ambiguity is checked according to the prior accuracy information of the initial coordinates and the Total Electron Content (TEC), and the part that fails the test is corrected by the Grey Wolf Optimization (GWO) Method. Finally, experimental studies based on a 522 m baseline and a 975 m baseline show that the identification success rates of the proposed method are both above 99%, which is 12% and 23% higher than that of traditional LAMBDA, respectively.

1. Introduction

With the characteristics of small size, flexible mobility, broad application scenarios, and low cost, unmanned aerial vehicles (UAVs) provide solid support for the construction of smart cities in the field of express logistics, smart agriculture, emergency rescue, remote sensing mapping [1,2]. Satellite positioning is one of the main navigation technologies used in UAVs. Positioning and navigational accuracy have a great impact on the performance of UAVs, such as safety, stability, flexibility and attitude control [3]. However, the positioning and navigational accuracy are affected greatly by the low update frequency of receiver data. Traditionally, to obtain high-precision positioning data needs acquire enough epochs of data over a long time. Therefore, fast positioning generally cannot reach high accuracy.

To improve the positioning accuracy of satellites, error sources need to be analyzed and compensated [4,5]. There are many sources of positioning errors in GNSS, such as receiver clock error, satellite clock error, satellite orbit error, tropospheric error, etc. Due to the lack of reference information, the influence of various errors must be considered in the traditional single-point positioning method, and its positioning accuracy is from meter level to decimeter level. Studies show that the error of observation data between stations with short distances is similar [6], thus, using a station with a known accurate position as a reference station to differ the observation data between the reference station and the station close to it can eliminate most of the observation errors of the station and get high-precision positioning results in real-time. That is the core idea of RTK (Real Time Kinematic), a carrier-phase difference technology, that provides real-time three-dimensional positioning results with centimeter-level accuracy. Differential positioning can be divided into pseudo-range difference and carrier-phase difference according to the different types of observations. The pseudo-range difference is a differential processing of the pseudo-range observation, which can be positioned at an epoch moment with positioning accuracy of meters scale. The carrier-phase difference is a differential processing of the carrier phase observation, which can obtain a positioning accuracy of centimeters scale. Compared with pseudo-range signals, carrier-range signals are cosine waves without any markers, which will lead to the problem of unknown cycle ambiguities in receivers. In addition to the algorithm based on RTK, more powerful hardware and satellite receivers, etc., are also effective ways to improve linearity, positioning, and resolution. Moreover, increasing the number of satellite observations and extending the observation time can reduce the pathology of the parameter identification matrix and obtain precision integer ambiguity, which is commonly used in static poisoning for they need more than 1 h to observe enough data. To achieve fast accuracy positioning, this manuscript proposes to improve the success rate of the integer ambiguity solution.

In fast positioning, unknown cycle calculation must be finished in several seconds or minutes with a few periods of observation data. However, the spatial structure of the satellites in a short time is of little change and great similarity. Thus, the ambiguity parameter identification matrix composed of these data is seriously ill-conditioned, which leads to great error or even unable to converge in the identification. There are two steps to get the integer ambiguity. The floating-point solution of integer ambiguity can be obtained first by identification. Then, the integer solution will be calculated by taking the floating-point solution as the initial value. Therefore, fast and accurate identification of the integer ambiguity is the key to improving positioning accuracy and is also the research focus in the field of GNSS position.

Traditionally, there are two methods for ill-conditioned problems i.e., ridge estimation [7] and truncated singular value decomposition (TSVD) [8]. While improving the ill-condition of the matrix, ridge estimation excessively introduces bias, which reduces the reliability of the solution results. While restoring the main properties of the solution, some precision information will be lost in TSVD. Thus, these two methods are not suitable for the identification of integer ambiguity in fast positioning. On the basis of analyzing the structural characteristics of the integer ambiguity identification matrix, Wang [9] proposed a construction method of regularization matrix based on the principle of Tikhonov regularization [10], in which the ill-condition of the integer ambiguity identification matrix is weakened by using a new regularization matrix. Then, a more accurate integer ambiguity floating-point solution and its corresponding mean square error matrix are obtained.

To calculate the integer solution of integer ambiguity, there are mainly three methods: Fast Ambiguity Resolution Approach (FARA) [11], Cholesky [12] and Least-square Ambiguity Decorrelation Adjustment (LAMBDA) [13], With the modernization of GNSS, the use of multi-frequency data for positioning has also been put into practice [14]. LAMBDA can reduce the correlation between integer ambiguities and the search range of integer ambiguities through integer transformation. It is a widely used integer ambiguity search algorithm with fast search speed and good effect. However, LAMBDA searches the solution from an initial value in the solution space, which has low fault tolerance and cannot directly correct the search results. Intelligent evolution algorithms and swarm intelligence algorithms have also achieved good results in solving the integer ambiguity [15] for their global search characteristics. Li [16] combined integer Gaussian transform and particle swarm optimization algorithm to search the integer ambiguity. However, optimization algorithms have the problem of falling into local optimal solutions. Grey Wolf Optimization (GWO) algorithm is a new kind of swarm intelligence optimization algorithm proposed in 2014 [17,18], which has the characteristics of simplicity, less parameter setting, strong global search ability, etc. It has been proven to be superior to particle swarm optimization algorithms in solution accuracy and convergence speed [19].

After the integer ambiguity of the solution is obtained, an effective confirmation method is required to determine whether the integer ambiguity is correct. The early method to confirm the integer ambiguity is to judge whether there is a significant difference between the optimal solution and the suboptimal solution of integer ambiguity through hypothesis testing, but the threshold value is often set according to experience [20]. The currently developed integer ambiguity confirmation method based on integer aperture estimation theory [21] cannot be applied to fast positioning due to the huge amount of calculation. According to the continuity and slow change of Total Electron Content (TEC), Han [22] used the TEC double difference of adjacent epochs to test the integer ambiguity. For the failed epoch, the ambiguity is searched again by removing one or more satellites with low altitude angles, but this method is limited by the number of satellites. Therefore, the traditional LAMBDA cannot directly correct the integer ambiguity, and the intelligent optimization methods also cannot guarantee the solution is globally optimal. And even if the global optimal solution is obtained under the designed objective function, it may not be the correct value. Thus, an efficient search strategy and reasonable integer ambiguity test means are necessary for the rapid positioning of GNSS.

To improve the solution efficiency and accuracy of the integer ambiguity in fast positioning, a search strategy based on LAMBDA-GWO is proposed in this paper, and the correctness test method of integer ambiguity with prior coordinate accuracy information and TEC as feedback index is introduced into the integer ambiguity solving process. Consequently, the problem of search efficiency of traditional methods and the low accuracy caused by the lack of checking and correction is solved.

To improve the solution efficiency and accuracy of the integer ambiguity in fast positioning, a search strategy based on LAMBDA-GWO is proposed in this paper, and the correctness test method of integer ambiguity with prior coordinate accuracy information and TEC as feedback index is introduced into the integer ambiguity solving process. Consequently, the problem of search efficiency of traditional methods and the low accuracy caused by the lack of checking and correction is solved. Finally, experimental verification and comparative analysis are then carried out.

2. Modeling and Analysis of Carrier-Phase Differential Positioning

2.1. Modeling of Carrier-Phase Differential Positioning

The carrier-phase observation is the phase difference between the satellite carrier signal received by the receiver and the same reference signal of the receiver itself. Since the phase difference can only measure the phase value within one cycle, unknown cycles have passed since the satellite carrier signal propagates to the receiver in the actual measurement, i.e., there is an unknown number of full cycles. The carrier-phase observation equation is shown as Equation (1). It indicates the number of cycles the carrier travels from the satellite to the ground station multiplied by its wavelength is the distance from the satellite to the station.

$$\left\{\begin{array}{c}\phi \lambda =\rho -c{V}_{tr}+c{V}_{ts}-N\lambda -V_{ion}-V_{trop}\hfill \\ \rho =\sqrt{{\left(x^s-X_{ref}\right)}^2+{\left(y^s-Y_{ref}\right)}^2+{\left(z^s-Z_{ref}\right)}^2}\hfill \end{array}\right.$$

(1)

where $\phi$ is the observation of the carrier phase, $\rho$ is the distance from the station to the satellite, $(x^s,y^s,z^s)$ and $(X_{ref},Y_{ref},Z_{ref})$ are satellite coordinates and approximate coordinates of ground stations, respectively, c is the speed of light, N is the integer ambiguity, $\lambda$ is the wavelength of the carrier, $V_{tr}$ and $V_{ts}$ are the receiver clock error and the satellite clock error, respectively, $V_{ion}$ is the ionospheric delay error, $V_{trop}$ is the tropospheric delay error.

Equation (2) can be obtained by Taylor expansion at the approximate coordinate $(X_{ref},Y_{ref},Z_{ref})$ of the station

$$\phi \lambda =\rho -\frac{x^s-X_{ref}}{\rho }dX-\frac{y^s-Y_{ref}}{\rho }dY-\frac{z^s-Z_{ref}}{\rho }dZ-c{V}_{tr}+c{V}_{ts}-N\lambda -V_{ion}-V_{trop}$$

(2)

where $dX$, $dY$, and $dZ$ are the coordinate correction quantities of the station coordinates in the three directions of X, Y, and Z. Let $l=\frac{x^s-X_{ref}}{\rho },m=\frac{y^s-Y_{ref}}{\rho },n=\frac{z^s-Z_{ref}}{\rho }$. l, m, and n are the cosine of the approximate position of the station to the satellite in three directions, then, Equation (2) can be simplified to Equation (3).

$$\phi \lambda =\rho -ldX-mdY-ndZ-c{V}_{tr}+c{V}_{ts}-N\lambda -V_{ion}-V_{trop}$$

(3)

Since differential positioning requires at least two receivers, one or more of which is set at a known location as the reference station, and one is used as a mobile station to measure unknown position. Simultaneous observation of satellite p on two stations i (reference station) and j (mobile station). Since station i is a reference station whose coordinates are known, there is no need for Taylor expansion. Hence, the carrier-phase observation equation Equation (4) can be obtained directly from Equation (1). Since station j is a mobile station, only the approximate value of its coordinates is required. Taylor expansion needs to be performed at the approximate coordinates. The carrier-phase observation equation Equation (5) can be obtained from Equation (3).

$${\phi }_i^p\lambda ={\rho }_i^p-c{V}_{tr}^i+c{V}_t^p-N_i^p\lambda -{\left(V_{ion}\right)}_i^p-{\left(V_{trop}\right)}_i^p$$

(4)

$${\phi }_j^p\lambda ={\rho }_j^p-l_j^{p}dX-m_j^{p}dY-n_j^{p}dZ-c{V}_{tr}^j+c{V}_t^p-N_j^p\lambda -{\left(V_{ion}\right)}_j^p-{\left(V_{trop}\right)}_j^p$$

(5)

By a differential between stations i.e., Equation (4) minus Equation (5), we can obtain Equation (6).

$$\left({\phi }_j^p-{\phi }_i^p\right)\lambda =-l_j^{p}dX-m_j^{p}dY-n_j^{p}dZ+c\left(V_{tr}^i\right.\left.-V_{tr}^j\right)+\left(N_i^p-N_j^p\right)\lambda +\left({\rho }_j^p-{\rho }_i^p\right)$$

(6)

From Equation (6), we can know that the satellite-related error terms are eliminated, and only the receiver-related error terms are left. Similarly, if the two stations observe q satellite simultaneously, we can obtain Equation (7).

$$\left({\phi }_j^q-{\phi }_i^q\right)\lambda =-l_j^{q}dX-m_j^{q}dY-n_j^{q}dZ+c\left(V_{tr}^i\right.\left.-V_{tr}^j\right)+\left(N_i^q-N_j^q\right)\lambda +\left({\rho }_j^q-{\rho }_i^q\right)$$

(7)

By a double-differential between stations i.e., Equation (6) minus Equation (7), we can obtain the observation equation of carrier-phase as shown in Equation (8).

$${\phi }_{ij}^{pq}=-\left(l_j^q-l_j^p\right)dX-\left(m_j^q-m_j^p\right)dY-\left(n_j^q-n_j^p\right)dZ-\mathsf{\Delta }{N}_{ij}^{pq}\lambda +L_{ij}^{pq}$$

(8)

where ${\phi }_{ij}^{pq}={\phi }_j^q-{\phi }_i^q-{\phi }_j^p+{\phi }_i^p$, $L_{ij}^{pq}={\rho }_j^q-{\rho }_i^q-{\rho }_j^p+{\rho }_i^p$, $\mathsf{\Delta }{N}_{ij}^{pq}$, is the double-difference integer ambiguity.

According to the double-difference observation equation of the carrier phase, the satellite clock error, the receiver clock error, and the error in the signal propagation path can be greatly reduced or even eliminated. If two dual-frequency GNSS receivers in a certain epoch have an observation of the same $k+1$ satellites, a carrier phase double-difference observation equation can be established, and the linearized double-difference observation equation can be abbreviated as:

$$L=\left[\begin{array}{cc}A\hfill & B\hfill \end{array}\right]\left[\begin{array}{c}X\hfill \\ N\hfill \end{array}\right]-\epsilon$$

(9)

where A is the $k\times 3$ dimensional coordinate coefficient matrix; B is the $k\times k$ dimensional integer ambiguity coefficient matrix; X is the three-dimensional baseline correction vector; N is an k-dimensional integer ambiguity vector; L is the k-dimensional difference vector between the double-difference observation and the calculated value; $\epsilon$ is the observed noise vector. Let $A=\left[\begin{array}{cc}A\hfill & B\hfill \end{array}\right]$, $Y={\left[\begin{array}{cc}X\hfill & N\hfill \end{array}\right]}^T$, then the least squares solution of Equation (9) can be written as:

$$\widehat{Y}={\left(A^{T}PA\right)}^{-1}{A}^{T}PL$$

(10)

where $N_0=A^{T}PA$ is the parameter identification matrix; p is the weight matrix; $Q_Y=N_0^{-1}$ is the covariance matrix.

2.2. Analysis of Ill-Conditioned Problems for the Identification Matrix

Fast positioning requires that the positioning calculation be completed in a relatively short time. But the spatial structure of satellites changes very little in a short time, which makes the identification matrix seriously ill-conditioned and the inversion matrix unstable. By least squares spectral decomposition for Equation (10), Equation (11) can be obtained.

$$\widehat{Y}=\sum _{i=1}^{k+3}\frac{u_i^T\widehat{L}}{{\delta }_i}{v}_i=\sum _{i=1}^{k+3}\frac{u_i^T\tilde{L}}{{\delta }_i}{v}_i+\sum _{i=1}^{k+3}\frac{u_i^T\epsilon }{{\delta }_i}{v}_i$$

(11)

where $u_i$ and $v_i$ are the left and right singular value vectors of the singular value decomposition of the coefficient matrix, ${\delta }_i$ is the decreasing singular value, $\widehat{L}$ and $\widehat{Y}$ are the true values. Although the spectral decomposition value $u_i^T\epsilon$ is small, its rate of convergence towards 0 is much lower than that of the singular value ${\delta }_i$. In fast positioning, there are three singular values that are close to 0 in the integer ambiguity parameter identification matrix. When ${\delta }_i\to 0$, then $\left|u_i^T\epsilon /{\delta }_i\right|\to \infty$. Thus, observation noise and other errors will cause instability of the least squares solution.

According to Tikhonov regularization, the estimation criteria used for the observation Equation (10) are as follows:

$$min\left\{\parallel A\widehat{Y}-L\parallel +\alpha {\widehat{Y}}^{T}R\widehat{Y}\right\}$$

(12)

where $\alpha$ is the regularization parameter; R is the regularization matrix, and A is the Euclidean 2-norm. The key to Tikhonov regularization to deal with ill-conditioned problems is how to select the regularization parameter $\alpha$ and the regularization matrix R. The process of constructing the regularization matrix R in this paper is as follows [23]:

Step 1: Solving the singular value decomposition of matrix A:

$$A=U_{k\times (k+3)}{D}_{(k+3)\times (k+3)}{V}_{(k+3)\times (k+3)}$$

(13)

Step 2: Decomposing matrices D and V:

$$\underset{(k+3)\times (k+3)}{D_{k\times 3}}=\left[\begin{array}{cc}\underset{k\times k}{D_1}& 0\\ 0& \underset{3\times 3}{D_2}\end{array}\right],\underset{(k+3)\times (k+3)}{V}=\left[\begin{array}{cc}\underset{3\times 3}{v_{11}}& \underset{3\times k}{v_{12}}\\ \underset{k\times 3}{v_{21}}& \underset{k\times k}{v_{22}}\end{array}\right]$$

(14)

Step 3: Calculating matrix S:

$$\underset{3\times (k+3)}{S}=\underset{3\times 3}{D_2^{1/2}}\left[\begin{array}{cc}\underset{3\times 3}{v_{11}^T}& 0\end{array}\right]$$

(15)

Step 4: Calculating matrix R with matrix S:

$$R=S^{T}S$$

(16)

where R is a $(k+3)\times (k+3)$ singular matrix, which is the regularization matrix. Combined Equation (12) Equation(10) can be rewritten as:

$$\widehat{Y}=\left[\begin{array}{c}X\hfill \\ N\hfill \end{array}\right]={\left(A^{T}PA+R\right)}^{-1}{A}^{T}PL$$

(17)

Compared with $N_0$ in Equation (10), the addition of R makes the inverse of $\left(A^{T}PA+R\right)$ normal, the essence of which is to add minor constraints to the part corresponding to the baseline component to overcoming the ill-conditioned of the identification matrix. The regularization leads to a more accurate floating-point solution of ambiguity, which uses ${\left(A^{T}PA+R\right)}^{-1}$ replace the covariance matrix to determine the search space of integer ambiguity.

3. Identification of the Integer Ambiguity Parameter

3.1. Modeling of the Integer Ambiguity Parameter Identification Based on LAMBDA

In the double-difference observation Equation (17), N is an integer. Thus, the solution of integer ambiguity can be treated as an integer least squares solution problem, which can be performed in three steps [24]. First, ignoring the integer characteristics of N, we can obtain the estimated value $\widehat{X}$ of X, the floating-point solution $\widehat{N}$ of N, and the covariance matrix $Q_{\widehat{N}}$ of $\widehat{N}$. Then, the corresponding covariance matrix of the estimated solution obtained by least squares of Equation (10) is:

$$Q_Y=\left[\begin{array}{cc}{Q}_{\widehat{X}}\hfill & Q_{\widehat{X}\widehat{N}}\hfill \\ Q_{\widehat{N}\widehat{X}}\hfill & Q_{\widehat{N}}\hfill \end{array}\right]$$

(18)

Then, the integer ambiguity N can be searched under the following conditions:

$${(\widehat{N}-N)}^T{Q}_{\widehat{N}}^{-1}(\widehat{N}-N)=min,N\in Z^n$$

(19)

The double-difference operation can lead to a certain correlation of the integer ambiguity, which will be further enhanced when the observation time is short. LAMBDA can convert the floating-point solution of the integer ambiguity and its variance-covariance matrix into a new space through integer Gaussian transformation, which reduces the correlation between the integer ambiguities and improves search efficiency. The conversion method is as follows:

$$\left\{\begin{array}{c}{Q}_N=z^T{Q}_{\widehat{N}}z\hfill \\ {\overline{N}}^0=z^T\widehat{N}\hfill \\ \overline{N}=z^{T}N\hfill \end{array}\right.$$

(20)

where N, $\widehat{N}$, and ${}_{\widehat{N}}$ are the integer solution, floating-point solution, and variance-covariance matrix of the integer ambiguity in the original search space, respectively. $\overline{N}$, ${\overline{N}}^0$ and $Q_{\overline{N}}$ are the integer solution, floating-point solution, and variance-covariance matrix of the integer ambiguity in the new search space; z is an integer transformation matrix. The objective function can be written as:

$${\left({\overline{N}}^0-\overline{N}\right)}^T{Q}_N^{-1}\left({\overline{N}}^0-\overline{N}\right)\le {\chi }^2$$

(21)

The equation determines a multi-dimensional ellipsoid search space centered on position $\widehat{N}$. ${\chi }^2$ determines the size of the ellipsoid. And the covariance matrix $Q_{\overline{N}}$ determines the shape of the ellipsoid. LAMBDA algorithm changes the shape of the original search space from an ellipsoid to an approximate sphere, reduces the combination of integer ambiguity, and transforms the integer ambiguity obtained in the new search space into the original space through the integer transformation matrix, which improves the search efficiency of the integer ambiguity.

3.2. Modeling of the Integer Ambiguity Parameter Identification Based on GWO

Gray wolf optimization (GWO) is a new kind of swarm intelligence optimization algorithm, which simulates the social hierarchy mechanism and hunting behavior of gray wolf groups in nature [17]. In the gray wolf population, there is a strict social hierarchy. The $\alpha$ wolf is the highest-level gray wolf. The $\beta$ and $\delta$ wolves are the two suboptimal gray wolves, and the lowest-grade gray wolf is called the $\tau$ wolf. Gray wolf hunting is mainly divided into three stages: tracking, encirclement, and attack. The gray wolf population is N and the search space is D dimension. Since the position of the gray wolf is related to the potential solution of the integer ambiguity, the position of the ith gray wolf needs to be rounded after the update, which can be denoted as $X_i=round\left(x_{i1},x_{i2},\dots ,x_{iD}\right)$. The iteration process of GWO can be described as follows:

$$\left\{\begin{array}{c}\hfill D=\left|C{X}_p\left(t\right)-X\left(t\right)\right|\\ \hfill X(t+1)=X_p\left(t\right)-AD\end{array}\right.$$

(22)

where t is the number of iterations; A and C are coefficient vectors; $X_p$ and X are the position vectors of prey and gray wolves. A and C are calculated as follows:

$$\left\{\begin{array}{c}A=2a{r}_1-a\hfill \\ C=2r_2\hfill \end{array}\right.$$

(23)

where a is the convergence factor which decreases linearly from 2 to 0 as the number of iterations increases; $r_1$ and $r_2$ are random numbers in the interval $[0,1]$.

Among the wolves, $\alpha$, $\beta$ and $\delta$ are closest to the prey. And the position of these three can be used to determine the location of the prey, which can be described mathematically as follows:

$$\left\{\begin{array}{c}{D}_{\alpha }=\left|C_1{X}_{\alpha }-X\right|\hfill \\ D_{\beta }=\left|C_2{X}_{\beta }-X\right|\hfill \\ D_{\delta }=\left|C_3{X}_{\delta }-X\right|\hfill \end{array}\right.$$

(24)

where $D_{\alpha }$, $D_{\beta }$ and $D_{\delta }$ denote the distance between $\alpha$, $\beta$ and $\delta$ and other individuals, respectively; $X_{\alpha }$, $X_{\beta }$ and $X_{\delta }$ denote the current positions of $\alpha$, $\beta$ and $\delta$; $C_1$, $C_2$ and $C_3$ are random vectors; X is the current position of the gray wolf. $X_1$, $X_2$ and $X_3$ indicate the position of $\tau$ wolf need to be adjusted by the influence of $\alpha$, $\beta$ and $\delta$ wolves. The direction in which the individual is moving towards the prey can be written as:

$$\left\{\begin{array}{c}{X}_1=X_{\alpha }-A_1{D}_a\hfill \\ X_2=X_{\beta }-A_2{D}_{\beta }\hfill \\ X_3=X_{\delta }-A_3{D}_{\delta }\hfill \end{array}\right.$$

(25)

Then, the next position of the gray wolf is:

$$X(t+1)=\frac{X_1+X_2+X_3}{3}$$

(26)

3.3. Testing and Correction Strategies

To solve the problem of low fault tolerance and no feedback of the commonly used LAMBDA, we propose to use the TEC test and station prior coordinate (position) accuracy to test the identified integer ambiguity. After the integer ambiguity is fixed, the difference between the calculated coordinate value and the prior coordinate will be calculated. If the difference exceeds the prior threshold value, the identified integer ambiguity is judged to be an invalid solution. By combining the dual-frequency observation data, a wavelength of 86 cm can be obtained, which can lead to much more deviation than the standard 19 cm and 24 cm wavelength. Therefore, the coordinate deviation calculated by the incorrect integer ambiguity is also enlarged. Generally, the coordinate deviation of the correct integer ambiguity solution is 1 cm grade, while the coordinate deviation of the incorrect integer ambiguity solution can reach more than 10 cm grade. Therefore, if the deviation exceeds the median value of more than 10 cm, the result is considered incorrect.Because the carrier signal propagation path has a strong correlation in time and space, the TEC values of adjacent epochs are very similar. Under the condition of fixed integer ambiguity, the double-difference ionospheric delay can be written as [22]:

$${\mathsf{\Delta }}_{ion}={\lambda }_1\nabla \mathsf{\Delta }{\varphi }_{L1}-{\lambda }_2\nabla \mathsf{\Delta }{\varphi }_{L2}-{\lambda }_1\nabla \mathsf{\Delta }{N}_{L1}-{\lambda }_2\nabla \mathsf{\Delta }{N}_{L2}$$

(27)

where ${\lambda }_1$, $\mathsf{\Delta }{\varphi }_{L1}$ and $\mathsf{\Delta }{N}_{L1}$ are the wavelength, phase and integer ambiguity of $L1$ carrier; ${\lambda }_2$, $\mathsf{\Delta }{\varphi }_{L2}$ and $\mathsf{\Delta }{N}_{L2}$ are the wavelength, phase and integer ambiguity of $L2$ carrier respectively.

If the integer ambiguity is fixed correctly, the value of the double-differential ionospheric delay changes little and steadily. Otherwise, there will be a big jump. By these two steps, most of the fixed ambiguity errors can be eliminated, and then appropriate corrective measures can be selected to correct the error solution. In this paper, Tikhonov regularization and LAMBDA are first used to identify the parameters of the integer ambiguity. Then, the TEC test and the prior coordinate accuracy test are used to analyze the validity of the integer ambiguity identification results. Finally, the GWO algorithm is used to correct the solution units that fail the test. The flowchart is shown in Figure 1.

4. Experiments

To verify the effectiveness of the proposed method, three known control points on campus were selected as the prior coordinates. Certain receivers were used to process the satellite signal. The processed observation data was acquired. The receivers at both ends of the baseline were required to acquire data at the same time during the data acquisition process. The data acquisition device was shown in Figure 2.

In the experiment, the carrier phase observation data of two baselines of 522 m and 975 m were collected for differential positioning modeling, and the sampling interval is 5 s. For the baseline of 522 (baseline 1), the total sampling time was 1 h, and 305 consecutive sampling values which can observe 5 satellites were selected. Every 6 values formed an epoch for position solving, so we can obtain 300 epochs. Similarly, for the baseline of 975 m (baseline 2), the total sampling time is 30 min, and 165 consecutive sampling values are selected. We can obtain 160 epochs. Each epoch is solved independently. Whether the epoch is solved correctly is determined by the value of deviation. If the deviation is more than 10 cm, the solution of the epoch is considered incorrect. The ratio of the correctly solved epoch number to the total epoch number is used as the success rate of the solution.

With the above two sets of data, LAMBDA was used to solve the integer ambiguity first. Then TEC test and prior coordinate accuracy test were used to analyze the correctness of the integer ambiguity solution. And GWO was used to correct the solution units that fail the test. The identification calculation results are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

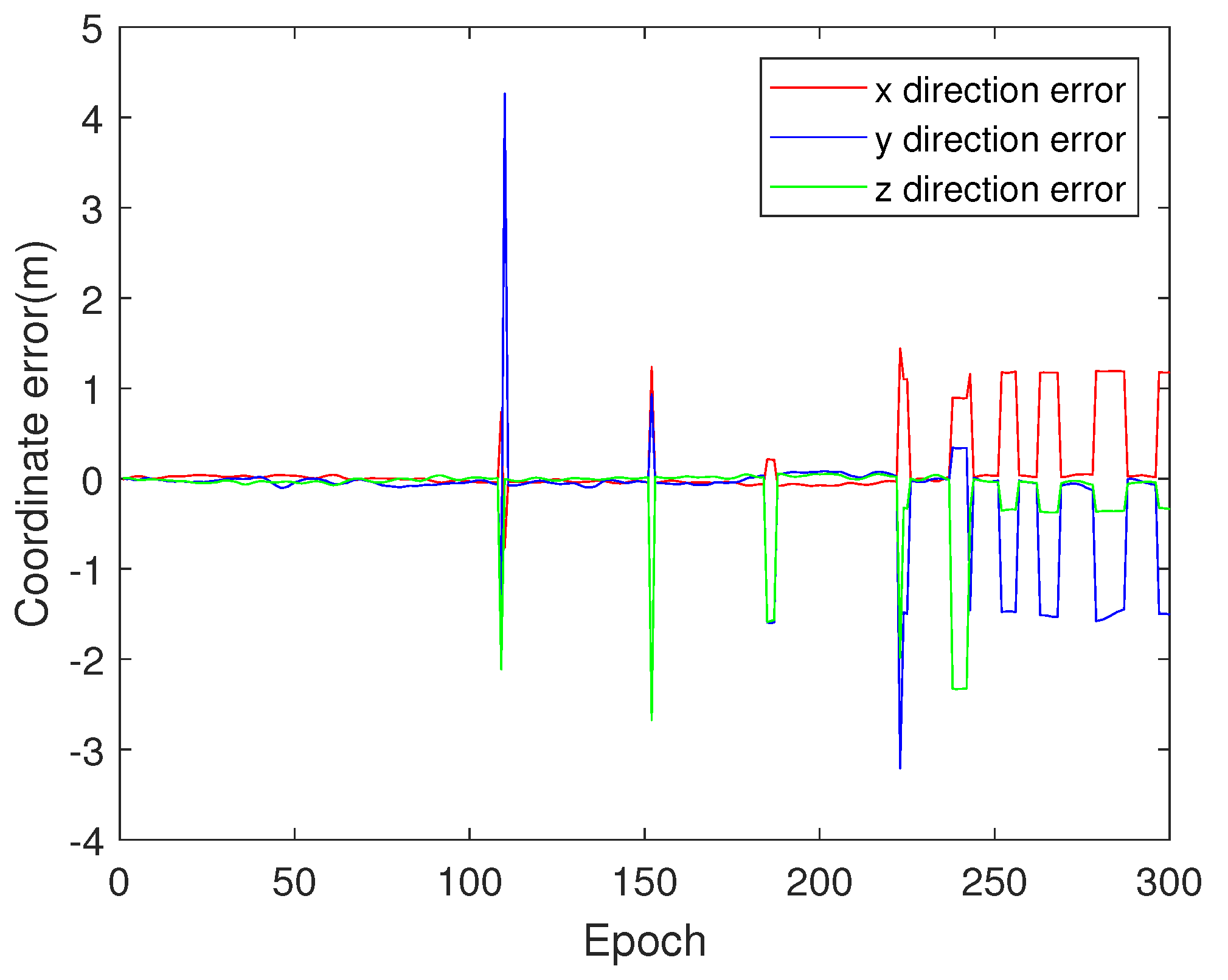
Figure 3 and Figure 4 show the deviation between the coordinates obtained by the traditional LAMBDA and the actual coordinates for the two baselines. Since traditional LAMBDA cannot correct the erroneously solved epochs, we can see there are many cases in Figure 3 and Figure 4 where the coordinates of the epoch have far deviated from the median for the solved integer ambiguity value is incorrect.

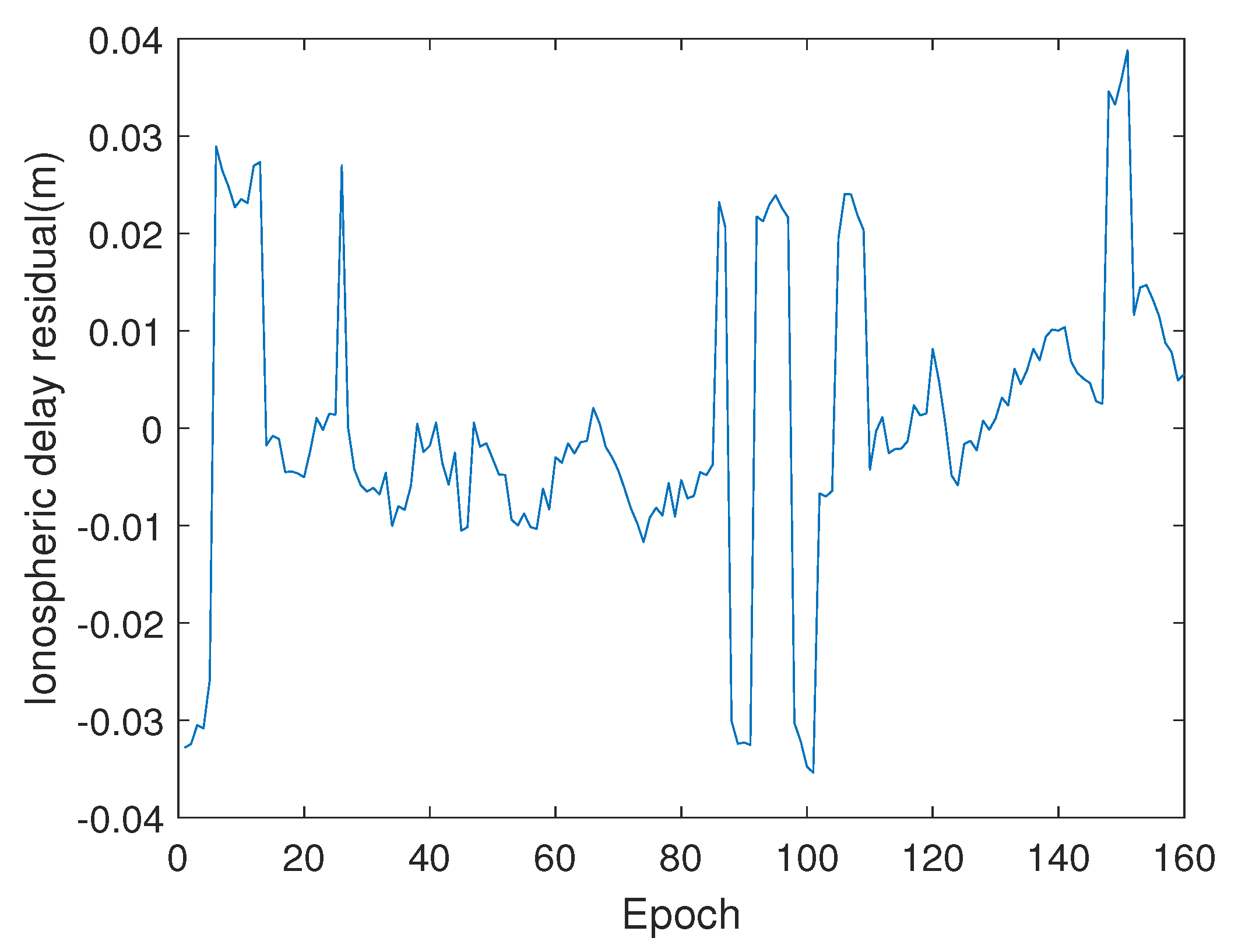
Figure 5 and Figure 6 show the Ionospheric delay residual of satellite 32 for the two baselines solved according to the traditional LAMBDA. The ionospheric delay residual value between adjacent epochs is similar due to the slow change of the ionosphere. When the integer ambiguity is incorrect, there will be a jump in the ionospheric delay residual between adjacent epochs, which is also the basis of ionospheric testing. The locations where the jump occurs in Figure 5 and Figure 6 also correspond to the epochs in Figure 3 and Figure 4 where the integer ambiguity is incorrect.

Moreover, if the ionospheric delay residual is used alone for testing, the calculation of the ionospheric delay residual of the first epoch is very important, because the subsequent test is also based on the first epoch. 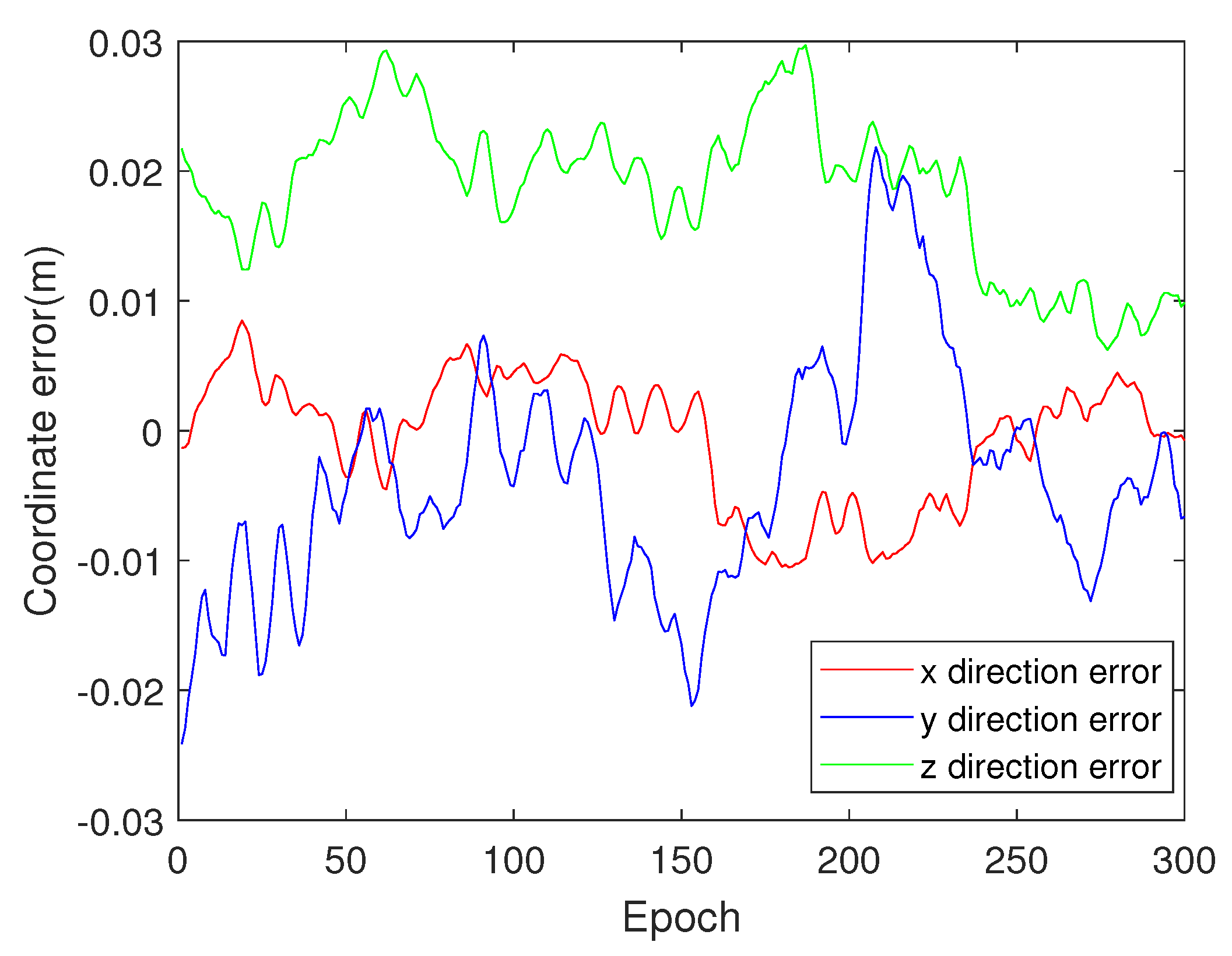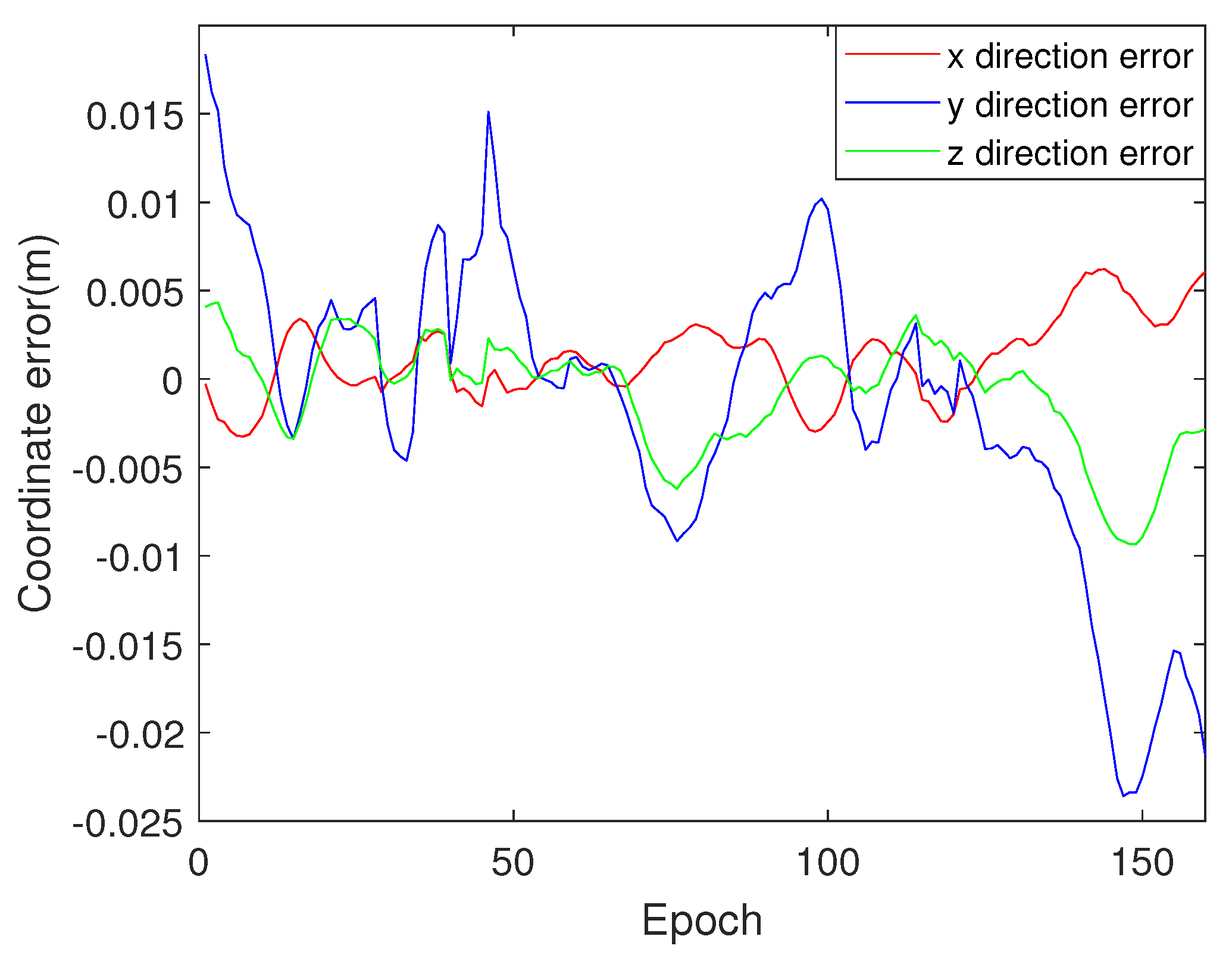It can be seen from Figure 4 that the integer ambiguity solution value of the first epoch is incorrect, so the ionospheric delay residual in the first epoch is incorrect as shown in Figure 6. Finally, the coordinate deviation of the two baselines is solved by the proposed test method and correction strategy, as shown in Figure 7 and Figure 8, which can correct the incorrect solution in traditional LAMBDA method shown in Figure 3 and Figure 4. To further verify the effectiveness of the method proposed in this paper, LAMBDA, IPSO-AR [16] and LAMBDA-GWO are used to solve the two sets of data collected, respectively. The results of the three methods are compared in

Table 1. Comparsion of three methods.

Base Line (m)	Method	Epochs	Success Rate (%)	Solution Time (s)
	LAMBDA	300	87.33	0.185
522	IPSO-AR	300	83.67	31.921
	LAMBDA-GWO	300	99.33	8.879
	LAMBDA	160	76.25	0.094
975	IPSO-AR	160	76.87	17.528
	LAMBDA-GWO	160	99.38	5.021

.

The results show that the solution success rates of the two baselines using LAMBDA are 87.33% and 76.25%, respectively. The solution success rates using IPSO-AR are 83.67% and 76.87%, respectively. The solution success rates using the proposed LAMBDA-GWO are 99.33% and 99.38%, respectively. The solution success rates are improved by 12% and 23% compared with LAMBDA. It can be seen that the success rates of LAMBDA and IPSO-AR are similar, but LAMBDA has a higher solving efficiency. With the increase of the baseline length, the success rate of the two solution methods decreases, but the proposed method (LAMBDA-GWO) is not significantly affected by the baseline distance. Therefore, while ensuring the solving efficiency, it has a higher success rate, which is also one of the advantages of the proposed method.

5. Conclusions

A carrier-phase differential positioning model is established based on RTK theory. To achieve fast accuracy positioning, this manuscript proposes to improve the success rate of the integer ambiguity solution. Experiments have shown that the proposed method (LAMBDA-GWO) is not significantly affected by the baseline length. While ensuring the solving efficiency, it also has a higher success rate. The main innovations of the work are as follows: (1) To solve the problem of low fault tolerance and no feedback of the traditional LAMBDA, TEC test, and station prior coordinate accuracy are used to test the identified integer ambiguity, and an intelligent optimization algorithm is used to search the optimal integer solution when the test results are invalid to improve the accuracy of parameter identification. (2) A parameter identification method for integer solution of the integer ambiguity based on LAMBDA- GWO is proposed to solve the problems of poor solution accuracy and algorithm instability of the traditional method when the measurement error is large.

However, the GNSS system cannot completely determine the flight state, position, and attitude of a UAV, especially in complex environments. Therefore, multi-sensor fusion such as GNSS and inertial navigation systems should be considered to obtain more reliable position and attitude information, which will be studied the future work.