Deep Q Network Based on a Fractional Political–Smart Flower Optimization Algorithm for Real-World Object Recognition in Federated Learning
Abstract
:1. Introduction
- FP-SFOA-DQN-FL for real-world object identification in FL: an efficacious model is developed for real-world object recognition in FL using FP-SFOA-DQN-FL.
- The object detection is conducted based on SegNet, and this classifier is optimally biased utilizing PSFOA.
- The object identification is accomplished utilizing DQN, and this network is optimally tuned based on modeled FP-SFOA.
- The FP-SFOA is derived by the consolidation of the FC concept with PO and SFOA.
2. Motivation
2.1. Literature Survey
2.2. Major Issues
- Achieving real-time detection in crowded areas becomes a challenging issue in the existing models.
- Imbalanced data handling is another major issue in the existing object-detection models.
- Owing to network slicing in resolution image sensing, it was unable to update the needs of resource allocation, computation offloading resolutions, and service caching.
- The communication overhead of the conventional models is high.
3. Proposed FP-SFOA-DQN-FL for Real-World Object Recognition in FL
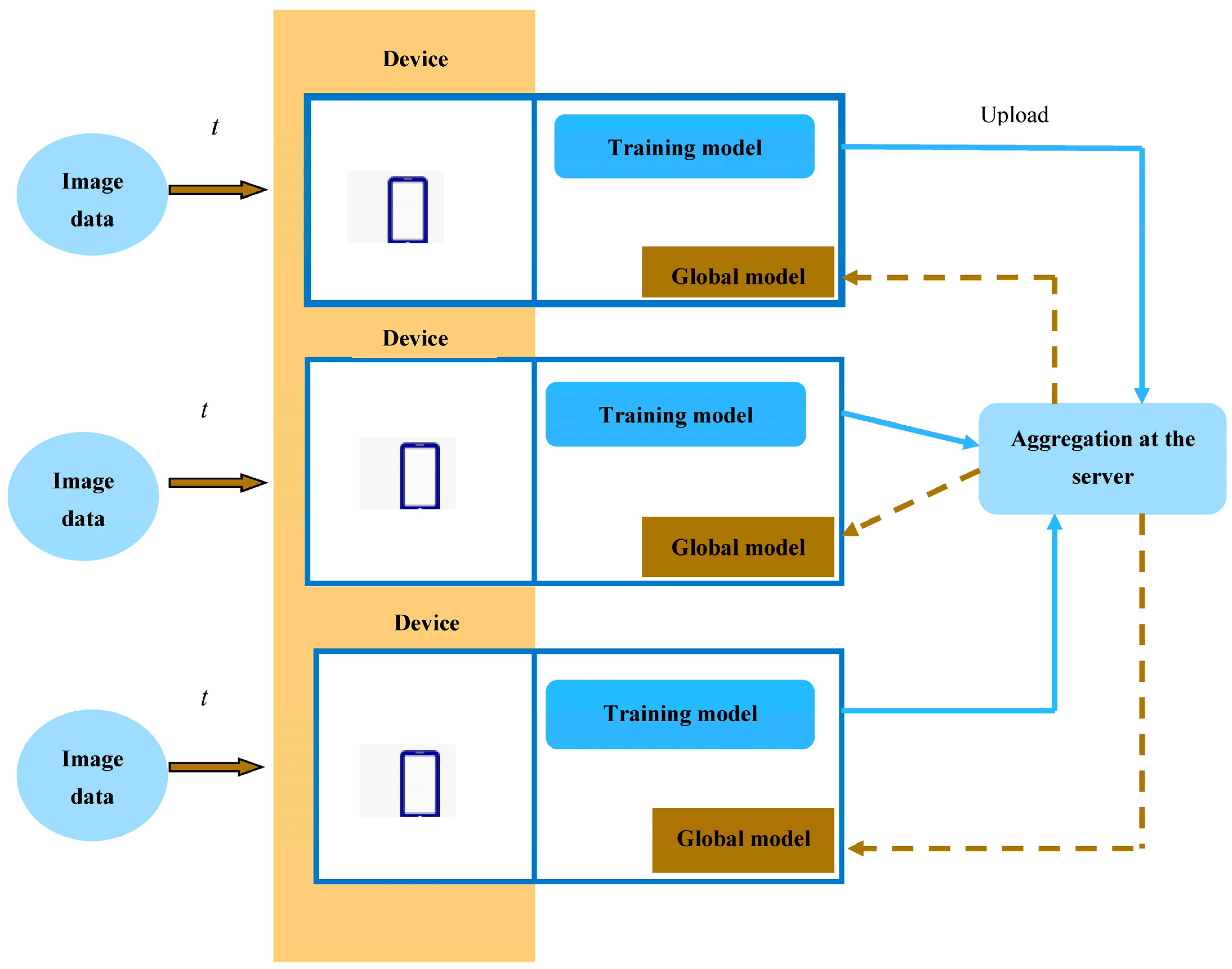
3.1. Local Training Depending upon Local Data
3.1.1. Training at Every Node
3.1.2. Training Model
3.2. Data Acquisition
3.3. Pre-Processing Utilizing Bilateral Filter
3.4. Object Detection Using SegNet
- Structural diagram of SegNet
- Encoder network
- 2.
- Decoder network
- 3.
- Softmax classifier
- ii.
- Training of SegNet using proposed PSFOA
- Smart Flower position encoding
- Objective function
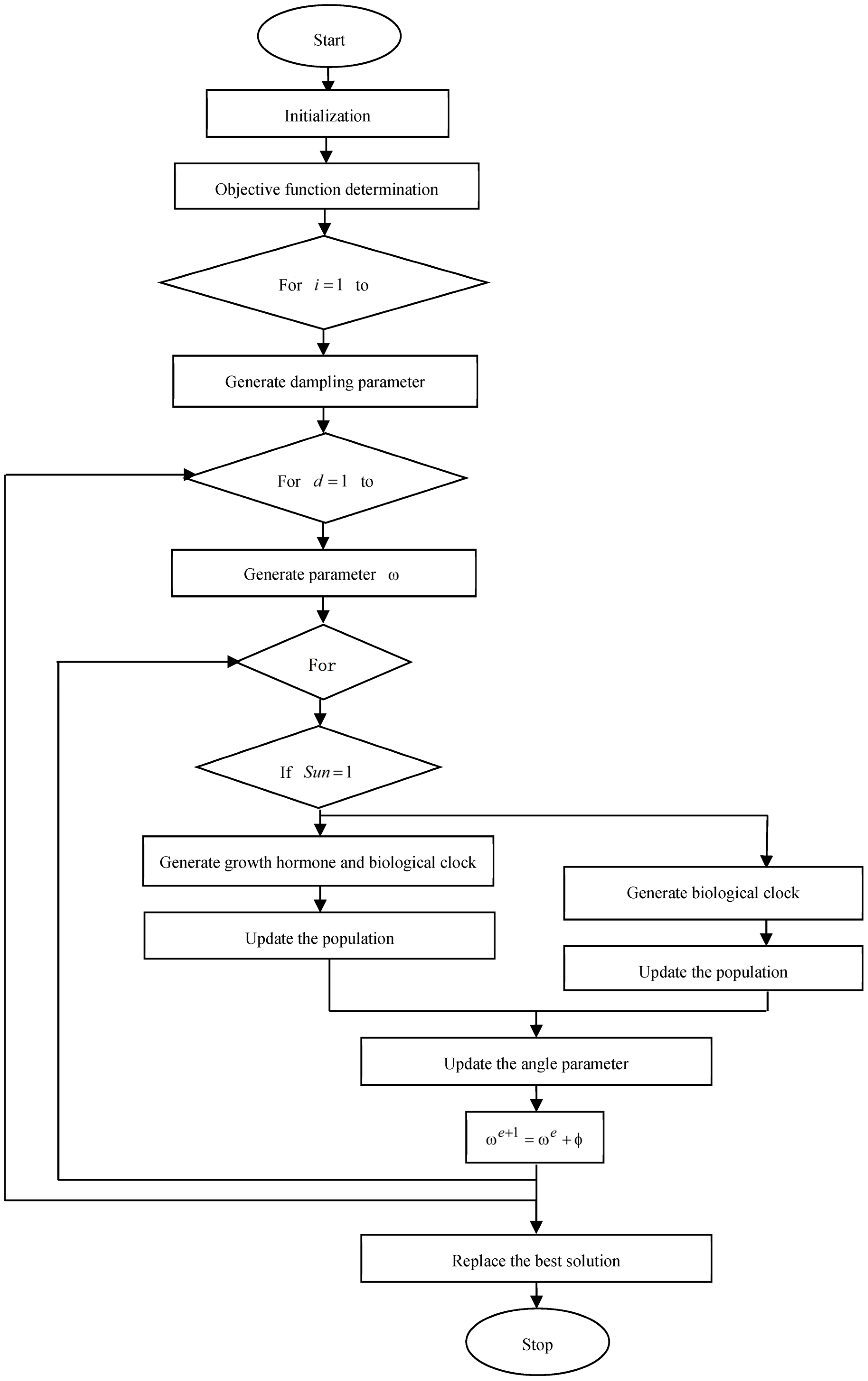
- Algorithmic steps of proposed PSFOA
- Step 1. Initialization of Sunflower population
- Step 2. Determine objective function
- Step 3. Evaluate the first mode
- Step 4. Generate damping parameter
- Step 5. Generate the Hours’ day parameter
- Step 6. Update the solution
- Step 7. Termination
| Algorithm 1 Pseudo-code of devised PSFOA |
| 1 Input: Population size , maximum count of iterations , Number of decision variables , Sun parameter 2 Output: 3 Begin 4 Initialized the population 5 Evaluate fitness function utilizing Equation (3) 6 for to 7 Generate damping parameter using Equation (6) 8 for to 9 Generate parameter 10 for to 11 if 12 Generate the growth hormone and biological clock 13 Update the population using Equation (5) 14 Else 15 Generate parameter 16 Update the population using Equation (18) 17 end if 18 Upgrade the angle parameter 19 20 end for 21 end for 22 Replace by 23 end for 24 Return best solution 25 Terminate |
3.5. Feature Extraction
- Shape Local Binary Texture (SLBT)
- ii.
- Speeded-Up Robust Feature (SURF);
- iii.
- Scale-Invariant Feature Transform (SIFT)
- iv.
- Oriented Fast and Rotated Brief (ORB)
- v.
- Gray-Level Co-Occurrence Matrix (GLCM);
- vi.
- Hierarchical skeleton features
- vii.
- ResNet features
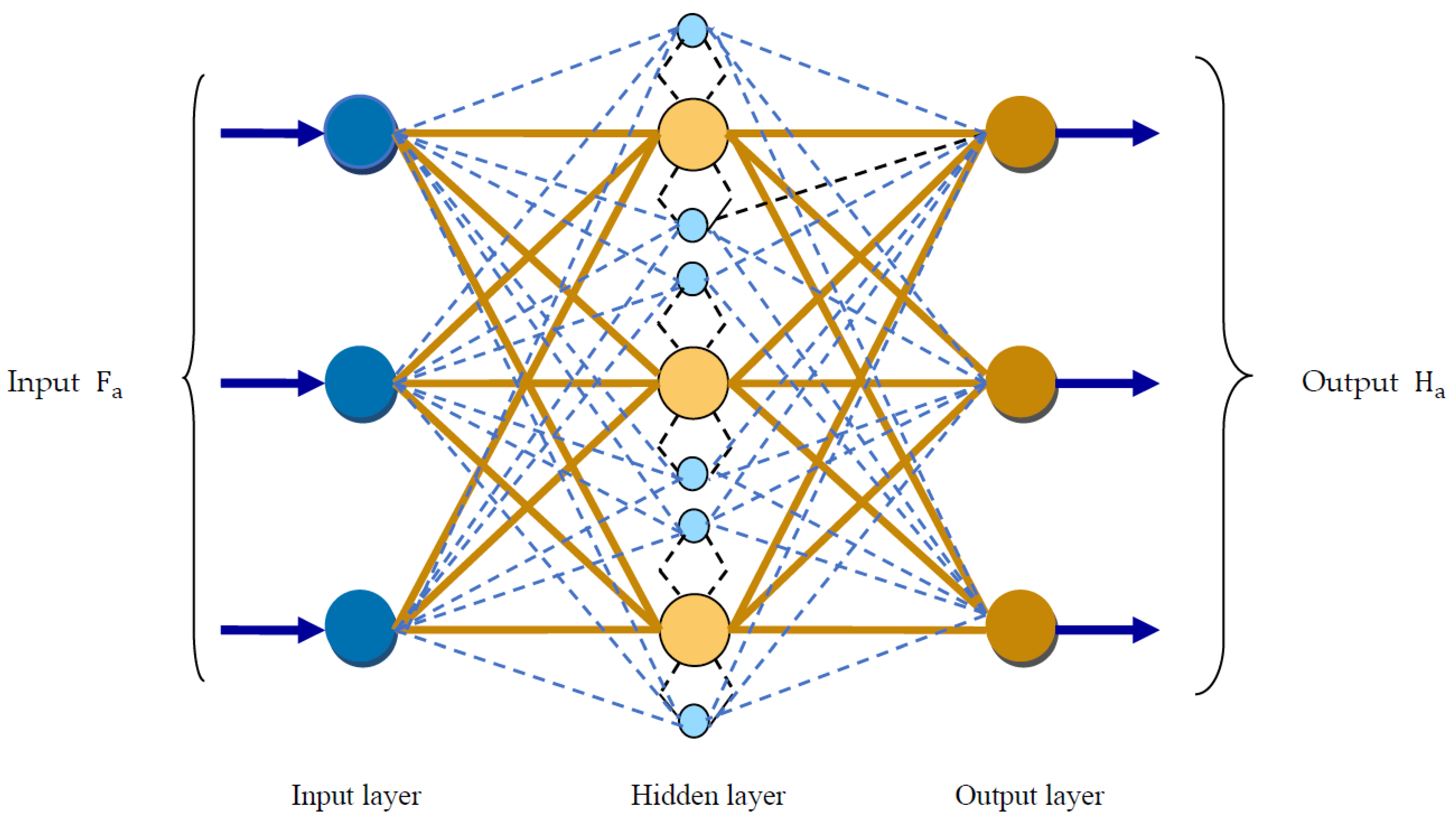
3.6. Object Recognition Using Proposed FP-SFOA
- Architecture of DQN
- ii.
- Training of DQN using FP-SFOA
3.7. Aggregation at the Server Using CAViaR Model
3.8. Apply Global Training Model to Every Local Node
4. Results and Discussion
4.1. Experimental Setup
4.2. Dataset Description
4.2.1. YOLO Object-Detection Dataset
4.2.2. MyNursingHome Dataset
4.3. Experimental Results
4.4. Evaluation Metrices
4.4.1. Accuracy
4.4.2. Loss Function
4.4.3. Mean Square Error (MSE)
4.4.4. Root Mean Square Error (RMSE)
4.4.5. False-Positive Rate (FPR)
4.4.6. Mean Average Precision
4.4.7. Communication Cost
4.5. Performance Analysis
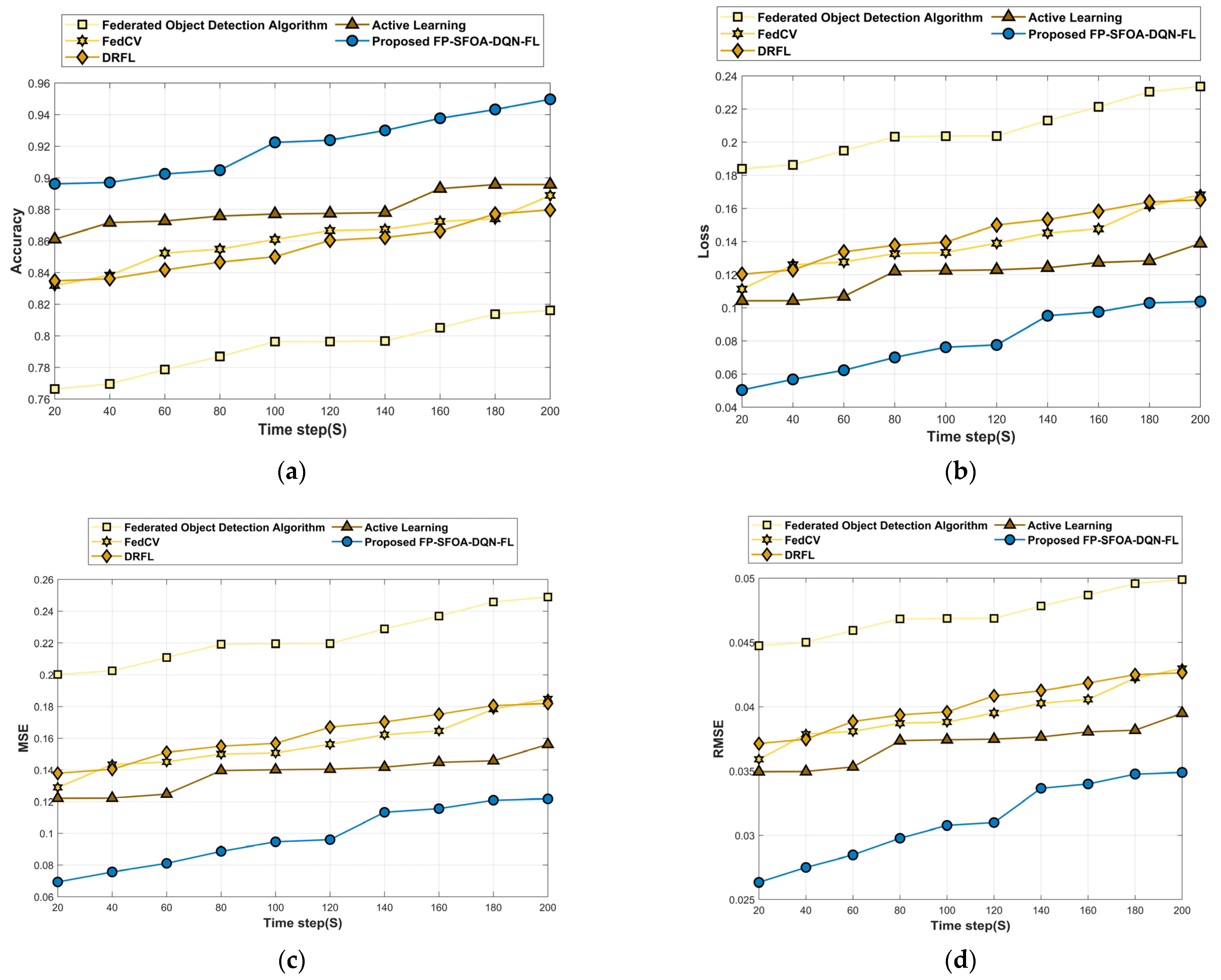
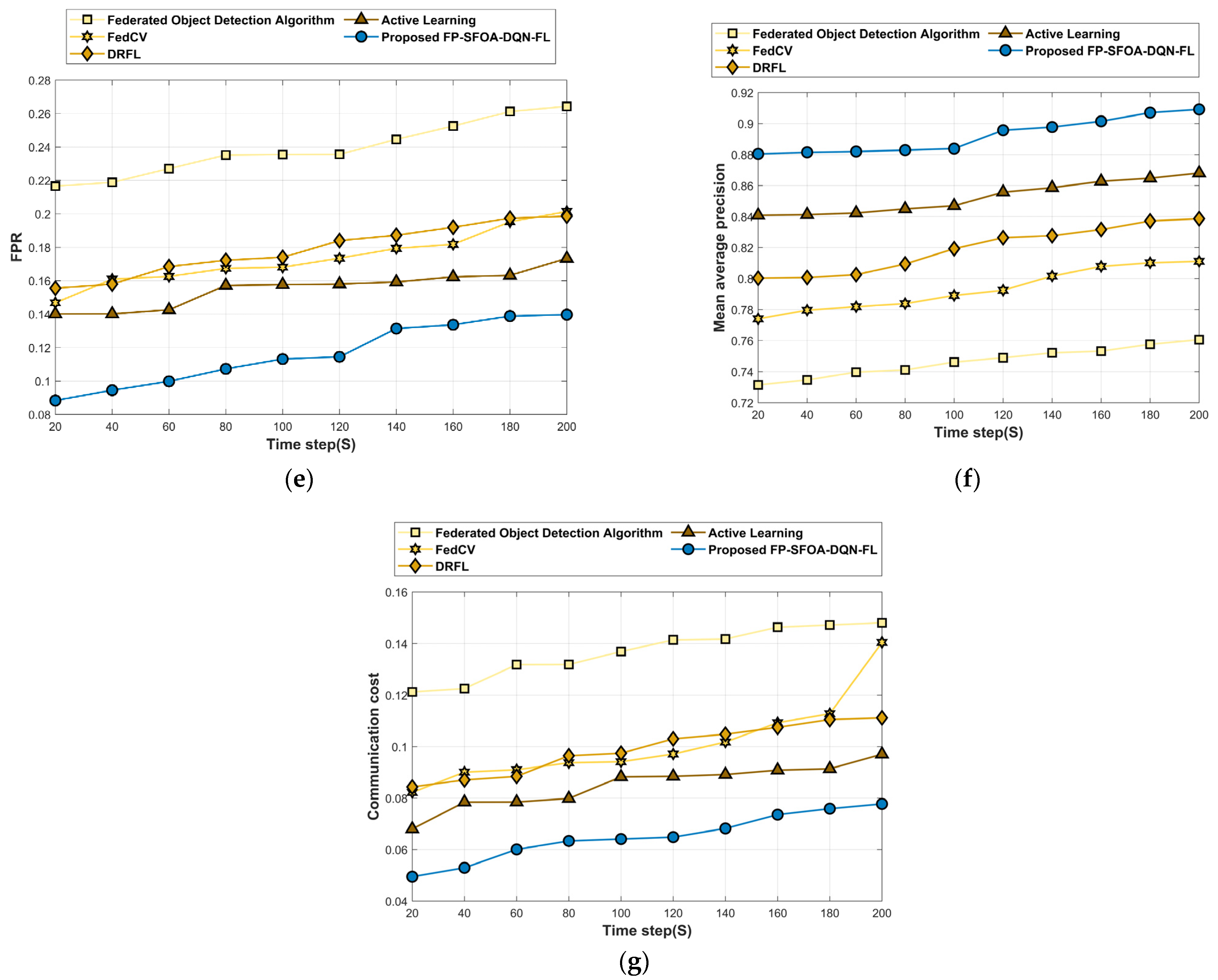
4.5.1. Performance Analysis Based on YOLO Object-Detection Dataset
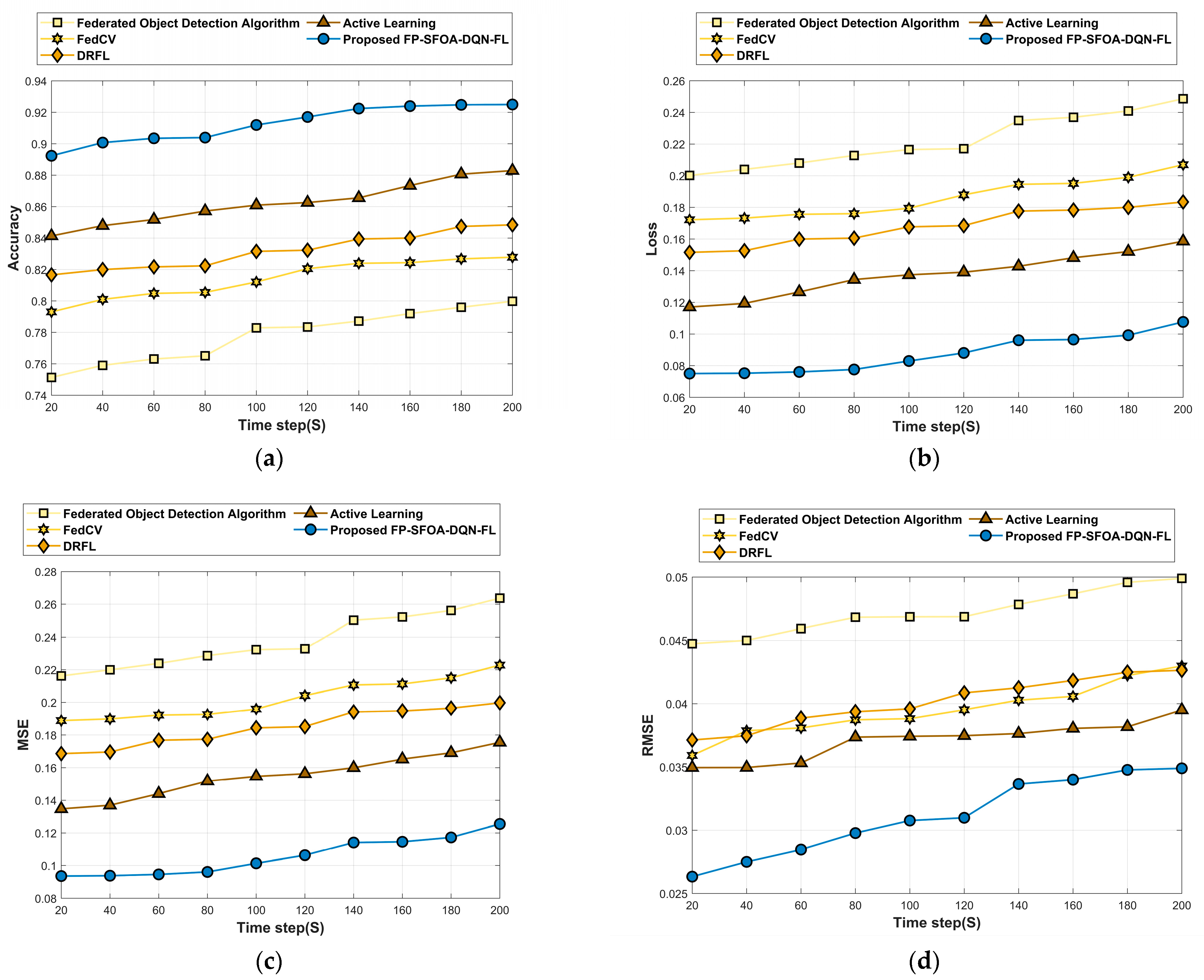
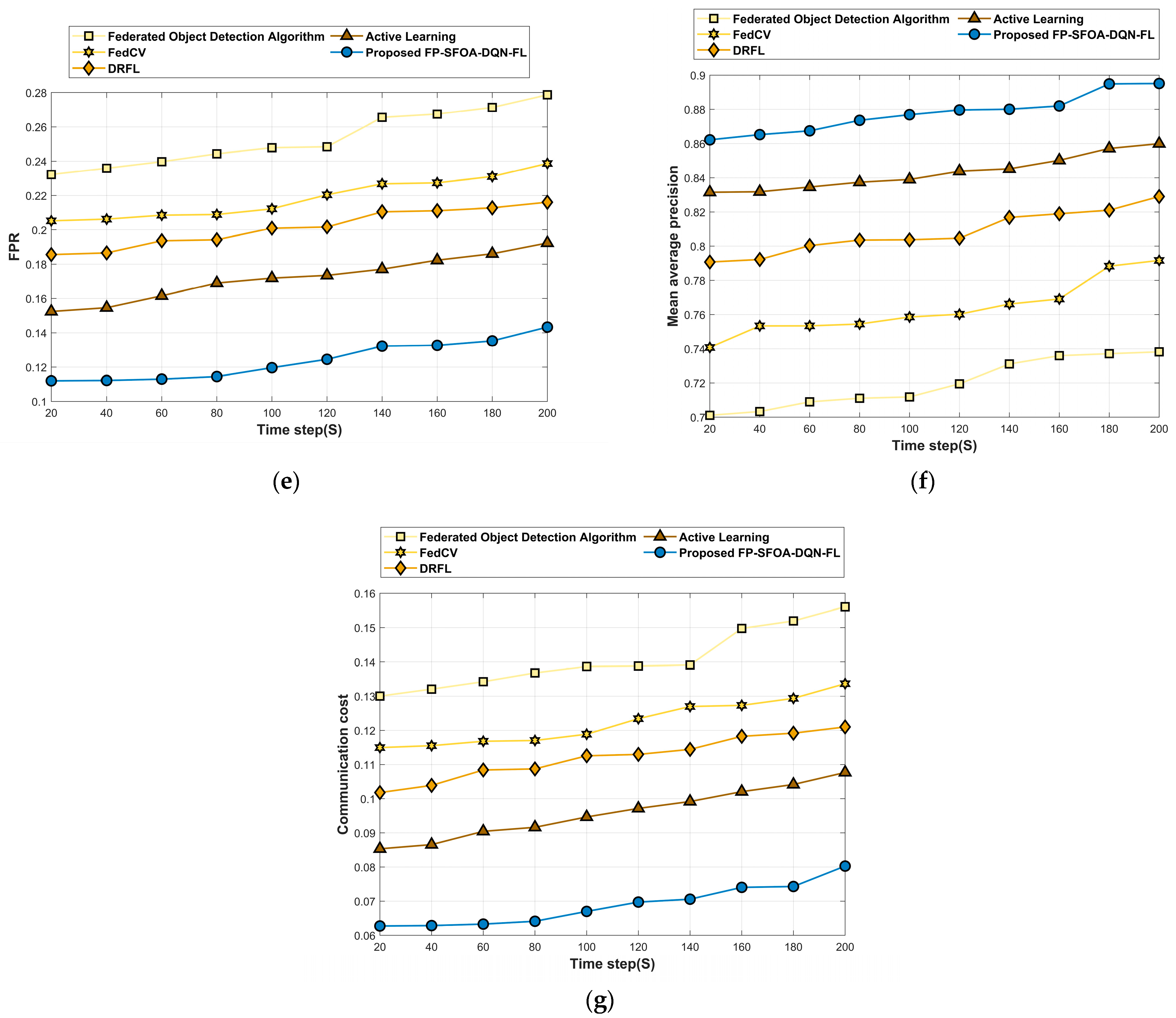
4.5.2. Performance Analysis Based on MyNursingHome Dataset
4.6. Comparative Methods
4.7. Comparative Evaluation
4.7.1. Analysis Based on YOLO Object-Detection Dataset
4.7.2. Evaluation Based on MyNursingHome Dataset
4.8. Comparative Discussion
4.9. Analysis of Computational Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FL | Federated learning. |
| CV | Computer Vision. |
| AI | Artificial Intelligence. |
| FC | Fractional Calculus. |
| SFOA | Smart Flower Optimization Algorithm. |
| FP-SFOA | Fractional Political–Smart Flower Optimization Algorithm. |
| CAViaR | Conditional Autoregressive Value at Risk by Regression Quantiles. |
| MPC | Multi-Party Computing. |
| CNNs | Convolutional neural networks. |
| DRFL | Dilation RetinaNet Face Location. |
| FedAvg | Federated Averaging. |
| DL | Deep learning. |
| DQL | Deep Q-Learning. |
| ICM | Inconsistency-Capture module. |
| PO | Political optimizer. |
| SLBT | Shape Local Binary Texture. |
| GLCM | Gray level co-occurrence matrix. |
| SURF | Speeded-Up Robust Feature. |
| ORB | Oriented Fast and Rotated Brief. |
| MSE | Mean Square Error. |
| RMSE | Root Mean Square Error. |
| FPR | False-Positive Rate. |
References
- Luo, J.; Wu, X.; Luo, Y.; Huang, A.; Huang, Y.; Liu, Y.; Yang, Q. Real-world image datasets for federated learning. arXiv 2019, arXiv:1910.11089. [Google Scholar]
- Hussain, F.; Hassan, S.A.; Hussain, R.; Hossain, E. Machine learning for resource management in cellular and IoT networks: Potentials, current solutions, and open challenges. IEEE Commun. Surv. Tutor. 2020, 22, 1251–1275. [Google Scholar] [CrossRef]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Deng, J.; Guo, J.; Ververas, E.; Kotsia, I.; Zafeiriou, S. Retinaface: Single-shot multi-level face localisation in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Mittal, M.; Verma, A.; Kaur, I.; Kaur, B.; Sharma, M.; Goyal, L.M.; Roy, S.; Kim, T.-H. An Efficient Edge Detection Approach to Provide Better Edge Connectivity for Image Analysis. IEEE Access 2019, 7, 33240–33255. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, A.; Luo, Y.; Huang, H.; Liu, Y.; Chen, Y.; Feng, L.; Chen, T.; Yu, H.; Yang, Q. Federated learning-powered visual object detection for safety monitoring. AI Mag. 2021, 42, 19–27. [Google Scholar] [CrossRef]
- He, C.; Shah, A.D.; Tang, Z.; Sivashunmugam, D.F.N.; Bhogaraju, K.; Shimpi, M.; Shen, L.; Chu, X.; Soltanolkotabi, M. Fedcv: A federated learning framework for diverse computer vision tasks. arXiv 2021, arXiv:2111.11066. [Google Scholar]
- Bayar, B.; Stamm, M.C. A deep learning approach to universal image manipulation detection using a new convolutional layer. In Proceedings of the 4th ACM Workshop on Information Hiding and Multimedia Security, Vigo, Spain, 20–22 June 2016. [Google Scholar]
- Karpathy, A.; Li, F.-F. Deep visual-semantic alignments for generating image descriptions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Mabrouk, A.; Redondo, R.P.D.; Elaziz, M.A.; Kayed, M. Ensemble Federated Learning: An approach for collaborative pneumonia diagnosis. Appl. Soft Comput. 2023, 144, 110500. [Google Scholar] [CrossRef]
- Alam, M.; Ahmed, T.; Hossain, M.; Emo, M.H.; Bidhan, K.I.; Reza, T.; Alam, G.R.; Hassan, M.M.; Pupo, F.; Fortino, G. Federated ensemble-learning for transport mode detection in vehicular edge network. Futur. Gener. Comput. Syst. 2023, 149, 89–104. [Google Scholar] [CrossRef]
- Yeganeh, A.; Pourpanah, F.; Shadman, A. An ANN-based ensemble model for change point estimation in control charts. Appl. Soft Comput. 2021, 110, 107604. [Google Scholar] [CrossRef]
- Mohammed, A.; Kora, R. A comprehensive review on ensemble deep learning: Opportunities and challenges. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Ye, Y.; Li, S.; Liu, F.; Tang, Y.; Hu, W. EdgeFed: Optimized federated learning based on edge computing. IEEE Access 2020, 8, 209191–209198. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wu, C.; Mao, S.; Ji, Y.; Bennis, M. Optimized computation offloading performance in virtual edge computing systems via deep reinforcement learning. IEEE Internet Things J. 2018, 6, 4005–4018. [Google Scholar] [CrossRef]
- Zhu, R.; Yin, K.; Xiong, H.; Tang, H.; Yin, G. Masked face detection algorithm in the dense crowd based on federated learning. Wirel. Commun. Mob. Comput. 2021, 2021, 8586016. [Google Scholar] [CrossRef]
- van Bommel, J. Active Learning during Federated Learning for Object Detection; University of Twente Enschede: Enschede, The Netherlands, 2021. [Google Scholar]
- Yu, P.; Liu, Y. Federated object detection: Optimizing object detection model with federated learning. In Proceedings of the 3rd International Conference on Vision, Image and Signal Processing, Vancouver, BC, Canada, 26–28 August 2019. [Google Scholar]
- Hu, Z.; Xie, H.; Yu, L.; Gao, X.; Shang, Z.; Zhang, Y. Dynamic-aware federated learning for face forgery video detection. ACM Trans. Intell. Syst. Technol. 2022, 13, 1–25. [Google Scholar] [CrossRef]
- Tam, P.; Math, S.; Nam, C.; Kim, S. Adaptive resource optimized edge federated learning in real-time image sensing classifications. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2021, 14, 10929–10940. [Google Scholar] [CrossRef]
- Ismail, A.; Ahmad, S.A.; Soh, A.C.; Hassan, M.K.; Harith, H.H. MYNursingHome: A fully-labelled image dataset for indoor object classification. Data Brief 2020, 32, 106268. [Google Scholar] [CrossRef]
- Engle, R.F.; Manganelli, S. CAViaR: Conditional autoregressive value at risk by regression quantiles. J. Bus. Econ. Stat. 2004, 22, 367–381. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Ahn, S.; Park, J.; Luo, L.; Chong, J. Adaptive Object-Region-Based Image Pre-Processing for a Noise Removal Algorithm. KSII Trans. Internet Inf. Syst. 2013, 7, 3160–3179. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Sattar, D.; Salim, R. A smart metaheuristic algorithm for solving engineering problems. Eng. Comput. 2021, 37, 2389–2417. [Google Scholar] [CrossRef]
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowl.-Based Syst. 2020, 195, 105709. [Google Scholar] [CrossRef]
- Lakshmiprabha, N.; Majumder, S. Face recognition system invariant to plastic surgery. In Proceedings of the 2012 12th International Conference on Intelligent Systems Design and Applications (ISDA), IEEE, Kochi, India, 27–29 November 2012. [Google Scholar]
- Dhivya, S.; Sangeetha, J.; Sudhakar, B. Copy-move forgery detection using SURF feature extraction and SVM supervised. Soft Comput. 2020, 24, 14429–14440. [Google Scholar] [CrossRef]
- Bicego, M.; Lagorio, A.; Grosso, E.; Tistarelli, M. On the use of SIFT features for face authentication. In Proceedings of the 2006 Conference on Computer Vision and Pattern Recognition Workshop (CVPRW’06), IEEE, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Bansal, M.; Kumar, M. 2D object recognition: A comparative analysis of SIFT, SURF and ORB feature descriptors. Multimed. Tools Appl. 2021, 80, 18839–18857. [Google Scholar] [CrossRef]
- Zulpe, N.; Pawar, V. GLCM textural features for brain tumor classification. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 354. [Google Scholar]
- Sheeba, P.T.; Murugan, S. Fuzzy dragon deep belief neural network for activity recognition using hierarchical skeleton features. Evol. Intell. 2019, 15, 907–924. [Google Scholar] [CrossRef]
- Sasaki, H.; Horiuchi, T.; Kato, S. A study on vision-based mobile robot learning by deep Q-network. In Proceedings of the 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), IEEE, Kanazawa, Japan, 19–22 September 2017. [Google Scholar]
- YOLO Object Detection Dataset. Available online: https://www.kaggle.com/code/rahulkumarpatro/yolo-object-detection (accessed on 14 November 2022).



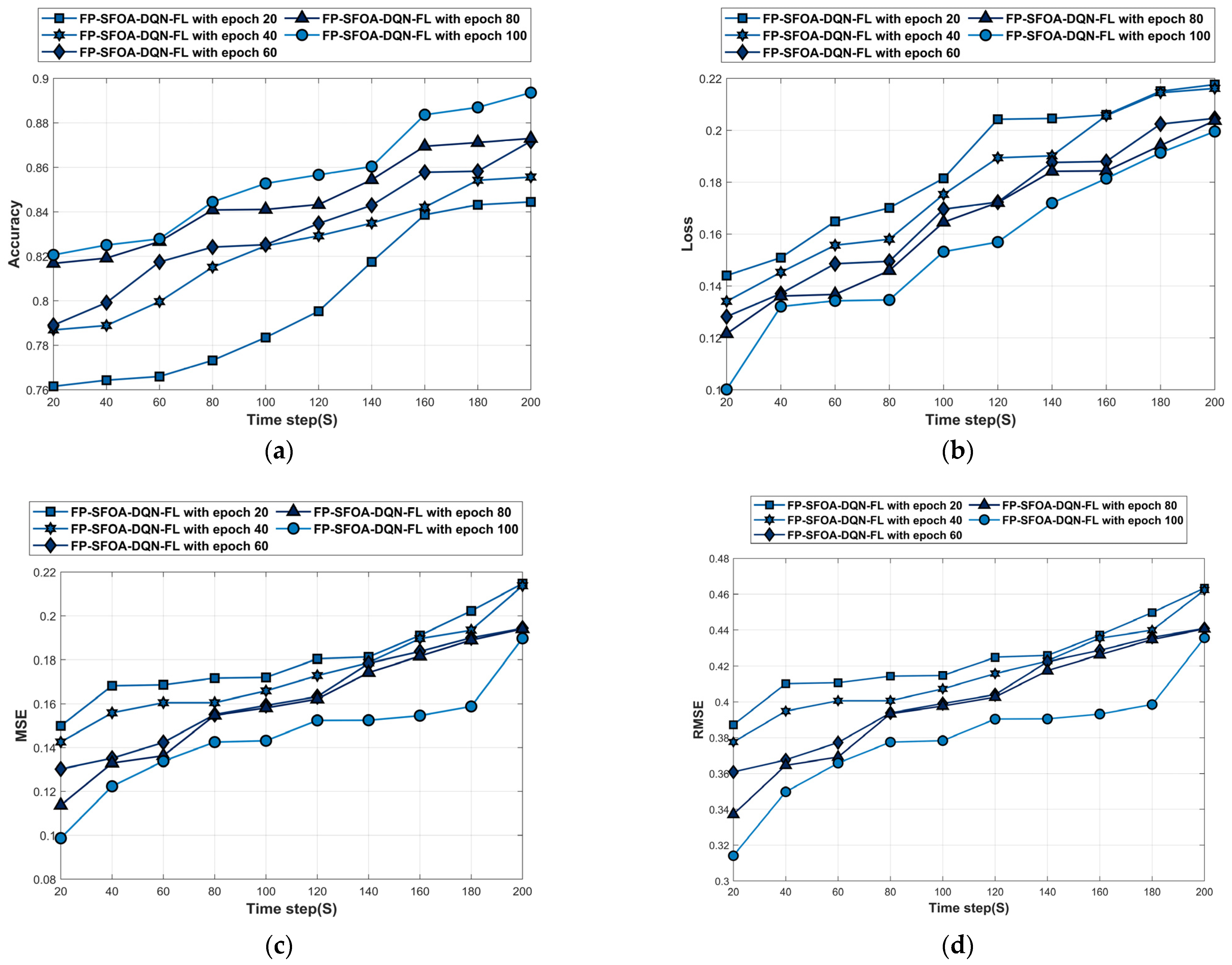
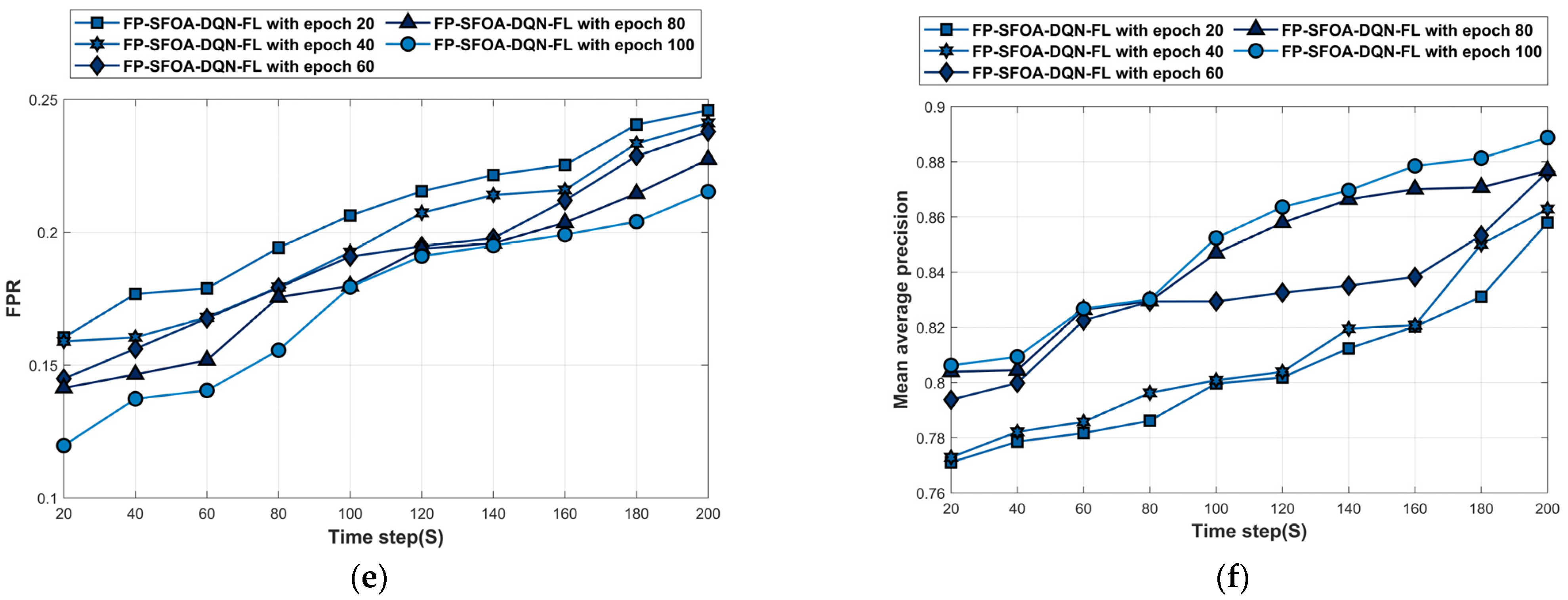
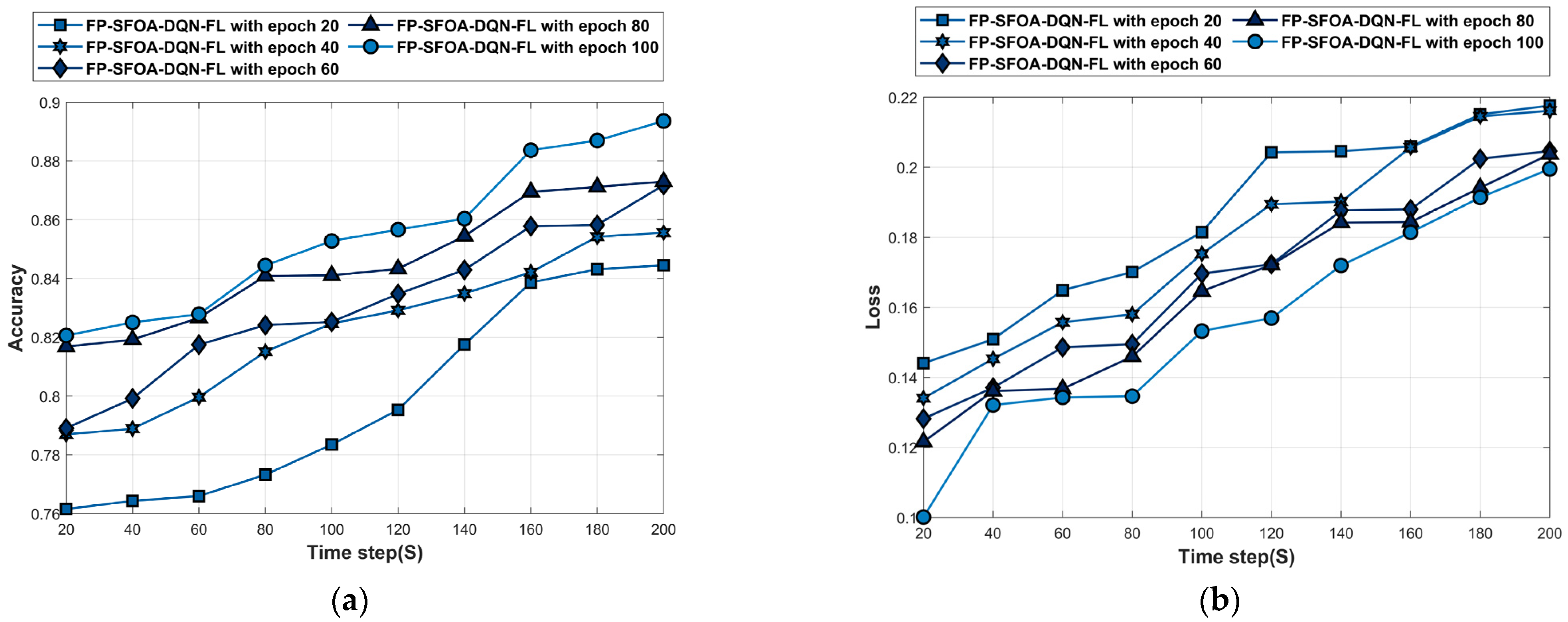
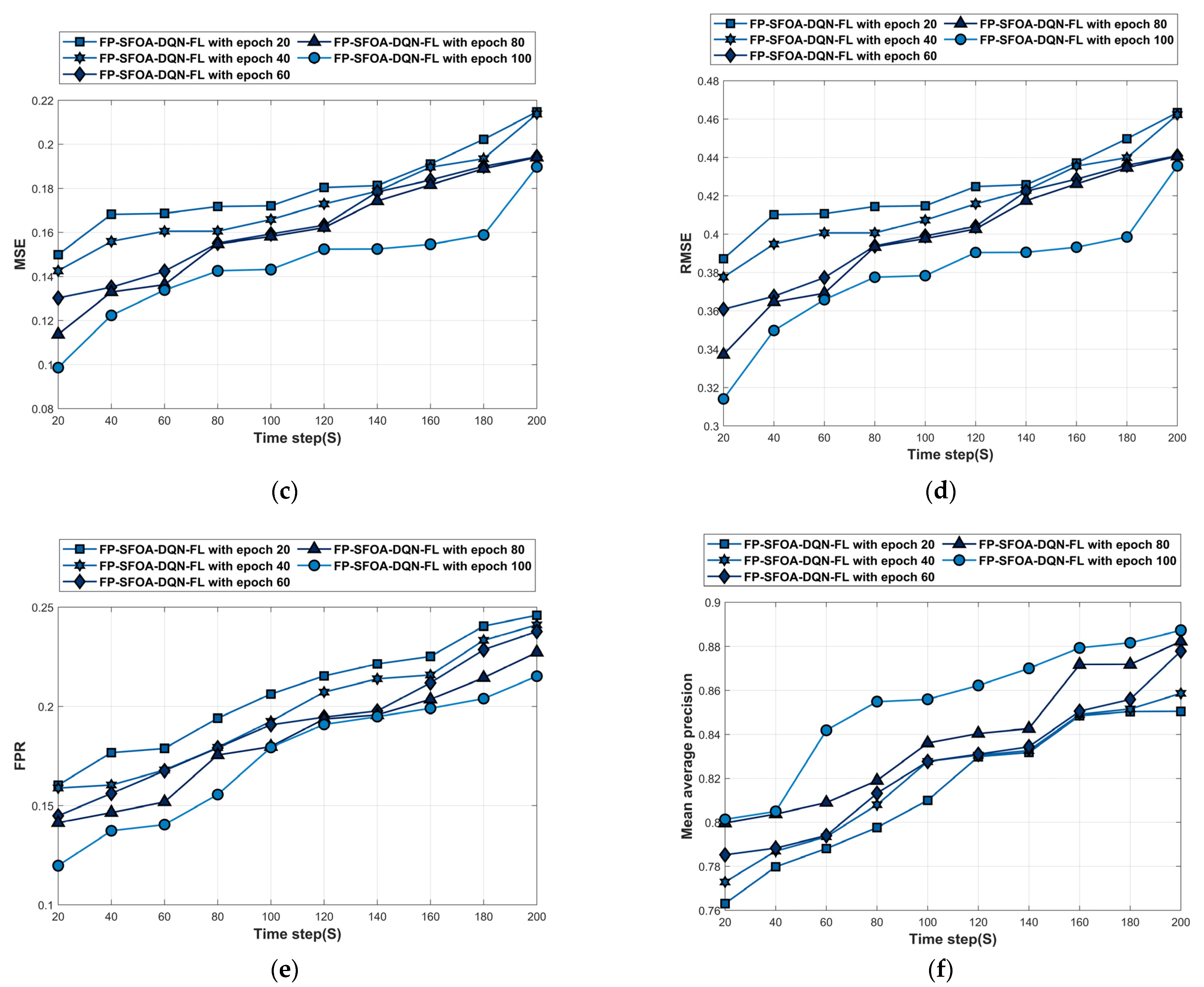
| Reference | Method | Advantages | Disadvantages |
|---|---|---|---|
| Luo, J. et al. [1] | Federated object-detection algorithms | It is able to mitigate non-IID issues. | It was not able to augment the dataset. |
| He, C. et al. [9] | FedCV | It is able to perform various computer vision tasks. | Increasing the effectiveness of federated learning was difficult. |
| Zhu, R. et al. [19] | DRFL | It provided better performance. | The implementation was not achieved using high-scale datasets. |
| Liu, Y. et al. [8] | FedVision | It reduced the communication overhead. | It failed to obtain sustainable mechanism. |
| Bommel, J.R. et al. [20] | Active learning | It increased the precision level. | It did not work well with non-homogeneous data. |
| Yu, P. and Liu, Y., [21] | FedAVg | It reduced the divergences. | It leads to reduction in mapping. |
| Hu, Z. et al. [22] | ICM | It effectively worked on decentralized data. It ensured high-level privacy and security. | It was incapable of enhancing the communication effectiveness of system factors. |
| Tam, P. et al. [23] | Adaptive model communication approach | It effectively deals with future congestion scenario. | It failed to compute the offloading decisions. |
| Parameters | Values |
|---|---|
| Learning rate | 0.01 |
| Batch size | 32 |
| Epoch | 50 |
| Datasets | Time Step | Metrics/ Methods | Federated Object Detection | FedCV | DRFL | Active Learning | FP-SFOA-DQN-FL |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.816 | 0.889 | 0.880 | 0.896 | 0.950 | ||
| Loss function | 0.234 | 0.168 | 0.165 | 0.139 | 0.104 | ||
| Dataset-1 | MSE | 0.249 | 0.185 | 0.182 | 0.156 | 0.122 | |
| Time Step = 200 s | RMSE | 0.050 | 0.043 | 0.043 | 0.040 | 0.035 | |
| FPR | 0.264 | 0.201 | 0.199 | 0.173 | 0.140 | ||
| Mean average Precision | 0.761 | 0.811 | 0.839 | 0.868 | 0.909 | ||
| Communication cost | 0.148 | 0.140 | 0.111 | 0.097 | 0.078 | ||
| Accuracy | 0.800 | 0.828 | 0.848 | 0.883 | 0.925 | ||
| Loss function | 0.249 | 0.207 | 0.183 | 0.159 | 0.108 | ||
| Dataset-2 | MSE | 0.264 | 0.223 | 0.200 | 0.175 | 0.125 | |
| Time Step = 200 s | RMSE | 0.049 | 0.042 | 0.042 | 0.039 | 0.034 | |
| FPR | 0.279 | 0.239 | 0.216 | 0.192 | 0.143 | ||
| Mean average Precision | 0.738 | 0.792 | 0.829 | 0.860 | 0.895 | ||
| Communication cost | 0.156 | 0.134 | 0.121 | 0.108 | 0.080 |
| Methods | Federated Object Detection | FedCV | DRFL | Active Learning | FP-SFOA-DQN-FL |
|---|---|---|---|---|---|
| Computational time (sec) | 9.521478523 | 8.255785244 | 7.258746581 | 6.258744698 | 5.254789502 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soomro, P.D.; Fu, X.; Aslam, M.; Mfungo, D.E.; Ali, A. Deep Q Network Based on a Fractional Political–Smart Flower Optimization Algorithm for Real-World Object Recognition in Federated Learning. Appl. Sci. 2023, 13, 13286. https://doi.org/10.3390/app132413286
Soomro PD, Fu X, Aslam M, Mfungo DE, Ali A. Deep Q Network Based on a Fractional Political–Smart Flower Optimization Algorithm for Real-World Object Recognition in Federated Learning. Applied Sciences. 2023; 13(24):13286. https://doi.org/10.3390/app132413286
Chicago/Turabian StyleSoomro, Pir Dino, Xianping Fu, Muhammad Aslam, Dani Elias Mfungo, and Arsalan Ali. 2023. "Deep Q Network Based on a Fractional Political–Smart Flower Optimization Algorithm for Real-World Object Recognition in Federated Learning" Applied Sciences 13, no. 24: 13286. https://doi.org/10.3390/app132413286
APA StyleSoomro, P. D., Fu, X., Aslam, M., Mfungo, D. E., & Ali, A. (2023). Deep Q Network Based on a Fractional Political–Smart Flower Optimization Algorithm for Real-World Object Recognition in Federated Learning. Applied Sciences, 13(24), 13286. https://doi.org/10.3390/app132413286








