Application of a Deep Learning Method to the Seismic Vulnerability Analysis of Cross-Fault Hydraulic Tunnels Based on MLE-IDA
Abstract
:1. Introduction
2. A Deep Learning Method to Enhance the Deterministic Evaluation of Seismic Responses
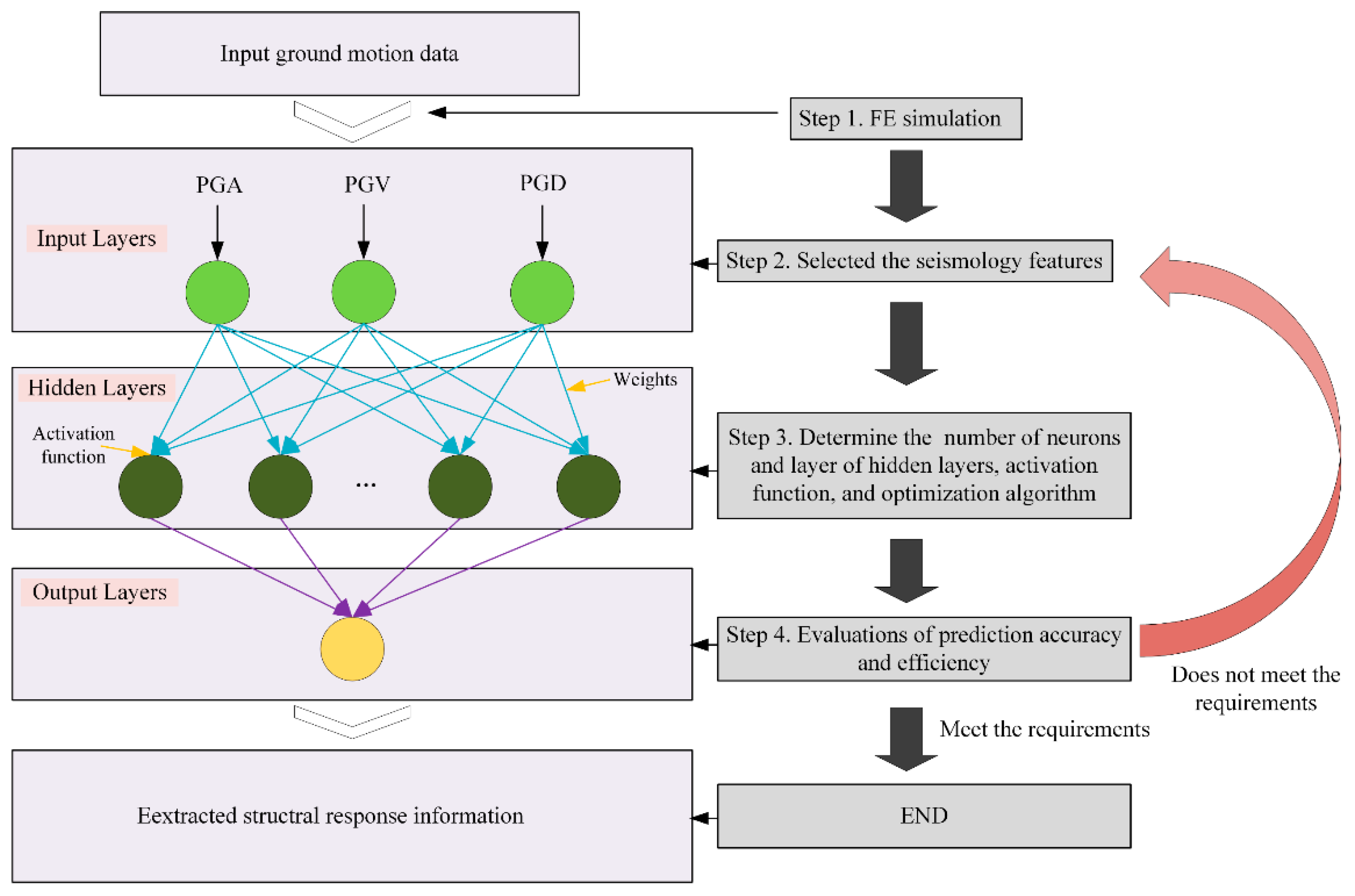
2.1. Artificial Neural Network Methodology
2.2. Prediction of Structural Responses by the Deep Learning Method
- (I)
- A database reflecting the inelastic dynamic response analysis of the FE simulations is generated using the CFHT–surrounding mass–fluid dynamic interaction system. After the FE simulations, the structural responses’ information time histories can be thus extracted.
- (II)
- The feature selection of the seismology characteristics of GM records is determined, such as the peak ground acceleration (PGA), peak ground velocity (PGV), and peak ground displacement (PGD), which are significant in the construction of the metamodel. Notably, one disadvantage is that the more feature elements that are selected, the more calculations will be required, because this approach requires a large number of repeated training steps of the metamodel.
- (III)
- The extracted structural response information and the seismology features of the GM records are merged together to predict the structural responses. During the process, the ratio of the training database size and testing database size is set as 7:3 to ensure the accuracy of the metamodel.
- (IV)
- The number of neurons and layers in the hidden layers, the activation function, and the optimization algorithm are studied in depth to determine the optimizable hyper-parameters of the ANNs, which can enhance the prediction accuracy.
- (V)
- Evaluations of the prediction accuracy and efficiency are performed using a range of quality measures, as well as discussions of the limitations and benefits of ANNs.
2.3. Quality Measures
3. Seismic Vulnerability Analysis Coupling Maximum Likelihood Estimation and Incremental Dynamic Analysis
- (a)
- Select the various seismology features of GM records from the PEER database and obtain the corresponding equivalent load time history from the velocity records and displacement records;
- (b)
- Establish the FE model of CFHTs considering the fluid–structure interaction effect and artificial boundary conditions;
- (c)
- Perform the IDA analysis on the CFHTs’ underground motion and excitation records;
- (d)
- Construct a training metamodel of ANNs for the CFHTs based on the numerical results;
- (e)
- Determine the control parameters and subsequently develop the probability damage curves according to the MLE-IDA.
4. Numerical Method
4.1. Numerical Model
4.2. Interaction System and Earthquake Records
4.3. Seismic Performance Assessment Index
5. Prediction Accuracy of Different Hyper-Parameter Configurations for the Proposed Trained ANN Model
5.1. Predictive Capability Evaluation of the Number of Layers and Neurons of Hidden Layers
5.2. Predictive Capability Evaluation of Activation Functions
5.3. Predictive Capability Evaluation of Optimization Algorithm
6. Analysis Results and Discussion
6.1. Investigation of the Effect of Seismology Features on Response Uncertainties
6.2. The Feasibility of the Predicted Database by the Proposed ANN Model
6.3. Seismic Fragility Analysis Using the Probabilistic ANN Model
7. Final Remarks
- (1)
- Compared with the hyper-parameters in terms of the mean square error, root mean square error, mean absolute error, and correlation based on the training database and testing database, it was found that two hidden layers and ten neurons are most suitable parameters for the ANN model. Meanwhile, it was demonstrated that the Bayesian optimization algorithm has higher predictive power for structural responses than other examined optimization algorithms. Furthermore, the direct use of the ANN model is not recommended to predict the structural response for the CFHT since different hyper-parameters have various abilities to change the predicted capacity of the model.
- (2)
- The predicted database of the integrated peak-value-type IMs of the input layers is more reliable than the scalar-valued IMs according to the examined methods. For the studied case, it was also confirmed that the amplitude type of seismology characteristics predicted by the ANN model has the highest prediction capacity compared with the other examined seismology features. On the other hand, the integral type of seismology characteristics is not suitable for the input layers of the ANN model to predict the structural response.
- (3)
- Only a slight difference was observed from the PSDM between the predicted EDPs and the calculated value of the CFHT, indicating that it is a reliable tool for the estimation of the seismic performance of CFHTs. Meanwhile, the ANN model is most suitable for the fragility analysis of the CFHTs because it can improve the computational efficiency and overcome the normally distributed assumption. For the seismic fragility curves, the traditional fragility analysis method may underestimate the probability of damage to CFHTs compared with MLE-IDA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hashash, Y.M.A.; Hook, J.J.; Schmidt, B.; Yao, J.I.C. Seismic design and analysis of underground structures. Tunn. Undergr. Sp. Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Li, T. Damage to mountain tunnels related to the Wenchuan earthquake and some suggestions for aseismic tunnel construction. Bull. Eng. Geol. Environ. 2012, 71, 297–308. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Xiao, M. Seismic damage assessment and mechanism analysis of underground powerhouse of the Yingxiuwan Hydropower Station under the Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2018, 113, 112–123. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Sp. Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A.; Shome, N.; Carballo, J.E. Three proposals for characterizing MDOF nonlinear seismic response. J. Struct. Eng. 1998, 124, 1281–1289. [Google Scholar] [CrossRef]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Kim, T.; Song, J.; Kwon, O.-S. Probabilistic evaluation of seismic responses using deep learning method. Struct. Saf. 2020, 84, 101913. [Google Scholar] [CrossRef]
- Kiani, J.; Camp, C.; Pezeshk, S. On the application of machine learning techniques to derive seismic fragility curves. Comput. Struct. 2019, 218, 108–122. [Google Scholar] [CrossRef]
- Wang, Z.; Pedroni, N.; Zentner, I.; Zio, E. Seismic fragility analysis with artificial neural networks: Application to nuclear power plant equipment. Eng. Struct. 2018, 162, 213–225. [Google Scholar] [CrossRef]
- Huang, Z.; Argyroudis, S.A.; Pitilakis, K.; Zhang, D.; Tsinidis, G. Fragility assessment of tunnels in soft soils using artificial neural networks. Undergr. Sp. 2022, 7, 242–253. [Google Scholar] [CrossRef]
- Noureldin, M.; Ali, A.; Memon, S.; Kim, J. Fragility-based framework for optimal damper placement in low-rise moment-frame buildings using machine learning and genetic algorithm. J. Build. Eng. 2022, 54, 104641. [Google Scholar] [CrossRef]
- Liu, C.; Macedo, J. Machine learning-based models for estimating seismically-induced slope displacements in subduction earthquake zones. Soil Dyn. Earthq. Eng. 2022, 160, 107323. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Z.; Lu, X.; Zhou, J.; Chen, J.; Liu, L.; Pei, L. Efficient seismic risk analysis of gravity dams via screening of intensity measures and simulated non-parametric fragility curves. Soil Dyn. Earthq. Eng. 2022, 152, 107040. [Google Scholar] [CrossRef]
- Jingchi, Y.U.; Aiyun, J.I.N.; Jianwen, P.A.N.; Jinting, W.; Chuhan, Z. GA-BP artificial neural networks for predicting the seismic response of arch dams. J. Tsinghua Univ. (Sci. Technol.) 2022, 62, 1321–1329. [Google Scholar]
- Dang-Vu, H.; Nguyen, Q.D.; Chung, T.; Shin, J.; Lee, K. Frequency-based Data-driven Surrogate Model for Efficient Prediction of Irregular Structure’s Seismic Responses. J. Earthq. Eng. 2022, 26, 7319–7336. [Google Scholar] [CrossRef]
- Ghasemi, A.; Stephens, M.T. Building clustering for regional seismic response and damage analysis. Earthq. Spectra 2022, 38, 2941–2969. [Google Scholar] [CrossRef]
- Işık, E.; Ademović, N.; Harirchian, E.; Avcil, F.; Büyüksaraç, A.; Hadzima-Nyarko, M.; Akif Bülbül, M.; Işık, M.F.; Antep, B. Determination of Natural Fundamental Period of Minarets by Using Artificial Neural Network and Assess the Impact of Different Materials on Their Seismic Vulnerability. Appl. Sci. 2023, 13, 809. [Google Scholar] [CrossRef]
- Jena, R.; Naik, S.P.; Pradhan, B.; Beydoun, G.; Park, H.-J.; Alamri, A. Earthquake vulnerability assessment for the Indian subcontinent using the Long Short-Term Memory model (LSTM). Int. J. Disaster Risk Reduct. 2021, 66, 102642. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Soleimani, F.; Liu, X. Artificial neural network application in predicting probabilistic seismic demands of bridge components. Earthq. Eng. Struct. Dyn. 2022, 51, 612–629. [Google Scholar] [CrossRef]
- Urlainis, A.; Shohet, I.M. Development of Exclusive Seismic Fragility Curves for Critical Infrastructure: An Oil Pumping Station Case Study. Buildings 2022, 12, 842. [Google Scholar] [CrossRef]
- Urlainis, A.; Shohet, I.M. Seismic Risk Mitigation and Management for Critical Infrastructures Using an RMIR Indicator. Buildings 2022, 12, 1748. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, J.; Shen, J.; Xiang, M. Regional-scale nonlinear structural seismic response prediction by neural network. Eng. Fail. Anal. 2023, 154, 107707. [Google Scholar] [CrossRef]
- Morgenroth, J.; Khan, U.T.; Perras, M.A. An overview of opportunities for machine learning methods in underground rock engineering design. Geosciences 2019, 9, 504. [Google Scholar] [CrossRef]
- Chimunhu, P.; Topal, E.; Ajak, A.D.; Asad, W. A review of machine learning applications for underground mine planning and scheduling. Resour. Policy 2022, 77, 102693. [Google Scholar] [CrossRef]
- Li, N.; Nguyen, H.; Rostami, J.; Zhang, W.; Bui, X.-N.; Pradhan, B. Predicting rock displacement in underground mines using improved machine learning-based models. Measurement 2022, 188, 110552. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ibrahim, H.H.; Noori, K.M.G.; Abdulhamid, S.N.; Ali, H.F.H. Forecasting sidewall displacement of underground caverns using machine learning techniques. Autom. Constr. 2021, 123, 103530. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Hall, R. Using machine learning approach for microseismic events recognition in underground excavations: Comparison of ten frequently-used models. Eng. Geol. 2020, 268, 105519. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S.; Guo, A.; Li, H. Comprehensive functional resilience assessment methodology for bridge networks using data-driven fragility models. Soil Dyn. Earthq. Eng. 2022, 159, 107326. [Google Scholar] [CrossRef]
- Ellingwood, B. Validation studies of seismic PRAs. Nucl. Eng. Des. 1990, 123, 189–196. [Google Scholar] [CrossRef]
- Vasavada, M.; Patel, V.R. Development of Fragility Curves for RC Buildings using HAZUS method. Int. Res. J. Eng. Technol. 2016, 3. [Google Scholar] [CrossRef]
- Goulet, J.-A. Probabilistic Machine Learning for Civil Engineers; MIT Press: Cambridge, MA, USA, 2020; ISBN 0262358018. [Google Scholar]
- Segura, R.; Padgett, J.E.; Paultre, P. Metamodel-based seismic fragility analysis of concrete gravity dams. J. Struct. Eng. 2020, 146, 04020121. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Sun, B.; Liu, W.; Deng, M.; Zhang, S.; Wang, C.; Guo, J.; Wang, J.; Wang, J. Compound intensity measures for improved seismic performance assessment in cross-fault hydraulic tunnels using partial least-squares methodology. Tunn. Undergr. Sp. Technol. 2023, 132, 104890. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D.; Beskos, D.E. Soil–structure interaction effects on seismic inelastic analysis of 3-D tunnels. Soil Dyn. Earthq. Eng. 2010, 30, 851–861. [Google Scholar] [CrossRef]
- Sun, B.; Deng, M.; Zhang, S.; Wang, C.; Cui, W.; Li, Q.; Xu, J.; Zhao, X.; Yan, H. Optimal selection of scalar and vector-valued intensity measures for improved fragility analysis in cross-fault hydraulic tunnels. Tunn. Undergr. Sp. Technol. 2023, 132, 104857. [Google Scholar] [CrossRef]
- Dobry, R.; Idriss, I.M.; Ng, E. Duration characteristics of horizontal components of strong-motion earthquake records. Bull. Seismol. Soc. Am. 1978, 68, 1487–1520. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Pearson Education India: Noida, India, 1996; ISBN 8131707180. [Google Scholar]
- Arias, A. Measure of Earthquake Intensity; Massachusetts Institute of Technology, Cambridge University of Chile: Santiago, Chile, 1970. [Google Scholar]
- Von Thun, J.L. Earthquake ground motions for design and analysis of dams. Earthq. Eng. Soil Dyn. II-Recent Adv. Ground-Motion Eval. 1988, 18, 227–239. [Google Scholar]
- Liu, J.B.; Du, Y.X.; Du, X. 3D viscous-spring artificial boundary in time domain. Earthq. Eng. Eng. Vib. 2006, 5, 93–102. [Google Scholar] [CrossRef]
- Andreotti, G.; Lai, C.G. Use of fragility curves to assess the seismic vulnerability in the risk analysis of mountain tunnels. Tunn. Undergr. Sp. Technol. 2019, 91, 103008. [Google Scholar] [CrossRef]
- Huang, P.; Chen, Z. Fragility analysis for subway station using artificial neural network. J. Earthq. Eng. 2021, 1–21. [Google Scholar] [CrossRef]















| Description | Symbol | Definition | Unit | Reference |
|---|---|---|---|---|
| Peak Ground Acceleration | PGA | g | - | |
| Peak Ground Velocity | PGV | m/s | - | |
| Acceleration Root-Mean-Square | Arms | g | [43] | |
| Velocity RMS | Vrms | m | [44] | |
| Arias Intensity | IA | m/s | [45] | |
| Acceleration Spectrum Intensity | ASI | m*s | [46] | |
| Velocity Spectrum Intensity | VSI | m | [46] |
| Damage State | Damage Level | Damage Measures | |
|---|---|---|---|
| Drift Ratio | Log Std | ||
| DS0 | No damage | - | - |
| DS1 | Slight/moderate damage | ||
| DS2 | Extensive damage | ||
| Case | Seismology Features | Database | RMSE | MSE | MAE | R2 |
|---|---|---|---|---|---|---|
| Case 1 | PGV | Train | 0.34 | 0.11 | 0.23 | 0.81 |
| Test | 0.34 | 0.11 | 0.24 | 0.81 | ||
| Case 2 | PGV and Vrms | Train | 0.32 | 0.10 | 0.22 | 0.84 |
| Test | 0.33 | 0.11 | 0.24 | 0.82 | ||
| Case 3 | Peak values (PGA, PGV, PGD) | Train | 0.29 | 0.09 | 0.21 | 0.86 |
| Test | 0.30 | 0.09 | 0.22 | 0.86 | ||
| Case 4 | Amplitude | Train | 0.24 | 0.06 | 0.17 | 0.91 |
| Test | 0.22 | 0.05 | 0.16 | 0.92 | ||
| Case 5 | Integral | Train | 0.47 | 0.22 | 0.37 | 0.66 |
| Test | 0.46 | 0.21 | 0.36 | 0.65 | ||
| Case 6 | Frequency content | Train | 0.37 | 0.13 | 0.27 | 0.80 |
| Test | 0.33 | 0.11 | 0.24 | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Sun, B.; Wang, P. Application of a Deep Learning Method to the Seismic Vulnerability Analysis of Cross-Fault Hydraulic Tunnels Based on MLE-IDA. Appl. Sci. 2023, 13, 13232. https://doi.org/10.3390/app132413232
Cao W, Sun B, Wang P. Application of a Deep Learning Method to the Seismic Vulnerability Analysis of Cross-Fault Hydraulic Tunnels Based on MLE-IDA. Applied Sciences. 2023; 13(24):13232. https://doi.org/10.3390/app132413232
Chicago/Turabian StyleCao, Wenyu, Benbo Sun, and Pengxiao Wang. 2023. "Application of a Deep Learning Method to the Seismic Vulnerability Analysis of Cross-Fault Hydraulic Tunnels Based on MLE-IDA" Applied Sciences 13, no. 24: 13232. https://doi.org/10.3390/app132413232
APA StyleCao, W., Sun, B., & Wang, P. (2023). Application of a Deep Learning Method to the Seismic Vulnerability Analysis of Cross-Fault Hydraulic Tunnels Based on MLE-IDA. Applied Sciences, 13(24), 13232. https://doi.org/10.3390/app132413232





