Abstract
In this article, the dependence of the operation states, dynamics, and noise of laser diodes (LD) with external optical feedback (OFB) on the linewidth enhancement factor (LEF) and spontaneous emission factor (SEF) have been investigated. We systematically studied the classification of the laser dynamics based on the bifurcation diagrams (BDs) of the photon numbers and the relative intensity noise (RIN) spectra at different levels of OFB, LEF, and SEF. The simulation results show that variations in the LEF and SEF lead to significant changes in the laser operation states and dynamics, which vary from continuous wave (CW), pulsation, and chaos states. The Hopf bifurcation (HB) point moves toward increasing/decreasing OFB intensity by increasing/decreasing the SEF/LEF. The laser state becomes more stable through a wide range of OFB by increasing/decreasing the SEF/LEF. The RIN reduces the solitary laser noise level at higher/lower values of SEF/LEF when the laser is operated under OFB. The relaxation frequency of the laser shifts toward higher values by increasing/decreasing the SEF/LEF through most laser states, and the RIN peak is higher than solitary laser noise by four orders of magnitude, especially in the pulsation regions. In the low-frequency region, the RIN is enhanced from one to two orders by reducing the LEF and SEF through laser states.
1. Introduction
Recent technology has witnessed the prominent role played by LDs in different disciplines, including optical communications, laser pumping, optoelectronics, and spectroscopy. The detailed and precise theoretical understanding of the roots of the analytical and numerical calculations is the bedrock for establishing highly efficient and practical solid lasers. Modulation bandwidths, enhanced output powers, and control spectral linewidths are fundamentally important for practical relevance. The spatial coherences of high-power semiconductor lasers, such as quantum dots or quantum wells, are significantly manipulated by the LEF. This factor plays a vigorous role as a critical parameter in manipulating the linewidth targeting high-frequency diode lasers [1,2].
The emission linewidth and the carrier dynamics are the two vital characteristics of lasers, which can be enhanced by engineering the coupling of the refractive index and gain medium to the carrier density. Potentially, in 1982, Henry introduced such a factor through the expression to enumerate the effect of the refractive index of the medium with the carrier density on the behaviors of LDs. Here, n is the refractive index, g is the gain per unit length, λ is the excitation wavelength, and N is the carrier density [3]. The insertion of the α-factor into the compacted set rate equations of laser dynamics has significantly explained the experimentally observed phenomenon related to broad linewidth and the onset of the coherent revival and collapse induced by OFB in many fields of LDs and amplifiers. This parameter also plays a vital role in the spectral features of the LD and its dynamic response and estimates the sensitivity of the LD to OFB [4].
The robust laser holds promising and fascinating applications for coherent communication and sensing devices, which has led to enormous efforts toward engineering narrow linewidth LDs to boost their performance beyond the conventional resonators. Many methodologies have been proposed, such as external cavities, phase shifted, chirped grating, fiber lasers, gain-loss interplay in non-Hermitian systems, and so on, with the aim of determining and reducing the spectral linewidth. A comprehensive related review can be found in [5,6].
One type of laser is called a spaser or plasmonic laser, which is a device that confines light at a sub-wavelength scale and enables localized or propagation light with high efficiency far below Rayleigh’s diffraction limit [7]. The spaser, surface plasmon amplification by stimulated emission of radiation, has been recently predicted and experimentally realized as an active element in nanostructures for generating coherent local fields [8]. If the spaser can be manipulated as an optical counterpart of the MOSFET, greater progress will be achieved for the coming promising devices. However, establishing a spaser for feature amplification is still challenging due to the intrinsic feedback amplification, causing the generation of nanolocalized plasmonic modes and saturation and the consequent elimination of the net gain. Alternatively, topological insulator lasers have been demonstrated theoretically and experimentally for crafting robust and topologically protected lasers [9,10]. Particularly, non-Hermitian systems with inherent gain and losses enable the occurrence of exceptional points (EPs), which leads to highly efficient lasers that are robust to disorder and defects, reaching single-mode lasing even high above the laser threshold.
In fact, the LEF, in several application aspects of LDs, similar to the linewidth, affects the chirp under current modulation, the mode stability, and the circumstance of filamentation in broad-area bias [3,11]. Many articles have studied the influences of the operation states and dynamics of time-delayed LD by the LEF and OFB [12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Al-Hosiny studied the impact of the LEF on the route to chaos of an LD subject to active external cavities [19]. He found that there is no difference in the route to chaos with minor changes in the LEF. Recently, Abdulrhmann et al. introduced an improved theoretical model of time delay, which is applicable through any OFB range and includes many round trips in the external cavity (EC) and optical phases due to OFB. This model has investigated the operation states and intensity noise of pumping LDs, which are used in fiber amplifier systems as a light source [26,27]. Moreover, Abdulrhmann et al. studied the impacts of gain saturation, the radiative and non-radiative recombination lifetime, the LEF, and the combined optical phase with OFB strength on the dynamic states and RIN of LDs with short external cavities [28,29].
On the other hand, the SEF specifies the ratio of the spontaneous field entered to the lasing mode, affecting the width of the laser linewidth. Since the emission rate is given in terms of fc(1 − fv)(S + 1) − fv(1 − fc)S, where fc, fv, and S represent the distribution functions of the electron in the conduction, valence bands, and photon density, respectively, accounting for the SEF and the stimulated emission coefficient for the laser. The SEF and the stimulated emission coefficient are identical in principle. Yamada investigated the impact of the SEF on the laser RIN and frequency noise levels [30]. He found that increasing the SEF and reducing the threshold current level gives low noise and a narrow linewidth when operating a micro-cavity laser at low power levels [30]. Many papers have studied the impacts of the SEF on the modulation and linewidth of the laser [31,32,33,34]. However, a thorough investigation of the influences of the SEF and LEF on the dynamic states and RIN in the presence of OFB is still missing. Here, we propose for the first time, the impacts of the LEF and the SEF on the dynamics state and RIN of the LD with short EC, which is very important in designing the LDs, using the model mentioned in [26,27]. This model can be used as the bedrock to cover a wide range of OFB, multiple round trips in the EC, and all the phase variations due to OFB, which leads to practically accurate results compared with the model in [25] used in many previous investigations. This work has novel features on the influences of the LEF, SEF, and OFB in LDs with short EC and their operation in optical communication systems, including fiber-optic communication networks. Moreover, LDs are used in optical data storage devices, such as CD and DVD players, for reading and writing data on optical discs. The main challenge for all these applications of LDs is the deformation of the signal due to OFB. This leads to difficulty in accurately positioning the laser spot on the application. Therefore, unnecessary OFB can cause data safety problems. During the writing or retrieval of data, any noise in the laser output due to OFB can result in the data being written or read with deformations.
In this article, we study the LDs subject to external OFB operation, dynamics, states, and noise aiming to the roles played by the LEF and SEF in a self-contained manner. We used the model in Ref. [26], which counts multiple round trips to study the impact of the LEF and SEF on the states and to characterize the route to chaos in LDs. The model in [26] is used to run ferocious numerical calculations of a short EC760 nm AlGaAs/GaAs LD. We have automatically included the impact of linewidth narrowing due to feedback from an EC, which is often described by the so-called chirp reduction factor. The dynamics of the LD are classified using the peak value of the photon number BDs at each feedback value. Here, we obtain a general view of the longitudinal excess factor of the SEF and the LEF taking into attentiveness the gain nonlinear impacts, the effects of the Kerr effect, and the dispersion of the gain of such a structure. The results show that when the LEF/SEF decreased/increased, the LD operation states were modified from a chaotic state to a CW or periodic oscillation (PO) state. This state is attractive due to its stability and lowest noise level compared with the solitary laser noise level. We anticipated that the LD with OFB would be highly stable and have a descending RIN level at lower/higher values of the LEF/SEF, adjusting the suitable value of the LEF and SEF.
The article is arranged as follows. A model of analysis that includes a modified rate equation for a time delay LD with any amount of OFB is presented in Section 2. The procedure of numerical simulation of the rate equations is induced. Section 3 presents the BDs of the peak value of the photon numbers of the LD at various LEF and SEF values, and varying OFB strengths are shown. The corresponding average RIN in the low-frequency region (f ≤ 10 MHz) of the LD are presented. The RIN spectrum at several dynamics regimes of the LD, such as the CW, PO, period doubling (PD) and chaos operation states, are introduced. Section 4 shows the conclusion.
2. Model of Analysis and Numerical Procedures
2.1. Modified Model of Analysis
The model in [26] was applied here to explore the impact of the LEF and SEF on the dynamics and RIN of an AlGaAs/GaAs LD with OFB. In long EC counting, a single round trip in the rate equation is sufficient to investigate the LD dynamics, while in a short EC, we have to include the multiple round trips in the rate Equations (1)–(3) [26]. The rate equations, which depict the time-delayed LD states, are given by the rate of the photon number S(t), the optical phase θ(t), and the electron number N(t) as
where aξ(N − Ng)/V is the gain linearity, with a and Ng as material constants, and ξ is the confinement factor of the optical field inside the active region with volume V, and C is the SEF. α is the LEF, I is the injected current, is the mean electron number, c is the speed of light, and τs is the lifetime. The threshold gain is given as Gth0, which is given by:
where k is the coefficient of loss of the LD. Many models have been introduced to introduce gain saturation [35,36,37]. The parameter B is the gain saturation, which is introduced by the gain third-order perturbation theory [35,36].
where Rcv is the dipole moment, τin is the intra-band relaxation time, is the plank constant, and Ns is an injection level.
The coefficient T, which represents the OFB term in the rate equation, is represented as [26]:
where m, Rf, nex, Lex, and ψ are the number of round trips, the front reflector reflectivity, the refractive index, the EC width, and the combined phase ψ = ϕex + ϕf + ωτ, respectively. Where ω, ϕex, and ϕf are the circular frequency emission, the phase retarded because of reflection from the external mirror, and the front facet, respectively, and is the time delay.
The OFB strength coefficient Kex is given by:
where Rex is the external mirror reflectivity. The argument ϕ of the OFB term T is given by:
where is an integer. The ϕ value is determined in the two-dimensional space (Re[T]-Im[T]).
FS(t), Fθ(t), and FN(t) are Langevin noise sources and are included in the rate Equations (1)–(3) to consider laser fluctuations due to intrinsic transitions [27,38]. These noise sources have Gaussian probability distributions to be δ-correlated processes and with zero means [27,38].
The spectra of the RIN are then calculated by instantaneous fluctuation values δS(t) = S(t) − and using the fast Fourier transform as [39]:
where and ω are the dc-value of S(t) and the Fourier frequency, respectively.
2.2. Numerical Simulations Procedures
The rate Equations (1)–(3) are simulated numerically with the aid of the fourth-order Runge Kutta method [39]. Short wavelength AlGaAs/GaAs LDs emitting at 760 nm are used in the simulation with the parameters given in Ref. [40]. The integration time step is adjusted to Δt = 5 ps, and the injection current is kept at I/Ith = 1.5, where Ith is the threshold value of the injection current. The effect of the OFB is taken by the OFB strength Kex. The steady states values and are determined from the steady states solution of the rate equation without OFB as:
The combined phase ψ and the averaged values are set as zero in this article. The OFB phase φ was chosen to vary continuously with the time evolution since the solution of the arc tangent is within the range of −π/2 to +π/2.
3. Simulation Results and Discussions
The dynamics of the laser output with OFB intensity Kex in terms of the LEF and SEF are examined using the BDs of the ratio of the S(t)/<S>, where <S> is the average photon numbers. The corresponding average RIN at low frequency (f ≤ 10 MHz) in LDs with short EC are examined at many values of the LEF and SEF.
3.1. Impacts of LEF and SEF on States of LD
The BDs of the output photon numbers from the back facet of the laser with OFB intensity at several LEF and SEF values are shown in Figure 1. In the calculations of the BDs, the Langevin noise sources in the rate Equations (1)–(3) are omitted to clarify the type of state induced by OFB. In these figures, we are interested in reporting the operation dynamic of the short EC LD through OFB wide range.
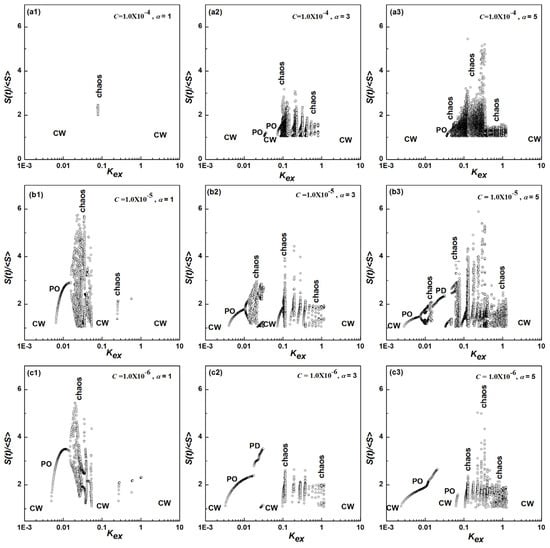
Figure 1.
BDs of an short EC LD at I/Ith0 = 1.5, with (a1) LEF α = 1, and SEF C = 10−4, (a2) LEF α = 3, and SEF C = 10−4, (a3) LEF α = 5, and SEF C = 10−4, (b1) LEF α = 1, and SEF C = 10−5, (b2) LEF α = 3, and SEF C = 10−5, (b3) LEF α = 5, and SEF C = 10−5, (c1) LEF α = 1, and SEF C = 10−6, (c2) LEF α = 3, and SEF C = 10−6, and (c3) LEF α = 5, and SEF C = 10−6.
Figure 1 shows the BDs of the laser when the LEF α = 1.0, 3.0, and 5.0 and the SEF C = 10−4, 10−5, and 10−6, respectively. In the weak OFB (Kex < 0.01) regime, the laser keeps in CW as no points are presented in the figures, which represents a stationary solution of the rate Equations (1)–(3). Figure 1 shows that increasing the LEF from 1.0 to 5.0 and the SEF from 10−6 to 10−4 led to decreases/increases in the width of the CW region. The same scenario occurs at Kex > 1.0 at strong OFB. By enhancing the OFB Kex, the CW state bifurcates into a PO region. The width of that region and the photon number intensity (S(t)/<S>) depend strongly on the values of the LEF and SEF. As shown in Figure 1(b1–b3,c1–c3), the PO width becomes the narrowest, and the intensity decreases, with increasing SEF. Figure 1(b2,b3,c2,c3) shows the reverse situation while increasing the LEF PO region width is the widest, and the intensity decreases with an increase in the LEF. The point at which the state changes is called the HB point, which moves toward decreasing the OFB Kex from 0.079 to 0.036 as the LEF increases from 1.0 to 5.0 and moves toward increasing the OFB Kex from 0.00495 to 0.079 when the SEF increases from 10−6 to 10−4, respectively.
By enhancing the OFB value Kex, the PO divaricates into two branches representing the PD dynamic state, as represented in Figure 1(b1–b3,c1,c2), which decreases the OFB Kex from 0.0154 to 0.0076 and changes the LEF from 1.0 to 5.0 and the SEF from 10−5 to 10−6, respectively. Under the moderate region of the OFB, the LD state transmits to a chaotic state, as indicated in Figure 1.
3.2. LEF and SEF with OFB Kex at HB Point
The OFB strength Kex at the HB point versus the LEF and SEF is shown in Figure 2a,b based on the results shown in Figure 1. In Figure 2a, the LEF changes as a nonlinear function (LEF exponential decay function) with the OFB Kex when the SEF C = 10−4, 10−5, and 10−6. Then, the OFB intensity Kex can be increased by reducing the LEF values, which is desired to set the LD into a stable dynamic, such as PD or PO. We notice that the effect of the LEF is noticeable when the SEF C = 10−4 and decreases by decreasing the SEF. Figure 2b shows the SEF with OFB Kex at many values of LEF α = 1.0, 3.0, and 5.0, and a nonlinear behavior representing an exponential function of the SEF with OFB intensity Kex is found. Then, by enhancing the OFB Kex, the SEF increases, which leads to a PO dynamic. The SEF has a strong effect when the LEF α = 1.0 and decreases by increasing the LEF. In Ref. [20], the change in the LEF with the phase due to OFB has been examined numerically and experimentally. We have included these characteristics in our proposal to enhance the predicted results shown in Figure 1 and Figure 2a with respect to the LEF and OFB intensity Kex and establish new calculated results on the SEF and OFB intensity Kex, of the LD with short EC shown in Figure 1 and Figure 2b. Figure 1 demonstrates that decreasing/increasing the LEF/SEF takes the LD into a more stable dynamic by enhancing the OFB Kex. As shown in the figures, decreases/increases in the LEF/SEF led to an increase/decrease in Kex with the HB point, which led to an increase in the threshold current. The calculated results in Figure 1 show that the LD with short EC dynamic state instability can be improved by decreasing/increasing the LEF/SEF and enhancing Kex, which, overall, helps in drawing LDs with better dynamics. The impacts of the LEF and SEF with OFB with selecting the LD design to adjust the values of the LEF and SEF are introduced for the first time here, which increases the stability of LDs with short EC.
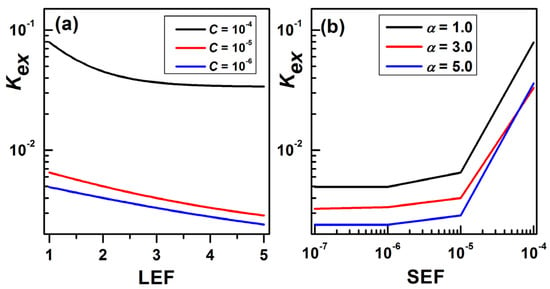
Figure 2.
OFB Kex variation with (a) LEF and (b) SEF, at HB point and I/Ith0 = 1.5.
3.3. RIN at Low Frequency with LEF and SEF
Figure 3, which corresponds to the BDs shown in Figure 1, shows the variation in the average value of the low-frequency RIN (f ≤ 10 MHz) with OFB intensity Kex when the LEF α = 1, 3, and 5 and the SEF C = 10−4, 10−5, and 10−6. One can see that the average RIN almost coincides with the solitary laser noise level (the LD without OFB) in the weak OFB regime. Through the route to chaos, the RIN displays higher levels and reaches maximum values when the laser state becomes chaotic in medium and some strong OFB regimes. At the Hopf bifurcation point, the average value of the RIN attains minimum levels, which happens to be lower than the solitary RIN level. Under strong OFB, the average value of the RIN exhibits lower levels than the corresponding solitary laser RIN level. As shown in Figure 3(a1), the average value of the RIN level almost coincides with the solitary laser noise level under the CW state and when the LEF α = 1. By increasing the LEF, the RIN becomes higher than that of the LD without OFB depending on the operating state of the LD (CW, PO, or chaos) and OFB intensity Kex, which is shown in Figure 3(a1–a3,b1–b3,c1–c3). Figure 3(a1–c1,a2–c2,a3–c3) exhibits the impact of the SEF on the average value of the low-frequency RIN. As shown in Figure 3(a1), the average value of the RIN level almost coincides with the solitary laser noise level under the CW state and when the SEF C = 10−4. By decreasing the SEF, the RIN attains higher values compared with the solitary laser noise level, which depends on the operating state of the LD (CW, PO, or chaos) and OFB intensity Kex, as shown in Figure 3(a1–c1,a2–c2,a3–c3). Figure 1 and Figure 3 show clearly the significant roles played by the SEF in the behavior of the dynamic state. As shown in Figure 3(a1,b1), the dynamic states have been changed dramatically, while in Figure 3(b1,c1), such a change is not noticeable when decreasing the SEF, which specifies the ratio of the spontaneous field entered to the lasing mode and affects the width of the laser linewidth. The SEF and stimulated emission coefficient are identical in principle. Decreasing the SEF and increasing the threshold current level gives a high noise level and a wide linewidth when operating a laser at low power levels.
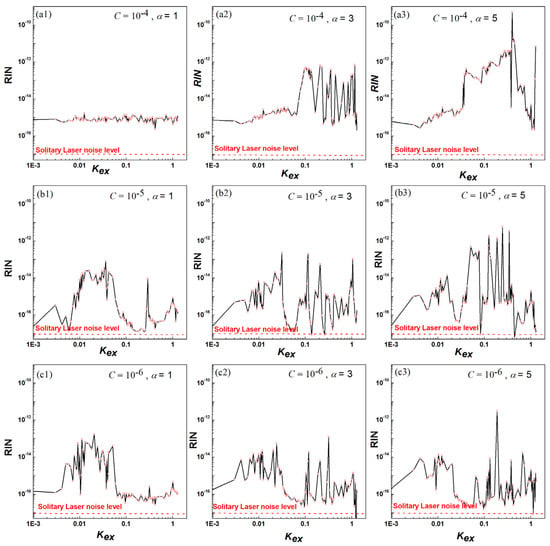
Figure 3.
RIN at low frequency (10 ≤ MHz) of a short EC LD, when I/Ith0 = 1.5 with (a1) LEF α = 1, and SEF C = 10−4, (a2) LEF α = 3, and SEF C = 10−4, (a3) LEF α = 5, and SEF C = 10−4, (b1) LEF α = 1, and SEF C = 10−5, (b2) LEF α = 3, and SEF C = 10−5, (b3) LEF α = 5, and SEF C = 10−5, (c1) LEF α = 1, and SEF C = 10−6, (c2) LEF α = 3, and SEF C = 10−6, and (c3) LEF α = 5, and SEF C = 10−6.
As shown in Figure 3, decreasing/increasing the LEF/SEF causes a reduction in the value of the average value of the RIN at low frequency, and this leads to an improvement in the properties of the LD with short EC, especially in applications such as optical communication systems and others. The simulated results in Figure 3 show that the average value of the RIN, which corresponds to the operation state instability of the LD with short EC shown in Figure 1, can be improved by decreasing/increasing the LEF/SEF, enhancing the OFB, which helps for drawing LDs with high dynamics and a low noise level. The impacts of the LEF and SEF with OFB on the average value of the RIN with selecting the LD design to adjust the values of the LEF and SEF are introduced for the first time, and this could be effective at increasing/decreasing the stability/RIN of LDs with short EC.
3.4. RIN Spectra of LD for Various States
Variations in the RIN of the LD with the LEF and SEF at various states of the LD, such as the CW, PO, PD, and chaos state, with two different values of OFB intensity, Kex = 0.01 (weak OFB) and Kex = 0.1 (moderate OFB), are presented in Figure 4 and Figure 5.
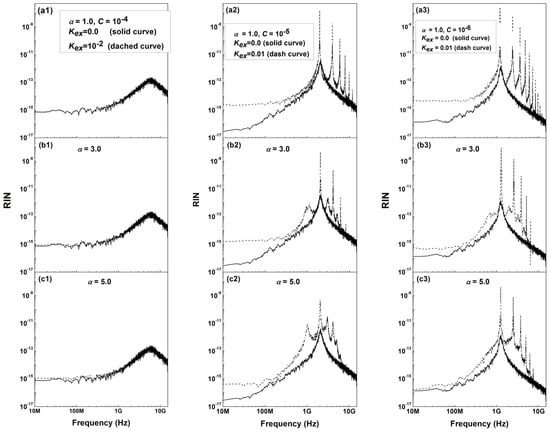
Figure 4.
Output RIN spectrum at Kex = 0.01 (weak OFB) as I/Ith0 = 1.5, with (a1) LEF α = 1, and SEF C = 10−4, (a2) LEF α = 1, and SEF C = 10−5, (a3) LEF α = 1, and SEF C = 10−6, (b1) LEF α = 3, and SEF C = 10−4, (b2) LEF α = 3, and SEF C = 10−5, (b3) LEF α = 3, and SEF C = 10−6, (c1) LEF α = 5, and SEF C = 10−4, (c2) LEF α = 5, and SEF C = 10−5, and (c3) LEF α = 5, and SEF C = 10−6.
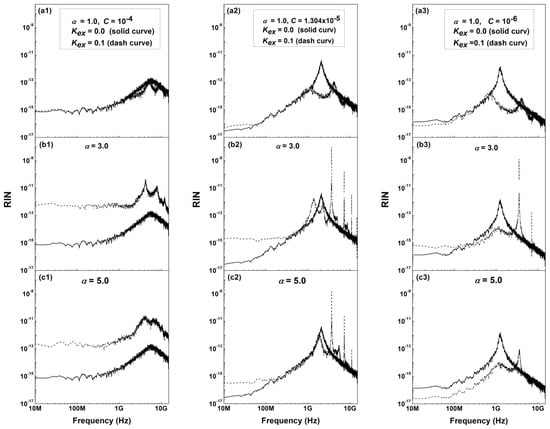
Figure 5.
Output RIN spectrum at Kex = 0.1 (moderate OFB) as I/Ith0 = 1.5, with (a1) LEF α = 1, and SEF C = 10−4, (a2) LEF α = 1, and SEF C = 10−5, (a3) LEF α = 1, and SEF C = 10−6, (b1) LEF α = 3, and SEF C = 10−4, (b2) LEF α = 3, and SEF C = 10−5, (b3) LEF α = 3, and SEF C = 10−6, (c1) LEF α = 5, and SEF C = 10−4, (c2) LEF α = 5, and SEF C = 10−5, and (c3) LEF α = 5, and SEF C = 10−6.
Figure 4 plots the RIN spectra at the OFB intensity Kex = 0.01 in the weak OFB regime, the LEF α = 1, 3, and 5, and the SEF C = 10−4, 10−5, and 10−6. It is clear from Figure 4(a1–c1) that when the laser operates in the CW state and when the SEF C = 10−4 and the LEF α = 1, 3, and 5, there is no difference in the RIN value with the OFB (dashed line) and solitary laser RIN (solid line) at a higher frequency regime (relaxation frequency fr). A frequency shift in the RIN peak is noticed and moves towards increasing frequency, where the relaxation frequency is fr = 5.5, 5.9, and 6.2 GHz when the LEF α = 1, 3, and 5, respectively. Moreover, in a low-frequency regime and by increasing the LEF, the RIN is enhanced to a level higher than the solitary laser RIN level.
By transmitting to the PO state, when the LEF α = 1 and the SEF C = 10−4, 10−5, and 10−6, the peak value of the RIN with OFB is enhanced to higher values (four orders of magnitude) (dashed line) compared with the solitary laser RIN (solid line) at the relaxation frequency fr, as shown in Figure 4(a1–a3). A small shift in the RIN peak is noticed and moves towards increasing frequency, where the relaxation frequency is fr = 1.2, 2, and 5.5 GHz by increasing the SEF C = 10−6, 10−5, and 10−4, respectively. At low frequency and by decreasing the SEF, the RIN is enhanced to almost one order of magnitude higher than the solitary laser noise. Under the PD state, the RIN behaves as under the PO state except that another peak is observed in the RIN spectrum, which represents a doubling in the period.
By increasing the intensity of the OFB kex = 0.1, we investigated the impacts of the LEF and SEF on the RIN spectra over various states of the LD in the OFB medium regime. Figure 5 shows the RIN spectra at the OFB intensity Kex = 0.1 in a moderate OFB regime, an LEF α = 1, 3, and 5, and an SEF C = 10−4, 10−5, and 10−6. When the laser operates in the CW state at an SEF C = 10−4 and an LEF α = 1, as shown in Figure 5(a1), the RIN shows a second harmonic peak, and its value of the relaxation frequency fr (dashed line) is lower than the solitary laser RIN (solid line) by about two orders of magnitude. A frequency shift was found between the RIN with OFB (fr = 4.9 GHz) and the solitary laser RIN (fr = 5.7 GHz). The frequency shift increases by decreasing the SEF C = 10−6 and 10−5, where the RIN with OFB occurs at (fr = 1.25 and 2.1 GHz) and the solitary laser RIN occurs at (fr = 0.75 and 1.25 GHz), as shown in Figure 5(b1,c1), respectively. At a low frequency, the RIN is enhanced to higher values (almost one order of magnitude) than the solitary laser RIN level and increases by decreasing the SEF, as shown in Figure 5(b1,c1).
Under the PO state, when the LEF α = 3 and the SEF C = 10−5, the peak intensity of the RIN with OFB is enhanced to higher values (four orders of magnitude) (dashed line) and shifted in the direction of increasing frequency comparing with the solitary laser RIN (solid line) at the relaxation frequency fr, as shown in Figure 5(b2). Figure 5(b2) exhibits a frequency shift between the RIN with OFB (fr = 3.6 GHz) and the solitary laser RIN (fr = 2.0 GHz). At low frequency, the RIN is enhanced to higher values (almost one order of magnitude) than the solitary laser RIN and increases by decreasing the SEF, as shown in Figure 5(b2,b3,c3).
In the chaos regime, when the LEF α = 3 and the SEF C = 10−4, the peak intensity of the RIN with OFB is enhanced to higher values (almost two orders of magnitude) (dashed line) and shifted in the direction of decreasing frequency compared with the solitary laser RIN (solid line) at the relaxation frequency fr, as shown in Figure 5(a2). Figure 5(a2) exhibits a frequency shift between the RIN with OFB (fr = 4.14 GHz) and the solitary laser RIN (fr = 5.9 GHz). At low frequency, the RIN is enhanced to higher values (almost two orders of magnitude) than the laser without OFB noise and increases/decreases by increasing/decreasing the LEF/SEF, as shown in Figure 5(a2,a3,c2).
This frequency shift found in the RIN at the relaxation oscillation frequency for both cases (solitary laser and laser with OFB) and due to the variation in the LEF and SEF is in agreement with the experimental and theoretical results mentioned in Refs. [29,30,31], which confirms our new results and expectations. From the results, under OFB in the weak region and when the LD is operating in the CW or PO region, we found that although the decrease/increase in the LEF/SEF causes an enhancement/reduction in the laser stability/noise, as presented in Figure 5, it causes considerable shifts in the lasing frequency and corrupts the LD efficiency in applications [32].
4. Conclusions
The effects of the LEF and SEF on the dynamics state and RIN of the short EC AlGaAs/GaAs LD 0.780 μm were investigated. In the simulation, multiple round trips have been considered in the time delay rate equation. The operations before and after the LD entered chaotic operation were identified using the BDs of the output photon number through wide range OFB. These operations were identified by computing the RIN spectrum at the OFB intensity, LEF, and SEF. The investigations found that the LEF and SEF caused considerable modifications in the LD dynamics. We report for the first time the impacts of the LEF and SEF on the dynamic states and RIN of the LD with short EC, which is very important in the designing of LDs. The results show that the OFB at which the dynamic moves from the CW to PO or chaos and decreases/increases at the LEF/SEF is enhancing/decreasing. The intensity of the OFB as the LD dynamic moves from the CW state to the PO, PD, or chaotic state decreased/increased when the LEF/SEF was enhanced. When the LEF/SEF decreased/increased, the LD operation states were modified from the chaotic state to the PO or CW state. This dynamic state is likely due to its stability and lowest noise level compared with the solitary laser noise level. We expected that the LD subject to OFB would be highly stable and have a descending RIN level at lower/higher values of the LEF/SEF, resulting in the selection of the appropriate LEF and SEF values.
Author Contributions
Conceptualization, S.A.; methodology, S.A. and J.H.; validation, S.A.; formal analysis, S.A.; investigation, S.A. and J.H.; resources, S.A. and J.H.; data curation, S.A. and J.H.; writing—original draft preparation, S.A.; writing—review and editing, S.A. and J.H.; visualization, S.A. and J.H.; supervision, S.A.; project administration, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Jazan University, Deanship of Scientific Research, Research Units Support Program, Support Number: RUP2-02, Jazan University, Jazan, Saudi Arabia.
Data Availability Statement
The data are contained within the article.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research, Jazan University for supporting this research through the Research Units Support Program, Support Number: RUP2-02.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kreinberg, S.; Chow, W.W.; Wolters, J.; Schneider, C.; Gies, C.; Jahnke, F.; Höfling, S.; Kamp, M.; Reitzenstein, S. Emission from quantum-dot high-β microcavities: Transition from spontaneous emission to lasing and the effects of superradiant emitter coupling. Light Sci. Appl. 2017, 6, e17030. [Google Scholar] [CrossRef] [PubMed]
- Stohs, J.; Bossert, D.J.; Gallant, D.J.; Brueck, S.R.J. Gain, Refractive Index Change, and Linewidth Enhancement Factor in Broad-Area Gaas and Ingaas Quantum-Well Lasers. IEEE J. Quantum Electron. 2001, 37, 11. [Google Scholar] [CrossRef]
- Henry, C.H. Theory of the linewidth of semiconductor lasers. IEEE J. Quantum Electron. 1982, QE-18, 259–264. [Google Scholar] [CrossRef]
- Yu, Y.; Xi, J. Influence of external optical feedback on the alpha factor of semiconductor lasers. Opt. Lett. 2013, 38, 1781. [Google Scholar] [CrossRef]
- Sobiesierski, A.; Smowton, P.M. Comprehensive Semiconductor Science and Technology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 6, pp. 353–384. [Google Scholar]
- Tong, K.; Du, Z.; Li, J.; Yuan, L. Optical frequency comb based on a distributed feedback semiconductor laser with direct injection current multi-frequency modulation. Opt. Laser Technol. 2021, 137, 106827. [Google Scholar] [CrossRef]
- Bergman, D.J.; Stockman, M.I. Surface Plasmon Amplification by Stimulated Emission of Radiation: Quantum Generation of Coherent Surface Plasmons in Nanosystems. Phys. Rev. Lett. 2003, 90, 027402. [Google Scholar] [CrossRef] [PubMed]
- Stockman, M.I. The spaser as a nanoscale quantum generator and ultrafast amplifier. J. Opt. 2010, 12, 024004. [Google Scholar] [CrossRef]
- Li, A.; Wei, H.; Cotrufo, M.; Chen, W.; Mann, S.; Ni, X.; Xu, B.; Chen, J.; Wang, J.; Fan, S.; et al. Exceptional points and non-Hermitian photonics at the nanoscale. Nat. Nanotechnol. 2023, 18, 706–720. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Demetrios; Christodoulides, N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, 6381. [Google Scholar] [CrossRef]
- Agrawal, G.; Bowden, C. Concept of linewidth enhancement factor in semiconductor lasers: Its usefulness and limitations. IEEE Photonics Technol. Lett. 1993, 5, 640–642. [Google Scholar] [CrossRef]
- Al-Hosiny, N.M. Dynamics of optically injected semiconductor lasers with zero linewidth enhancement factor. J. Taibah Univ. Sci. 2023, 17, 2163607. [Google Scholar] [CrossRef]
- Osinski, M.; Buus, J. Linewidth broadening factor in semiconductor lasers—An overview. IEEE J. Quantum Electron. 1987, 23, 9–29. [Google Scholar] [CrossRef]
- Masoller, C.; Abraham, N.B. Stability and dynamical properties of the coexisting attractors of an external-cavity semiconductor laser. Phys. Rev. A 1998, 57, 1313. [Google Scholar] [CrossRef]
- Rodriguez, D.; Esquivias, I.; Deubert, S.; Reithmaier, J.P.; Forchel, A.; Krarowski, M.; Calligaro, M.; Parillaud, O. Gain, index variation, and linewidth-enhancement factor in 980-nm quantum-well and quantum-dot lasers. IEEE J. Quantum Electron. 2005, 41, 117. [Google Scholar] [CrossRef]
- Ryan, A.T.; Agrawal, G.P.; Gray, G.R.; Gage, E.C. Optical-feedback-induced chaos and its control in multimode semiconductor lasers. IEEE J. Quantum Electron. 1994, 30, 668. [Google Scholar] [CrossRef]
- Mi, Z.; Bhattacharya, P.; Fathpour, S. High-speed 1.3 μm tunnel injection quantum-dot lasers. Appl. Phys. Lett. 2005, 86, 153109. [Google Scholar] [CrossRef]
- Mi, Z.; Bhattacharya, P. Analysis of the linewidth-enhancement factor of long-wavelength tunnel-injection quantum-dot lasers. IEEE J. Quantum Electron. 2007, 43, 363. [Google Scholar] [CrossRef]
- Al-Hosiny, N.M. Effect of Linewidth Enhancement Factor on the Stability Map of Optically Injected Distributed Feedback Laser. Opt. Rev. 2014, 21, 261. [Google Scholar] [CrossRef]
- Chuang, C.-F.; Liao, Y.-H.; Lin, C.-H.; Chen, S.-Y.; Grillot, F.; Lin, F.-Y. Linewidth enhancement factor in semiconductor lasers subject to various external optical feedback conditions. Opt. Express 2014, 22, 5651. [Google Scholar] [CrossRef]
- Bowers, J.E.; Hemenway, B.R.; Gnauck, A.H.; Wilt, D.P. High-speed InGaAsP constricted-mesa lasers. IEEE J. Quantum Electron. 1986, 22, 833. [Google Scholar] [CrossRef]
- Petermann, K. Laser Diode Modulation and Noise; Kluwer Academic: Dordrecht, The Netherlands, 1988; Chapter 7; p. 152. [Google Scholar]
- Arsenijević, D.; Bimberg, D. Phase noise and jitter reduction by optical feedback on passively mode-locked quantum dot lasers. Appl. Phys. Lett. 2013, 103, 231101. [Google Scholar] [CrossRef]
- Asghar, H.; Wei, W.; Kumar, P.; Sooudi, E.; Mcinerney, J.G. Stabilization of self-mode-locked quantum dash lasers by symmetric dual-loop optical feedback. Opt. Express 2018, 26, 4581. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Ahmed, M.; Okamoto, T.; Ishimori, W.; Yamada, M. An improved analysis of semiconductor laser dynamics under strong optical feedback. IEEE J. Select. Top. Quantum Electron. 2003, 9, 1265–1274. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Ahmed, M.; Yamada, M. New model of analysis of semiconductor laser dynamics under strong optical feedback in fiber communication system. Proc. SPIE 2003, 4986, 490–501. [Google Scholar]
- Abdulrhmann, S.; Altowyan, A.S.; Hakami, J. Impact of Optical Feedback and Radiative and Non-radiative Recombination Rates on the Dynamics and Intensity Noise of Semiconductor Laser. Photonics 2022, 9, 541–554. [Google Scholar] [CrossRef]
- Abdulrhmann, S.; Hakami, J.; Alhasan, A.M.; Altowyan, A.S.; Afifi, G. Impact of α-factor, combined optical phase and gain saturation on the onset of chaos of short external cavity semiconductor lasers. Optik 2023, 286, 171030. [Google Scholar] [CrossRef]
- Yamada, M. Variation of intensity noise and frequency noise with the spontaneous emission factor in semiconductor lasers. IEEE J. Quantum Electron. 1994, 30, 1511–1519. [Google Scholar] [CrossRef]
- Sattar, Z.A.; Shore, K.A. External Optical Feedback Effects in Semiconductor Nanolasers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 500–505. [Google Scholar] [CrossRef]
- Suelzer, J.S.; Prasad, A.; Ghosh, R.; Vemuri, G. Effects of quantum noise on the nonlinear dynamics of a semiconductor laser subject to two spectrally filtered, time-delayed optical feedbacks. Opt. Commun. 2016, 370, 209–221. [Google Scholar] [CrossRef][Green Version]
- Lam, W.-S.; Guzdar, P.N.; Roy, R. Effect of Spontaneous Emission Noise and Modulation on Semiconductor Lasers Near Threshold with Optical Feedback. Int. J. Mod. Phys. B 2003, 17, 4123–4138. [Google Scholar] [CrossRef]
- Chow, W.W.; Wan, Y.; Bowers, J.E.; Grillot, F. Analysis of the Spontaneous Emission Limited Linewidth of an Integrated III–V/SiN Laser. Laser Photonics Rev. 2022, 16, 2100620. [Google Scholar] [CrossRef]
- Ahmed, M.; Yamada, M. An infinite order perturbation approach to gain calculation in injection semiconductor lasers. J. Appl. Phys. 1998, 84, 3004. [Google Scholar] [CrossRef]
- Yamada, M.; Suematsu, Y. Analysis of gain suppression in undoped injection lasers. J. Appl. Phys. 1981, 52, 2653. [Google Scholar] [CrossRef]
- Nishimura, Y.; Nishimura, Y. Spectral hole-burning and nonlinear-gain decrease in a band-to-level transition semiconductor laser. IEEE J. Quantum Electron. 1973, 9, 1011. [Google Scholar] [CrossRef]
- Ahmed, M.; Yamada, M. Field Fluctuations and Spectral Line Shape in Semiconductor Lasers Subjected to Optical Feedback. J. Appl. Physics 2004, 95, 7573–7583. [Google Scholar] [CrossRef]
- Spiteri, R.J.; Wei, S. Fractional-step runge–kutta methods: Representation and linear stability analysis. J. Comput. Phys. 2023, 476, 111900. [Google Scholar] [CrossRef]
- Bakry, A.; Abdulrhmann, S.; Ahmed, M. Theoretical Modeling of the Dynamics of Semiconductor Laser Subject to Double-Reflector Optical Feedback. J. Exp. Theor. Phys. 2016, 149, 960–969. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).