Characterizing the Vibration Responses of Flexible Workpieces during the Turning Process for Quality Control
Abstract
:Featured Application
Abstract
1. Introduction
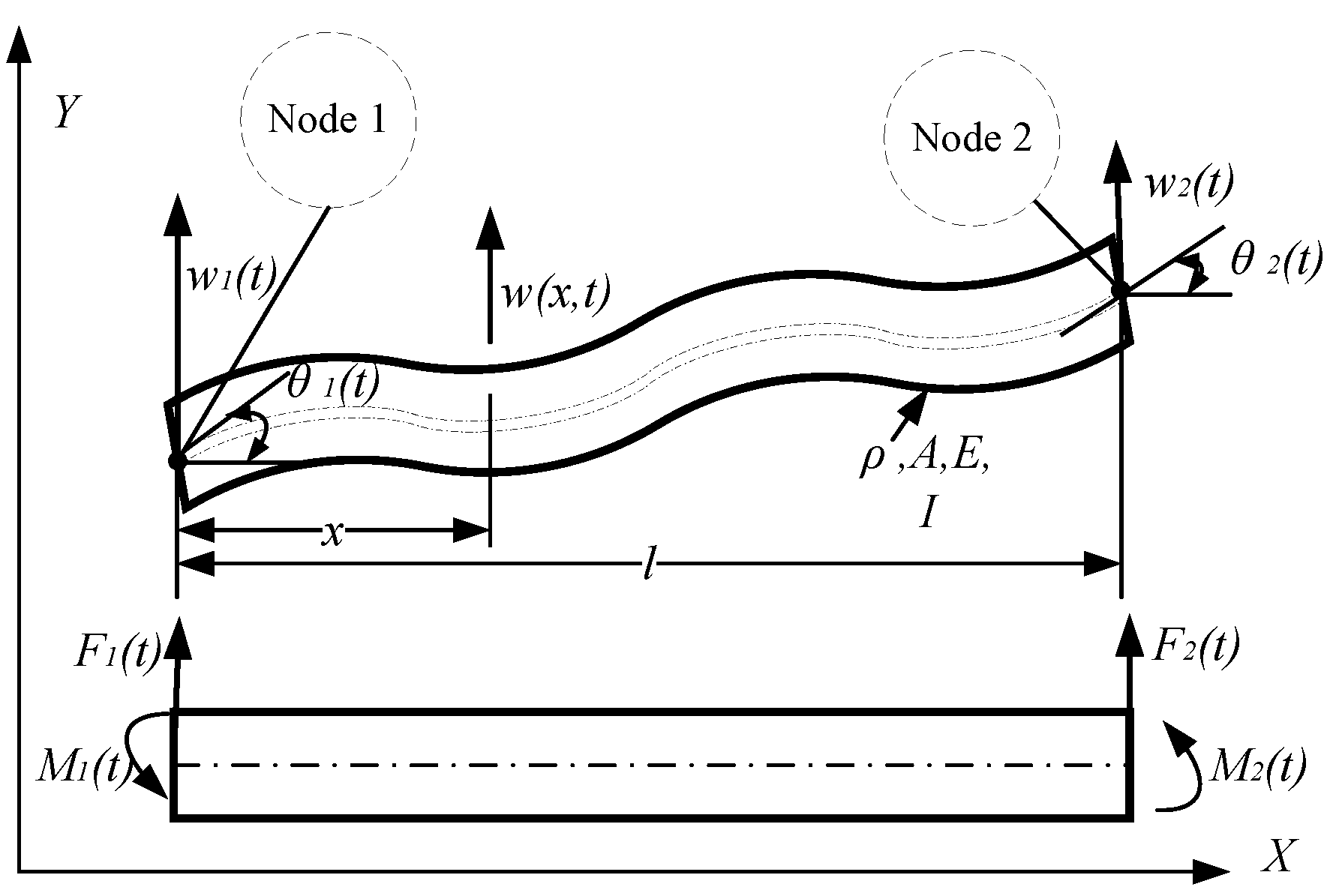
2. Dynamic Model of Turning a Slender Shaft
3. Finite Element Analysis Considering Support Stiffness and Axial Force
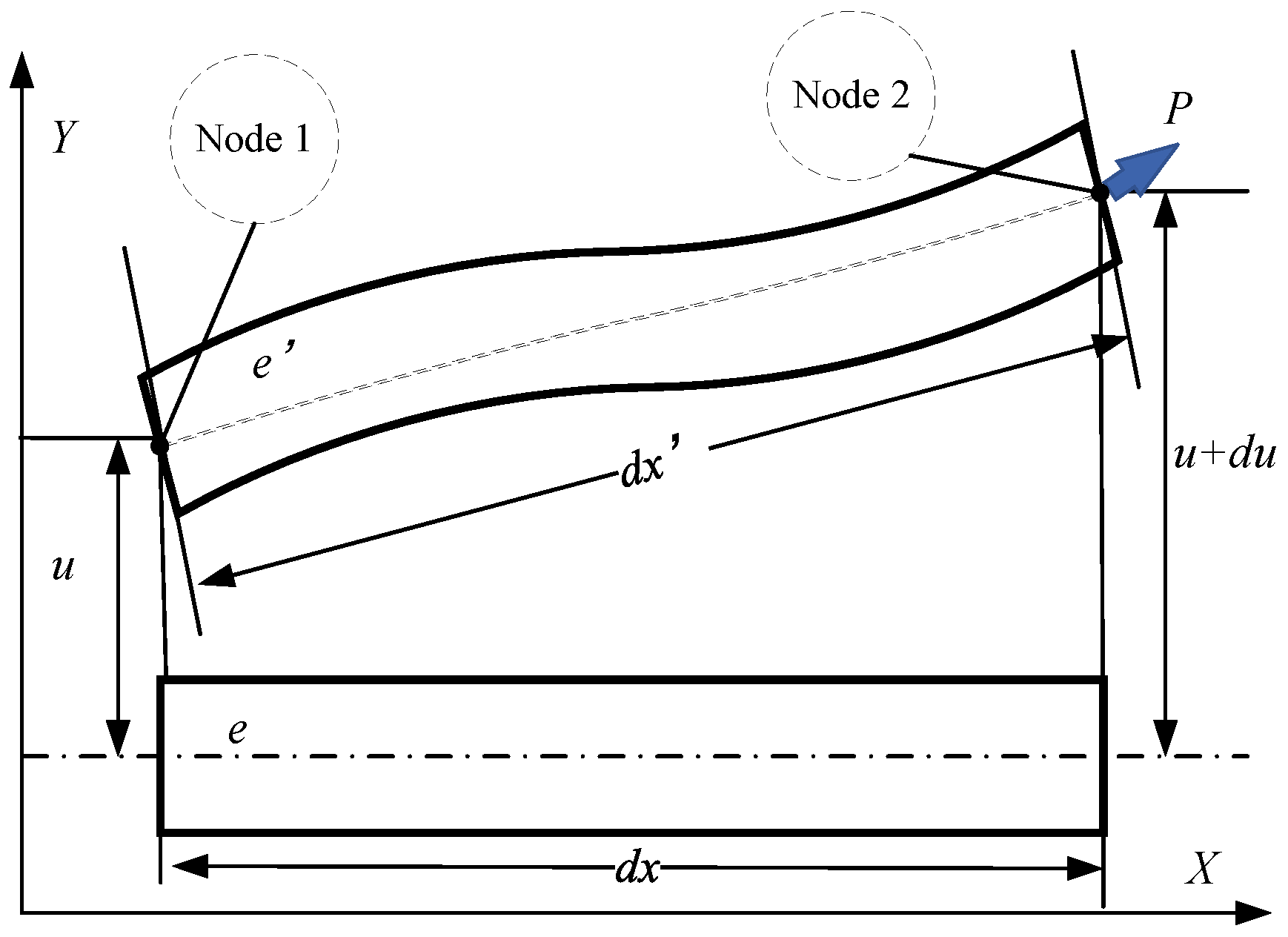
3.1. Stiffness and Mass Matrices of the Shaft Element
3.2. Support Stiffness of the Tailstock
3.3. Influence of Axial Force on Stiffness Matrix
4. Simulation Results Using FEA Method
4.1. Influence of Tailstock Radial Stiffness on the Shaft’s Mode Frequency
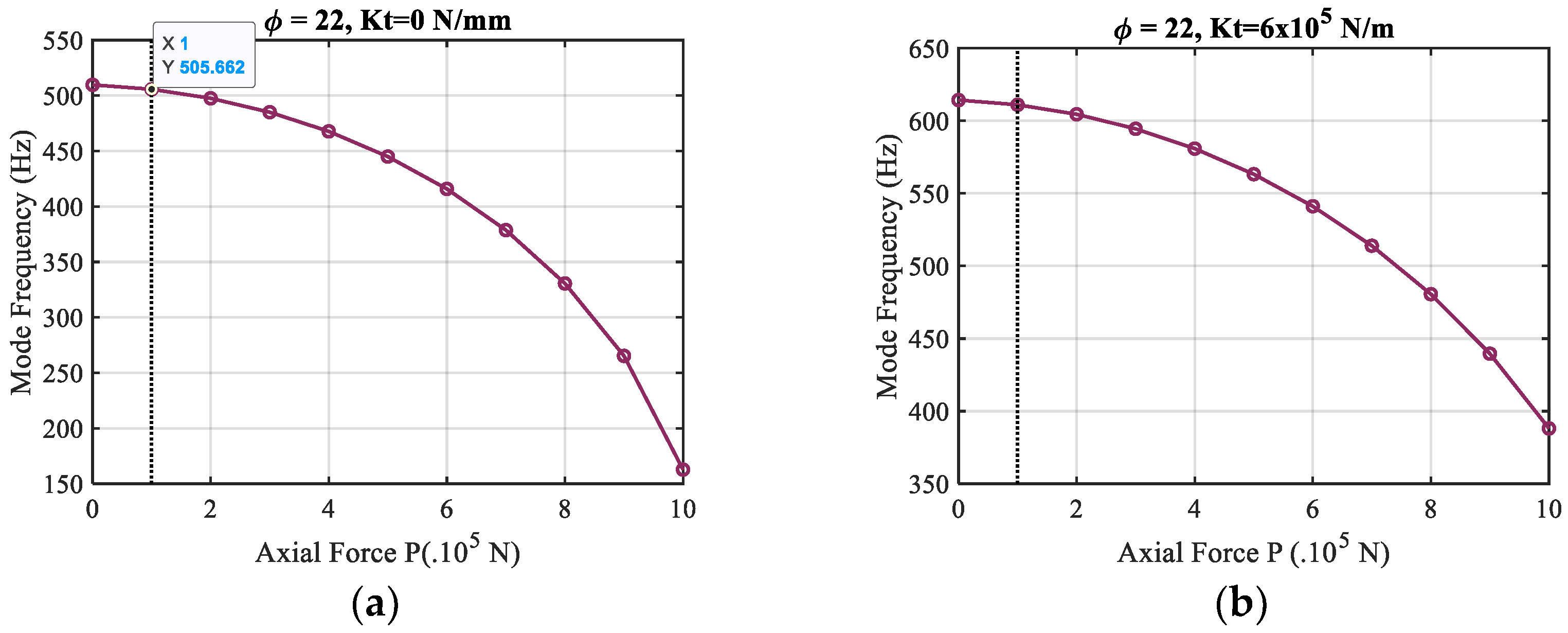
4.2. Influence of Axial Force on Shaft’s Mode Frequency
4.3. Influence of Shaft Diameter on Mode Frequency
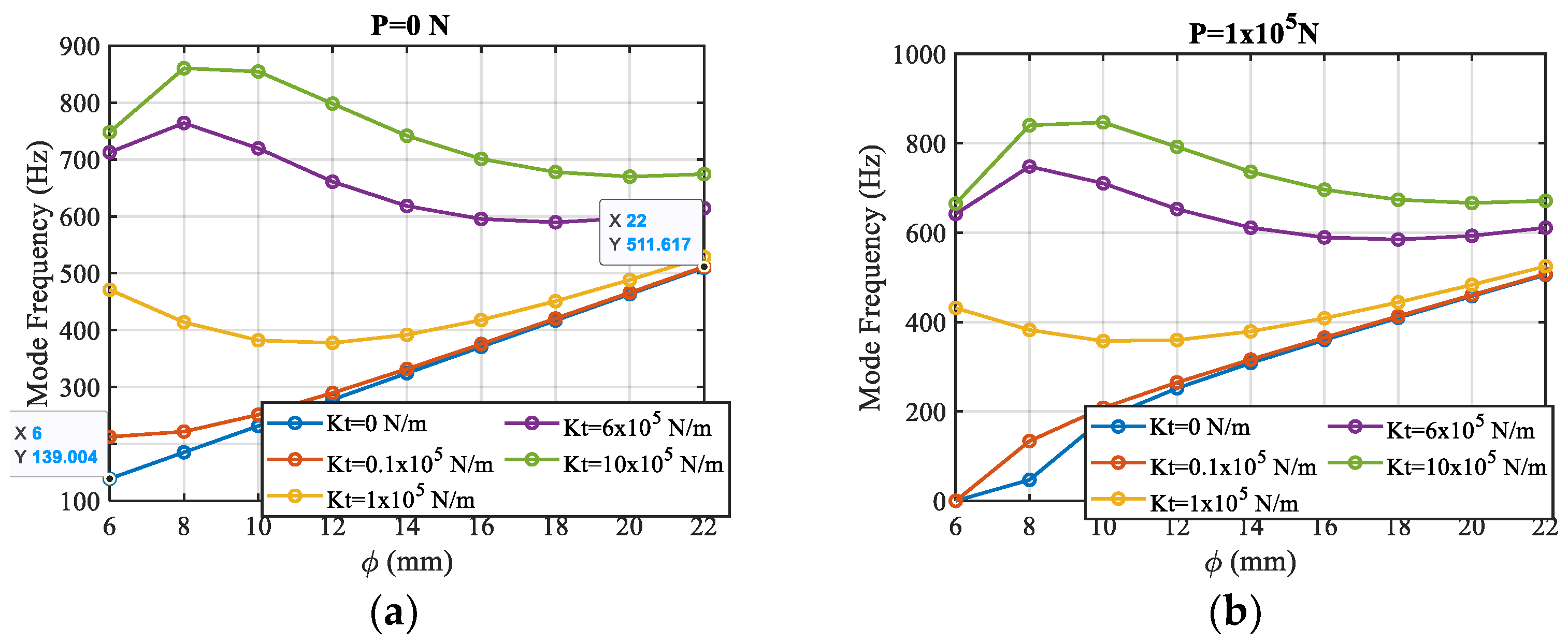
4.4. Influence of Coupling of Shaft Diameter and Tailstock Stiffness
4.5. Effect of the Coupling of Shaft Diameter and Axial Force
5. Experimental Verification
5.1. Frequency Response Function Analysis
5.2. Analysis of the Transverse Vibration Signal of the Shaft
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sekar, M.; Srinivas, J.; Kotaiah, K.R.; Yang, S.H. Stability Analysis of Turning Process with Tailstock-Supported Workpiece. Int. J. Adv. Manuf. Technol. 2009, 43, 862–871. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Chen, H.; Zou, J.; Ma, L.; Yin, G. Study on Surface Quality and Subsurface Damage Mechanism of Nickel-Based Single-Crystal Superalloy in Precision Turning. J. Manuf. Process. 2023, 99, 230–242. [Google Scholar] [CrossRef]
- Stepan, G.; Kiss, A.K.; Ghalamchi, B.; Sopanen, J.; Bachrathy, D. Chatter Avoidance in Cutting Highly Flexible Workpieces. CIRP Ann. Manuf. Technol. 2017, 66, 377–380. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Song, Q.; Wang, B. Development of Constrained Layer Damping Toolholder to Improve Chatter Stability in End Milling. Int. J. Mech. Sci. 2016, 117, 299–308. [Google Scholar] [CrossRef]
- Chen, C.K.; Tsao, Y.M. A Stability Analysis of Turning a Tailstock Supported Flexible Work-Piece. Int. J. Mach. Tools Manuf. 2006, 46, 18–25. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Song, Q.; Wang, B. Analysis and Implementation of Chatter Frequency Dependent Constrained Layer Damping Tool Holder for Stability Improvement in Turning Process. J. Am. Acad. Dermatol. 2018, 266, 687–695. [Google Scholar] [CrossRef]
- Chanda, A.; Dwivedy, S.K. Nonlinear Dynamic Analysis of Flexible Workpiece and Tool in Turning Operation with Delay and Internal Resonance. J. Sound Vib. 2018, 434, 358–378. [Google Scholar] [CrossRef]
- Lu, K.; Lian, Z.; Gu, F.; Liu, H. Model-Based Chatter Stability Prediction and Detection for the Turning of a Flexible Workpiece. Mech. Syst. Signal. Process. 2018, 100, 814–826. [Google Scholar] [CrossRef]
- Tang, L.; Landers, R.G.; Balakrishnan, S.N. Parallel Turning Process Parameter Optimization Based on a Novel Heuristic Approach. J. Manuf. Sci. Eng. Trans. ASME 2008, 130, 0310021–03100212. [Google Scholar] [CrossRef]
- Carrer, J.A.M.; Corrêa, R.M.; Mansur, W.J.; Scuciato, R.F. Dynamic Analysis of Continuous Beams by the Boundary Element Method. Eng. Anal. Bound. Elem. 2019, 104, 80–93. [Google Scholar] [CrossRef]
- Östling, D.; Magnevall, M. Modelling the Dynamics of a Large Damped Boring Bar in a Lathe. Procedia CIRP 2019, 82, 285–289. [Google Scholar] [CrossRef]
- Beri, B.; Meszaros, G.; Stepan, G. Machining of Slender Workpieces Subjected to Time-Periodic Axial Force: Stability and Chatter Suppression. J. Sound Vib. 2021, 504, 116114. [Google Scholar] [CrossRef]
- Yekdane, A.; Movahedian, B.; Boroomand, B. An Efficient Time-Space Formulation for Dynamic Transient Analyses: Application to the Beam Assemblies Subjected to Moving Loads and Masses; Elsevier Inc.: Amsterdam, The Netherlands, 2020; ISBN 8415683111. [Google Scholar]
- Ozturk, E.; Comak, A.; Budak, E. Tuning of Tool Dynamics for Increased Stability of Parallel (Simultaneous) Turning Processes. J. Sound Vib. 2016, 360, 17–30. [Google Scholar] [CrossRef]
- Saffury, J.; Altus, E. Chatter Resistance of Non-Uniform Turning Bars with Attached Dynamic Absorbers-Analytical Approach. J. Sound Vib. 2010, 329, 2029–2043. [Google Scholar] [CrossRef]
- Nachum, S.; Altus, E. Natural Frequencies and Mode Shapes of Deterministic and Stochastic Non-Homogeneous Rods and Beams. J. Sound Vib. 2007, 302, 903–924. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Cheng, C.J. Natural Frequencies and Mode Shapes for Axisymmetric Vibrations of Shells in Turning-Point Range. Int. J. Solids Struct. 2006, 43, 5525–5540. [Google Scholar] [CrossRef]
- Sun, Y.; Yan, S. Dynamics Identification and Stability Analysis in Turning of Slender Workpieces with Flexible Boundary Constraints. Mech. Syst. Signal. Process. 2022, 177, 109245. [Google Scholar] [CrossRef]
- Subbarao, R.; Dey, R. Selection of Lathe Spindle Material Based on Static and Dynamic Analyses Using Finite Element Method. Mater. Today Proc. 2019, 22, 1652–1663. [Google Scholar] [CrossRef]
- Duran, A.; Nalbant, M. Finite Element Analysis of Bending Occurring While Cutting with High Speed Steel Lathe Cutting Tools. Mater. Des. 2005, 26, 549–554. [Google Scholar] [CrossRef]
- Mahdavinejad, R. Finite Element Analysis of Machine and Workpiece Instability in Turning. Int. J. Mach. Tools Manuf. 2005, 45, 753–760. [Google Scholar] [CrossRef]
- Jorge, P.C.; Da Costa, A.P.; Simões, F.M.F. Finite Element Dynamic Analysis of Finite Beams on a Bilinear Foundation under a Moving Load. J. Sound Vib. 2015, 346, 328–344. [Google Scholar] [CrossRef]
- Shang, H.Y.; Machado, R.D.; Abdalla Filho, J.E. Dynamic Analysis of Euler-Bernoulli Beam Problems Using the Generalized Finite Element Method. Comput. Struct. 2016, 173, 109–122. [Google Scholar] [CrossRef]
- Joseph, S.; Deepak, B.S. Virtual Experimental Modal Analysis of a Cantilever Beam. Int. J. Eng. Res. Technol. 2017, 6, 921–928. [Google Scholar]
- Jianliang, G.; Rongdi, H. A United Model of Diametral Error in Slender Bar Turning with a Follower Rest. Int. J. Mach. Tools Manuf. 2006, 46, 1002–1012. [Google Scholar] [CrossRef]
- Li, C.; Li, B.; Gu, L.; Feng, G.; Gu, F.; Ball, A.D. Online Monitoring of a Shaft Turning Process Based on Vibration Signals from On-Rotor Sensor. In Proceedings of the 2020 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMENIM), Shanghai, China, 4–6 December 2020; pp. 402–407. [Google Scholar] [CrossRef]
- Segonds, S.; Cohen, G.; Landon, Y.; Monies, F.; Lagarrigue, P. Characterising the Behaviour of Workpieces under the Effect of Tangential Cutting Force during NC Turning: Application to Machining of Slender Workpieces. J. Mater. Process. Technol. 2006, 171, 471–479. [Google Scholar] [CrossRef]
- Huang, D.; Bian, Y.; Huang, D.; Zhou, A.; Sheng, B. An Ultimate-State-Based-Model for Inelastic Analysis of Intermediate Slenderness PSB Columns under Eccentrically Compressive Load. Constr. Build. Mater. 2015, 94, 306–314. [Google Scholar] [CrossRef]
- Soleimanimehr, H. Analysis of the Cutting Ratio and Investigating Its Influence on the Workpiece’s Diametrical Error in Ultrasonic-Vibration Assisted Turning. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2021, 235, 640–649. [Google Scholar] [CrossRef]
- Li, B.; Gu, L.; Lin, Y.; Zou, Z.; Pang, S.; Lu, K.; Feng, G.; Gu, F.; Ball, A.D. Vibration Monitoring of Turning a Shaft on a Lathe Based on Signals from an On-Rotor Sensor. In Proceedings of the Mechanisms and Machine Science; Springer Science and Business Media B.V.: Berlin/Heidelberg, Germany, 2021; Volume 105, pp. 910–922. [Google Scholar]
- Rao, S.S. Vibration of Continuous Systems; Wiley: Hoboken, NJ, USA, 2006; ISBN 9786468600. [Google Scholar]
- Gritsenko, D.; Xu, J.; Paoli, R. Transverse Vibrations of Cantilever Beams: Analytical Solutions with General Steady-State Forcing. Appl. Eng. Sci. 2020, 3, 100017. [Google Scholar] [CrossRef]
- Li, C.; Zou, Z.; Lu, K.; Wang, H.; Cattley, R.; Ball, A.D. Assessment of a Three-Axis on-Rotor Sensing Performance for Machining Process Monitoring: A Case Study. Sci. Rep. 2022, 12, 16813. [Google Scholar] [CrossRef]
- Li, C.; Li, B.; Wang, H.; Shi, D.; Gu, F.; Ball, A.D. Tool Wear Monitoring in CNC Milling Process Based on Vibration Signals from an On-Rotor Sensing Method. In International Conference on the Efficiency and Performance Engineering Network; Springer Nature: Cham, Switzerland, 2022; pp. 268–281. [Google Scholar] [CrossRef]
- Zerti, O.; Yallese, M.A.; Khettabi, R.; Chaoui, K.; Mabrouki, T. Design Optimization for Minimum Technological Parameters When Dry Turning of AISI D3 Steel Using Taguchi Method. Int. J. Adv. Manuf. Technol. 2017, 89, 1915–1934. [Google Scholar] [CrossRef]







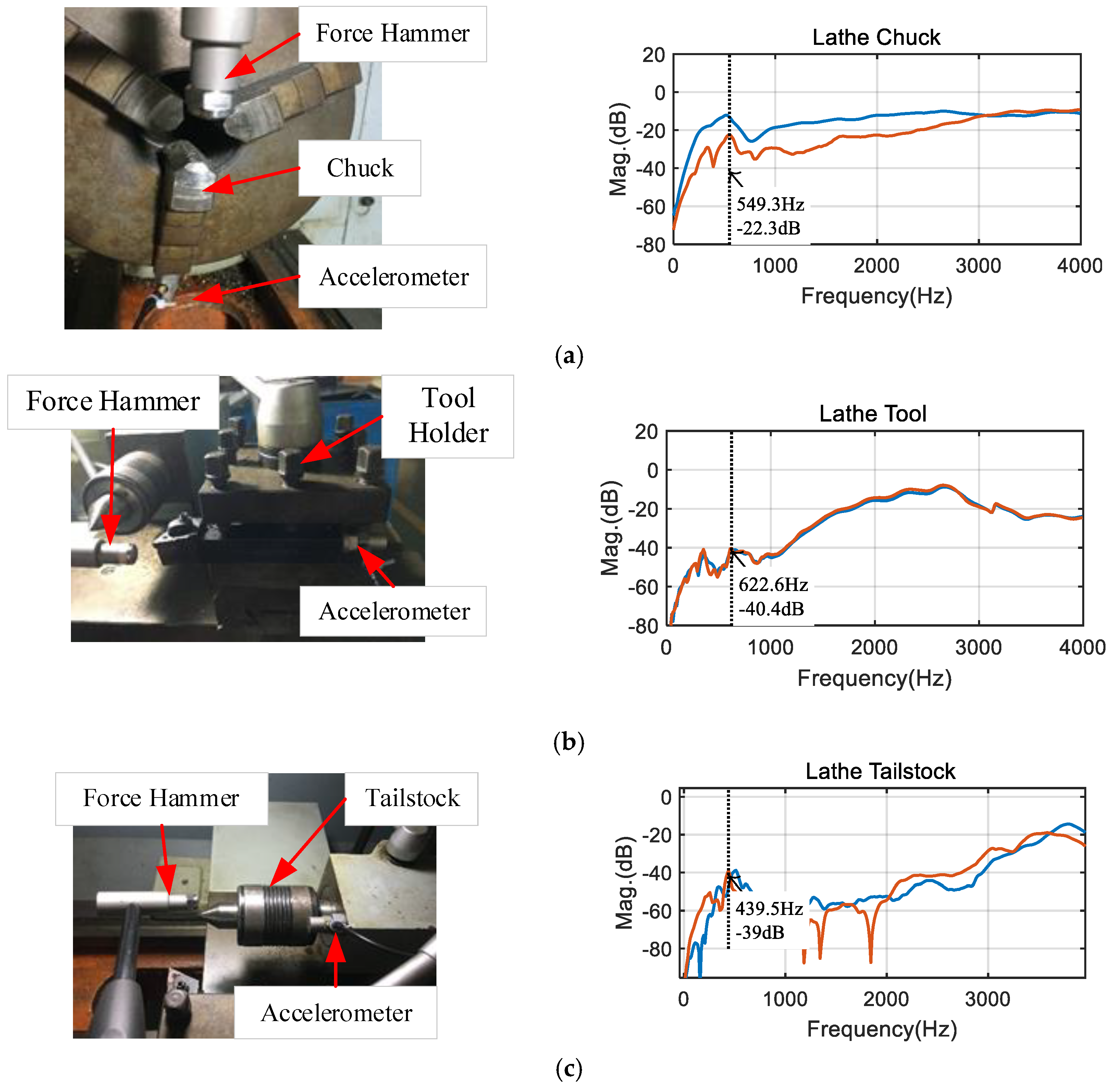

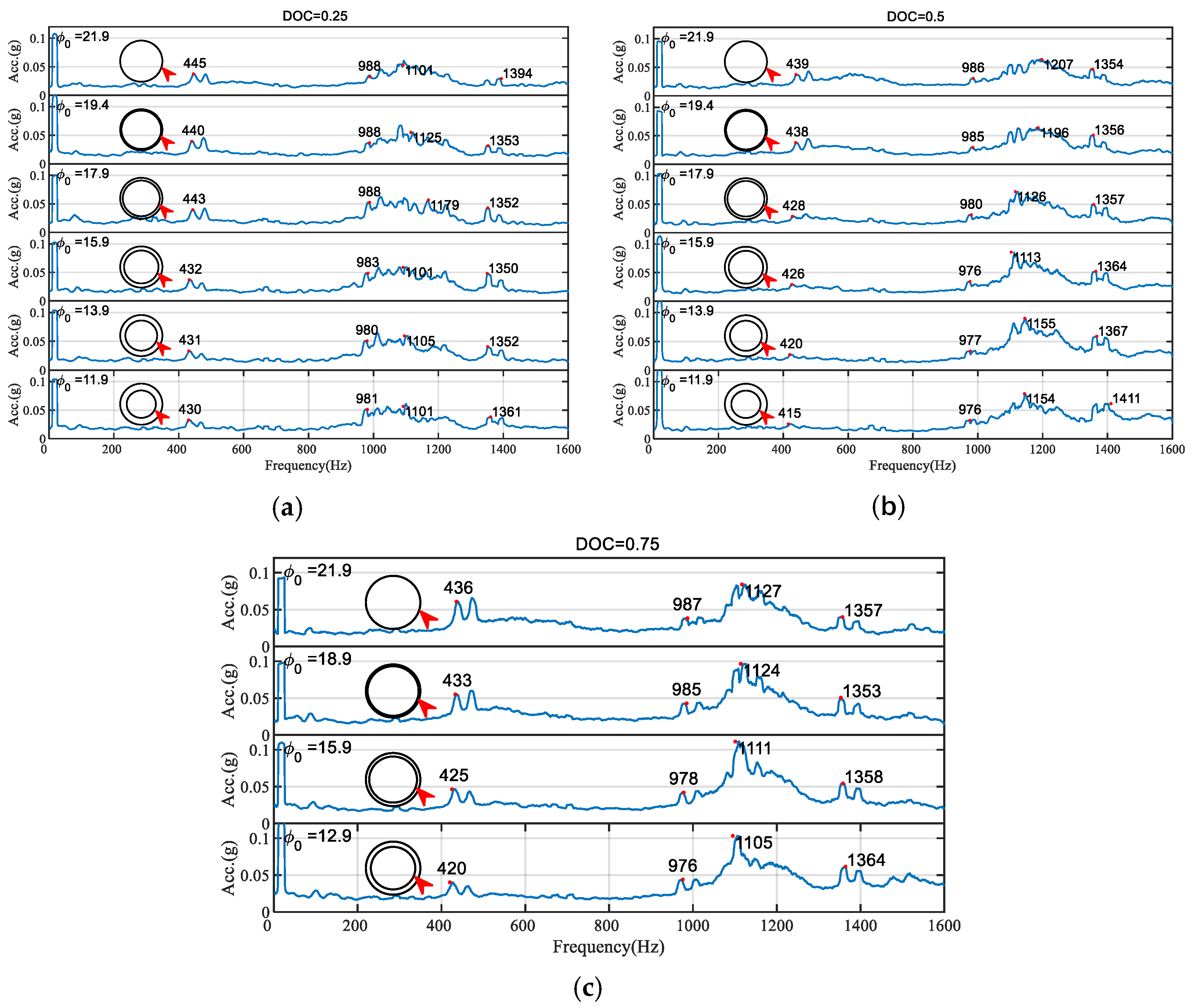

| Shaft Material | Initial Diameter | Length | Young’s Modulus E | Mass Density ρ |
|---|---|---|---|---|
| Q235 | 22 mm | 215 mm | 200 GPa | 7850 kg m−3 |
| Cutting Tool | Feed Rate | Spindle Speed | Depth of Cut (mm) | Number of Cuts |
|---|---|---|---|---|
| Kyocera TNGG 160402R-S PR930 | 0.05 mm/r | 1080 rpm | 0.25 mm | 12 |
| 0.5 mm | 8 | |||
| 0.75 mm | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zou, Z.; Duan, W.; Liu, J.; Gu, F.; Ball, A.D. Characterizing the Vibration Responses of Flexible Workpieces during the Turning Process for Quality Control. Appl. Sci. 2023, 13, 12611. https://doi.org/10.3390/app132312611
Li C, Zou Z, Duan W, Liu J, Gu F, Ball AD. Characterizing the Vibration Responses of Flexible Workpieces during the Turning Process for Quality Control. Applied Sciences. 2023; 13(23):12611. https://doi.org/10.3390/app132312611
Chicago/Turabian StyleLi, Chun, Zhexiang Zou, Wenbo Duan, Jiajie Liu, Fengshou Gu, and Andrew David Ball. 2023. "Characterizing the Vibration Responses of Flexible Workpieces during the Turning Process for Quality Control" Applied Sciences 13, no. 23: 12611. https://doi.org/10.3390/app132312611
APA StyleLi, C., Zou, Z., Duan, W., Liu, J., Gu, F., & Ball, A. D. (2023). Characterizing the Vibration Responses of Flexible Workpieces during the Turning Process for Quality Control. Applied Sciences, 13(23), 12611. https://doi.org/10.3390/app132312611











