Multilevel Regularization Method for Building Outlines Extracted from High-Resolution Remote Sensing Images
Abstract
:1. Introduction
- The calculation of the Hausdorff distance is improved by considering the distribution characteristics of nodes in the building outline.
- An MBR algorithm is presented based on the improved Hausdorff distance method, addressing the issue of directional deviation present in commonly used MBR methods.
- A new “overall–local–detail” multilevel regularization method was designed for building outlines.
2. Materials and Methods
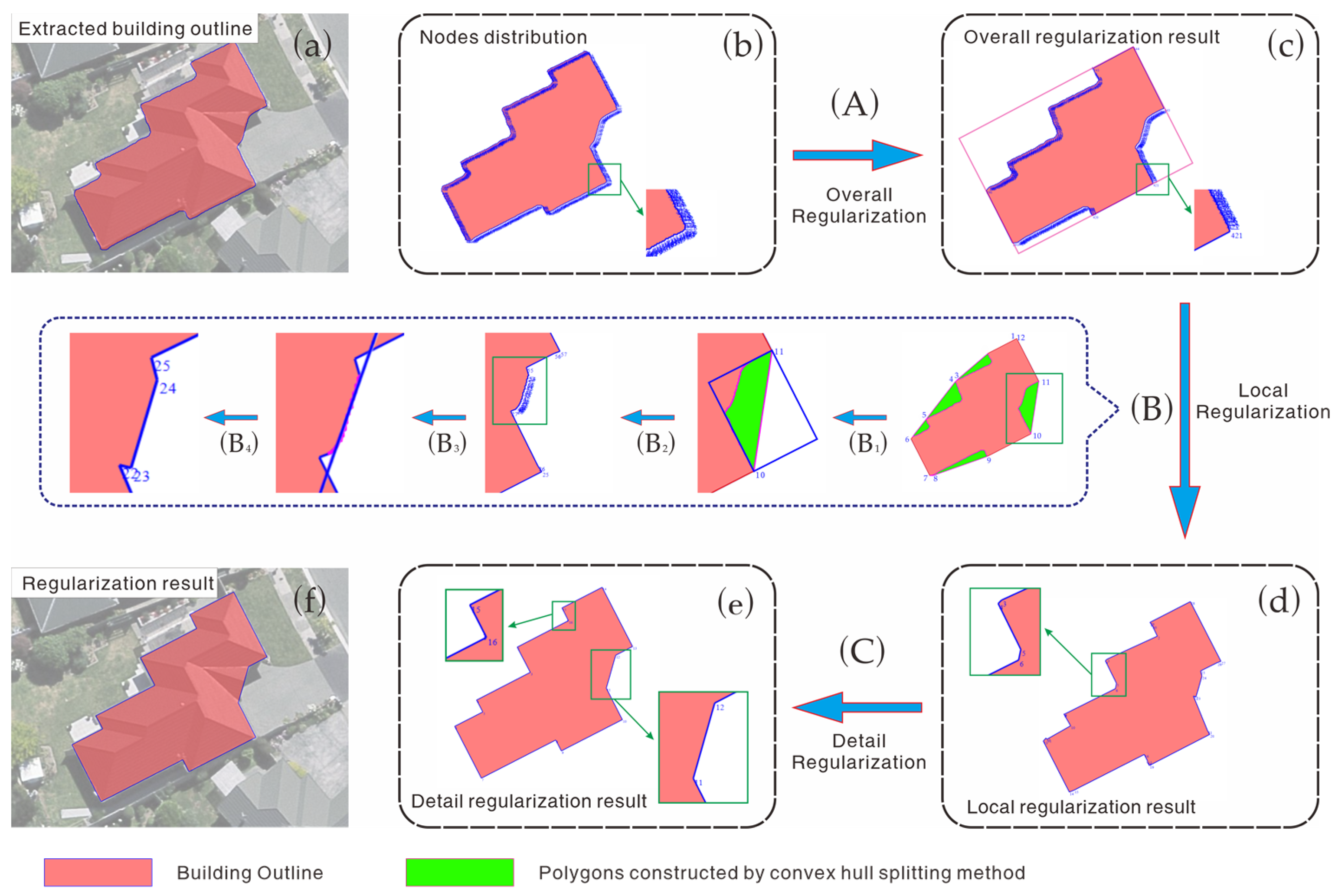
2.1. Principles and Specific Steps
2.2. Overall Regularization of Building Outlines Using Hausdorff Distance and MBR
2.2.1. Calculation of Hausdorff Distance
2.2.2. Building Outline Regularization Using the Hausdorff Distance Method and Its Improvement
- 1.
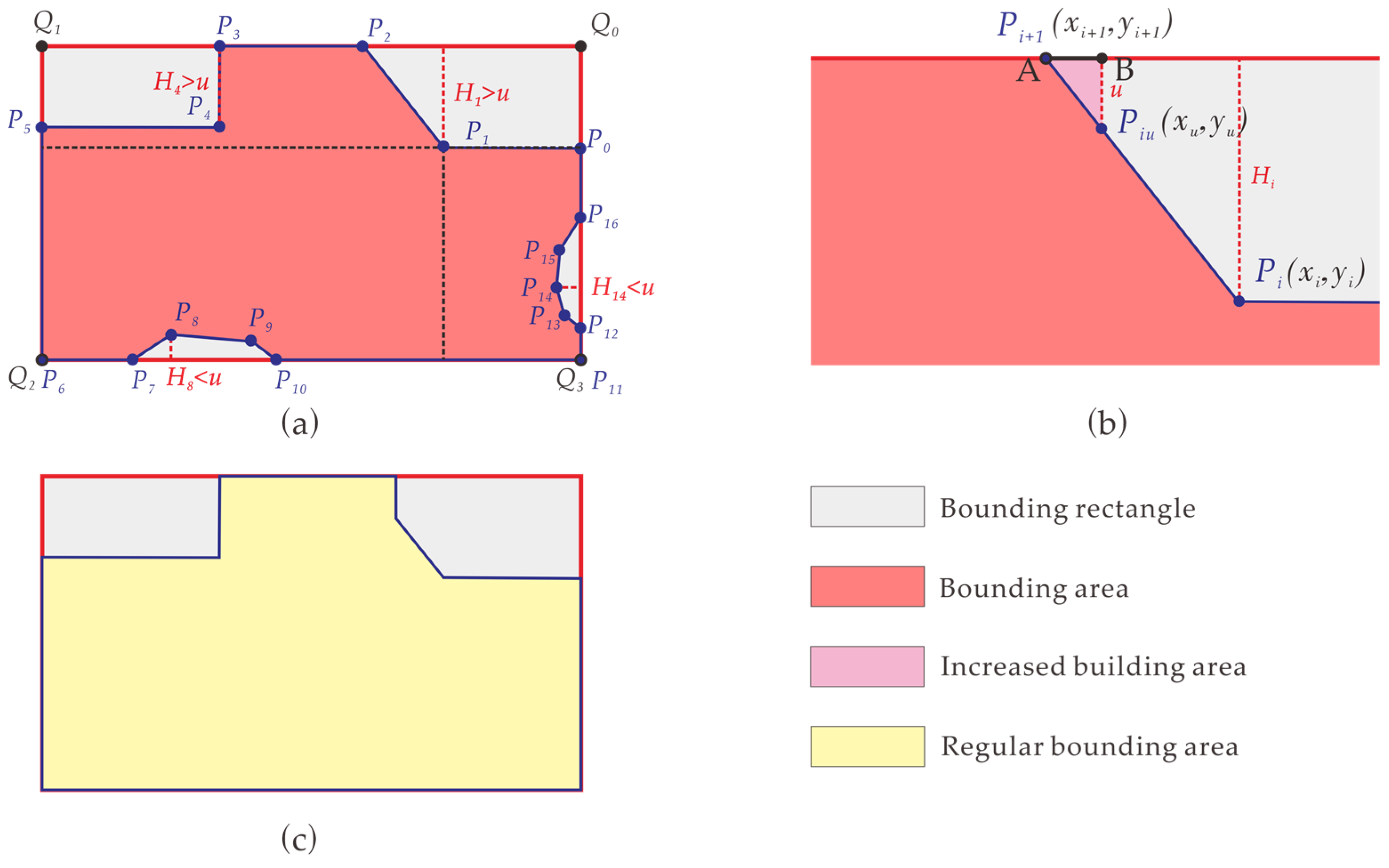
- Take the ordered set of nodes from the building outline as the point set P and treat the four corner points of the MBR as the point set Q. Then, in sequence, calculate the perpendicular distance from each point in set P to the line segments formed by adjacent points in set Q. Use the minimum distance among the four distances as the distance Hi from point Pi to the MBR. As shown in Figure 4a, calculate the perpendicular distances from point P1 to line segments Q0Q1, Q1Q2, Q2Q3, and Q3Q0, and then, select the minimum distance H1 as the distance from point P1 to the MBR.
- 2.
- For any line segment PiPi+1 on the building outline, take the larger of Hi and Hi+1 as .
- 3.
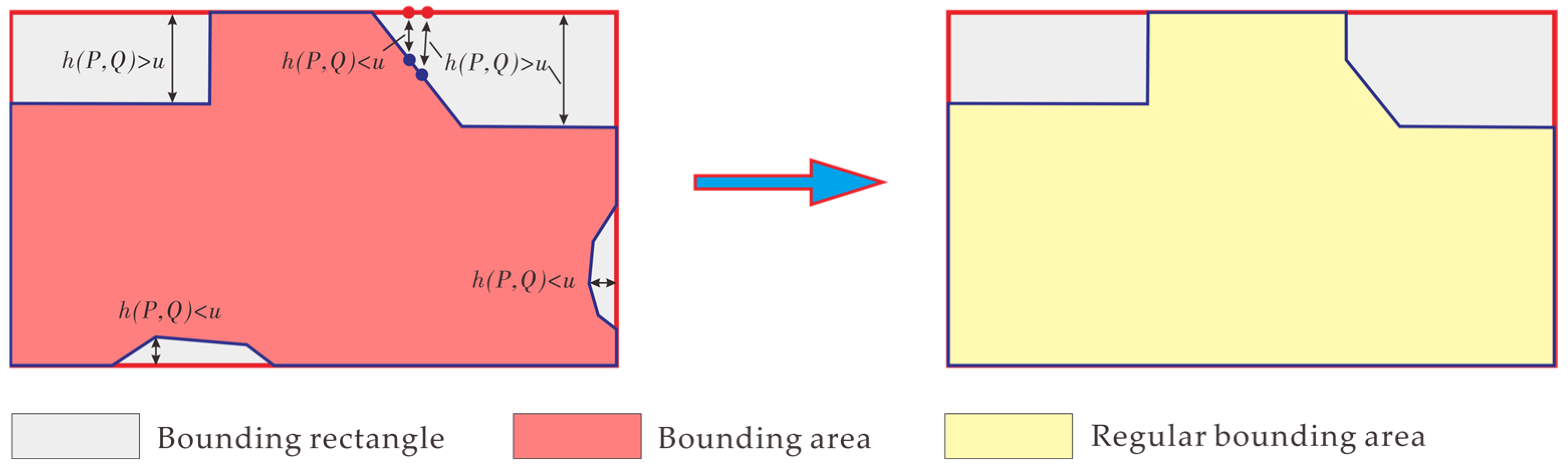
- If < u, replace the line segment on the building outline with the corresponding orthographically projected line segment on the nearest edge of the MBR. If > u, there are two possible cases: either both endpoints of the line segment are farther from the MBR than u, in which case the outline segment remains unchanged, or only one endpoint has a distance greater than u from the MBR. In the latter case, use Equation (4) to calculate point (xu, yu) on the line segment where the distance to the MBR equals u, and replace the part of Hausdorff distances less than u with the corresponding segments on the MBR.where Hi and Hi+1 are the minimum distances from the endpoints Pi and Pi+1 of the line segment, respectively, to an edge of the MBR.
- 4.
- After iteratively processing all points on the building outline, the overall regularization result is obtained, as shown in Figure 4c.
2.2.3. MBR Calculation Method and Its Improvement
- 1.
- 2.
- Calculate all MBRs aligned with the edges of the convex hull and record the area and perimeter for each direction, as depicted in Figure 6c.
- 3.
- Select the MBR with the smallest area as the MABR and the one with the shortest perimeter as the MPBR, as illustrated in Figure 6d, where the green rectangle represents the MABR, and the pink rectangle represents the MPBR of the building outline.
- 1.
- Compute the convex hull of the building outline.
- 2.
- Calculate the MBRs corresponding to each edge of the convex hull.
- 3.
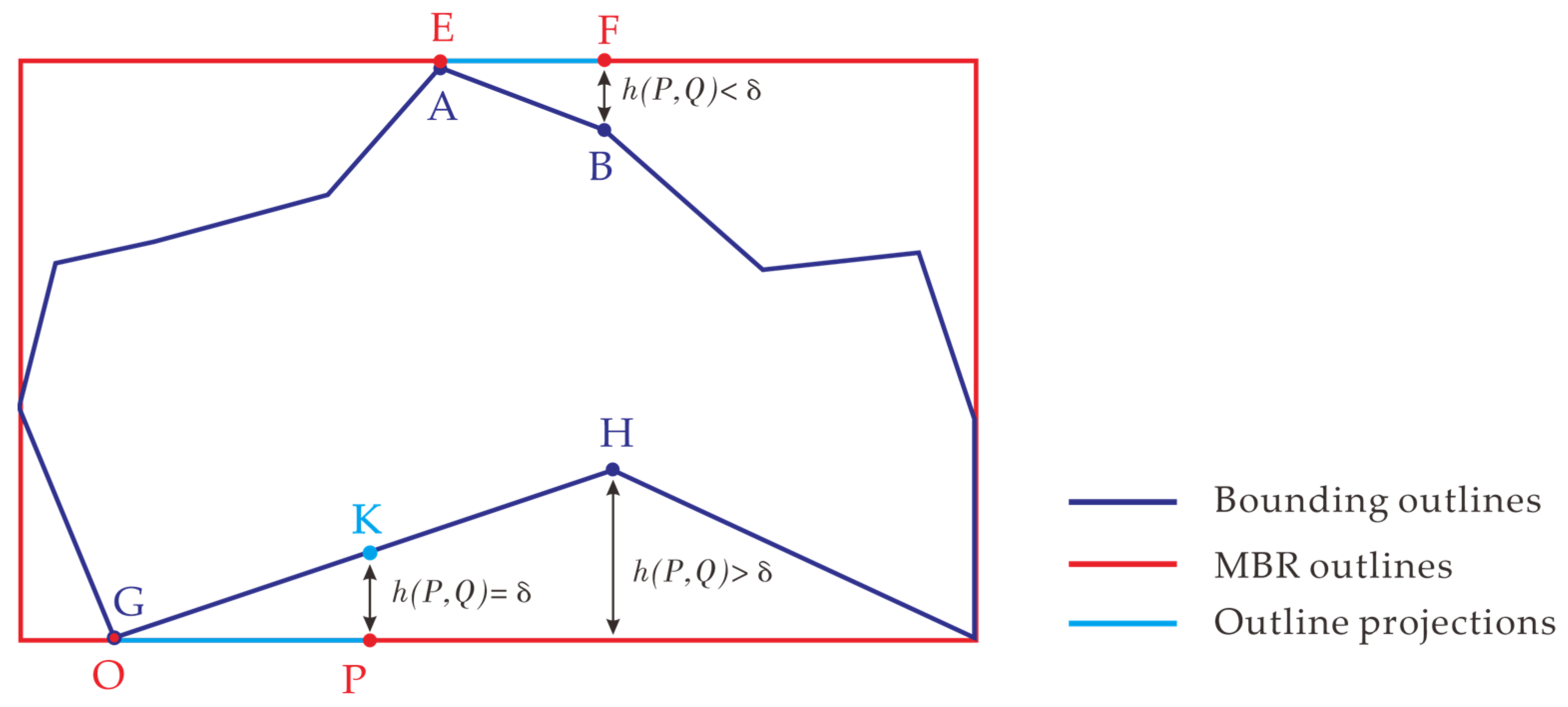
- Set a threshold δ (based on extensive experiments, δ can be set to the same value as the data resolution, e.g., 0.5 m for data with resolution of 0.5 m). If the line segment on building outline P to any side of the MBR Q satisfies < δ, record the length of the projected line segment on Q. As shown in Figure 8, because segment AB satisfies < δ, the length of its projected line segment EF on Q is recorded. For a line segment satisfying > δ, if there is a part with < δ, record the length of the projected segment of that part on Q. As shown in Figure 8, part GK of line segment GH satisfies < δ, and thus the length of its projected line segment OP on Q is recorded. Then, calculate the ratio p = Lsum/Crec, where Lsum is the sum of the lengths of projected segments on the current MBR outline, and Crec is the perimeter of the MBR.
- 4.
- Select the MBR corresponding to the maximum p value as the result based on the Hausdorff distance.
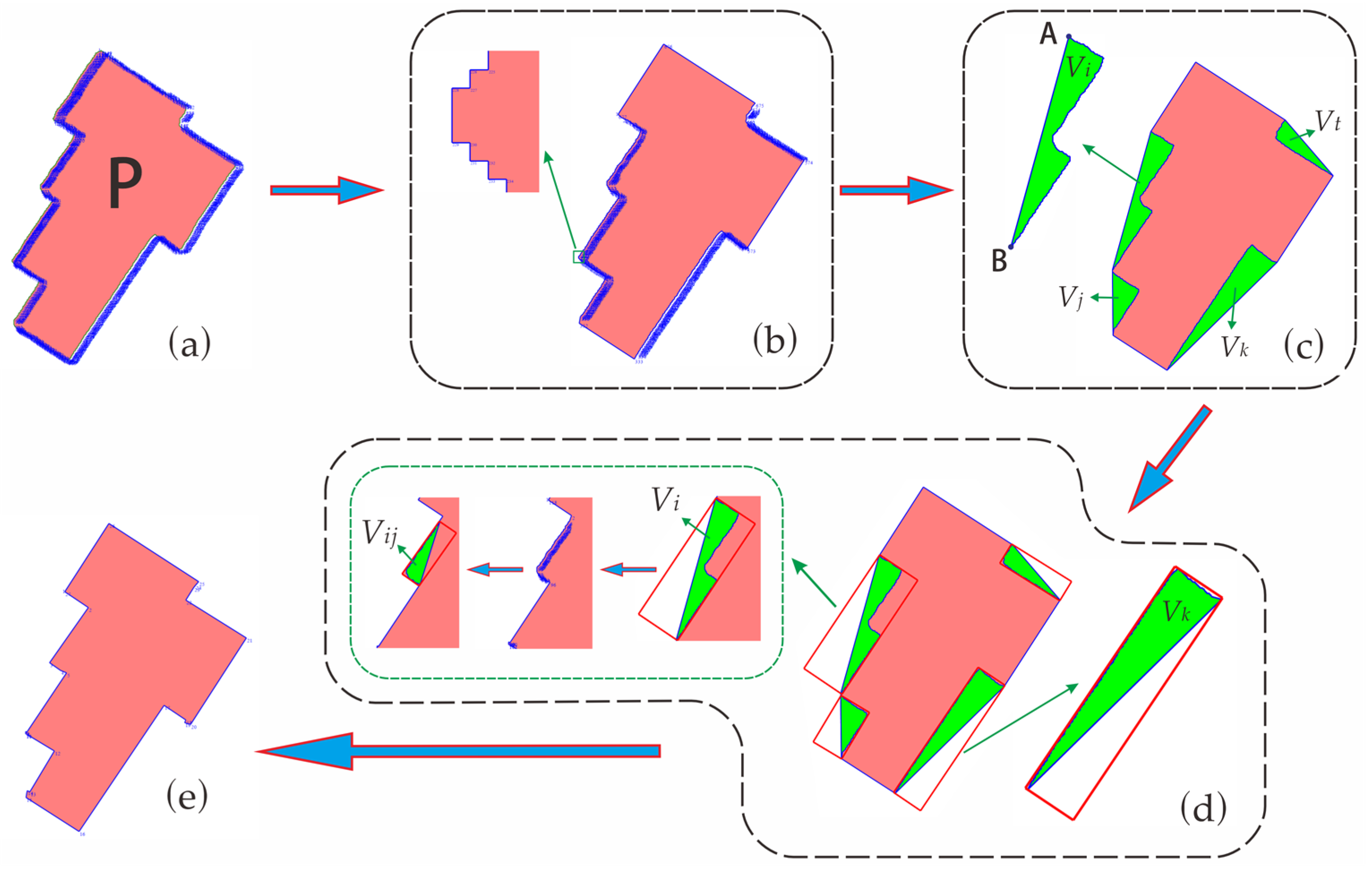
2.3. Local Regularization of Building Outline-Based Convex Hull Grouping
2.3.1. Grouping Unregularized Nodes Using the Convex Hull Method
2.3.2. Regularization of Point-like Node Set Using Centroid Coordinate Replacement
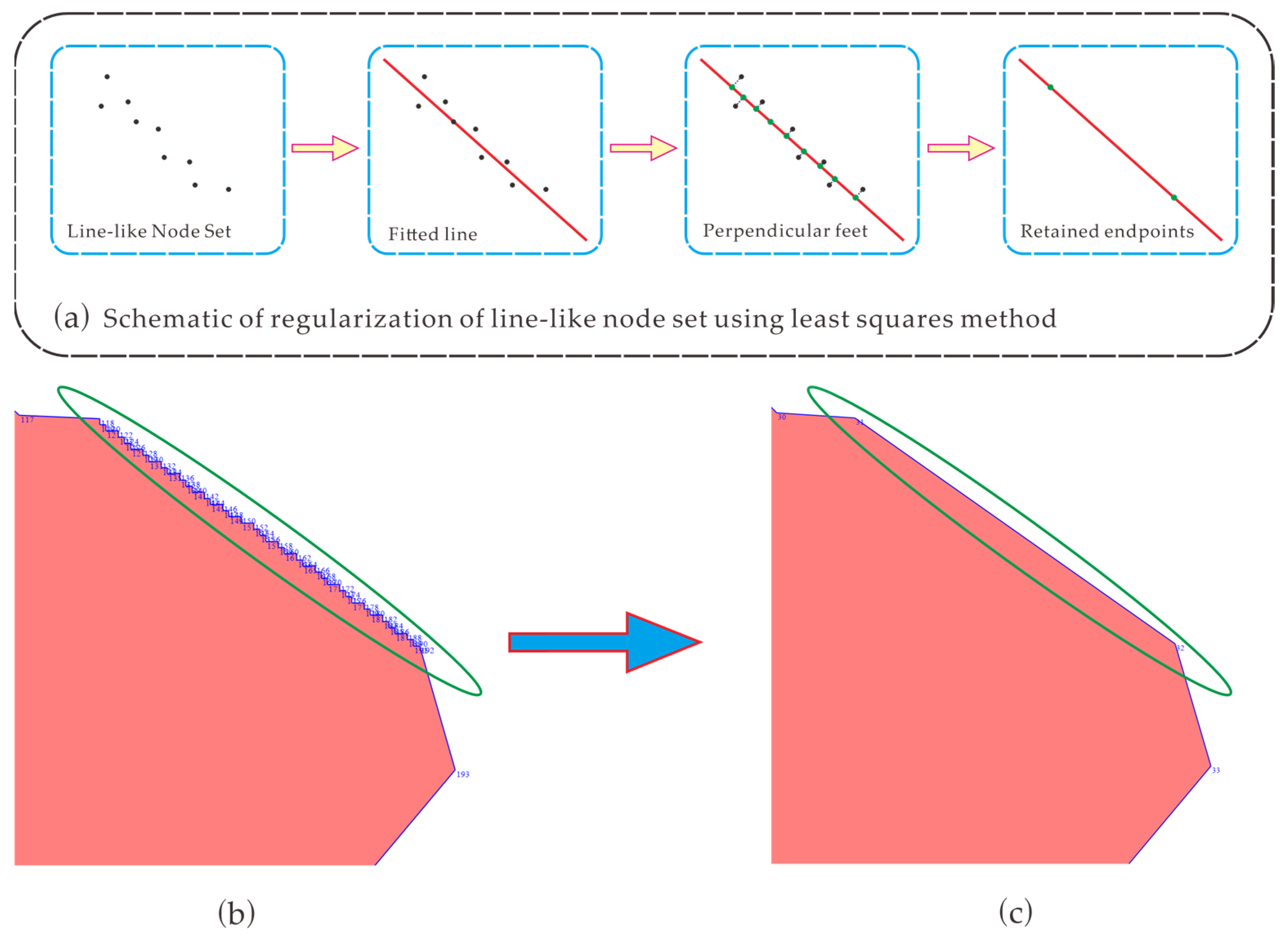
2.3.3. Regularization of Line-like Node Set Using Least Squares Method
2.3.4. Regularization of Area-like Set Using the Hausdorff Distance Method
- 1.
- Connect the starting and ending nodes of the area-like set to form a closed surface. Regularize it using the method described in Section 2.2. The difference here is that, when calculating the MBR and using the Hausdorff distance method for regularization, only the line segments composed of adjacent nodes that belong to the building outline are calculated and processed. Line segments that overlap with the convex hull outline and do not belong to the building outline are not considered. As shown in Figure 11c, during the regularization of Vi, segment AB is not part of the building outline. Thus, including it in calculations may affect the regularization results.
- 2.
- Continue to calculate the convex hull for area-like set V and construct unregularized point sets by category. Figure 11d shows the regularization of area-like sets Vi, Vj, Vk, and Vt, as well as the continued use of the convex hull method to split and classify the unregularized portions of Vi.
- 3.
- Iteratively execute the above steps. Once all nodes have been processed, local regularization results are obtained.
2.4. Detailed Regularization and Enhancement of Parallel and Perpendicular Relationships
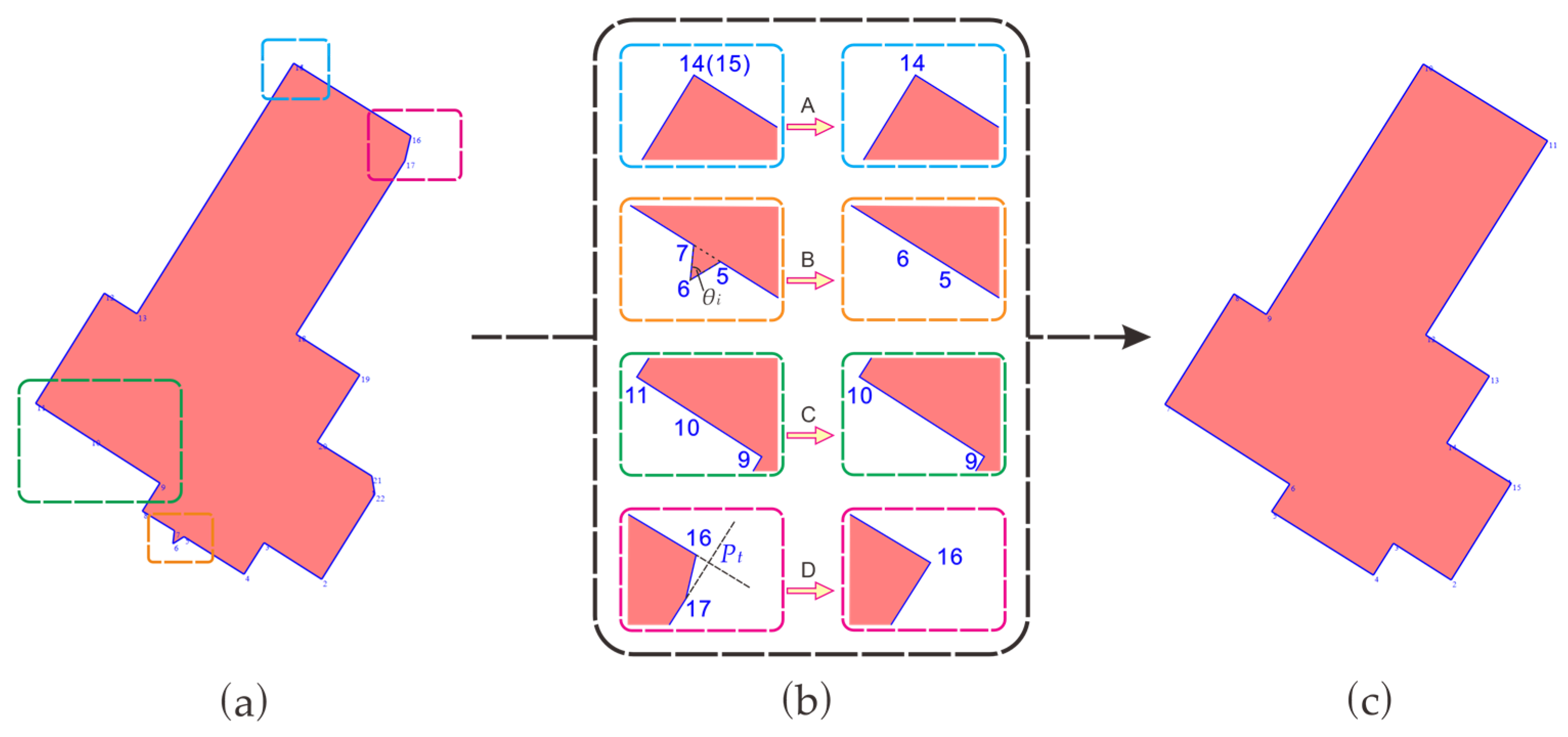
2.4.1. Detailed Regularization
2.4.2. Enhancement of Parallel and Perpendicular Relationships Based on the Main Direction of the Building Outline
- 1.
- Calculate the MBR of the building outline and take one of its long sides as vector a.
- 2.
- Calculate the angles θ between vectors b (consists of two neighboring nodes) and a in a counterclockwise direction, as described by Equation (9):
- 3.
- Set a threshold γ to 15°. If , then the line segment is approximately perpendicular to the main direction, and the method shown in Figure 13a is applied. A line is drawn through the midpoint Pm of line segment PiPi+1, perpendicular to the main direction. This line intersects the extensions of the two adjacent line segments at points Pi′ and Pi+1′. Replace Pi with Pi′ and Pi+1 with Pi+1′. If or , then the line segment is parallel to the main direction, and the method shown in Figure 13b is applied. After that, a line is drawn through the midpoint Pn of line segment PjPj+1, parallel to the main direction. This line intersects the extensions of the adjacent two line segments at points Pj′ and Pj+1′. Replace Pj with Pj′ and Pj+1 with Pj+1′. If the line segment is not parallel or perpendicular to the main direction, no further action is taken, as shown in Figure 13c.
3. Experimental Design
3.1. Descriptions of the Datasets
3.2. Experimental Settings
3.3. Evaluation Metrics
4. Results and Analysis
4.1. Experimental Analysis
4.1.1. Qualitative Evaluation
4.1.2. Quantitative Evaluation
4.2. Applicability of Analysis for Data of Different Resolutions
4.3. Analyzing Applicability to Complex Types of Building Outlines
4.4. Overall Discussion of the Algorithms and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kwak, E.; Habib, A. Automatic representation and reconstruction of DBM from LiDAR data using recursive minimum bounding rectangle. ISPRS J. Photogram. Remote Sens. 2013, 93, 171–191. [Google Scholar] [CrossRef]
- Yan, L.; Li, Y.; Xie, H. Urban building mesh polygonization based on 1-ring patch and topology optimization. Remote Sens. 2021, 13, 4777. [Google Scholar] [CrossRef]
- Hu, R.; Huang, X.; Huang, Y. An enhanced morphological building index for building extraction from high-resolution images. Acta Geod. Cartogr. Sin. 2014, 43, 514–520. [Google Scholar] [CrossRef]
- Gao, X.; Wang, M.; Yang, Y.; Li, G. Building extraction from RGB VHR images using shifted shadow algorithm. IEEE Access 2018, 6, 22034–22045. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, X.; Liao, X.; Zhuang, D. B-FGC-Net: A building extraction network from high resolution remote sensing imagery. Remote Sens. 2022, 14, 269. [Google Scholar] [CrossRef]
- Chang, J.; Gao, X.; Yang, Y.; Wang, N. Object-oriented building contour optimization methodology for image classification results via generalized gradient vector flow snake model. Remote Sens. 2021, 13, 2406. [Google Scholar] [CrossRef]
- Gao, X.; Zheng, X.; Shen, D.; Yang, Y.; Zhang, J. Automatic building extraction based on shadow analysis from high resolution images in suburb areas. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 1350–1357. [Google Scholar] [CrossRef]
- Wang, W.X.; Du, J.; Li, X.M.; Hu, H.; Xu, W.; Guo, H.; Ding, Y. A grid filling based rectangular building outlines regularization method. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 318–324. [Google Scholar] [CrossRef]
- Ding, Y.; Feng, F.; Li, J.; Hu, Y.; Cui, W. Right-angle buildings extraction from high-resolution aerial image based on multi-stars constraint segmentation and regularization. Acta Geod. Cartogr. Sin. 2018, 47, 1630–1639. [Google Scholar] [CrossRef]
- Zhou, S.; Sun, J.; Fan, L.; Xiang, J.; Chen, C. Extraction of building contour from high resolution images. Remote Sens. Land Resour. 2015, 27, 52–58. [Google Scholar] [CrossRef]
- Zhao, K.; Kang, J.; Jung, J.; Sohn, G. Building extraction from satellite images using Mask R-CNN with building boundary regularization. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 247–251. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Chang, J.X.; Gao, X.J.; Yang, Y.W.; Wang, S. Building contour optimization method integrating multitemporal and high-resolution images. Bull. Survey. Mapp. 2020, 7, 112–115. [Google Scholar] [CrossRef]
- Xiang, H.; Jianhua, W.; Ning, W.; Haowen, T. A building contour optimization method for multi-source data. Acta Opt. Sin. 2023, 12, 330–342. [Google Scholar]
- Wang, S.X.; Yang, Y.W.; Chang, J.X.; Gao, X.J. Optimization of building contours by classifying high-resolution images. Laser Optoelectron. Prog. 2020, 57, 329–338. [Google Scholar] [CrossRef]
- Shen, W.; Li, J.; Chen, Y.H.; Deng, L.; Peng, G.X. Algorithms study of buildings boundary extraction and normalization based on LIDAR data. J. Remote Sens. 2008, 5, 692–698. [Google Scholar]
- Mousa, Y.A.; Helmholz, P.; Belton, D.; Bulatov, D. Building detection and regularisation using DSM and imagery information. Photogramm. Rec. 2019, 34, 85–107. [Google Scholar] [CrossRef]
- Li, Y.F.; Gong, W.P.; Lin, Y.X.; Wang, B. The extraction of building boundaries based on LiDAR point cloud data and imageries. Remote Sens. Land Resour. 2014, 26, 54–59. [Google Scholar] [CrossRef]
- Wei, S.; Ji, S.; Lu, M. Toward automatic building footprint delineation from aerial images using CNN and regularization. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2178–2189. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Xu, J.W.; Liu, W.; Shan, H.Y.; Shi, J.; Li, E.; Zhang, L.; Li, X. High-resolution remote sensing image building extraction based on PRCUnet. J. Geo-Inf. Sci. 2021, 23, 1838–1849. [Google Scholar] [CrossRef]
- Chang, J.X.; Wang, S.X.; Yang, Y.W.; Gao, X. Hierarchical optimization method of building contour in high-resolution remote sensing images. Chin. J. Lasers 2020, 47, 1010002. [Google Scholar] [CrossRef]
- Cheng, P.; Yan, H.; Han, Z. An algorithm for computing the minimum area bounding rectangle of an arbitrary polygon. J. Eng. Graph. 2008, 29, 122–126. [Google Scholar]
- Zhongle, W.; Limin, L. Deformable simple polygon reconstruction algorithm. J. Southeast Univ. (Nat. Sci. Ed.) 2003, 33, 86–89. [Google Scholar]
- Ji, S.; Wei, S.; Lu, M. Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set. IEEE Trans. Geosci. Remote Sens. 2019, 57, 574–586. [Google Scholar] [CrossRef]
- Qiu, Y.; Wu, F.; Yin, J.; Liu, C.; Gong, X.; Wang, A. MSL-Net: An efficient network for building extraction from aerial imagery. Remote Sens. 2022, 14, 3914. [Google Scholar] [CrossRef]
- Bayer, T. Automated building simplification using a recursive approach. In Cartography in Central and Eastern Europe; Gartner, G., Ortag, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 121–146. [Google Scholar] [CrossRef]
- Feng, M.; Zhang, T.; Li, S.; Jin, G.; Xia, Y. An improved minimum bounding rectangle algorithm for regularized building boundary extraction from aerial LiDAR point clouds with partial occlusions. Int. J. Remote Sens. 2019, 41, 300–319. [Google Scholar] [CrossRef]
- He, S.; Jiang, W. Boundary-assisted learning for building extraction from optical remote sensing imagery. Remote Sens. 2021, 13, 760. [Google Scholar] [CrossRef]
- Cui, W.; Li, J.; Liu, Y. Semi-automatic extraction and regularization of buildings of different shapes from high-resolution remote sensing images. J. Appl. Sci. 2022, 40, 372–388. [Google Scholar] [CrossRef]













| Data Resolution | Pre-Improvement | Post-Improvement | Efficiency Improvement |
|---|---|---|---|
| 0.075 m | 1:38′56″ | 3′26″ | 96.53% |
| 0.5 m | 16′21″ | 1′05″ | 93.83% |
| Method | Total Number of Buildings | Number of Correctly Counted | Correct Ratio |
|---|---|---|---|
| MABR | 300 | 263 | 87.67% |
| Maximum number of co-linear nodes method | 300 | 286 | 95.33% |
| Proposed method | 300 | 300 | 100% |
| Method | P (%) | R (%) | IOU (%) | F1 (%) |
|---|---|---|---|---|
| A | 91.62 | 96.74 | 88.88 | 94.11 |
| B | 94.96 | 96.45 | 91.75 | 95.70 |
| C | 93.42 | 88.85 | 83.62 | 91.08 |
| Proposed method | 95.97 | 98.41 | 94.50 | 97.17 |
| Method | Time Complexity | |||
|---|---|---|---|---|
| First Step | Second Step | Third Step | Sum | |
| A | O(n2) | O(n2) | -- | O(n2) |
| B | O(n2) | O(n2) | O(n) | O(n2) |
| C | O(n2) | O(n2) | … | O(n2) |
| Proposed method | O(n2) | O(n2) | O(n) | O(n2) |
| Data Resolution | Method | P (%) | R(%) | IOU (%) | F1(%) |
|---|---|---|---|---|---|
| 0.075 m | A | 92.43 | 94.31 | 87.55 | 93.36 |
| B | 98.06 | 97.61 | 95.76 | 97.83 | |
| C | 96.71 | 90.16 | 87.47 | 93.32 | |
| Proposed method | 98.27 | 98.43 | 96.75 | 98.35 | |
| 0.5 m | A | 88.07 | 94.62 | 83.87 | 91.23 |
| B | 94.41 | 91.58 | 86.87 | 92.97 | |
| C | 91.28 | 94.28 | 86.49 | 92.76 | |
| Proposed method | 92.57 | 94.82 | 88.11 | 93.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Qian, H.; Xie, L.; Huang, Z.; Qiu, Y.; Bian, C. Multilevel Regularization Method for Building Outlines Extracted from High-Resolution Remote Sensing Images. Appl. Sci. 2023, 13, 12599. https://doi.org/10.3390/app132312599
Kong L, Qian H, Xie L, Huang Z, Qiu Y, Bian C. Multilevel Regularization Method for Building Outlines Extracted from High-Resolution Remote Sensing Images. Applied Sciences. 2023; 13(23):12599. https://doi.org/10.3390/app132312599
Chicago/Turabian StyleKong, Linghui, Haizhong Qian, Limin Xie, Zhekun Huang, Yue Qiu, and Chenglin Bian. 2023. "Multilevel Regularization Method for Building Outlines Extracted from High-Resolution Remote Sensing Images" Applied Sciences 13, no. 23: 12599. https://doi.org/10.3390/app132312599
APA StyleKong, L., Qian, H., Xie, L., Huang, Z., Qiu, Y., & Bian, C. (2023). Multilevel Regularization Method for Building Outlines Extracted from High-Resolution Remote Sensing Images. Applied Sciences, 13(23), 12599. https://doi.org/10.3390/app132312599








