New Interval Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithms under Different Distance Measures for Symbolic Interval Data Analysis
Abstract
:1. Introduction
2. Definition and Distance Measures for Symbolic Interval Data
3. Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithm
4. Interval Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithm
4.1. Interval Improved Fuzzy Partitions Fuzzy C-Means under Euclidean Distance
4.2. Interval Improved Fuzzy Partitions Fuzzy C-Means under City Block Distance
| Algorithm 1: Procedures of the proposed IIFPFCME clustering algorithm in the following steps |
| Step 1: Initialization fix ; fix ; fix ; Set iteration counter and iteration limit ; Initialization . |
| Step 2: Update the and . |
| Step 3: Update the . |
| Step 4: Update the . |
| Step 5: if ( or ) Stop. Else and go to Step 2. |
| Algorithm 2: Procedures of the proposed IIFPFCMC clustering algorithm in the following steps |
| Step 1: Initialization fix ; fix ; fix ; Set iteration counter and iteration limit ; Initialization . |
| Step 2: Update the and . |
| Step 3: Update the . |
| Step 4: Update the . |
| Step 5: If ( or ) Stop. Else and go to Step 2. |
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DS | Datasets |
| FCM | Fuzzy C-means |
| FMD | Fuzzy membership degree |
| IDS | Interval datasets |
| IFCMC | Interval fuzzy C-means with city block distance |
| IFCME | Interval fuzzy C-means with Euclidean distance |
| IFPFCM | Improved fuzzy partitions for fuzzy regression models |
| IIFPFCM | Interval improved fuzzy partitions fuzzy C-means |
| IIFPFCMC | IIFPFCM with city block distance |
| IIFPFCME | IIFPFCM with Euclidean distance |
| IPFCM | Interval possibilistic FCM |
| PMD | Possibilistic membership degree |
| RMSE | Root-mean-square error |
| SID | Symbolic interval data |
| SIDA | Symbolic interval data analysis |
References
- Billard, L.; Diday, E. Symbolic Data Analysis: Conceptual Statistics and Data Mining; John Wiley & Sons: London, UK, 2006. [Google Scholar]
- Chuang, C.-C.; Jeng, J.-T.; Chang, S.-C. Hausdorff distance measure based interval fuzzy possibilistic c-means clustering algorithm. Int. J. Fuzzy Syst. 2013, 15, 471–479. [Google Scholar]
- He, Q.; He, Z.; Duan, S.; Zhong, Y. Multi-objective interval portfolio optimization modeling and solving for margin trading. Swarm Evol. Comput. 2022, 75, 101141. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Zhou, J.; Jing, C. Trajectory recovery based on interval forward–backward propagation algorithm fusing multi-source information. Electronics 2022, 11, 3634. [Google Scholar] [CrossRef]
- Yamaka, W.; Phadkantha, R.; Maneejuk, P. A convex combination approach for artificial neural network of interval data. Appl. Sci. 2021, 11, 3997. [Google Scholar] [CrossRef]
- Fordellone, M.; De Benedictis, I.; Bruzzese, D.; Chiodini, P. A maximum-entropy fuzzy clustering approach for cancer detection when data are uncertain. Appl. Sci. 2023, 13, 2191. [Google Scholar] [CrossRef]
- Freitas, W.W.F.; Souza, R.M.C.R.; Getúlio, J.A.; Bastian, F. Exploratory spatial analysis for interval data: A new autocorrelation index with COVID-19 and rent price applications. Expert Syst. Appl. 2022, 195, 116561. [Google Scholar] [CrossRef]
- Chang, W.; Ji, X.; Liu, Y.; Xiao, Y.; Chen, B.; Liu, H.; Zhou, S. Analysis of university students’ behavior based on a fusion k-means clustering algorithm. Appl. Sci. 2020, 10, 6566. [Google Scholar] [CrossRef]
- Zhang, R.-L.; Liu, X.-H. A novel hybrid high-dimensional pso clustering algorithm based on the cloud model and entropy. Appl. Sci. 2023, 13, 1246. [Google Scholar] [CrossRef]
- Dougherty, E.R.; Brun, M. A probabilistic theory of clustering. Pattern Recognit. Soc. 2004, 37, 917–925. [Google Scholar] [CrossRef]
- Volkovich, Z.; Avros, R.; Golani, M. On initialization of the expectation maximization clustering algorithm. Glob. J. Technol. Optim. 2011, 2, 1–4. [Google Scholar]
- Sun, T.; Shu, C.; Li, F.; Yu, H.; Ma, L.; Fang, Y. An efficient hierarchical clustering method for large datasets with map-reduce. In Proceedings of the 2009 International Conference on Parallel and Distributed Computing, Applications and Technologies, Boston, MA, USA, 24–26 September 2009; pp. 494–499. [Google Scholar]
- Li, M.; Deng, S.; Wang, L.; Feng, S.; Fan, J. Hierarchical clustering algorithm for categorical data using a probabilistic rough set model. Knowl. Based Syst. 2014, 65, 60–71. [Google Scholar] [CrossRef]
- Patel, S.; Sihmar, S.; Jatain, A. A study of hierarchical clustering algorithms. In Proceedings of the 2015 2nd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 11–13 March 2015; pp. 537–541. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Park, H.S.; Jun, C.H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A. A survey of clustering algorithms for big data: Taxonomy and empirical analysis. IEEE Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Mújica-Vargas, D.; Kinani, J.M.V.; Rubio, J.D. Color-based image segmentation by means of a robust intuitionistic fuzzy c-means algorithm. Int. J. Fuzzy Syst. 2020, 22, 901–916. [Google Scholar] [CrossRef]
- Gao, Y.; Li, H.; Li, J.; Cao, C.; Pan, J. Patch-based fuzzy local weighted c-means clustering algorithm with correntropy induced metric for noise image segmentation. Int. J. Fuzzy Syst. 2023, 25, 1991–2006. [Google Scholar] [CrossRef]
- Hussain, I.; Sinaga, K.P.; Yang, M.-S. Unsupervised multiview fuzzy c-means clustering algorithm. Electronics 2023, 12, 4467. [Google Scholar] [CrossRef]
- Shi, Y. Application of FCM clustering algorithm in digital library management system. Electronics 2022, 11, 3916. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, R.; Xia, B. VSFCM: A novel viewpoint-driven subspace fuzzy c-means algorithm. Appl. Sci. 2023, 13, 6342. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Q.; Zhou, J.; Chen, Y.; Han, S.; Wang, L.; Du, T.; Ji, K.; Zhao, Y.O.; Zhang, K. Guided filter-based fuzzy clustering for general data analysis. Int. J. Fuzzy Syst. 2023, 25, 2036–2051. [Google Scholar] [CrossRef]
- Sousa, Á.; Silva, O.; Bacelar-Nicolau, L.; Cabral, J.; Bacelar-Nicolau, H. Comparison between two algorithms for computing the weighted generalized affinity coefficient in the case of interval data. Stats 2023, 6, 1082–1094. [Google Scholar] [CrossRef]
- Roh, S.B.; Oh, S.K.; Pedrycz, W.; Wang, Z.; Fu, Z.; Seo, K. Design of iterative fuzzy radial basis function neural networks based on iterative weighted fuzzy c-means clustering and weighted LSE estimation. IEEE Trans. Fuzzy Syst. 2022, 30, 4273–4285. [Google Scholar] [CrossRef]
- Huang, Y.P.; Bhalla, K.; Chu, H.C.; Lin, Y.C.; Kuo, H.C.; Chu, W.J.; Lee, J.H. Wavelet k-means clustering and fuzzy-based method for segmenting MRI images depicting Parkinson’s disease. Int. J. Fuzzy Syst. 2021, 23, 1600–1612. [Google Scholar] [CrossRef]
- Elsheikh, S.; Fish, A.; Zhou, D. Exploiting spatial information to enhance DTI segmentations via spatial fuzzy c-means with covariance matrix data and non-euclidean metrics. Appl. Sci. 2021, 11, 7003. [Google Scholar] [CrossRef]
- Höppner, F.; Klawonn, F. Improved fuzzy partitions for fuzzy regression models. Int. J. Approx. Reason 2003, 32, 85–102. [Google Scholar] [CrossRef]
- Hazarika, I.; Mahanta, A.K. A New Semimetric for Interval Data. Int. J. Recent Technol. Eng. 2019, 8, 3278–3285. [Google Scholar] [CrossRef]
- De Souza, R.M.C.R.; De Carvalho, F.A.T. Clustering of interval data based on city–block distances. Pattern Recognit. Lett. 2004, 25, 353–365. [Google Scholar] [CrossRef]
- De Carvalho, F.D.A.T.; Brito, P.; Bock, H.-H. Dynamic clustering for interval data based on L₂ distance. Comput. Statist. 2006, 21, 231–250. [Google Scholar] [CrossRef]
- Peng, W.; Li, T. Interval Data Clustering with Applications. In Proceedings of the 18th IEEE International Conference on Tools with Artificial Intelligence, Arlington, VA, USA, 13–15 November 2006; pp. 355–362. [Google Scholar]
- De Carvalho, F.D.A.T. Fuzzy c-means clustering methods for symbolic interval data. Pattern Recognit. Lett. 2007, 28, 423–437. [Google Scholar] [CrossRef]
- Jeng, J.-T.; Chen, C.-M.; Chang, S.-C.; Chuang, C.-C. IPFCM clustering algorithm under Euclidean and Hausdorff distance measure for symbolic interval data. Int. J. Fuzzy Syst. 2019, 21, 2102–2119. [Google Scholar] [CrossRef]
- Chen, C.-M.; Chang, S.-C.; Chuang, C.-C.; Jeng, J.-T. Rough IPFCM clustering algorithm and its application on smart phones with Euclidean distance. Appl. Sci. 2022, 12, 5195. [Google Scholar] [CrossRef]
- Kato, J.; Okada, K. Simplification and shift in cognition of political difference: Applying the geometric modeling to the analysis of semantic similarity judgment. PLoS ONE 2011, 6, e20693. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Shahapure, K.R.; Nicholas, C. Cluster Quality Analysis Using Silhouette Score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, NSW, Australia, 6–9 October 2020; pp. 747–748. [Google Scholar]
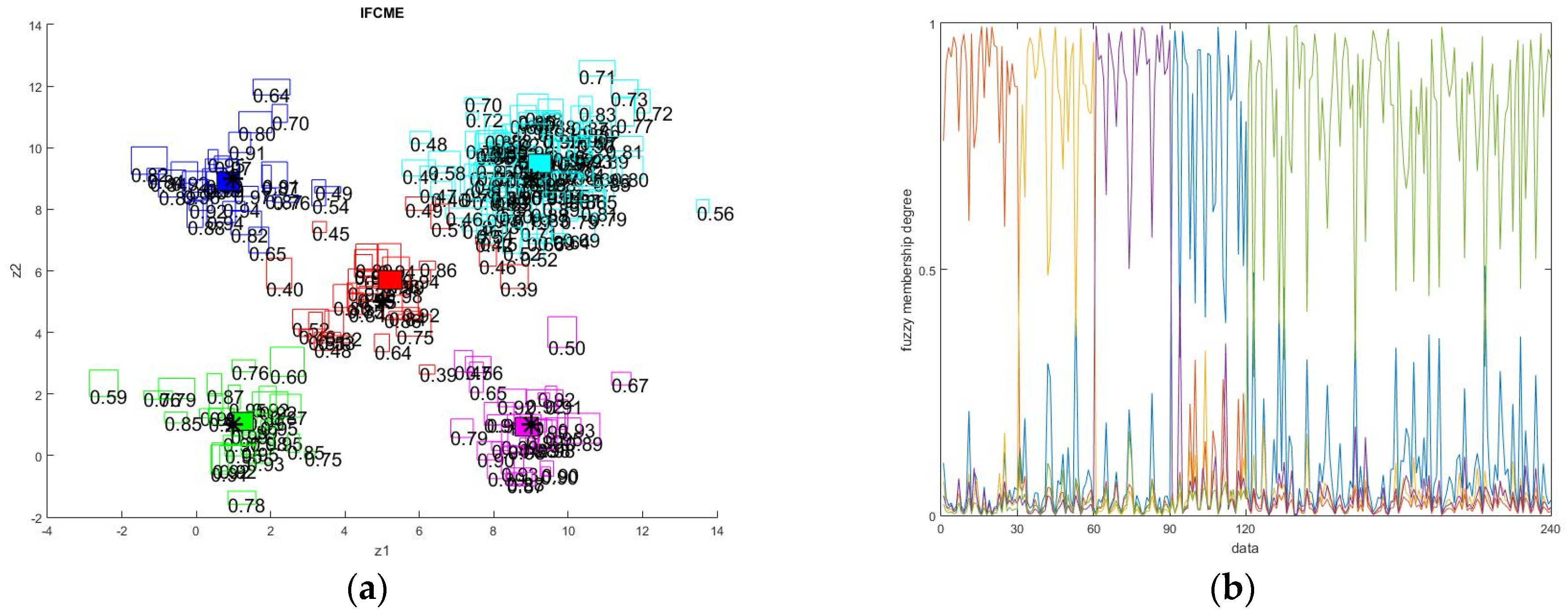
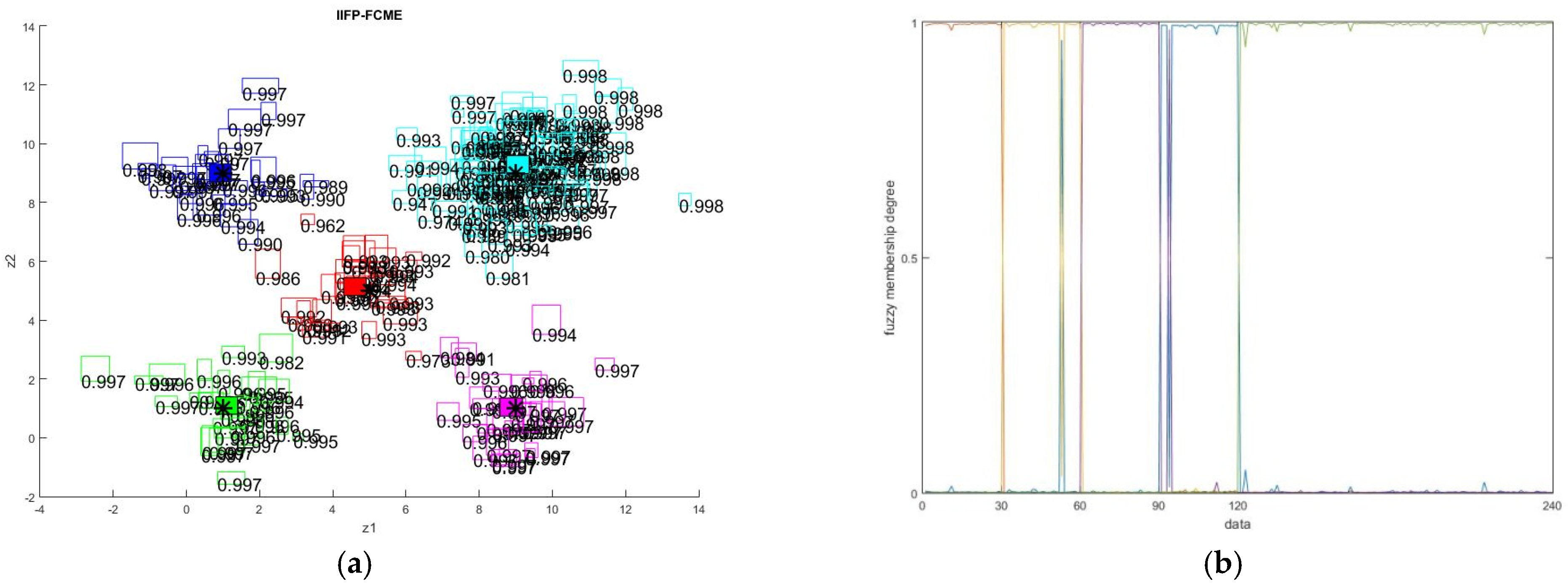

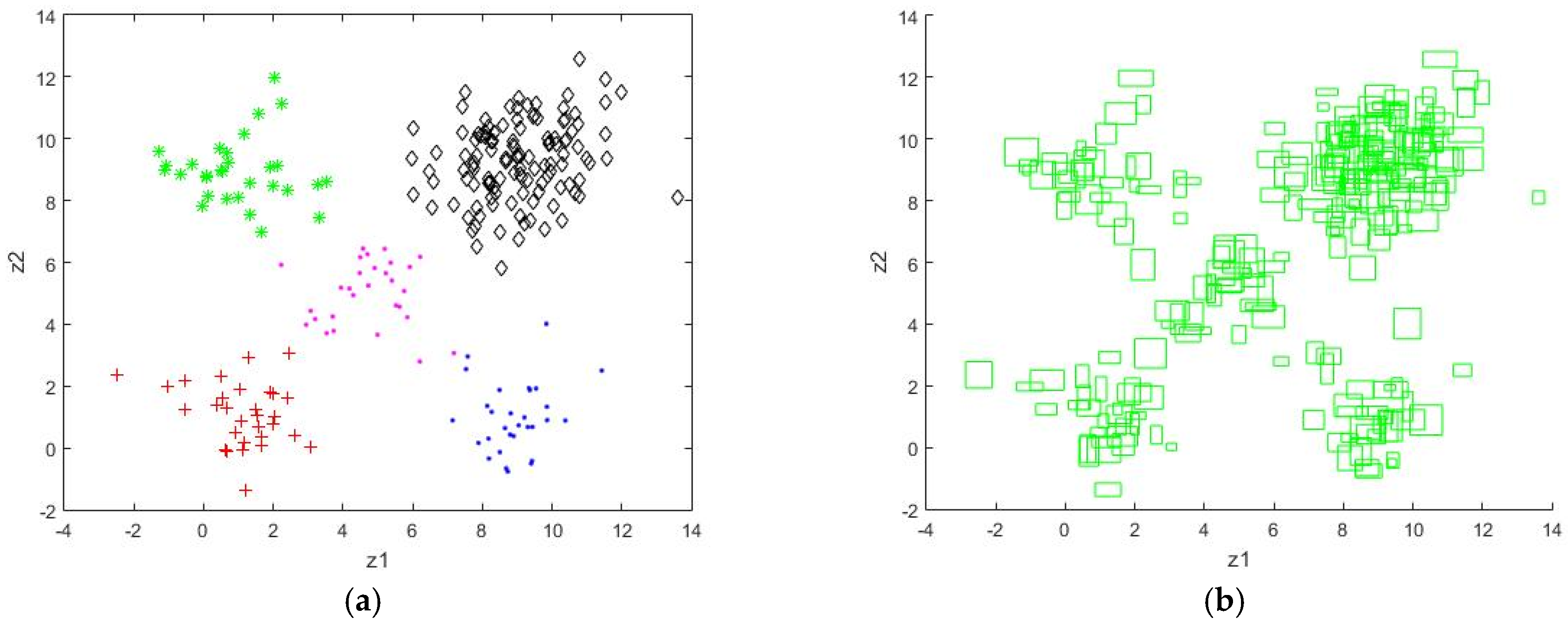
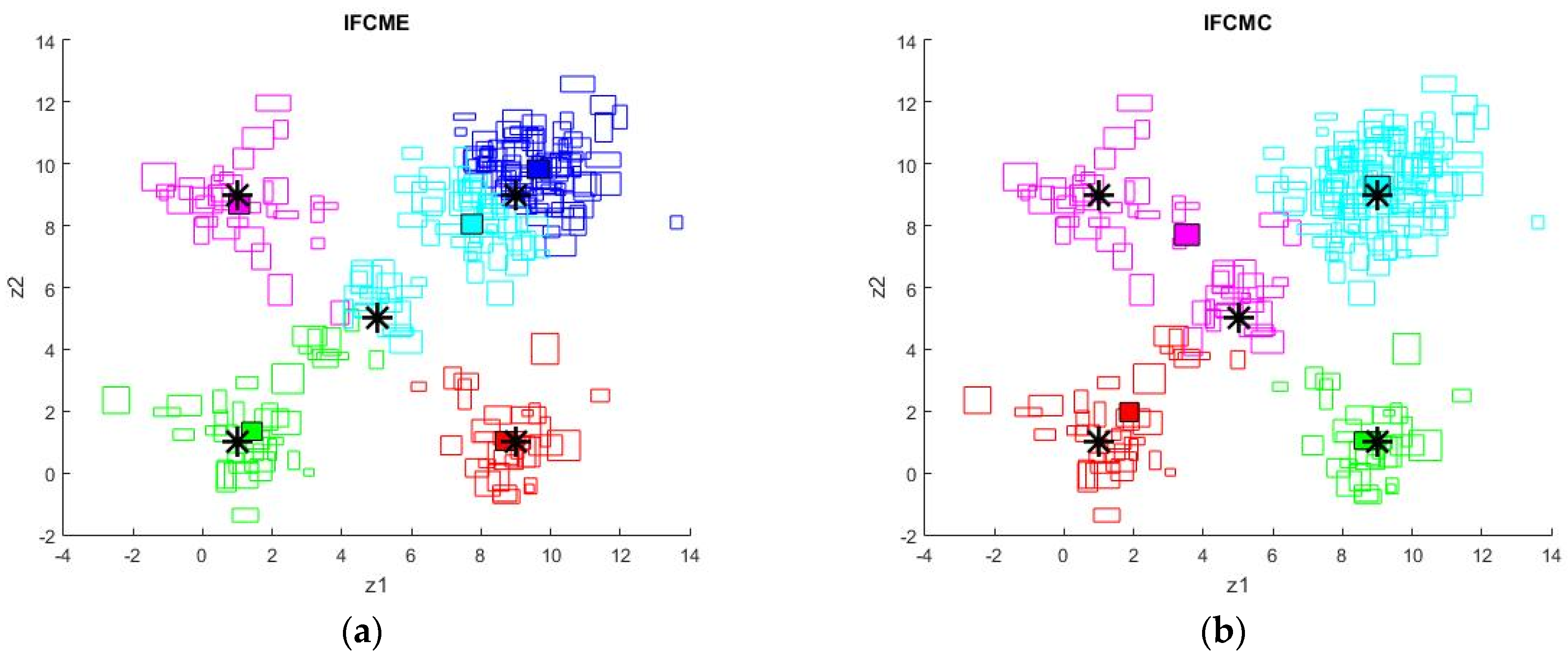




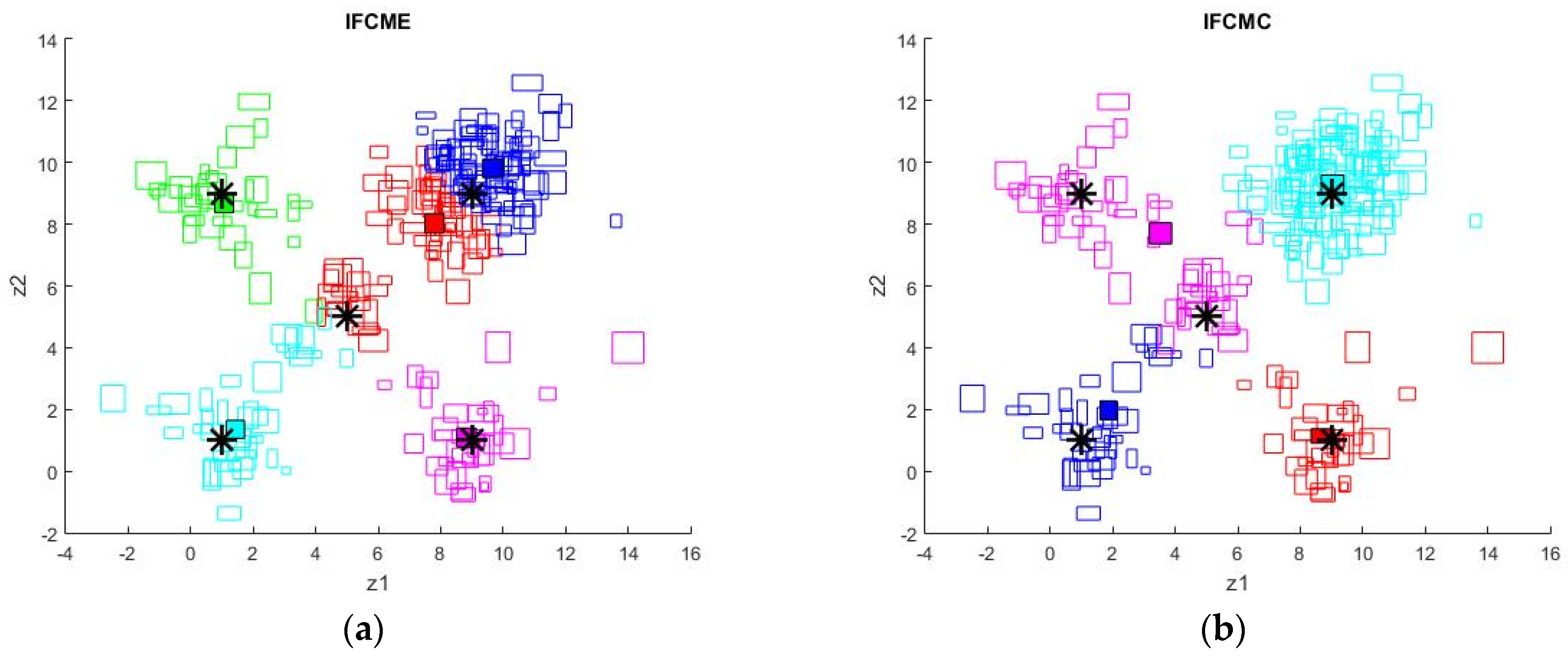

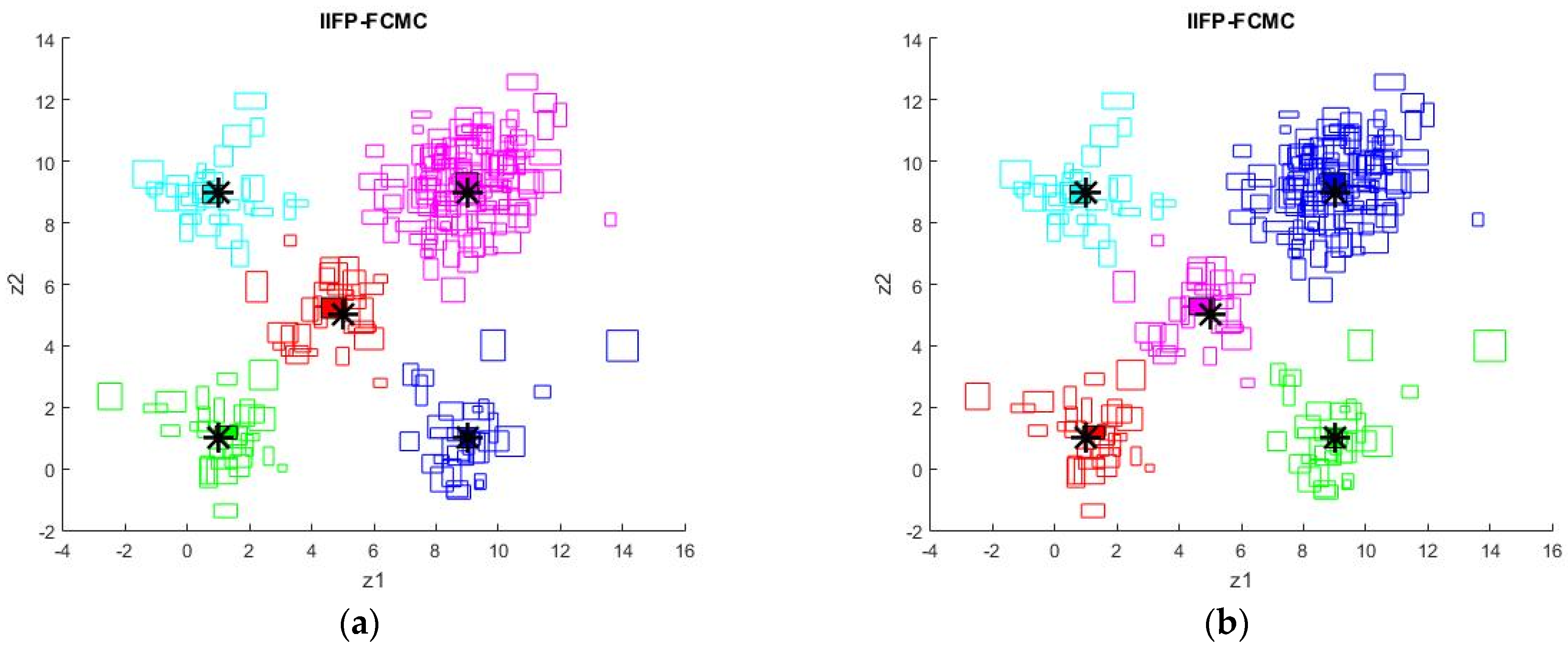
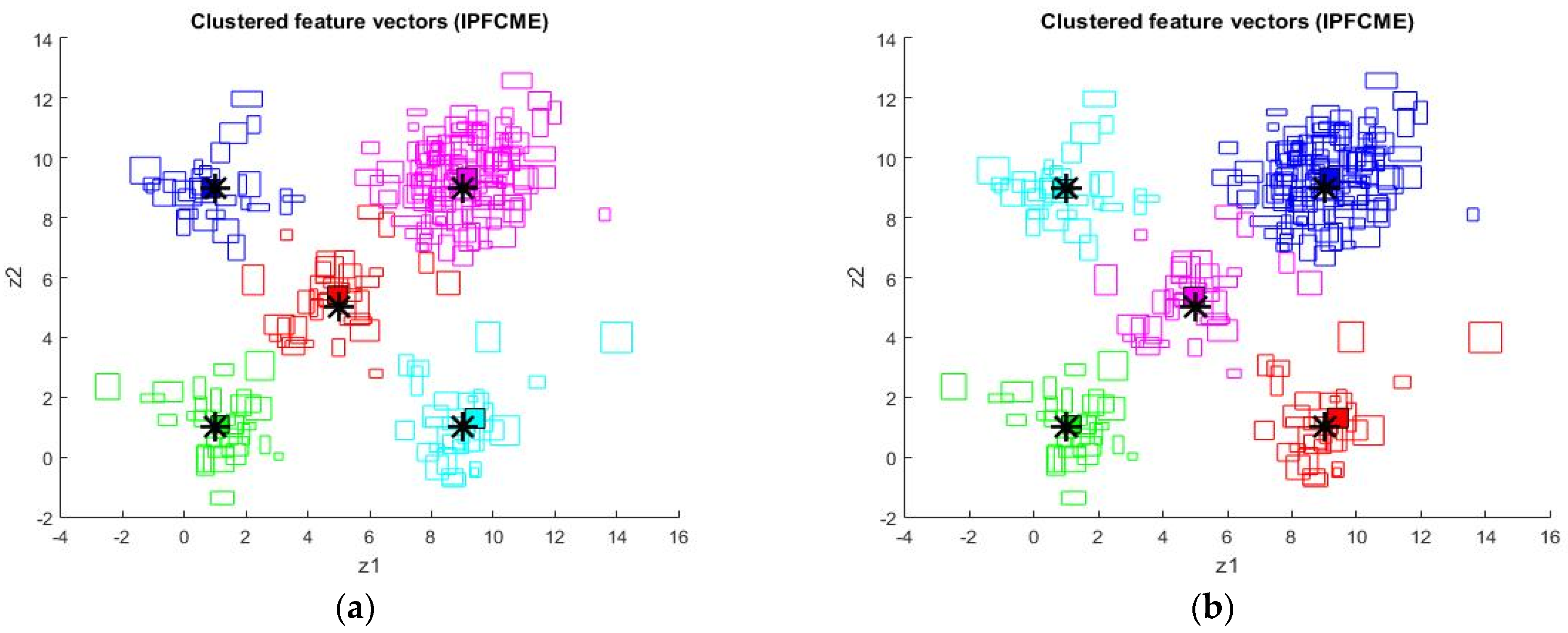
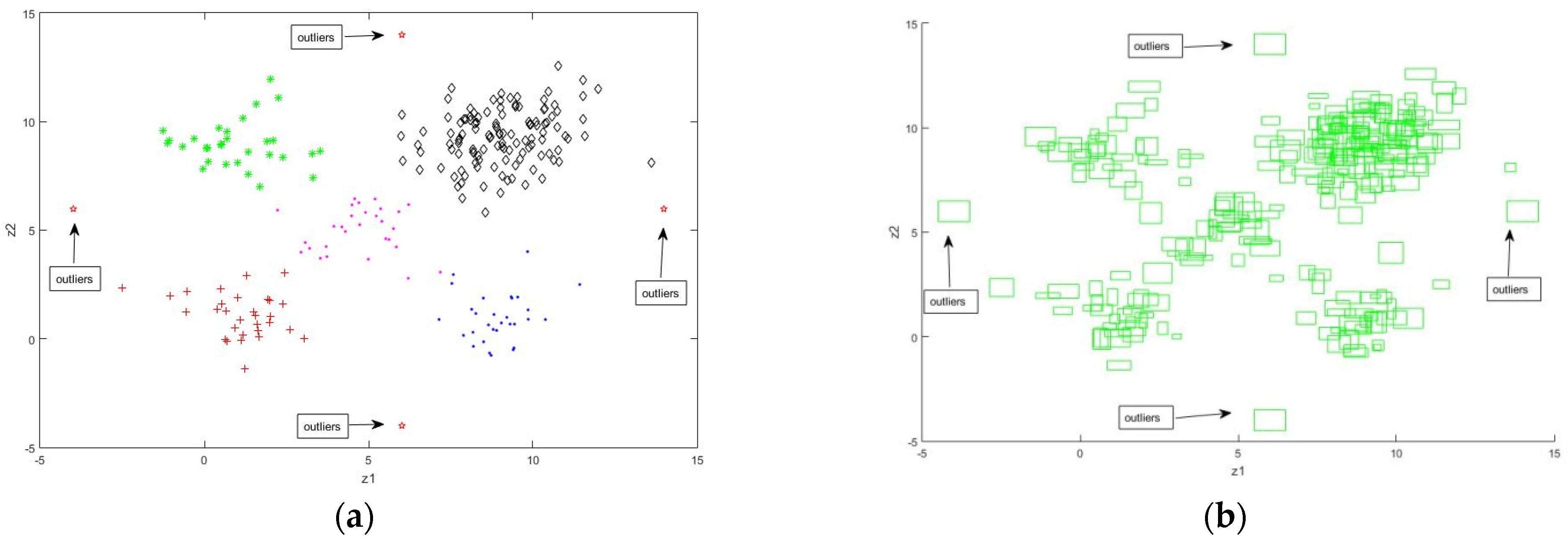

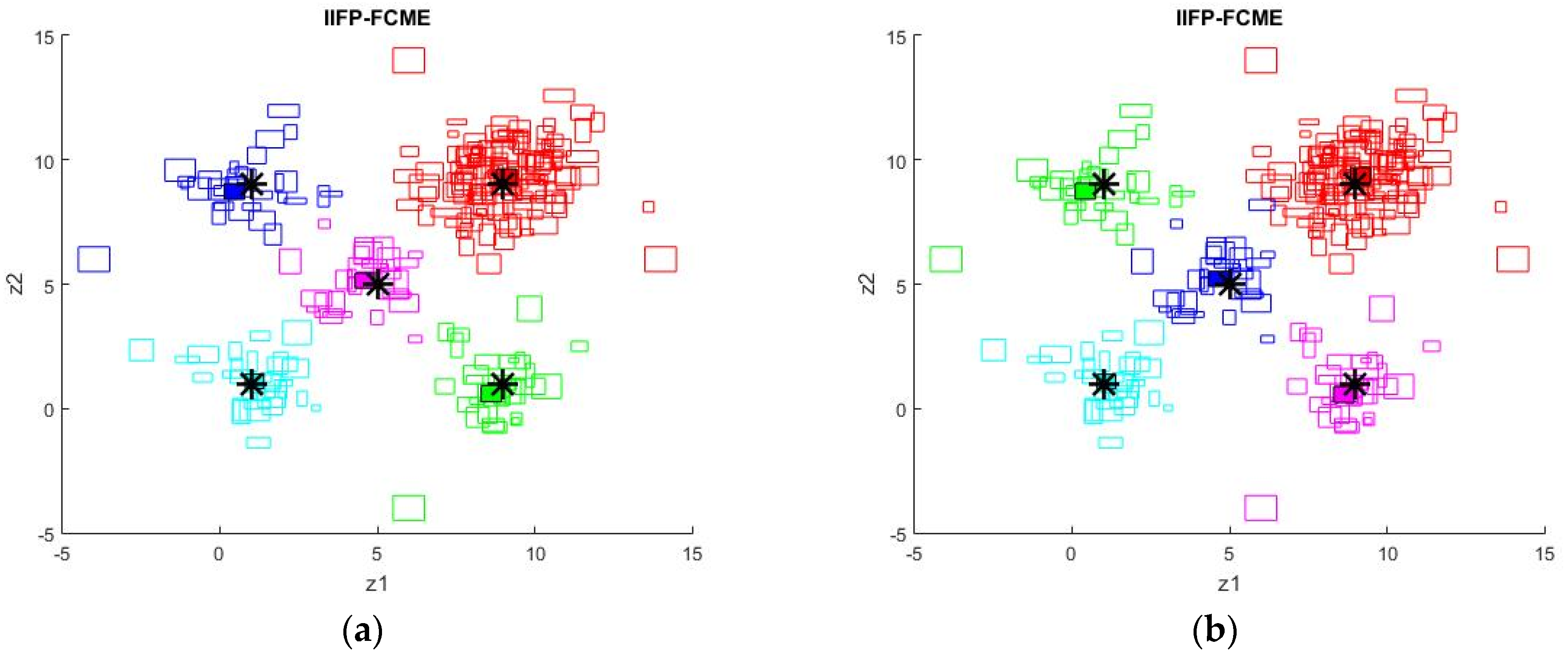
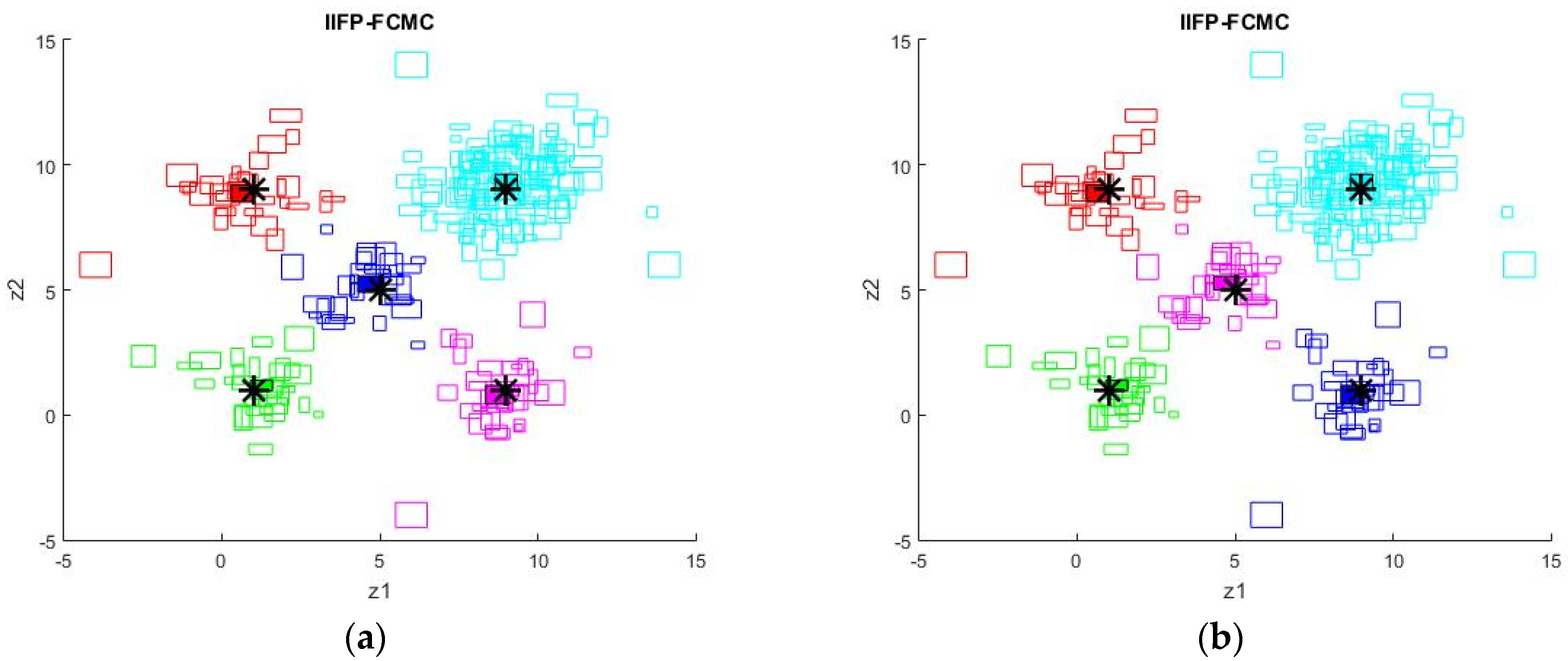




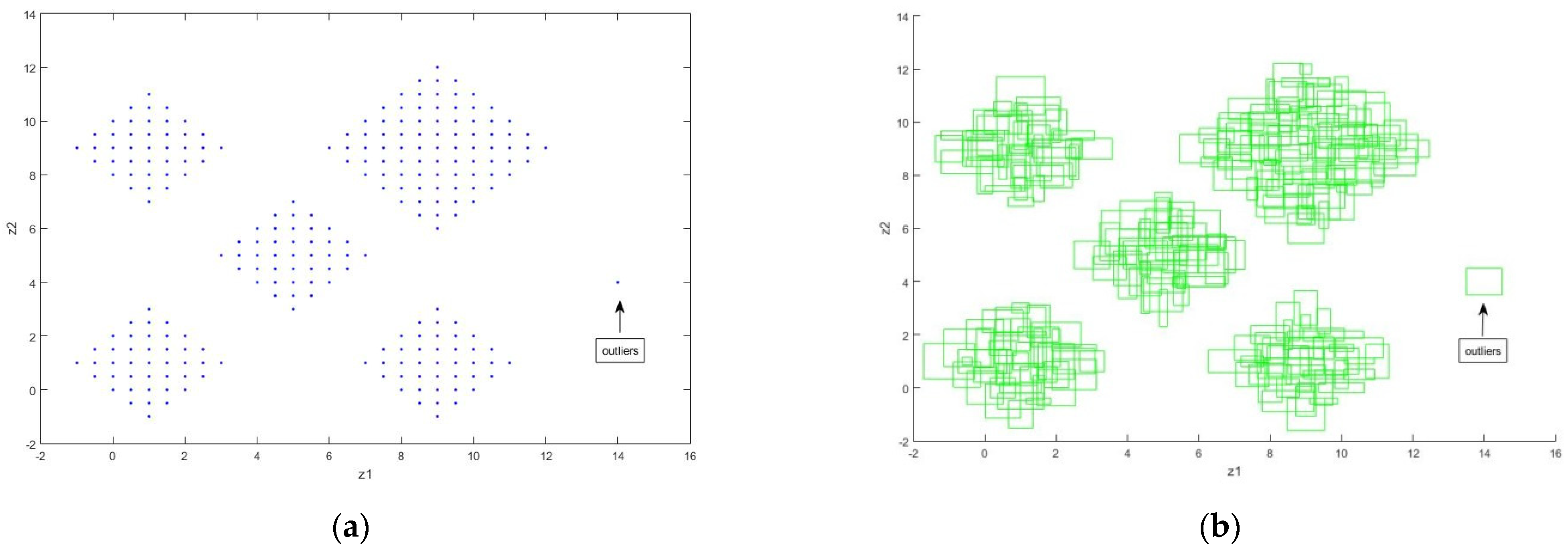






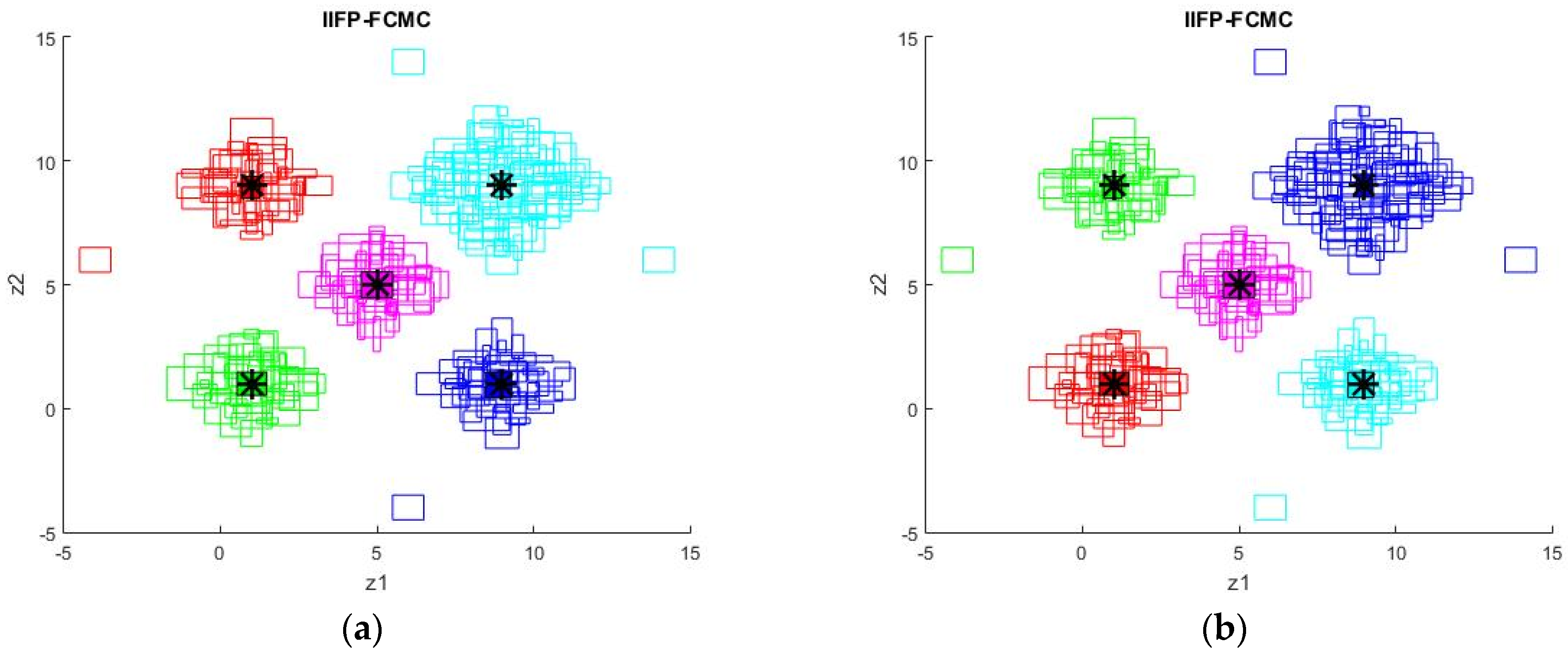




| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| RMSE | --- | 0.2470 | 0.2470 | 0.2513 |
| Average times on ten (sec.) | 0.007468 | 0.004497 | 0.003814 | 0.00735 |
| Average of ten iterations () | 42.8 | 23.2 | 19.4 | 39.2 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| RMSE | --- | 0.2924 | 0.2964 | 0.2955 |
| Average times on ten (sec.) | 0.011596 | 0.005645 | 0.006696 | 0.006356 |
| Average number of ten iterations () | 18.5 | 11 | 12 | 11.7 |
| (c) | ||||
| Compared Index/Method | IPFCME ( ) | IPFCME ( ) | ||
| RMSE | 0.2885 | 0.2733 | ||
| Average times on ten (sec.) | 0.01856 | 0.019446 | ||
| Average number of ten iterations () | 35.6 | 37.5 | ||
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| RMSE | --- | 0.3124 | 0.3124 | 0.3159 |
| Average times on ten (sec.) | 0.007727 | 0.004025 | 0.005414 | 0.006802 |
| Average number of ten iterations () | 42.5 | 20.1 | 27.8 | 34.6 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| RMSE. | --- | 0.273 | 0.2773 | 0.2736 |
| Average times on ten (sec.) | 0.010524 | 0.008881 | 0.007854 | 0.006761 |
| Average number of ten iterations () | 16.8 | 12.8 | 11.6 | 11.3 |
| (c) | ||||
| Compared Index/Method | IPFCME ( ) | IPFCME ( ) | ||
| RMSE | 0.3545 | 0.3505 | ||
| Average times on ten (sec.) | 0.023422 | 0.020567 | ||
| Average number of ten iterations () | 44.1 | 38.4 | ||
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| RMSE | --- | 0.4437 | 0.4428 | 0.4616 |
| Average times on ten (sec.) | 0.007077 | 0.003865 | 0.006962 | 0.00694 |
| Average number of ten iterations () | 39.6 | 18.9 | 35.2 | 34.7 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| RMSE | --- | 0.3449 | 0.3484 | 0.3356 |
| Average times on ten (sec.) | 0.009187 | 0.007241 | 0.00958 | 0.005183 |
| Average number of ten iterations () | 15.1 | 10.5 | 14.3 | 8.9 |
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| RMSE | 0.1668 | 2.7094 × 10−4 | 0.0027 | 0.0233 |
| Average times on ten (sec.) | 0.005133 | 0.00203 | 0.001978 | 0.002283 |
| Average number of ten iterations () | 28.7 | 8.9 | 9.1 | 10.9 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| RMSE | 0.6604 | 0 | 0 | 0 |
| Average times on ten (sec.) | 0.008365 | 0.006414 | 0.007366 | 0.006735 |
| Average number of ten iterations () | 13.3 | 8.5 | 10 | 9.2 |
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| RMSE | 0.1871 | 0.1778 | 0.1780 | 0.1810 |
| Average times on ten (sec.) | 0.004011 | 0.001845 | 0.002007 | 0.002452 |
| Average number of ten iterations () | 22.1 | 8.4 | 9.3 | 11.7 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| RMSE | 0.6437 | 0.0522 | 0.0522 | 0.0522 |
| Average times on ten (sec.) | 0.008791 | 0.006091 | 0.005886 | 0.006728 |
| Average number of ten iterations () | 12.6 | 8.1 | 7.8 | 9 |
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| RMSE | 0.1801 | 0.2549 | 0.2555 | 0.2604 |
| Average times on ten (sec.) | 0.008623 | 0.003292 | 0.00311 | 0.004102 |
| Average number of ten iterations () | 26.7 | 10.3 | 10.8 | 16.5 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| RMSE | 0.6522 | 0.0626 | 0.0626 | 0.0626 |
| Average times on ten (sec.) | 0.007367 | 0.006087 | 0.007714 | 0.006814 |
| Average number of ten iterations () | 10 | 7.6 | 9.8 | 8.6 |
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| Average times on ten (sec.) | 0.011177 | 0.004754 | 0.005224 | 0.005234 |
| Average number of ten iterations () | 39.6 | 13 | 16.4 | 16.5 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| Average times on ten (sec.) | 0.008484 | 0.008062 | 0.009802 | 0.009563 |
| Average number of ten iterations () | 13.9 | 10.3 | 11.4 | 10.4 |
| (a) | ||||
| Compared Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
| Average times on ten (sec.) | 0.007042 | 0.003014 | 0.003111 | 0.003673 |
| Average number of ten iterations () | 23.2 | 8.2 | 8.1 | 9.7 |
| (b) | ||||
| Compared Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
| Average times on ten (sec.) | 0.007925 | 0.007317 | 0.006542 | 0.007304 |
| Average number of ten iterations () | 13.5 | 8.8 | 7.8 | 8 |
| Silhouette Index/Method | IFCME () | IIFPFCME () | IIFPFCME () | IIFPFCME () |
|---|---|---|---|---|
| SI of IDS7 | 0.613169 | 0.670552 | 0.669509 | 0.669509 |
| SI of IDS8 | 0.678284 | 0.764616 | 0.764616 | 0.764616 |
| Silhouette Index/Method | IFCMC () | IIFPFCMC () | IIFPFCMC () | IIFPFCMC () |
|---|---|---|---|---|
| SI of IDS7 | 0.612450 | 0.655276 | 0.655276 | 0.655276 |
| SI of IDS8 | 0.733026 | 0.760424 | 0.760424 | 0.760424 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, S.-C.; Chuang, W.-C.; Jeng, J.-T. New Interval Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithms under Different Distance Measures for Symbolic Interval Data Analysis. Appl. Sci. 2023, 13, 12531. https://doi.org/10.3390/app132212531
Chang S-C, Chuang W-C, Jeng J-T. New Interval Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithms under Different Distance Measures for Symbolic Interval Data Analysis. Applied Sciences. 2023; 13(22):12531. https://doi.org/10.3390/app132212531
Chicago/Turabian StyleChang, Sheng-Chieh, Wei-Ching Chuang, and Jin-Tsong Jeng. 2023. "New Interval Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithms under Different Distance Measures for Symbolic Interval Data Analysis" Applied Sciences 13, no. 22: 12531. https://doi.org/10.3390/app132212531
APA StyleChang, S.-C., Chuang, W.-C., & Jeng, J.-T. (2023). New Interval Improved Fuzzy Partitions Fuzzy C-Means Clustering Algorithms under Different Distance Measures for Symbolic Interval Data Analysis. Applied Sciences, 13(22), 12531. https://doi.org/10.3390/app132212531





