Abstract
Temporal knowledge graph completion (TKGC) refers to the prediction and filling in of missing facts on time series, which is essential for many downstream applications. However, many existing TKGC methods suffer from two limitations: (1) they only consider direct relations between entities and fail to express high-order structural dependencies between entities; and (2) they only leverage relation quadruples of temporal knowledge graphs, ignoring attribute information that contains rich semantic information. This makes them vulnerable to sparsity and incompleteness problems. In response, we propose HCAE, a temporal knowledge graph completion model that includes high-order connectivity and attribute information. This consists mainly of a recursive embedding propagation layer and a multi-head attention aggregation layer. The former leverages a recursive mechanism to update entity embeddings and can learn high-order connectivity information between entities in linear complexity time. The latter leverages an attention mechanism to understand the importance of different attributes for entity representation automatically. Combining high-order connectivity and attribute information can lead to more diverse entity representations and help enhance the model’s ability to infer unknown entities. Comparative experiments on three real-world datasets show that the model’s inference accuracy significantly outperforms other benchmark methods, especially regarding knowledge graphs with many unknown entities or relations.
1. Introduction
A knowledge graph (KG) is a structured representation of entities and their attribute relationships in the real world. It has been widely applied in various fields, such as natural language processing [1], recommendation systems [2], and information retrieval [3]. However, traditional KGs are static, snapshot-like knowledge representations that typically form facts in the form of triplets , where S represents the subject entity, O represents the object entity, and represents the relationship between entities. Static knowledge graphs (SKGs) fail to capture the evolution of entities and relationships over time, limiting their modeling and predicting capabilities in terms of temporal aspects. This has led to the development and application of temporal knowledge graphs (TKGs). TKGs introduce timestamps and extend the representation to quadruplets . TKGs are a collection of snapshot graphs with different timestamps, where facts about entities and relationships coexist within the same snapshot [4].
TKGs provide a new perspective for downstream applications such as resource allocation [5], question answering [6], and stock prediction [7]. However, many TKGs need help with the problem of incompleteness, which affects their reliability and accuracy, severely limiting their usage. Therefore, it is of great significance to design an efficient and adaptive method with which to enhance the completeness of traditional TKGs. The TKGC task aims to predict missing facts based on the existing information in TKGs. It can be divided into two subtasks: predicting missing entities for queries like or and predicting missing relationships for queries like . The symbol represents the missing entity or relation. The main challenge lies in effectively integrating timestamps into the model to accurately capture and leverage the temporal dynamics of entities, relationships, and the underlying graph, thereby enhancing the ability to predict missing facts [8]. In this regard, researchers have explored various timestamp integration strategies, such as tensor decomposition based on timestamps [9], timestamp transformation-based methods [10], dynamic embeddings [11], and predictions based on historical contexts [12]. The goal is to incorporate timestamps into the fact-scoring function. However, these methods mainly model the structural features and temporal dependencies of TKGs at a single timescale, and they do not consider the potential temporal variability of TKGs, which leads to the limited performance of TKGC solutions. Building upon this, the MtGCN [13] model utilizes a gated recurrent unit (GRU) to learn the temporal dependencies of TKGs across multiple timescales. Additionally, it combines organically with graph convolutional networks (GCNs) to achieve end-to-end temporal link prediction and synergistic enhancement of temporal modeling and graph structure learning. However, existing research still has some limitations: firstly, it only considers direct relationships between entities while overlooking the high-order connectivity among entities. Secondly, it models only the relationship quadruples, neglecting the abundant attribute information in the KG. These limitations make these methods susceptible to the sparsity and incompleteness of the KG. Additionally, the structural information cannot express the specific meanings between entities and relations, severely inhibiting model prediction ability enhancement.
To overcome these limitations, this paper proposes HCAE, a temporal knowledge graph completion model that fuses high-order connectivity and attribute information, which continues the idea of MtGCN multi-timescale modeling. There are two novelties: (1) Explicitly capturing the high-order connectivity between entities. High-order structured relationships contain rich semantic information that can reflect the complex connections between entities, which is conducive to multi-step prediction and to improving the matching ability of KG representation learning. As shown in Figure 1, the relationship between and can be mined through the facts of . Existing path construction methods attempt to capture the high-order connectivity of KGs using multi-step relationship chains [14]. However, the vast paths pose a significant computational complexity challenge for such methods. These methods can only perform path sampling or select approximate treatments for efficient path modeling. Our analysis reveals that such approximations can significantly impact the final model performance. (2) Explicitly modeling attribute information in KGs. There is a large amount of attribute information in real KGs, as shown in a statistic of Sun et al. [15] on the English version of the DBpedia dataset (2016-04), in which attribute triples are three times as many as relation triples. Attribute triples (denoted as , with indicating attribute values) form a rich network of associations between entities that can characterize specific meanings of entities and relationships. As shown in Figure 1, attributes such as and associated with the entity can provide insights into his educational background and personal profile, facilitating the extraction of rich semantic information and enhancing the model’s prediction and completion capabilities. Such information cannot be obtained from relationship quadruplets alone. Existing works have attempted to incorporate attribute information into TKGC models [16,17]. However, they suffer from two limitations. On the one hand, some methods only utilize partial attribute information, such as AATE_E [17], that solely uses entity description information. On the other hand, both relational and attribute information are optimized in a unified framework, but the loss function must be balanced for both tasks. For instance, JAPE [15] adjusts hyperparameters to achieve the optimal balance between the two loss functions.
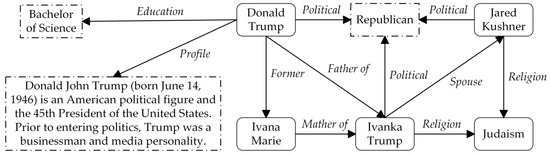
Figure 1.
A subgraph of the knowledge graph containing information about entities, relations, and attributes.
The limitations of existing methods severely restrict the performance of the models. Given this, designing a model that can learn attribute information and high-order connectivity uniformly and efficiently is essential. Modeling high-order connectivity allows for the capturing of dependencies and semantic associations among entities, thus enabling a more comprehensive understanding of entity characteristics from multiple perspectives. Attribute information explicitly describes entity features and complements structural information, allowing the model to generalize better to unseen entities. The joint modeling of structure and attributes enables the learning of representations that fuse connectivity patterns and content features, leading to a more comprehensive understanding of entity characteristics. The combination of both approaches provides complementary benefits.
Unlike existing approaches, HCAE computes entity-specific representations by weighting attribute information and performing embedding propagation based on high-order structural relationships. Specifically, HCAE elaborates on two improvement strategies. Firstly, recursive embedding propagation of relational quaternions using a GCN-based architecture aims at the real-time updating of entity embedding representations. Using a recursive embedding mechanism enables HCAE to learn high-order connectivity between entities with linear time complexity. Secondly, the automatic learning of the importance of different attributes to entity representation through the multi-attention mechanism, which adequately fuses structural and attribute information to enhance the ability to model entities from multiple perspectives.
The main contributions of this work are as follows:
- We emphasize the importance of attribute information and high-order connectivity in temporal knowledge graph completion, highlighting the complementary benefits of their combination.
- We propose the HCAE model based on the limitations of existing work, aiming to utilize attribute information and higher-order structural information to improve the model’s prediction of unknown facts.
- The experimental results on three real-world datasets demonstrate that HCAE improves the predicting ability for missing facts, indicating that learning high-order connectivity and attribute information enhances the model’s TKGC capability.
2. Related Works
2.1. Static Knowledge Graph Completion
Static knowledge graph completion (SKGC) methods are based mainly on knowledge representation learning, which captures semantic associations and patterns between entities and relations by mapping them to low-dimensional vector representations [13]. The standard approaches are broadly categorized into three types: (1) Translation-based models: both TransE [18] and RotateE [19] follow the idea that a relationship causes head and tail entities to be translated in the embedding space. The difference lies in the technique of using translation and rotation, respectively. The higher the proximity of the transformed vectors of head and tail entities, the higher the matching degree. ComTR [20] uses double-quadratic number-based multiplication to model timestamps and relations as translation and rotation operations. MuRMP [21] embeds multi-relationship KGs into the hybrid curvature space of the SKGC task. (2) Bilinear model: also known as tensor decomposition. For example, RESCAL [22] decomposes the relationship matrix into the product of three matrices using singular value decomposition. The result represents the association scores between entities and relationships. However, it suffers from high computational complexity and the risk of overfitting. DistMult [23] is a simplified version of RESCAL that represents relationships as dot products between entity vectors, using a symmetric bilinear function to compute scores between entity pairs, offering advantages in terms of computational efficiency but with limitations in multi-relational modeling. ComplEx [24] is an extension of DistMult that represents relationships as complex products of entity vectors, which is more advantageous in handling multiple relationships. GIE [25] learns interaction structures in various single spaces, such as Euclidean, hyperbolic, or spherical spaces, to capture more complex topological structures in KGs, including chain-like, hierarchical, and cyclical structures. (3) Neural network models: rGCN [26] is a multi-layer relation aware GCN that performs representation learning directly on the KG structure. It incorporates relationship-type information to differentiate relationships and employs de-featurization and batch normalization to improve training stability. ConvE [27] maps entities and relations to a continuous vector space and calculates similarity between entities and relationships using element-wise multiplication and pooling operations. FTL-LM [28] is a language model that combines topological structure information and logical rules. MKGformer [29] utilizes a hybrid transformer and multi-level fusion architecture, achieving multi-level fusion of visual and textual multimodal knowledge representations through prefix-guided coarse-grained interaction and correlation-aware fine-grained fusion modules. KRAT [30] leverages graph context to project neighboring triplets into different latent spaces and jointly aggregates messages with attention mechanisms.
2.2. Temporal Knowledge Graph Completion
Many TKGC models extend existing SKGC models by introducing time embeddings or modeling the temporal dimension, to capture the evolution of entities and relationships at different time points. For example, TTransE [31] is an extension of the TransE model that encodes timestamps as translation operations to perform additional translation on the representations of head entities. TBDRI [32] is a block term decomposition (similar to a variant of Tucker decomposition) model based on binary tensor representation of KG quadruples. It enhances the binding of forward and backward relations and introduces a core tensor as temporal information to capture temporal relationships between entities better. ChronoR [33] uses the RotatE model as a foundation and combines the timestamp with the relation representation to form a unified rotation vector. This enables the representation of temporal relationship pairs with rotation and scaling in the embedding space. TComplEx [34] and TNTComplEx [34] are extensions of ComplEx. The former applies factorization methods to model a fourth-order tensor, while the latter decomposes the tensor into temporal and non-temporal components during the factorization process. TASTER [35] represents different TKGs using sparse transformation matrices to reduce the complexity of entity relation evolution.
Fusion neural networks are another vital research direction for TKGC models. TA-DistMult [36] learns time-aware relationship representations using recursive neural networks (RNN) based on DistMult and TransE models, injecting the capability of temporal modeling into these two SKGC models. TeMP [37] utilizes message-passing graph neural networks (GNN) to learn structure-based entity representations at each timestamp. It aggregates the representations of all timestamps using TeMP-GRU and TeMP-SA encoders, capturing both time dependency and structure dependency. FTMF [38] encodes entities using self-attention mechanisms, aggregates parameter sets using RNNs, and employs a fault-tolerant mechanism to handle incorrect information. It effectively handles few-shot TKGC tasks. SANe [39] maps facts corresponding to different timestamps to different latent spaces using a convolution neural network (CNN). It explores the overlap in the latent space through a time-aware parameter generator to capture contextual information about timestamps. Many existing studies rely on handcrafted GNNs, which cannot fully explore the diverse topology and temporal information of TKGs. To address this, SPA [40] adopts neural architecture search (NAS) techniques to design a general framework. Through single-path sampling training, it efficiently searches for the optimal message-passing structure on various datasets. RoAN [41] is a time-oriented attention network that embeds time features by applying attention mechanisms to multi-chain relationships in TKGs. ExKGR [42] employs GNNs to achieve interpretable multi-hop completion. TARGCN [43] is a simple but powerful graphical encoder with valid parameters. The contextual information of each entity can be extensively mined.
The two types of methods described above require predefined temporal granularity and modeling based on this granularity. Nevertheless, temporal information in TKG exhibits multi-granularity, and the time scales for the evolution of different facts or relationships are other. Using a fixed single time scale makes capturing historical information at additional time granularities challenging and will lead to inadequate modeling of specific temporal patterns, thus reducing the expressive power of the model. Therefore, designing a model that can support multi-timescale modeling in the TKGC task is a direction worth exploring in depth. Based on multi-timescale modeling, HCAE enhances the model’s ability to complement TKG by learning attribute information and high-order connectivity.
3. Proposed Model
3.1. Problem Formulation
This study involves both relationship quadruples and static attribute triples. However, considering the dimensional conflicts between them and the difficulty of accurately predicting the properties of unknown entities using fixed attribute values, this paper introduces additional timestamps to static attribute triples, expanding them into dynamic attribute quadruples.
Definition 1.
Temporal Knowledge Graph: A TKG consists of a relation quadruple and an attribute quadruple . Therefore, a TKG can be denoted as , while , , and denote the set of entities, relations, attributes and the timestamps, respectively.
The research objective of this study is to generate continuous vector representations for elements in each relationship quadruple and attribute quadruple by mining the high-order connectivity and attribute information of the TKG. This includes generating complete vector representations for and facts, where the bolded elements represent vectors. Here, the subject entity is ( is the dimension of the embedding representation), the relation is , the object entity is , the attribute is , and the timestamp t is a scalar.
In this work, the inputs are all facts (including relations and attributes) in a given TKG before the timestamp t, and the goal is to maximize the performance metrics (using MRR and Hits@n) for the following two tasks:
- Entity prediction: given or , predict the missing subject or object entity at t moment.
- Relation prediction: given , predict the missing relationship at the t moment.
3.2. Overall Structure
The HCAE model takes as input all relation quadruples and attribute quadruples in the TKG. It consists of four parts: (1) Attribute embedding layer: using long short-term memory (LSTM), it maps semantically related attributes to nearby positions in the vector space to capture attribute correlations. (2) Embedding propagation layer: entity and attribute vectors are used as inputs, and graph attention embedding is employed to learn high-order connectivity between entities. (3) Temporal encoding layer: multiple layers of GRU are set up to learn historical information at different time granularities. represents the time window size used to control the length of historical information. Finally, multi-granularity temporal features are fused. (4) Decoder: the entity vectors and relationship vectors generated by the structure mentioned above are used as inputs to compute entity-relation scores for all quadruples. The model’s overall structure is shown in Figure 2, and the notation used in the paper is summarized in Table 1.
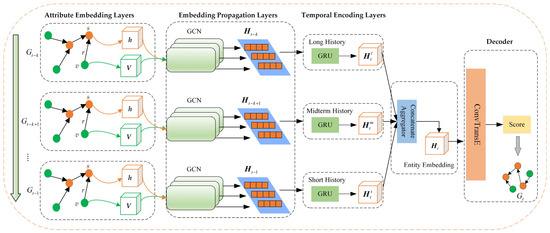
Figure 2.
Architecture of HCAE.

Table 1.
Notations used in the paper.
3.3. Attribute Embedding Layer
The performance of machine learning algorithms relies heavily on the consistency of interpreting input vectors. Poor data interpretation can lead to suboptimal results. Therefore, feature extraction is crucial in machine learning algorithms [44]. Attribute values are often in the form of variable-length text, and to obtain dense feature representations, an encoder is required to encode the text into fixed-length vector representations. The bag-of-words (BOW) encoder is a commonly used method for feature representation in natural language processing (NLP) due to its simplicity and ability to capture word frequency information. However, it disregards word order and semantic information, making it unable to handle contextual relationships and word sense ambiguity. Hence, this paper adopts LSTM as the encoder. Deep learning techniques, on the other hand, facilitate faster information extraction, enabling scientists to extract discriminative features without relying solely on limited domain knowledge and manual effort [44]. The attribute value is denoted as , where denotes the position of i word, and the output of the last hidden state of LSTM is taken as the attribute vector . Figure 3 shows the detailed process of the attribute embedding layer.
where denotes the word embedding vector and denotes the LSTM network.
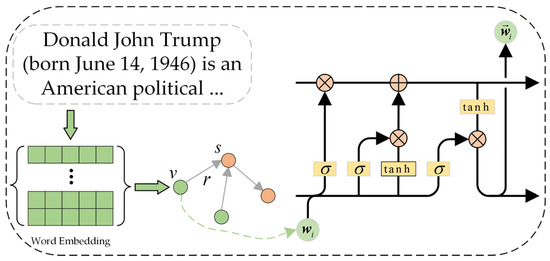
Figure 3.
Attribute embedding layer detailed process.
3.4. Embedding Propagation Layer
This layer is primarily based on the GCN architecture for recursive embedding propagation, including attention embedding propagation and embedding aggregation. Specifically, the graph attention mechanism is employed to learn the attention weights of neighboring entities for each entity, enabling selective cascading embedding propagation. The entity embeddings are then recursively propagated and aggregated onto the central entity in the KG, ultimately achieving entity representation learning. The detailed structure of the embedding propagation layer is illustrated in Figure 4.
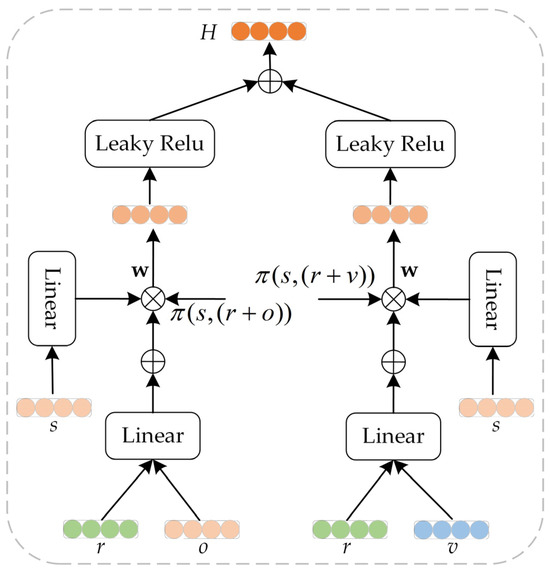
Figure 4.
The structure of the embedding propagation layer.
Attention Embedding Propagation. Its inputs are entities, relations, and attribute embeddings. The embedding representation of entity as at timestamp t and the set of its neighbors as , aims to obtain an updated embedded representation of entity by encoding neighbor entity information and attribute information. In this paper, we take the quadruple as an example:
where is a learnable linear transformation that transforms the input embedding into a high-order feature space. is an attention coefficient representing the importance of entity O to entity .
The attention coefficient is used to control the amount of information propagation between the entities, and is computed by the softmax function for all quadruple connected to entity :
In this paper, the attention coefficients are realized by a simple single-layer feedforward neural network:
where denotes the activation function.
Embedding Aggregation. To learn more stable entity representations and obtain richer semantic information, the last layer of HCAE uses a multi-head attention mechanism. The role of embedding aggregation is to integrate the embedding representations of each head in order to obtain the final embedding representation of the center entity. In this paper, the average aggregation method is used to extend Equation (2):
where m denotes the number of attention heads, indicates the j normalized attention coefficient, and is a linear transformation.
Next, multiple layers of embedding propagation are stacked to aggregate features from multi-hop neighboring entities, encoding deeper-level connectivity information to capture semantic information within the high-order connectivity structures in the TKG. The embedding representation of the l layer of entity is:
3.5. Temporal Encoding Layer
The temporal encoding layer consists of multiple layers of GRU. Its input is the entity embedding sequences at different time granularities, which incorporate attribute and high-order structural information. Controlled by the time window, it models the short-term, medium-term, and long-term historical information of entities separately. Finally, the outputs of GRUs at different granularities are concatenated and passed to the next layer. The multi-granularity temporal features provide abundant temporal information for TKGC tasks and help improve the model’s prediction accuracy:
where , and denote the temporal aggregation generated from short-term, medium-term and long-term historical information, respectively. denote the number of entities and represents the time window size, which is used to regulate the timescale of the input. is a weighted sum of , and , controlled by predefined weighting coefficients , and , respectively, and represents the final output of the temporal coding layer.
3.6. Decoder
The HCAE model employs ConvTransE [45] as the decoder. Its input consists of entity and relationship representations learned from the embedding propagation layer and the temporal encoding layer. The decoder outputs scores for quadruples, which are used to link the features learned by the encoder and compute the conditional probability of quadruples, thereby completing the TKGC task of the entire model. The scoring function can be represented as follows:
where represents the spliced subject entities and relations, is the convolution kernel matrix for performing convolution operations on the spliced vectors, ∗ denotes the convolution operation, W represents the linear transformation matrix of the fully connected layer, and is a nonlinear function containing a convolution step.
3.7. Optimization
According to the above, the loss function of the HCAE model is defined as:
where T is the number of timestamps controlling the number of sampled training quadruple, N denotes the number of entities, and is a labelled value that takes the value 0/1. A value of 1 denotes the existence of a quadruple of entity i in TKG at timestamp . Otherwise, it is 0. In addition, this paper uses Adam as the optimization algorithm.
3.8. Applications
HCAE is a general framework that can be applied to different scenarios such as transportation, healthcare, social networks, economy, and finance. Take transportation scenarios as an example: (1) Construct TKG, using vehicles, routes, and events, etc. as entities: A specific vehicle travelling on a particular route during a certain period, and a special event occurring on a specific route, etc., are represented as relationships. Vehicle type, color, the route starting and ending points, and event type, etc. are used as entity attributes. (2) Encoding attribute information: This can reflect behavioral patterns under different conditions, such as route selection varying based on weekdays or weekends and other start and endpoints. It helps in learning the correlations between entities, such as certain events that significantly impact specific types of vehicles. It also provides decision-making foundations, such as planning public transportation routes based on road segment attributes. (3) Mining high-order structural information: Learning high-order relationships between vehicles and roads can reflect the way in which a vehicle drives certain road sections for an extended period, while high-order connections between roads can demonstrate the way in which congestion on a road section often affects neighboring road sections, and high-order relationships between events and related entities, such as a road construction events, affect related vehicles and road sections. (4) Multi-scale historical modeling: Long-term history can capture vehicle driving habits and patterns. A medium-term account can learn changes in road congestion over the past month or two. A short-term history can predict traffic peaks during daily traffic hours. Therefore, the HCAE model can predict future traffic conditions, traffic flow, and optimal route planning. Compared with the use of KG or historical data alone, HCAE effectively combines attribute, structural, and multi-scale historical information, improving traffic-related prediction and planning tasks.
4. Experimentation
4.1. Datasets
To evaluate the performance of the HCAE model, we will conduct experiments on the following three publicly available datasets: (1) Subset of the Global Database of Events, Language, and Tone (GDELT) known as GDELT [46]. (2) Two subsets of the Integrated Crisis Early Warning System (ICEWS), namely ICEWS14 and ICEWS05-15 [36]. Among these, GDELT records daily timestamped facts from 1 April 2015, to 31 March 2016, and contains the most common 500 entities and 20 common relations. ICEWS14 focuses on political and military events on a global scale and records facts between entities that occurred frequently in 2014. Due to limitations in its design, ICEWS14 is more limited in its temporal patterns, and geopolitical events between different entities are often not correlated in time. ICEWS05-15 records frequent entity-to-entity facts with a longer period from 2005 to 2015. To help select the best model parameters and hyperparameters, this paper divides the dataset into a training set (80%), a validation set (10%), and a test set (10%). The time interval indicates the time granularity between neighboring facts. More statistical information is shown in Table 2.

Table 2.
The statistics of datasets.
4.2. Baselines
To verify the validity of the HCAE model, comparative tests with the four SKGC methods and the existing state-of-the-art TKGC methods will be conducted in this paper. The introduction of the benchmark methods is described below:
- TransE [18] learns low-dimensional embeddings by translating entity and relationship vectors, achieving KGC tasks.
- DistMult [23] learns entity and relationship representations by using the inner product of entity and relationship triplets.
- ComplEx [24] represents entities and relationships as complex-valued embeddings and utilizes complex-valued inner products to capture symmetric/antisymmetric relationships, thereby improving KG link prediction performance.
- R-GCN [26] effectively captures complex relationships and contextual information between nodes.
- TTransE [31] innovatively embeds spatiotemporal information into KG, which provides richer contextual information for entity and relationship representation.
- TA-DistMult [36] is the first approach to introduce a time-sensitive attention mechanism in the TKGC task, which can enhance the presentation of relations across time.
- ChronoR [33], in which the representations of the relationship and timestamp are concatenated and applied as a rotation vector to the entity, enabling the temporal representation of the relationship to possess time dependency.
- TNTComplEx [34] decomposes the KG fourth-order tensor into material and non-temporal components and then specializes in learning the earthly manifestation of relations to achieve dynamic completion of KG.
- TeMP [37], in which, using message passing GNN, the structured representation of each entity at each time step is learned. The dynamic entity representation is obtained by aggregating all of the representations through an encoder.
- MtGCN [13] uses GCN to mine latent semantic information in TKG. GRU explicitly models historical information at different scales and uses the generated valid entity and relationship representations to complete TKGC.
- BoxTE [47] introduces dedicated time embedding representations, enabling the relationship representation at each time point to be unique and highly expressive.
- RoAN [41] directly encodes relationships and captures their temporal characteristics through a multi-chain structure and relationship attention mechanism.
- TASTER [35] learns global and local TKG embeddings using a sparse transition matrix, considering global statistics and local temporal evolution information.
- RotateQVS [48] represents entities and relationships in a quaternion vector space, utilizing rotation to represent the temporal evolution of relationships while also considering patterns such as symmetry and antisymmetry in relationships.
4.3. Evaluation Metrics
This paper adopts two commonly used metrics in the TKGC task, mean reciprocal rank (MRR) and Hits@{1, 3, 10}, which usually appear together. MRR denotes the average of the reciprocal rank of the correct answers in the prediction results, which is used to measure the model’s ranking of the correct answers in the prediction results, and higher values indicate higher model predicting ability, which is defined as follows:
Hits@1, Hits@3, and Hits@10 denote the percentage of correct answers ranked in the top 1/3/10, respectively, reflecting the model’s accuracy in incorporating the correct answers into the top n predictions. The higher the value of Hits@{1, 3, 10} the more effective is the model, which is defined as follows:
where and denote the ranking of the two-query subject and object entities, respectively. represents the indicator function.
4.4. Implementation and Hyperparameters
The HCAE model was implemented using PyCharm 2021.3.3 (Professional Edition) as the IDE platform. The operating system used was Windows 10 Home Chinese Edition, and the programming language utilized was Python 3.8. The CPU employed was an i7-7700HQ, and the PyTorch version utilized was 1.4. After the grid search, the hyperparameters of the HCAE model were set as follows: in this paper, the training set was first batch-processed, and the batch size set to 128. The number of training round epochs was set to 400. The learning rate lr was set to 0.01. The embedding dimensionality d of the entities and relationships was set to 128. The lengths of the time windows used to control the long-term, medium-term, and short-term historical information N1, N2, and N3 were set to 2, 4, and 10, respectively. The weighting coefficients , , and were 0.4, 0.4, and 0.2, respectively.
4.5. Experimental Results
To verify the validity of the HCAE model, this paper conducts a comparison experiment with the benchmark method in Section 4.2. It should be noted that the results of the comparison models are derived from the best results reported in the respective papers. For visualization, the MRR values are expanded by a factor of 100 in this paper, while the Hits@n values indicate percentages. The experimental results on the three datasets are shown in Table 3.

Table 3.
Comparison of prediction results on the GDELT, ICEWS14, and ICEWS05-15 datasets.
4.5.1. Comparison Experiment
The experimental results of the three datasets indicate that temporal knowledge graph completion methods generally outperform static methods. This is because TKG contains temporal information between facts, which provides crucial contextual information for time-sensitive link prediction tasks. Additionally, TKG can capture the patterns of facts changing over time, such as adding or deleting facts, which helps predict missing entities or relationships. HCAE demonstrates significant performance improvements compared with the four static methods. For example, compared with the best-performing static method R-GCN, HCAE achieves improvements of 10.1, 14.6, and 19.6 in Hits@1/3/10 on the GDELT dataset. This highlights the effectiveness of modeling temporal dependencies between facts.
The HCAE model was compared with several TKGC methods on the GDELT dataset, and from Table 3, it can be observed that HCAE outperformed TTransE by significant margins in all four metrics. Specifically, HCAE achieved improvements of 24.6, 27.3, 23.6, and 22.2 percentage points in the respective metrics. Because TTransE only models the translation operations of entities and relations, it cannot effectively model complex event evolution. Compared with TA-DistMult, HCAE achieved 15.5, 14.9, 17.7, and 17.5 improvements in the respective metrics. This is primarily because TA-DistMult relies on matrix factorization, which cannot handle large-scale datasets. Additionally, TeMP-SA and TeMP-GRU struggle to model complex long-term dependencies due to their reliance on temporal ordering information. Furthermore, MtGCN only considers direct relationships between entities, disregarding the rich attribute information present in TKG. These factors contribute to the significant differences in results when compared with HCAE. BoxTE achieved relatively similar results, with slight decreases of 0.9, 0.4, 1.9, and 2.9 in the four metrics. BoxTE models temporal order constraints and KG structural constraints while effectively modeling uneven time spans using the Box embedding model. It can handle the temporal characteristics of TKG well. However, BoxTE’s model tends to be overly smooth, leading to the loss of fine-grained information related to sudden events. This makes it challenging for BoxTE to identify and link such events. RoAN and RotateQVS exhibit similar results but differ significantly from HCAE in performance. This is because RoAN’s relation attention mechanism is too simplistic to learn complex temporal patterns thoroughly. At the same time, RotateQVS’s quaternion space assumption is overly idealized and unsuitable for capturing complex relationships in real-world TKGs. Additionally, both methods assume fixed time intervals, whereas time gaps often exhibit irregular patterns. HCAE achieves the best results because the GDELT dataset has a relatively small number of entities and relationships but a highly complex topology. Furthermore, some facts persist across multiple consecutive timestamps, while others are instantaneous and sparse. These benchmark methods struggle to extract and model structural information in such scenarios effectively. HCAE, on the other hand, has improved attribute embedding and embedding propagation layers, allowing it to adapt effectively to complex graph structures. It demonstrates strong capabilities in learning complex topology and temporal induction.
Table 3 presents the comparison results between HCAE and several TKGC methods on ICEWS14 and ICEWS05-15 datasets. On the ICEWS14 dataset, ChronoR(b) outperforms HCAE by 0.4 in terms of MRR metric, while TeMP-SA surpasses HCAE by 0.3 in the Hits@10 metric. On the ICEWS05-15 dataset, TeMP-GRU outperforms HCAE by 0.4 in Hits@10 metric. This is because the time information provided by ICEWS14, and ICEWS05-15 is limited. The relationships in these two datasets could be sparser as they involve fewer events such as negotiations, visits, and conflicts. Additionally, different entities are primarily unrelated in time and exhibit limited patterns, resulting in reduced richness and variability of temporal information in the dataset, relying more on entity-based predictions. On the other hand, HCAE models multi-scale historical details, to some extent depending on temporal information, leading to slightly lower performance than the baseline methods in specific cases. However, it is essential to note that HCAE significantly outperforms other baseline methods in most cases. For instance, it exceeds ChronoR(b) by 0.2, 1.8, and 6.4 percentage points in Hits@1/3/10 metrics. Additionally, the performance of TeMP-SA and TeMP-GRU is notably inferior to HCAE in other metrics. Specifically, HCAE is substantially improved when compared with recent TKGC methods such as RoAN, RotateQVS, and TASTER. Due to the inclusion of many unprecedented new events in event-based KG datasets, HCAE can exploit these new events’ historical and non-historical dependencies to uncover latent patterns that have not been observed. Ultimately, it is proven that HCAE, which integrates high-order connectivity and attribute information, is an effective TKGC method.
4.5.2. Model Robustness Analysis
To validate the robustness of the HCAE model, we conducted TKGC experiments on an irregular timestamp dataset called ICEWS14-irregular. The goal was to evaluate the performance of HCAE in handling unevenly distributed timestamp intervals. The construction of the dataset follows [43], where a snapshot graph is randomly sampled from ICEWS14, ensuring that the time interval between two consecutive snapshots does not exceed 4. The experimental results are presented in Figure 5.
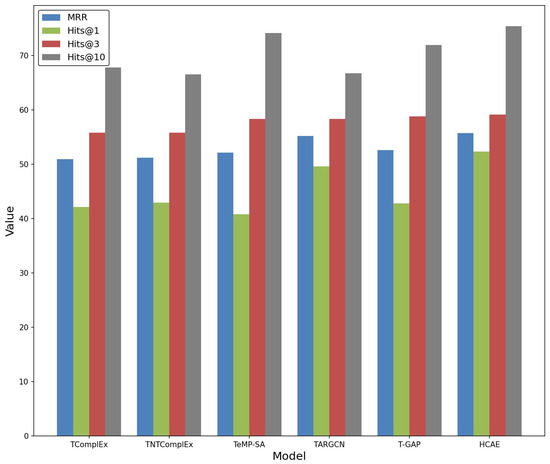
Figure 5.
Generalization performance on irregular timestamp data.
From the experimental results, it can be observed that HCAE performs the best in all four metrics. Notably, it achieves significant improvement in Hits@1. For instance, it outperforms TeMP-SA by 11.5. This is because HCAE adopts the idea of multi-scale historical modeling, which allows it to explore temporal dependency patterns at different granularities without overly relying on a specific temporal regularity. On the other hand, TComplEx’s temporal modeling approach is relatively simple, representing temporal influence through a single time weight parameter with limited expressive power. TNTComplEx does not delve deep into modeling temporal regularities and primarily relies on linear transformations, which fail to capture the semantic information related to entities and time effectively. TeMP-SA only utilizes graph information within a fixed short time range for embedding learning, disregarding the rich graph information in other time intervals. T-GAP [12] employs time-shifted embeddings to encode different time differences. However, HCAE’s modeling of attribute information reduces the reliance on structural information and mitigates the impact of irregular timestamps. Moreover, mining high-order structural information enables the capture of more complex entity relationships, allowing HCAE to effectively withstand fluctuations in timestamp intervals and better adapt to irregular time gaps.
4.5.3. Parameter Sensitivity Analysis
Hyperparameters , and are used to control the importance of short-term, medium-term, and long-term historical information, respectively, for the task in the HCAE model. To investigate their impact on the performance of HCAE in knowledge graph completion, this paper conducted parameter sensitivity experiments on the ICEWS14 dataset. The values of these hyperparameters were gradually increased from 0.1 to 0.9 with a step size of 0.2. When exploring one hyperparameter, the values of the other two hyperparameters were fixed at 0.3. Additionally, other parameter settings remained unchanged.
A larger attention coefficient indicates a higher importance of the corresponding period’s historical information for the completion task. From Figure 6, it can be observed that the HCAE model performs the best when the value of is 0.3. Subsequently, the performance gradually decreases as the weight of short-term historical information increases. This is because an excessive reliance on short-term history can lead to neglecting long-term patterns, resulting in the model overfitting the current situation. Short-term situations are more susceptible to various random factors and exhibit greater dynamism. Figure 7 shows that the HCAE performs best when the value of is 0.5. The ICEWS14 dataset has one year, and the distribution of event times is relatively uniform. The medium-term history captures the development patterns of international relations over a specific period, and paying appropriate attention to medium-term history helps understand the global context. However, excessive reliance on medium-term history leads to neglect of current changes, making it challenging to explain sudden events and predict future trends. Figure 8 shows that the model achieves the best performance when the value of is 0.7. Long-term history has a larger time window and can capture temporal dependencies overlooked by short-term and medium-term history. However, excessive reliance on long-term history fails to perceive the short-term patterns of new events, so an increase in beyond a certain point leads to a decline in performance.
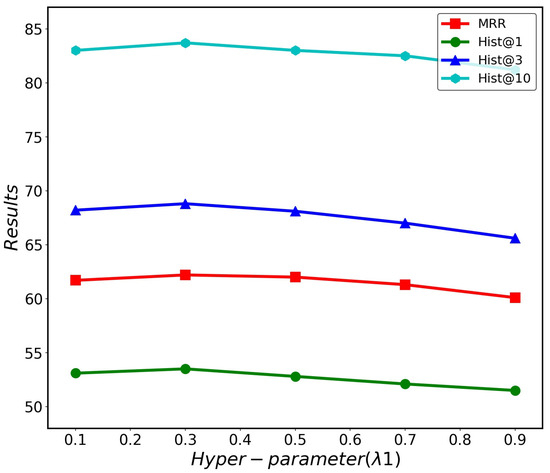
Figure 6.
Effects of different λ1 on HCAE performance.
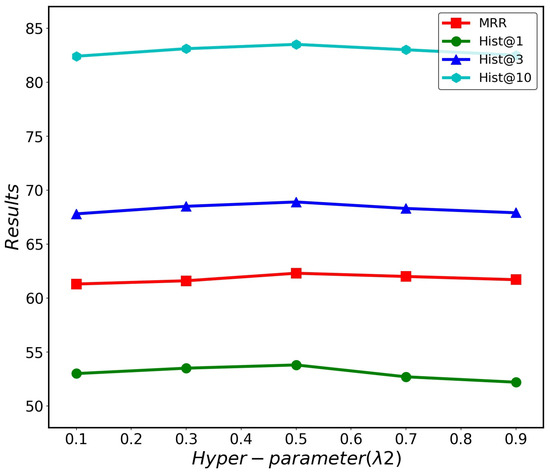
Figure 7.
Effects of different λ2 on HCAE performance.
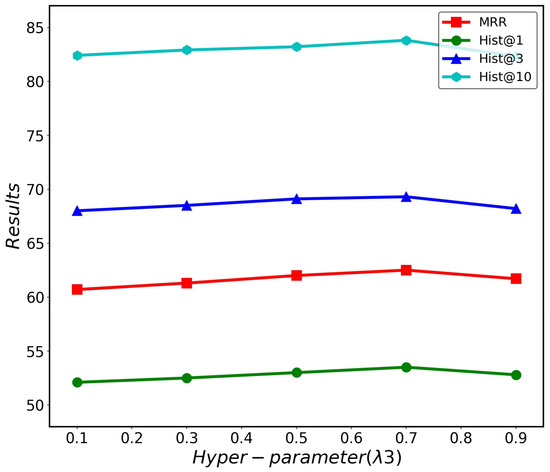
Figure 8.
Effects of different λ3 on HCAE performance.
In conclusion, historical information from different periods plays unique roles, and neglecting the history from any period can result in a partial understanding of the evolution of events and difficulty in capturing global patterns. Therefore, when dealing with datasets with different patterns, it is advisable to adjust the hyperparameters , and appropriately to strike a balance between the influences of historical information from different periods, thus achieving optimal performance.
5. Conclusions
This paper proposes a temporal knowledge graph completion (TKGC) model that combines high-order connectivity between entities and attribute information. The model utilizes LSTM networks to extract rich semantic information from attribute values, providing additional supervision and addressing the problem of indistinguishable structural information for entities and relations with different meanings. Additionally, it employs graph attention networks to model high-order connectivity between entities, enhancing the model’s ability to learn complex relationships between entities, implicit dependencies between events, and constraints. Experimental results on the GDELT and ICEWS demonstrate that the proposed HCAE model performs well in terms of mean reciprocal rank (MRR) and Hits@n metrics, outperforming other baseline models. It is particularly suitable for addressing complex temporal evolution tasks involving unknown entities or relations. The model also holds significant value for practical engineering tasks. However, compared with other models, HCAE has a larger number of parameters and computational efficiency limitations. Future work will focus on designing a more lightweight yet powerful model and improving its applicability in real-world engineering tasks.
Author Contributions
Conceptualization, M.W.; methodology, M.W.; software, H.M.; validation, M.W., H.M., W.W. and X.Z.; formal analysis, X.Z.; investigation, M.W.; resources, M.W.; data curation, M.W.; writing—original draft preparation, M.W.; writing—review and editing, H.M.; visualization, M.W.; supervision, W.W.; project administration, M.W.; funding acquisition, H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (grant number No. 62273170), the Liaoning Education Department Scientific Research Project (grant number No. JZL202015404, grant number No. LJKZ0625), the General project of Liaoning Provincial Department of Education (grant number No. LJKZ0618).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Q.; Li, M.; Wang, X.; Parulian, N.; Han, G.; Ma, J.; Tu, J.; Lin, Y.; Zhang, H.; Liu, W.; et al. COVID-19 literature knowledge graph construction and drug repurposing report generation. arXiv 2020, arXiv:2007.00576. [Google Scholar]
- Yang, Y.; Huang, C.; Xia, L.; Li, C. Knowledge graph contrastive learning for recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 1434–1443. [Google Scholar]
- Reinanda, R.; Meij, E.; de Rijke, M. Knowledge graphs: An information retrieval perspective. Found. Trends Inf. Retr. 2020, 14, 289–444. [Google Scholar] [CrossRef]
- Xu, Y.; Ou, J.; Xu, H.; Fu, L. Temporal knowledge graph reasoning with historical contrastive learning. Proc. AAAI Conf. Artif. Intell. 2023, 37, 4765–4773. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, M.; Chen, J.; Qu, T.; Huang, G.Q. Digital twin-enabled dynamic spatial-temporal knowledge graph for production logistics resource allocation. Comput. Ind. Eng. 2022, 171, 108454. [Google Scholar] [CrossRef]
- Saxena, A.; Chakrabarti, S.; Talukdar, P. Question answering over temporal knowledge graphs. arXiv 2021, arXiv:2106.01515. [Google Scholar]
- Feng, F.; He, X.; Wang, X.; Luo, C.; Liu, Y.; Chua, T.S. Temporal relational ranking for stock prediction. ACM Trans. Inf. Syst. (TOIS) 2019, 37, 1–30. [Google Scholar] [CrossRef]
- Cai, B.; Xiang, Y.; Gao, L.; Zhang, H.; Li, Y.; Li, J. Temporal knowledge graph completion: A survey. arXiv 2022, arXiv:2201.08236. [Google Scholar]
- Shao, P.; Zhang, D.; Yang, G.; Tao, J.; Che, F.; Liu, T. Tucker decomposition-based temporal knowledge graph completion. Knowl.-Based Syst. 2022, 238, 107841. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Chen, X.; Lei, J.; Lai, X. 3drte: 3d rotation embedding in temporal knowledge graph. IEEE Access 2020, 8, 207515–207523. [Google Scholar] [CrossRef]
- Goel, R.; Kazemi, S.M.; Brubaker, M.; Poupart, P. Diachronic embedding for temporal knowledge graph completion. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3988–3995. [Google Scholar] [CrossRef]
- Jung, J.; Jung, J.; Kang, U. Learning to walk across time for interpretable temporal knowledge graph completion. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 786–795. [Google Scholar]
- Peng, C.C.; Shi, X.; Yu, R.; Ma, C.; Wu, L.; Zhang, D. Multi-timescale History Modeling for Temporal Knowledge Graph Completion. In Proceedings of the 2022 18th International Conference on Mobility, Sensing and Networking (MSN), Guangzhou, China, 14–16 December 2022; pp. 477–484. [Google Scholar]
- Toutanova, K.; Lin, X.V.; Yih, W.T.; Poon, H.; Quirk, C. Compositional learning of embeddings for relation paths in knowledge base and text. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Berlin, Germany, 7–12 August 2016; pp. 1434–1444. [Google Scholar]
- Sun, Z.; Hu, W.; Li, C. Cross-lingual entity alignment via joint attribute-preserving embedding. In Proceedings of the Semantic Web–ISWC 2017: 16th International Semantic Web Conference, Vienna, Austria, 21–25 October 2017; Proceedings, Part I 16. Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 628–644. [Google Scholar]
- Fatemi, B.; Ravanbakhsh, S.; Poole, D. Improved knowledge graph embedding using background taxonomic information. Proc. AAAI Conf. Artif. Intell. 2019, 33, 3526–3533. [Google Scholar] [CrossRef]
- An, B.; Chen, B.; Han, X.; Sun, L. Accurate text-enhanced knowledge graph representation learning. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), New Orleans, LA, USA, 1–6 June 2018; pp. 745–755. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013, 26, 2787–2795. [Google Scholar]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv 2019, arXiv:1902.10197. [Google Scholar]
- Yu, R.; Liu, T.; Yu, J.; Zhang, W.; Zhao, Y.; Yang, M.; Zhao, M.; Guo, J. Combination of Translation and Rotation in Dual Quaternion Space for Temporal Knowledge Graph Completion. In Proceedings of the 2023 International Joint Conference on Neural Networks (IJCNN), Gold Coast, Australia, 18–23 June 2023; pp. 1–8. [Google Scholar]
- Wang, S.; Wei, X.; Nogueira dos Santos, C.N.; Wang, Z.; Nallapati, R.; Arnold, A.; Xiang, B.; Yu, P.S.; Cruz, I.F. Mixed-curvature multi-relational graph neural network for knowledge graph completion. Proc. Web Conf. 2021, 2021, 1761–1771. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.P. A three-way model for collective learning on multi-relational data. ICML 2011, 11, 3104482–3104584. [Google Scholar]
- Yang, B.; Yih, W.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and inference in knowledge bases. arXiv 2014, arXiv:1412.6575. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2071–2080. [Google Scholar]
- Cao, Z.; Xu, Q.; Yang, Z.; Cao, X.; Huang, Q. Geometry interaction knowledge graph embeddings. Proc. AAAI Conf. Artif. Intell. 2022, 36, 5521–5529. [Google Scholar] [CrossRef]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the Semantic Web: 15th International Conference, ESWC 2018, Heraklion, Greece, 3–7 June 2018; Proceedings 15. Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 593–607. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. In Proceedings of the AAAI’18: AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 1811–1818. [Google Scholar]
- Lin, Q.; Mao, R.; Liu, J.; Xu, F.; Cambria, E. Fusing topology contexts and logical rules in language models for knowledge graph completion. Inf. Fusion 2023, 90, 253–264. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, N.; Li, L.; Deng, S.; Tan, C.; Xu, C.; Huang, F.; Si, L.; Chen, H. Hybrid transformer with multi-level fusion for multimodal knowledge graph completion. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 904–915. [Google Scholar]
- Tan, Z.; Chen, Z.; Feng, S.; Zhang, Q.; Zheng, Q.; Li, J.; Luo, M. KRACL: Contrastive learning with graph context modeling for sparse knowledge graph completion. Proc. ACM Web Conf. 2023, 2023, 2548–2559. [Google Scholar]
- Leblay, J.; Chekol, M.W. Deriving validity time in knowledge graph. Companion Proc. Web Conf. 2018, 2018, 1771–1776. [Google Scholar]
- Yu, M.; Guo, J.; Yu, J.; Xu, T.; Zhao, M.; Liu, H.; Li, X.; Yu, R. TBDRI: Block decomposition based on relational interaction for temporal knowledge graph completion. Appl. Intell. 2023, 53, 5072–5084. [Google Scholar] [CrossRef]
- Sadeghian, A.; Armandpour, M.; Colas, A.; Wang, D.Z. Chronor: Rotation based temporal knowledge graph embedding. Proc. AAAI Conf. Artif. Intell. 2021, 35, 6471–6479. [Google Scholar] [CrossRef]
- Lacroix, T.; Obozinski, G.; Usunier, N. Tensor decompositions for temporal knowledge base completion. arXiv 2020, arXiv:2004.04926. [Google Scholar]
- Wang, X.; Lyu, S.; Wang, X.; Wu, X.; Chen, H. Temporal knowledge graph embedding via sparse transfer matrix. Inf. Sci. 2023, 623, 56–69. [Google Scholar] [CrossRef]
- García-Durán, A.; Dumančić, S.; Niepert, M. Learning sequence encoders for temporal knowledge graph completion. arXiv 2018, arXiv:1809.03202. [Google Scholar]
- Wu, J.; Cao, M.; Cheung, J.C.K.; Hamilton, W.L. Temp: Temporal message passing for temporal knowledge graph completion. arXiv 2020, arXiv:2010.03526. [Google Scholar]
- Bai, L.; Zhang, M.; Zhang, H.; Zhang, H. FTMF: Few-shot temporal knowledge graph completion based on meta-optimization and fault-tolerant mechanism. World Wide Web 2023, 26, 1243–1270. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Zhang, B.; Ren, H. Each snapshot to each space: Space adaptation for temporal knowledge graph completion. In International Semantic Web Conference; Springer International Publishing: Cham, Switzerland, 2022; pp. 248–266. [Google Scholar]
- Wang, Z.; Du, H.; Yao, Q.; Li, X. Search to Pass Messages for Temporal Knowledge Graph Completion. arXiv 2022, arXiv:2210.16740. [Google Scholar]
- Bai, L.; Ma, X.; Meng, X.; Ren, X.; Ke, Y. RoAN: A relation-oriented attention network for temporal knowledge graph completion. Eng. Appl. Artif. Intell. 2023, 123, 106308. [Google Scholar] [CrossRef]
- Yan, C.; Zhao, F.; Jin, H. Exkgr: Explainable multi-hop reasoning for evolving knowledge graph. In International Conference on Database Systems for Advanced Applications; Springer International Publishing: Cham, Switzerland, 2022; pp. 153–161. [Google Scholar]
- Ding, Z.; Ma, Y.; He, B.; Tresp, V. A simple but powerful graph encoder for temporal knowledge graph completion. arXiv 2022, arXiv:2112.07791. [Google Scholar]
- Chinnasamy, P.; Sathya, K.B.S.; Jebamani, B.J.A.; Nithyasri, A.; Fowjiya, S. Deep Learning: Algorithms, Techniques, and Applications—A Systematic Survey. In Deep Learning Research Applications for Natural Language Processing; IGI Global: Hershey, PA, USA, 2023; pp. 1–17. [Google Scholar]
- Shang, C.; Tang, Y.; Huang, J.; Bi, J.; He, X.; Zhou, B. End-to-end structure-aware convolutional networks for knowledge base completion. Proc. AAAI Conf. Artif. Intell. 2019, 33, 3060–3067. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, R.; Dai, H.; Wang, Y.; Song, L. Know-evolve: Deep temporal reasoning for dynamic knowledge graphs. In Proceedings of the ICML’17: Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3462–3471. [Google Scholar]
- Messner, J.; Abboud, R.; Ceylan, I.I. Temporal knowledge graph completion using box embeddings. Proc. AAAI Conf. Artif. Intell. 2022, 36, 7779–7787. [Google Scholar] [CrossRef]
- Chen, K.; Wang, Y.; Li, Y.; Li, A. Rotateqvs: Representing temporal information as rotations in quaternion vector space for temporal knowledge graph completion. arXiv 2022, arXiv:2203.07993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).