Macro–Micro-Coupled Simulations of Dilute Viscoelastic Fluids
Abstract
1. Introduction
2. Governing Equations
2.1. Macroscopic Flow Equations
- The Reynolds number, , which is the ratio of inertial to viscous forces.
- The ratio of the solvent to total zero-shear viscosity: .
- The Deborah number, , which is the ratio of the fluid relaxation time to a characteristic time for the macroscopic flow. Note that in the case of viscometric flow, in which , this is also referred to as the Weissenberg number.
2.2. Constitutive Equations for Extra Stress
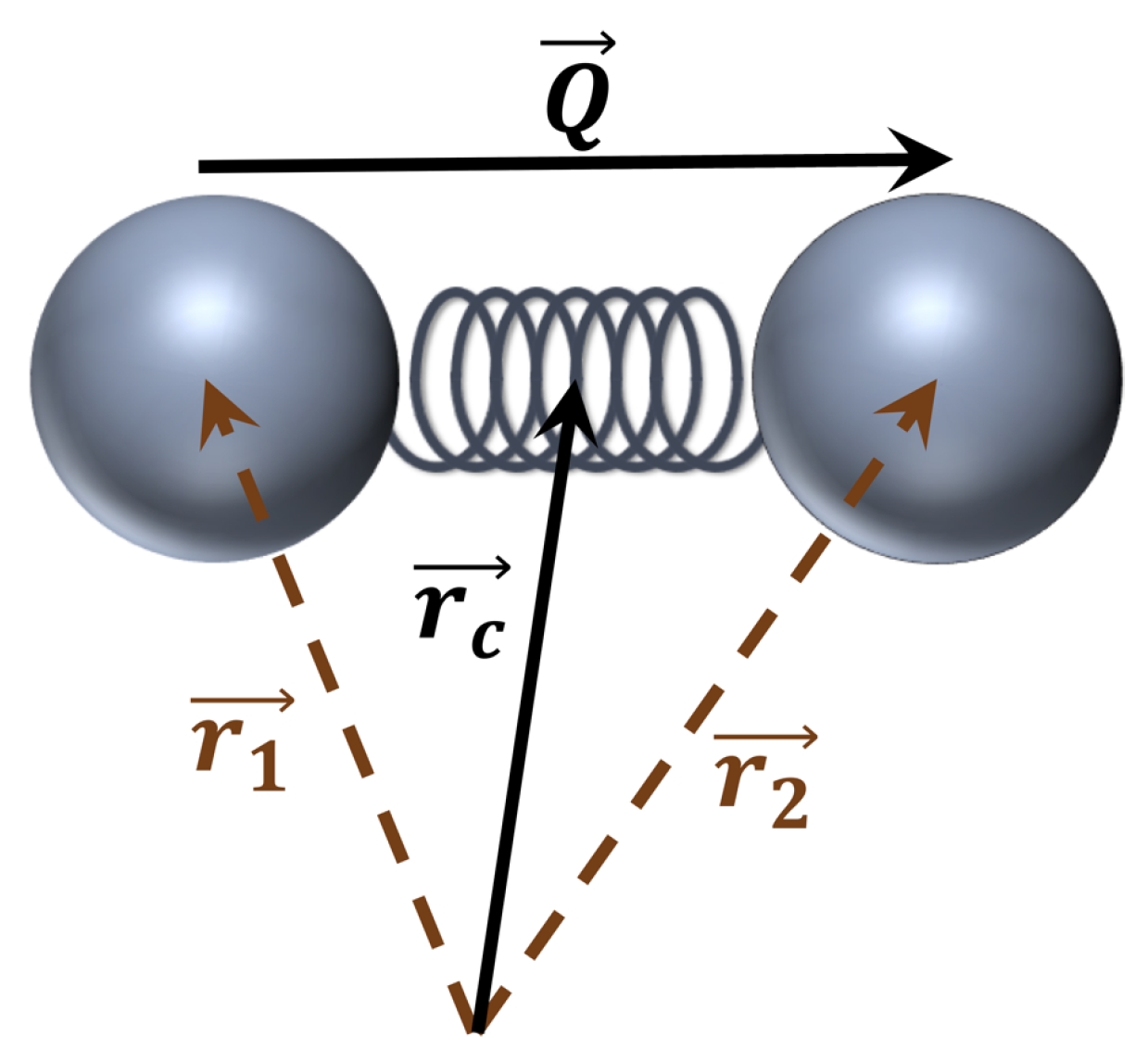
2.2.1. Microscopic Description—Dumbbell Models
- Hookean dumbbells:For Hookean dumbbells, a linear form is assumed for the spring force, , where H is the spring constant. With this, Equations (5) and (6) becomeThese equations are scaled using Equation (3) and the characteristic microscopic length,With these,In addition, the longest relaxation time is defined asThe resulting non-dimensional equations are thenwhere the Deborah number is defined as before, .
- FENE DumbbellsIf instead of a linear spring connector a finitely extensible spring is considered, we obtain FENE-type models. These models are derived by introducing Warner’s finitely extensible nonlinear connector force law [15],where and is the maximum allowed extension of the dumbbell.Introducing this spring law into Equation (5) and non-dimensionalizing as before giveswhere the nonlinear FENE parameters are .
2.2.2. Macro-Constitutive Equations—Closure Models
- Upper convected Maxwell model:If the spring is linear (Hookean), where , the resulting constitute equation obtained from Equation (14) is known as the upper convected Maxwell (UCM) modelUsing the same scaling as before leads to the following non-dimensional constitutive equations:
- FENE-P modelIn a FENE model, with the spring law given by Equation (12), the evolution equation, Equation (14), becomesDifferent FENE models can be formulated based on the approximation used to calculate the second term in Equation (18). Here, we focus on the FENE-P model, which is obtained by the approximationWith this approximation, the constitutive equations becomeScaling as before, we obtainFor convenience, one can define the non-dimensional configuration tensor, , aswhere is the mean-square end-to-end spring length at equilibrium (absence of flow) and d is the dimensionality [15].Note that if we scale the end-to-end vector as before, we haveIn addition, traceThe constitutive equation for in two dimensions is
2.3. Numerical Considerations
- Parameter values: Unless otherwise noted, the parameter values used in the simulations are given in Table 1.
| Parameter | Symbol—Eqn | Units | Value | Ref. |
|---|---|---|---|---|
| Density | kg/m | 1000 | ||
| Solvent viscosity | Pa s | 0.001 | ||
| Zero shear rate viscosity | Pa s | 0.0037 | [33] | |
| Characteristic relaxation time | s | 0.010 | [34] | |
| Characteristic velocity | m/s | 0.260 | ||
| Characteristic length | L | m | 0.003 | |
| Surface tension | N/m | 0.070 | [34] | |
| Initial jet radius | m | 0.001 | [34] | |
| Reynolds number | Dimensionless | 78 | ||
| Ratio of viscosities | Dimensionless | 0.270 | ||
| Deborah number | Dimensionless | 0.800 | ||
| Ohnesorge number | Dimensionless | 0.038 | ||
| FENE parameter | b | Dimensionless | ||
| Wavenumber | k | Dimensionless | 0.8 |
2.3.1. Hookean Dumbbells
2.3.2. FENE Dumbbells
3. Results
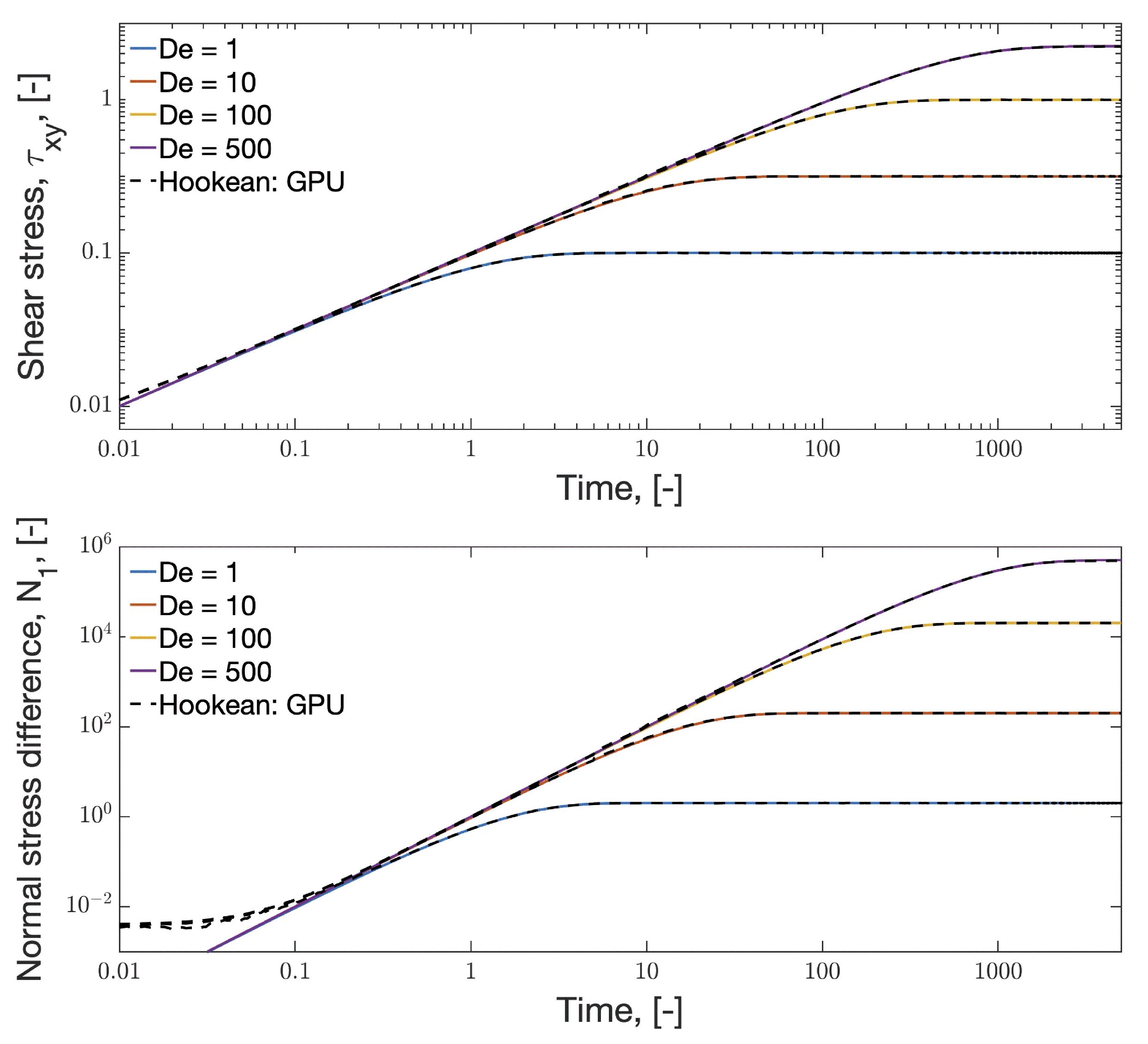
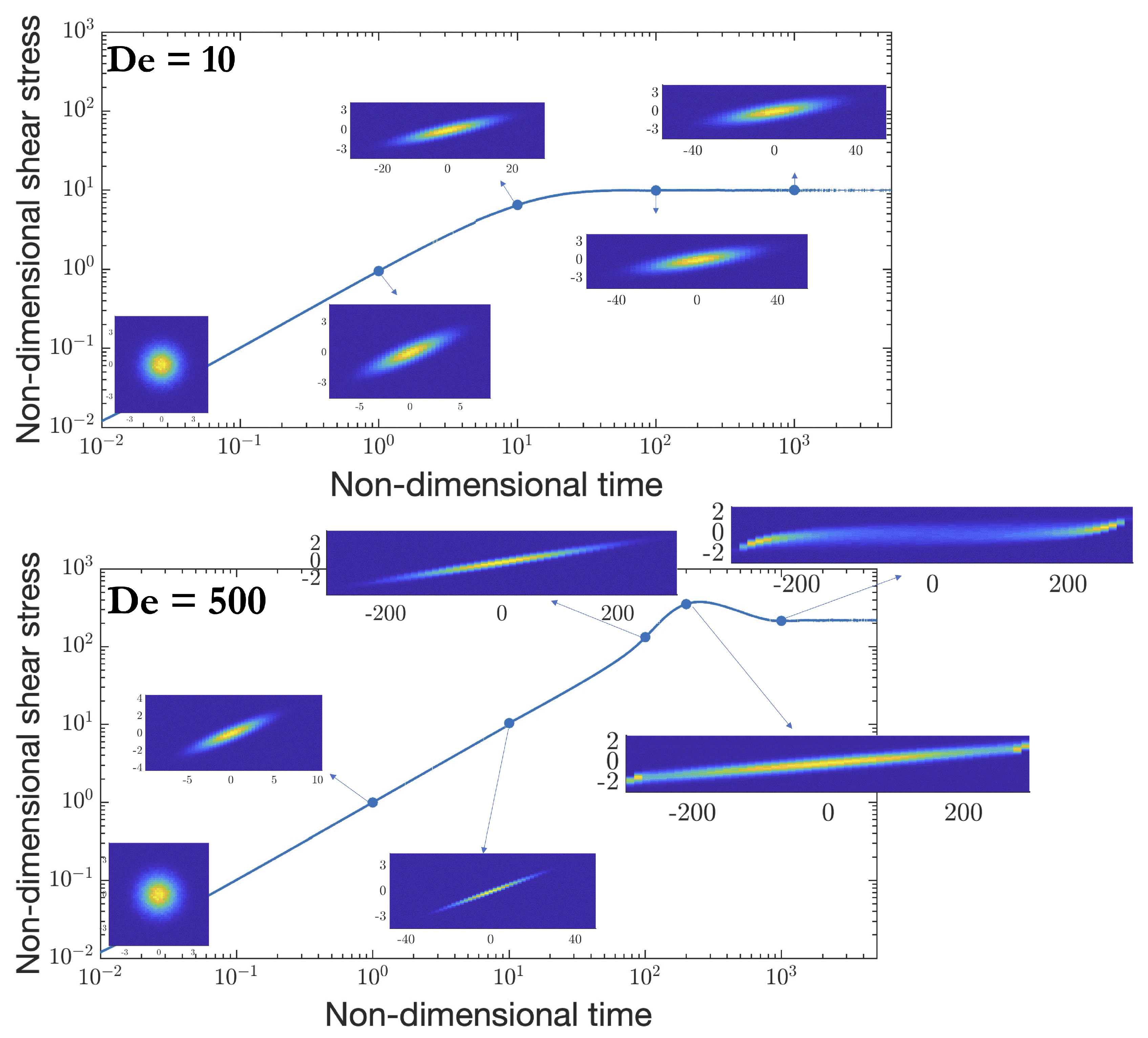
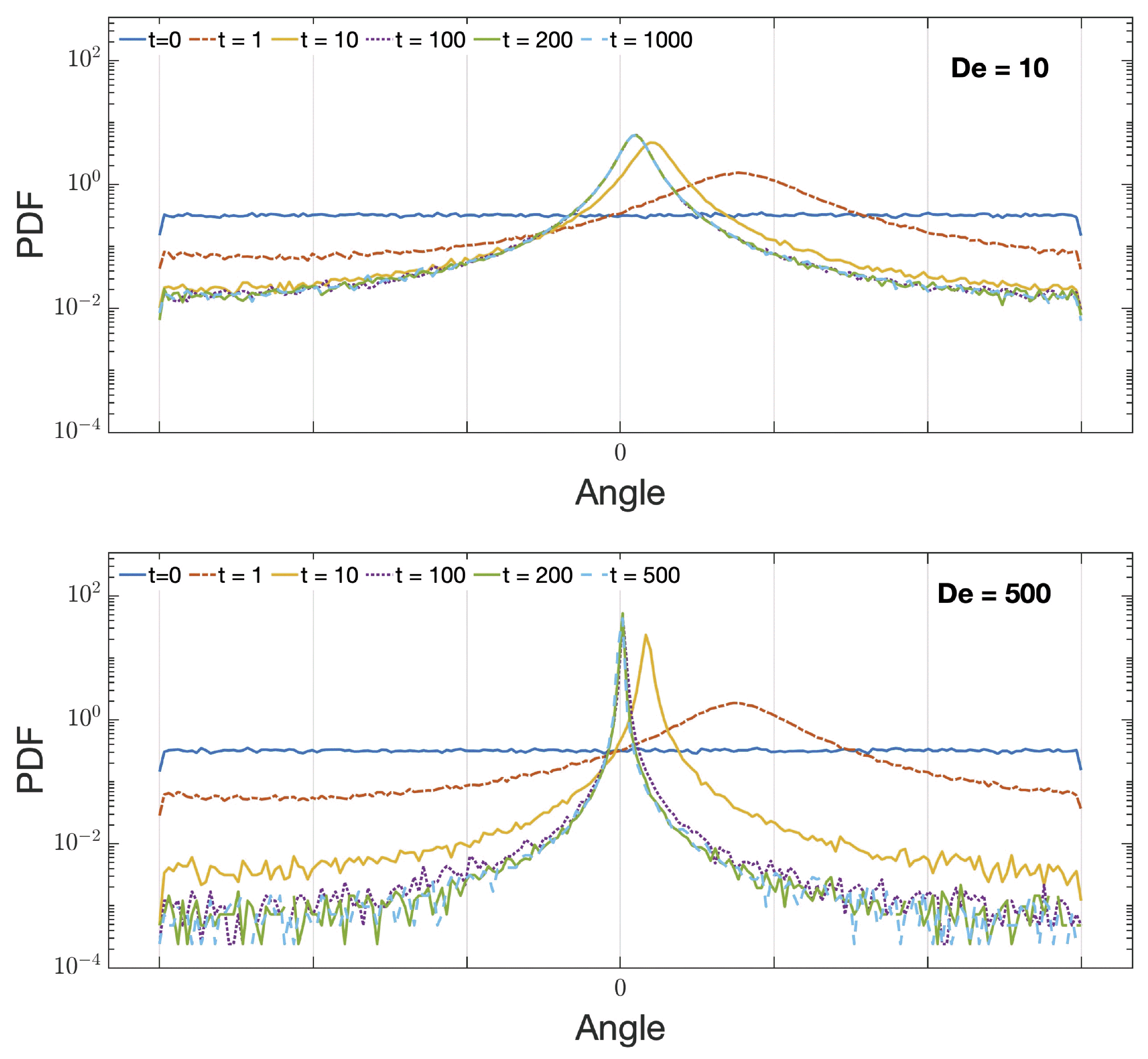
3.1. Simple Shear
3.2. Elongational Flow
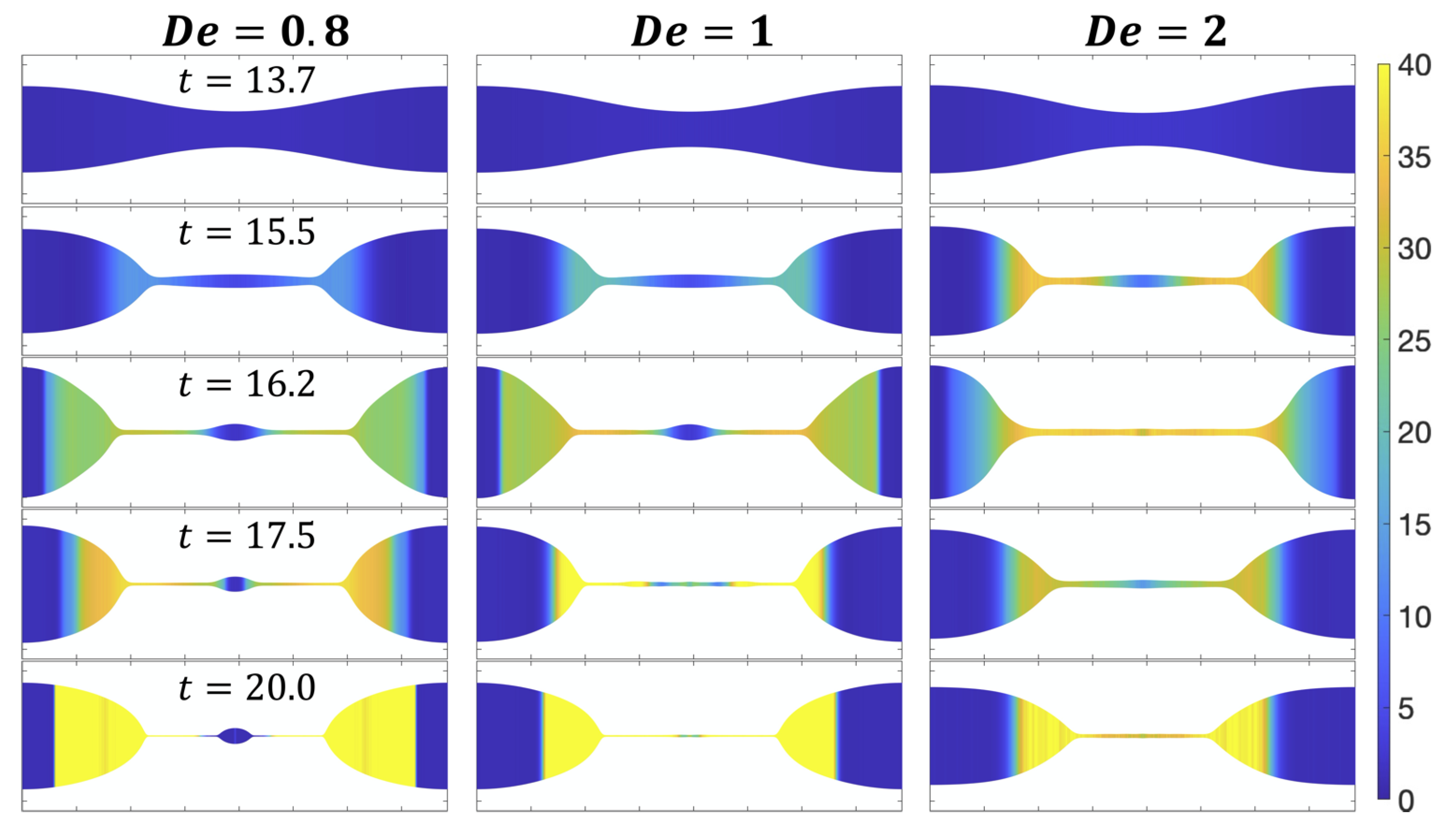
3.3. Capillary Thinning
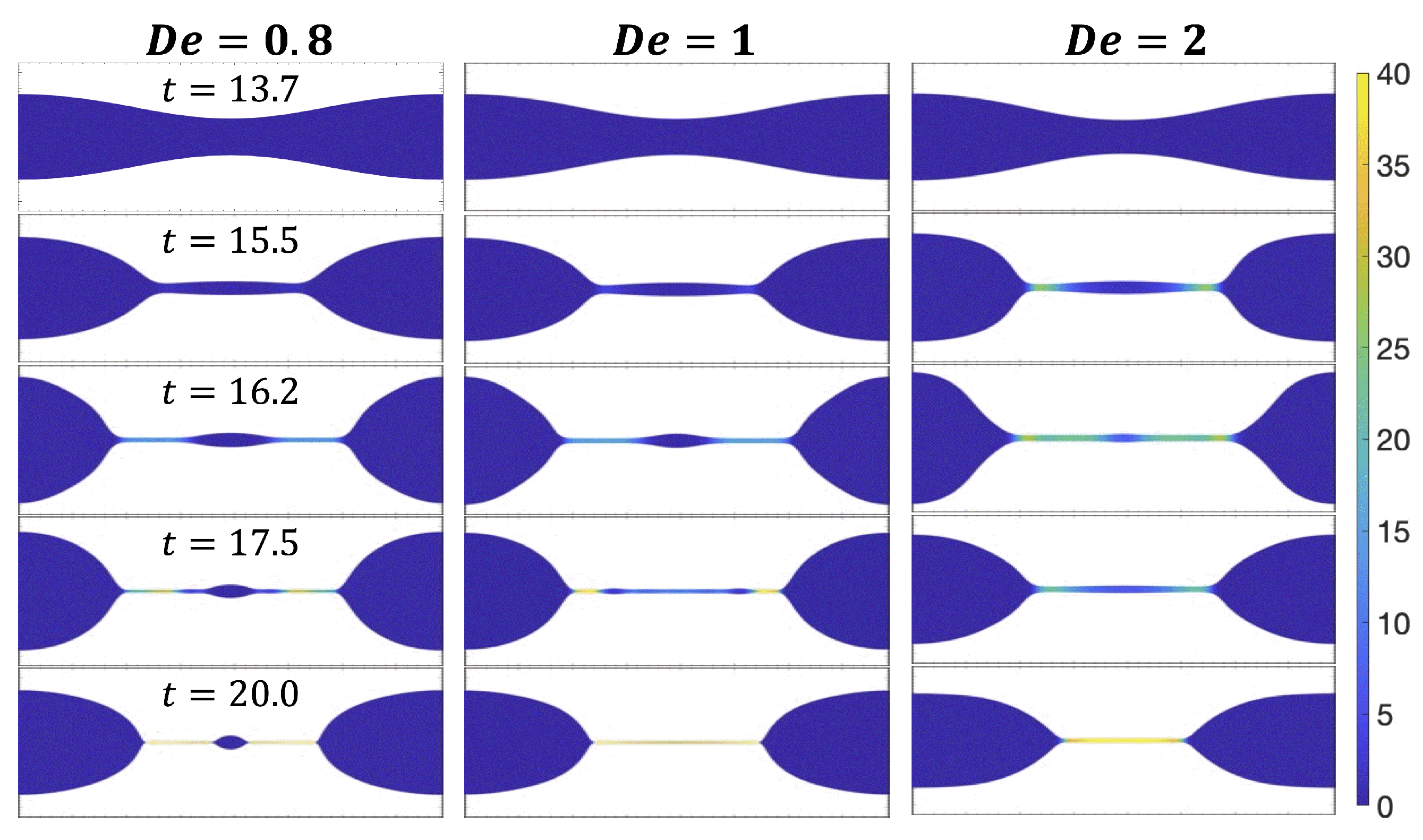
3.3.1. Deborah Number
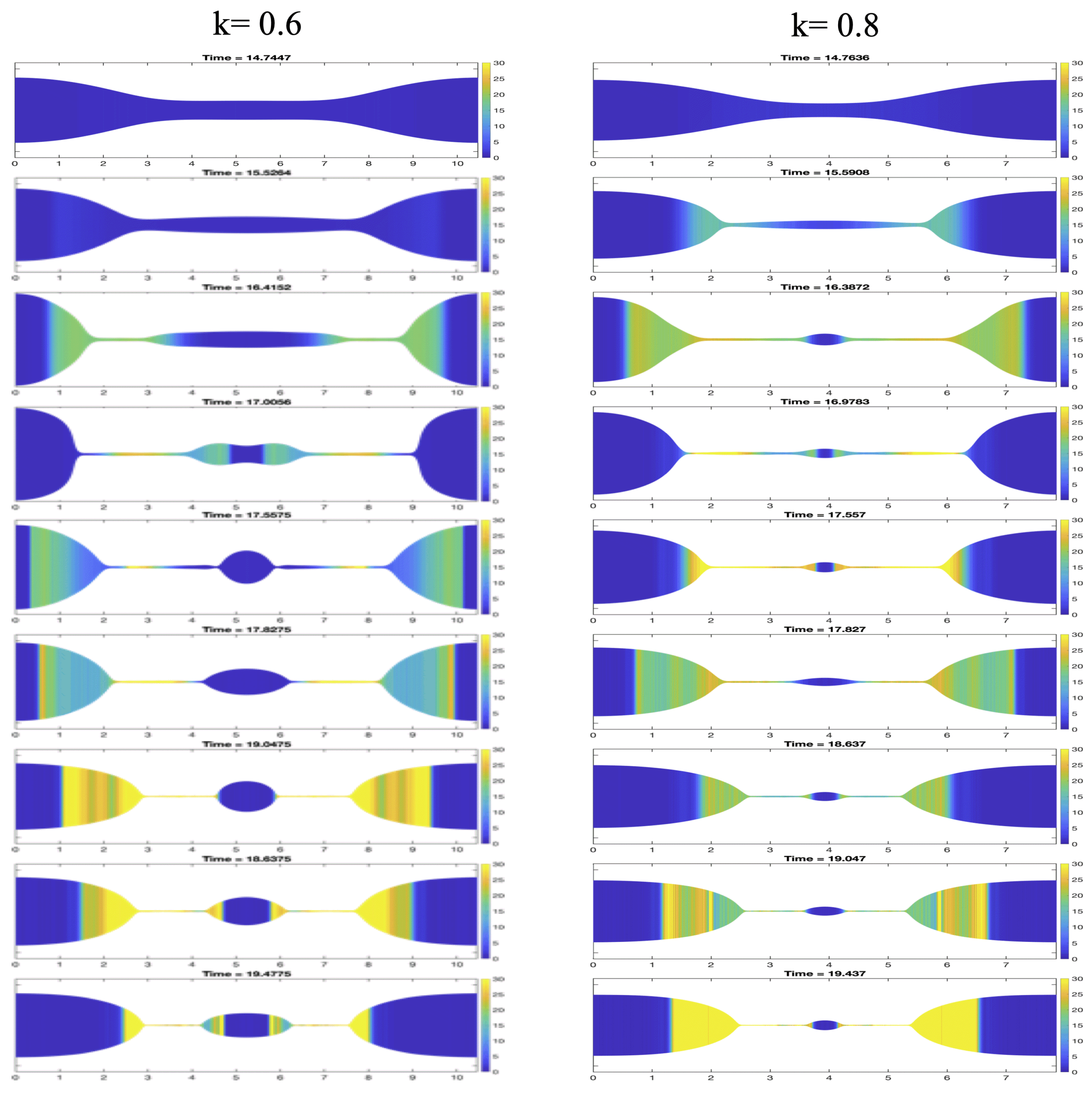
3.3.2. Wavelength
3.3.3. Nonlinear FENE Parameter
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Flow Diagram
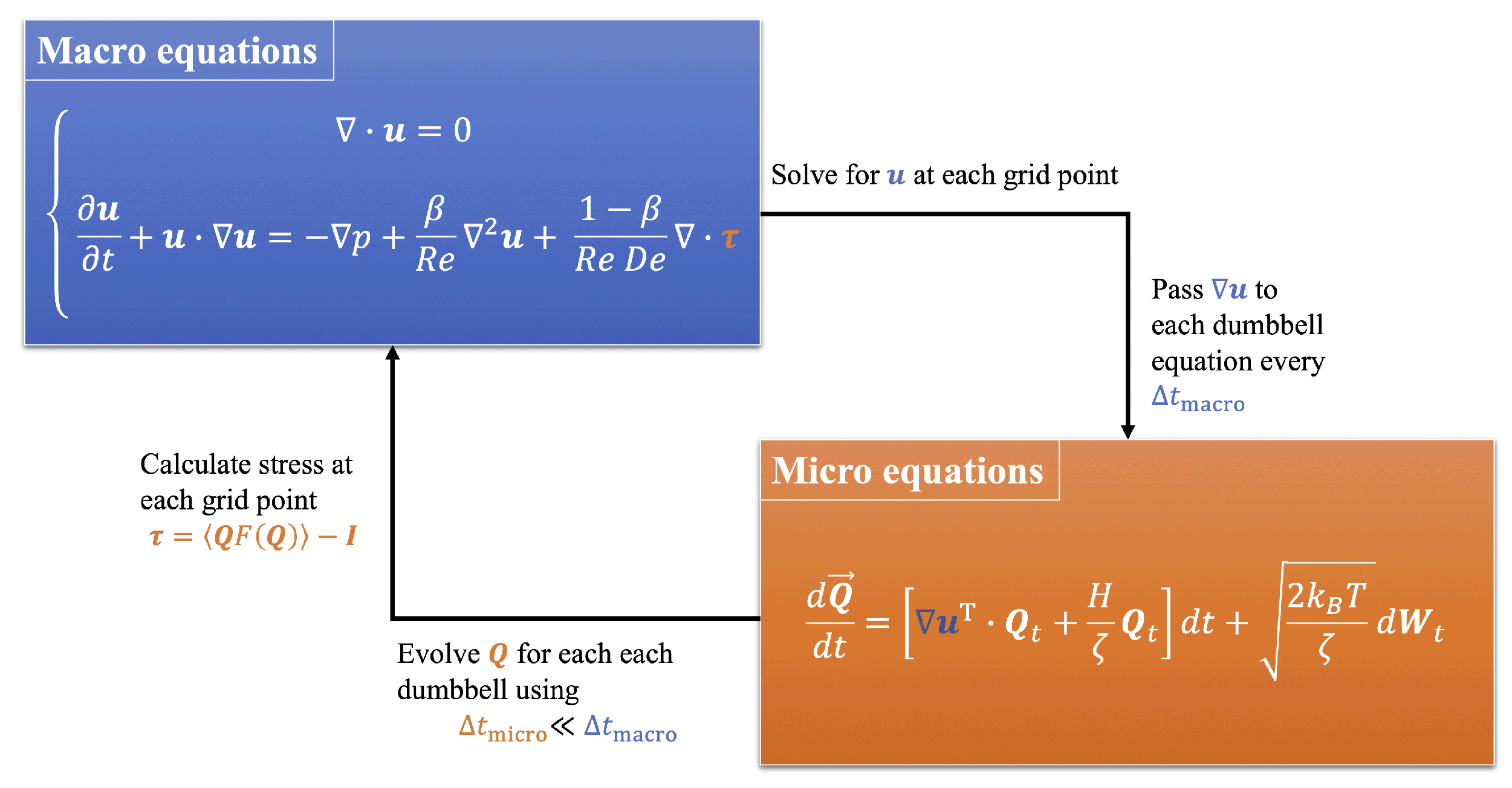
Appendix A.2. Computational Resources
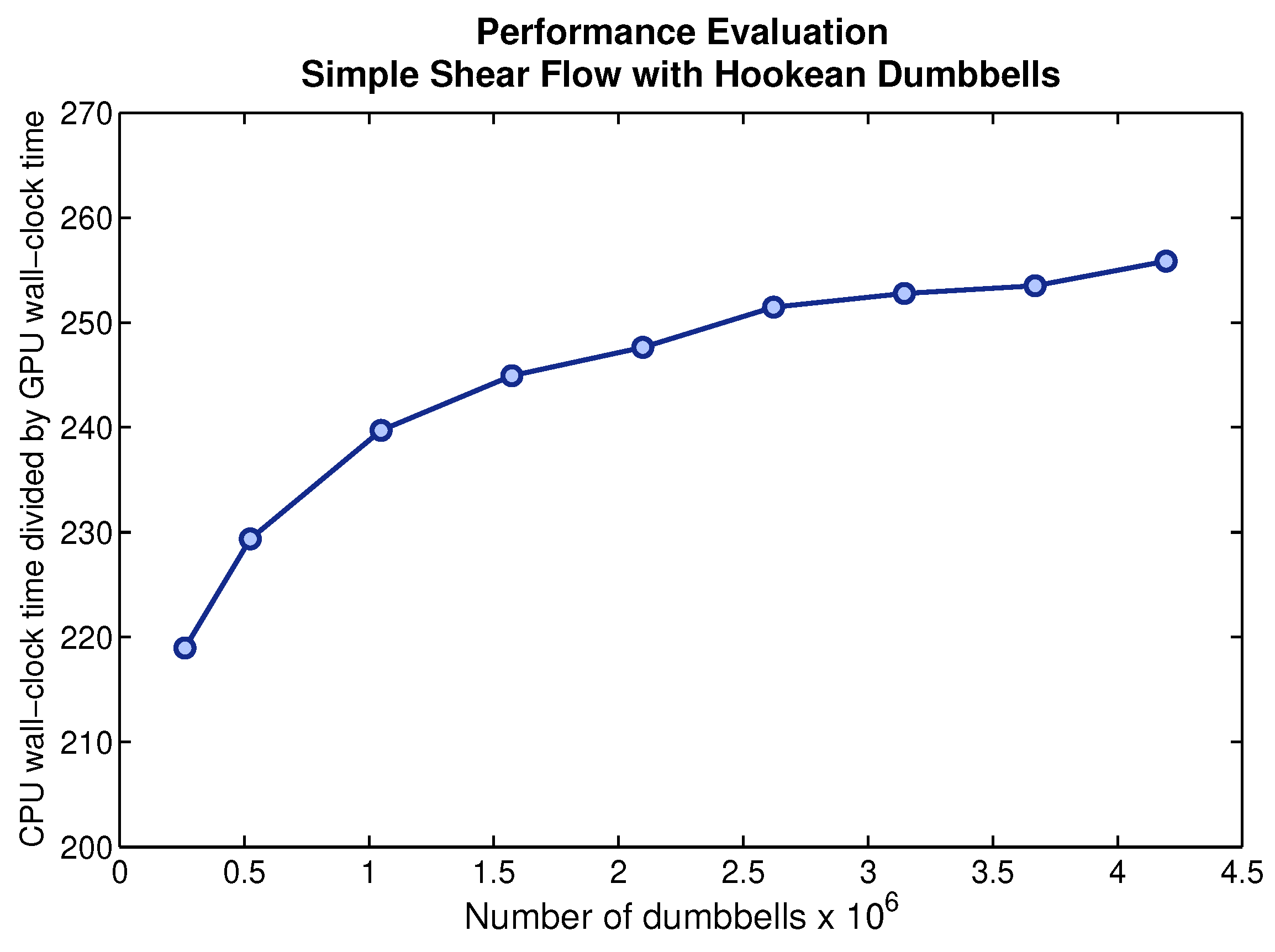
Appendix A.3. Capillary Thinning Results Using FENE-P Model
References
- Hutchings, I.; Tuladhar, T.; Mackley, M.; Vadillo, D.; Hoath, S.; Martin, G. Links between ink rheology, drop-on-demand jet formation, and printability. J. Imaging Sci. Technol. 2009, 53, 1–8. [Google Scholar] [CrossRef]
- Krishnan, J.; Deshpande, A.; Kumar, P. Rheology of Complex Fluids; Springer: New York, NY, USA, 2010. [Google Scholar]
- Ulery, B.; Nair, L.; Laurencin, C. Biomedical applications of biodegradable polymers. J. Polym. Sci. Part Polym. Phys. 2011, 49, 832–864. [Google Scholar] [CrossRef] [PubMed]
- Barbati, A.; Desroches, J.; Robisson, A.; McKinley, G. Complex fluids and hydraulic fracturing. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 415–453. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Patanwala, H.; Bognet, B.; Ma, A. Inkjet and inkjet-based 3D printing: Connecting fluid properties and printing performance. Rapid Prototyp. J. 2017, 23, 562–576. [Google Scholar] [CrossRef]
- Ewoldt, R.; Saengow, C. Designing complex fluids. Annu. Rev. Fluid Mech. 2022, 54, 413–441. [Google Scholar] [CrossRef]
- Reith, D.; Mirny, L.; Virnau, P. GPU Based Molecular Dynamics Simulations of Polymer Rings in Concentrated Solution: Structure and Scaling. Prog. Theor. Phys. Suppl. 2011, 191, 135–145. [Google Scholar] [CrossRef]
- José dos Santos Brito, C.; Vieira-e-Silva, A.L.B.; Almeida, M.W.S.; Teichrieb, V.; Marcelo Xavier Natario Teixeira, J. Large Viscoelastic Fluid Simulation on GPU. In Proceedings of the 2017 16th Brazilian Symposium on Computer Games and Digital Entertainment (SBGames), Curitiba, Brazil, 2–4 November 2017; pp. 134–143. [Google Scholar] [CrossRef]
- Ingelsten, S.; Mark, A.; Jareteg, K.; Kádár, R.; Edelvik, F. Computationally Efficient Viscoelastic Flow Simulation Using a Lagrangian-Eulerian Method and GPU-acceleration. J. Non-Newton. Fluid Mech. 2020, 279, 104264. [Google Scholar] [CrossRef]
- Yang, K.; Su, J.; Guo, H. GPU accelerated numerical simulations of viscoelastic phase separation model. J. Comput. Chem. 2012, 33, 1564–1571. [Google Scholar] [CrossRef]
- Bergamasco, L.; Izquierdo, S.; Ammar, A. Direct numerical simulation of complex viscoelastic flows via fast lattice-Boltzmann solution of the Fokker–Planck equation. J. Non-Newton. Fluid Mech. 2013, 201, 29–38. [Google Scholar] [CrossRef]
- Gutierrez-Castillo, P.; Kagel, A.; Thomases, B. Three-dimensional viscoelastic instabilities in a four-roll mill geometry at the Stokes limit. Phys. Fluids 2020, 32, 023102. [Google Scholar] [CrossRef]
- Schram, R.; Barkema, G. Simulation of ring polymer melts with GPU acceleration. J. Comput. Phys. 2018, 363, 128–139. [Google Scholar] [CrossRef]
- Behbahani, A.; Schneider, L.; Rissanou, A.; Chazirakis, A.; Bacova, P.; Jana, P.; Li, W.; Doxastakis, M.; Polinska, P.; Burkhart, C. Others Dynamics and rheology of polymer melts via hierarchical atomistic, coarse-grained, and slip-spring simulations. Macromolecules 2021, 54, 2740–2762. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Alves, M.; Oliveira, P.; Pinho, F. Numerical Methods for Viscoelastic Fluid Flows. Annu. Rev. Fluid Mech. 2021, 53, 509–541. [Google Scholar] [CrossRef]
- Cruz, C.; Chinesta, F.; Régnier, G. Review on the Brownian Dynamics Simulation of Bead-Rod-Spring Models Encountered in Computational Rheology. Arch. Comput. Methods Eng. 2012, 19, 227–259. [Google Scholar] [CrossRef]
- Keunings, R. Micro-Macro Methods for the Multiscale Simulation of Viscoelastic Flow Using Molecular Models of Kinetic Theory. Rheol. Rev. 2004, 2004, 67–98. [Google Scholar]
- Owens, R.G.; Phillips, T.N. Computational Rheology; World Scientific: Singapore, 2002. [Google Scholar]
- Walters, K.; Webster, M.F. The Distinctive CFD Challenges of Computational Rheology. Int. J. Numer. Methods Fluids 2003, 43, 577–596. [Google Scholar] [CrossRef]
- Feigl, K.; Laso, M.; Oettinger, H.C. CONNFFESSIT approach for solving a two-dimensional viscoelastic fluid problem. Macromolecules 1995, 28, 3261–3274. [Google Scholar] [CrossRef]
- Halin, P.; Lielens, G.; Keunings, R.; Legat, V. The Lagrangian Particle Method for Macroscopic and Micro–Macro Viscoelastic Flow Computations. J. Non-Newton. Fluid Mech. 1998, 79, 387–403. [Google Scholar] [CrossRef]
- Le Bris, C.; Lelievre, T. Micro-macro models for viscoelastic fluids: Modelling, mathematics and numerics. Sci. China Math. 2012, 55, 353–384. [Google Scholar] [CrossRef]
- Lozinski, A.; Owens, R.G.; Phillips, T.N. The Langevin and Fokker–Planck Equations in Polymer Rheology. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2011; Volume 16, pp. 211–303. [Google Scholar] [CrossRef]
- Xu, X.; Yu, P. A multiscale SPH method for simulating transient viscoelastic flows using bead-spring chain model. J. Non-Newton. Fluid Mech. 2016, 229, 27–42. [Google Scholar] [CrossRef]
- Bhave, A.V.; Armstrong, R.C.; Brown, R.A. Kinetic theory and rheology of dilute, nonhomogeneous polymer solutions. J. Chem. Phys. 1991, 95, 2988–3000. [Google Scholar] [CrossRef]
- Herrchen, M.; Öttinger, H.C. A detailed comparison of various FENE dumbbell models. J. Non-Newton. Fluid Mech. 1997, 68, 17–42. [Google Scholar] [CrossRef]
- Chase, D.; Cromer, M. Roles of chain stretch and concentration in capillary thinning of polymer solutions. Fluid Dyn. Res. 2023; in revision. [Google Scholar]
- Öttinger, H.C. Stochastic Processes in Polymeric Fluids: Tools and Examples for Developing Simulation Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Öttinger, H.C.; Van Den Brule, B.; Hulsen, M. Brownian configuration fields and variance reduced CONNFFESSIT. J. Non-Newton. Fluid Mech. 1997, 70, 255–261. [Google Scholar] [CrossRef]
- Jourdain, B.; Le Bris, C.; Lelièvre, T. On a variance reduction technique for micro–macro simulations of polymeric fluids. J. Non-Newton. Fluid Mech. 2004, 122, 91–106. [Google Scholar] [CrossRef]
- Bonvin, J.; Picasso, M. Variance reduction methods for CONNFFESSIT-like simulations. J. Non-Newton. Fluid Mech. 1999, 84, 191–215. [Google Scholar] [CrossRef]
- Bertola, V. Dynamic wetting of dilute polymer solutions: The case of impacting droplets. Adv. Colloid Interface Sci. 2013, 193, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ardekani, A.; Sharma, V.; McKinley, G. Dynamics of bead formation, filament thinning and breakup in weakly viscoelastic jets. J. Fluid Mech. 2010, 665, 46–56. [Google Scholar] [CrossRef]
- Prieto, J.L.; Bermejo, R.; Laso, M. A semi-Lagrangian micro–macro method for viscoelastic flow calculations. J. Non-Newton. Fluid Mech. 2010, 165, 120–135. [Google Scholar] [CrossRef][Green Version]
- Lee, E.C.; Solomon, M.J.; Muller, S.J. Molecular orientation and deformation of polymer solutions under shear: A flow light scattering study. Macromolecules 1997, 30, 7313–7321. [Google Scholar] [CrossRef]
- Ghosh, I.; McKinley, G.H.; Brown, R.A.; Armstrong, R.C. Deficiencies of FENE dumbbell models in describing the rapid stretching of dilute polymer solutions. J. Rheol. 2001, 45, 721–758. [Google Scholar] [CrossRef]
- Li, J.; Fontelos, M.A. Drop dynamics on the beads-on-string structure for viscoelastic jets: A numerical study. Phys. Fluids 2003, 15, 922–937. [Google Scholar] [CrossRef]
- Clasen, C.; Eggers, J.; Fontelos, M.A.; Li, J.; McKinley, G.H. The beads-on-string structure of viscoelastic threads. J. Fluid Mech. 2006, 556, 283–308. [Google Scholar] [CrossRef]
- Bhat, P.P.; Appathurai, S.; Harris, M.T.; Pasquali, M.; McKinley, G.H.; Basaran, O.A. Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 2010, 6, 625–631. [Google Scholar] [CrossRef]
- Wagner, C.; Bourouiba, L.; McKinley, G.H. An analytic solution for capillary thinning and breakup of FENE-P fluids. J. Non-Newton. Fluid Mech. 2015, 218, 53–61. [Google Scholar] [CrossRef]
- Eggers, J. Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 1997, 69, 865. [Google Scholar] [CrossRef]
- Forest, M.G.; Wang, Q. Change-of-type behavior in viscoelastic slender jet models. Theor. Comput. Fluid Dyn. 1990, 2, 1–25. [Google Scholar] [CrossRef]
- Guzel, A.; Layton, W. Time filters increase accuracy of the fully implicit method. BIT Numer. Math. 2018, 58, 301–315. [Google Scholar] [CrossRef]
- Middleman, S. Stability of a viscoelastic jet. Chem. Eng. Sci. 1965, 20, 1037–1040. [Google Scholar] [CrossRef]
- Goldin, M.; Yerushalmi, J.; Pfeffer, R.; Shinnar, R. Breakup of a laminar capillary jet of a viscoelastic fluid. J. Fluid Mech. 1969, 38, 689–711. [Google Scholar] [CrossRef]
- Brenn, G.; Liu, Z.; Durst, F. Linear analysis of the temporal instability of axisymmetrical non-Newtonian liquid jets. Int. J. Multiph. Flow 2000, 26, 1621–1644. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cromer, M.; Vasquez, P.A. Macro–Micro-Coupled Simulations of Dilute Viscoelastic Fluids. Appl. Sci. 2023, 13, 12265. https://doi.org/10.3390/app132212265
Cromer M, Vasquez PA. Macro–Micro-Coupled Simulations of Dilute Viscoelastic Fluids. Applied Sciences. 2023; 13(22):12265. https://doi.org/10.3390/app132212265
Chicago/Turabian StyleCromer, Michael, and Paula A. Vasquez. 2023. "Macro–Micro-Coupled Simulations of Dilute Viscoelastic Fluids" Applied Sciences 13, no. 22: 12265. https://doi.org/10.3390/app132212265
APA StyleCromer, M., & Vasquez, P. A. (2023). Macro–Micro-Coupled Simulations of Dilute Viscoelastic Fluids. Applied Sciences, 13(22), 12265. https://doi.org/10.3390/app132212265






