Abstract
In public places, pedestrian panic behaviors have received increasing attention due to their dangerous impact on normal pedestrian flow. To address this issue, this study considered crowd panic behaviors as two-dimensional Gaussian disturbances quantitatively triggered by accidents and analyzed the stability of the pedestrian crowd based on Lyapunov criterion. First, this study established a two-dimensional static model for the disturbance pressure in a crowd. Then, a dynamic disturbance–propagation model (DPM) of crowd panic behaviors was proposed based on the conservation law of fluid dynamics. The anisotropy of the disturbance pressure propagation was proven with theoretical derivations and simulation experiments, which kept consistent with ground truth. Further, a stability criterion was proposed for pedestrian crowd flow under disturbances based on Lyapunov theory. To validate the proposed DPM, we simulated a disturbance scenario in the waiting hall of Shanghai Hongqiao Railway Station. Subsequently, the visual disturbance propagation dynamics and crowd state evolution due to a panic behavior disturbance in a pedestrian crowd were investigated; Finally, the experimental results demonstrated that disturbance pressures and pedestrian density fluctuated and diffused with the panic behavior outbreak point as the disturbance center, showing heterogeneous characteristics. This study shows how we can locate the high-risk areas affected by pedestrian panic behaviors in advance, and further help control crowd flow to keep a pedestrian crowd safe in public buildings.
1. Introduction
The scientific management of crowd-gathering scenarios is a significant issue regarding public safety. Using physics, transportation, and mathematical tools to describe the characteristics of a crowd flow, crowd flow dynamics has been a well-known academic hotspot for several decades. It comprises the processes of establishing a mathematical model of a crowd flow and then carrying out numerical simulations and solving them.
There were some similarities between crowd flows and continuous fluids. Since Swiss mathematician and mechanics scientist Euler proposed a classical assumption for fluid continuity [1], the irregular thermal motion of molecules in a fluid were simplified as the regular motion of the molecules; i.e., the fluid was considered as a continuous medium. Then, fluids were mainly studied based on a macro-mechanical motion theory of a continuous medium.
In general, a crowd flow consists of pedestrians, with physical gaps between them. From a micro point of view, crowd flows are not continuously distributed, but if the distance between pedestrians and the surrounding environment is defined as a pedestrian area, it is feasible to assume a crowd flow as a continuous pedestrian fluid. Therefore, like the continuum hypothesis in fluid dynamics, the macroscopic quantities of crowd flows are the velocities, densities, and flows, which also conform to the physical laws of mass conservation, momentum conservation, and energy conservation. Henderson first proposed a macroscopic model for pedestrian flow [2,3]..
It was shown that the distribution functions for crowd densities and velocities were consistent with the results from the Maxwell–Boltzmann theory, except for significant deviations near the frequency mode of each distribution [3]. Henderson further proposed a hydrodynamic model of a pedestrian crowd, in which a particle collision was used to describe the interactions between macroscopic pedestrian groups [3]. Hughes considered pedestrian flow as a continuous fluid medium and used fluid dynamics equations to describe the relationships between the speed, density, and flow rate of pedestrians. According to references [4,5], a typical macro dynamic model for the field of crowd flows is established in the form of Equation (1).
where represents the horizontal velocity, and represents the lateral velocity.
Most studies on macro crowd flow used this crowd flow model in Equation (1) as their primary theory base. This model assumed that the behaviors of the crowds were homogeneous, i.e., that crowds make approximately the same responses under the same stimulus; however, this was not sufficiently realistic in practice.
In real pedestrian-gathering scenarios, the panic behavior characteristics of crowd flows were relatively complex. Due to the subjective initiatives of the crowds and external environments, once internal panic disturbances due to emergencies such as pedestrian falls, stampedes, shootings, terrorist attacks, explosions, and fires occur, the stop-and-go phenomena of crowds can cause a chaotic phenomenon of the sudden acceleration and deceleration of pedestrians. In this context, more complex crowd trampling and other accidents often easily occur [5].
It was significant to keep a pedestrian crowd stable considering that a large-scale crowd (including more than 2000 pedestrians) system consisted of a large number of autonomous individual pedestrians, movement rules, and the scene environment [6]. As a continuous flow, a large-scale crowd flow also had three typical system states: stability, critical stability, and instability.
Large-scale crowd trample disasters were typical phenomena of crowd instability owing to internal disturbances. Most of the existing literature about crowd stability is based on traffic flow theory and lacks systematic consideration. The panic characteristics of pedestrian self-organization behaviors and crowd-merging flow layouts make crowd flows more complex, while few studies have been conducted on the propagation characteristics of sudden panic disturbances in crowd flows, which motivate us to study this issue further.
The main contributions of this study are the following: (1) we propose a dynamic disturbance model of crowd panic behaviors, considering the anisotropy of crowd movements based on the conservation law of fluid dynamics; (2) the anisotropy property of the disturbance propagation is proven with theoretical derivations and simulation experiments; (3) a crowd stability criterion is put forward under internal disturbances based on Lyapunov theory.
The outline of this paper is as follows: in Section 2, we investigate the related work with a literature survey; in Section 3, we propose a dynamic disturbance model of crowd panic behaviors; in Section 4, we analyze the stability of crowd flow considering disturbances due to panic behaviors; in Section 5, simulation experiments conducted in the waiting hall of Shanghai Hongqiao Railway Station to validate the proposed DPM are presented.
2. Related Work
2.1. Internal Disturbances of Drowd Panic Behaviors
In general, pedestrian panic behaviors are trigged by dangerous emergencies including pedestrian falls, stampedes, shootings, terrorist attacks, explosions, and fires. The crowd will change rapidly from an orderly and stable state into a disordered and chaotic state in the case of these emergencies. In most cases, the disturbance is caused by the physical environment or by pedestrian panic behaviors (running under scattering) in crowd-intensive locations. These panic behaviors, acting as the disturbance center points, probably change a stable pedestrian crowd into a disordered state.
At present, there are relatively few systematic studies on the modeling of internal disturbances in a crowd flow; the existing studies are scattered among fields such as biological populations, human disasters, and traffic flows, for example, in order to investigate the causes of crowd disasters and propose preventive measures and possible methods for mitigating disasters, J. J. Fruin stated that turbulent waves were experienced in dozens of crowd-intensive events each year all over the world [7]. Once a pedestrian was able to pass the narrowing, pedestrians with the same walking direction can easily follow. Hence, the number and “pressure” of waiting, “pushy” pedestrians on one side of the bottleneck becomes less than on the other side [8]. Pascal and Levin [9] described the interactions of disturbance distributions in a real biological population, which were considered temporal, nonlinear, and random. The disturbances were affected by the crowd density. With an increase in pedestrian density, the sensitivity to interference increased. Lu [10] regarded a crowd as a continuous medium considering that any disturbance in the crowd would spread in the form of waves.
J. Ma [11] studied a crowd disaster in Germany from the perspective of crowd flow patterns. The results showed that the force generated by physical contact between pedestrians led to unstable movements, and the disturbed crowd velocity characteristics fluctuated and diffused, finally forming crowd turbulence. W. Qin [12] constructed a distributed parameter system to describe the disturbed crowd dynamics based on the conservation law of mass. Unit sliding mode control was used to eliminate disturbances and stabilize the crowd dynamic system to a reference density. J. Wei [13] improved the social force model by introducing disturbance fluctuation force, to characterize the disturbance fluctuation of pedestrian flow caused by the disturbance during evacuation and the state of change in pedestrian flow.
Most of the macro-crowd flow models above were established based on conservation law. G. Grinstein [14] pointed out that a system with conservation deterministic dynamics has noise interference and requires spatial anisotropy to describe the self-organized criticality. In summary, as triggers of unstable crowd flow and stampede disasters, internal disturbances due to pedestrian panic behaviors were random and complex. Research on pedestrian disturbance dynamics and the disturbance propagation remains challenging but meaningful, which motivates us to focus on the dynamic disturbance model of pedestrian panic behaviors and Lyapunov-based crowd stability analysis.
2.2. Stability Analysis for Crowd Flow
Investigations on crowd flows began later than those on traffic flows; as such, there are relatively few studies on crowd stability, most of which are based on theories of traffic flow stability analysis, such as boundary control, sliding mode control, and feedback control [15,16,17]. However, owing to the stochastics of crowd movement without expected lanes in vehicle traffic, it is more complex to study crowd flow stability than only traffic flow stability. The existing research methods of macro crowd flow stability remain in the initial stages and can be mainly divided into four categories: methods based on statistical analysis, methods based on computer vision, methods based on control theory, and methods based on mathematical calculation, as shown below.
(1) Methods based on statistical analysis. These methods rely on data collection, literature retrieval, and statistical analysis of past crowd disaster events, aiming to explore the unstable factors of the crowds and to provide advice on crowd management. The Guide to Safety at Sports Grounds (the “Green Guide”) in the United Kingdom established a safety standard for pedestrian crowds based on experience analysis. It considered a crowd with a density between 4 p/m2 and 7 p/m2 as a crowd in a critical state [18]. Jaime Santos Reyes and Samuel Olmos-Peña Santos and Olmos [19] analyzed the stampede in Mexico City on 20 June 2008. The management oversight risk tree technique and the FIST model have also been proposed and can be used to analyze and extract the unstable and fatal factors in a disaster. In 2021, Y. Feng [20] systematically reviewed 145 studies and found that although the instability factors of pedestrian behaviors in traditional emergency situations (i.e., free traffic accidents) have been widely studied, new high-risk situations (such as earthquakes, terrorist attacks, and stampedes) have not received sufficient attention.
(2) Methods based on computer vision. Using optical flow theory, the movement characteristics of a crowd can be according to abnormal behaviors. At present, a variety of anomaly detection algorithms have been proposed for crowded scenes, such as abnormal crowd behavior detection [21,22], human abnormal action detection [23], and traffic event detection [24]. However, this type of abnormal event detection method is only suitable for small-and medium-sized crowds, the scene equipment cost is large, and the calculations are complex.
(3) Methods based on control theory. A group interaction matrix has been used to qualitatively predict group behaviors, and the stability of the system was analyzed to determine whether the system structure was reasonable. In general, if a system has high stability, it is reasonable, and if the system has low stability, it is necessary to adjust the system structure to reduce the conflict(s) in the evacuation process. W. Qin [25] established a cold dynamics model based on a conservation law, and the relationship between density and speed was expressed using a diffusion model. The feedback linearization method of a partial differential equation was used to design a feedback controller for controlling crowd stability so that pedestrians could evacuate in a certain direction and at a fixed speed. S. A. Wadoo [26] designed nonlinear feedback controllers for providing convection, diffusion, and convection/diffusion control, and discussed the control stability using partial differential equations. Based on a study of fluid dynamics and traffic flow, W. Qin [27] designed a time-limited controller for solving the finite time-tracking problem, and for making the density converge to a given steady-state density.
(4) Methods based on mathematical deduction. In one example of these methods, based on fluid dynamics and traffic flow theory, a conservation equation for macro crowd flow dynamics is established, and the stability of a crowd flow is analyzed using the system stability judgment theory. Q. Wang [6] studied the stability of a crowd system based on the determination method of the M-matrix and the Perron Frobenius theorem. S. Mukherjee [28] proposed a crowd dynamics modeling method based on the Lagrange method, which considered various forces exerted by the crowd members, constructed an appropriate Lyapunov energy function, and proved the stability of the established motion system. In modern mathematical models describing group systems, the Lyapunov method is the primary and most effective method for analyzing the stability of a complex system, whether linear or nonlinear. Most of the research on group systems is based on the Lyapunov method, i.e., analyzing and judging the stability of the system [29].
Among the four methods above, the following points can be made: (1) in statistical analysis-based methods, most of the achievements comprise qualitative crowd management guidance conclusions; (2) computer vision-based methods are generally only suitable for small and medium-sized crowd flow scenes, owing to the high cost of monitoring equipment and complex calculations; and (3) for approaches based on control theory, it is necessary to construct a controller to control the external scene, such as exit numbers and indicator signs, to achieve crowd stability control; moreover, without considering the evolution of internal disturbances, the influence of internal disturbances on the stability of crowds cannot be explained in depth; in contrast, (4) a mathematical derivation method is a systematic approach, which is based on a macro crowd flow model and generally uses the Lyapunov stability determination method to quantitatively analyze crowd flows; it can deeply explore the characteristics of disturbance propagation dynamics and the evolution characteristics of crowd flow stability in crowd flow scenes.
3. Dynamic Disturbance Model of Crowd Panic Behaviors
In fact, a point in the crowd movement area will be disturbed when sudden changes in some physical environment or sudden changes in pedestrian behavior occur. These cause the crowd flow to gradually change from a stable and orderly state to a chaotic unstable state, and these key points are referred to as perturbation points. According to the formation principle of a crowd-disturbing point, such points can be divided into mutation-disturbing points and release-disturbing points [30,31]. Among them, a mutation-disturbing point is a sudden abnormal behavior inside a crowd of pedestrians; it mainly manifests as abnormal postures, expressions, and voices.
Abnormal postures are the most conductive and harmful and include pedestrian speed mutations, pedestrian U-turns, pedestrian falls, disease assistance, group fights, and violent terrorist attacks. These types of abnormalities can easily cause massive disturbing forces in the crowd, thereby disturbing an originally stable crowd flow. A release disturbance point corresponds to external disturbance factors such as insufficient numbers of entrances and exits in crowded places, insufficient numbers of passageways, or evacuation passageways and stairs in inappropriate places, leading to limited crowd flow movements. Release disturbances are generally discussed before the establishment of the scenarios. For public places already in use, sudden pedestrian abnormal behavior disturbances are worthier of attention. Moreover, based on statistics, mutant crowd disturbances are more likely to lead to serious crowd accidents. The disturbances discussed in this paper are mutation disturbance points, that is, they represent disturbance forces suddenly generated in a crowd.
3.1. Dynamic Model of Internal Crowd Disturbance
In time domains, the dynamic behavior of a sudden internal disturbance of a crowd is similar to a sudden white noise disturbance in the crowd movement. Its randomness cannot be completely expressed by deterministic variables but can be expressed by a stochastic process. However, the numerical solutions of stochastic equations and the inherent mathematical complexity of stochastic calculus are challenging problems. Based on a probability density function, a Langevin equation can be used to describe the turbulent velocity of fluid particles, which is modeled as Brownian motion. Initially, this equation was applied to homogeneous and isotropic turbulence. The Brownian motion model was widely used in internal random disturbance modeling.
If the random process with value R satisfies the following properties:
(1) The orbit is almost necessarily continuous:
(2) For any and Borel set
where if , then is called the standard Brownian motion. The standard Brownian motion satisfies a Gaussian distribution. For the sake of simplicity, this study only considers the disturbances of single pedestrian behaviors, so the probability distribution of the random disturbance intensity can be expressed by a single Gaussian function. Figure 1a shows the two-dimensional Gaussian distributions of four groups of different expectation values (mu) and standard deviations (sigma). Figure 1b shows the standard three-dimensional Gaussian distribution when the expectation value is 0 and the standard deviation is 5.
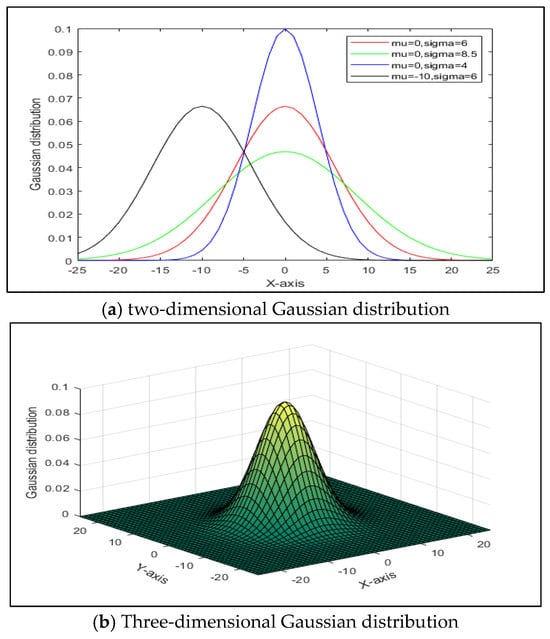
Figure 1.
Standard Gaussian distribution.
When a crowd moves forward in a crowded state, it will produce a certain “pressure” among the crowd. In this study, the crowd is regarded as fluid, and a crowd flow model is established based on fluid dynamics. Therefore, the pressure among a crowd can be established according to the characteristics of fluid dynamics, as shown in Equation (4) as follows:
Here, is a pressure factor. In the case of sudden abnormal situations occurring in crowds, such as pedestrian falls and terrorist attacks, a disturbing force will be produced and disturb the balanced crowd flow; this can be directly assumed as the change in “pressure” among the crowd. To construct the dynamic model of a disturbance caused by an abnormal behavior in a pedestrian crowd, we assumed that the disturbance burst point is , then the crowd pressure at this point is the largest, and the crowd pressure around it decays exponentially in the form of e, with same character of a Gaussian distribution in Figure 1. This result showed a single disturbance without damping from the neighboring pedestrians. Therefore, under the influence of random disturbances in the crowd, an equivalent pressure at can be defined as follows:
Here is the pedestrian density, is the power of density, is the pressure intensity coefficient of the random disturbance, is the position of the disturbance center, and is the duration of a disturbance burst. Therefore, the equivalent pressure is a comprehensive and dimensionless definition considering the pedestrian density, scenario-based pressure intensity, disturbance propagation time, and two-dimensional layout of observed measurement points.
3.2. Dynamic Disturbance Model of Crowd Panic Behaviors
The Hughes crowd flow model, as shown in Equation (1), is widely used in the study of crowd macro flows. However, the crowd behavior represented by the Hughes model is homogeneous; that is, it assumes that pedestrians make the same responses under the same stimuli. In reality, as affected by individual subjective consciousness, pedestrian movements exhibit evident acceleration inconsistencies. For example, the rear crowd can directly observe the movement changes of the front crowd, and then change their movement characteristics. However, the front crowd cannot see the rear crowd, so the front crowd is hardly disturbed by the rear crowd, reflecting the anisotropy of crowd disturbance propagation. Therefore, in addition to the hyperbolic conservation equation shown in Equation (1), another equation is needed to reflect the anisotropy of crowd disturbance propagation.
Pedestrian acceleration, velocity, and density, as the three basic motion variables, have complex nonlinear couplings, but meet the basic momentum conservation. Therefore, many scholars in fluid mechanics have proposed second equation models based on momentum conservation. Aw and Rascle used a convection derivative to replace the spatial derivative of “pressure” in a second-order model, and developed the Aw–Rascle prediction (AR) model, thereby improving the non-physical characteristics pointed out by Daganzo [32]. The AR model is a typical anisotropic traffic flow model.
In this study, based on the AR model and the proposed crowd disturbance pressure as shown in Equation (5), a propagation dynamic model for the internal disturbance of a crowd is established, as shown in Equations (6)–(8).
where represent the horizontal and lateral equilibrium velocities, respectively; these are represented by the steady-state relationship between velocity and density (fundamental diagrams). is a relaxation factor. , are the horizontal and lateral crowd disturbance pressures, as shown in Equations (9) and (10).
3.3. Proof of Anisotropy of Dynamic Disturbance Model
As mentioned above, the anisotropy of pedestrians determines that the propagation of internal disturbances in crowd movement is anisotropic. The proof of the anisotropy of the model is given below.
The propagation dynamic model of an internal disturbance of a crowd can be expressed in a conservation form as shown in Equation (11).
here, the conserved vector, , , and .
Therefore, the eigenvalues in the horizontal and lateral directions of Equations (6)–(8) are shown in Equation (12).
It is evident that the characteristic velocity of the propagation dynamic model of the internal disturbance of the crowd is less than or equal to the macroscopic fluid velocity . Daganzo indicated that a continuum model with a characteristic velocity greater than the macroscopic fluid velocity is not heterogeneous. Moreover, it is difficult to demonstrate the nonphysical effects of vehicle flows in some cases. Crowd flows based on hydrodynamics have the same properties. The characteristic velocity of the model proposed in this study is not greater than the macroscopic fluid velocity; therefore, the model is anisotropic.
4. Stability Analysis of Crowd Flow Considering Internal Disturbances
4.1. Lyapunov-Based Crowd Stability Analysis
The definition of crowd stability based on Lyapunov is as follows. Assume that the equilibrium flow of the macro crowd flow model is . The disturbance flow is . If the spatial gradient of the disturbance flow is bounded, then the propagation of the crowd flows is stable under the disturbance of , i.e., and at , . is the whole region of the crowd movement scenario. In addition, when and , the propagation of the equilibrium flow is asymptotically stable.
Based on the above definition of crowd stability, this study uses the wavefront theory in fluid dynamics to express the crowd disturbance propagation, as shown in Figure 2 [33]. The equilibrium state of the crowd flow is disturbed suddenly at position . The wavefront propagation curve of crowd flow is shown in Figure 2.
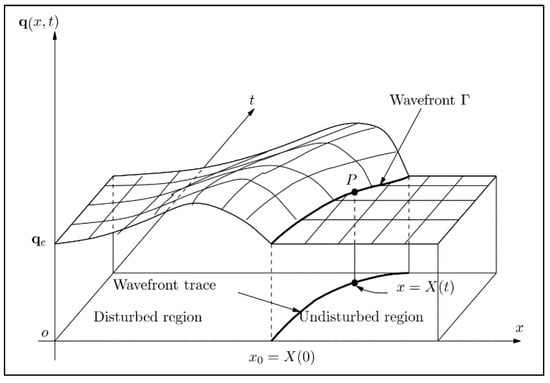
Figure 2.
Wavefront of crowd disturbance propagation.
If the crowd flow system is stable, then the initial disturbance will not increase in the process of its propagation, and will gradually disappear; that is, the wavefront curve of the disturbance flow is bounded. However, if the crowd flow system is unstable, the disturbed flow wave may increase in the propagation process and eventually form a shock wave or bottleneck in the crowd flow scenario.
4.2. Stability Analysis of Crowd Flow with Internal Disturbance
Based on the wavefront theory, the nonlinear dynamic model of crowd disturbance propagation, that is, Equations (6)–(8), are linearized, and then the stability of crowd flow is analyzed based on Lyapunov.
It is assumed that internal disturbances occur in the equilibrium state . The initial solutions of Equations (6)–(8) are and . First, the solutions of the equations near the wavefront are expanded by the power series, as follows:
Here, is the location of the wavefront at time . Because the wavefront is the boundary of the disturbance influence range under the crowd equilibrium state, the eigenvalue method remains valid near the wavefront. Thus, the derivatives of and Y can be obtained using the eigenvalues, as follows:
According to Equation (13), we can obtain the power series expansions of , , and as follows:
where , , , . Therefore, the partial derivatives of , and are as follows:
Similarly, the partial derivatives of the pressure term and equilibrium velocities are obtained as follows:
here, , , , , , , , , and , .
By substituting Equations (16)–(29) into Equations (6)–(8) and retaining the previous two terms and , we can obtain the following formulas:
In the above equations, . Substituting Equation (30) into Equation (32) yields the following:
We can see that the coefficients of and are linearly independent, and can be estimated by Equations (31) and (33). It can be concluded from Equation (30) that , which is substituted into Equations (31) and (33) to obtain the Bernoulli equation, as follows:
here, and .
Assuming that in Figure 2, is the slope of the wavefront at position P. The solution of the Bernoulli equation is . Therefore, the Bernoulli equation can show the evolution of the wavefront slope. In the case of a disturbance, generally, the crowd density increases sharply and the crowd velocity decreases sharply, , and , , so the stable range is . Then, we can determine the followings:
here, “-” indicates the direction, and is the relaxation factor. Let . is the critical acceleration function, and is related to the disturbance pressure in the crowd. Substituting into yields the following:
Therefore, the stability criterion of the horizontal crowd flow can be obtained as follows:
Similarly, the stability criterion of the lateral crowd flow can be obtained as follows:
5. Experiments and Discussion
5.1. Numerical Simulation for Dynamic Model of Disturbance Propagation in a Crowd
To reveal the characteristics of internal disturbance propagation in a crowd and verify the anisotropy of the proposed dynamic model, numerical examples were implemented. Using the numerical analysis method of crowd flow described in reference [34] and the MATLAB R2022a simulation tool, a simulation scenario with internal disturbance propagation in a crowd was simulated.
The simulation scenario was a 30 m × 30 m square area with a 10 m-wide exit at the top and a 5 m × 5 m square obstacle at the bottom left of the scene. In the lower half of the square space, pedestrians were waiting to be evacuated. The maximum crowd equilibrium state was , . The pressure between the crowd in the equilibrium state was . The initial disturbance pressure intensity was generated by a sudden disturbance at position P(20,5).
The simulation stopped when the pressure of observation point P reached the maximum value of 7, indicating with a yellow color, at the step = 150. The specific characteristics of the propagation of the disturbance pressure are shown in Figure 3. The contour color indicates the intensity of the disturbance pressure and point P in Figure 3 indicates the burst point of the disturbance pressure in the crowd. We can see from Figure 3 that the sudden disturbance pressure of the crowd fluctuates and spreads with the crowd movements. Moreover, the pressure gradient of the crowd near the obstacle is large.
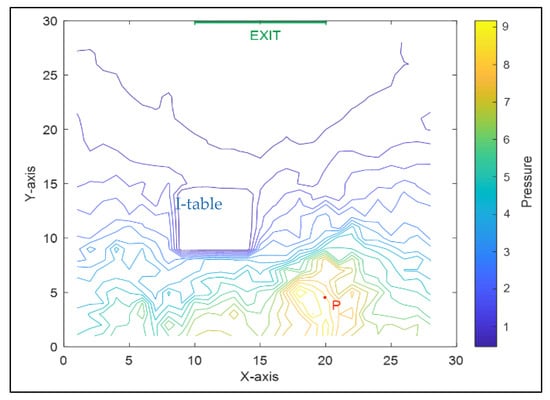
Figure 3.
Internal disturbance pressure propagation of crowd around I-table (information table as a block in a waiting hall). Note: pressure is a dimensionless parameter defined in Equation (5).
In reality, the pressure propagation of a crowd flow is anisotropic. Using the same numerical analysis method, a crowd flow based on the Hughes model was constructed. The crowd density distribution in the scenario when the simulation step was equal to 150 is shown in Figure 4, where the contour color indicates the crowd density. Comparing Figure 3 and Figure 4, the simulation results of the proposed dynamic model for disturbance propagation in the crowd indicate that the upstream crowd is greatly affected by the disturbance of the downstream population, reflecting the anisotropy of the pressure propagation.
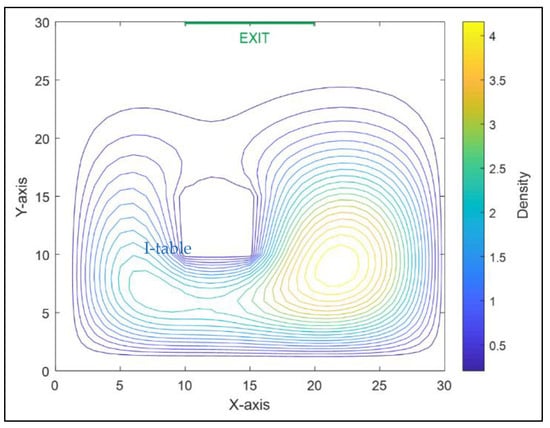
Figure 4.
Crowd density distribution based on Hughes crowd flow model (information table as a block in a waiting hall).
5.2. Discussion on the Critical Stability Function
The critical stability function of the crowd stability criterion proposed in this study is inversely proportional to the crowd density; that is, the larger the crowd density, the smaller the critical stability value of the crowd. In other words, to maintain the stability of the crowd, the denser the crowd, the stricter the required control of pedestrian acceleration, which is consistent with reality. It is worth noting that the value of the critical stability function in the criterion should vary with the duration of the disturbance and distance from the disturbance center [35,36].
First, the influence of the disturbance duration on the stability of the crowd flow is discussed. According to the reference [37], assuming that the pedestrian walking acceleration range is , then Equation (39) takes , , .
The relationship between the critical stability function and duration of the disturbance is shown by the blue line in Figure 5. Assuming that the maximum allowable acceleration of the studied scenario is , the relationship between the probability of crowd flow instability and the disturbance duration is obtained, as shown by the red line in Figure 5. It can be seen from Figure 5 that the critical stability function value increases with time, and the instability probability decreases. When the simulation time is 6.87 min, the instability probability is 80%. This shows that the disturbance energy decays and the risk probability of the unstable crowd flow decreases with time.
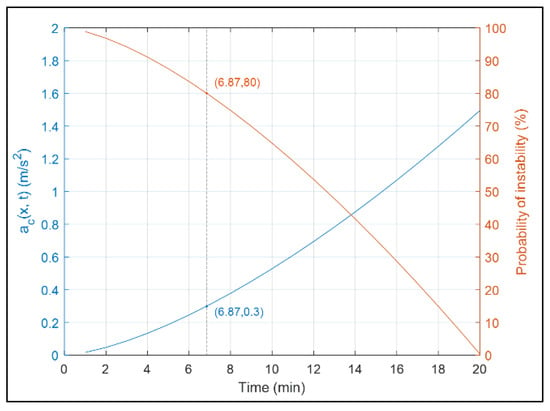
Figure 5.
Relationship between the critical stability function value, the probability of crowd flow instability, and the duration of disturbance outbreak.
Similarly, taking Equation (39) as an example, the influence of the distance from the disturbance center on the critical stability function value and instability probability of the crowd flow is discussed. If , , it can be seen from Figure 5 that the attenuation time of the disturbance is approximately 20 min. Therefore, in Equation (39), t = 20 min, and the abscissa of the disturbance center . The relationship between the distance from the disturbance center and the critical stability function is shown by the blue line in Figure 6. Similarly, assuming that the maximum allowable acceleration of the studied scenario is , the relationship between the distance from the disturbance center and the probability of crowd flow instability is obtained, as shown by the red line in Figure 6. As shown in Figure 6, with the expansion of displacement, the disturbance energy at a certain point fluctuates and spreads, affecting the stability of the surrounding crowd flow. Without considering the influence of the crowd flow direction, the instability probability of the crowd with the disturbance outbreak point as the center whose radius length is between 1.55–8.57 m is greater than 80%. This indicates that in the safety management of crowd flows, an area of approximately 10 m around the disturbance center needs to be specifically guided and controlled.
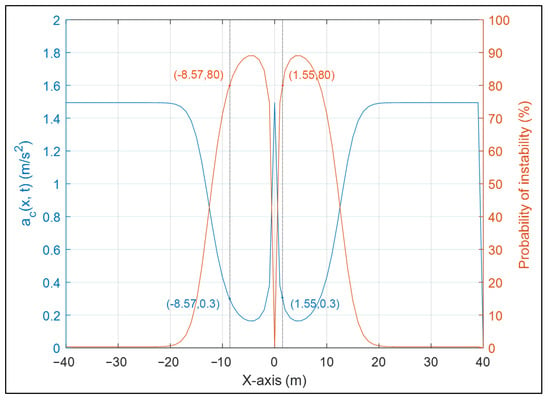
Figure 6.
Relationship between the value of critical stability function, probability of crowd flow instability, and distance from the center of disturbance.
5.3. Experiment and Simulation
In large-scale crowd-gathering places with high crowd densities, unconventional internal disturbances will quickly spread and ferment, which can easily cause large-scale crowd stampedes. Shanghai Hongqiao Railway Station is an integral part of the Shanghai Hongqiao comprehensive transportation hub and one of the largest railway passenger transport hubs in East Asia. The waiting hall of Shanghai Hongqiao Railway Station, as shown in Figure 7, was considered as a case scenario. Based on the hybrid crowd aggregation risk assessment model proposed by our research team [36], we demarcated the high-risk area of the waiting hall as shown in Figure 8. We can see that the crowd aggregation risk for the four major intersections and eight major exits is high.

Figure 7.
Waiting hall of Shanghai Hongqiao Railway Station. Note: captured by Tongji University CIMS group on 30 April 2023. Note: point A is the center of panic disturbance, B is the observer position.
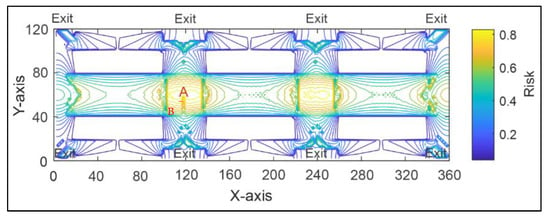
Figure 8.
Distribution of crowd aggregation risk discretion based on the hybrid crowd aggregation risk assessment model. Note: point A is the center of panic disturbance, B is the observer position.
Sudden internal disturbances in high-risk areas were more likely to cause crowd disasters. Among simulation experiments, point A where the crowd converged first reached the peak density, which was the peak risk. Therefore, we focused on the A-centered area (shown as the Information table in Figure 3 and Figure 4). Therefore, this study selected the representative high-risk area intersection A in Figure 8 as the scenario for the case study of the internal disturbance propagation in a crowd and Lyapunov-based crowd stability.
Actual scenario data were obtained from the waiting hall of Shanghai Hongqiao Railway Station. The simulated scenario was a 40 × 40 m rectangular area. It was assumed that the internal disturbance position was (11,11) and that a sudden disturbance occurred when the simulation step was step = 310, i.e., time t = 3.09 min. Special restrictions on the directions of crowd movements were not mentioned in the following experiments. The experiment data were synthesized as follows.
Experiment 1: The initial density of the crowd was set as , and the disturbance pressure ; the propagation of the disturbance pressure and the probability distribution of the crowd flow instability are shown in Figure 9. The Z-axis represents the crowd pressure, and the graph color represents the probability of crowd instability.
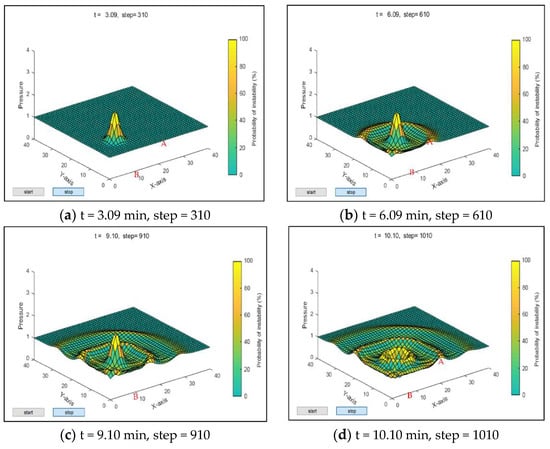
Figure 9.
Propagation of disturbance pressure and probability distribution of crowd flow instability when and Note: point A is the center of disturbance, B is the observer position.
Experiment 2: The initial density of the crowd was still and the disturbance pressure increased to . The propagation of the disturbance pressure and probability distribution of the crowd flow instability are shown in Figure 10.
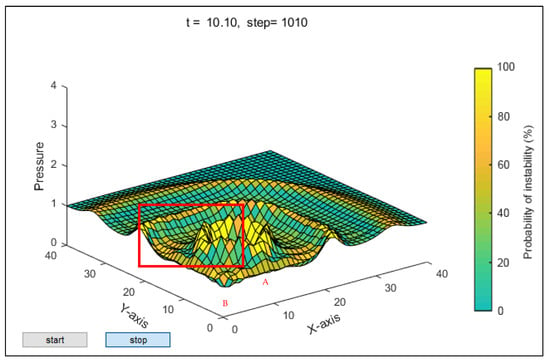
Figure 10.
Propagation of disturbance pressure and probability distribution of crowd flow instability when and . Note: point A is the center of disturbance, B is the observer position.
Experiment 3: The initial density of the crowd was increased to , and the disturbance pressure was still . The propagation of disturbance pressure and probability distribution of the crowd flow instability are shown in Figure 11.
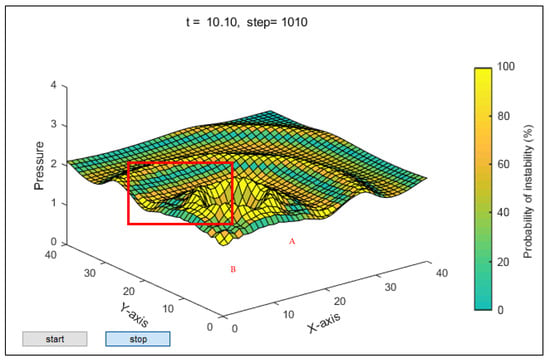
Figure 11.
Propagation of disturbance pressure and probability distribution of crowd flow instability when and . Note: point A is the center of disturbance, B is the observer position.
Based on the three experiments above, we can find that the propagation of the crowd disturbance pressure and changes in crowd stability are based on wave theory, consistent with the indications in the references [10,36,37], i.e., that any disturbance in the crowd will propagate in the form of a wave. Therefore, the panic disturbance pressure in a crowd would be enlarged, then the pedestrian flow direction would be consistent with the current panic disturbance pressure, and vice versa. Comparing Experiment 1 with Experiment 2, it can be seen that when the disturbance pressure is larger, the propagation fluctuation of the crowd disturbance pressure is larger, and the area with a high probability of crowd instability is larger. Experiments 2 and 3 show that when the crowd density is larger, the area with a high probability of crowd instability is larger under the same disturbance. Moreover, from the areas marked by the red boxes in Figure 10 and Figure 11, it can be seen that the three-dimensional curve of the pressure propagation is evidently not smooth, reflecting the anisotropy of disturbance propagation. When the sudden disturbance pressure is large, in the areas with relatively small pressure, the probability of crowd instability is also large. This indicates that crowd stability is a complex problem worthy of further study in the future.
6. Conclusions and Future Work
In this study, a dynamic disturbance model of crowd panic behaviors based on fluid dynamics was proposed to quantitatively investigate the disturbance dynamics of pedestrian panic behaviors. Further, the anisotropy property of this model was proven to keep consistent with the ground truth of real pedestrian movement.
In addition, based on the Lyapunov stability theory, a criterion of crowd stability for sudden internal disturbances was proposed; Experimental results in Hongqiao railway station showed that the equivalent pressure was related to the pedestrian density, duration of the disturbance, and distance from the center of the disturbance. In the Lyapunov-based crowd stability analysis, two main conclusions have been drawn:
(1) The dynamic propagation of panic disturbance pressure in a crowd was mainly affected by the density, direction of flow, and obstacles, indicating the heterogeneous characteristics of the propagation.
(2) Regardless of the limitations on crowd movement directions, the dynamic disturbance of crowd behaviors changed in crowd stability, revealing the characteristics of wave diffusion.
Further work on model calibration based on measured data with more complex scenarios is suggested to be conducted, which can support more pedestrian flow control in public places.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis and investigation, resources, data curation, writing—original draft preparation, C.L., R.Z. and C.H.; writing—review and editing, and visualization, R.A., Q.L. and Y.M.; supervision and project administration, R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 72074170 and No. 23AZD073).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lions, P.L. Mathematical Topics in Fluid Mechanics, 1st ed.; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Henderson, L.F. The statistics of crowd fluids. Nature 1971, 229, 381–383. [Google Scholar] [CrossRef]
- Henderson, L.F. On the fluid mechanics of human crowd motion. Transp. Res. 1974, 8, 509–515. [Google Scholar] [CrossRef]
- Hughes, R.L. The flow of large crowds of pedestrians. Math. Comput. Simul. 2000, 53, 367–370. [Google Scholar] [CrossRef]
- Zhao, R.Y.; Wang, D.; Wang, Y.; Han, C.F.; Jia, P.; Li, C.L.; Ma, Y.L. Macroscopic view: Crowd evacuation dynamics at T-shaped street junctions using a modified Aw-Rascle traffic flow model. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6612–6621. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.B. The research status of the stability of population system and the stability determination method of linear time-varying system. J. Univ. Sci. Technol. Liaoning 2010, 33, 517–524. [Google Scholar]
- Fruin, J.J. Engineering for Crowd Safety; Smith, R.A., Dickie, J.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1993; pp. 99–108. [Google Scholar]
- Helbing, D.; Johansson, A. Pedestrian, Crowd, and Evacuation Dynamics. arXiv 2013, arXiv:1309.1609. [Google Scholar]
- Pascual, M.; Levin, S.A. Spatial Scaling in a Benthic Population Model with Density-Dependent Disturbance. Theor. Popul. Biol. 1999, 56, 106–122. [Google Scholar] [CrossRef]
- Lu, C.X. Analysis on the Wave of Pedestrians. China Saf. Sci. J. 2006, 16, 30–34. [Google Scholar]
- Ma, J.; Song, W.G.; Lo, S.M.; Fang, Z.M. New insights into turbulent pedestrian movement pattern in crowd-quakes. J. Stat. Mech. Theory Exp. 2013, 2013, 02028. [Google Scholar] [CrossRef]
- Qin, W.; Cui, B.; Lou, X. Tracking control of disturbed crowd dynamic system using unit sliding mode control and feedback linearization. Nonlinear Dyn. 2019, 98, 2247–2260. [Google Scholar] [CrossRef]
- Wei, J.; Fan, W.J.; Guo, Y.Y.; Hu, J.; Fang, Y.Y. An extended social force model for pedestrian evacuation under disturbance fluctuation force. Int. J. Mod. Phys. C 2020, 31, 2050102. [Google Scholar] [CrossRef]
- Grinstein, G.; Lee, D.H.; Sachdev, S. Conservation laws, anisotropy, and ‘‘self-organized criticality’’ in noisy nonequilibrium systems. Phys. Rev. Lett. 1990, 64, 1927–1930. [Google Scholar] [CrossRef]
- Qin, W.; Zhuang, B.; Cui, B.T. Boundary Control of Crowd Evacuation System Based on Continuum Model. Control Decis. 2017, 33, 2073–2079. [Google Scholar]
- Zhong, R.X.; Chen, C.; Huang, Y.P.; Sumalee, A.; Lam, W.H.K.; Xu, D.B. Robust Perimeter Control for Two Urban Regions with Macroscopic Fundamental Diagrams: A Control-Lyapunov Function Approach. Transp. Res. Procedia 2017, 23, 922–941. [Google Scholar] [CrossRef]
- Wadoo, S.A.; Sabiha, A. Sliding Mode Control of Crowd Dynamics. IEEE Trans. Control Syst. Technol. 2013, 21, 1008–1015. [Google Scholar] [CrossRef]
- Thorburn, S. Safety at Sports Grounds in the UK. Struct. Eng. Int. 1999, 9, 186–188. [Google Scholar] [CrossRef]
- Santos-Reyes, J.; Olmos-Peña, S. Analysis of the ‘News Divine’ stampede disaster. Saf. Sci. 2017, 91, 11–23. [Google Scholar] [CrossRef]
- Feng, Y.; Duives, D.; Daamen, W.; Hoogendoorn, S. Data collection methods for studying pedestrian behaviour: A systematic review. Build. Environ. 2021, 187, 107329. [Google Scholar] [CrossRef]
- Cho, S.; Kang, H. Integrated multiple behavior models for abnormal crowd behavior detection. In Proceedings of the 2012 IEEE Southwest Symposium on Image Analysis and Interpretation, Santa Fe, NM, USA, 22–24 April 2012. [Google Scholar]
- Varadarajan, J.; Odobez, J. Topic models for scene analysis and abnormality detection. In Proceedings of the 12th IEEE International Conference on Computer Vision Workshops, Kyoto, Japan, 27 September–4 October 2009. [Google Scholar]
- Suriani, N.; Hussain, A.; Zulkifley, M. Sudden Event Recognition: A Survey. Sensors 2013, 13, 9966–9998. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Fei, F.; Fang, Y.; Lee, C.; Xiong, N.; Shu, L.; Chen, S. Abnormal event detection in crowded scenes based on deep learning. Multimed. Tools Appl. 2016, 75, 14617–14639. [Google Scholar] [CrossRef]
- Qin, W.; Cui, B.; Lou, X. Feedback control design of crowd evacuation system based on the diffusion model. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar]
- Wadoo, S.A.; Kachroo, P. Feedback Control of Crowd Evacuation in One Dimension. IEEE Trans. Intell. Transp. Syst. 2010, 11, 182–193. [Google Scholar] [CrossRef]
- Qin, W.; Cui, B.T.; Jiang, Z.X. Finite-Time Control of One Dimensional Crowd Evacuation System. J. Adv. Transp. 2019, 2019, 6597360. [Google Scholar] [CrossRef]
- Mukherjee, S.; Goswami, D.; Chatterjee, S. A Lagrangian Approach to Modeling and Analysis of a Crowd Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 865–876. [Google Scholar] [CrossRef]
- Liao, X.X. Mathematical theory and application of stability. Huazhong Norm. Univ. Press 2001, 23, 51–52. [Google Scholar]
- Qu, M.Z. Research on Disturbance Model of Stampede Accident in Crowded Places; Capital University of Economics and Business: Beijing, China, 2016. [Google Scholar]
- Zhao, R.Y.; Dong, D.H.; Wang, Y.; Li, C.L.; Ma, Y.L.; Enríquez, V.F. Image-Based Crowd Stability Analysis Using Improved Multi-Column Convolutional Neural Network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5480–5489. [Google Scholar] [CrossRef]
- Aw, A.; Rascle, M. Resurrection of “second order” models of traffic flow. Siam J. Appl. Math. 2000, 60, 916–938. [Google Scholar] [CrossRef]
- Yi, J.G.; Lin, H.; Alvarez, L.; Horowitz, R. Stability of macroscopic traffic flow modeling through wavefront expansion. Transp. Res. Part B 2003, 37, 661–679. [Google Scholar] [CrossRef]
- Huang, L.; Wong, S.C.; Zhang, M.P.; Shu, C.W.; Lam, W.H.K. Revisiting Hughes’ dynamic continuum model for pedestrian flow and the development of an efficient solution algorithm. Transp. Res. Part B Methodol. 2009, 43, 127–141. [Google Scholar] [CrossRef]
- Zhao, R.Y.; Liu, Q.; Wang, Y.; Jia, P.; Li, C.L.; Ma, Y.L.; Zhu, W.J. Dynamic Crowd Accident-Risk Assessment Based on Internal Energy and Information Entropy for Large-scale Crowd Flow Considering COVID-19 Epidemic context. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17466–17478. [Google Scholar] [CrossRef]
- Bain, N.; Bartolo, D. Dynamic response and hydrodynamics of polarized crowds. Science 2019, 363, 46–49. [Google Scholar] [CrossRef]
- Liu, Q. Crowd Aggregation Risk Assessment and Stability Analysis Considering Internal Disturbances. Master’s Thesis, Tongji University, Shanghai, China, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).