Abstract
The stability and accuracy of explicit high-order finite difference (HOFD) algorithms have been research hotspots in different fields. To improve the stability and accuracy of the HOFD algorithms in thermal simulations, we present a Lax-Wendroff high-order finite difference (LHOFD) algorithm to solve the 2D transient heat transfer equation in this paper and develop an improved LHOFD (IHOFD) algorithm to improve the stability of the LHOFD algorithm. The formulas of the general high-order central FD (HOCFD) coefficients and the truncation error coefficient as well as the high-order non-central FD (HONFD) coefficients and the truncation error coefficient of the fourth-order spatial derivative are derived concisely in a different way. Furthermore, a unified analytical formula of the general HOCFD and HONFD coefficients, which can calculate the spatial derivative of any integer order, is derived. A new strategy of combination with the HOCFD and HONFD approximations under the same high-order accuracy as the internal computational domain is proposed to calculate the mixed derivatives of the boundary domains with high accuracy, no additional computational cost, and easy implementation. Then, the accuracy analysis, stability analysis, and comparative analysis of numerical simulation results obtained by the LHOFD and IHOFD algorithms with the exact solution show the correctness and validity of the proposed algorithms and their stability formulas, and the advantages of the proposed algorithms. The proposed algorithms are valid under both symmetric and asymmetric boundary conditions. The stability factor of the LHOFD algorithm is slightly higher than that of the conventional algorithm. The stability factor of the IHOFD algorithm is twice that of the conventional algorithm, and the maximum absolute error of the thermal simulation is within 0.015 (°C).
1. Introduction
The explicit high-order finite difference (FD) method is widely used in thermal simulation due to its low computational complexity and low memory usage [1,2,3,4]. The computational performance of the explicit FD method is mainly affected by three factors, namely accuracy, stability, and efficiency. Where the computational accuracy involves the difference operator accuracy of the numerical approximation of temporal and spatial derivatives. Stability is determined by the Courant–Friedrich–Levy (CFL) condition, while computational efficiency is mainly determined by the FD operator, spatial grid size, and time step. The conventional high-order FD (HOFD) algorithm with high-order spatial accuracy usually has a low temporal accuracy and stability. Usually, small time steps are needed to obtain simulation results that meet certain accuracy requirements, which are often smaller than the upper limit value calculated by the CFL condition, thus consuming a lot of computation time. Therefore, the researchers used the standard Lax-Wendroff method and its improvement method to increase the time accuracy and improve the stability of the FD algorithms [5,6,7,8,9,10]. Additionally, stencil-based methods for increasing the temporal accuracy usually use smaller computational amounts than Lax-Wendroff methods with a similar calculation accuracy [11,12,13]; however, the calculation of the coefficients of these stencils is more complicated. These methods are mainly used for acoustic field simulation; however, there are a few literature reports on boundary value problems such as heat conduction problems due to the difficulty of boundary treatment. At the same time, some researchers have studied ADER methods, which are another class of Lax-Wendroff methods [14,15,16] to solve the computational flow dynamics (CFD) problem. The implicit (compact) HOFD algorithms often used in thermal simulation significantly improve the simulation stability and computational accuracy [17,18,19]. The explicit FD algorithms typically use less computational cost than the implicit FD ones. Therefore, we prefer to study the explicit HOFD algorithm to improve the numerical simulation stability and accuracy and reduce computational costs. In addition, a small number of scholars have explored releasing the upper limit of the time step restrained by the stability condition of the explicit FD algorithm based on the spatial filtering method [20,21,22] and the eigenvalue-type method [23,24,25], however, these need a large amount of memory.
As mentioned above, the Lax-Wendroff HOFD algorithms have been studied in many fields and have achieved good results. The implicit HOFD algorithms are mostly used in thermal simulation, while the Lax-Wendroff HOFD algorithm has been poorly studied.
In order to improve the accuracy and stability of the existing HOFD algorithm, first, this paper presents a Lax-Wendroff high-order finite difference (LHOFD) algorithm to numerically solve the 2D transient heat conduction equations (HCEs). Using the stability analysis and operator combination optimization strategy, an improved LHOFD (IHOFD) algorithm was developed to improve the stability of the LHOFD algorithm. Secondly, we develop the formulas of general high-order central FD (HOCFD) coefficients and the truncation error coefficient as well as general high-order non-central FD (HONFD) coefficients and the truncation error coefficient of the fourth-order spatial derivative. A unified formula for general HOCFD and HONFD coefficients that can calculate the spatial derivative of any order is also derived. In the domain of wavenumbers, we analyze the accuracy of the HOCFD operator of the fourth-order spatial derivative and derive the stability formulas of the algorithms. Then, we use a strategy of combining the high-order non-central and central FD approximation with the same high-order accuracy as the internal computational domain to calculate the derivatives of the boundary regions. Finally, the stability, accuracy, and effectiveness of the proposed algorithms are analyzed by examples.
2. Methods
In this section, we present an LHOFD algorithm to numerically solve the 2D transient HCEs, and developed an IHOFD algorithm using stability analysis and an operator combination optimization strategy to improve the stability of the LHOFD algorithm. Then, based on the standard Taylor expansion and the Lagrange interpolation formula, we derive the formulas of general HOCFD coefficients and the truncation error coefficient as well as general HONFD coefficients and the truncation error coefficient of the 4th-order spatial derivative. Finally, we derive a unified formula for general HOCFD and HONFD coefficients that can calculate the spatial derivative of any integer order.
The two-dimensional transient thermal simulation is mainly implemented based on the two-dimensional transient HCEs. As a continuous, isotropic material, the two-dimensional transient HCEs can be rewritten as [1,18]
where represents the thermal conductivity coefficient, represents the density, represents the specific heat capacity, represents the thermal conductivity. The thermal parameters of the material are constant, including its density, specific heat capacity, and thermal conductivity. represents a two-dimensional transient temperature field.
Equation (1), a continuous heat conduction problem, is transformed into a discrete time-evolving heat conduction problem by the computational domain meshing. In this paper, the explicit HOFD method discretizes the HCEs by the HOFD operators in the time–space domain.
Based on the idea of the reference [5], this paper presents a Lax-Wendroff high-order finite difference (LHOFD) algorithm with the second-order temporal accuracy and 2M-order spatial accuracy to solve the numerical solution of the two-dimensional HCEs in Equation (1). An improved LHOFD (IHOFD) algorithm was developed, which significantly improved the stability of the LHOFD algorithm.
2.1. LHOFD Scheme
By Taylor expansion, the LHOFD algorithm for the two-dimensional HCEs can be expressed as
where represents a transient temperature of the point on the two-dimensional plane at time, , , , , and represent the 2M-order operators of the second-order derivative, the fourth-order derivative, and the fourth-order mixed derivative in the space of the two-dimensional transient temperature field along the and coordinates, respectively. represents the thermal conductivity as a constant, represents the magnitude of the time step, and represents the number of time step iterations.
In Equation (2), the two-dimensional LHOFD algorithm is a combination of two types of stencils, namely a cross-shaped stencil and a box-shaped stencil, where the 2M-order stencils of the second-order and the fourth-order spatial derivative belong to the cross-shaped stencil, and the 2M-order stencil of the fourth-order spatial mixed derivative belongs to the box-shaped stencil. When ignoring the third term of Equation (2), the LHOFD algorithm degenerates to a general HOFD (GHOFD) algorithm [26].
Based on the stability analysis (see Appendix C), the LHOFD algorithm is slightly more stable compared to the GHOFD algorithm. Therefore, further studies on the algorithm to improve the stability is needed.
2.2. IHOFD Scheme
Based on the stability analysis of Equation (2) (see Appendix C), let the term in Equation (A18) be equal to zero, and we obtain a new algorithm (CHOFD) modified for the LHOFD algorithm. The CHOFD algorithm of the two-dimensional HCEs can be written as
From Equation (A18), it can be seen that the stability of Equation (3) is significantly improved compared to Equation (2).
In order to reduce the effects of the truncation error of the time derivative in Equation (2) and the omitted approximation of Equation (3) on the accuracy, based on the idea of [27], a weight coefficient is introduced in Equation (3) to realize the optimal combination of the two operators and further improve the algorithm performance. The improved CHOFD (IHOFD) algorithm for the two-dimensional HCEs can be expressed as
The optimal weighting coefficient is determined by Equation (5) based on the maximum norm.
where represents the numerical simulation results and represents the exact solution. This method is a relatively simple method compared with the conventional methods.
Through the optimization numerical calculation of Equation (5), it can be obtained that the optimal values of the fourth-order and sixth-order IHOFD algorithms are 0.7502 and 0.7503, respectively. All calculations in the following are taken as 0.75.
The derivatives calculation of the temperature field in Equations (2)–(4) involves the internal computational domain and the boundary region. We adopted the HOCFD operator in the internal computational domain and used a strategy of combining the HONFD and HOCFD approximation under the same high-order accuracy as the internal computational domain to calculate the derivatives in the boundary region.
2.3. Difference Operators and Coefficient Formulas
2.3.1. HOCFD Operator and Coefficient Formula
For the two-dimensional transient HCEs, the 2M-order HOCFD operator of the second-order spatial derivative along the and coordinates can be expressed as [26]
and the 2M-order HOCFD operator of the fourth-order spatial derivative along the and coordinates can be can be expressed as
as well as the 2M-order HOCFD operator of the fourth-order spatial mixed derivative
where and represent the mesh interval along the and coordinates, respectively. represents half the length of the HOCFD operator. There are other similarities along the coordinate.
The HOCFD operator coefficient can be determined by the analytic formula of Equation (9a) (see [26] for a detailed derivation).
and can be determined by the analytic formula of Equation (9b) (see Appendix A for a detailed derivation).
- (1)
- , ,
- (2)
- , , ,
- (3)
For the fourth-order spatial mixed derivatives , from , using the product of the 2M-order HOFD coefficients of the second-order spatial derivatives along the x and y coordinates (see Equation (9a)), respectively, one can calculate the 2M-order HOFD coefficients matrix of the fourth-order spatial mixed derivative by means of a simple method that can easily treat the boundary (see Equation (10)).
where represents the 1/4 block matrix of the coefficient matrix .
The 2M-order HOFD coefficients matrix of the fourth-order spatial mixed derivatives is a symmetric matrix, i.e., , , , represent the 2M-order HOFD coefficients of the second-order spatial derivatives along the and coordinates, respectively (see Equation (9a)), and .
The coefficient formula for an explicit higher-order FD operator in a regular grid can also be determined by the Taylor expansion method in the wavenumber domain [28,29]; this paper derives the coefficient formulas using the standard Taylor expansion, and the derivation process is concise and clear, and provides another way to calculate high-order FD coefficients and its truncation error coefficient.
2.3.2. HONFD Operator and Coefficient Formulas
Hicks and Wei [30] give fourth-order-accuracy FD operators to approximate the second-order spatial derivative in the boundary region. Inspired by the reference [31], we develop a formula for the coefficients of the HONFD operator, and use a strategy of combining the HONFD and HOCFD approximation to calculate the spatial derivatives of the boundary region.
The HONFD operator of the fourth-order spatial derivative along the coordinate with ()-order accuracy, which can be written as
where represents the HONFD coefficient, which can be calculated through Equation (12) (see Appendix B for detailed derivation)
where the stencil vector , represents the length of the operator, , ,
and , , are all positive integers and is also a vector. represents the spatial interval in the direction. represents the derivative at the mesh point in the boundary area, and also represents the zero point position of the operator vector. The left boundary area of the two-dimensional model in the direction, , represents the number of meshes from the derivative mesh point or operator zero point to the left boundary point. represents the length to the right side of the zero value point of the operator, . The right boundary area, , represents the number of meshes from the zero position of the operator to the right boundary point, and the represents the length to the left side of the zero position of the operator, . The derivatives in the direction in the boundary area are calculated the same as in the direction. represents the sequence number of the difference operator vector element from left to right .
The sixth-order HONFD operators and coefficients for the fourth-order spatial derivative are shown in Table 1. The operators’ lengths are . The and of different operators with serial numbers 1–5 are 1, 2, 5, 4, 3 and 5, 4, 1, 2, 3, respectively. Table 1 only shows the sixth-order HONFD operators and their difference coefficients for the left boundary zone (serial numbers 1, 2) and right boundary zone (serial numbers 3, 4) as well as the internal zone (serial number 5) of the two-dimensional model in the direction. The sixth-order HONFD operator in the top and bottom boundary zone and its difference coefficients in the direction are the same as in the direction. As can be seen from Table 1, the HONFD coefficients of the right boundary zone are consistent with the difference coefficients of the same operator (such as serial numbers 1 and 3) in the left boundary zone arranged in reverse order. Therefore, the two-dimensional model only needs to calculate the HONFD coefficients for either boundary region without an additional computational cost.

Table 1.
Sixth-order HONFD operators of the fourth-order spatial derivative and their coefficients.
Moreover, Table 1 demonstrates that, when the HONFD operator becomes an HOCFD operator (see Table 1 serial number 5), The coefficients calculated using the coefficient formula (see Equation (12)) of the HONFD operator are consistent with the results calculated using the coefficient formula (see Equation (9b)) of the HOCFD operator.
The comparison shows that the HONFD operator and its coefficient formula are universal, while the HOCFD operator has a clearer mathematical meaning, the coefficient formula is more concise, and its truncation error coefficient (see Appendix A (A5), where the operator length is ), is smaller than that of the HONFD operator (see Appendix B (A12), where the operator length is equal to ). It can be seen that the HOCFD operator and its coefficient formula presented in this paper are more suitable for the numerical simulation of the internal computational domain, and the HONFD operator and its coefficient formula are more suitable for the numerical simulation of the boundary region, and the organic combination of these two algorithms forms a new explicit HOFD algorithm proposed in this paper, which can solve the two-dimensional transient HCEs with high accuracy.
In the same manner, we obtain the HONFD and the HOCFD coefficients of the 2M-order-accuracy of the L-order derivative in space, namely
where represents an arbitrary order of the space derivative. represents the length of the shortest operator. When is even, . When is odd, then . represents the length of the operator, is an odd number greater than or equal to . When is even, ; when is odd, . Equation (13) can be applied to the numerical calculation of the HOFD methods in the regular mesh domain for all different types of integer-order partial differential equations including heat transfer equations.
3. Schemes Analysis
Firstly, we theoretically inspect the accuracy and truncation error of the different-order HOFD operators of the fourth-order spatial derivative. The focus here is on the HOCFD operator. Secondly, the LHOFD and IHOFD algorithm’s stability formulas are derived, and the stability factors of different orders are given.
3.1. Accuracy Analysis
In the wavenumber domain, the 2M-order HOCFD operator of a one-variable function (see Appendix A (A1)) can be expressed as
Among them, represents the size of the spatial mesh, indicates the wavenumber, and indicates the HOCFD coefficient. Let
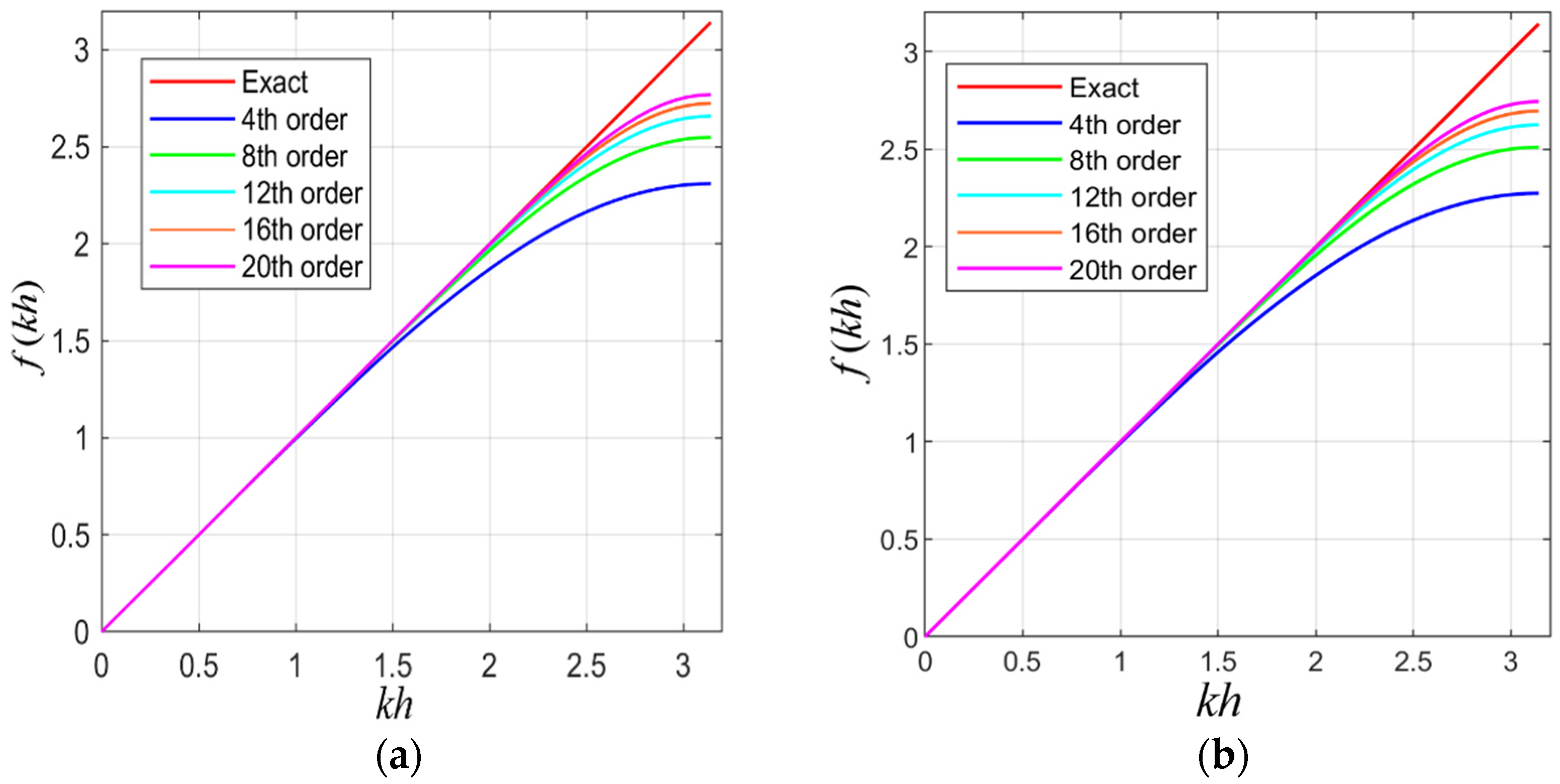
According to Shannon’s law of sampling, there is . According to the HOCFD coefficients of different orders, Equation (15) can be used to obtain the comparison relationship between the accuracy of the different-order HOCFD operators and exact solution (see Figure 1). It can be concluded that the accuracy of the HOCFD operator can be significantly improved with the increase in the different-order number. The HOFD operator of the same order of the fourth-order spatial derivatives are less accurate than the second-order spatial derivatives.
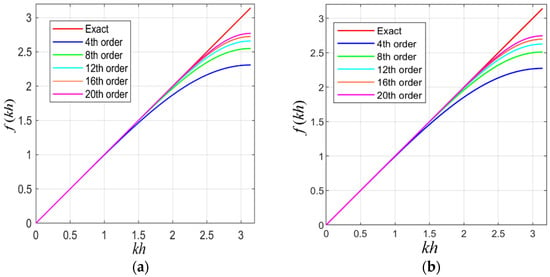
Figure 1.
Comparison chart of the accuracy of the 4th–20th-order HOCFD operators of the different order spatial derivative and exact solution: (a) 2nd-order spatial derivative [26] and (b) 4th-order spatial derivative.
The qualitative evaluation is previously given. Based on Equation (16a) [26] and Equation (16b), the values corresponding to different-order HOCFD operators of the second- and fourth-order spatial derivative with errors less than or equal to can be solved, respectively. According to these values, the accuracy of different-order HOCFD operators can be quantitatively evaluated.
and
From Table 2 and Table 3, with the admissible error reduction, the value corresponding to the different HOCFD operator of the same order significantly decreases, and under the same admissible error conditions, the value corresponding to the HOCFD operator of the second-order derivative in space under the same order is a little greater than the value corresponding to the fourth-order spatial derivative; in other words, under the same order, the accuracy of the HOCFD operator of the second-order spatial derivative is higher than that of the fourth-order spatial derivative.

Table 2.
The values corresponding to different-order HOCFD operators of the 2nd-order spatial derivatives under different admissible error conditions.

Table 3.
The values corresponding to different-order HOCFD operators of the 4th-order spatial derivatives under different admissible error conditions.
In addition, based on the truncation error coefficient Formula (17) of the 2M-order HOCFD operator of the fourth-order spatial derivation (see Appendix A for detailed derivation),
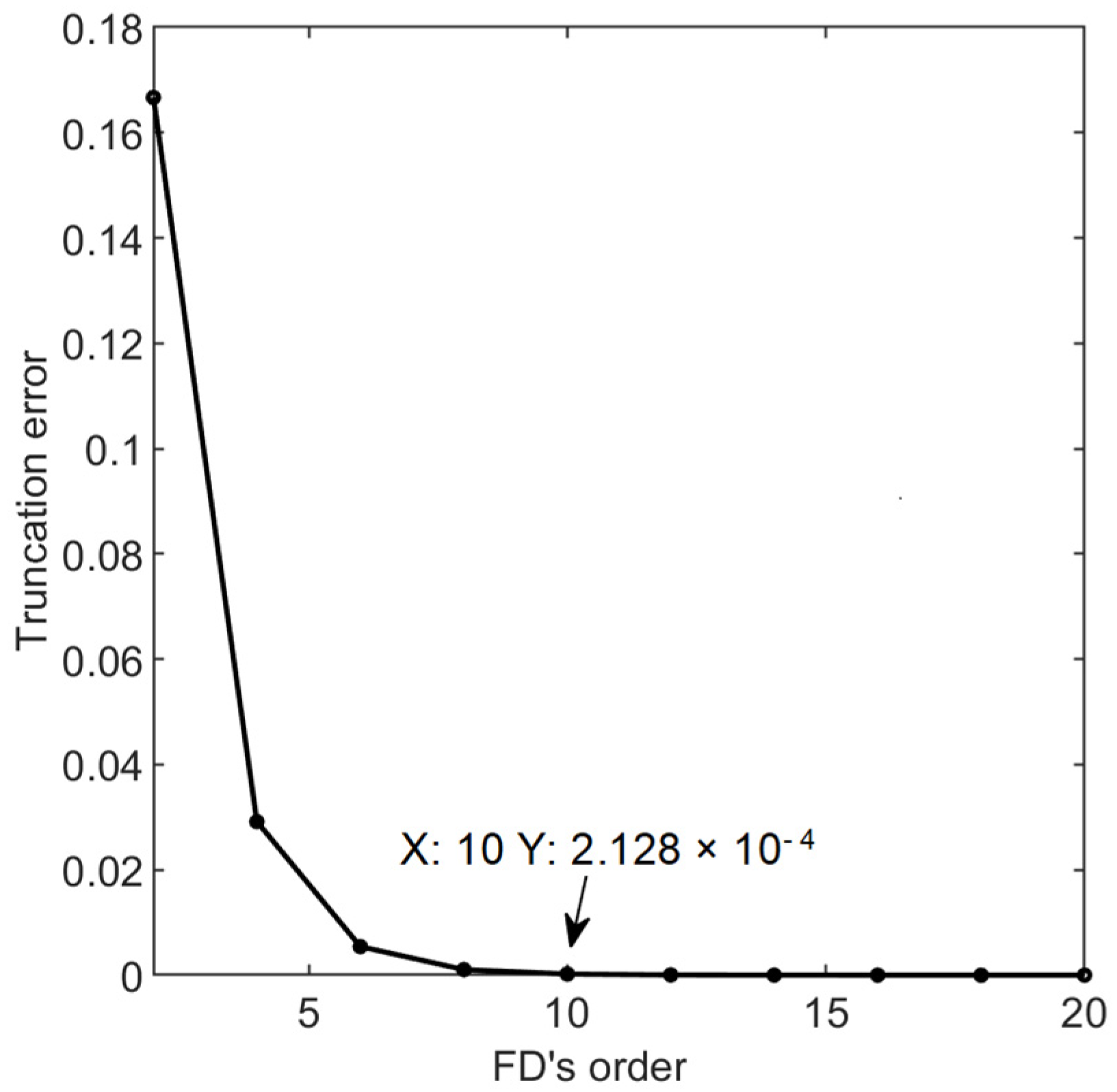
The curve of the truncation error (TE) coefficient of the different-order HOCFD operators can be obtained (see Figure 2). The TE coefficient of the different-order HOCFD operator swiftly decreases with an increasing order, as shown in Figure 2; in other words, its accuracy rapidly increases. When 2M = 10, the TE coefficients of the 10th-order HOCFD operators of the 2nd-order and the 4th-order spatial derivations are 6.013 × 10−5 ( [26]) and 2.128 × 10−4 (see the arrow in Figure 2), respectively.
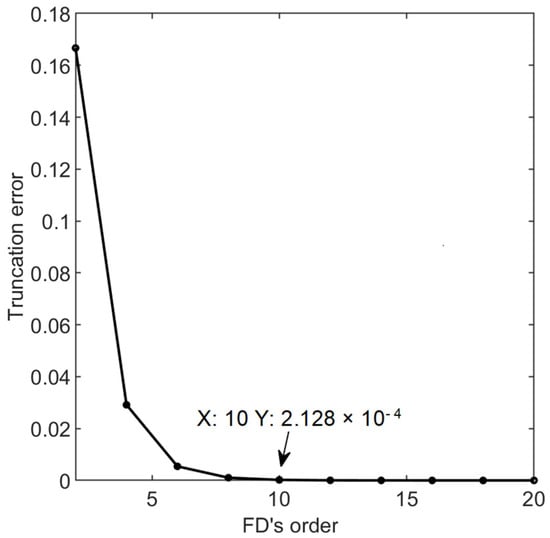
Figure 2.
Curve of the TE coefficient of the different-order HOCFD operator of the 4th-order spatial derivative.
It can be concluded that the accuracy of the HOCFD operator can be significantly improved with the increase in the different-order number. And, under the same order, the TE coefficient of the HOCFD operator of the fourth-order spatial derivative is significantly higher than that of the second-order spatial derivative.
Using the product of the 2M-order HOFD coefficients of the second-order spatial derivatives along the x and y coordinates (see Equation (9a)), respectively, can calculate the 2M-order HOFD coefficients matrix of the fourth-order mixed-derivative in space, and its corresponding TE is . Compared with Equation (17), the TE of the HOFD operator of the fourth-order spatial mixed derivatives is comparable to it.
3.2. Stability Formulas and Analysis
We derive the stability formula of the LHOFD algorithm of the two-dimensional HCEs (see Appendix C for details) as
where represents the maximum odd number that does not exceed . And,
When , Equation (18a) degenerates into the stability condition formula of the GHOFD algorithm of the two-dimensional transient HCEs [26].
When , from Equation (18a), we obtain
Let , .
The stability factor of the LHOFD algorithm is .
And, derive the stability formula of the CHOFD algorithm of the two-dimensional transient HCEs as
When , from Equation (19a), we obtain
Let , and the stability factor of the CHOFD algorithm is ; thus, the stability factors of the difference algorithms are as shown in Table 4. According to Table 4, as the order of the difference algorithms increases, their stability factor decreases; that is, when the size of the spatial mesh remains unchanged, the time interval needs to be reduced to ensure that these algorithms are stable. The stability factor of the LHOFD algorithm is slightly larger compared to that of the GHOFD algorithm, while the stability factor of the CHOFD algorithm of the same order is two times that of the GHOFD algorithm. This shows that the time step of the CHOFD algorithm (as can be seen in Equation (19a)) is twice that of the GHOFD algorithm () (see [26]) for the same mesh size. In addition, when the order of different algorithms is greater than the 10th order, their stability factors increase with the order, and its increase is not obvious. It can be seen that, in practical applications, with comprehensive stability (see Table 4) and accuracy (see Figure 2), it is generally reasonable to take within 10th order.

Table 4.
Stability factors (×10−1) of the difference algorithms for two-dimensional transient HCEs.
4. Integration Procedure
4.1. Initial Condition and Boundary Conditions
For convenience, take the square 2D model for example. An exact solution of the two-dimensional transient HCEs shown in Equation (1) in the conditions of Equation (20) was given in reference [26]. The boundary conditions and the initial condition are
4.2. Boundary Process for the High-Order FD Schemes
When numerically solving HCEs utilizing an HOFD algorithm, it is important to calculate the derivative at the boundary point and its neighbor points [32].
The algorithms proposed in this paper include the HOCFD and HONFD methods of three different spatial derivatives, such as the second derivative, fourth derivative, and fourth mixed derivative. The HOCFD and HONFD methods of the second-order spatial derivative in the boundary zone are shown in reference [26], while the HOCFD and HONFD methods of the fourth-order spatial derivative are similar to that of the second-order spatial derivative. The boundary processing strategy of the fourth-order spatial mixed derivatives is highlighted here.
For the Dirichlet boundary conditions, we present a new strategy of combination with the HOCFD and the HONFD approximations under the same high-order accuracy as the internal computational domain to calculate the derivatives of the boundary domains, which has very high accuracy and does not add an additional computational cost.
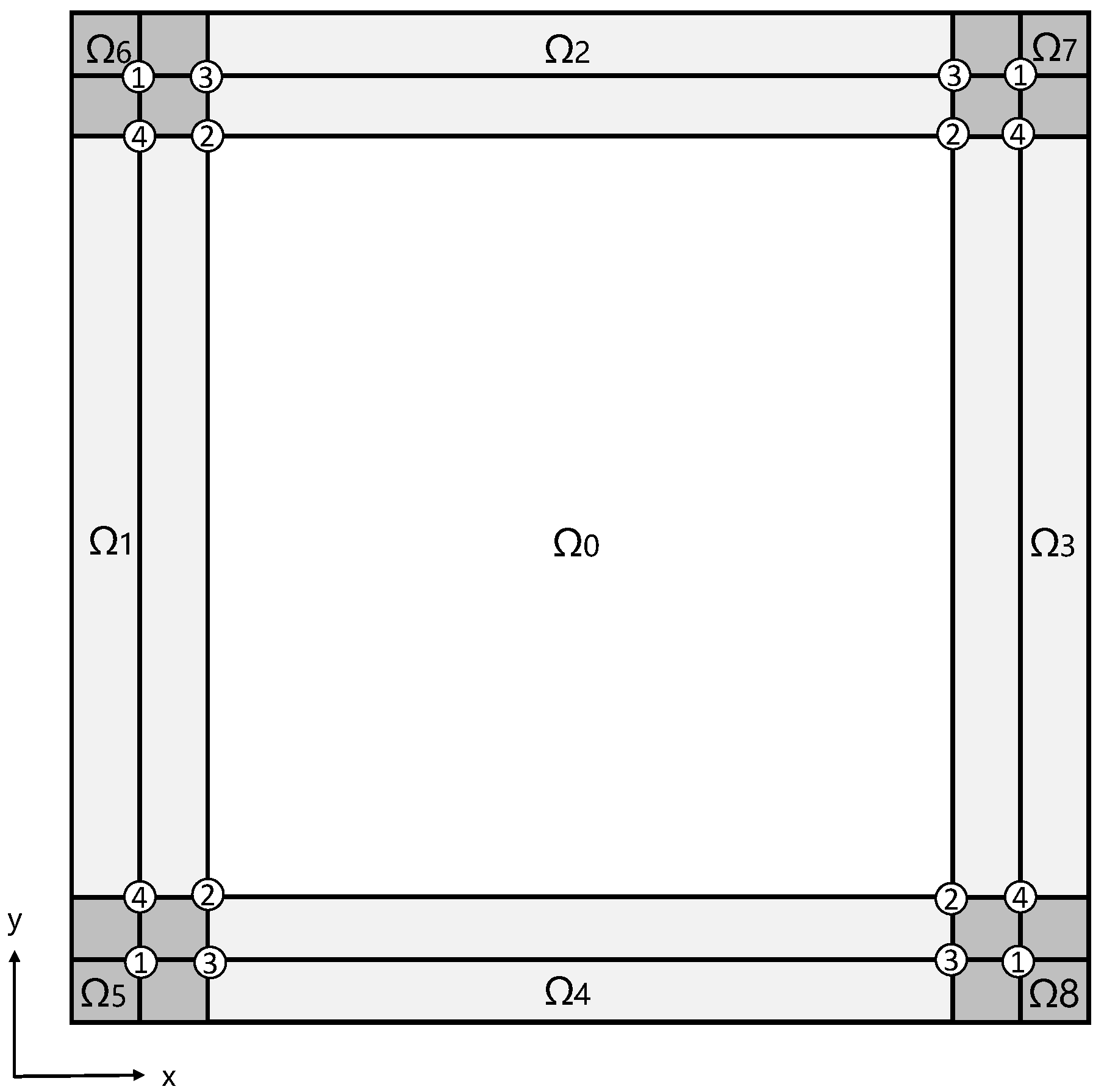
Generally, the HOFD numerical calculation of the transient thermal field in a two-dimensional model includes two parts, namely the internal computational domain and the boundaries domain. A sketch of the internal computational domain and the boundaries domain of the two-dimensional model for the HOFD numerical simulation of the transient thermal field in two dimensions is displayed in Figure 3.
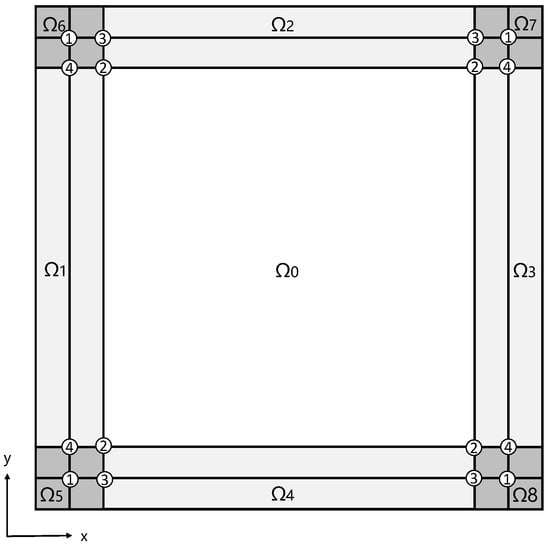
Figure 3.
Sketch of the internal computational domain and the boundaries domain of the two-dimensional model for an HOFD numerical simulation of the two-dimensional transient thermal field.
The width of the , the grid points, and the boundary domains are , where is half the length of the HOFD operator in the internal calculation domain. When the meshes of the two-dimensional model are , represents the number of meshes along the and coordinates, respectively, and the internal computational domain . represents the mesh size in space. The HONFD operators in the boundary domains have the same order as the HOCFD operators in the internal computing domain.
In the sixth-order LHOFD and IHOFD algorithms, the corner domain (see Figure 3) is taken as an example to briefly introduce the calculation method and the process of the fourth-order spatial mixed derivative in the boundary region. Specifically, the first step is to calculate the coefficients of HONFD along the and coordinates of four mesh points. The first point, marked as ① in the corner domain, its corresponding stencil, and the sixth-order HONFD coefficients of the second-order spatial derivative along the coordinate, are shown in Table 5 serial number 1, and the coefficients along the coordinate are the same as those along the coordinate. The second point marked as ②, its stencil, and the sixth-order HONFD coefficients in the coordinate are shown in Table 5 by serial number 2, and the coefficients along the y coordinate are the same as those along the coordinate. The third point marked as ③, the stencil, and the sixth-order HONFD coefficients along the coordinate are the same as those of the second point, the stencil, and the sixth-order HONFD coefficients along the coordinate are the same as those of the first point. And, the fourth point marked as ④, the stencil, and the sixth-order HONFD coefficients along the coordinate are the same as those of the first point, the stencil, and the sixth-order HONFD coefficients along the coordinate, which are also the same as those of the second point. In the second step, a matrix of HONFD coefficients of the fourth-order spatial mixed derivative on the four mesh points is calculated, which can be determined by Equation (10). The fourth-order spatial mixed derivatives for the four mesh points can be calculated in the third step.

Table 5.
Sixth-order HONFD operators of the 2nd-order spatial derivative and their coefficients [26].
In the left and right domains , the HONFD operators are used along the coordinate, and the HOCFD operators are used along the coordinate, constituting other similarities.
This paper uses the Matlab software(Version R2018b) programming to implement the LHOFD and IHOFD algorithms of the two-dimensional transient HCEs derived previously.
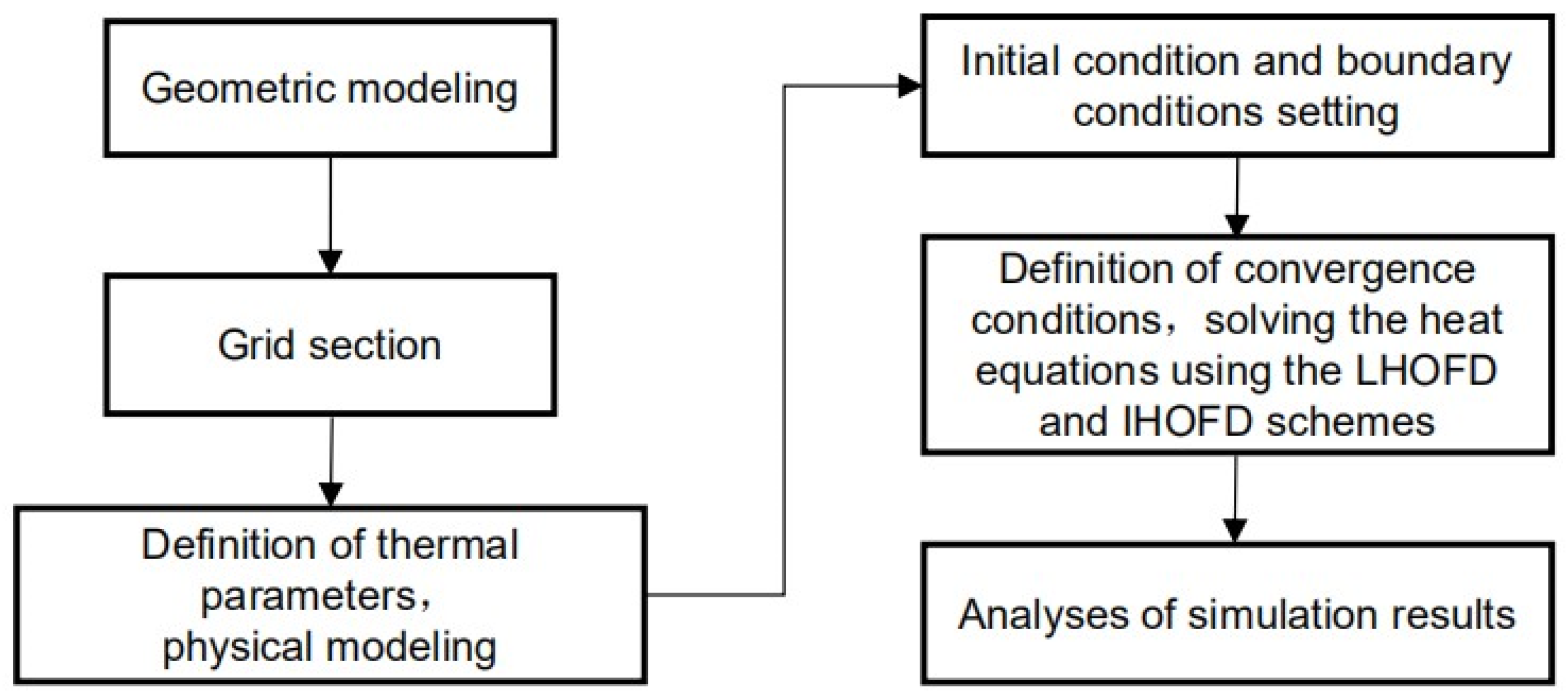
A diagram of the procedure used to solve the two-dimensional transient HCEs by the proposed algorithms in the computational model is shown in Figure 4.
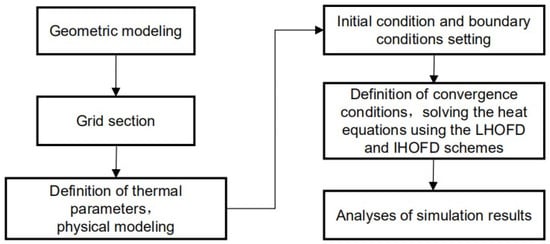
Figure 4.
Diagram of the procedure used to solve the two-dimensional transient HCEs by the proposed algorithms in the computational model.
5. Results of Numerical Experimentation
To be able to confirm the theoretical results and examine the accuracy and effectiveness of the algorithms proposed in this paper, by comparing them with the exact (analytical) solution, we analyze several examples, give their results, and discuss them in this section.
5.1. Stability Formula Analysis of the Different Schemes
In the following, the correctness of the stability condition formulas of the LHOFD and IHOFD algorithms for the two-dimensional transient HCEs is verified. Here, the sixth-order LHOFD and IHOFD algorithms (M = 3) and the corresponding stability factors (see Table 4) are used. Assuming the thermal conductivity , the calculation domain was divided into 41 × 41 rectangular mesh nodes with a mesh size of 0.025 m, a time of 1.0 s, and the stability Equations (18c) and (19b) determine the time step .
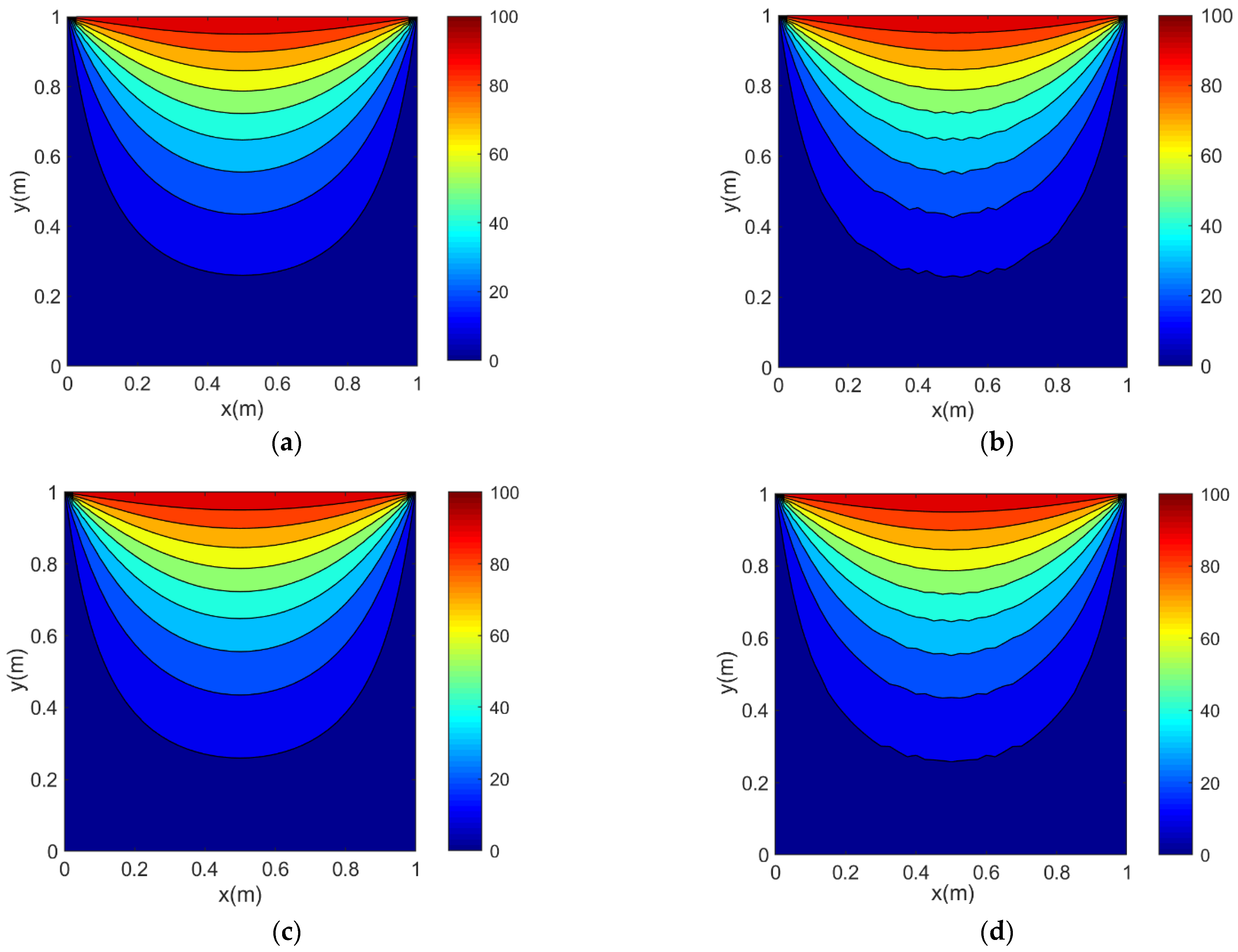
Figure 5 shows the numerical simulation results of the two-dimensional transient HCEs by the sixth-order LHOFD and IHOFD algorithms with the stability factors F = 1.713 × 10−1 and F = 3.309 × 10−1, respectively. The numerical simulation results of the sixth-order LHOFD and IHOFD algorithms for the two-dimensional transient HCEs are stable, when the stability factors are calculated by the Formulas (18c) and (19b) (see Figure 5a,c). When the stability factors are marginally greater than the calculated value (the relative errors of the stability factor are +0.0004 and +0.0017, respectively), the numerical simulation results show obvious instability (see the high-frequency fluctuations or waves of the contours) (see Figure 5b,d). The simulation results confirm the correctness of the stability condition formulas of the LHOFD and IHOFD algorithms. In addition, from the slightly larger relative error of the stability factor, it can also be concluded that the optimal combination of operators is also beneficial to improve the stability of the IHOFD algorithm.
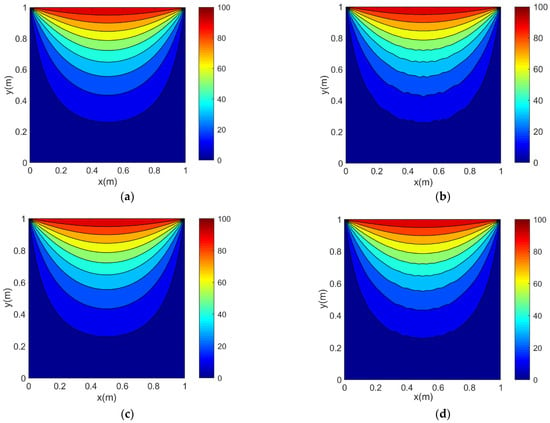
Figure 5.
Numerical simulation results of two-dimensional HCEs by the LHOFD and IHOFD algorithms with different stability factors: (a) LHOFD algorithm with stability factor (F = 1.713 × 10−1), (b) LHOFD algorithm with stability factor (F = 1.713 × 10−1 + 0.365 × 10−2), (c) IHOFD algorithm with stability factor (F = 3.309 × 10−1) and (d) IHOFD algorithm with stability factor (F = 3.309 × 10−1 + 0.017 × 10−1).
5.2. Comparison of the Different-Order LHOFD Schemes
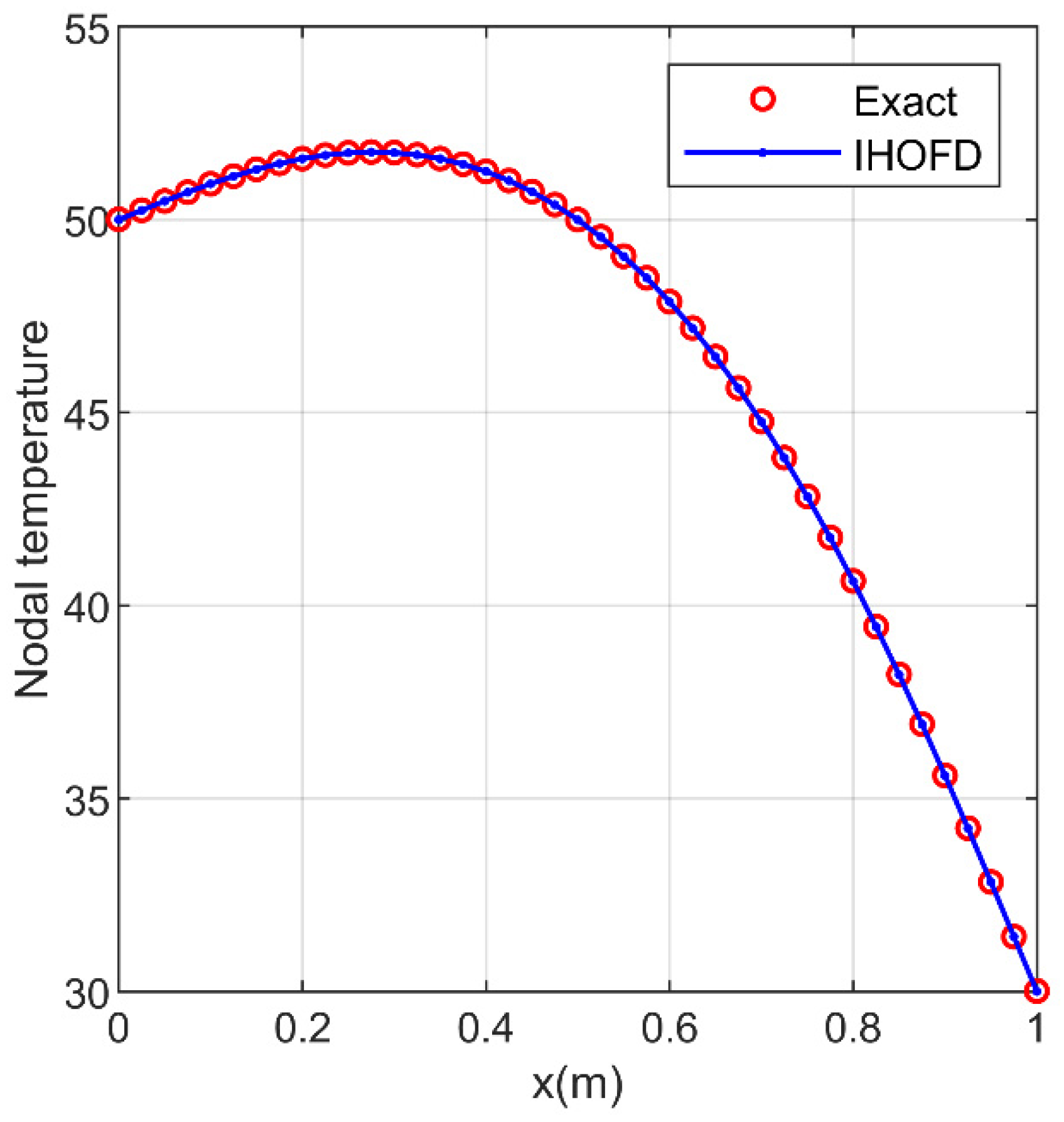
Assuming the thermal conductivity , the calculation domain was divided into 41 × 41 rectangular mesh nodes with a mesh size of 0.025 m, time of 1.0 s, and stability factors for the fourth-order and sixth-order LHOFD algorithms of 0.1938 and 0.1713, respectively, corresponding to the upper limit of the time steps determined by the stability Equation (18c), which are 1.211 × 10−4 s and 1.071 × 10−4 s, respectively. It can be concluded that the temperature distribution curves using a numerical simulation of the LHOFD algorithm with different orders (fourth and sixth order) coincide with that of the exact solution along the axis of the center line = 0.5 m in Figure 6. The relative error (RE) calculated by , where represents the total point numbers, represents the numerical simulation results, and represents the exact solution, and the maximum absolute error (MAE) determined by the error maximum norm of the numerical simulation results of the LHOFD algorithm with different orders (fourth and sixth order) and the exact solution of two-dimensional transient HCEs are 2.702 × 10−4, 6.281 × 10−3 (°C) and 2.156 × 10−4, 4.763 × 10−3 (°C), respectively.
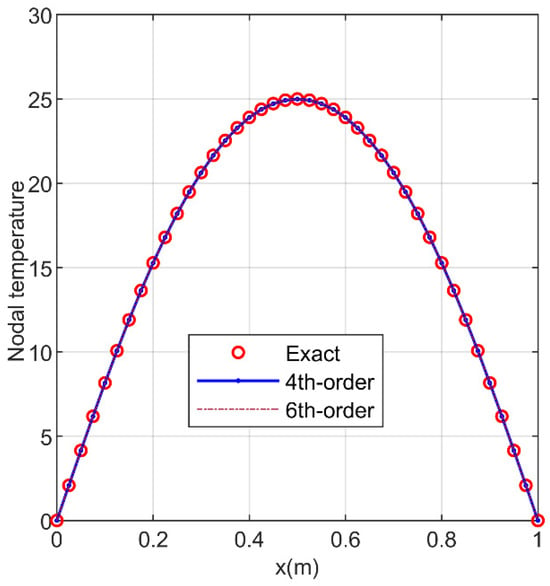
Figure 6.
Numerical simulation comparison of the LHOFD method with different orders (fourth and sixth) and the exact solution of two-dimensional HCEs (the centerline of = 0.5 m is distributed along the axis, temperature in (°C)).
When the time step is 1.071 × 10−4 s, the RE and MAE of the numerical simulation results of the fourth-order LHOFD algorithm and the exact solution of two-dimensional transient HCEs are 2.535 × 10−4, 5.569 × 10−3 (°C), respectively. It can be seen from the above that the LHOFD algorithm is correct and effective, and with the increase in the order of the LHOFD algorithm, its simulation accuracy is significantly improved. At the same time, the computational complexity and cost of the LHOFD algorithm also increases significantly.
In addition, under the same conditions, the RE and MAE of the numerical simulation results of the fourth-order GHOFD algorithm (see [26]) are 7.525 × 10−7, 3.606 × 10−5 (°C), respectively, which are much smaller than those of the LHOFD algorithm results. These results are consistent with the theoretical analysis results presented in Section 3.1.
5.3. Comparison of the Different Schemes
First, the numerical simulation results of the IHOFD method with different orders under the same grid size condition are given, and their results are compared with the LHOFD method in this section. Secondly, the results obtained by the IHOFD method with different orders and time steps are given and discussed. Here, the thermal parameters and model parameters are the same as in the previous section.
When the mesh size and the time step are the same as that of the fourth- and sixth-order LHOFD algorithms (∆t1 = 1.211 × 10−4 s, ∆t2 = 1.071 × 10−4 s), the RE and MAE between the results of the fourth- and sixth-order IHOFD algorithms and the exact solution are 3.126 × 10−4, 7.279 × 10−3 (°C) and 2.761 × 10−4, 6.435 × 10−3 (°C), respectively. Compared with the LHOFD algorithm (see Section 5.2), the simulation accuracy of the IHOFD algorithm of the same order is slightly lower under the same grid size and the same time step. This is mainly due to the fact that the IHOFD algorithm (see Equation (4)) omits other fourth-order spatial derivatives in the LHOFD algorithm (see Equation (2)) except for the fourth-order spatial mixed derivative term.
When the grid size is the same, under different time steps (∆t1 = 1.172 × 10−4 s, ∆t2 = 1.034 × 10−4 s), the errors analysis between the results of the fourth-order and sixth-order IHOFD algorithms and the exact solution are shown in Table 6. When the time step (1.4∆t1 = 1.641 × 10−4 s) of the fourth-order IHOFD algorithm is slightly less than the time step (1.6∆t2 = 1.654 × 10−4 s) of the sixth-order, the accuracy of the former is still slightly higher than that of the latter. And, when the time step (2∆t1) of the fourth-order IHOFD algorithm is greater than the time step (2∆t2) of the sixth-order, the latter has a slightly higher accuracy compared to the former. When the time step reaches the upper limits (2∆t1, 2∆t2) of the stability condition, the simulation accuracy of the fourth-order and sixth-order IHOFD algorithms decreases to a certain extent, but their accuracy errors are less than ±0.015 (°C).

Table 6.
The RE and MAE of the numerical simulation results of the IHOFD algorithm with different orders (4th- and 6th-order) and time steps and the exact solution of two-dimensional transient HCEs.
When the mesh size and time step (∆t = 2 × 10−4 s) remain the same, the REs and MAEs between the fourth-order and sixth-order IHOFD algorithm and the exact solution are 5.172 × 10−4, 1.2036 × 10−2 (°C) and 5.171 × 10−4, 1.2040 × 10−2 (°C), respectively. It can be seen that the accuracy of the two is almost the same. It can be concluded from above that the simulation accuracy of the fourth-order and sixth-order IHOFD algorithms is very close and the simulation accuracy improvement of the latter is very small when the grid size is the same.
Based on the comprehensive analysis of stability (see Table 4), accuracy, and computational cost, it can be concluded that the fourth-order IHOFD algorithm is more advantageous than the sixth-order IHOFD algorithm. The 2D stencil of the fourth-order IHOFD algorithm is a 25-point stencil consisting of an optimized combination of the cross stencil and the box stencil, which is similar to the popular 25-point stencil [33] in the acoustic field simulation; however, the former realizes the high-order differential accuracy calculation of temporal and spatial derivatives in the time–space domain, while the latter is a box stencil with a fixed structure and only the high-order differential accuracy calculation of spatial derivatives in the frequency–space domain.
5.4. Comparison of the IHOFD Scheme under Asymmetric Boundary Conditions
For comparison, take the square 2D model like the same one as before for example. An exact solution of the two-dimensional transient HCEs shown in Equation (1) in the conditions of Equation (21) was given in [26]. Here, the solution of the reference [26] is easily extended to satisfy the non-homogeneous boundary conditions. The asymmetric boundary conditions and the initial condition are
Here, the thermal parameters and model parameters are the same as in the previous section.
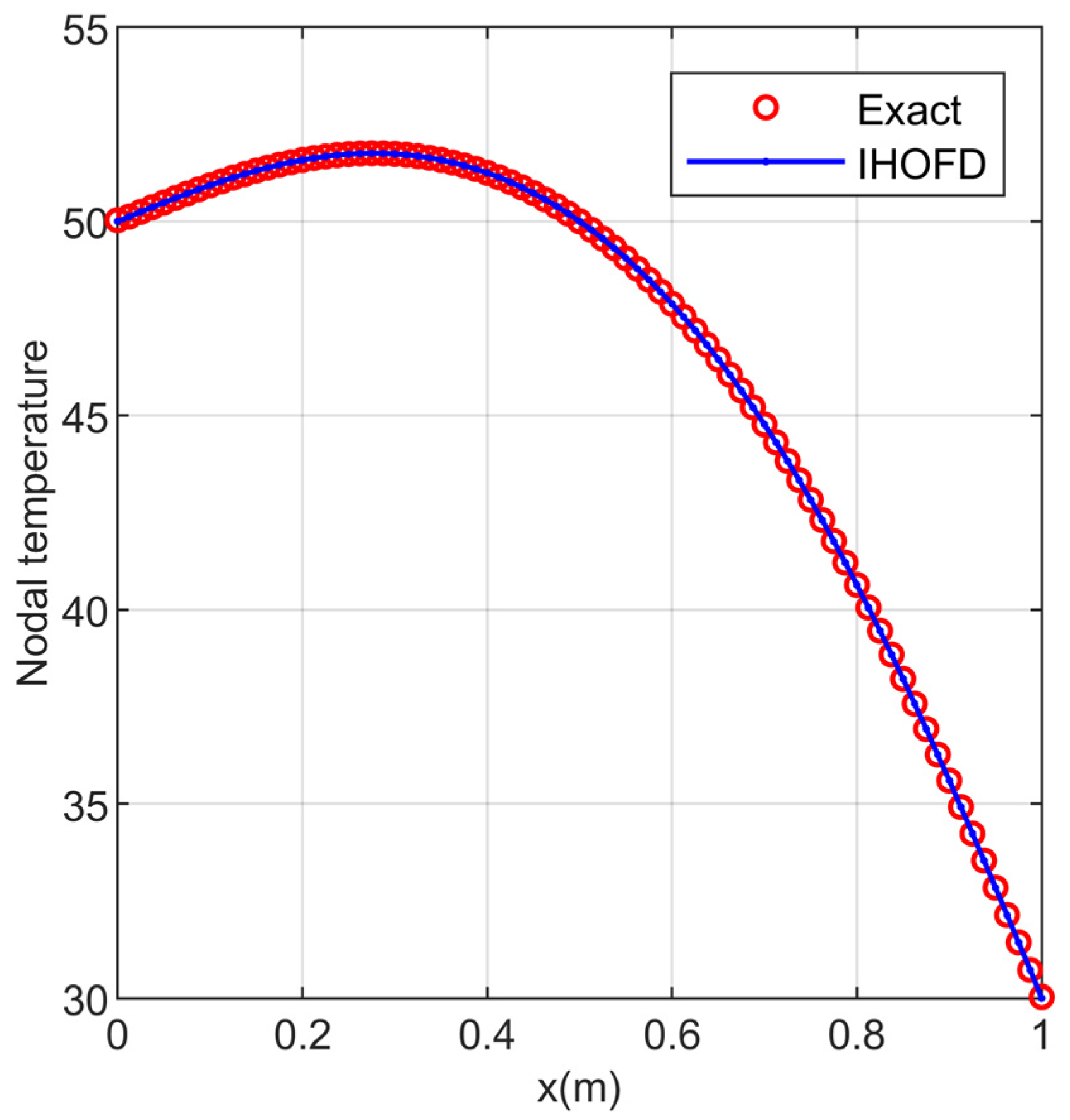
When the mesh size and the time step are the same as that of the fourth-order IHOFD algorithms in Section 5.3, the RE and MAE between the simulation result of the fourth-order IHOFD algorithm and the exact solution under the asymmetric boundary conditions are 6.082 × 10−4 and 1.412 × 10−2 (°C) in Figure 7. Compared with the result of the fourth-order IHOFD algorithm (see Table 6), it can be seen that the accuracy of the two is almost the same. It can be concluded that the IHOFD algorithm is also valid for the asymmetric boundary conditions.
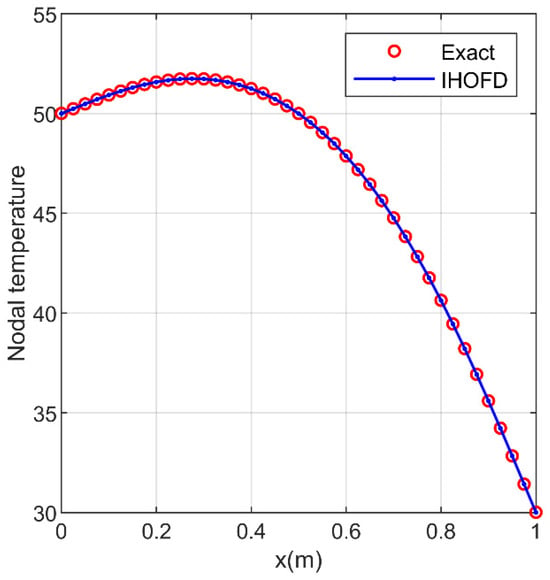
Figure 7.
Numerical simulation of the fourth-order IHOFD algorithm under the asymmetric boundary conditions and the exact solution of two-dimensional HCEs (the centerline of = 0.5 m is distributed along the axis, with temperature in (°C)).
To compare the results of the IHFOD algorithm for different grid densities (sizes), here, the thermal parameters are the same as in the above. the calculation domain was divided into 81 × 81 rectangular mesh nodes with a mesh size of 0.0125 m, the time is 1.0 s, and the stability Equation (19b) determines the time step . The RE and MAE between the simulation result of the fourth-order IHOFD algorithm with a grid density of 81 × 81 and the exact solution are 2.675 × 10−5 and 3.633 × 10−3 (°C) in Figure 8, respectively. The simulation errors of the fourth-order IHOFD algorithm with a grid density of 81 × 81 are significantly smaller compared to that with a grid density of 41 × 41 (see Figure 7). It can be concluded that the simulation accuracy of the IHOFD algorithm also improves significantly as the grid density increases.
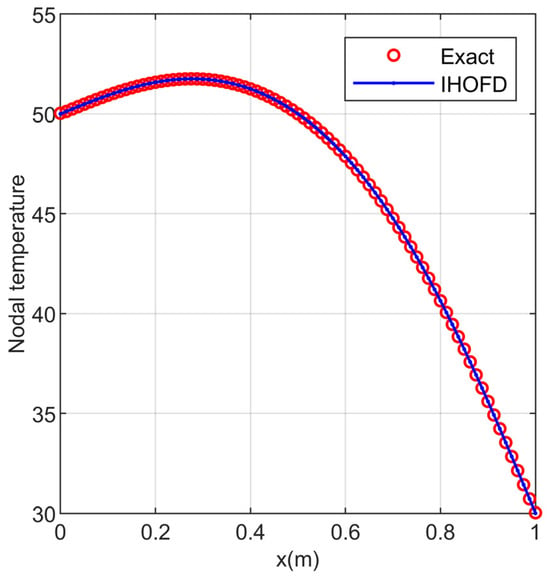
Figure 8.
Numerical simulation of the 4th-order IHOFD algorithm with a grid density of 81 × 81 and the exact solution of two-dimensional HCEs (the centerline of = 0.5 m is distributed along the axis, with temperature in (°C)).
In summary, the main advantages of the proposed algorithms can be obtained as follows: (1) The stability factor of the LHOFD algorithm is slightly higher than that of the conventional algorithm (such as the GHOFD algorithm [26]). The stability factor of the IHOFD algorithm is twice the conventional algorithm, and the maximum absolute error of the thermal simulation is within 0.015 (°C). (2) The proposed algorithms are valid under both symmetric and asymmetric boundary conditions. (3) The simulation accuracy of the proposed algorithms also improves significantly as the grid density increases.
6. Conclusions
In this paper, the main contributions of this work are as follows:
- (1)
- We present an LHOFD algorithm to numerically solve the 2D transient HCEs, and develop an IHOFD algorithm using stability analysis and a stencil combination optimization strategy to improve the stability of the LHOFD algorithm. The proposed algorithms are valid under both symmetric and asymmetric boundary conditions. The stability factor of the LHOFD algorithm is slightly higher than that of the conventional algorithm. The stability factor of the IHOFD algorithm is twice the conventional algorithm, and the maximum absolute error of the thermal simulation is within 0.015 (°C).
- (2)
- Based on the standard Taylor expansion and the Lagrange interpolation formula, we derive the formulas of the general high-order central FD (HOCFD) coefficients and the truncation error coefficient as well as the high-order non-central FD (HONFD) coefficients and the truncation error coefficient of fourth-order spatial derivative in a concise and clear way, and provide another way to calculate high-order FD coefficients and its truncation error coefficient.
- (3)
- A unified analytical formula for the general HOCFD and HONFD coefficients that can calculate the spatial derivative of any integer order is also derived, which can be applied to the numerical calculation of the HOFD methods in a regular mesh domain for different types of integer-order partial differential equations, including heat conduction equation.
- (4)
- We propose a new strategy of combination with the HOCFD and HONFD approximations under the same high-order accuracy, namely that of using the internal computational domain to calculate the mixed derivatives of the boundary domains, which has higher accuracy, no additional computational cost, and is easy to implement.
Author Contributions
Methodology, Validation, Writing—original draft, Y.P.; Writing—review and editing, H.J.; Conceptualization, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon request due to restrictions privacy. The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to the project containing this study is still in development.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Thermal conductivity coefficient | Density | ||
| Specific heat capacity | Thermal conductivity | ||
| Time step | Temperature field | ||
| Number of time step iterations | HONFD operator coefficient | ||
| Operator of derivative | Length of the HONFD operator | ||
| Order number of the operator | Stencil vector element of the HONFD operator | ||
| Weighting coefficient | Arbitrary order of the space derivative | ||
| Numerical simulation result | Length of the shortest operator | ||
| Exact solution | Stability factor | ||
| Mesh interval along the x coordinate | Parameters of stability factor | ||
| Mesh interval along the y coordinate | Total point numbers | ||
| Operator coefficient of the second-order spatial derivative | Number of meshes along the x coordinate | ||
| Operator coefficient of the fourth-order spatial derivative | Number of meshes along the y coordinate | ||
| Coefficients matrix of the fourth-order spatial mixed derivative | Mesh interval () |
Appendix A. The Formula for the HOCFD Coefficients of the Fourth-Order Spatial Derivative
An HOCFD operator of the fourth-order derivative in space with the -order-accuracy can be approximated as
Based on the Taylor expansion of at the points , we obtain (2L + 2)-order expression as
where is the length of the HOCFD operator, is the spatial mesh size in the direction , represents the number of mesh points, and , represents the th order derivative of at the point .
Then, Equation (A2) can be expressed as a matrix form and simplified, thus we obtain
By solving Equation (A3), the formula of the HOCFD operator coefficients can be obtained as
- (1)
- , ,
- (2)
- , , ,
- (3)
From Equation (A2), the truncation error coefficient of the HOCFD operator can be written as
Appendix B. The Formula for the HONFD Coefficients of the Fourth-Order Spatial Derivative
An HONFD operator of the fourth-order derivative in space with the ()-order-accuracy can be approximated as
The general form of the HONFD operator can be also expressed as a vector , represents the length of the operator, and is an odd number greater than or equal to 5. Where , and , , are all positive integers, and is also a vector. represents the ordinal numbers of the vector elements of the HONFD operator from left to right, ,. and represents the mesh size along the coordinate.
Similar to the above, we obtain the following expression as
where represents the number of mesh points, indicates the derivation at the location . represents with a derivative of the order at the location .
Equation (A7) can be expressed as a matrix form and simplified to obtain
The coefficient matrix is a Vandermonde matrix. Directly using Cramer’s rule, Equation (A8) can be easily solved to obtain the HONFD coefficients . However, for a higher-order Vandermonde problem, it is quite commonly a singularity, thus affecting the accuracy of the HONFD coefficients. Inspired by [32], we develop a general HONFD coefficient formula in different ways, so as to solve the problem well.
Consider Equation (A8) as a polynomial function, that is
and , , denotes the column vector or column matrix element, where , and the other is zero. The elements of the vector of the HONFD operator are different from each other. Thus, the coefficient matrix determinant , therefore can be expressed as the Lagrange interpolation formula, i.e.,
Expanding the numerator of Equation (A10) into a polynomial form and comparing it with Equation (A9), we obtain
where represents different natural numbers.
From Equation (A7), we can obtain the truncation error coefficient of the HONFD operator of the fourth-order derivative in space with ()-order-accuracy, namely
Appendix C. Stability Formula of the LHOFD Scheme
According to the von Neumann stability analysis [34], in the wavenumber domain, let , and then the LHOFD Algorithm (2) for 2D transient HCEs can be expressed as
where
where , , represent the HOFD coefficients of the second-order derivative, the fourth-order derivative, and the fourth-order mixed derivative in space, respectively. Similarly, L represents half the length of the HOFD operator. From (A13), we obtain
According to Shannon’s law of sampling, then
Combining Equations (A14) and (A16) with (A15) and simplifying to obtain
where , , is a maximum odd number not exceeding L, and . From Equation (A14), the stability formula of the LHOFD algorithm for 2D transient HCEs can be expressed as
References
- Ali, M.E.; Loskor, W.Z.; Taher, S.; Bilkis, F. Solution of a One-Dimension Heat Equation Using Higher-Order Finite Difference Methods and Their Stability. J. Appl. Math. Phys. 2022, 10, 877–886. [Google Scholar] [CrossRef]
- Hassan, H.; Shafey, N.Y.A.; Uddin, Z.; Hawwash, A.A. 3D investigation on the impact of chips positions and number on their cooling inside cavity. J. Mech. Sci. Technol. 2021, 35, 5233–5244. [Google Scholar] [CrossRef]
- Xiong, Z.; Wang, X.; He, M.; Benabou, L.; Feng, Z. Investigation on thermal conductivity of silver-based porous materials by finite difference method. Mater. Today Commun. 2022, 33, 104897. [Google Scholar] [CrossRef]
- Zhang, H.; Geng, J.; Zhu, S.; Zhao, Y.; Ji, S.; Guo, X.; Tong, Z.; Li, D. An effective method for large-scale temperature simulation in SLM based on the finite difference. Numer. Heat Transfer Part A Appl. 2022, 83, 503–521. [Google Scholar] [CrossRef]
- Lax, P.D.; Wendroff, B. Difference schemes for hyperbolic equations with high order of accuracy. Commun. Pure Appl. Math. 1964, 17, 381–398. [Google Scholar] [CrossRef]
- Blanch, J.O.; Robertsson, J.O.A. A modified Lax-Wendroff correction for wave propagation in media described by Zener elements. Geophys. J. Int. 1997, 131, 381–386. [Google Scholar] [CrossRef]
- Chen, J.-B. A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation. Geophysics 2011, 76, T37–T42. [Google Scholar] [CrossRef]
- Amundsen, L.; Pedersen, Ø. Time step n-tupling for wave equations. Geophysics 2017, 82, T249–T254. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, H. Reducing computation cost by Lax-Wendroff methods with fourth-order temporal accuracy. Geophysics 2019, 84, T109–T119. [Google Scholar] [CrossRef]
- Ren, Z.; Bao, Q.; Gu, B. Time-dispersion correction for arbitrary even-order Lax-Wendroff methods and the application on full-waveform inversion. Geophysics 2021, 86, T361–T375. [Google Scholar] [CrossRef]
- Tan, S.; Huang, L. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation. Geophys. J. Int. 2014, 197, 1250–1267. [Google Scholar] [CrossRef]
- Wang, E.; Liu, Y.; Sen, M.K. Effective finite-difference modelling methods with 2-D acoustic wave equation using a combination of cross and rhombus stencils. Geophys. J. Int. 2016, 206, 1933–1958. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Wang, Z.; Zhang, S. Dispersion-relationship-preserving seismic modelling using the cross-rhombus stencil with the finite-difference coefficients solved by an over-determined linear system. Geophys. Prospect. 2020, 68, 1771–1792. [Google Scholar] [CrossRef]
- Titarev, V.A.; Toro, E.F. ADER: Arbitrary High Order Godunov Approach. J. Sci. Comput. 2002, 17, 609–618. [Google Scholar] [CrossRef]
- Toro, E.; Titarev, V. ADER schemes for scalar non-linear hyperbolic conservation laws with source terms in three-space dimensions. J. Comput. Phys. 2005, 202, 196–215. [Google Scholar] [CrossRef]
- Toro, E.F.; Titarev, V.A. TVD Fluxes for the High-Order ADER Schemes. J. Sci. Comput. 2005, 24, 285–309. [Google Scholar] [CrossRef]
- Arar, N.; Kaki, L.A.; Ben Makhlouf, A. Highly Efficacious Sixth-Order Compact Approach with Nonclassical Boundary Specifications for the Heat Equation. Math. Probl. Eng. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Yosaf, A.; Rehman, S.U.; Ahmad, F.; Ullah, M.Z.; Alshomrani, A.S. Eighth-Order Compact Finite Difference Scheme for 1D Heat Conduction Equation. Adv. Numer. Anal. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Hajipour, M.; Jajarmi, A.; Malek, A.; Baleanu, D. Positivity-preserving sixth-order implicit finite difference weighted essentially non-oscillatory scheme for the nonlinear heat equation. Appl. Math. Comput. 2018, 325, 146–158. [Google Scholar] [CrossRef]
- Ecer, A.; Gopalaswamy, N.; Akay, H.U.; Chien, Y.P. Digital Filtering Techniques for Parallel Computation of Explicit Schemes. Int. J. Comput. Fluid Dyn. 2000, 13, 211–222. [Google Scholar] [CrossRef]
- Sarris, C.D. Extending the Stability Limit of the FDTD Method With Spatial Filtering. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 176–178. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, J.; Yao, Z. Extending the stability limit of explicit scheme with spatial filtering for solving wave equations. J. Comput. Phys. 2019, 397, 108853. [Google Scholar] [CrossRef]
- Gaffar, M.; Jiao, D. Alternative Method for Making Explicit FDTD Unconditionally Stable. IEEE Trans. Microw. Theory Tech. 2015, 63, 4215–4224. [Google Scholar] [CrossRef]
- Li, X.; Sarris, C.D.; Triverio, P. Overcoming the FDTD stability limit via model order reduction and eigenvalue perturbation. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–3. [Google Scholar]
- Gao, Y.; Zhang, J.; Yao, Z. Removing the stability limit of the explicit finite-difference scheme with eigenvalue perturbation. Geophysics 2018, 83, A93–A98. [Google Scholar] [CrossRef]
- Pei, Y.; Liu, J.; Li, W. A general high-order finite difference scheme for two-dimensional transient thermal simulation. Numer. Heat Transf. B Fundam. 2023; Unpublished Manuscript. [Google Scholar]
- Jo, C.; Shin, C.; Suh, J.H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics 1996, 61, 529–537. [Google Scholar] [CrossRef]
- Fornberg, B. Classroom Note:Calculation of Weights in Finite Difference Formulas. SIAM Rev. 1998, 40, 685–691. [Google Scholar] [CrossRef]
- Liu, Y.; Sen, M.K. A new time–space domain high-order finite-difference method for the acoustic wave equation. J. Comput. Phys. 2009, 228, 8779–8806. [Google Scholar] [CrossRef]
- Hicks, J.S.; Wei, J. Numerical Solution of Parabolic Partial Differential Equations With Two-Point Boundary Conditions by Use of the Method of Lines. J. ACM 1967, 14, 549–562. [Google Scholar] [CrossRef]
- Fukuchi, T. Finite difference method and algebraic polynomial interpolation for numerically solving Poisson’s equation over arbitrary domains. AIP Adv. 2014, 4, 060701. [Google Scholar] [CrossRef]
- Dai, W. A new accurate finite difference scheme for Neumann (insulated) boundary condition of heat conduction. Int. J. Therm. Sci. 2010, 49, 571–579. [Google Scholar] [CrossRef]
- Li, S.; Sun, C. An improved 25-point finite-difference scheme for frequency-domain elastic wave modelling. Geophys. Prospect. 2022, 70, 702–724. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).