A Modified Model for Identifying the Characteristic Parameters of Machine Joint Interfaces
Abstract
:1. Introduction
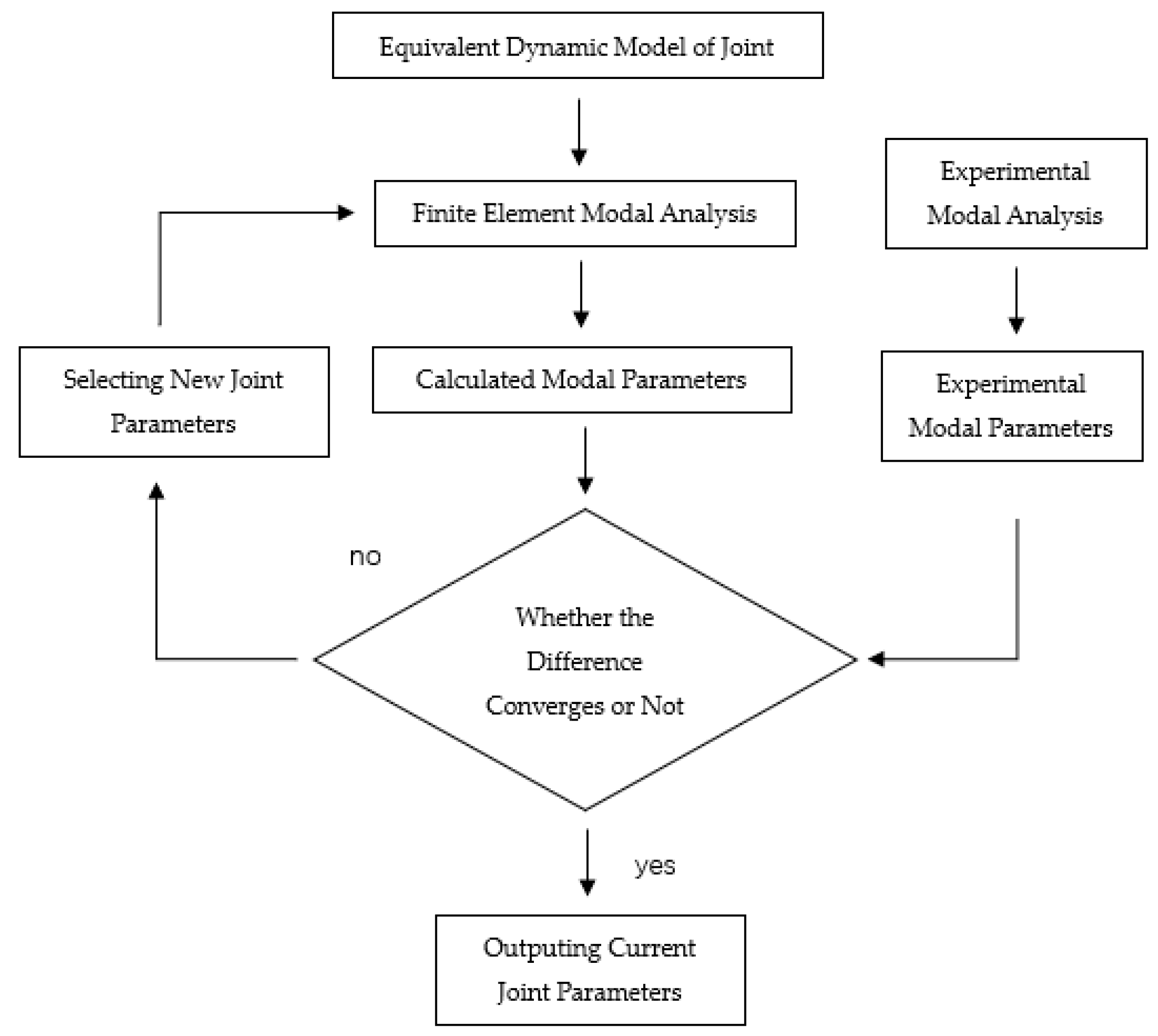
2. Stiffness Identification Method Based on Joint Simulation
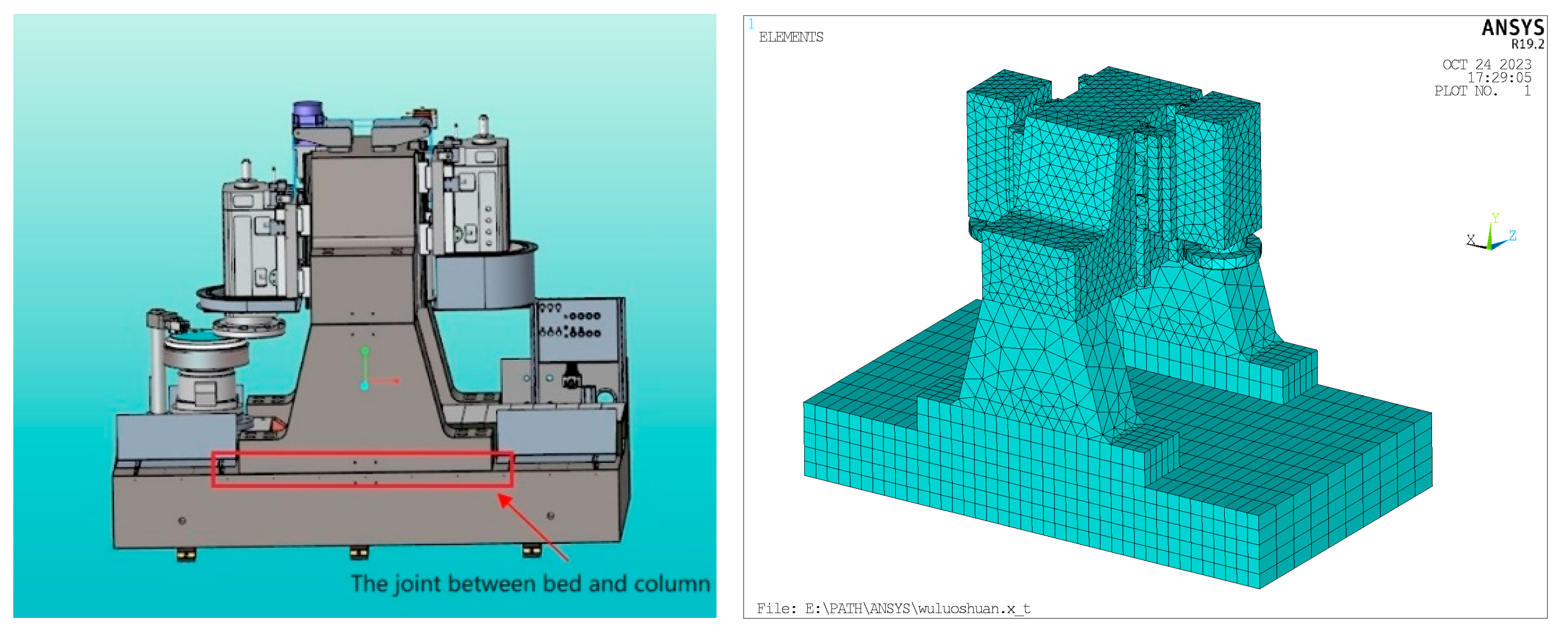
2.1. Principle of Joint Simulation Method Based on Matlab and Ansys
2.2. Method Verification
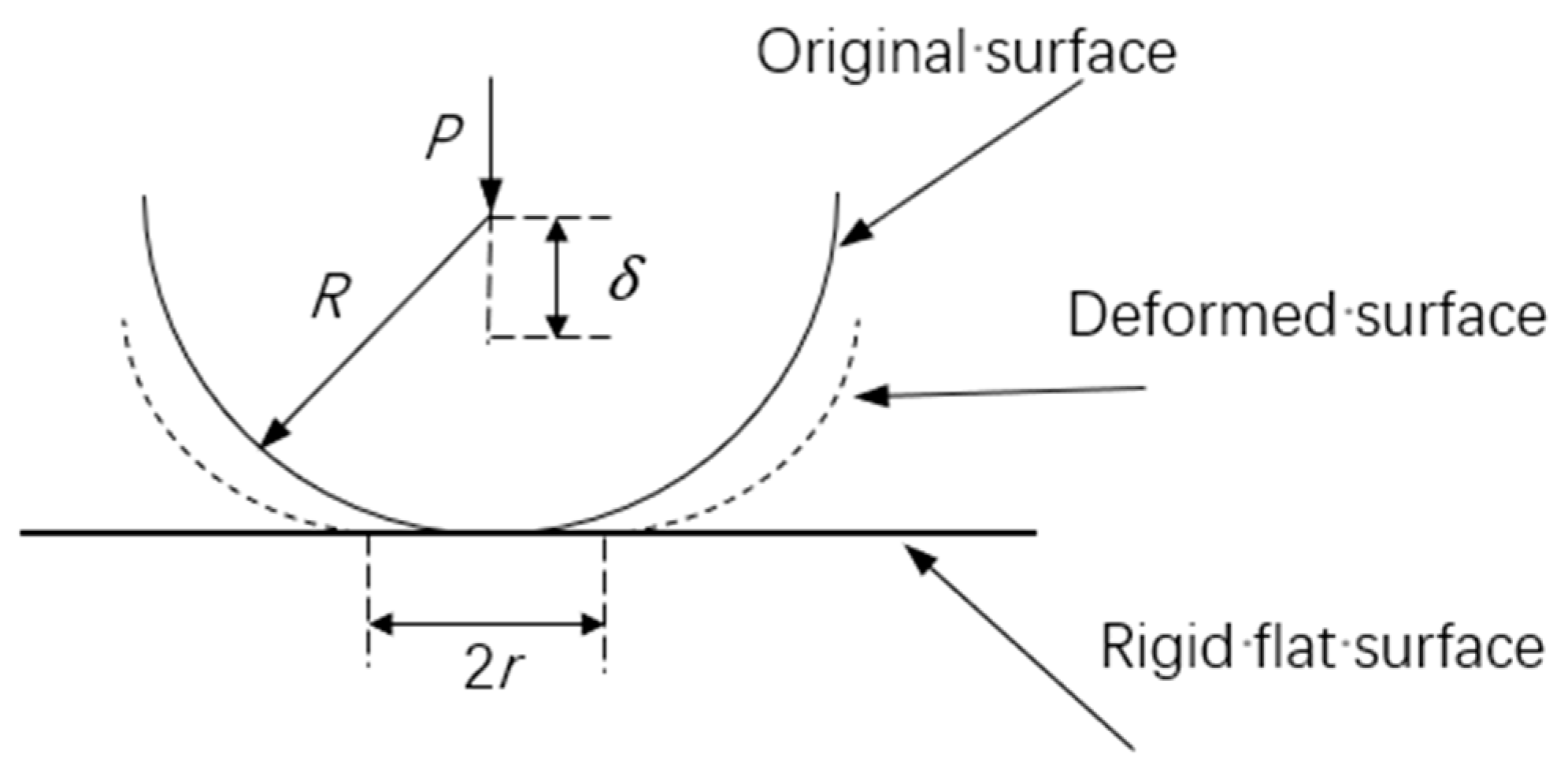
3. Modification of the Normal Stiffness Fractal Model for Joint
3.1. Total Normal Load of Joint
3.2. Total Normal Stiffness of Joint
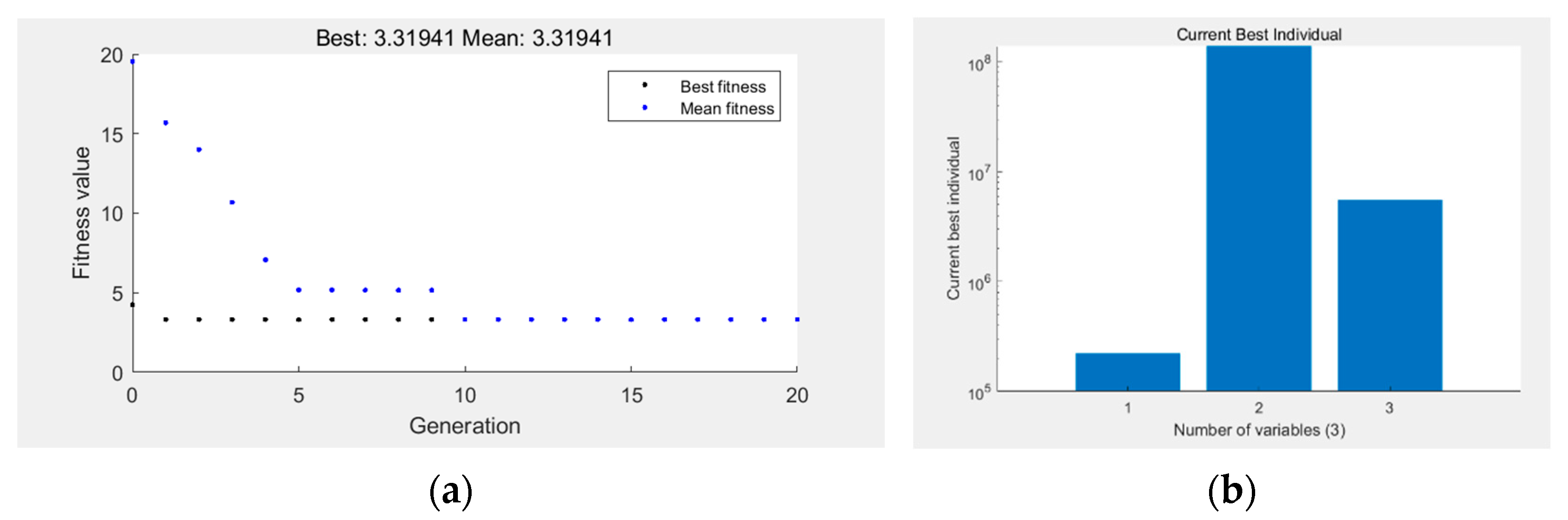
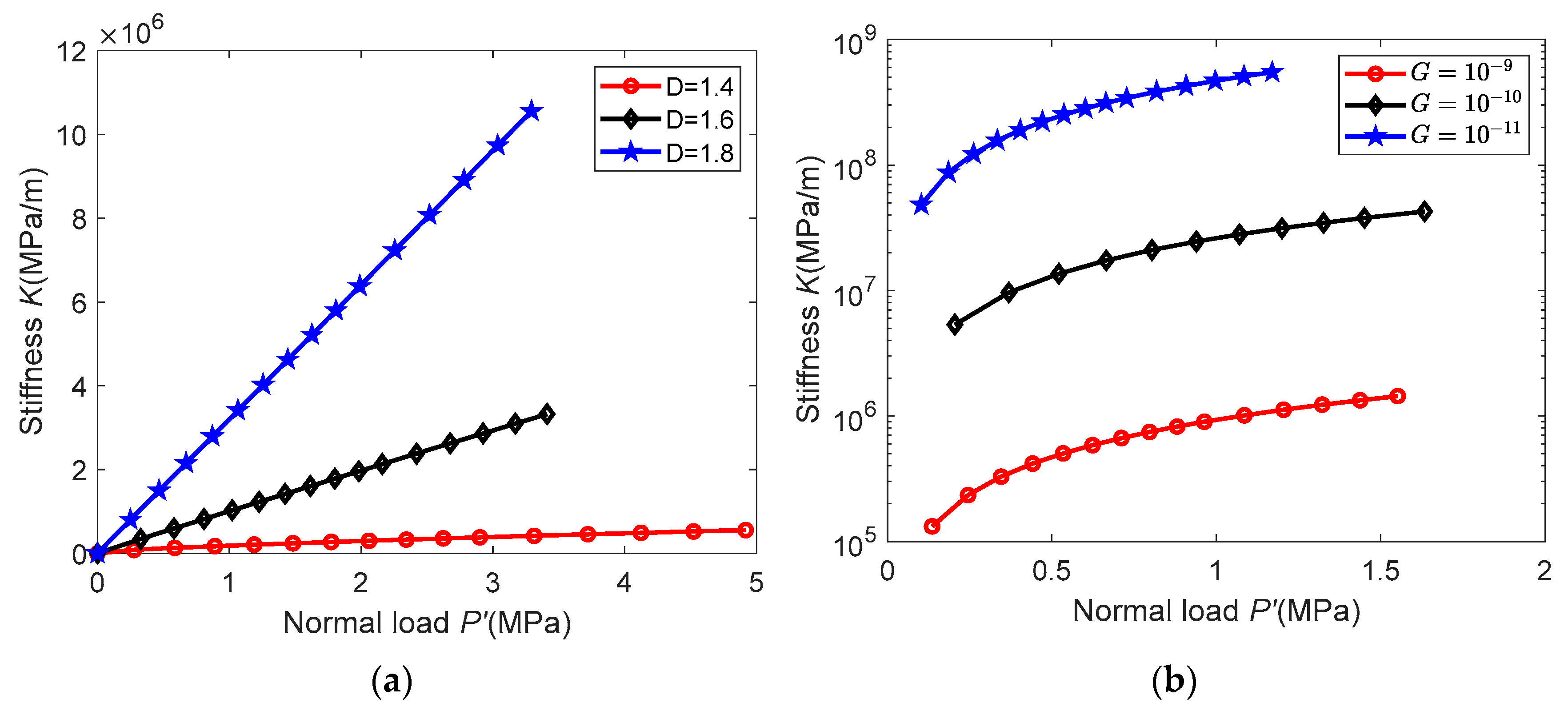
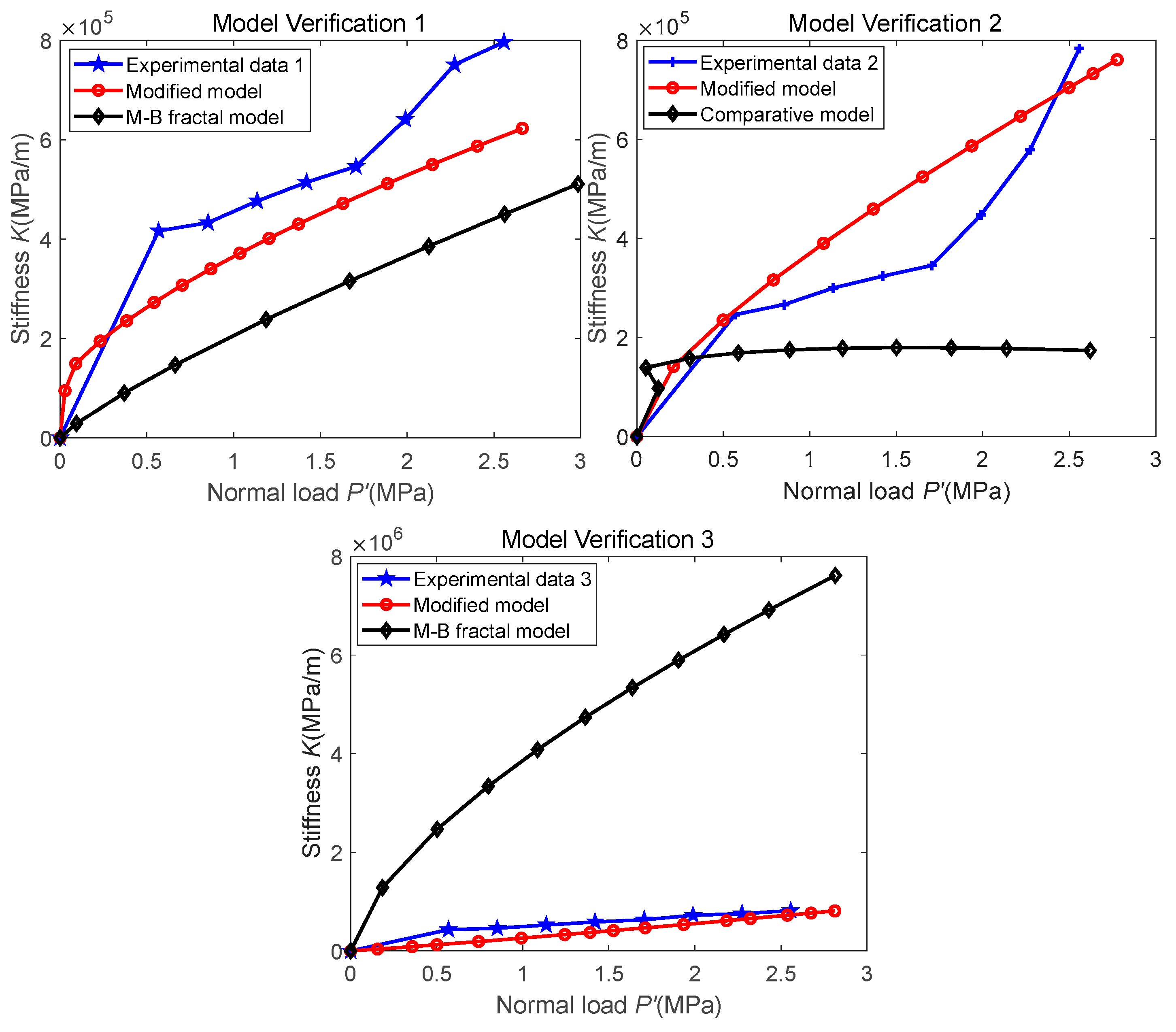
3.3. Numerical Simulation and Model Verification
4. Three-Dimensional Fractal Model
4.1. Total Load and Total Stiffness
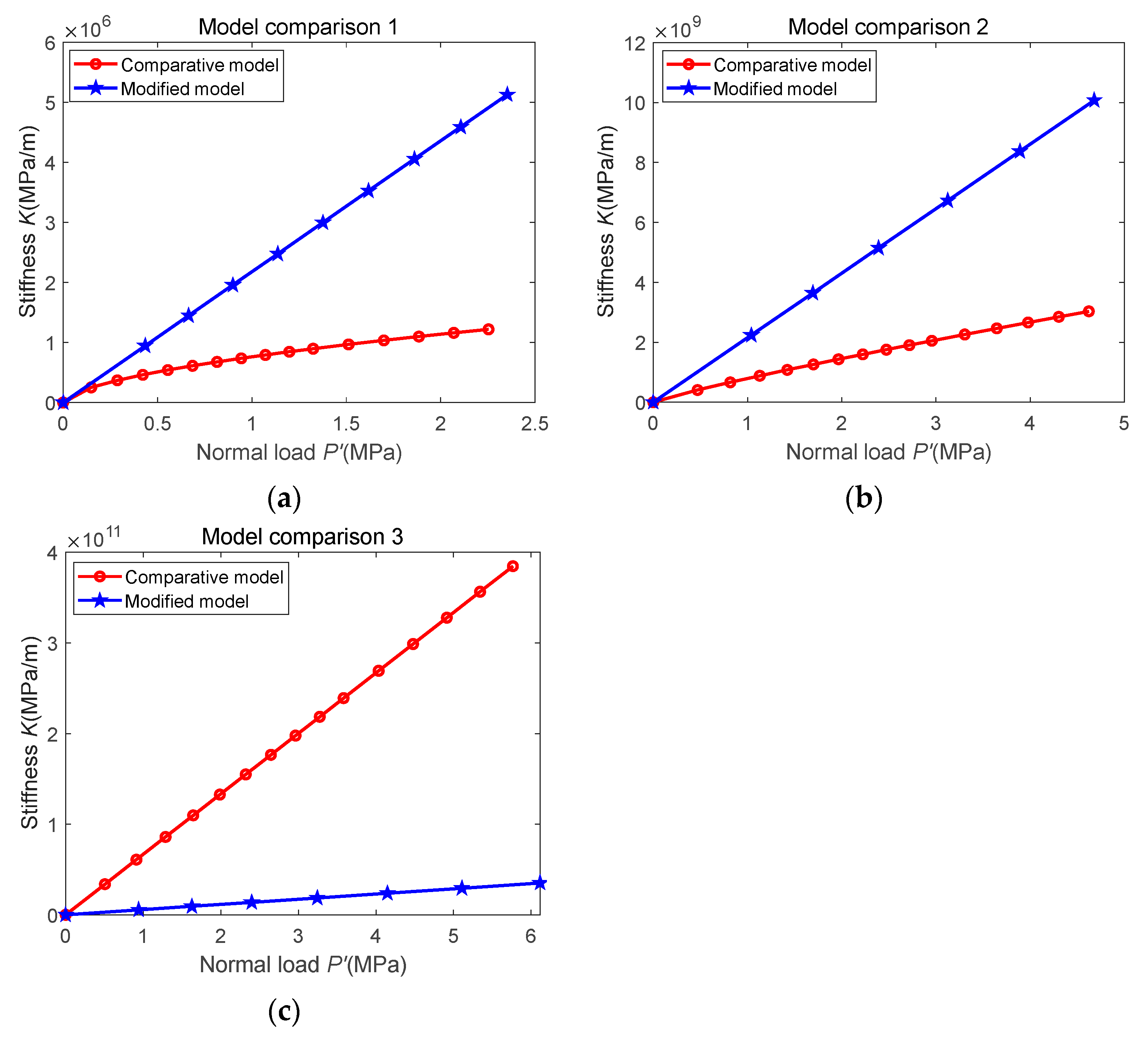
4.2. Numerical Simulation
5. Conclusions
- The method based on joint simulation in Matlab and Ansys can identify the joint stiffness quickly and accurately;
- Simulation of the dynamic performance of a machine tool considering the joint is closer to the experimental data than without considering the joint;
- The existence of the joint reduces the overall natural frequencies of the machine tool;
- The 2D fractal model is more accurate after considering the asperity interaction and elastic–plastic deformation. The normal stiffness increases with the increase in normal load and D and increases with the decrease in G;
- The calculated stiffness of the 3D fractal model is greater than that of the 2D fractal model, and the 3D fractal model can more accurately characterize the actual surface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.L. Dynamic Characterization and Applications for Machine Joint Interfaces; Science and Technology of China Press: Beijing, China, 2002. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A finite element based elastic-plastic model for the contact of rough surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Chang, W.R.; Etsion, I.; Bogy, D.B. An elastic-plastic model for the contact of rough surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Ciavarella, M.; Greenwood, J.A.; Paggi, M. Inclusion of “interaction” in the Greenwood and Williamson contact theory. Wear 2008, 265, 729–734. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, L.; Zhu, C. Research on fractal model of normal contact stiffness for mechanical joint considering asperity interaction. Int. J. Mech. Sci. 2017, 134, 357–369. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, J.; Zhang, Z.; Hong, J. Normal contact stiffness model considering 3D surface topography and actual contact status. Mech. Sci. 2021, 12, 41–50. [Google Scholar] [CrossRef]
- Xue, P.; Zhu, C.; Wang, R.; Zhu, L. Research on dynamic characteristics of oil-bearing joint surface in slide guides. Mech. Based Des. Struct. Mach. 2022, 50, 1893–1913. [Google Scholar] [CrossRef]
- Jiang, K.; Liu, Z.; Yang, C.; Zhang, C.; Tian, Y.; Zhang, T. Effects of the joint surface considering asperity interaction on the bolted joint performance in the bolt tightening process. Tribol. Int. 2022, 167, 107408. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Shi, X.; Ma, S.; Cai, A. Contact stiffness model of joint surface considering continuous smooth characteristics and asperity interaction. Tribol. Lett. 2021, 69, 1–12. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Stanway, R. Identification of structural vibration parameters by using a frequency domain filter. J. Sound Vib. 1986, 109, 495–506. [Google Scholar] [CrossRef]
- Tsai, J.S.; Chou, Y.F. The identification of dynamic characteristics of a single bolt joint. J. Sound Vib. 1988, 125, 487–502. [Google Scholar] [CrossRef]
- Syed Asif, S.A.; Wahl, K.J.; Colton, R.J.; Warren, O.L. Quantitative imaging of nanoscale mechanical properties using hybrid nanoindentation and force modulation. J. Appl. Phys. 2001, 90, 1192–1200. [Google Scholar] [CrossRef]
- Kartal, M.E.; Mulvihill, D.M.; Nowell, D.; Hills, D.A. Determination of the frictional properties of titanium and nickel alloys using the digital image correlation method. Exp. Mech. 2011, 51, 359–371. [Google Scholar] [CrossRef]
- Mulvihill, D.M.; Brunskill, H.; Kartal, M.E.; Dwyer-Joyce, R.S.; Nowell, D. A comparison of contact stiffness measurements obtained by the digital image correlation and ultrasound techniques. Exp. Mech. 2013, 53, 1245–1263. [Google Scholar] [CrossRef]
- Jamia, N.; Jalali, H.; Taghipour, J.; Friswell, M.I.; Khodaparast, H.H. An equivalent model of a nonlinear bolted flange joint. Mech. Syst. Signal Process. 2021, 153, 107507. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, L. A model of asperity interactions in elastic-plastic contact of rough surfaces. J. Trib. 2001, 123, 857–864. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Li, X.P.; Zhao, G.H.; Liang, Y.M. Fractal model and simulation of normal contact stiffness between two cylinders’ joint surfaces. Trans. Chin. Soc. Agric. Mach. 2013, 44, 277–281. [Google Scholar]
- Li, X.P.; Wang, X.; Yun, H.M.; Gao, J.Z. Investgation into normal contact stiffness of fixed joint surface with three-dimensional fractal. J. S. China Univ. Technol. Nat. Sci. Ed. 2016, 1, 114–122. [Google Scholar]

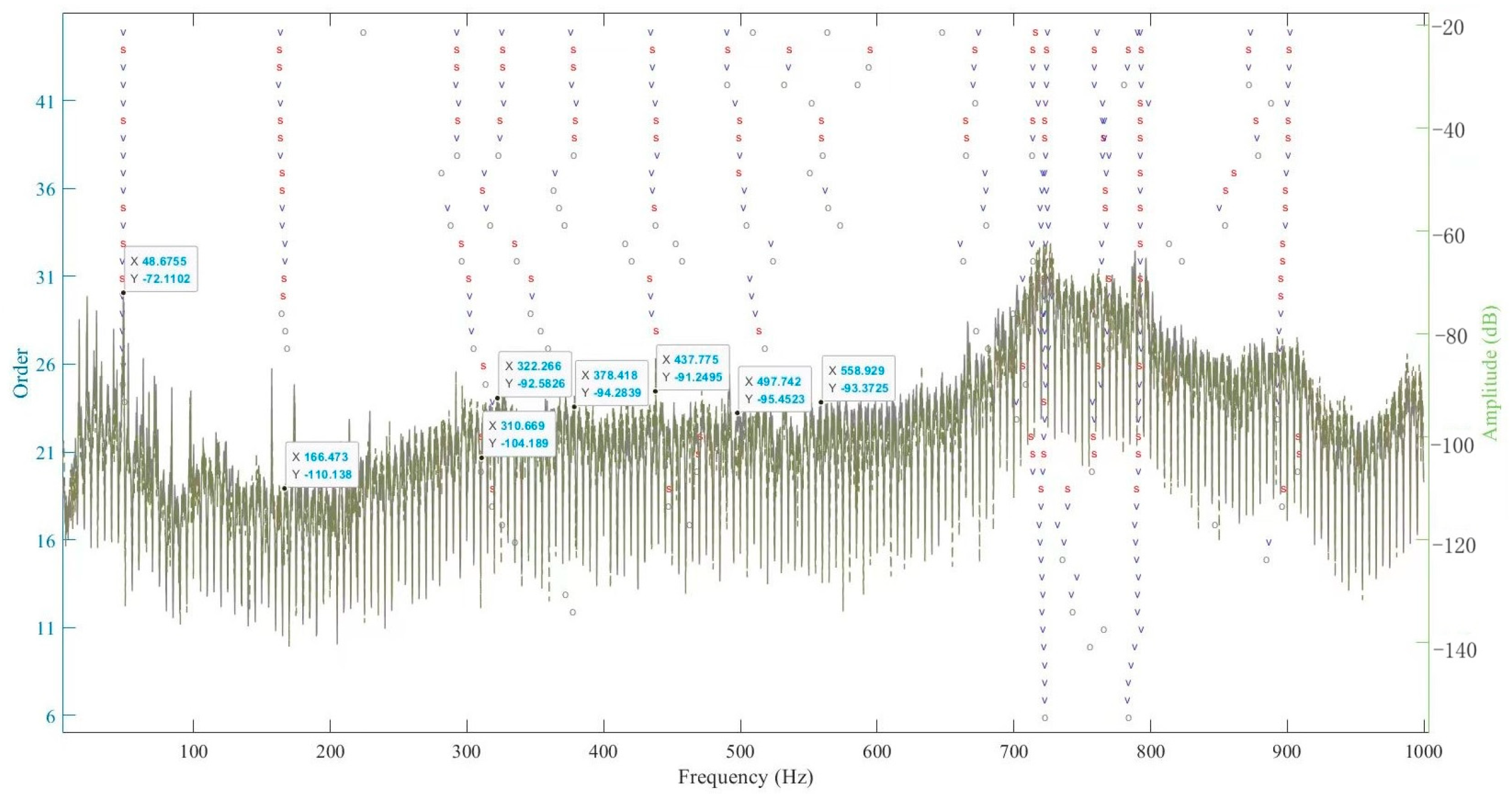



| First Order (Hz) | Second Order (Hz) | Third Order (Hz) | |
|---|---|---|---|
| Experiment | 48.7 | 166.5 | 310.7 |
| Considering joint | 48.8 | 165.8 | 313.6 |
| Without considering joint | 402.1 | 842.5 | 1068.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Liu, J.; Wang, L.; Zhao, Y.; Li, F. A Modified Model for Identifying the Characteristic Parameters of Machine Joint Interfaces. Appl. Sci. 2023, 13, 11680. https://doi.org/10.3390/app132111680
Liu K, Liu J, Wang L, Zhao Y, Li F. A Modified Model for Identifying the Characteristic Parameters of Machine Joint Interfaces. Applied Sciences. 2023; 13(21):11680. https://doi.org/10.3390/app132111680
Chicago/Turabian StyleLiu, Kexian, Junfeng Liu, Linfeng Wang, Yuqian Zhao, and Fei Li. 2023. "A Modified Model for Identifying the Characteristic Parameters of Machine Joint Interfaces" Applied Sciences 13, no. 21: 11680. https://doi.org/10.3390/app132111680
APA StyleLiu, K., Liu, J., Wang, L., Zhao, Y., & Li, F. (2023). A Modified Model for Identifying the Characteristic Parameters of Machine Joint Interfaces. Applied Sciences, 13(21), 11680. https://doi.org/10.3390/app132111680







