Cardiac Electrophysiology Meshfree Modeling through the Mixed Collocation Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mixed Collocation Form of the Monodomain Equation
2.1.1. Deriving the Mixed Collocation Form
2.1.2. Boundary Conditions Imposition
2.2. Interpolating Meshfree Approximants
2.2.1. Radial Point Interpolation
2.2.2. Moving Kriging Interpolation
3. Results
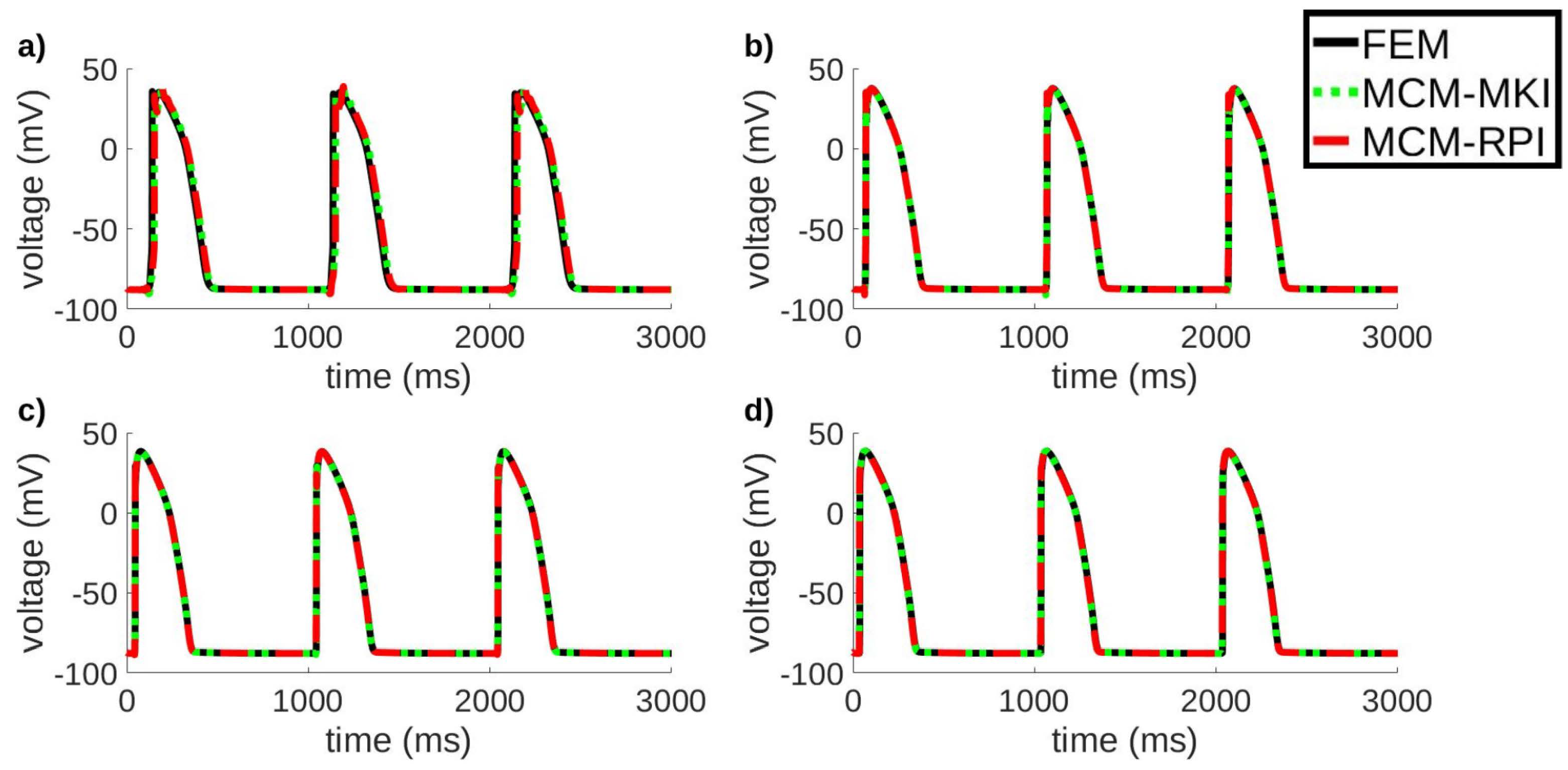
3.1. Electrical Propagation in a 2D Tissue Sheet
3.2. Electrical Propagation in a 3D Tissue Slab
3.3. Electrical Propagation in the Niederer Benchmark Geometry
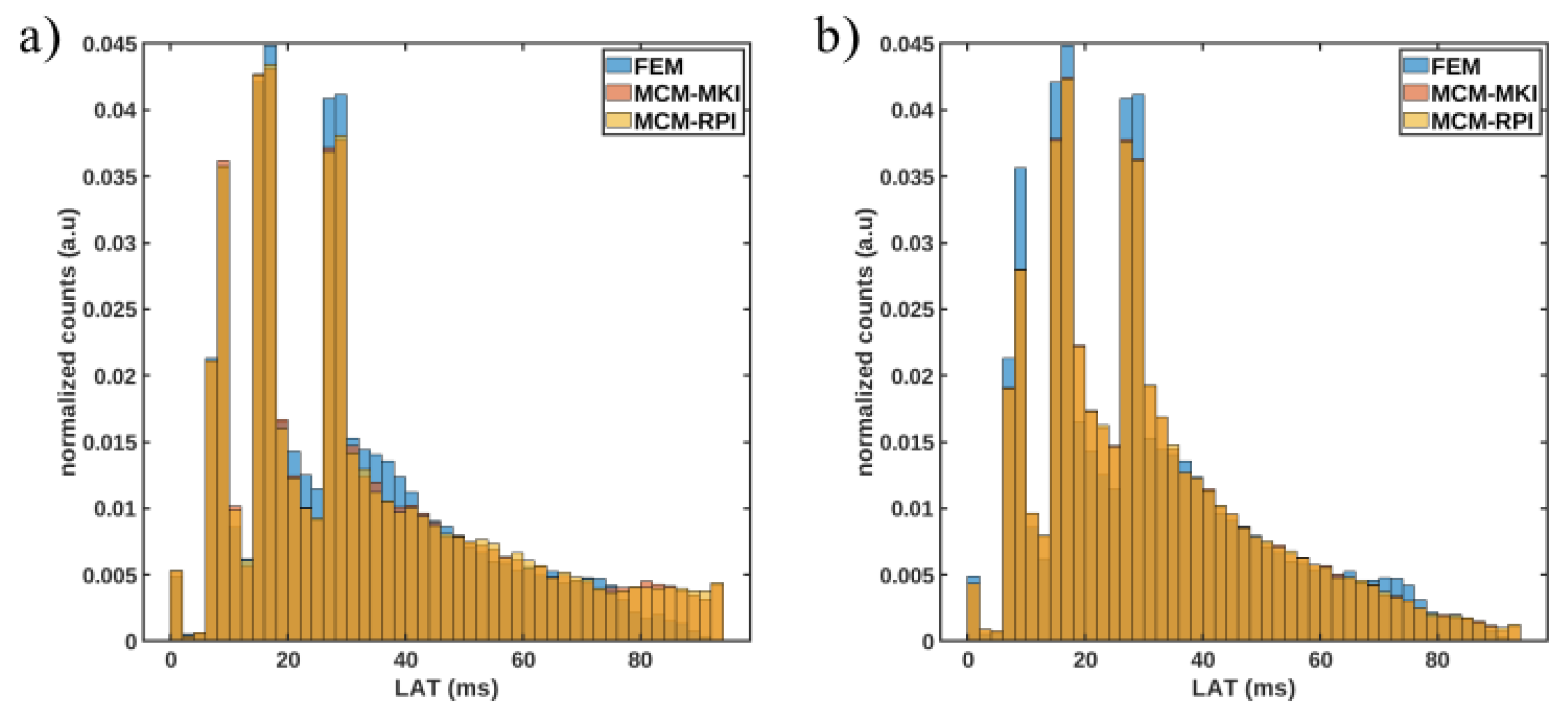
3.4. Electrical Propagation in 3D Biventricular Geometry with Irregular Nodal Distribution
3.5. Electrical Propagation in 3D Biventricular Geometry with Immersed Grid Nodal Distribution
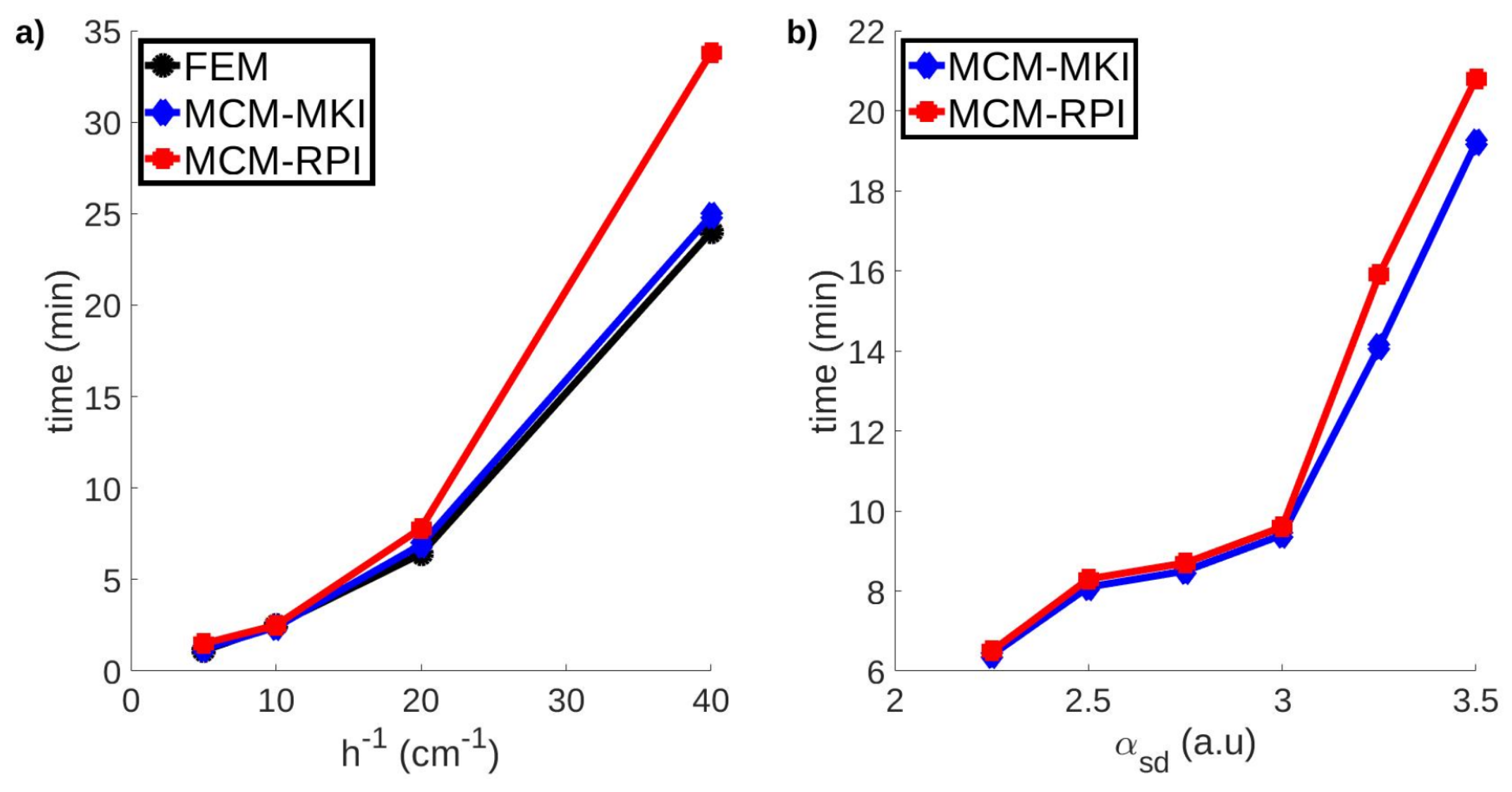
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lopez-Perez, A.; Sebastian, R.; Ferrero, J.M. Three-dimensional cardiac computational modelling: Methods, features and applications. Biomed. Eng. Online 2015, 14, 35. [Google Scholar] [CrossRef] [PubMed]
- Niederer, S.A.; Lumens, J.; Trayanova, N.A. Computational models in cardiology. Nat. Rev. Cardiol. 2019, 16, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Sampedro-Puente, D.A.; Raphel, F.; Fernandez-Bes, J.; Laguna, P.; Lombardi, D.; Pueyo, E. Characterization of spatio-temporal cardiac action potential variability at baseline and under β-adrenergic stimulation by combined unscented Kalman filter and double greedy dimension reduction. IEEE J. Biomed. Health Inform. 2020, 25, 276–288. [Google Scholar] [CrossRef] [PubMed]
- Rama, R.R.; Skatulla, S. Towards real-time cardiac mechanics modelling with patient-specific heart anatomies. Comput. Methods Appl. Mech. Eng. 2018, 328, 47–74. [Google Scholar] [CrossRef]
- Pueyo, E.; Dangerfield, C.; Britton, O.; Virág, L.; Kistamás, K.; Szentandrássy, N.; Jost, N.; Varró, A.; Nánási, P.P.; Burrage, K.; et al. Experimentally-based computational investigation into beat-to-beat variability in ventricular repolarization and its response to ionic current inhibition. PLoS ONE 2016, 11, e0151461. [Google Scholar] [CrossRef]
- Chabiniok, R.; Wang, V.Y.; Hadjicharalambous, M.; Asner, L.; Lee, J.; Sermesant, M.; Kuhl, E.; Young, A.A.; Moireau, P.; Nash, M.P.; et al. Multiphysics and multiscale modelling, data–model fusion and integration of organ physiology in the clinic: Ventricular cardiac mechanics. Interface Focus 2016, 6, 20150083. [Google Scholar] [CrossRef]
- Tung, L. A Bi-Domain Model for Describing Ischemic Myocardial DC Potentials. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1978. [Google Scholar]
- Keener, J.P.; Sneyd, J. Mathematical Physiology: Systems Physiology. II; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Potse, M.; Dubé, B.; Richer, J.; Vinet, A.; Gulrajani, R.M. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans. Biomed. Eng. 2006, 53, 2425–2435. [Google Scholar] [CrossRef]
- Mirams, G.R.; Arthurs, C.J.; Bernabeu, M.O.; Bordas, R.; Cooper, J.; Corrias, A.; Davit, Y.; Dunn, S.J.; Fletcher, A.G.; Harvey, D.G.; et al. Chaste: An open source C++ library for computational physiology and biology. PLoS Comput. Biol. 2013, 9, e1002970. [Google Scholar] [CrossRef]
- Vigmond, E.J.; Hughes, M.; Plank, G.; Leon, L.J. Computational tools for modeling electrical activity in cardiac tissue. J. Electrocardiol. 2003, 36, 69–74. [Google Scholar] [CrossRef]
- Lluch, È.; De Craene, M.; Bijnens, B.; Sermesant, M.; Noailly, J.; Camara, O.; Morales, H.G. Breaking the state of the heart: Meshless model for cardiac mechanics. Biomech. Model. Mechanobiol. 2019, 18, 1549–1561. [Google Scholar] [CrossRef]
- Lluch, E.; Doste, R.; Giffard-Roisin, S.; This, A.; Sermesant, M.; Camara, O.; De Craene, M.; Morales, H.G. Smoothed particle hydrodynamics for electrophysiological modeling: An alternative to finite element methods. In Proceedings of the International Conference on Functional Imaging and Modeling of The Heart, Toronto, ON, Canada, 11–13 June 2017; pp. 333–343. [Google Scholar]
- Zhang, H.; Ye, H.; Huang, W. A meshfree method for simulating myocardial electrical activity. Comput. Math. Methods Med. 2012, 2012, 936243. [Google Scholar] [CrossRef] [PubMed]
- Mountris, K.A.; Sanchez, C.; Pueyo, E. A novel paradigm for in silico simulation of cardiac electrophysiology through the Mixed Collocation Meshless Petrov-Galerkin Method. In Proceedings of the 2019 Computing in Cardiology (CinC), Singapore, 8–11 September 2019; p. 1. [Google Scholar]
- Legner, D.; Skatulla, S.; MBewu, J.; Rama, R.; Reddy, B.; Sansour, C.; Davies, N.; Franz, T. Studying the influence of hydrogel injections into the infarcted left ventricle using the element-free Galerkin method. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 416–429. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Wittek, A.; Joldes, G.; Jin, X.; Miller, K. A three-dimensional nonlinear meshfree algorithm for simulating mechanical responses of soft tissue. Eng. Anal. Bound. Elem. 2014, 42, 60–66. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Mountris, K.A.; Bourantas, G.C.; Millán, D.; Joldes, G.R.; Miller, K.; Pueyo, E.; Wittek, A. Cell-based maximum entropy approximants for three-dimensional domains: Application in large strain elastodynamics using the meshless total Lagrangian explicit dynamics method. Int. J. Numer. Methods Eng. 2020, 121, 477–491. [Google Scholar] [CrossRef]
- Chen, J.; Beraun, J.; Carney, T. A corrective smoothed particle method for boundary value problems in heat conduction. Int. J. Numer. Methods Eng. 1999, 46, 231–252. [Google Scholar] [CrossRef]
- Bonet, J.; Lok, T.S. Variational and momentum preservation aspects of smooth particle hydrodynamic formulations. Comput. Methods Appl. Mech. Eng. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Atluri, S.N. The Meshless Method (MLPG) for Domain and BIE Discretizations; Tech Science Press: Henderson, NV, USA, 2004; p. 677. [Google Scholar]
- Atluri, S.N.; Shen, S. The basis of meshless domain discretization: The meshless local Petrov-Galerkin (MLPG) method. Adv. Comput. Math. 2005, 23, 73–93. [Google Scholar] [CrossRef]
- Libre, N.; Emdadi, A.; Kansa, E.; Rahimian, M.; Shekarchi, M. A stabilized RBF collocation scheme for Neumann type boundary value problems. Comput. Model. Eng. Sci. 2008, 24, 61–80. [Google Scholar]
- Atluri, S.N.; Liu, H.T.; Han, Z.D. Meshless local Petrov-Galerkin (MLPG) mixed collocation method for elasticity problems. Comput. Model. Eng. Sci. 2006, 4, 141. [Google Scholar]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G. A point interpolation meshless method based on radial basis functions. Int. J. Numer. Methods Eng. 2002, 54, 1623–1648. [Google Scholar] [CrossRef]
- Mountris, K.A.; Pueyo, E. The radial point interpolation mixed collocation method for the solution of transient diffusion problems. Eng. Anal. Bound. Elem. 2020, 121, 207–216. [Google Scholar] [CrossRef]
- Gu, L. Moving kriging interpolation and element-free Galerkin method. Int. J. Numer. Methods Eng. 2003, 56, 1–11. [Google Scholar] [CrossRef]
- Qu, Z.; Garfinkel, A. An advanced algorithm for solving partial differential equation in cardiac conduction. IEEE Trans. Biomed. Eng. 1999, 46, 1166–1168. [Google Scholar]
- Hundsdorfer, W.; Verwer, J.G. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 33. [Google Scholar]
- Overvelde, J.T. The Moving Node Approach in Topology Optimization. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Mountris, K.A.; Pueyo, E. A dual adaptive explicit time integration algorithm for efficiently solving the cardiac monodomain equation. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3461. [Google Scholar] [CrossRef]
- O’Hara, T.; Virág, L.; Varró, A.; Rudy, Y. Simulation of the undiseased human cardiac ventricular action potential: Model formulation and experimental validation. PLoS Comput. Biol. 2011, 7, e1002061. [Google Scholar] [CrossRef]
- Niederer, S.A.; Kerfoot, E.; Benson, A.P.; Bernabeu, M.O.; Bernus, O.; Bradley, C.; Cherry, E.M.; Clayton, R.; Fenton, F.H.; Garny, A.; et al. Verification of cardiac tissue electrophysiology simulators using an N-version benchmark. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 4331–4351. [Google Scholar] [CrossRef]
- Ten Tusscher, K.H.; Panfilov, A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol.-Heart Circ. Physiol. 2006, 291, H1088–H1100. [Google Scholar] [CrossRef]
- Fang, Q.; Boas, D.A. Tetrahedral mesh generation from volumetric binary and grayscale images. In Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, USA, 28 June–1 July 2009; pp. 1142–1145. [Google Scholar]
- Tristán-Vega, A.; Aja-Fernández, S. DWI filtering using joint information for DTI and HARDI. Med Image Anal. 2010, 14, 205–218. [Google Scholar] [CrossRef]
- Barmpoutis, A.; Vemuri, B.C. A unified framework for estimating diffusion tensors of any order with symmetric positive-definite constraints. In Proceedings of the 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Barcelona, Spain, 2–5 May 2010; pp. 1385–1388. [Google Scholar]
- Costabal, F.S.; Hurtado, D.E.; Kuhl, E. Generating Purkinje networks in the human heart. J. Biomech. 2016, 49, 2455–2465. [Google Scholar] [CrossRef] [PubMed]
- Mountris, K.A.; Pueyo, E. Next-generation In Silico Cardiac Electrophysiology Through Immersed Grid Meshfree Modeling: Application To Simulation Of Myocardial Infarction. In Proceedings of the 2020 Computing in Cardiology, Rimini, Italy, 13–16 September 2020; pp. 1–4. [Google Scholar]
- Liu, J.; Chen, Y.; Maisog, J.M.; Luta, G. A new point containment test algorithm based on preprocessing and determining triangles. Comput.-Aided Des. 2010, 42, 1143–1150. [Google Scholar] [CrossRef]
- Mongillo, M. Choosing basis functions and shape parameters for radial basis function methods. SIAM Undergrad. Res. Online 2011, 4, 2–6. [Google Scholar] [CrossRef]

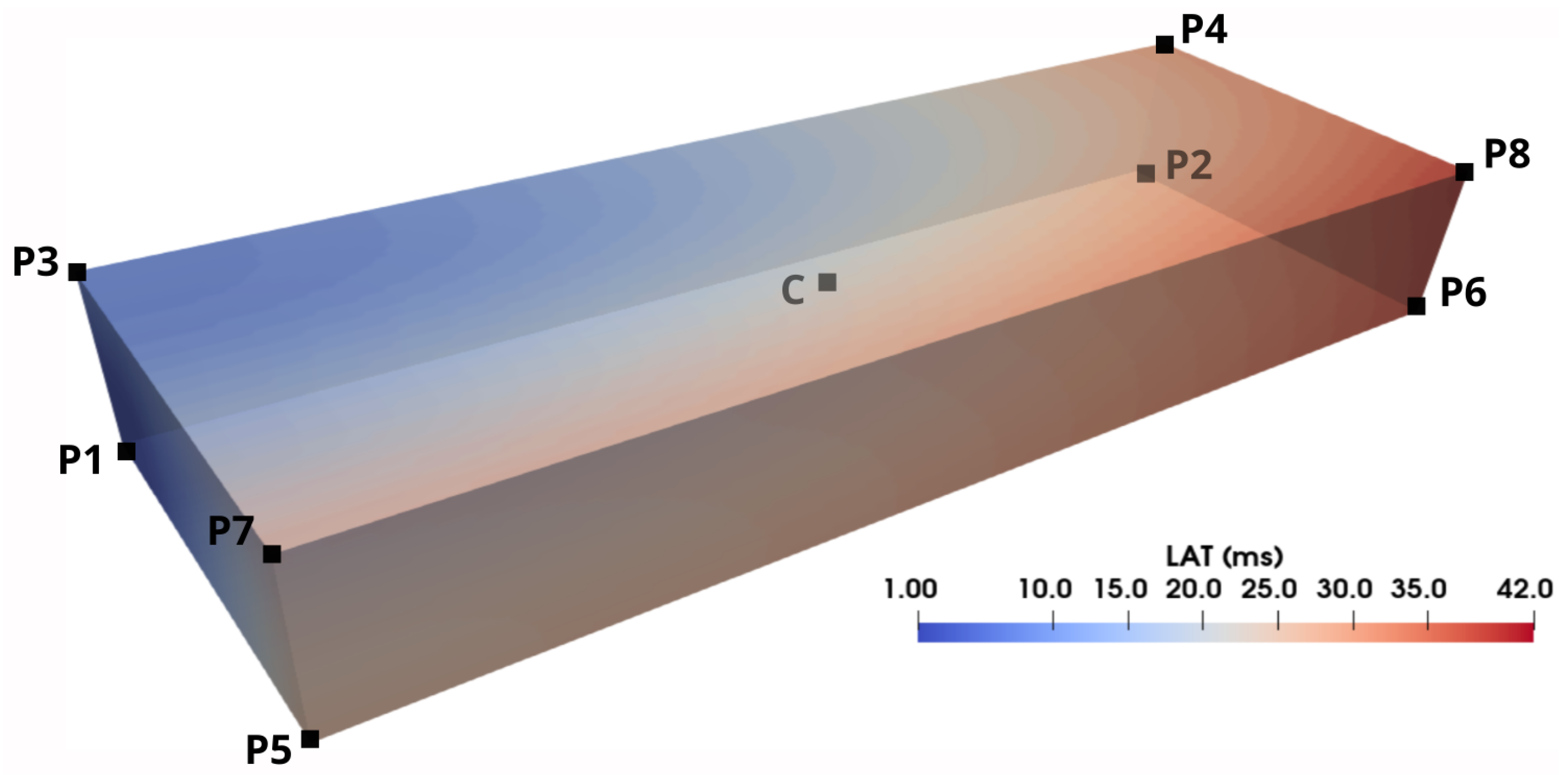



| h (mm) | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | C |
|---|---|---|---|---|---|---|---|---|---|
| MCM-RPI activation time (ms) | |||||||||
| 0.5 | 1 | 51 | 23 | 59 | 99 | 115 | 107 | 120 | 56 |
| 0.2 | 1 | 34 | 11 | 36 | 37 | 53 | 42 | 58 | 26 |
| 0.1 | 1 | 30 | 8 | 33 | 29 | 42 | 31 | 44 | 2 |
| MCM-MKI activation time (ms) | |||||||||
| 0.5 | 1 | 49 | 24 | 60 | 99 | 111 | 101 | 119 | 58 |
| 0.2 | 1 | 33 | 12 | 36 | 36 | 55 | 39 | 55 | 26 |
| 0.1 | 1 | 30 | 8 | 32 | 29 | 42 | 31 | 42 | 2 |
| FEM activation time (ms) | |||||||||
| 0.5 | 1 | 49 | 22 | 58 | 94 | 109 | 98 | 111 | 54 |
| 0.2 | 1 | 31 | 11 | 35 | 35 | 51 | 39 | 54 | 25 |
| 0.1 | 1 | 29 | 8 | 31 | 27 | 41 | 29 | 41 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mountris, K.A.; Pueyo, E. Cardiac Electrophysiology Meshfree Modeling through the Mixed Collocation Method. Appl. Sci. 2023, 13, 11460. https://doi.org/10.3390/app132011460
Mountris KA, Pueyo E. Cardiac Electrophysiology Meshfree Modeling through the Mixed Collocation Method. Applied Sciences. 2023; 13(20):11460. https://doi.org/10.3390/app132011460
Chicago/Turabian StyleMountris, Konstantinos A., and Esther Pueyo. 2023. "Cardiac Electrophysiology Meshfree Modeling through the Mixed Collocation Method" Applied Sciences 13, no. 20: 11460. https://doi.org/10.3390/app132011460
APA StyleMountris, K. A., & Pueyo, E. (2023). Cardiac Electrophysiology Meshfree Modeling through the Mixed Collocation Method. Applied Sciences, 13(20), 11460. https://doi.org/10.3390/app132011460







