Data Knowledge Dual-Driven Rate of Penetration Prediction Method for Horizontal Wells
Abstract
:1. Introduction
2. Horizontal Well Drilling Characteristics
2.1. Characteristics
- (1)
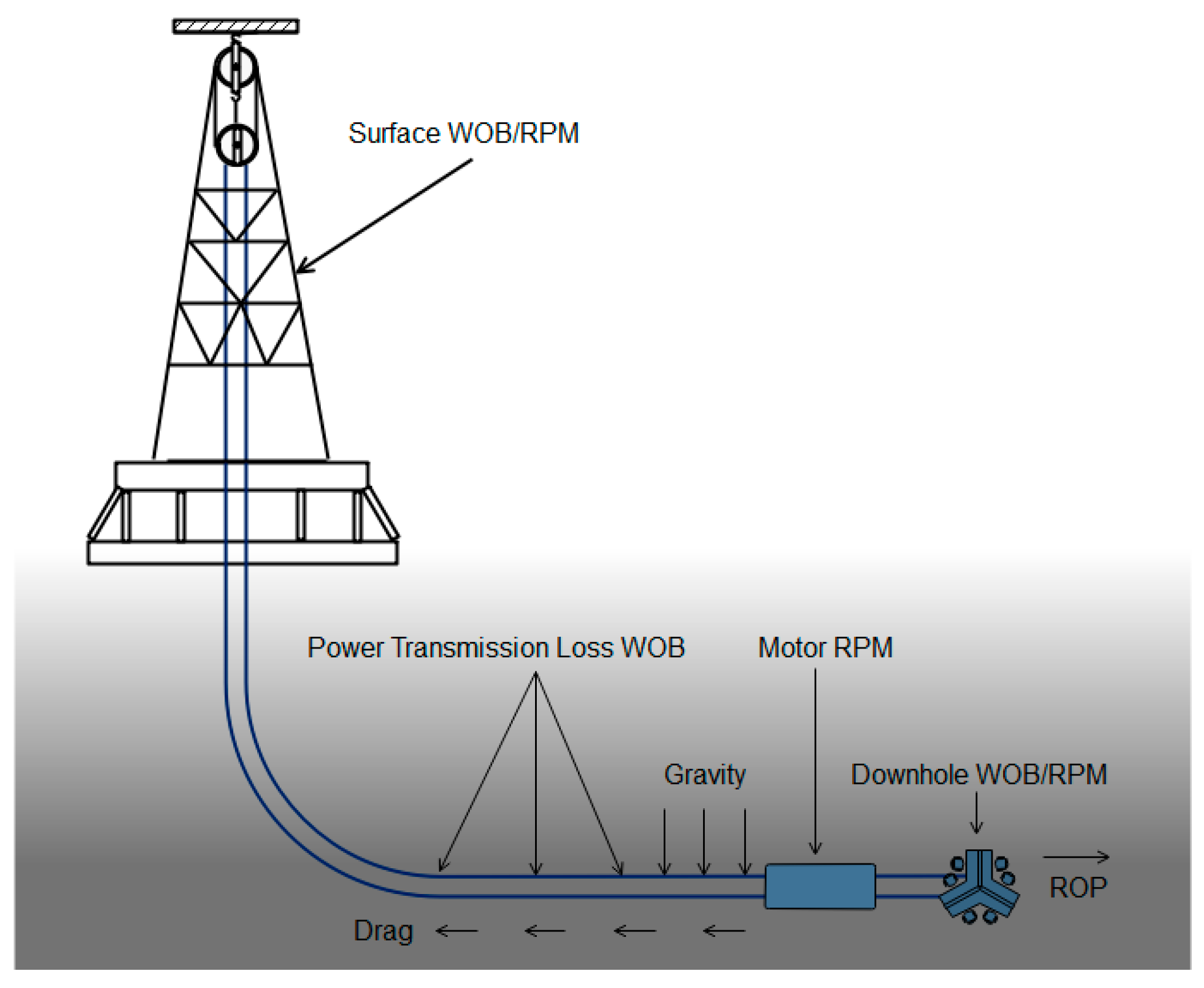
- Drag and torque. The direct contact of the BHA with the wellbore under the action of gravity from the build-up section leads to large drag and torque. Drag counteracts part of the weight applied to the bit by BHA, causing the weight on bit (WOB) reflected by the surface WOB (SWOB) to be inconsistent with the downhole WOB [23].
- (2)
- Eccentric annulus and hole cleaning. The drill string in the horizontal part of the wellbore is eccentric to the lower side by gravity, forming an eccentric annulus, while in the eccentric annulus, the flow velocity is not uniform, and the cuttings settle radially to form a cutting bed in the lower wellbore, which affects the friction coefficient between the drill string and the wellbore and subsequently affects the WOB transfer [24,25].
- (3)
- Trajectory control. Horizontal wells require directional operations due to the need for a well incline and azimuth adjustment [26]. The positive displacement motor (PDM) is a commonly used tool for trajectory control. In a PDM, the power section converts the hydraulic energy of mud flow into mechanical rotary power to drive the drill bit to rotate rapidly at the bottom hole to achieve trajectory control [27]. Rotary Steerable Systems are employed as tools for trajectory control, which enables directional drilling while the drill string is rotating. However, in order to enhance drilling efficiency, it is commonly deployed in tandem with a PDM. As a result, the bit’s RPM surpass that of the surface RPM.
2.2. Horizontal Well Data Processing Method
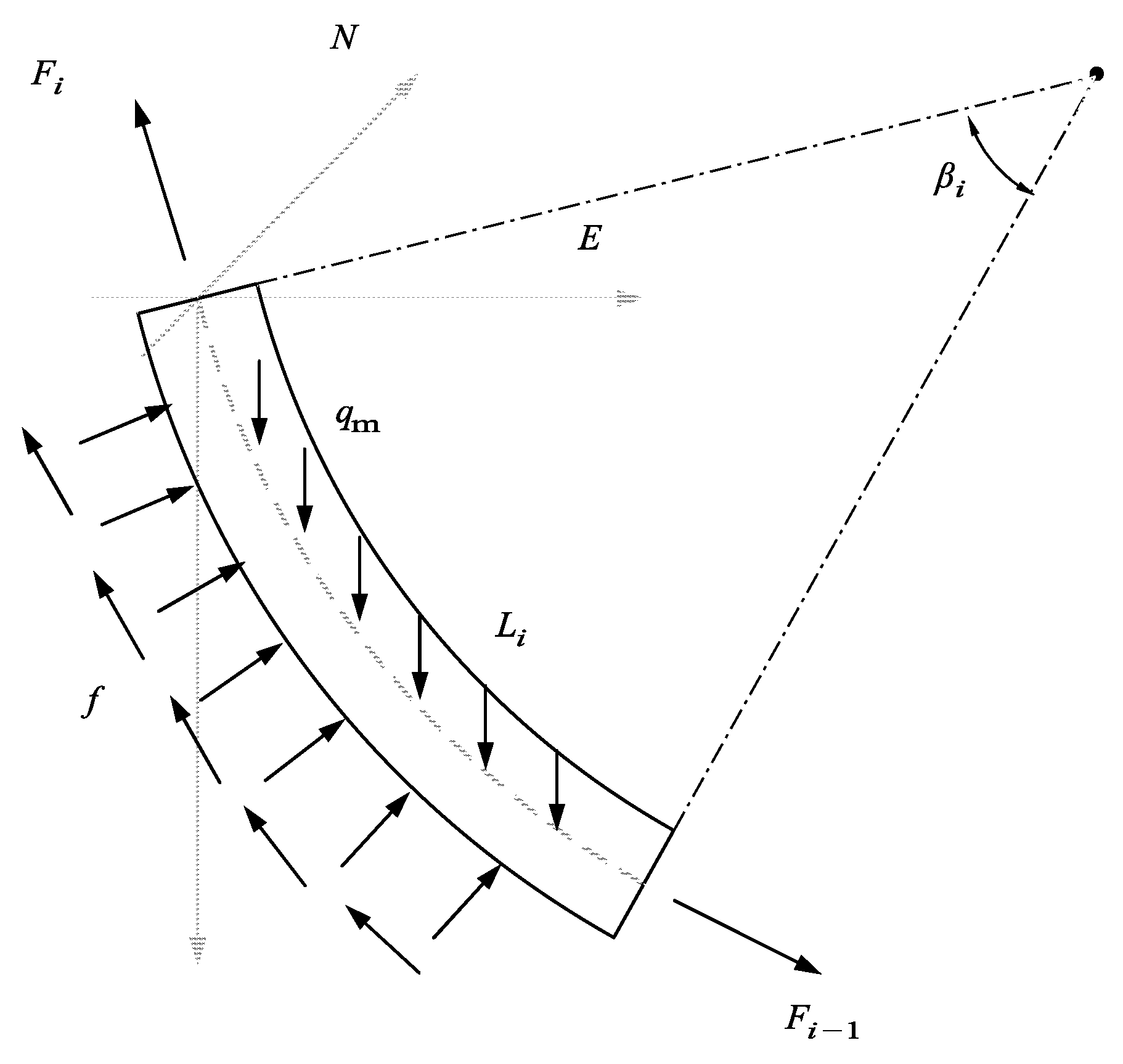
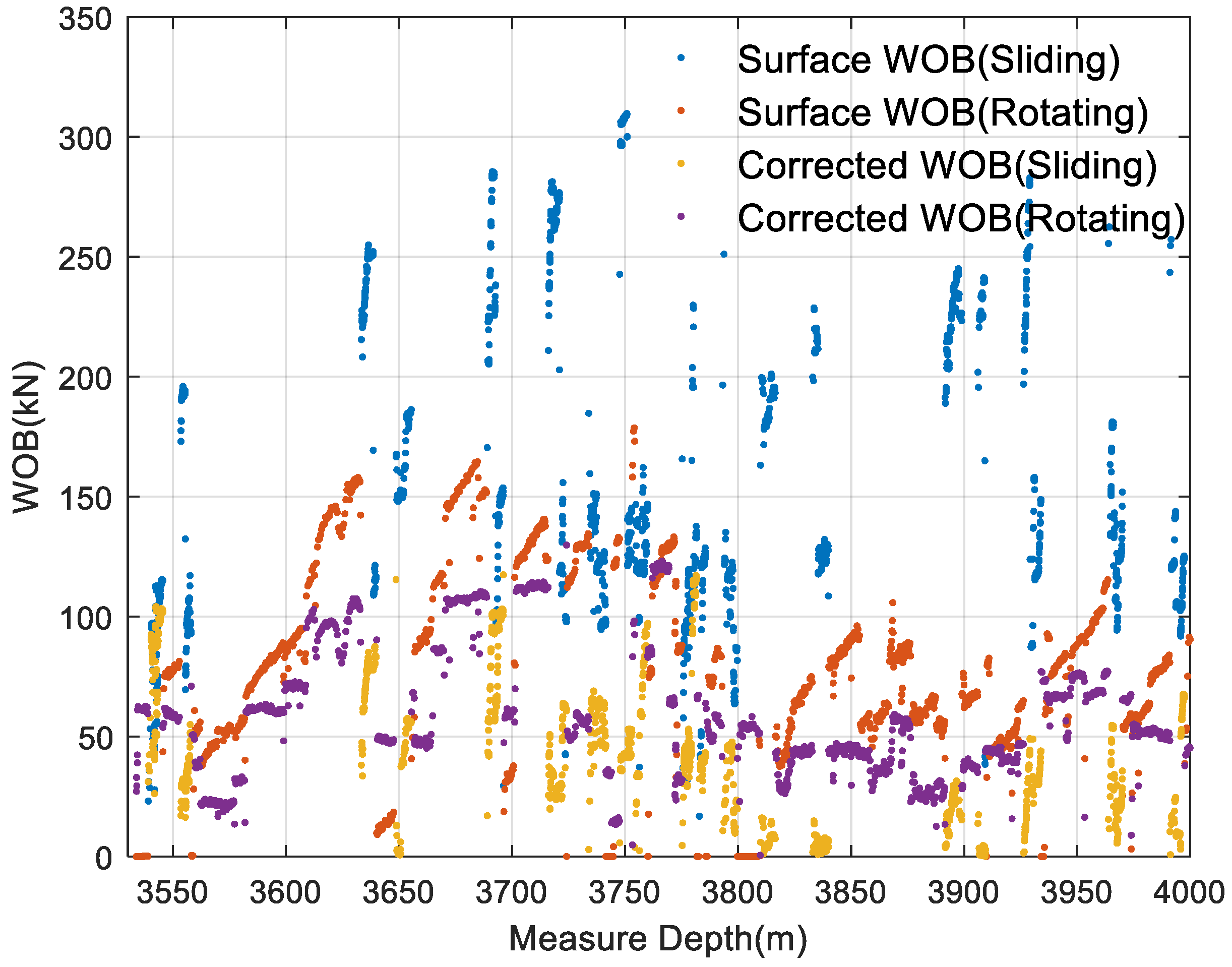
2.2.1. Corrected WOB
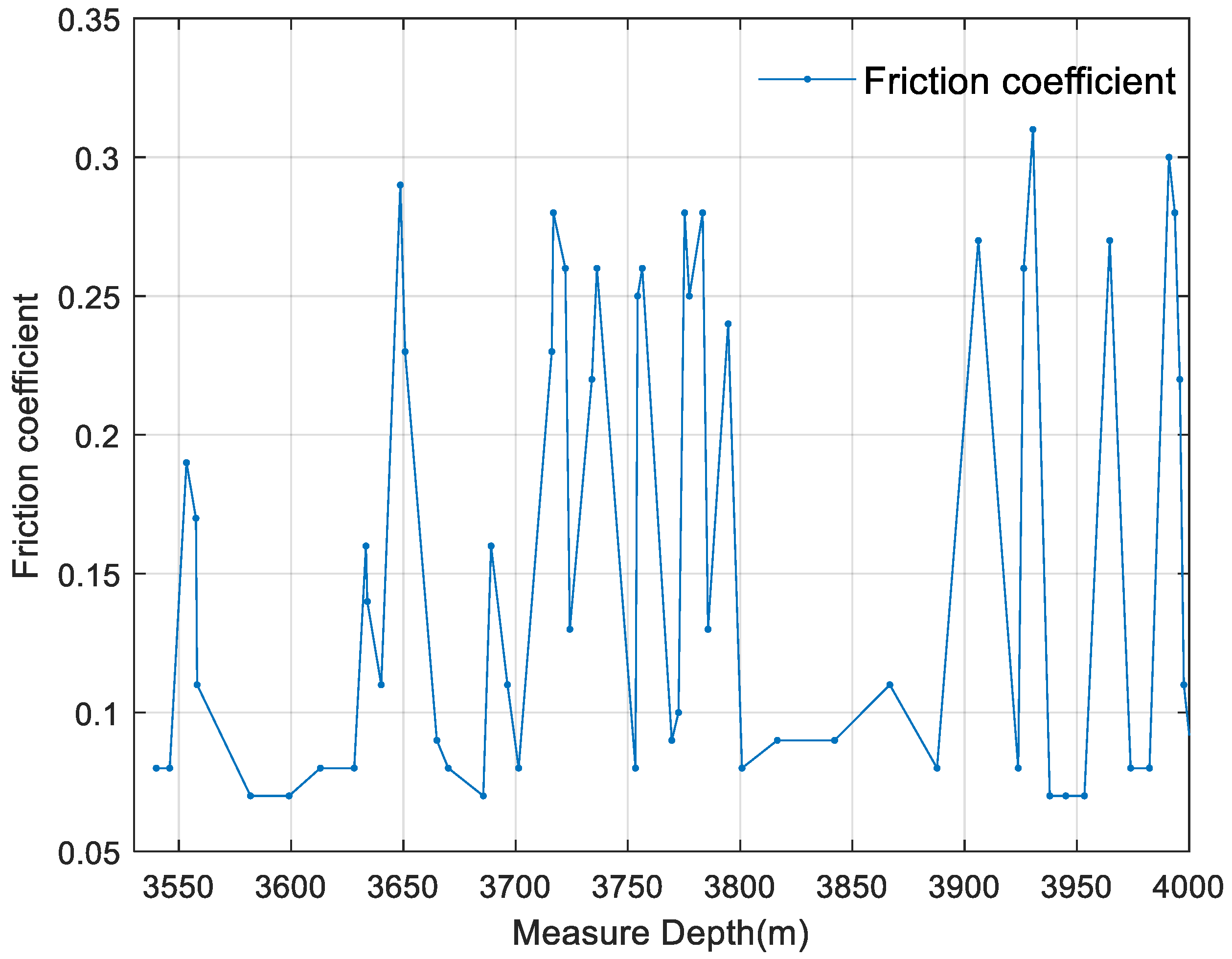
2.2.2. Friction Coefficient Calculation
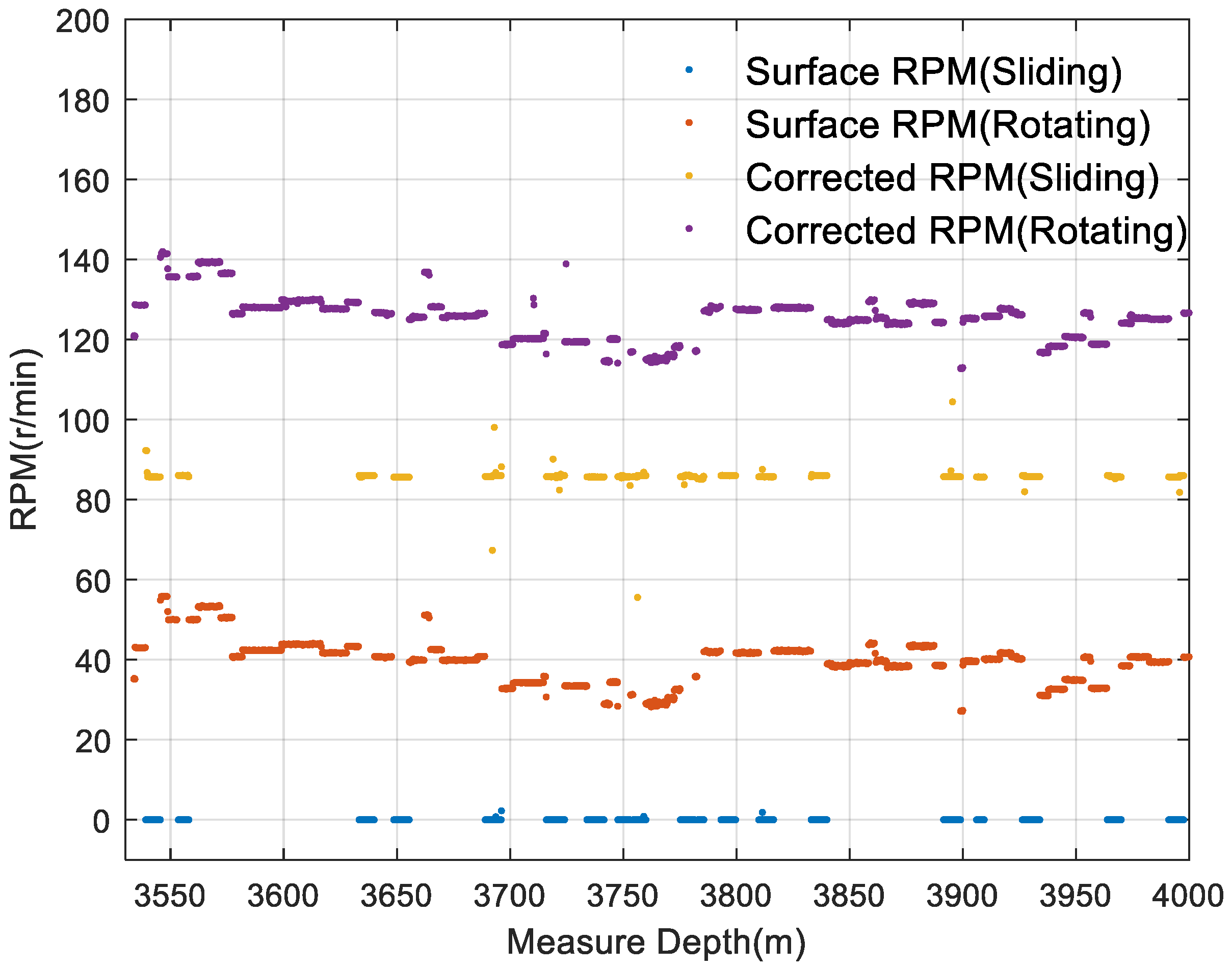
2.2.3. Corrected RPM
2.3. Data Statistics and Processing Results
3. Methodology
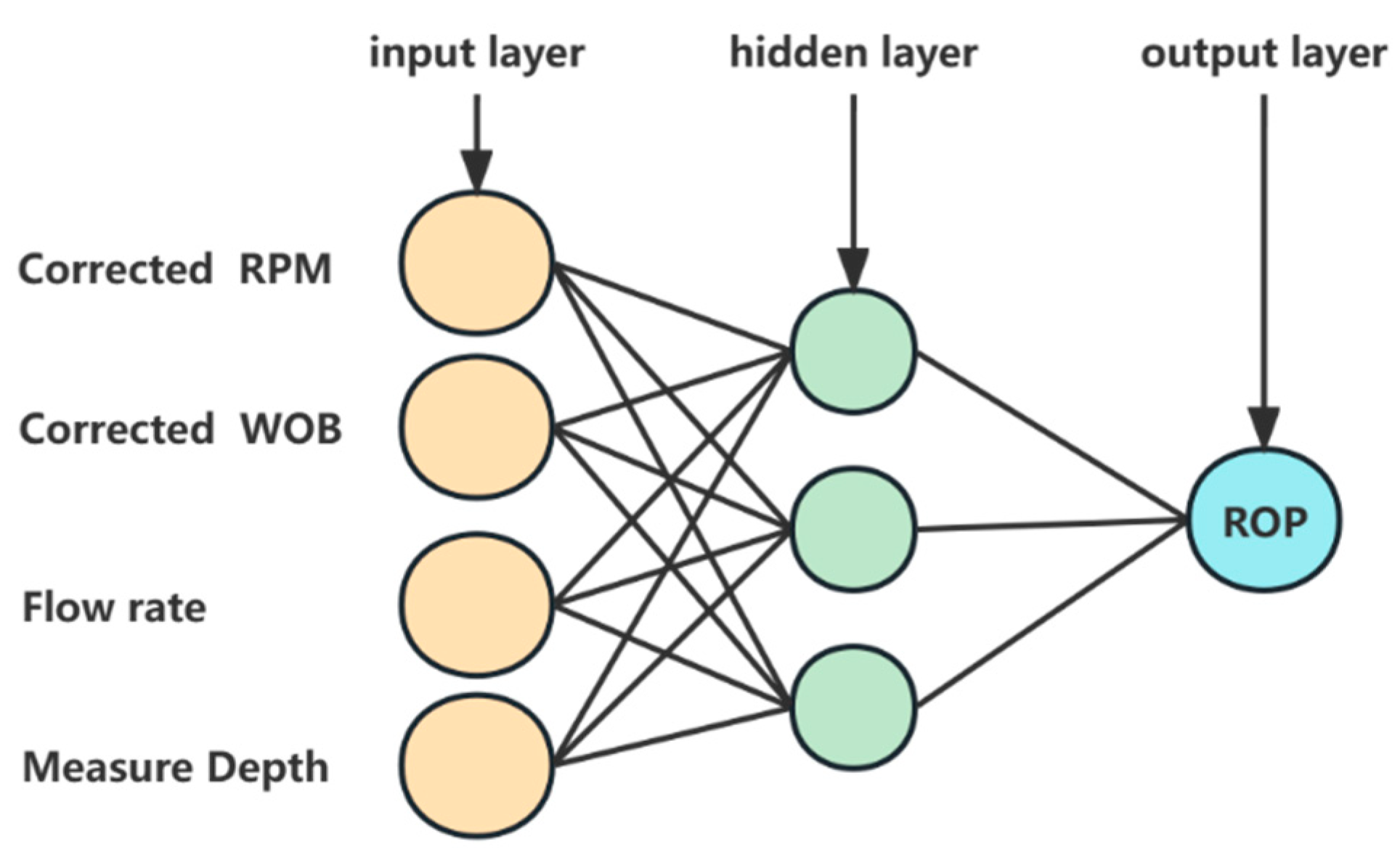
3.1. Feature Selection
3.2. Data Pre-Processing
3.3. ROP Prediction
4. Case Study
4.1. Data-Set Attributes
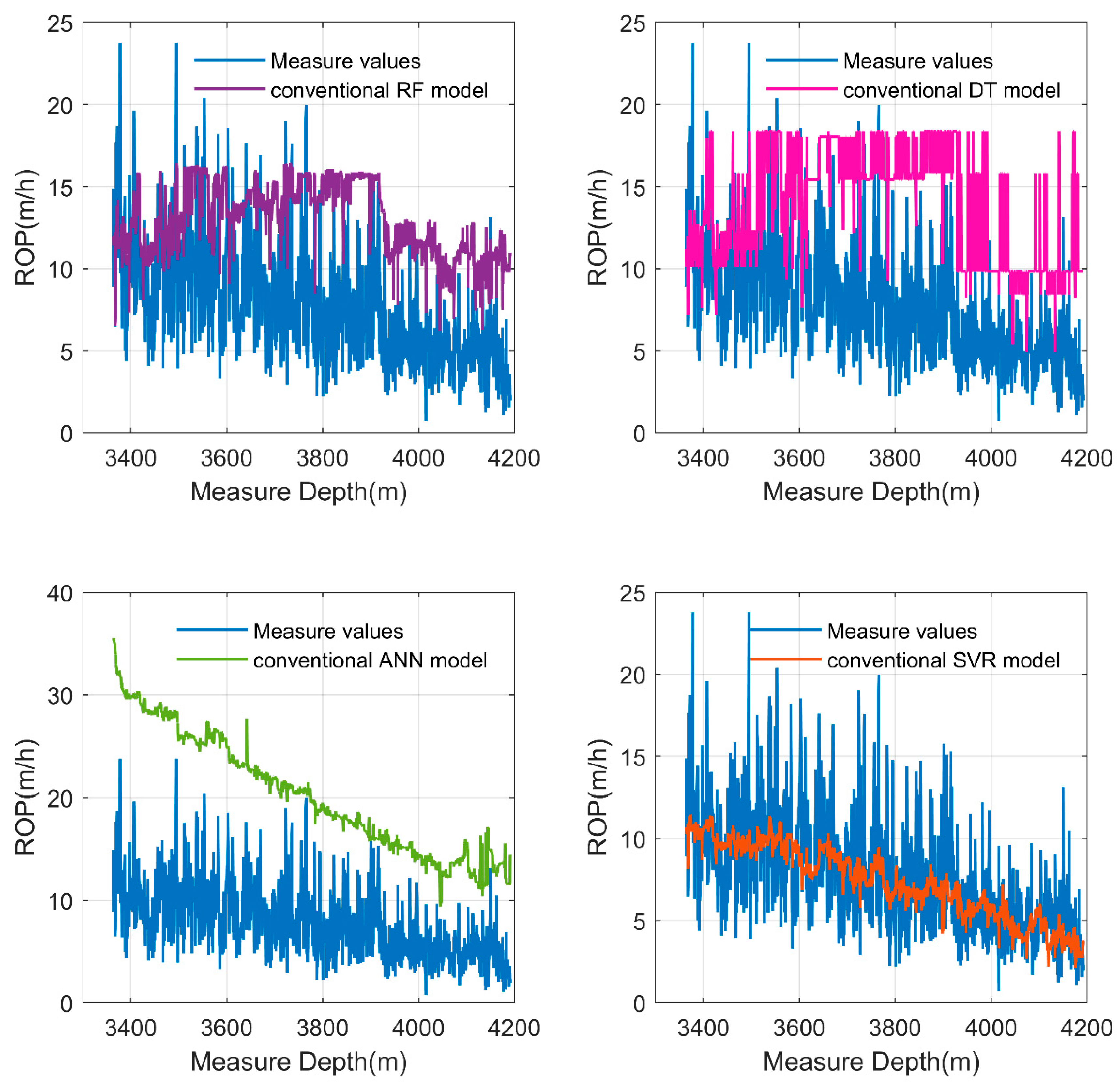
4.2. ROP Prediction Experiments
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahmoud, H.; Hamza, A.; Nasser, M.S.; Hussein, I.A.; Ahmed, R.; Karami, H. Hole cleaning and drilling fluid sweeps in horizontal and deviated wells: Comprehensive review. J. Petrol. Sci. Eng. 2020, 186, 106748. [Google Scholar] [CrossRef]
- Zhu, X.; Li, K.; An, J. Calculation and analysis of dynamic drag and torque of horizontal well strings. Nat. Gas Ind. B 2019, 6, 183–190. [Google Scholar] [CrossRef]
- Akgun, F. A finite element model for analyzing horizontal well BHA behavior. J. Petrol. Sci. Eng. 2004, 42, 121–132. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, K. Three-dimensional trajectory design for horizontal well based on optimal switching algorithms. ISA Trans. 2015, 58, 348–356. [Google Scholar] [CrossRef] [PubMed]
- Najjarpour, M.; Jalalifar, H.; Norouzi-Apourvari, S. Half a century experience in rate of penetration management: Application of machine learning methods and optimization algorithms—A review. J. Petrol. Sci. Eng. 2022, 208, 109575. [Google Scholar] [CrossRef]
- Bingham, G. A new approach to interpreting rock drillability. Tech. Man. Repr. Oil Gas J. 1965, 93, 1965. [Google Scholar]
- Bourgoyne, A.T.; Young, F.S. A multiple regression approach to optimal drilling and abnormal pressure detection. Soc. Pet. Eng. J. 1974, 14, 371–384. [Google Scholar] [CrossRef]
- Hegde, C.; Daigle, H.; Millwater, H.; Gray, K. Analysis of rate of penetration (ROP) prediction in drilling using physics-based and data-driven models. J. Petrol. Sci. Eng. 2017, 159, 295–306. [Google Scholar] [CrossRef]
- Soares, C.; Daigle, H.; Gray, K. Evaluation of PDC bit ROP models and the effect of rock strength on model coefficients. J. Nat. Gas Sci. Eng. 2016, 34, 1225–1236. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.; Wu, M.; Chen, X.; Hu, Y.; Liu, K.; Wang, F.; Zhang, S. Prediction of drilling rate of penetration (ROP) using hybrid support vector regression: A case study on the Shennongjia area, Central China. J. Petrol. Sci. Eng. 2019, 181, 106200. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.; Wu, M.; Liu, K.; Chen, X.; Hu, Y.; Ning, F. Two-level intelligent modeling method for the rate of penetration in complex geological drilling process. Appl. Soft Comput. 2019, 80, 592–602. [Google Scholar] [CrossRef]
- Sabah, M.; Talebkeikhah, M.; Wood, D.A.; Khosravanian, R.; Anemangely, M.; Younesi, A. A machine learning approach to predict drilling rate using petrophysical and mud logging data. Earth Sci. Inform. 2019, 12, 319–339. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.; Liu, K.; Wu, M. A novel dynamic model for the online prediction of rate of penetration and its industrial application to a drilling process. J. Process Control 2022, 109, 83–92. [Google Scholar] [CrossRef]
- Elkatatny, S. Real-time prediction of rate of penetration while drilling complex lithologies using artificial intelligence techniques. Ain Shams Eng. J. 2021, 12, 917–926. [Google Scholar] [CrossRef]
- Keshavarz Moraveji, M.; Naderi, M. Drilling rate of penetration prediction and optimization using response surface methodology and bat algorithm. J. Nat. Gas Sci. Eng. 2016, 31, 829–841. [Google Scholar] [CrossRef]
- Jiang, W.; Samuel, R. Optimization of rate of penetration in a convoluted drilling framework using ant colony optimization. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 1–3 March 2016. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Zhao, H.; Wu, M.; Cao, W.; Zhang, Y.; Liu, H. A novel rate of penetration prediction model with identified condition for the complex geological drilling process. J. Process Control 2021, 100, 30–40. [Google Scholar] [CrossRef]
- Soares, C.; Gray, K. Real-time predictive capabilities of analytical and machine learning rate of penetration (ROP) models. J. Petrol. Sci. Eng. 2019, 172, 934–959. [Google Scholar] [CrossRef]
- Abbas, A.K.; Rushdi, S.; Alsaba, M. Modeling rate of penetration for deviated wells using artificial neural network. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 12–15 November 2018. [Google Scholar] [CrossRef]
- Hazbeh, O.; Aghdam, S.K.; Ghorbani, H.; Mohamadian, N.; Ahmadi Alvar, M.; Moghadasi, J. Comparison of accuracy and computational performance between the machine learning algorithms for rate of penetration in directional drilling well. Pet. Res. 2021, 6, 271–282. [Google Scholar] [CrossRef]
- Najjarpour, M.; Jalalifar, H.; Norouzi-Apourvari, S. The effect of formation thickness on the performance of deterministic and machine learning models for rate of penetration management in inclined and horizontal wells. J. Petrol. Sci. Eng. 2020, 191, 107160. [Google Scholar] [CrossRef]
- Kuang, Y.; Lin, W.; Liu, Y.; Wang, Q.; Zhang, J. Numerical modelling and field experimental validation of the axial load transfer on the drill-strings in deviated wells. J. Nat. Gas Sci. Eng. 2020, 75, 103124. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, T.; Chen, P.; Yang, C. Method and apparatus for monitoring of downhole dynamic drag and torque of drill-string in horizontal wells. J. Petrol. Sci. Eng. 2018, 164, 320–332. [Google Scholar] [CrossRef]
- Guan, Z.; Liu, Y.; Liu, Y.; Xu, Y. Hole cleaning optimization of horizontal wells with the multi-dimensional ant colony algorithm. J. Nat. Gas Sci. Eng. 2016, 28, 347–355. [Google Scholar] [CrossRef]
- El Sabeh, K.; Gaurina-Međimurec, N.; Mijić, P.; Medved, I.; Pašić, B. Extended-Reach Drilling (ERD)—The Main Problems and Current Achievements. Appl. Sci. 2023, 13, 4112. [Google Scholar] [CrossRef]
- Tunkiel, A.T.; Sui, D.; Wiktorski, T. Training-while-drilling approach to inclination prediction in directional drilling utilizing recurrent neural networks. J. Petrol. Sci. Eng. 2021, 196, 108128. [Google Scholar] [CrossRef]
- Chen, X.; Fan, H.; Guo, B.; Gao, D.; Wei, H.; Ye, Z. Real-time prediction and optimization of drilling performance based on a new mechanical specific energy model. Arab. J. Sci. Eng. 2014, 39, 8221–8231. [Google Scholar] [CrossRef]
- Johancsik, C.A.; Friesen, D.B.; Dawson, R. Torque and Drag in Directional Wells-Prediction and Measurement. J. Pet. Technol. 1984, 36, 987–992. [Google Scholar] [CrossRef]
- Motahhari, H.R.; Hareland, G.; James, J.A. Improved drilling efficiency technique using integrated PDM and PDC bit parameters. J. Can. Pet. Technol. 2010, 49, 45–52. [Google Scholar] [CrossRef]
- Alali, A.M.; Abughaban, M.F.; Aman, B.M.; Ravela, S. Hybrid data driven drilling and rate of penetration optimization. J. Petrol. Sci. Eng. 2021, 200, 108075. [Google Scholar] [CrossRef]
- Hegde, C.; Soares, C.; Gray, K. Rate of penetration (ROP) modeling using hybrid models: Deterministic and machine learning. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar] [CrossRef]




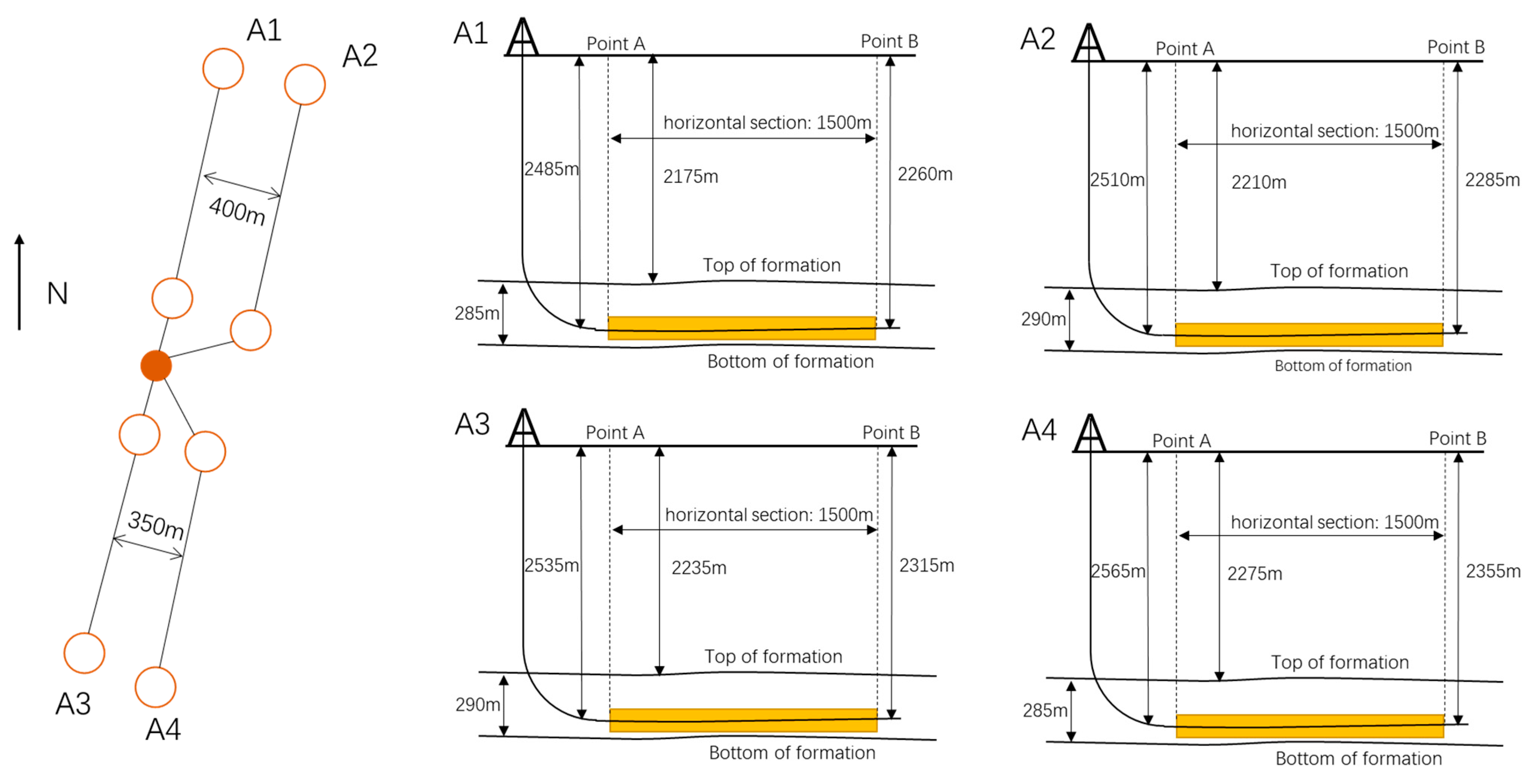

| Well | Footage (m) | Data Amount (Number) | Percentage (%) | |||
|---|---|---|---|---|---|---|
| Sliding | Rotating | Sliding | Rotating | Rotating Data | Rotating Footage | |
| A1 | 69.56 | 631.99 | 50,666 | 75,734 | 59.92% | 90.08% |
| A2 | 74.44 | 684.04 | 67,026 | 77,130 | 53.50% | 90.19% |
| A3 | 93.32 | 697.4 | 62,354 | 73,438 | 54.08% | 88.20% |
| A4 | 112.9 | 690.6 | 83,674 | 69,463 | 45.36% | 85.95% |
| Proposed Method | R2 | RMSE | MAE | Conventional Method | R2 | RMSE | MAE |
|---|---|---|---|---|---|---|---|
| RF | 0.96 | 1.08 | 0.65 | RF | 0.65 | 1.87 | 1.31 |
| ANN | 0.95 | 1.12 | 0.71 | ANN | 0.55 | 2.1 | 1.53 |
| DT | 0.93 | 1.21 | 0.75 | DT | 0.52 | 2.18 | 1.53 |
| SVR | 0.94 | 1.2 | 0.68 | SVR | 0.6 | 1.98 | 1.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Yin, H.; Li, Q. Data Knowledge Dual-Driven Rate of Penetration Prediction Method for Horizontal Wells. Appl. Sci. 2023, 13, 11396. https://doi.org/10.3390/app132011396
Zhao X, Yin H, Li Q. Data Knowledge Dual-Driven Rate of Penetration Prediction Method for Horizontal Wells. Applied Sciences. 2023; 13(20):11396. https://doi.org/10.3390/app132011396
Chicago/Turabian StyleZhao, Xiuwen, Hu Yin, and Qian Li. 2023. "Data Knowledge Dual-Driven Rate of Penetration Prediction Method for Horizontal Wells" Applied Sciences 13, no. 20: 11396. https://doi.org/10.3390/app132011396
APA StyleZhao, X., Yin, H., & Li, Q. (2023). Data Knowledge Dual-Driven Rate of Penetration Prediction Method for Horizontal Wells. Applied Sciences, 13(20), 11396. https://doi.org/10.3390/app132011396






