Abstract
This paper presents an approach to a go-kart chassis design, vehicle dynamics calculation, Li-ion battery capacity analysis, and electric motor choice for optimized vehicle performance. The chassis analysis shown in this paper was performed using a CAD/FEA software package, SolidWorks Student Edition. Three highlights can be found in this paper: (1) An original design was implemented; the basic analysis was composed of chassis optimization using beam elements and modeling such an optimized chassis “locally” with solid elements for sub-modeling purposes. (2) The most stressed tube joint was sub-modeled to calculate the risk of tube wall stability. (3) Vehicle dynamics were calculated for the case of braking on a curved path and the case of a collision with the front tire due to road imperfection. The authors intend to install a data acquisition system in the future to analyze the stress of local chassis tubes. The results of the SolidWorks analysis indicate a safety design for the chassis concept. The results for the sub-model stability (buckling) analysis show that the chosen tube wall thickness-to-diameter ratio gives safety factor values ranging from 1.6 to 5. Based on the stress distribution, some improvement in the middle part of the chassis can be made by using a half-a-millimeter-thicker wall tube or a larger tube diameter of a few millimeters to lower the stress. The latter will be described in this paper.
1. Introduction
A go-kart, in accordance with the definition given by the International Karting Commission–Federation International Automobile (CIK–FIA), is a land vehicle with or without bodywork, with four outstanding wheels in contact with the ground, two of which are steered using a steering wheel, while the other two transmit power. In addition to the engine and connected wheels, a go-kart chassis usually consists of a body frame composed of steel tubes that are welded together. The go-kart is a racing vehicle, small and light, powered mostly by an internal combustion engine (ICE), without a driver or with one person in it with no suspension. The go-kart is specially designed for racing and has very low ground clearance when compared to other vehicles. Many studies have been conducted on “karting” [1,2,3]. This includes studies on the design of the go-kart frame or chassis; at times, researchers were concerned about choosing materials for the structure—put simply, structure analysis, safety, and structure stability. The common parts of a go-kart are the engine, wheels, steering, tires, axle, and chassis [4,5,6]. The idea presented in this paper is a concept design for a chassis and other self-produced parts for a self-built electrically powered go-kart inspired by references [7,8,9], since the trend in chassis design involves producing lighter vehicle structures at lower costs but with good safety efficiency. As a drive, a brushless direct current electric motor (BDCEM) was chosen for this concept for, firstly, ecological reasons, and secondly, for its favorable torque characteristics, since it provides large torque at a low rotational speed [10,11,12,13,14,15]. A commercially available go-kart most often has a two-stroke internal combustion engine as its power source, which is quite low in fuel efficiency and moment characteristics while also producing exhaust emissions and noise. Our motivation is to show an alternative to ICE-powered go-karts, the limitation of Li-ion batteries combined with a DC motor as a power source, and the details of designing such a go-kart [16,17].
The chassis of a go-kart is mostly designed from circular thin-walled tubes welded into a frame, as presented in references [18,19,20,21,22,23]. The stability of the tube wall is the detail for which the most attention has been given in the mechanical integrity “domain” [24,25]. In an engineering sense, the “local” stability analysis of thin-walled structures is relatively difficult to conduct without the utilization of computer finite element analysis (FEA) programs [26,27,28]. The SolidWorks application was chosen for the modeling and analysis of displacement and stress in most cases. Every aspect of the vehicle was considered for optimization, so that the energy demand for a given race (drive) was minimal, as mentioned in references [29,30].
One of the first issues in go-kart driving condition safety is the braking system design [31,32]. Firstly, in order to have loads for any analysis, the driving scenarios of braking in a curved trajectory, acceleration in a straight trajectory, and the impact with (on) a road imperfection (a bulge or a dent) in a straight trajectory were chosen as extreme cases of wheel loads. The wheel loads were calculated based on the assumption of “linear” behavior, i.e., the vehicle chassis does not rotate sideways (i.e., rock) more than a few degrees in a curved trajectory, so that the initial geometry can be used in modeling a free body diagram and setting the equilibrium equations [33,34]. As we advance in this paper, the wheel’s normal and tangential forces are calculated with a predictor–corrector method [35]. Calculated forces are the base for a rear wheel shaft design and as load cases in the FEA model [36,37].
The shaft’s mechanical integrity depends on the load spectrum, an analysis of which is omitted here for the sake of brevity, and partially because it depends on the track configuration. However many curved parts of the track there are and how long the straight parts are influence the load spectrum and steering mechanism [38]. The worst wheel load is taken as a design base, with awareness that it is only a part of the load spectrum. Finally, in reference [39], an approach toward updating finite element models through a frequency analysis of a karting structure was proposed in order to obtain dynamic structural properties, i.e., the natural frequencies, damping ratios, and the mode shapes of the structure. This is an applicable and useful technique known as model calibration, which proved to be a good method in reducing deviations.
Other very important systems of a go-kart, such as the selection of an appropriate electrical vehicle control system, published in reference [40], are currently in the background for the authors. Moreover, the battery management system (BMS) in this paper is discussed and selected only in a theoretical manner, similar to in reference [41]. Nevertheless, the positions of the two battery system containers and DC motor had to be determined to calculate the chassis stress parameters. The battery system capacity was calculated for a 10–20 min ride at maximum speed, as described in reference [42]. This covers some average races evidenced in go-kart races, regarding the number of accelerations, straight parts, braking, and so on.
Moreover, the steering system of a go-kart, as a fully developed and accepted system in this paper, is not the subject of a detailed discussion. The justifiable reason as to why this has not yet been worked out is of great importance, safety, and reliability to vehicle management, to which special attention, time, and effort should be paid. As mentioned, the systems are not elaborated and described in detail; they will be the subjects of other scientific research and investigations in the near future. The authors are aware that it will be necessary to significantly strengthen the chassis construction in the part related to the steering wheel support and the design solution for the brake pedal and acceleration control [43]. This will need to be completed in the second step of the concept design of the go-kart.
2. Materials and Methods
The materials and methods are described with sufficient detail in this paper. The choice of chassis material plays a vital role in the construction of the entire light vehicle in providing reliability, security, and durability. The choice of the chassis material is considered depending on various factors, such as maximum load capacity, absorption force capacity, strength, rigidity, durability, and toughness, and is designed so that the chassis can withstand a total load of 130 kg. The low (mild) carbon steel was chosen for its weld ability. The chassis is intended to be thin-walled, lowering the weight while maintaining wall stability (local buckling problem). Another criterion proven to be significant in choosing materials is availability. An overall issue in the design is the price, so the material had to be of a low price. In Croatia, a common steel marking is EN 10027-1 [44]. Considering all of the criteria, the chassis of an electric go-kart was selected from S355 seamless steel tubes with a yield strength of σT = 355 MPa. For the shaft material, S355 mild steel was chosen. S355 has a high fracture toughness since it has high plasticity at the conditions of use. For the dynamic strength of the shaft design, the key parameters are inverse bending dynamic strength σd−1 = 280 MPa and inverse torsional dynamic strength τd,t−1 =180 MPa. In contrast, the material chosen in [16] is AISI 4130, with a yield strength of σT = 435 MPa. It also has good weld ability, high fracture toughness, and plasticity, so it is an excellent choice of material for the chassis. It is marked according to AISI, the American-based institution. It is not readily available in Croatia. In [11], AISI 4130 was also selected for the chassis material. In [22], the chassis material was not marked, only the yield strength of 250 MPa was stated, which was close to S235, according to EN 10027-1. In several papers [10,15,18,19], the material chosen was AISI 1018, with a very similar yield strength of 370 MPa. One quite different choice of material, aluminum alloy 6063, was chosen in [13], with a yield strength of around 220 MPa. The difficulty with aluminum alloy involves the additional material in the welding process, i.e., the electrode. Overall, one can argue that the material most chosen for chassis is a mild structural steel, with yield strengths ranging from 250 to 440 MPa, with good weld ability. Hence, our choice of material falls within this range.
In Figure 1, the flow chart of our go-kart concept design methodology is presented.
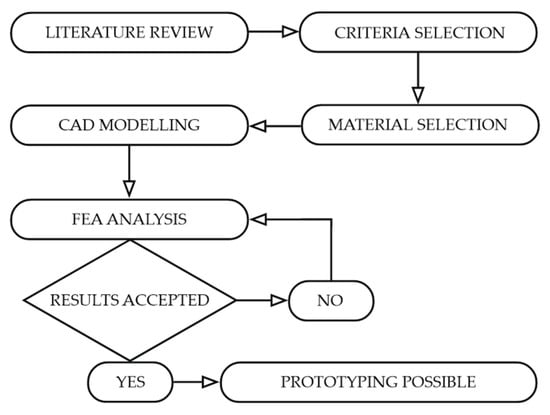
Figure 1.
Flow chart of our go-kart concept design methodology.
2.1. Vehicle Dynamics Modeling
In this section, we present the vehicle dynamics modeling. For the loads on the chassis, the major parameter is the static distribution of loads from the weight of the vehicle and driver. Additionally, dynamical loads arriving from road imperfections, such as a bulge or a dent, and accelerations on curved trajectories were taken into account for the approximation of a maximum load on each wheel. Dynamical loads are shown in Figure 2. For the approximation of maximum acceleration at braking and on a curve, the friction coefficient, in case of a dry tarmac, is presumed to be 0.8, according to references [35,36]. With an approximated average of the driver’s anthropometric parameters, the maximum force on each tire is derived based on a concept sketch presented in Figure 3. The driver is presumed to have a maximal mass of 80 kg, and the vehicle 50 kg.
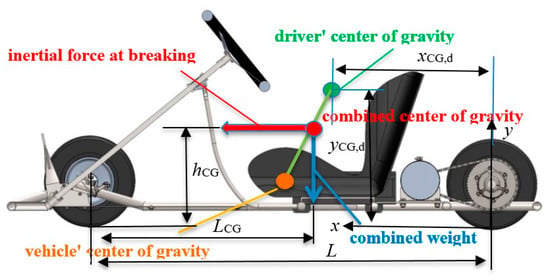
Figure 2.
The inertial force of go-kart with the driver, side view.
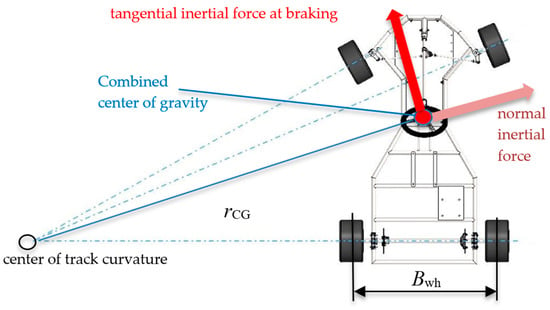
Figure 3.
Inertial force of the go-kart, top view, while driving on a curved trajectory.
The combined center of gravity position was approximated by the available equations for the mass of body segments found in [45,46] for the expected sitting position in driving. The body segments were drawn symbolically as lines with the center of gravity and respective mass omitted here for the sake of brevity. Then, the driver’s COG components in the coordinate system Oxy, shown in Figure 2 with origins in the contact point of the rear wheel, were calculated according to
The human body can be described by 14 segments in the calculation of its kinetics, according to [Hall]. Each segment’s center of gravity coordinates, , were derived from geometry based on the drawing of the driver sitting in the go-kart seat. Further on, the vehicle’s COG was calculated in SolidWorks and introduced as information into the calculation of the combined COG. The driver’s COG alone was approximated for an adult person, as well as the average height, according to [45,46]. Specific parameters for the chosen go-kart and driver are: The same way the driver’s COG was calculated by Equation (1), the combined COG was calculated by
In Equation (2), L is the wheel base, md is the driver’s mass, and mv is the vehicle mass. The final COG position according to Figure 2 is Figure 2 and Figure 3 depict the inertial forces at acceleration, causing redistribution of ground reactions on a vehicle concept design.
In Figure 2, the driver’s center of gravity is shown with a green circle, the vehicle’s center of gravity with orange, and the combined center of gravity (COG) with a red circle, with its height relative to the ground level marked by hCG, and the distance from the front wheels marked by LCG. The inertial force at braking in a straight trajectory is shown with the red arrow, and the combined weight with the blue arrow.
In Figure 3, the inertial force components at braking in a curved trajectory are shown, with tangential in red and normal (centrifugal) in light purple. Kinematics of this case were determined by combined COG moving on a curve with radius rCG. The inertial forces in Figure 2 were used to determine the normal reaction forces on wheels in the “worst” case scenario, braking in the curved trajectory, to determine loads for the finite element model analysis. The normal inertial force in a curved trajectory was calculated according to
In Equation (3), is the normal inertial force, mcom is the combined driver’s and vehicle’s mass, v is the COG velocity, and rCG is the COG’s trajectory curvature radius. The tangential inertial force is calculated as
In Equation (4), is the tangential inertial force and is the tangential acceleration component. Details of the vehicle’s geometry at the curved trajectory in calculating the normal reaction forces at the wheels are shown in Figure 4.
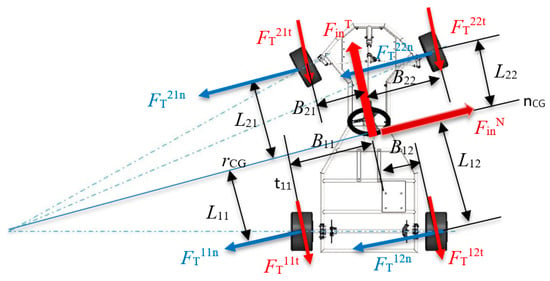
Figure 4.
Geometry in calculating the redistribution of forces in a curved trajectory at vehicle acceleration.
Distances in radial and longitudinal directions of the contact points of the tires to the COG are presented in Figure 4, marked as, for instance, L11 for longitudinal distance from the contact of the rear left tire to the COG, and B11 for the radial distance from the contact of the rear left tire to the COG, etc. In Figure 4, the nomenclature for the ground reaction forces is, for instance, is a friction force on the outer rear tire on the normal line to the combined COG, and is a friction force component on the inner front tire on the tangential line to the combined COG. The maximum expected friction force on any given tire, according to the dry friction Coulomb’s law, is , where μ0 is the static friction coefficient. The friction force on each contact surface, in Figure 4, is depicted by two components, radial and tangential.
This, written in scalar form, gives the amount of the friction force on a tire contact surface from its components [35,36], in the form of
Indices i and j in Equation (5) take the values 1 and 2. The combined vehicle’s and driver’s weight is the sum of the normal reaction forces on all tires, i.e.,
The sum of all friction forces on the tangential line is equal to the vehicle’s tangential inertial force, . For the following equilibrium equations, the presumption is the constant (or close to that) position of the vehicle’s chassis, or, in other words, a rigid-like behavior [35,36]. Setting the equilibrium moment of force equation around the tangential line, passing through the inner most wheel’s surface contact center, in Figure 4, denoted t11, yields
Next is the equilibrium moment of force equation around the radial line passing through the combined center of gravity of the vehicle and driver, in Figure 4, denoted nCG, yielding
The force equilibrium on the tangential and normal line, respectively, yields
Moreover, the equilibrium moment of force equation around the vertical axis, passing through the combined center of gravity, is in the form of
The most intense redistribution of normal reaction forces and friction forces is in the case of braking in a curved trajectory, as shown in Figure 2. Additionally, the redistribution, due to normal (centrifugal) and tangential (braking) inertial forces, is presumed linearly independent, and so calculated [35,36]. Omitting the details of solving the system of Equations (6)–(10) by an iterative predictor–corrector method, the solution with the following parameters: rCG = 16 m, hCG = 0.32 m, v = 10 m/s, LCG = 0.62 m, mcom = 130 kg, aT = 1.6 m/s2, is shown in Table 1. This set of parameters is within the friction coefficient, i.e., for each wheel within the friction cone.

Table 1.
Normal reaction forces at braking in a curved trajectory.
The redistribution shown in Table 1 is further used as load conditions for the chassis finite element model, depicted later on. An additional load is considered an impact force, in the amount of 200 N, without detailing it further. It will be modeled on one wheel, for instance, on the front right-hand side, and then on the rear right-hand side wheel, simulating driving over the same road imperfection. This force will be added to the “steady-state” normal force distribution.
2.2. Vehicle Power Train
The go-kart is presumed to be powered by an electric direct current motor, with lithium-ion batteries as an energy storage form. For the design of the drive shaft, chain gear selection of the chain, and selection of the motor, there were a few iterations of calculations of possible battery volumes, their capacities, and desired vehicle kinematics. The load on the rear shaft was combined from bending due to normal and tangential forces on tire contact surfaces, and torsional, due to the power transmission from the chain gear to the wheels. Cycles of normal stress components due to bending are different in their amplitudes because the normal reaction forces on each wheel are different in different time instances, depending on the driving conditions. The shear stress component values vary, rather than the direction, since the torque on the shaft acts mostly in one direction (drive), but the opposite rarely occurs since generation mode-braking is not the dominant mode of braking the vehicle. Given the stress component dependence of time, the stress has a spectrum, however, the calculation will be carried out with the highest expected stress components. The rear shaft with wheels, chain gear, bearings, and the braking disk is shown in Figure 5.
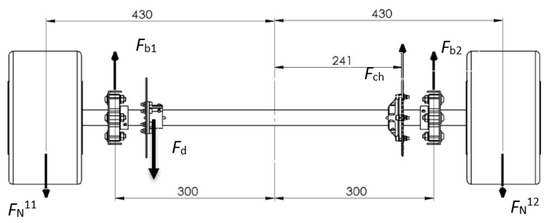
Figure 5.
Rear shaft with loads.
In Figure 5, along with the prior mentioned normal reaction forces, , are the bearing radial reaction forces; is the chain force, not in the same plane as previous forces, yet shown as such for simplicity, is the force on the disk at braking (red vector color), also not in the same plane. All of the forces cause bending of particular parts of the shaft, and the chain and disk forces cause torque, depending on the distribution of normal reaction forces, hence, the friction forces. Harmonically changing normal stresses, due to bending and constant shear stresses (due to torque) are transformed into equivalent mean and amplitude stresses, and they are used in the accepted criteria. In the calculation of the equivalent stress, mean and amplitude values incorporate the stress concentration factors in the context of material properties, starting from the Neuber’s notch sensitivity q criteria calculated from the transition radius between two shaft cylindrical parts, or in the keyway slot root, shown in detail in [24,25]. The drive shaft connecting the rear wheels is designed based on Soderberg’s dynamic strength criteria [29].
The power requirement, as the base for the DC motor choice, is based on the calculation of rolling resistance and aerodynamic resistance at the limit speed [5]. A DC motor rated 1.6 kW nominal power at nominal 48 V was chosen for this vehicle. It is also presumed that the overall efficiency rate is 0.9 [6]. The following equation is used for calculating the power consumption and the limit speed:
The chosen motor has a nominal rotational speed of 4600 min−1. The chosen wheels with a diameter of 255 mm would have an angular speed at the limit speed This leads to a rotational speed of To reduce the rotational speed from the motor to the wheel, a simple chain drive is presumed. The transmission ratio should be zw stands for the number of teeth on the rear shaft chain gear, and zm stands for the number of teeth on the motor chain gear. If the motor chain gear is chosen with 13 teeth, then the rear shaft chain gear should have . The chain that could be used to drive the vehicle has a pitch of at least 8 mm, for “reason” of the minimum pitch diameter of the small chain gear, following the diameter of the sleeve for the motor shaft. Such a chain gear would have a pitch diameter . The force acting on the chain gear on the rear shaft is .
Based on the wheel loads, the moment and torque diagrams were calculated and drawn. In this paper, they are not detailed, i.e., shown, for the sake of brevity. The equations for design of the shaft were based on dynamic strength conditions according to Soderberg, ASME, Gerber, Goodman, and others found in [29]. The stress components are firstly transformed into equivalent mean and amplitude stresses according to the von Mises theory (HMH, or distortion energy density theory):
In Equation (12), for calculation of equivalent amplitude and mean stress values, the akb stands for the stress concentration factor at bending, the upper index “t” stands for torsion, and “a” for axial load case. Further on, is the bending induced normal stress amplitude, is the axial load induced stress amplitude, is the torsion induced stress amplitude, while all stress components with lower index “m” are mean values of, respectively, depicted stress components. The Soderberg criterion is chosen as the simplest and most conservative condition in the form of:
In the Soderberg criteria (13), on the left-hand side is the form without an explicit member, which takes into account the influence of the surface roughness and size of the part, which are introduced into the right-hand side as k1 and k2, respectively, [37]. stands for inverse dynamic bending strength [29,37], stands for yield strength, and fs the chosen safety factor. These dynamic strength conditions use the stress components transformed into equivalent stresses, as shown in Equation (12). It is one of the best suited explicit equations for the case of combined non-proportional stress components (i.e., one stress component changing with time, differently from other stress components).
In the calculation of the equivalent stress, mean and amplitude values incorporate the stress concentration factors in the context of material properties, starting from the Neuber notch sensitivity q, calculated from the transition radius between two shaft cylindrical parts, or in the keyway slot root, shown in detail in [24,25]. The notch sensitivity is calculated for bending induced stress (normal) and torsional (shear) separately, and the stress concentration factors for each load case. The notch sensitivity is the value connecting the effective and geometrical stress concentration factor values, according to
In Equation (14), represents the geometrical value of the stress concentration factor for bending load case, which is calculated by the equation shown in the first row on the right-hand side. Mean and amplitude values of individual stress components are calculated as Taking that the normal stress component caused by the axial force is at least one order of magnitude smaller than the normal stress component caused by the bending moment, and constant, it is omitted from the equation for the shaft diameter, which, after some algebraic transformations, gives
The first critical section was identified at the wheel keyway root end, the end of the shaft where the wheel is pressed on the shaft’s ring surface (axial force caused by the nut on the M14), the ϕ20 measure. The second critical section is the starting position of the bearing from the wheel side, and the third is the keyway root, the section of it identified in more detail in [33,34]. In all of the identified sections, the load case is the torque and bending moment. The load cases, or in other words, forces acting on the wheels, and shaft, consequently, are listed in Table 2. Cases are numbered as follows: 1—braking in a curved trajectory, 2—acceleration in a straight trajectory, 3—normal drive in a straight trajectory with a road imperfection.

Table 2.
Load cases via reaction forces.
The normal reaction force and friction force normal component create bending moments in the shaft, and the friction force tangential component creates torque in the shaft. One circle of driving (a lap) consists of various kinematical conditions; acceleration in a straight trajectory, braking in a curved trajectory, braking in a straight trajectory, driving through a curved trajectory, and other possible combinations of drive parameters, so the loads on the shaft change through the lap. Looking at the distribution of loads through the shaft cycles, i.e., rotations, gives a load (directly proportional stress) spectrum, not analyzed here. Values of the bending moment and torque as functions of tire loads are in the form of
The ± sign in the first and second Equation (16) are related to the “direction” of the turn; a left-hand or a right-hand side turn. In the case of a left-hand turn, as shown in Figure 2, the signs in the bending moment calculation are the “upper” signs, i.e., + in the first and—in the second equation. The x coordinate is set at the middle of the left-hand side wheel. D is the wheel diameter.
In the case of a left-hand turn, as shown in Figure 2, with parameters described above, the maximum values of the bending moment and torque for the radius root on the cylindrical part on which the wheel rim sets are denoted as I, and the root of the keyway on the chain gear are denoted as II, or the disk in the right-hand side turn. The maximum bending moment on the sections, respectively, are MbI = 20.15 Nm, MbII = 51.5 Nm, MtII = 10.4 Nm.
Without detailing the calculation of the diameters at the mentioned sections, for various load cases, diameters for the highest loads are shown in Table 3. For the shaft material, S355 mild steel (St 60) was chosen with a yield strength of = 350 MPa, an inverse bending dynamic strength of σd−1 = 280 MPa, and an inverse torsional dynamic strength of σd,t−1 =180 MPa.

Table 3.
Shaft section diameters for the worst load case.
After calculating the diameters for the chosen sections in the worst-case scenario, by Equation (15), a final shaft geometry was chosen with respect to the available bearings, chain gears, the rod to manufacture it from, and technology, which is detailed with measures in Figure 6.
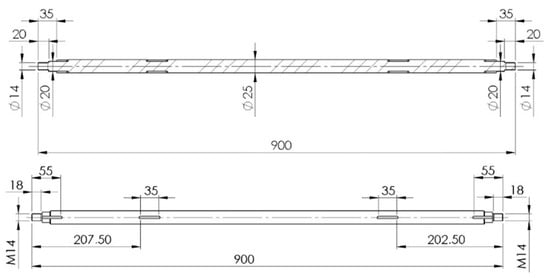
Figure 6.
The go-kart rear drive shaft. Upper: a cross section; lower: front view.
3. Finite Element Analysis
In this section of the paper, we present a detailed analysis of the pipe wall stability. The aim was to find the most loaded tube joint that was sub-modulated to calculate the risk of tube wall stability failure of the vehicle’s chassis conceptual design (Figure 7). The tube presumed for the chassis was seamless, had an outer diameter of 25 mm, and a wall thickness of 2 mm. Chassis analysis was performed using the finite element analysis module in the SolidWorks package. For a rough analysis, before the sub-modeling, the basic beam element was used to optimize the tube cross-section according to the strength criterion. The basic beam element [27,28] has two nodes with two degrees of freedom in each node, a transverse component, a deflection, and a rotational component. The displacement field can be described as a polynomial of the third-degree. The bending moment that could be described over the element was linear. The longitudinal displacement component and the torsional angle described in the element were linear. Thus, the longitudinal force and the torsional moment in the element were constant. The normal stress component over the element cross section was linear. The welded joints needed to be calculated for the strength criterion separately, based on the stress distribution in the tube joints. Here, it was omitted for the sake of brevity. Welded joints were presumed to be made by an active gas arc welding process.

Figure 7.
Chassis geometry modeled for the finite element analysis: (a) isometric “real” view; (b) chassis tubes and plates.
For purposes of sub-modeling and a detailed analysis of tube wall stability, basic solid elements with three components of displacements per node were used. This element has the “properties” of describing a linear displacement component field over the element; therefore, it can describe constant stress components over the element.
The idea used to model the chassis in the sub-modeling context is to use the beam elements in the first step of the analysis. Then, based on the stress distribution, the modeling is continued with the introduced solid elements on the chassis part with the highest stress value, combined with the beam elements in the remaining part, using the loads at the sub-model boundary for stability analysis. The software version available to the author performing the analysis has limitations of such a sub-model combination. It allows modeling of only the entire chassis with solid elements, and later the sub-model is analyzed only for stability. Figure 8 shows the chassis loads and boundary conditions selected for the finite element analysis.
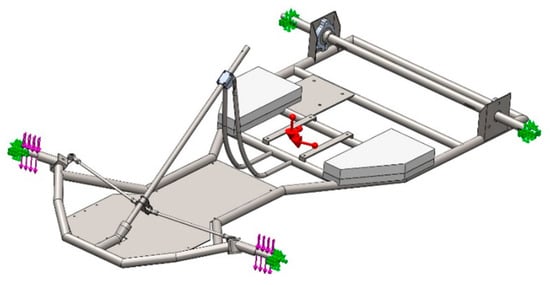
Figure 8.
Chassis loads and boundary conditions for the finite element analysis.
Figure 9 shows the coarsest and finest networks of solid elements. In addition to “medium”, they were used to analyze the components of stress and displacement. The results for the von Mises (equivalent) stress for the finest mesh model are shown in Figure 10. The calculation proved good convergence of both displacement and stress components (not detailed in this paper). Most of the chassis had a “low” equivalent stress, as the front wheel joint had the highest local stress, around 275 MPa, while the yield strength was around 355 MPa. Here, as a significant limit, the maximum normal forces, i.e., the chassis stresses, were not considered to occur in many cycles of stress (load) in one circuit, assuming that the circuits were more or less the same in kinematic conditions. This maximum stress was, for example, 10 or 15% of the total stress cycle. This particular joint was taken as a significant part of the chassis and sub-model and was calculated under safety conditions due to the possibility of local pipe wall bending. This is the topic of the next chapter.

Figure 9.
Meshes based on beam elements: (a) coarsest mesh; (b) finest mesh.
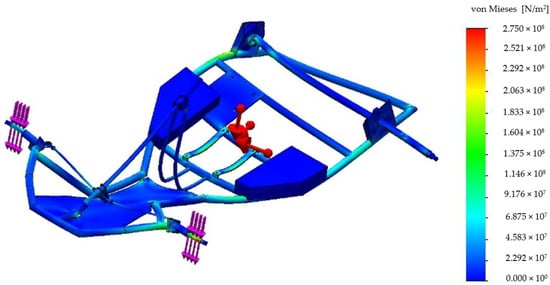
Figure 10.
Results of analysis, with respect to equivalent stress for the finest mesh (von Mises stress).
4. Tube Wall Stability Analysis (Buckling)
The most stressed part of the chassis is the steering area—the front wheel joint, as can be deduced from the previous analysis. Therefore, the steering part of the vehicle was further analyzed for local stability, as additional criteria for the chassis mechanical integrity. For this purpose, basic solid elements were chosen. They had the ability to describe the linear displacement field in each coordinate axis and the fields of the constant stress component [27]. The geometry of the steering part taken for a sub-model is shown in Figure 11a. An analysis of the stress components and equivalent stresses give the stress distributions, as shown in Figure 11b. The finest solid element mesh utilized for stability analysis is shown in Figure 11c. To compare the cross-sectional thickness of the tube wall, Figure 12 shows three different sizes of solid elements. After the displacement and stress analysis, the load at the sub-model boundary nodes were imported for the analysis of the sub-model stability.
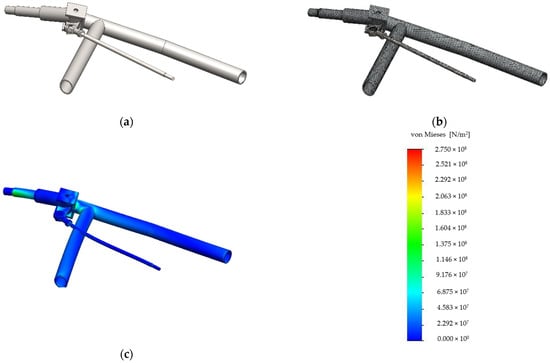
Figure 11.
Sub-modeling of the most stressed joint: (a) geometry of the chassis, part view; (b) view of joint sub-model mesh based on solid elements; (c) von Mises stress distribution in the sub-model.
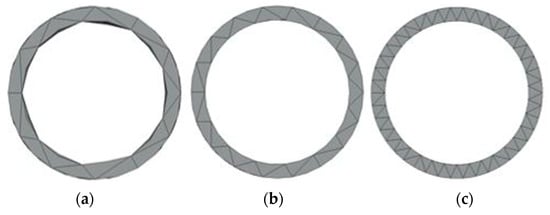
Figure 12.
The size of the solid elements compared to the cross-sectional thickness of the tube wall: (a) coarsest mesh; (b) medium mesh; (c) finest mesh.
The stability analysis of the sub-model of the steering part, known as a “stub axle” for the finest mesh, is shown in Figure 13. The lowest value of the safety factor on the scale is 1.537, which is still satisfactory, as it should be noted that this stress is localized on a smaller part of the pipe wall (Figure 13) and is calculated from the most severe load case.
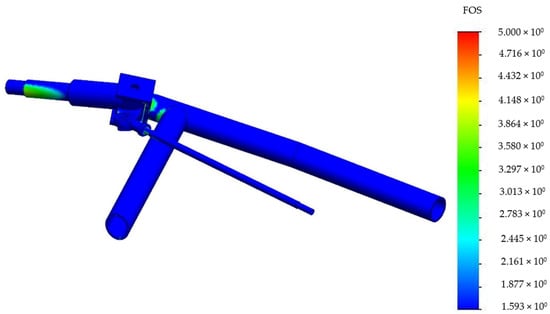
Figure 13.
Sub-modeling of the most stressed joint–stub axle in the steering mechanism: calculated factor of safety (FOS).
In the mechanical part of the design process, shown above, the small detail of the welded joint has been omitted. The joints made by active gas arc welding have lower mechanical parameters than the base metal, and therefore need to be locally strengthened in order to satisfy the strength criterion. Adding a new tube section, in length of about its outer diameter, provides significant improvement in welded joint strength and tube wall stability in the most stressed area. This was not modeled for the FEA (in order to keep the results as conservative as possible and the modeling as simple as possible). Any reinforcement in the most stressed areas will lower the stress and increase safety from local buckling (tube wall).
Furthermore, a few details not directly numerically addressed involve the planned measurements. The first step involves plans to install the strain gages on as much of the most stressed (based on the FEA) tube joints, depending on the available gages. These serve a purpose in validating FEA results in the context of “usual” drive loads, i.e., braking and accelerating in a straight and curved trajectory, and braking in a straight trajectory, as identified in most severe load cases. Another important plan involves installing accelerometers on or adjacent to the king pin of each wheel, and on a few points around the vehicle’s center of gravity position, to determine the relative motion of the wheel to the chassis as the cause of impact with the road imperfection. In the case of impact with a road imperfection, we concluded that an experiment is a much more appropriate and acceptable solution to determine “true” loads for any further developments and calculations of critical load combinations, revealing the findings to the scientific community. Any reliable numerical simulation would require very complex modeling, material behavior parameters, mathematical and numerical competences, and possibly experience. All of this is omitted through conducting an in vivo measurement, although with the awareness that some calculations stand between measurements of king pin kinematics and actual impact forces. This is an issue to address in further investigation steps and actions. Additional measurements planned involve the measurements of steering mechanism dynamics, with the aim of determining an optimal steering ration, geometry, and other design details to “bring” the steering in the most severe road dynamic conditions to within an average driver’s biomechanical capabilities.
5. Design of Electrical System
Although, in this paper, we did not focus on detailed designs of the electrical controlling system and battery power supply, with a multitude of particular Li-ion battery cells, and the belonging control system elements, it was nevertheless necessary to conduct a thorough conceptual analysis of some essential parameters. The power supply system of electric vehicles is most often based on battery cells. Different kinds of cells have a number of limitations related to energy density and power, mass, charge, and discharge currents, the number of charge cycles, and compliance with safety requirements. Proper selections and linking of cells to modules is crucial for subsequent operations of a system. The aim is to ensure the longest possible operation system. Currently, the most commonly used cells in vehicles are Li-ion cells [47]. They are used mainly due to their high energy and power density, long life cycles, and no memory repercussions. As a result, Li-ion batteries can be smaller and take up less space than batteries built from other stations (Figure 14), as presented in reference paper [47].
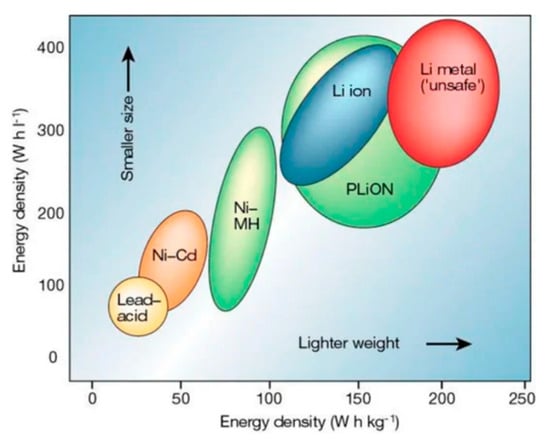
Figure 14.
Energy density comparison of battery cell materials.
Mechanical damage to Li-ion cells is the type of failure that is most likely to occur in kart racing, and it is important to keep this in mind at the design stage of the housing and the position of the vehicle battery system. When designing the size of the battery system space, another problem in the case of electric go-karts for entertainment purposes is to ensure operation during at least one race (approximately 10–20 min) so that there is no need to charge the cells or replace them while driving. When calculating the chassis stress parameters, in addition to determining the position of the battery system, the position of the DC motor with the support bracket should also be determined in time. Therefore, certain positions of the two battery tanks are placed symmetrically on the chassis on both sides of the driver’s seat (Figure 8), as well as the position of the DC motor conceptually placed behind the driver’s seat on the corresponding support bracket (Figure 2 and Figure 8).
5.1. Energy Demand
The battery system of an electric go-kart depends on several related limitations on the vehicle dimensions, weight, efficiency, and range of the cell. The main problem that arises in the case of an electric go-kart power supply system is the limited capacity of battery cells, resulting in limited driving time and radius [47]. The main challenge is to ensure the longest possible operation time, fast charging, and weight reduction of the vehicle. Battery weight should not be significant in relation to the mass of the whole vehicle. The first way is to assemble a large number of battery cells. A large number of stations connected in parallel will increase the battery capacity, which will extend the operating time. The disadvantage is the mass of the batteries. Being overweight causes more strain and faster wear of the components, including bearings and tires. Obviously, there is a need to develop a concept for this case of the power supply system as well.
5.2. Battery System Modeling
The most important issues in power supply system development are battery cells, and more precisely, the type to be used. To choose the most appropriate station, it was decided to use a morphological analysis. The analysis included, among other things, performance, safety, price, service life, power, energy density, operating temperature, and charging times. The most important criterion was the safety of the vehicle users. For this reason, cell types that meet high safety standards have been reduced to two cell types—LTO (Li4 Ti5 O12—“lithium titanate”) and LFP (Li Fe Po4—“lithium iron phosphate”). These two types do not burn or explode compared to the other cells considered. The number of cycles for both types is large, and the range of operating temperatures of the cells is also very wide and sufficient to operate in the initially assumed conditions. Comparing LTO and LFP cells, the biggest difference, and also the disadvantage of LTO cells, is their high cost.
Different batteries have different energy value densities and specific energy. Li-ion cells used in the automotive industry (NMC—“nickel manganese cobalt”, NCA—“nickel cobalt aluminum”) have much higher values than LTO and LFP. Table 4 shows the basic parameters of these cells.

Table 4.
Specific energy and energy density of Li-ion cells.
Nominal vehicle voltage of a 48 VDC for a BDCEM drive can be achieved by a series connection of several Li-ion batteries with a nominal voltage of 3.6 V and a 3000 mAh capacity. The battery type 18650 was selected for this concept. This leads to a simple calculation of the required number of battery units connected in the serial connection: 48 V/3.6 V = 13.333; rounded to an integer, it is a value of 14. Therefore, the expected nominal battery system voltage is UN = 14 ⋅ 3.6 = 50.4 V. According to the go-kart standard, driving with maximum power can take 10–20 min. For further design of the power supply, the chosen energy capacity is 1.6 kWh (E = 1600 Wh). Since one battery has an approximate or expected capacity of 3 Ah, this means that one serial “package” has the same energy capacity E1:E1 = 50.4 V·3 Ah = 151.2 Wh. Thus, when designed, ten of such packages should be connected in parallel and then the energy capacity would be ten times more, equal to E10 = 1512 Wh. This is close to the planned power consumption and is also within some geometric parameters that are suitable for mounting on chassis tubes. Details of the battery holder box and the design of the battery cell inter-connections are shown in Figure 15.
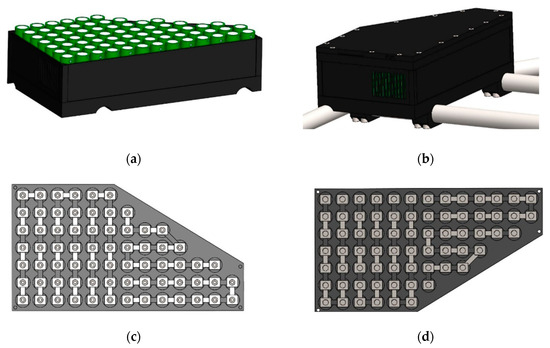
Figure 15.
Battery system concept design: (a) cell placement in a holder box; (b) box with the cover attached to the chassis distribution as the basis for the sub-modeling view; (c) lower battery cell inter-connecting plate view; (d) upper battery cell inter-connecting plate view.
Since a Li-ion battery is the most expensive part of the electric go-kart, improving battery performance is one of the most important factors in promoting the electric vehicle market, extending battery life, reducing the cost of purchase, and giving potential customers confidence in the product. Designers of electric battery systems must consider a method to improve battery performance that prolongs battery life and increases grip ability. This can be achieved by finding the best filling profile for the EV battery by identifying that battery time can accept charging and the charging profile, with minimal impact on battery life. The analysis presented in reference [48] shows that including rest periods reduces battery degradation in two parts while charging the battery’s ways.
On the other hand, the reliable battery management system, or BMS, is required for the safe use of Li-ion batteries [47]. Its purpose is to control the polarity of the connected battery cells, limiting current, temperature, overload, and other possible anticipated faults. The main purpose of the controller is to check each battery to make the most of its capacity and extend its life. Two main types of controllers are common—centralized and divided. In the case of centralized, the main controller and battery management system are located in one housing. In a split system, each battery has its own control system, which sends information to the controller. The centralized system has more wiring; however, its cost is significantly lower compared to the split system because there is no need for a board for each battery. The system described in this paper was chosen because of its simplicity and cost. The BMS controller was selected from the manufacturer Deligreen [49].
Another purpose of the BMS is to maintain balance between batteries or the designed battery groups or packages regarding nominal voltages. Not all batteries are produced the same due to unavoidable manufacturing errors, i.e., margins and, therefore, balancing functions. The whole series of batteries depends on the weakest, which means that the weakest battery determines the capacity of the series. It also means that charging the weakest battery determines how much energy can be stored in a series. For this reason, BMS can maintain balance in a passive or active way. In a passive way, the difference in capacity between the batteries is converted into heat until they all reach the same capacity. In an active way, BMS uses energy from “stronger” batteries and charges weaker ones until they all reach the same capacity.
It is envisaged that each of the designed battery tanks in the presented conceptual design has its own BMS, and in the case of one empty series, the vehicle still runs on a different series. The selected BMS Deligreen is marked “14S 60A 48V”. The “14S” refers to the number of batteries in the series; “60A” is the maximum current at which the BMS switches off the system. Such a BMS is shown in Figure 16 [47]. The scheme of connecting the “14S 60A 48V” BMS assumes the connection to a maximum of 10 battery groups (B1 to B10) to the input connectors shown in Figure 16.
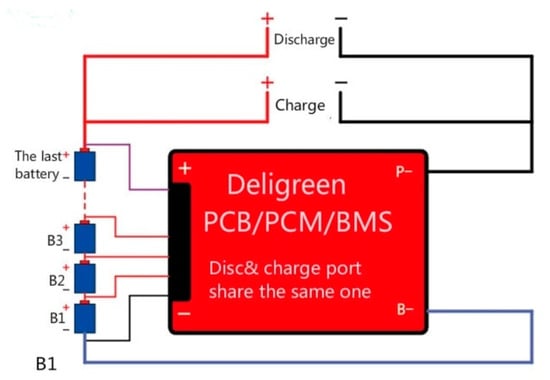
Figure 16.
Battery management system Deligreen PCB/PCM/BMS connecting scheme.
6. Discussion
This paper presents a comprehensive approach to a conceptual design of a modular electrical go-kart. The power train was calculated for a constant drive at a nominal motor power rated 1.6 kW. The wheel normal forces cause harmonic changes of the normal stress components while rotating and constant shear stress components caused by the torque. This disproportional stress state was taken into design by Soderberg’s criteria of dynamic strength, as described in [29]. The drive shaft was detailed in a calculation following the principles from [24,25,29], which is not seen in many listed references. Power transmission is presumed by a chain transmission, as in among others [12,30]. Our approach to the development of a concept, modular, electrically-powered go-kart has a few key oversized parts, namely, the battery pack, the drive shaft, the chassis joints holding the vehicle’s power train, and the bolts connecting the power train elements. All of this allows a “modular” ability of improving, testing, and simply changing those parts.
The described battery pack can be used for a powerful motor in a shorter period of time. The shaft allows the use of approximately 150% more of the powerful motor, taking into account the load spectrum [6,12,30], which is omitted here. This is based on the S–N curve [24,25,29,33,37], while the number of the most severe load cycles is dependent on the driving conditions and does not construct all of the load cases [41]. Increasing the power also demands increasing or adding a controller for a higher current [42].
Vehicle dynamics is calculated for a case of braking in a curved trajectory [30,35,36], and presumed for a case of impact with a front tire on a road imperfection. While the redistributions of normal reaction wheel forces in any case of a flat road are reliable, the road imperfection impact force is only at the level of presumption. We plan to conduct an in vivo measurement of chassis kinematics at road imperfection impact conditions in order to determine the reaction force indirectly. This, we intend to conduct on a manufactured go-kart by adding accelerometers on chosen “key” vehicle points, such as king pin, as close to the wheel as possible, on the seat joints, and depending on the results, a few more. The indirect force measurement in this manner means we need to analyze the dynamical behavior of the chassis loaded by an impulse (a step function) force [39], with a very short duration, approximated from tire geometry, rigid imperfection behavior, and vehicle velocity. By the chassis response, we will be able to adjust the force amplitude to have some base for a parametric analysis of load spectrum caused by impacts on road imperfections as a function of velocity, imperfection geometry, and chassis characteristics, i.e., elasticity. This alone would be, we consider, a significant contribution to the community of small electric vehicle designers. This parametric analysis was not explicitly noticed in the references listed.
The normal reaction forces redistribution was calculated by a predictor–corrector method [30,37]. We showed a free body diagram for the vehicle dynamics, equations of equilibrium, and solutions for three COG kinematics cases that we considered the most intense cases for the wheel reaction force redistribution, i.e., driving conditions. A similar display in all of the details could be seen in reference [30]. Those forces are used as the loads in the chassis finite element model. The model consists of basic beam finite elements [27,28,39] for establishing the global stress distribution, and determining which joint is the most stressed one, so that it would be modeled with linear solid finite elements [27,28] for a more detailed analysis. Three different element characteristic measures, the length of the beam elements, and the edge length of solid elements, i.e., “mesh size”, were used to control the displacement and stress component convergence [27,28]. The analysis showed good convergence for both beam and solid element meshes. The results for the sub-model stability (buckling) analysis showed that the chosen tube wall thickness to diameter gives a safety factor value of five in most of the chassis. The lowest safety factor is around 1.6 in a small area around the front wheel axle tube joint. A large portion of the chassis was oversized (regarding the cross section). This leaves enough “space” for improvement upon the test ride and measurement and an increase in power if needed/desired.
Another important feature after manufacturing the vehicle would be installing strain gages on the most stressed chassis parts, in order to validate the analysis results. The accelerometers and strain gages, along with a battery state monitoring device, would be installed in the vehicle and connected by Wi-Fi with a stationary computer to have recording of the in-drive measured data. This would provide important feedback on the accuracy of the predicted vehicle’s behavior in a curved trajectory, and to relate the chassis elasticity with the redistribution of ground reaction forces.
Based on the stress distribution, some improvement in the middle part of the chassis, the tubes passing along (under) the driver, have in the overall view, high stress. Our choice of the tube’s cross section is 25 mm of the outer diameter, a wall thickness of 2 mm, which is similar to a heavier go-kart, overall mass of 190 kg, the tube’s outer diameter of 25.4 mm (1”), but no wall thickness in [11], or 26/20 mm for 190 kg of mass in [15], up to the thickest wall tube of 3.125 mm in [21], so that part of the chassis could be made from a half-a-millimeter thicker wall tube, or a larger (by a few millimeters) diameter tube to lower the stress. Moreover, we would consider including an innovative addition to improve the strength and rigidity of the same tubes with either hydro-tubing, cold rolling (plastic deformation) of the circular tube to give it a “directional” rigidity, or some similar solution, with as little added mass and involved energy as possible.
There is a “drawback” in our possibilities of sub-modeling; the software version used has limitations of sub-modeling in the sense that it “needs” to have a mesh of solid finite elements to continue the analysis and form the linear static analysis to, in our case, an elastic stability analysis. Therefore, we were limited in utilizing the basic idea of sub-modeling, to use as simple (basic beam) and as few as possible finite elements for an initial analysis for the load distribution, and parts of the chassis with “higher” stress components (i.e., the equivalent von Mises stress), and to sub-model those regions with solid elements, more refined in size. This is firstly to reduce the modeling time, computational time, and demand on the computer’s CPU and RAM “capacity”, or to show how to control the computational model for such a design, and where the pitfalls of using simple and coarse meshes are [28,39].
One mechanical subsystem involves the steering mechanism or system—the development of which has not been at the center of our efforts thus far, in the sense of a detailed analysis of forces acting on the wheels in the most severe driving conditions, and the resistance on the steering wheel to control or execute the maneuver in question [10,13,30,43]. This is directly related to the angles of a king pin (i.e., the wheel) and inflation of the tire; hence, its deformation [30], redistribution of ground reaction forces, and so on, which we intend to measure to validate all of the design presumptions. The restriction is to find the steering ratio [30] that provides acceptable resistance at the steering wheel for a child [45,46], since it is intended for children and adults up to an expected 80 kg of mass. There are not many details available in the references listed regarding detailed parametric displays of influence of mechanical components on the steering wheel torque; rather, a few papers show calculations of steering wheel torque [10,13].
Another important aspect of chassis analysis is impact, shown in some papers [10,11,15,19,20]. The forces calculated are somewhat “averaged” through the impact time, with not enough descriptions on the assumptions of the impact conditions. In case of sufficient funding, we intend to build several chassis with rigid masses instead of battery packs, motors, and so on, so as to have a realistic enough model for crash tests, with possibly high-speed cameras. One of the goals in the concept development is determining and improving crashworthiness [30].
A braking system was not detailed in the calculation; however, there is sufficient published numerical simulations for heavier karts, with higher limit speeds, with similar weight distribution ratios [2,12,31], so as to have reliable choices for disk and pad sizes and characteristics. Detailed calculations of braking systems is the next step planned in the measurement stage of development.
In the power supply assembly, much care has been placed into designing its capacity [47] so as to maximize the battery life span and have the lowest cost battery management system. Batteries’ lifetime is mainly influenced by the highest electrode temperature [48]. For that reason, we oversized the battery pack so we could use the two sides of the pack in a way to shortly have the ability to “boost” power (torque) as much as the DC motor allowed [3] by employing all the batteries, hence lowering the highest current on roughly a half the value with the doubled number of batteries as in the nominal drive. Another aspect of doubling the battery pack is the regenerative braking mode [40,42]. Since a race is composed of accelerating and braking, the new way of planning the usage of batteries is somewhat innovative to have a roughly up to one-third of capacity charged pack on one side, which can be used in a short-term acceleration mode to aid the “main” pack, and in the braking mode, to make the highest possible energy “recovery” from braking. This is all easily achievable by programming the BMS in such a way [40,42]. The connecting plate that connects batteries is designed to be very simple in the sense that it is composed of prefabricated contact tin plates, which have been incorporated into the connecting plate and soldered together. The battery packs alone have been designed in an “original” manner, such to incorporate them into a chassis shape. They are easily interchangeable, making it modular.
7. Conclusions
In this paper, we provided an overview of a conceptual design and development of an electric go-kart chassis for undergraduate students in vehicle dynamics and stress applications. The go-kart, as a light racing vehicle, has a high level of demands, pertaining to structural, driving, and overall economic conditions, i.e., the lowest possible prices. The structural demand represents the lowest possible mass (weight), which ensures strength and rigidity for the presumed loads, the lowest possible costs of the joints (mostly welds), the “most possible” standard part installed, and so on. The drive demand represents a replacement of the conventional gasoline ICE with Li-ion batteries powered with a BDCEM motor for the most efficient drive and battery management system with a centralized system. The drive shaft on the rear wheels is designed for higher torque, in case a more powerful motor is installed. Special care was invested in calculating the thin-walled tube’s local stability, i.e., to optimize the chassis by utilizing the sub-modeling technique.
This paper, as a preliminary design, emphasizes the importance of modeling and analysis of the obtained results as well as possible improvements in both construction methods and material selection. The authors hope that the presented work will inspire readers and students, leading them to further develop new methods and applications of go-kart design solutions. This concept is intended to be modular, i.e., replaceable battery packages, adaptable steering wheel position, driver’s seat position, and “drive” motor replacement. The most important feature of the proposed approach is to utilize it for in vivo measurements of vehicle dynamics, the most stressed joint stresses of the chassis (by strain gages), the steering wheel resistance as a function of mechanical parameters, such as tire inflation pressure, steering mechanism geometry, and drive conditions, to parametrically research the overall safety of such a design. We will continue our research on the go-kart mechanical system and BMS system, respectively.
Author Contributions
Conceptualization, J.H., V.T. and T.M.; methodology, V.T. and J.H.; software, T.K. and J.H.; validation, T.M.; formal analysis, J.H.; investigation, T.K.; resources, J.H.; data curation, T.M.; writing—original draft preparation, J.H.; writing—review and editing, V.T.; visualization, J.H., T.K. and V.T.; supervision, V.T. and T.M.; project administration, J.H. and V.T. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was funded by Zagreb University of Applied Sciences, 10000 Zagreb, Croatia.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ehsani, M.; Gao, Y. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles—Fundamentals, Theory and Design; CRC Press: Boca Raton, FL, USA, 2005; pp. 142–154. [Google Scholar] [CrossRef]
- Cardoso, C.; Ferreira, J.; Alves, V.; Araújo, R.E. The design and implementation of an electric go-kart for educational in motor control. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2006, Taormina, Italy, 23–26 May 2006. [Google Scholar] [CrossRef]
- Vitols, K.; Reinberg, N.; Sokolovs, A.; Galkins, I. Drive Selection for Electric Kart. In Proceedings of the 14th International Power Electronics and Motion Control Conference (EPE/PEMC), Ohrid, Macedonia, 6–8 September 2010. [Google Scholar] [CrossRef]
- Heffernan, B.; Duke, R.; Zhang, R.; Gaynor, P.; Cusdin, M. A go-cart as an electric vehicle for undergraduate teaching and assessment. In Proceedings of the 20th Australasian Universities Power Engineering Conference (AUPEC), Christchurch, New Zealand, 5–8 December 2010; IEEE: Piscataway, NJ, USA, 2010. ISBN 978-1-4244-8380-8. [Google Scholar]
- Burridge, M.; Alahakoon, S. The Design and Construction of a Battery Electric Vehicle Propulsion System—High Performance Electric Kart Application. In Proceedings of the International Conference on Sustainable Energy Engineering, Perth, Australia, 12–14 June 2017; Volume 73. [Google Scholar] [CrossRef]
- Krishnamoorthi, S.; Prabhu, L.; Shadan; Raj, H.; Akram, N. Design and analysis of electric Go-Kart. Mater. Today Proc. 2020, 45, 5997–6005. [Google Scholar] [CrossRef]
- Wegert, D.; Mauer, C.; Huth, P.; Karlin, J.; Altschaffel, F. Development and Assembly of o Go-Kart Sized Fuel Cell Research Vehicle; F2008-Sc-037; University of Applied Sciences: Bingen, Germany, 2008. [Google Scholar]
- Faieza, A.A.; Sapuan, S.M.; Ariffin MK, A.; Baharudin BT, H.T.; Supeni, E.E. Design and fabrication of a student competition based racing car. Sci. Res. Essays 2009, 4, 361–366. [Google Scholar]
- Sharma, C. Design and Fabrication of Environment Friendly Kart. In Proceedings of the International Conference on Emerging Trends in Mechanical and Electrical Engineering, Tekanpur, India, 13–14 March 2014. [Google Scholar]
- Jha, M.K.; Singh, A.; Gupta, N.; Renwal, N.; Suman, S.K. Design and Simulation of an ECO-Friendly kart. In Proceedings of the 15th International Conference on Recent Trends in Engineering, Applied Science and Management, Hyderabad, India, 1 April 2018. [Google Scholar]
- Kumar, P.K.; Kumar, K.S.; Hemanth, P.; Sai Chandu, V.; Babu, D.N. Design of IC Engine Go-Kart and Analysis of its Chassis. J. Emerg. Technol. Innov. Res. 2020, 7, 96–105. [Google Scholar]
- Larminie, J.; Lowry, J. Electric Vehicle Technology Explained, 2nd ed; Wiley: London, UK, 2012; pp. 183–187. ISBN 978-1-119-94273-3. [Google Scholar]
- Kumar, N.S.; Vignesh, A. Design and Analysis of an Electric Kart. Int. J. Res. Eng. Technol. 2015, 4, 9–17. [Google Scholar]
- Ravikanth, D.; Rajagopal, K.; Murty, V.S.S.; Harikrishna, A. Design of a Go Kart Vehicle. Int. J. Sci. Eng. Technol. Res. 2017, 6, 448–456. [Google Scholar]
- Kumar, R.S.; Rohith, R.; Srinivas, S. Design of a Compact Go Kart Vehicle. Int. Res. J. Eng. Technol. 2019, 6, 1611–1623. [Google Scholar]
- Porwal, A.; Chohuan, N.; Chohuan, K.; Chatur, J. Design and Fabrication of Electric Go-Kart. Int. J. Eng. Res. Technol. 2020, 9. [Google Scholar] [CrossRef]
- Chau, K.T. Electric Vehicle Machines and Drives Design Analysis and Applications; John Wiley and Sons: Singapore, 2015; pp. 18–19. ISBN 978-1-118-75252-4. [Google Scholar]
- Raghunandan, D.; Pandiyan, A.; Majeed, S. Design and Analysis of Go-Kart Chassis. Int. J. Eng. Sci. Res. Technol. 2016, 5, 134–141. [Google Scholar] [CrossRef]
- Aniket, S.S.; Sameer, S.R.; Shubham, K.A.; Nehatrao, S.A. Design and Analysis of Go-kart Chassi. Int. J. Adv. Res. Innov. Ideas Educ. 2017, 3, 2763–2769. [Google Scholar]
- Kumar, N.S.; Rana, R.; Hassan, M.N.; Goswami, K. Design and Impact Analysis of Go-kart Chassis. Int. J. Appl. Eng. Res. 2019, 14, 46–52. [Google Scholar]
- Hajare, K.; Shet, Y.; Khot, A. A Review Paper on Design and Analysis of a Go-Kart Chassis. Int. J. Eng. Technol. Manag. Appl. Sci. 2016, 4, 150–164. [Google Scholar]
- Renuke, P.A. Dynamic Analysis of a Car Chassis. Int. J. Eng. Res. Appl. 2012, 2, 955–959. [Google Scholar]
- Patil, N.R.; Kulkarni, R.R.; Mane, B.R.; Malve, S.H. Static analysis of Go-Kart Chassis frame by Analytical and SolidWorks Simulation. Int. J. Sci. Eng. Technol. 2014, 3, 661–663. [Google Scholar]
- Neuber, H. Theory of Notch Stresses; Office of Technical Services; U.S. Department of Commerce: Washington, DC, USA, 1961.
- Neuber, H. Theory of Stress Concentration for Shear Strained Prismatic Bodies with Nonlinear Stress-Strain Law. J. Appl. Mech. 1961, 28, 544–550. [Google Scholar] [CrossRef]
- Heisler, H. Advanced Vehicle Technology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 9780080493442. [Google Scholar]
- Sorić, J. Metoda Konačnih Elemenata; Golden Marketing: Zagreb, Croatia, 2008. (In Croatian) [Google Scholar]
- Sorić, J. Uvod u Numeričke Metode u Strojarstvu; Golden Marketing: Zagreb, Croatia, 2008. (In Croatian) [Google Scholar]
- Budynas, R.G.; Nisbett, K.J. Shigley’s Mechanical Engineering Design, 9th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; SAE International: Warrendale, PA, USA, 2021; 470p, ISBN 978-1-4686-0176-3. [Google Scholar]
- Rajkumar, M.; Soundar Rajan, M.; Queen Florence, M. Design Optimization and Analysis of Braking system of Go-Kart. Int. J. Eng. Res. Technol. 2020, 9, 558–563. [Google Scholar] [CrossRef]
- Ambashta, H.; Mehndiratta, C.; Waghmare, N. Design of Braking System of Go-kart. Int. J. Emerg. Technol. Eng. Res. 2017, 5, 57–59. [Google Scholar]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors, 3rd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Young, C.W.; Budynas, G.R. Roark’s Formulas for Stress and Strain, 7th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Doumiati, M.; Baffet, G.; Lechner, D.; Victorino, A.; Charara, A. Embedded estimation of the tire/road forces and validation in a laboratory vehicle. In Proceedings of the 9th International Symposium on Advanced Vehicle Control (AVEC’08), Kobe, Japan, 6–9 October 2008. [Google Scholar]
- Doumiati, M.; Victorino, A.; Charara, A.; Baffet, G.; Lechner, D. An estimation process for vehicle wheel-ground contact normal forces. In Proceedings of the 17th World Congress of the International Federation of Automatic Control, Seoul, Republic of Korea, 6–11 July 2008. [Google Scholar]
- Alfirević, I. Inženjerski Priručnik IP 1; Školska knjiga d.d.: Zagreb, Croatia, 1996. (In Croatian) [Google Scholar]
- Babu, B.; Prabhu, M.; Dharmaraj, P.; Sampath, R. Stress analysis on steering knuckle of the automobile steering system. Int. J. Res. Eng. Technol. 2014, 3, 363–366. [Google Scholar]
- Abdullah, N.; Sani, M.; Husain, N.; Rahman, M.; Zaman, I. Dynamics properties of a Go-kart chassis structure and its prediction improvement using model updating approach. Int. J. Automot. Mech. Eng. 2017, 14, 3887–3897. [Google Scholar] [CrossRef]
- Wang, H.; Sun, T.; Zhou, X.; Fan, Q. Research on the Electric Vehicle Control System. Int. J. U. E-Serv. Sci. Technol. 2015, 8, 103–110. [Google Scholar] [CrossRef]
- Krzysztof, M. Battery System Design for Electric Go-Kart, Transdisciplinary Engineering for Resilience: Responding to System Disruptions; IOS Press Ebook: Amsterdam, The Netherlands, 2021; pp. 395–404. [Google Scholar] [CrossRef]
- Gabbar, H.; Othman, A.; Abdussami, M. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Anwar, M.; Shaik, A.; Sohail, M. Steering System of Go-Kart. Int. Adv. Res. J. Sci. Eng. Technol. 2017, 4, 21–24. [Google Scholar] [CrossRef]
- EN 10027-1:2005; Designation Systems for Steels—Part 1: Steel Names Bezeichnungssysteme für Stähle—Teil 1: Kurznamen. Available online: https://sanyosteel.com/files/EN/EN%2010027-1.pdf (accessed on 10 July 2023).
- McDowell, M.A.; Fryar, C.D.; Ogden, C.L.; Flegal, K.M. Anthropometric Reference Data for Children and Adults: United States, 2003–2006; National Health Statistics Reports, no 10; National Center for Health Statistics: Hyattsville, MD, USA, 2008. [Google Scholar]
- Hall, S.J. Basic Biomechanics, 6th ed.; McGraw-Hill: Boston, MA, USA, 2012. [Google Scholar]
- Miao, Y.; Hynan, P.; von Jouanne, A.; Yokochi, A. Current Li-Ion Battery Technologies in Electric, Vehicles and Opportunities for Advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef]
- Al-karakchi, A.A.; Lacey, G.; Putrus, G. A method of electric vehicle charging to improve battery life. In Proceedings of the 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Available online: www.deligreenpower.com (accessed on 15 January 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).