Magnetic Vortex Phase Diagram for a Non-Optimized CaKFe4As4 Superconductor Presenting a Wide Vortex Liquid Region and an Ultra-High Upper Critical Field
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
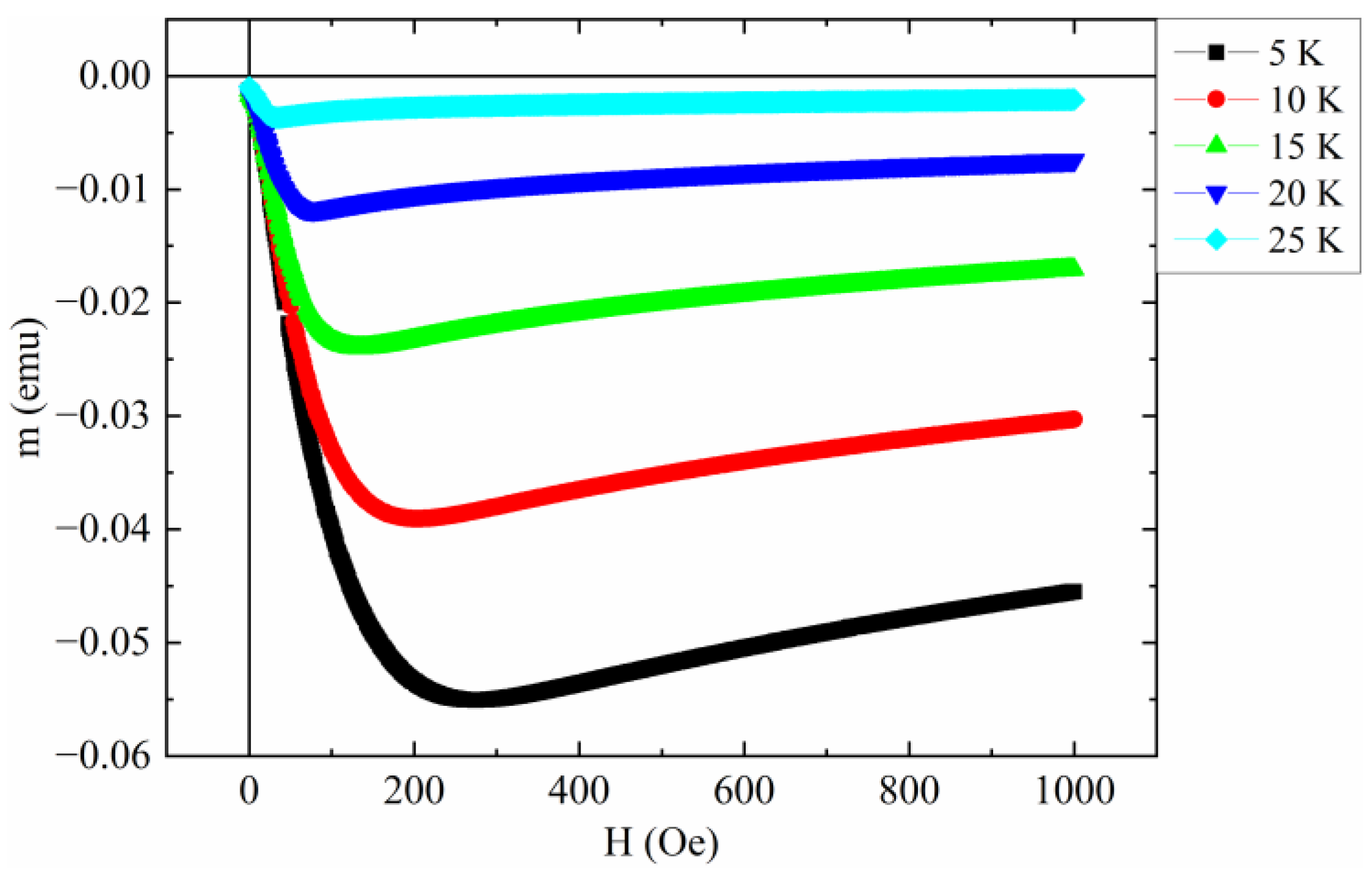
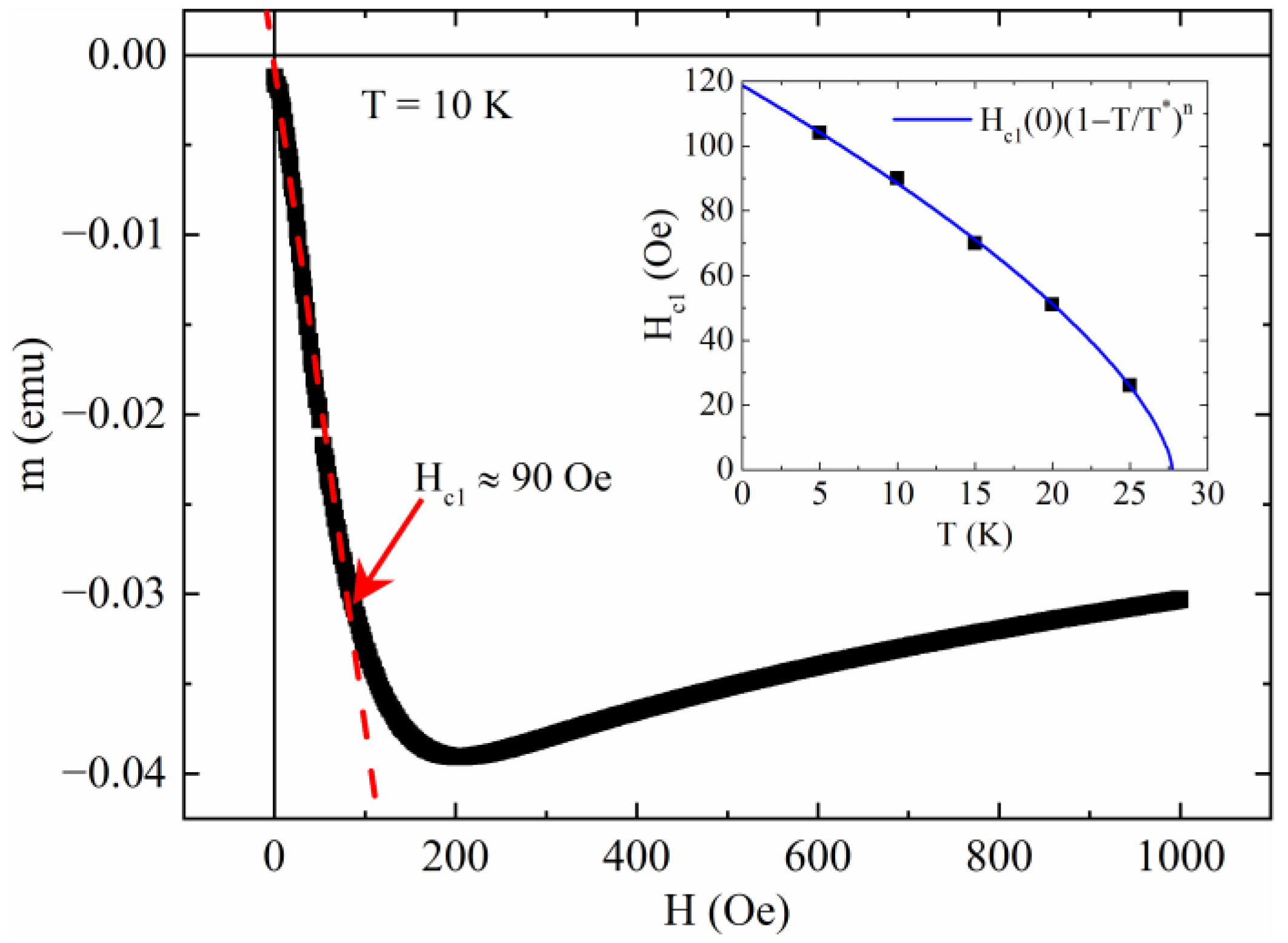
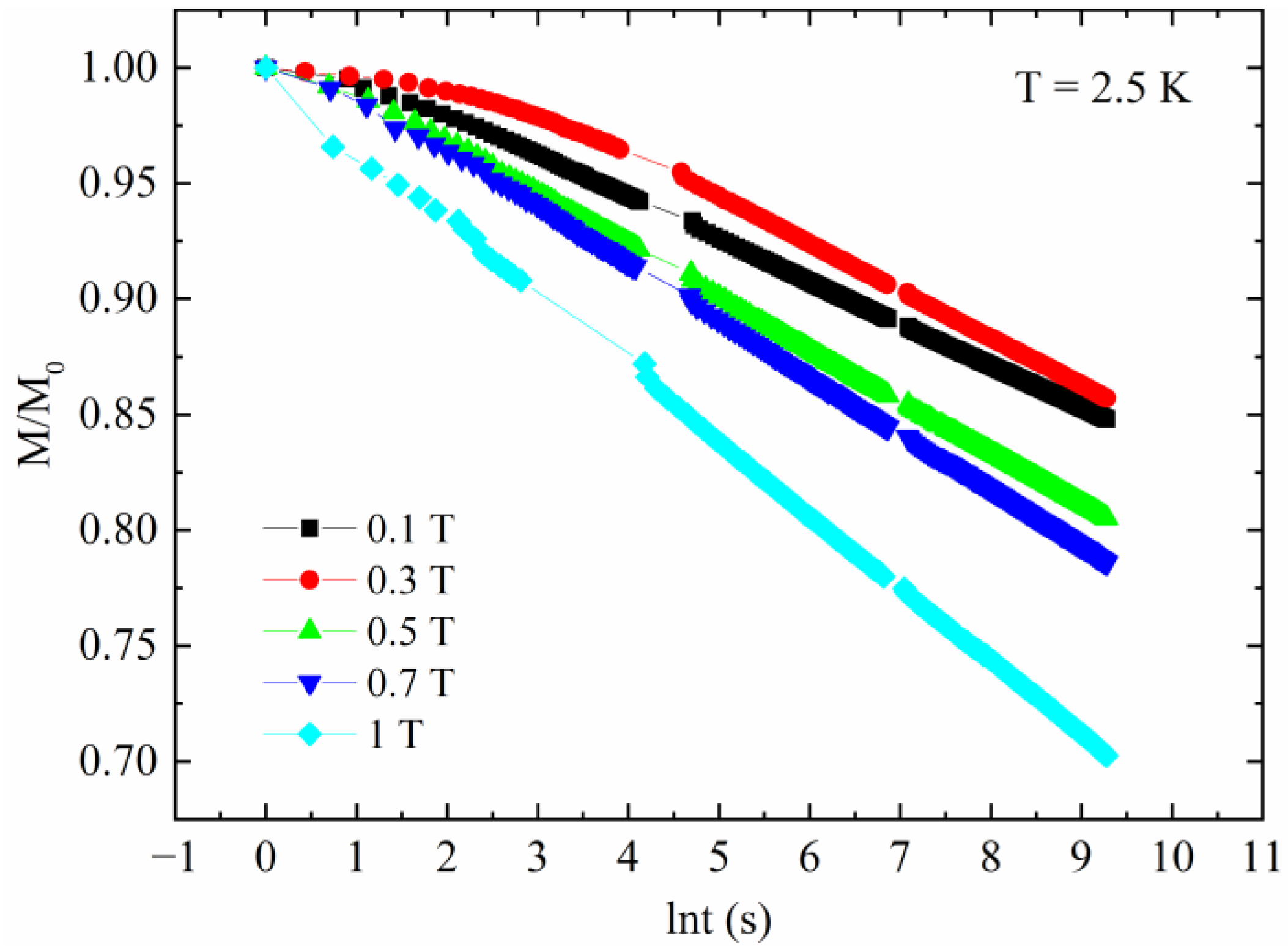
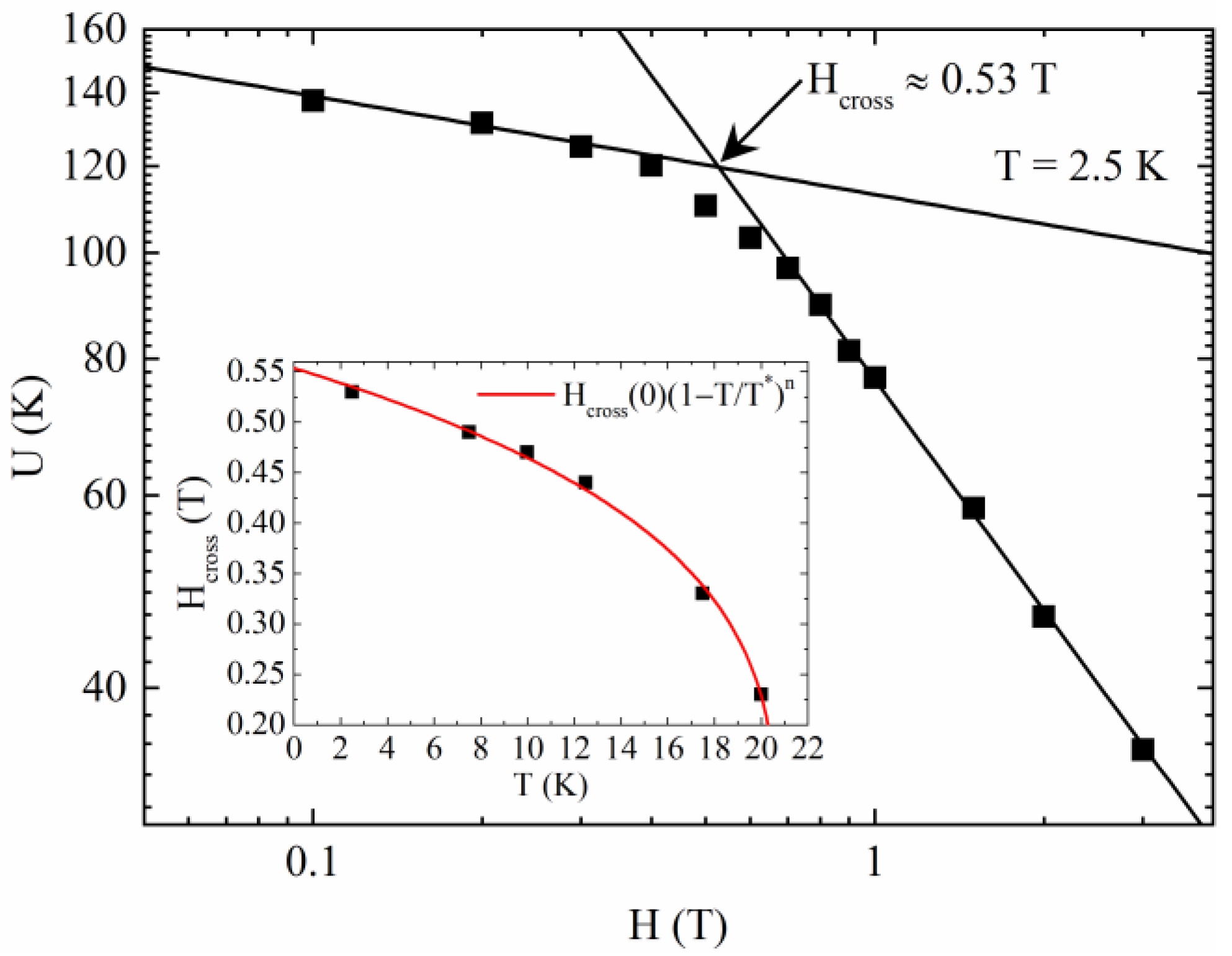
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La[O(1-x)F(x)]FeAs (x = 0.05-0.12) with T(c) = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Moodera, J.S.; Meservey, R.; Tkaczyk, J.E.; Hao, C.X.; Gibson, G.A.; Tedrow, P.M. Critical-magnetic-field anisotropy in single-crystal YBa2Cu3O7. Phys. Rev. B 1988, 37, 619–622. [Google Scholar] [CrossRef] [PubMed]
- Naughton, M.J.; Yu, R.C.; Davies, P.K.; Fischer, J.E.; Chamberlin, R.V.; Wang, Z.Z.; Jing, T.W.; Ong, N.P.; Chaikin, P.M. Orientational anisotropy of the upper critical field in single-crystal YBa2Cu3O7 and Bi2.2CaSr1.9Cu2O8+x. Phys. Rev. B 1988, 38, 9280–9283. [Google Scholar] [CrossRef] [PubMed]
- Ambegaokar, V.; Baratoff, A. Tunneling Between Superconductors. Phys. Rev. Lett. 1963, 10, 486–489. [Google Scholar] [CrossRef]
- Delin, K.A.; Kleinsasser, A.W. Stationary properties of high-critical-temperature proximity effect Josephson junctions. Supercond. Sci. Technol. 1996, 9, 227–269. [Google Scholar] [CrossRef]
- Yuan, H.Q.; Singleton, J.; Balakirev, F.F.; Baily, S.A.; Chen, G.F.; Luo, J.L.; Wang, N.L. Nearly isotropic superconductivity in (Ba,K)Fe2As2. Nature 2009, 457, 565–568. [Google Scholar] [CrossRef]
- Grimaldi, G.; Leo, A.; Martucciello, N.; Braccini, V.; Bellingeri, E.; Ferdeghini, C.; Galluzzi, A.; Polichetti, M.; Nigro, A.; Villegier, J.-C.; et al. Weak or Strong Anisotropy in Fe(Se,Te) Superconducting Thin Films Made of Layered Iron-Based Material? IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Katase, T.; Ishimaru, Y.; Tsukamoto, A.; Hiramatsu, H.; Kamiya, T.; Tanabe, K.; Hosono, H. Advantageous grain boundaries in iron pnictide superconductors. Nat. Commun. 2011, 2, 409. [Google Scholar] [CrossRef]
- De Gennes, P.G. Boundary effects in superconductors. Rev. Mod. Phys. 1964, 36, 225–237. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.; Nazarova, E.; Tomov, V.; Grimaldi, G.; Leo, A.; Pace, S.; Polichetti, M. Transport properties and high upper critical field of a Fe(Se,Te) iron based superconductor. Eur. Phys. J. Spec. Top. 2019, 228, 725–731. [Google Scholar] [CrossRef]
- Fiamozzi Zignani, C.; De Marzi, G.; Corato, V.; Mancini, A.; Vannozzi, A.; Rufoloni, A.; Leo, A.; Guarino, A.; Galluzzi, A.; Nigro, A.; et al. Improvements of high-field pinning properties of polycrystalline Fe(Se,Te) material by heat treatments. J. Mater. Sci. 2019, 54, 5092–5100. [Google Scholar] [CrossRef]
- Rotter, M.; Tegel, M.; Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1-xKx)Fe2As2. Phys. Rev. Lett. 2008, 101, 107006. [Google Scholar] [CrossRef]
- Iyo, A.; Kawashima, K.; Kinjo, T.; Nishio, T.; Ishida, S.; Fujihisa, H.; Gotoh, Y.; Kihou, K.; Eisaki, H.; Yoshida, Y. New-Structure-Type Fe-Based Superconductors: CaAFe4As4 (A = K, Rb, Cs) and SrAFe4As4 (A = Rb, Cs). J. Am. Chem. Soc. 2016, 138, 3410–3415. [Google Scholar] [CrossRef] [PubMed]
- Galluzzi, A.; Leo, A.; Masi, A.; Varsano, F.; Nigro, A.; Grimaldi, G.; Polichetti, M. Critical Current and Pinning Features of a CaKFe4As4 Polycrystalline Sample. Materials 2021, 14, 6611. [Google Scholar] [CrossRef] [PubMed]
- Meier, W.R.; Kong, T.; Kaluarachchi, U.S.; Taufour, V.; Jo, N.H.; Drachuck, G.; Böhmer, A.E.; Saunders, S.M.; Sapkota, A.; Kreyssig, A.; et al. Anisotropic thermodynamic and transport properties of single-crystalline CaKFe4As4. Phys. Rev. B 2016, 94, 064501. [Google Scholar] [CrossRef]
- Singh, S.J.; Bristow, M.; Meier, W.R.; Taylor, P.; Blundell, S.J.; Canfield, P.C.; Coldea, A.I. Ultrahigh critical current densities, the vortex phase diagram, and the effect of granularity of the stoichiometric high-Tc superconductor CaKFe4As4. Phys. Rev. Mater. 2018, 2, 74802. [Google Scholar] [CrossRef]
- Wang, C.; He, T.; Han, Q.; Ji, Z.; Lei, Q.; Tang, Q.; Li, Y.; Yu, B. Vortex creep activation energies and depinning currents in CaKFe4As4 and Ba0.6K0.4Fe2As2 revealed by AC susceptibility measurements. J. Phys. Condens. Matter 2020, 32, 415607. [Google Scholar] [CrossRef]
- Cheng, Z.; Dong, C.; Huang, H.; Liu, S.; Zhu, Y.; Wang, D.; Vlasko-Vlasov, V.; Welp, U.; Kwok, W.K.; Ma, Y. Chemical stability and superconductivity in Ag-sheathed CaKFe4As4 superconducting tapes. Supercond. Sci. Technol. 2019, 32, 015008. [Google Scholar] [CrossRef]
- Pyon, S.; Miyawaki, D.; Veshchunov, I.; Tamegai, T.; Takano, K.; Kajitani, H.; Koizumi, N.; Awaji, S. Fabrication and characterization of CaKFe4As4 round wires sintered at high pressure. Appl. Phys. Express 2018, 11, 123101. [Google Scholar] [CrossRef]
- Adesso, M.G.; Polichetti, M.; Pace, S. Harmonics of the AC susceptibility for the study of I-V curves in melt grown YBCO. Phys. C Supercond. Its Appl. 2004, 401, 196–200. [Google Scholar] [CrossRef]
- Senatore, C.; Polichetti, M.; Zola, D.; Matteo, T.D.; Giunchi, G.; Pace, S. Vortex dynamics and pinning properties analysis of MgB 2 bulk samples by ac susceptibility measurements. Supercond. Sci. Technol. 2003, 16, 183–187. [Google Scholar] [CrossRef]
- Oliveira, A.A.M.; Hur, N.; Cheong, S.W.; Ortiz, W.A. Vortex glass melting in Mg-deficient MgB2. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 104506. [Google Scholar] [CrossRef]
- Oliveira, A.A.M.; Lisboa-Filho, P.N.; Ortiz, W.A. Solid-liquid transition in Nb powder determined by third harmonic susceptibility. J. Magn. Magn. Mater. 2008, 320, e510–e512. [Google Scholar] [CrossRef]
- Masi, A.; Angrisani Armenio, A.; Celentano, G.; La Barbera, A.; Rufoloni, A.; Silva, E.; Vannozzi, A.; Varsano, F. Mechanochemically assisted low temperature synthesis route of the 1144 Ca-K Iron Based Superconductor. Supercond. Sci. Technol. 2020, 33, 74003–74010. [Google Scholar] [CrossRef]
- Galluzzi, A.; Nigro, A.; Fittipaldi, R.; Guarino, A.; Pace, S.; Polichetti, M. DC magnetic characterization and pinning analysis on Nd1.85Ce0.15CuO4 cuprate superconductor. J. Magn. Magn. Mater. 2019, 475, 125–129. [Google Scholar] [CrossRef]
- Polichetti, M.; Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Leo, A.; Grimaldi, G.; Pace, S. A precursor mechanism triggering the second magnetization peak phenomenon in superconducting materials. Sci. Rep. 2021, 11, 7247. [Google Scholar] [CrossRef]
- Galluzzi, A.; Polichetti, M.; Buchkov, K.; Nazarova, E.; Mancusi, D.; Pace, S. Critical current and flux dynamics in Ag-doped FeSe superconductor. Supercond. Sci. Technol. 2017, 30, 025013. [Google Scholar] [CrossRef]
- Felner, I.; Kopelevich, Y. Magnetization measurement of a possible high-temperature superconducting state in amorphous carbon doped with sulfur. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 79, 233409. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.M.; Nazarova, E.; Tomov, V.; Grimaldi, G.; Leo, A.; Pace, S.; Polichetti, M. Pinning energy and anisotropy properties of a Fe(Se,Te) iron based superconductor. Nanotechnology 2019, 30, 254001. [Google Scholar] [CrossRef]
- Yeshurun, Y.; Malozemoff, A.P.; Shaulov, A. Magnetic relaxation in high-temperature superconductors. Rev. Mod. Phys. 1996, 68, 911–949. [Google Scholar] [CrossRef]
- Blatter, G.; Feigel’Man, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Yeshurun, Y.; Malozemoff, A.P. Giant flux creep and irreversibility in an Y-Ba-Cu-O crystal: An alternative to the superconducting-glass model. Phys. Rev. Lett. 1988, 60, 2202–2205. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Leo, A.; Grimaldi, G.; Nigro, A.; Pace, S.; Polichetti, M. Evidence of pinning crossover and the role of twin boundaries in the peak effect in FeSeTe iron based superconductor. Supercond. Sci. Technol. 2018, 31, 015014. [Google Scholar] [CrossRef]
- Ionescu, A.M.; Miu, D.; Crisan, A.; Miu, L. Pinning-Induced Vortex-System Disordering at the Origin of the Second Magnetization Peak in Superconducting Single Crystals. J. Supercond. Nov. Magn. 2018, 31, 2329–2337. [Google Scholar] [CrossRef]
- Pramanik, A.K.; Harnagea, L.; Nacke, C.; Wolter, A.U.B.; Wurmehl, S.; Kataev, V.; Büchner, B. Fishtail effect and vortex dynamics in LiFeAs single crystals. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 83, 094502. [Google Scholar] [CrossRef]
- Miu, D.; Noji, T.; Adachi, T.; Koike, Y.; Miu, L. On the nature of the second magnetization peak in FeSe1−xTex single crystals. Supercond. Sci. Technol. 2012, 25, 115009. [Google Scholar] [CrossRef]
- Yang, H.; Luo, H.; Wang, Z.; Wen, H.-H. Fishtail effect and the vortex phase diagram of single crystal Ba0.6K0.4Fe2As2. Appl. Phys. Lett. 2008, 93, 142506. [Google Scholar] [CrossRef]
- Prozorov, R.; Ni, N.; Tanatar, M.A.; Kogan, V.G.; Gordon, R.T.; Martin, C.; Blomberg, E.C.; Prommapan, P.; Yan, J.Q.; Bud’ko, S.L.; et al. Vortex phase diagram of Ba(Fe0.93Co0.07)2As2 single crystals. Phys. Rev. B 2008, 78, 224506. [Google Scholar] [CrossRef]
- Salem-Sugui, S.; Ghivelder, L.; Alvarenga, A.D.; Cohen, L.F.; Yates, K.A.; Morrison, K.; Pimentel, J.L.; Luo, H.; Wang, Z.; Wen, H.H. Flux dynamics associated with the second magnetization peak in the iron pnictide Ba1-xKxFe2As2. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 054513. [Google Scholar] [CrossRef]
- Sharma, S.; Vinod, K.; Sundar, C.S.; Bharathi, A. Critical current density and magnetic phase diagrams of BaFe 1.29Ru0.71As2 single crystals. Supercond. Sci. Technol. 2012, 26, 015009. [Google Scholar] [CrossRef]
- Shabbir, B.; Wang, X.; Ghorbani, S.R.; Shekhar, C.; Dou, S.; Srivastava, O.N. Hydrostatic pressure: A very effective approach to significantly enhance critical current density in granular iron pnictide superconductors. Sci. Rep. 2015, 5, 8213. [Google Scholar] [CrossRef]
- Shen, B.; Cheng, P.; Wang, Z.; Fang, L.; Ren, C.; Shan, L.; Wen, H.H. Flux dynamics and vortex phase diagram in Ba(Fe1-xCox)2As2 single crystals revealed by magnetization and its relaxation. Phys. Rev. B 2010, 81, 014503. [Google Scholar] [CrossRef]
- Das, P.; Thakur, A.D.; Yadav, A.K.; Tomy, C.V.; Lees, M.R.; Balakrishnan, G.; Ramakrishnan, S.; Grover, A.K. Magnetization hysteresis and time decay measurements in FeSe 0.50Te 0.50: Evidence for fluctuation in mean free path induced pinning. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 84, 214526. [Google Scholar] [CrossRef]
- Buchkov, K.; Galluzzi, A.; Mancusi, D.; Nazarova, E.; Pace, S.; Polichetti, M. Harmonic AC magnetic susceptibility analysis of FeSe crystals with composite morphology. Phys. Scr. 2019, 94, 085804. [Google Scholar] [CrossRef]
- Galluzzi, A.; Buchkov, K.; Tomov, V.; Nazarova, E.; Leo, A.; Grimaldi, G.; Pace, S.; Polichetti, M. Mixed state properties analysis in AC magnetic field of strong pinning Fe(Se,Te) single crystal. Supercond. Sci. Technol. 2020, 33, 094006. [Google Scholar] [CrossRef]
- Singh, S.J.; Shimoyama, J.; Yamamoto, A.; Ogino, H.; Kishio, K. Transition temperature and upper critical field in SmFeAsO 1-xFx synthesized at low heating temperatures. IEEE Trans. Appl. Supercond. 2013, 23, 7300605. [Google Scholar] [CrossRef]
- Polichetti, M.; Adesso, M.G.; Pace, S. Response of glass and liquid phases in the vortex lattice to an external AC magnetic field at different frequencies. Phys. A Stat. Mech. Its Appl. 2004, 339, 119–124. [Google Scholar] [CrossRef]
- Adesso, M.G.; Senatore, C.; Polichetti, M.; Pace, S. Harmonics of the AC susceptibility as probes to differentiate the various creep models. Phys. C Supercond. 2004, 404, 289–292. [Google Scholar] [CrossRef]
- Marziali Bermúdez, M.; Pasquini, G.; Bud’Ko, S.L.; Canfield, P.C. Correlated vortex pinning in slightly orthorhombic twinned Ba(Fe1-xCox)2As2 single crystals: Possible shift of the vortex-glass/liquid transition. Phys. Rev. B 2013, 87, 054515. [Google Scholar] [CrossRef]
- Singh, S.J.; Cassidy, S.J.; Bristow, M.; Blundell, S.J.; Clarke, S.J.; Coldea, A.I. Optimization of superconducting properties of the stoichiometric CaKFe4As4. Supercond. Sci. Technol. 2019, 33, 025003. [Google Scholar] [CrossRef]
- Miu, L.; Miu, D. On the sensitivity of the Maley technique for the analysis of vortex-creep activation energy in disordered superconductors. Supercond. Sci. Technol. 2010, 23, 025033. [Google Scholar] [CrossRef]
- Miu, L.; Miu, D.; Petrisor, T.; El Tahan, A.; Jakob, G.; Adrian, H. Origin of the plateau in the temperature dependence of the normalized magnetization relaxation rate in disordered high-temperature superconductors. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 78, 212508. [Google Scholar] [CrossRef]
- El Tahan, A.; Jakob, G.; Miu, D.; Ivan, I.; Badica, P.; Miu, L. Vortex creep crossover in YBCO/PrBCO superlattices during standard magnetization relaxation measurements. Supercond. Sci. Technol. 2011, 24, 045014. [Google Scholar] [CrossRef]



| Measurement | Minimum Value | Maximum Value | Rate |
|---|---|---|---|
| m(T) | 2.5 K | 300 K | 0.5 K/min |
| m(H) | −9 T | +9 T | 0.01 T/s |
| m(t) | 100 s | 10,800 s | 1 datapoint/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galluzzi, A.; Leo, A.; Masi, A.; Varsano, F.; Nigro, A.; Grimaldi, G.; Polichetti, M. Magnetic Vortex Phase Diagram for a Non-Optimized CaKFe4As4 Superconductor Presenting a Wide Vortex Liquid Region and an Ultra-High Upper Critical Field. Appl. Sci. 2023, 13, 884. https://doi.org/10.3390/app13020884
Galluzzi A, Leo A, Masi A, Varsano F, Nigro A, Grimaldi G, Polichetti M. Magnetic Vortex Phase Diagram for a Non-Optimized CaKFe4As4 Superconductor Presenting a Wide Vortex Liquid Region and an Ultra-High Upper Critical Field. Applied Sciences. 2023; 13(2):884. https://doi.org/10.3390/app13020884
Chicago/Turabian StyleGalluzzi, Armando, Antonio Leo, Andrea Masi, Francesca Varsano, Angela Nigro, Gaia Grimaldi, and Massimiliano Polichetti. 2023. "Magnetic Vortex Phase Diagram for a Non-Optimized CaKFe4As4 Superconductor Presenting a Wide Vortex Liquid Region and an Ultra-High Upper Critical Field" Applied Sciences 13, no. 2: 884. https://doi.org/10.3390/app13020884
APA StyleGalluzzi, A., Leo, A., Masi, A., Varsano, F., Nigro, A., Grimaldi, G., & Polichetti, M. (2023). Magnetic Vortex Phase Diagram for a Non-Optimized CaKFe4As4 Superconductor Presenting a Wide Vortex Liquid Region and an Ultra-High Upper Critical Field. Applied Sciences, 13(2), 884. https://doi.org/10.3390/app13020884










