A Simple Solution for the General Fractional Ambartsumian Equation
Abstract
1. Introduction
2. On the Fractionalisation Problem
- not distinguishing between constant and Heaviside functions;
- not giving the derivative of the ;
- the derivative of a sinusoid is not a sinusoid;
- (Riemann–)Liouville derivative [30]The usual Riemann–Liouville derivative is a particular case of this one, obtained for functions null outside any interval .
- Liouville–Caputo derivative [25]The Caputo derivative is a particular case of this one as happens with the RL derivative.
- Regularized Liouville derivative [40]where the summation is taken as being null, when .
- Linearity;
- Additivity and Commutativity of the orders;
- Neutral and inverse elementsFrom (10) we conclude that there is always an inverse element; that is, for every there is always the order that we called above the anti-derivative.
- Backward compatibility ()If , then:We obtain this expression repeating the first order derivative.
- The generalized Leibniz ruleThis rule gives the FD of the product of two functions and assumes the format [30]
3. Problem Formulation and a First Solution
4. Solution Using Mittag–Leffler Functions
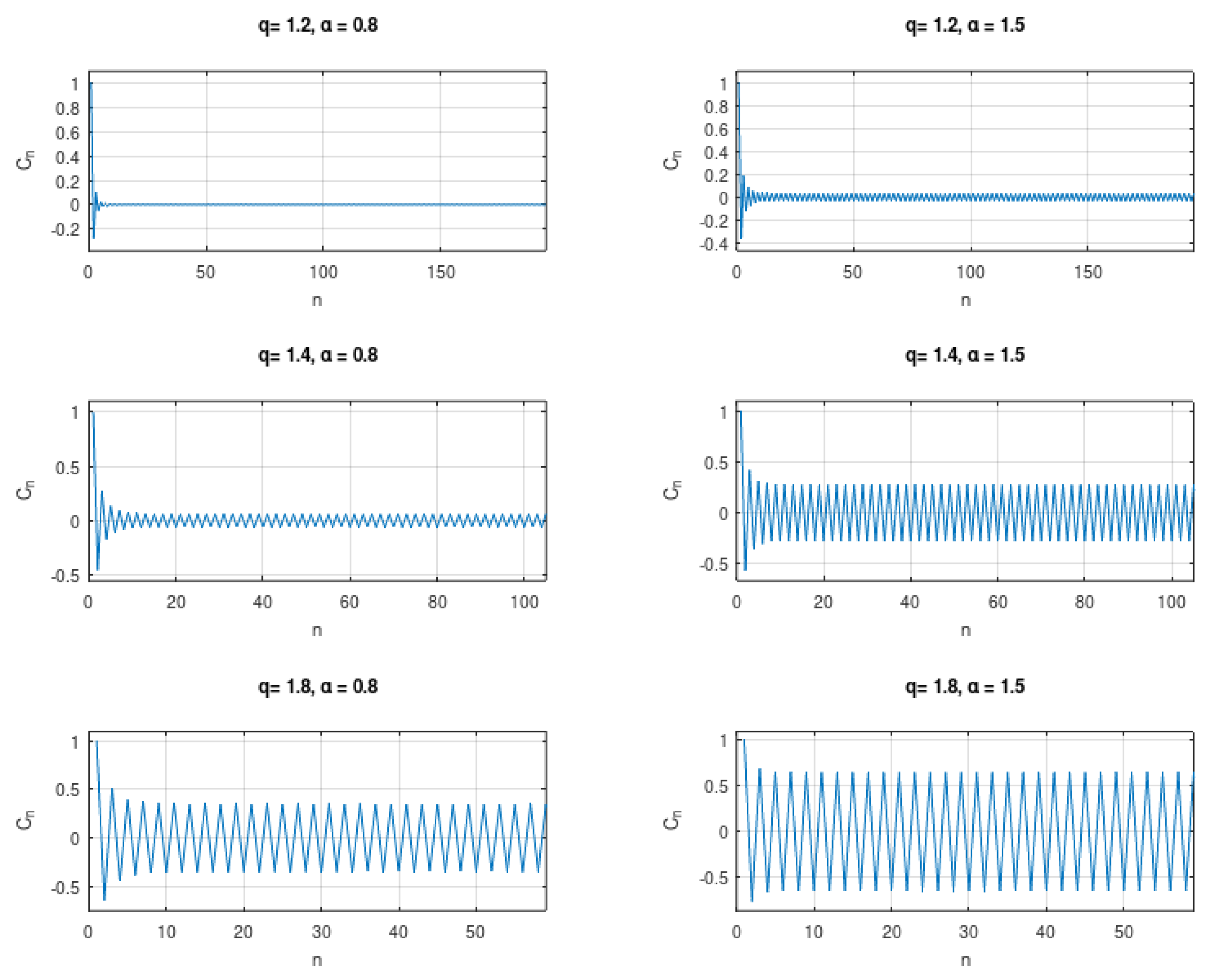
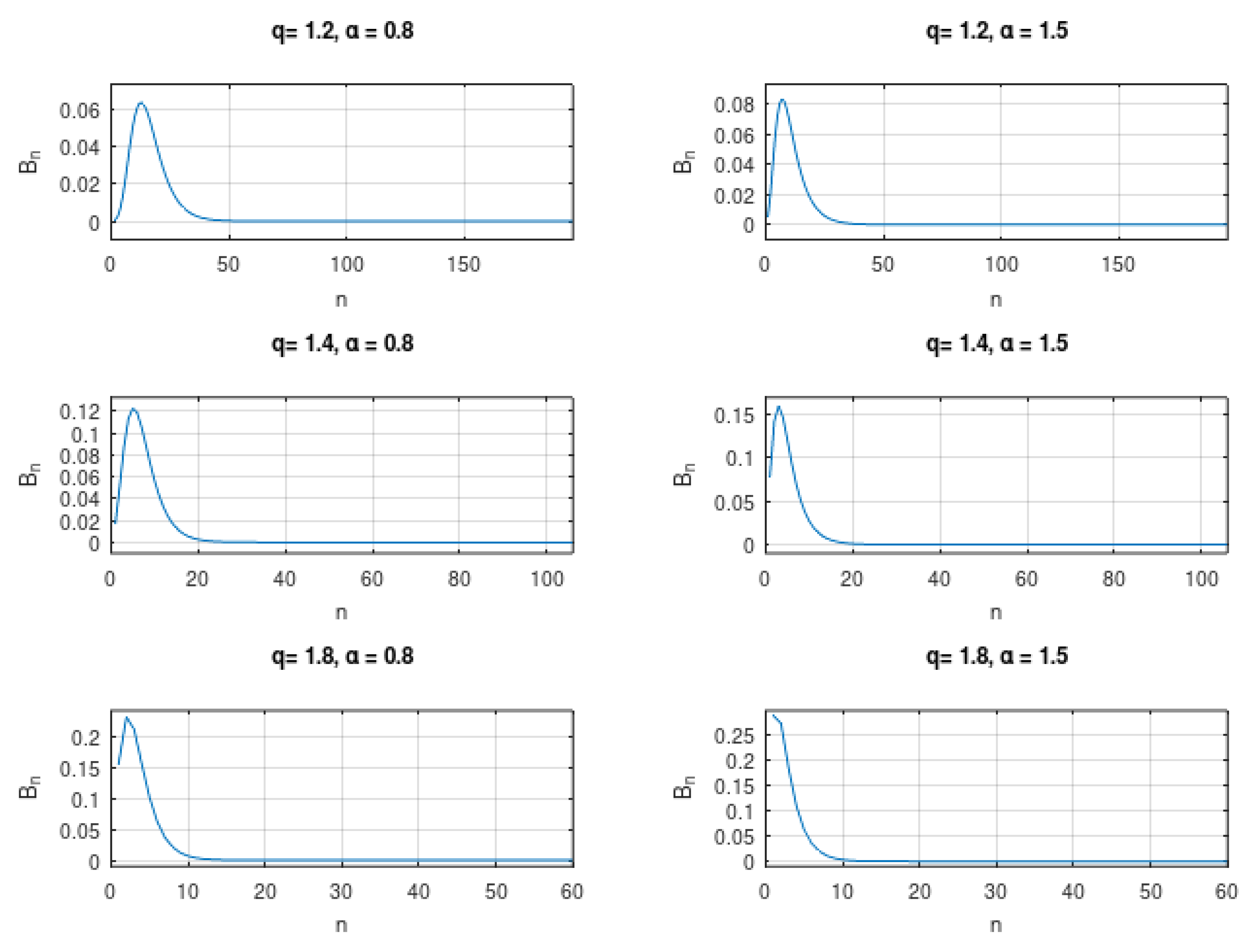
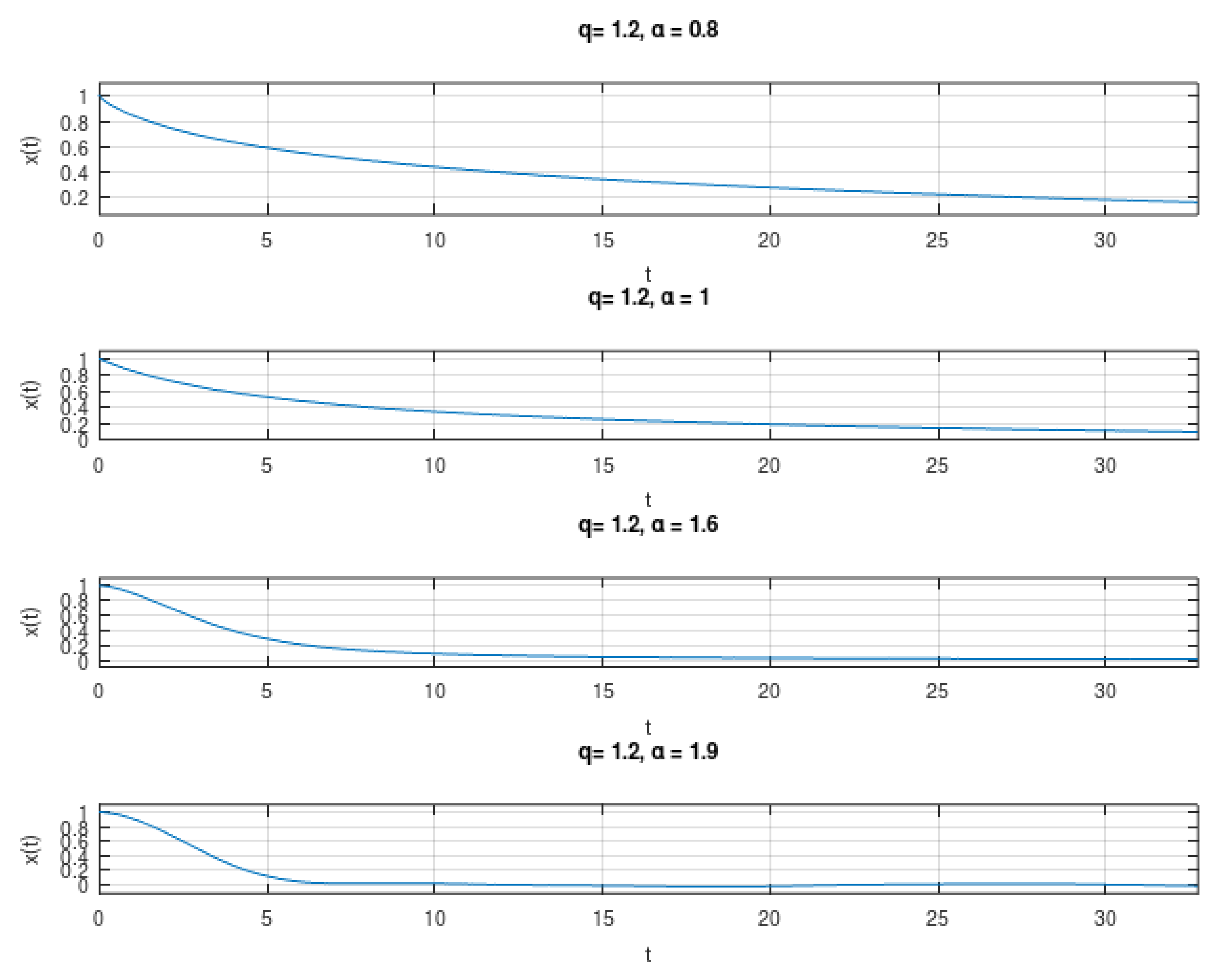
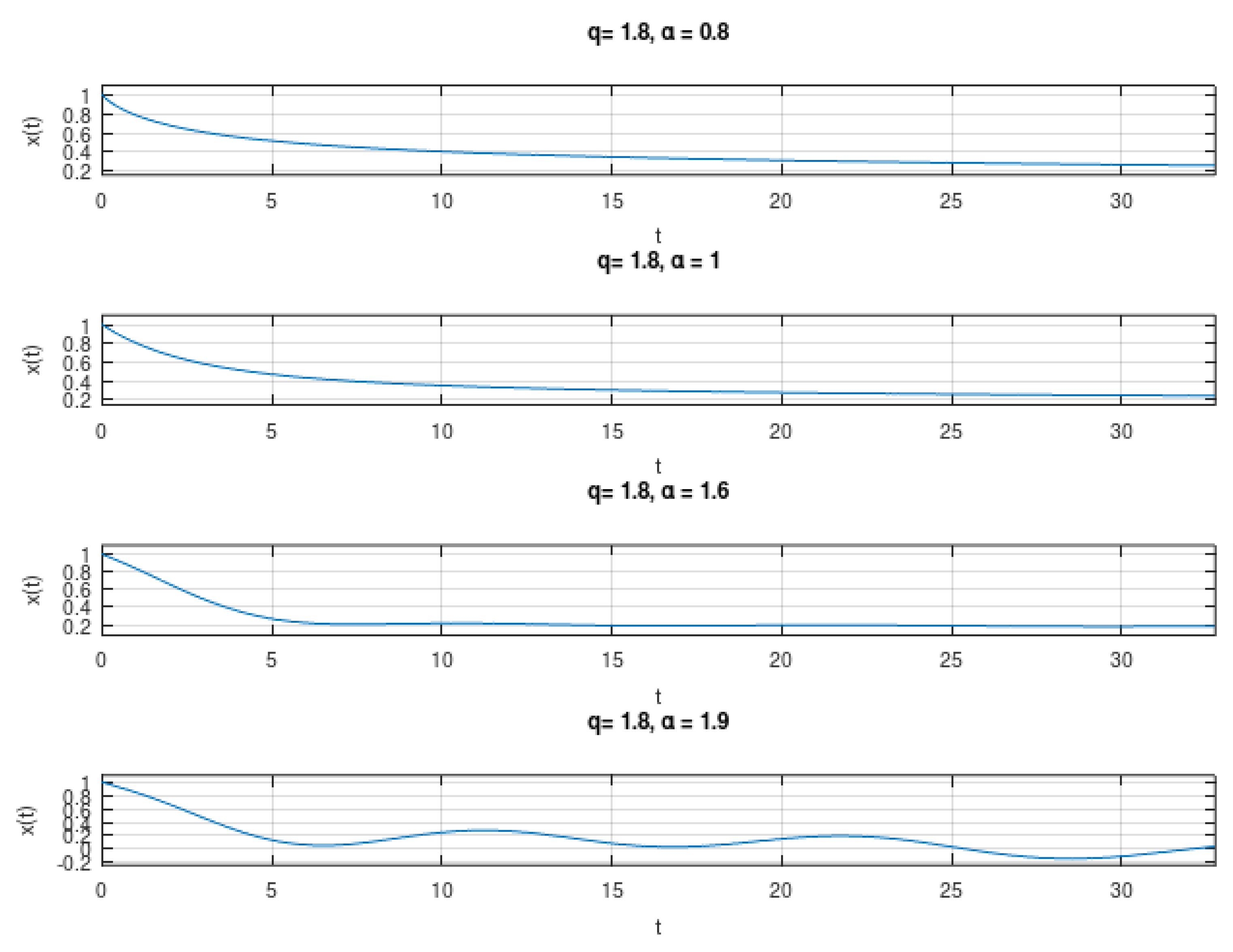
5. Numerical Aspects
- Use the bilinear transformation [8]to pass from a continuous-time to a sampled (discrete) function. T is the sampling interval. We obtain the function
- Set , to get a discrete-time Fourier transform of [39]. To avoid the effect of the branchcut points at , we found it better to move them slightly into the unit circle. This is accomplished by settingWe can use a simple procedure that consists of the following steps:
- (a)
- Set , where represents the discrete Fourier transform that is implemented by the fast Fourier transform algorithm;
- (b)
- Similarly, set ;
- (c)
- Compute ;
- (d)
- Obtain the approximation to
- Sample in a uniform grid, making , where N is in high enough agreement with T and the interval where we want to compute the function. In our simulations, we used and .
- We could use the fast Fourier transform to compute the inverse of , . However, this is not very good from numerical aspects, due to the singularity at the origin. We found it was better to separate the computation in three steps:
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambartsumian, V. On the fluctuation of the brightness of the Milky Way. Dokl. Akad. Nauk SSSR 1944, 44, 223–226. [Google Scholar]
- Patade, J.; Bhalekar, S. On analytical solution of Ambartsumian equation. Natl. Acad. Sci. Lett. 2017, 40, 291–293. [Google Scholar] [CrossRef]
- Bakodah, H.O.; Ebaid, A. Exact solution of Ambartsumian delay differential equation and comparison with Daftardar-Gejji and Jafari approximate method. Mathematics 2018, 6, 331. [Google Scholar] [CrossRef]
- Alharbi, F.M.; Ebaid, A. New analytic solution for Ambartsumian equation. J. Math. Syst. Sci. 2018, 8, 182–186. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D.; Rathore, S. Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 2018, 133, 1–7. [Google Scholar] [CrossRef]
- Ebaid, A.; Cattani, C.; Al Juhani, A.S.; El-Zahar, E.R. A novel exact solution for the fractional Ambartsumian equation. Adv. Differ. Equations 2021, 2021, 1–18. [Google Scholar] [CrossRef]
- Alharbi, W.; Hristova, S. New Series Solution of the Caputo Fractional Ambartsumian Delay Differential Equationation by Mittag-Leffler Functions. Mathematics 2021, 9, 157. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.A.T. New discrete-time fractional derivatives based on the bilinear transformation: Definitions and properties. J. Adv. Res. 2020, 25, 1–10. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. The 21st century systems: An updated vision of continuous-time fractional models. IEEE Circuits Syst. Mag. 2022, 22, 36–56. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor Theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Westerlund, S. Dead Matter has Memory! Causal Consulting: Kalmar, Sweden, 2002. [Google Scholar]
- Heaviside, O. Electromagnetic Theory 2; Ernest Benn Limited: London, UK, 1925; Volume 2. [Google Scholar]
- Nahin, P.J. Oliver Heaviside, Fractional Operators, and the Age of the Earth. IEEE Trans. Educ. 1985, 28, 94–104. [Google Scholar] [CrossRef]
- Rogosin, S.; Mainardi, F. George William Scott Blair–the pioneer of factional calculus in rheology. arXiv 2014, arXiv:1404.3295. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Laskin, N. Fractional quantum mechanics. Phys. Rev. E 2000, 62, 3135. [Google Scholar] [CrossRef] [PubMed]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef] [PubMed]
- Naber, M. Time fractional Schrödinger equation. J. Math. Phys. 2004, 45, 3339–3352. [Google Scholar] [CrossRef]
- Laskin, N. Time fractional quantum mechanics. Chaos, Solitons Fractals 2017, 102, 16–28. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Nonlinear Physical Science; Springer: Beijing, China; Heidelberg, Germany, 2011. [Google Scholar]
- Ortigueira, M.D.; Rivero, M.; Trujillo, J.J. From a generalised Helmholtz decomposition theorem to fractional Maxwell equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1036–1049. [Google Scholar] [CrossRef]
- Gulgowski, J.; Kwiatkowski, D.; Stefański, T.P. Signal Propagation in Electromagnetic Media Modelled by the Two-Sided Fractional Derivative. Fractal Fract. 2021, 5, 10. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers. Vol. I: Background and Theory. Vol. II: Applications; Nonlinear Physical Science; Springer and Higher Education Press: Heidelberg, Germany, 2012. [Google Scholar]
- Uchaikin, V.; Sibatov, R. Fractional Kinetics in Solids: Anomalous Charge Transport in Semiconductors, Dielectrics and Nanosystems; World Scientific Publishing Company: Singapore, 2013. [Google Scholar]
- Herrmann, R. Fractional Calculus, 3rd ed.; World Scientific: Singapore, 2018. [Google Scholar]
- Mandelbrot, B.; Van Ness, J. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Nossenson, N.; Bobrovsky, B.Z. Analysis of direct spectrum measurement of a sinusoidal signal impaired by either fractional gaussian phase noise or fractional Brownian phase motion. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2351–2362. [Google Scholar] [CrossRef]
- Lilly, J.M.; Sykulski, A.M.; Early, J.J.; Olhede, S.C. Fractional Brownian motion, the Matérn process, and stochastic modeling of turbulent dispersion. Nonlinear Process. Geophys. 2017, 24, 481–514. [Google Scholar] [CrossRef]
- Dugowson, S. Les Différentielles Métaphysiques (Histoire et Philosophie de la Généralisation de L’ordre de Dérivation). Ph.D. Thesis, Université Paris Nord, Paris, France, 1994. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Ortigueira, M.D.; Tenreiro Machado, J. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Trigeassou, J.C.; Maamri, N. Initial conditions and initialization of linear fractional differential equations. Signal Process. 2011, 91, 427–436. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C. Comments on the description and initialization of fractional partial differential equations using Riemann–Liouville’s and Caputo’s definitions. J. Comput. Appl. Math. 2018, 339, 30–39. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. Revisiting the 1D and 2D Laplace Transforms. Mathematics 2020, 8, 1330. [Google Scholar] [CrossRef]
- Ortigueira, M.D. A New Look at the Initial Condition Problem. Mathematics 2022, 10, 1771. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. Which Derivative? Fractal Fract. 2017, 1, 3. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. Fractional derivatives: The perspective of system theory. Mathematics 2019, 7, 150. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valério, D. Fractional Signals and Systems; De Gruyter: Berlin, Germany, 2020. [Google Scholar]
- Ortigueira, M.D. Two-sided and regularised Riesz-Feller derivatives. Math. Methods Appl. Sci. 2021, 44, 8057–8069. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Lecture Notes in Electrical Engineering; Springer: Dordrecht, The Netherlands; Heidelberg, Germany, 2011. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Ortigueira, M.; Bengochea, G. A new look at the fractionalisation of the logistic equation. Phys. A Stat. Mech. Appl. 2017, 467, 554–561. [Google Scholar] [CrossRef]
- Ortigueira, M.; Coito, F. System initial conditions vs derivative initial conditions. Comput. Math. Appl. 2010, 59, 1782–1789. [Google Scholar] [CrossRef]
- Kac, V.G.; Cheung, P. Quantum Calculus; Springer: Berlin/Heidelberg, Germany, 2002; Volume 113. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2014; Second Edition in Preparation. [Google Scholar]
- Ortigueira, M.D.; Lopes, A.M.; Machado, J.A.T. On the Numerical Computation of the Mittag-Leffler function. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 4879. [Google Scholar] [CrossRef]
- Zemanian, A.H. Distribution Theory and Transform Analysis: An Introduction to Generalized Functions, with Applications; Lecture Notes in Electrical Engineering, 84; Dover Publications: New York, NY, USA, 1987. [Google Scholar]
- Ortigueira, M.D.; Machado, J.T.; Rivero, M.; Trujillo, J.J. Integer/fractional decomposition of the impulse response of fractional linear systems. Signal Process. 2015, 114, 85–88. [Google Scholar] [CrossRef]
- Andrews, G. q-Hypergeometric and Related Functions, NIST Handbook of Mathematical Functions, 419–433, US Dept; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortigueira, M.D.; Bengochea, G. A Simple Solution for the General Fractional Ambartsumian Equation. Appl. Sci. 2023, 13, 871. https://doi.org/10.3390/app13020871
Ortigueira MD, Bengochea G. A Simple Solution for the General Fractional Ambartsumian Equation. Applied Sciences. 2023; 13(2):871. https://doi.org/10.3390/app13020871
Chicago/Turabian StyleOrtigueira, Manuel Duarte, and Gabriel Bengochea. 2023. "A Simple Solution for the General Fractional Ambartsumian Equation" Applied Sciences 13, no. 2: 871. https://doi.org/10.3390/app13020871
APA StyleOrtigueira, M. D., & Bengochea, G. (2023). A Simple Solution for the General Fractional Ambartsumian Equation. Applied Sciences, 13(2), 871. https://doi.org/10.3390/app13020871