Comparison of 210Pb Age Models of Peat Cores Derived from the Arkhangelsk Region
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Area and Sample Collection
2.2. Study of Physical and Radioactive Characteristics of Peat Samples
2.2.1. Determining the Plant Material
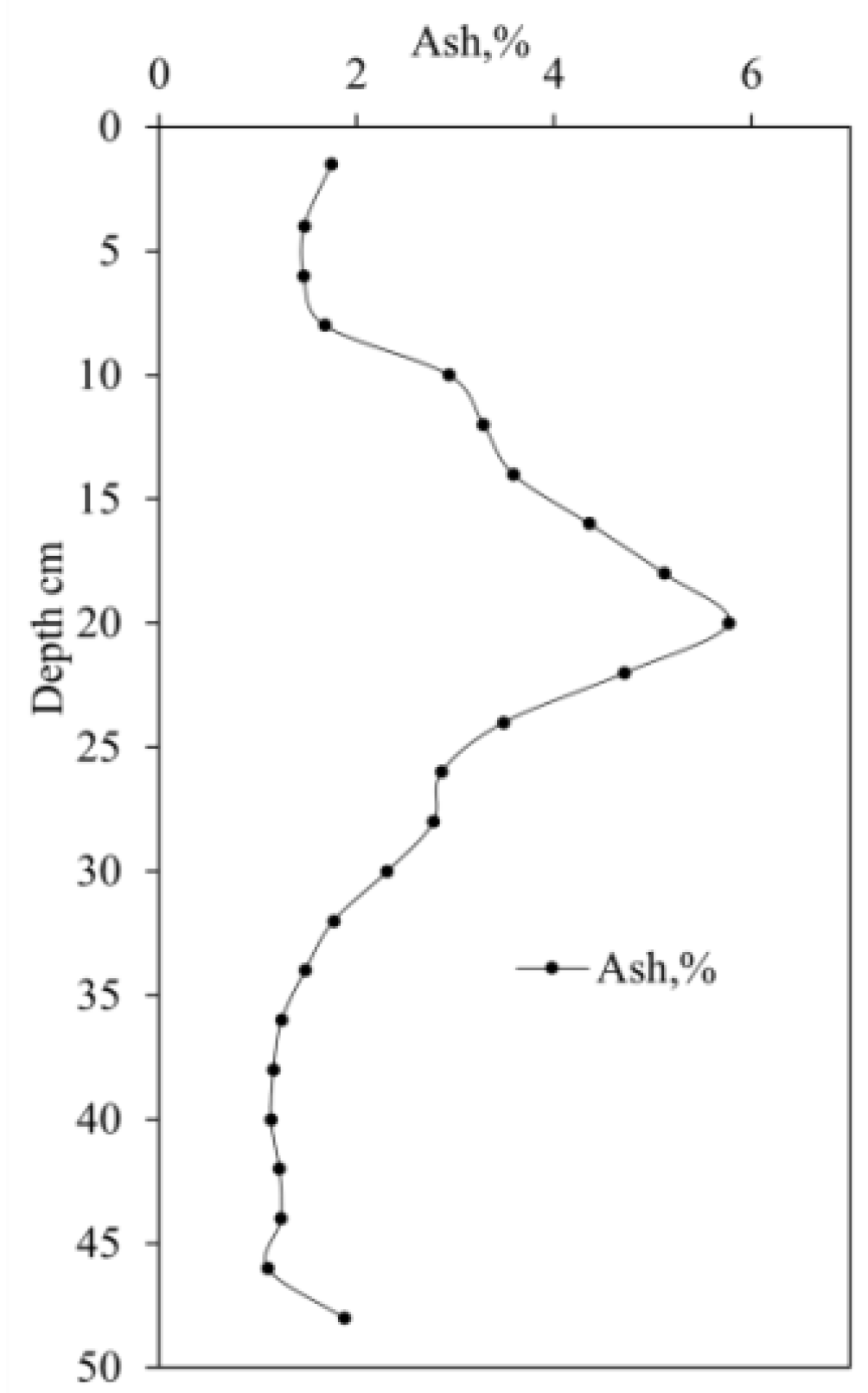
2.2.2. Determining the Ash Content of Peat
2.2.3. Determining the Bulk Density of Peat
2.2.4. Determining 137Cs and 210Pb Isotopes
2.2.5. The Dating Procedure
3. Results and Discussion
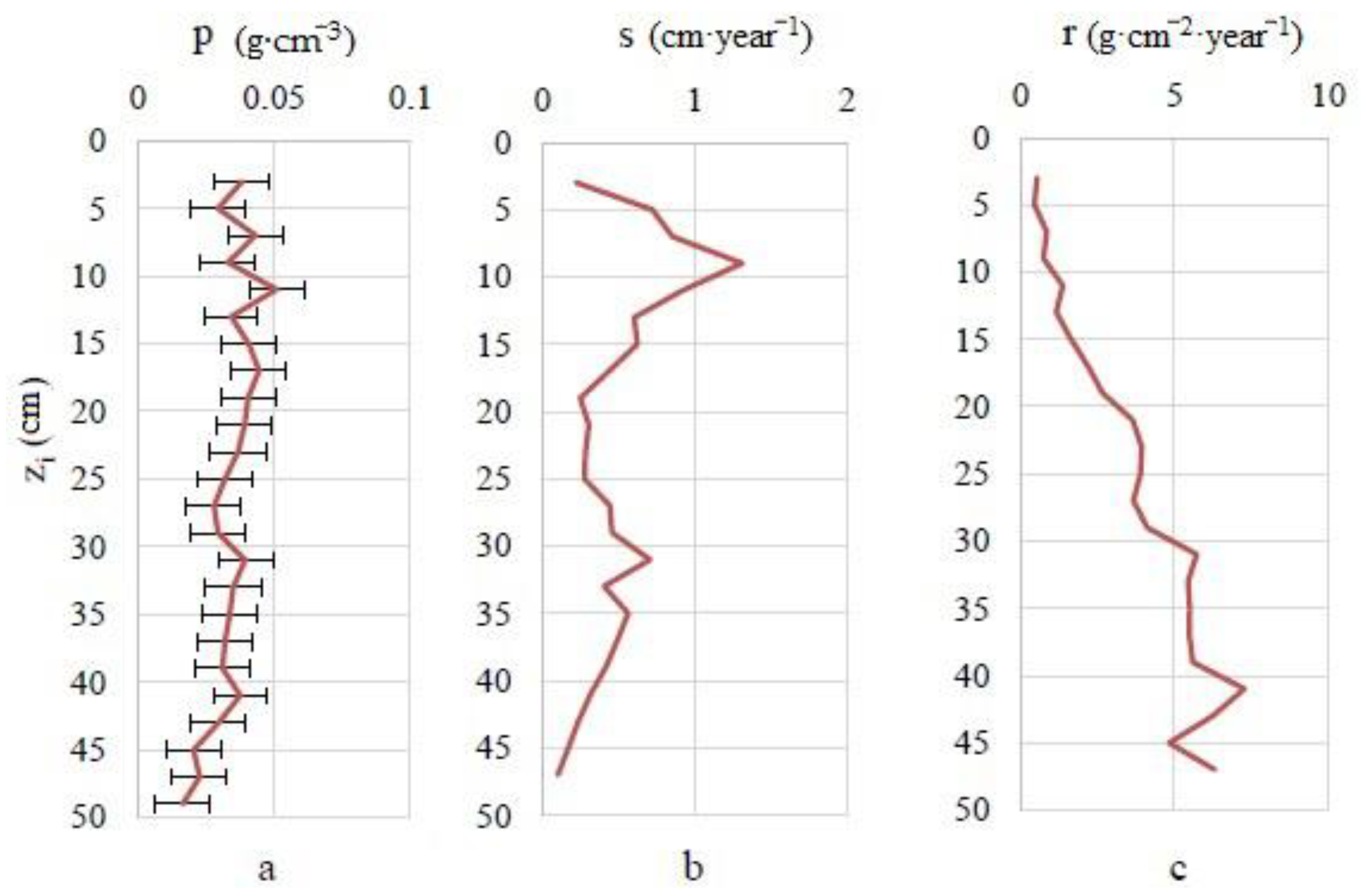
3.1. Physico-Chemical Parameters of Peat
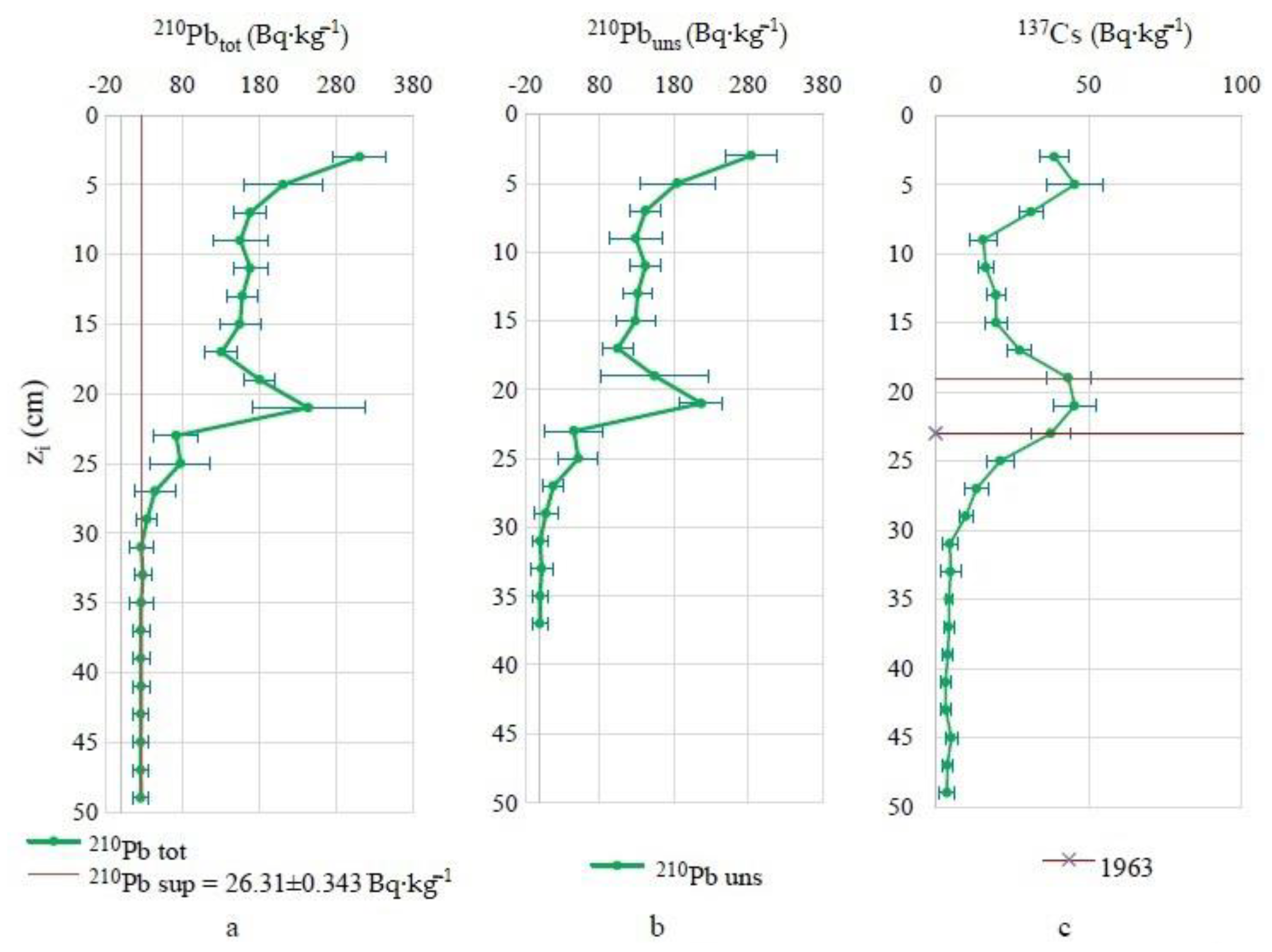
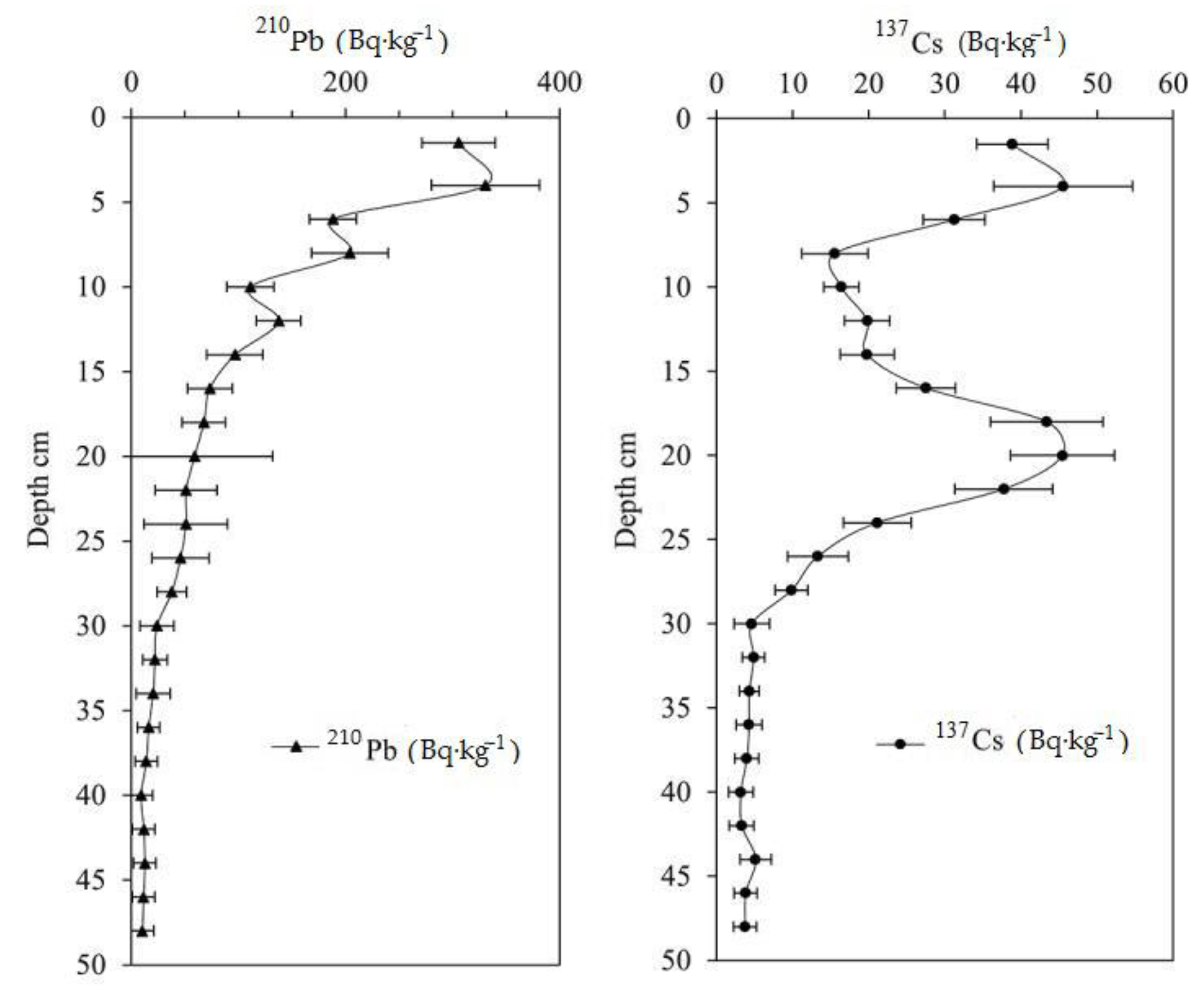
3.2. Vertical Distribution of the Peat Profile of Radionuclides
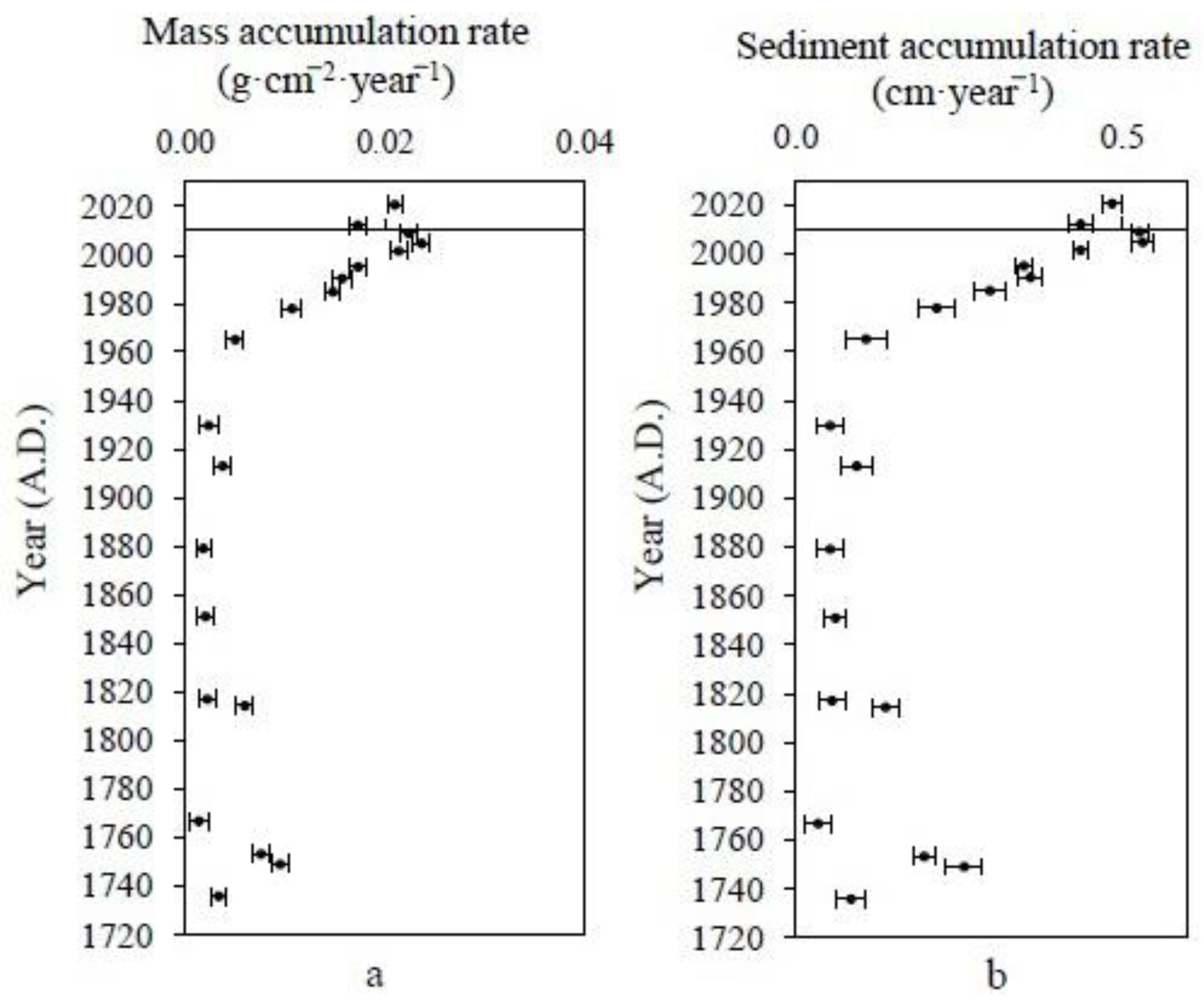
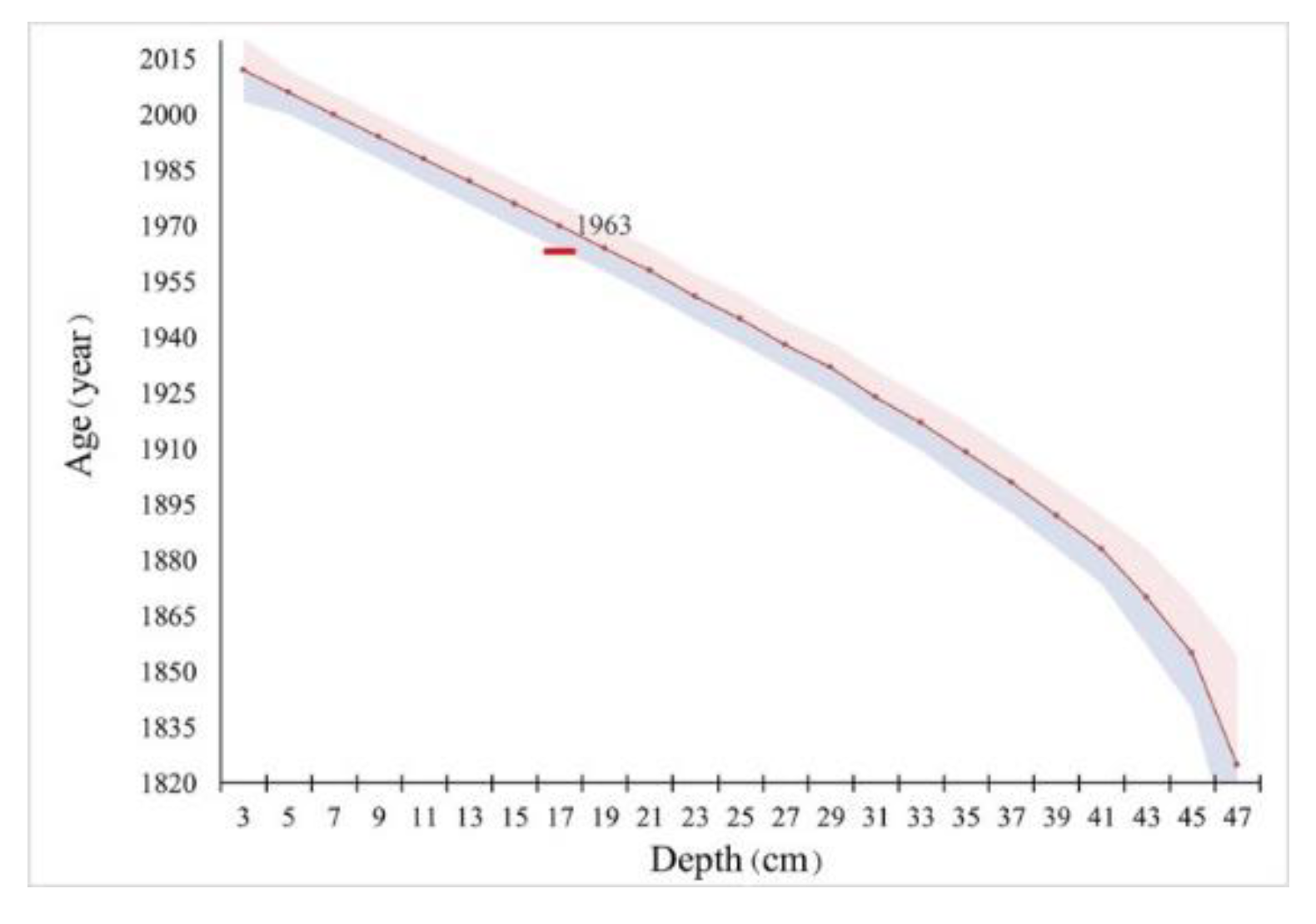
3.3. Chronology 210Pb and Rate of Peat Accumulation
- –
- Sample code.
- –
- Concentration 210Pb (Ci, Bq·kg−1).
- –
- Uncertainty (u(210Pb))—Its calculation is specific to the analytical method used. The sources of uncertainty are as follows: the number of samples, efficiency or indicator activity, and sample weight.
- –
- Contents 226Ra (Bq·kg−1)—we calculated the arithmetic mean and standard deviation for the three lowest sites (43–49 cm), which, in our case, were 226Ra = 26.2 ± 0.1 Bq·kg−1.
- –
- Uncertainty (u(226Ra), Bq·kg−1) corresponded to the calculated standard deviation.
- –
- Excess 210Pbex (Ci, Bq·kg−1) was computed as follows: 210Pbex = 210Pb − 226Ra, except for the areas used to calculate 226Ra, where 210Pbex was missing.
- –
- Uncertainty (u (Ci), Bq·kg−1) was computed as follows:
- –
- Reserve 210Pbex (Ai, Bq·m−2) was computed as follows: multiplying Ci by the air-dried mass . We used a factor of 10 to obtain kg·m−2, and Ai = .
- –
3.3.1. Application of the CA Model
- –
- Age (ti; years): .
- –
- Uncertainty (u(ti)): .
- –
- In order to compute the accumulation rate, it is necessary to obtain the age of the layers. The age 0 is assigned to layer 0 (t = 0), and the average age of each of the layers is computed as follows: .
- –
- The calculation used to determine the age of the last horizon should be carried out as follows: .
- –
- Uncertainty (u(t(i))) was computed as follows (one section): .
- –
- Section formation time (Δt1; years) was defined as the difference between two successive layers: .
- –
- Uncertainty (u(Δt)) was computed as follows (one section): .
- –
- Mean sediment accumulation rate (si, cm·year−1) was the relationship between the transect width and formation time. For Section 1, we used the following equation: .
- –
- Uncertainty (u(s)): .
- –
- Mean mass accumulation rate (ri, g·cm−2·year−1): .
- –
- Uncertainty (u(r)): .
3.3.2. Application of the CF/CS Model
3.3.3. Application of the PF Model
- –
- The time of formation of the profile (∆ti, year) was calculated using the following equation: .
- –
- Uncertainty (u(Δt1)) was defined as follows: .
- –
- MAR (ri) was calculated using the equation , and the uncertainty was determined as follows: [21].
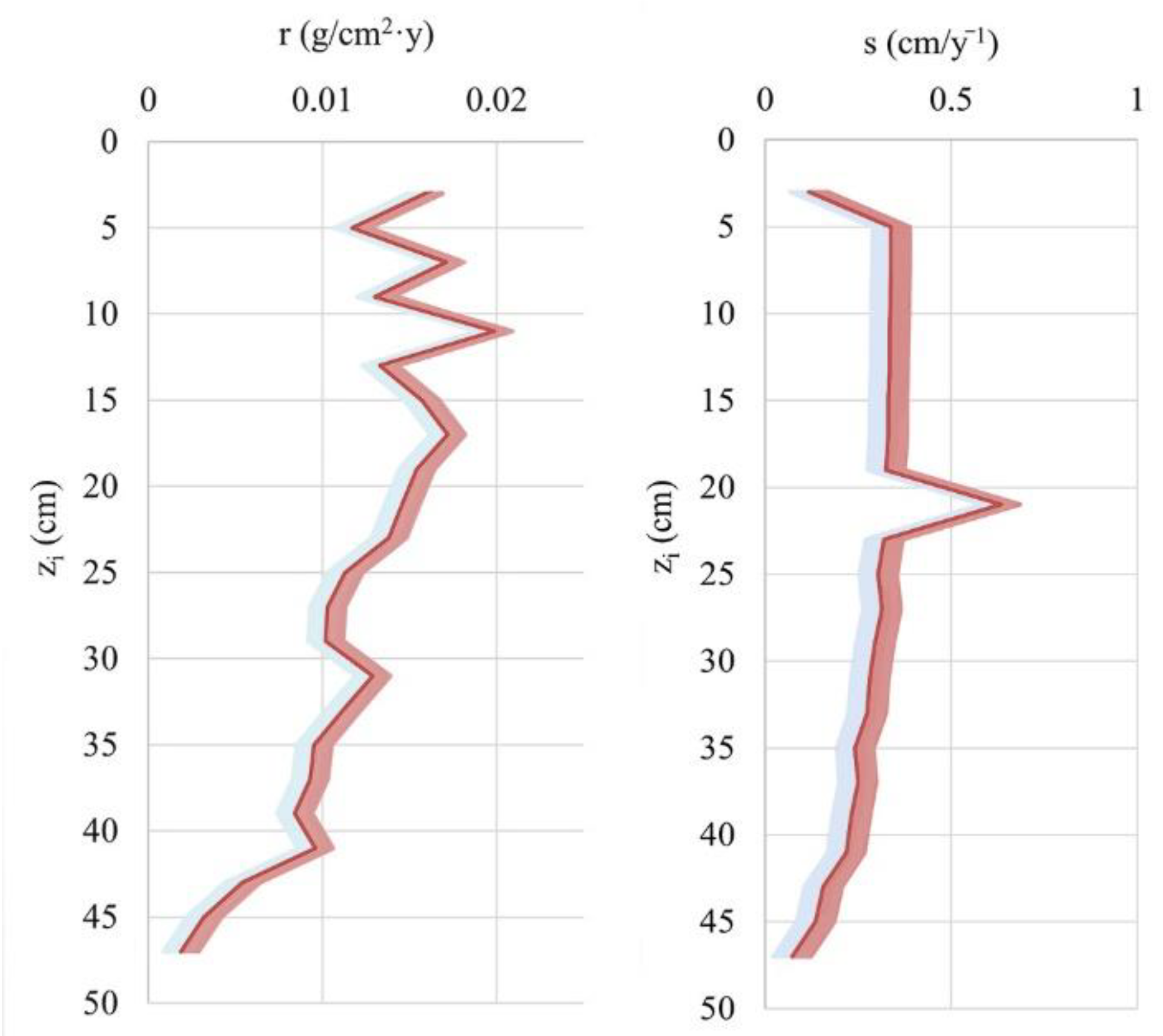
3.3.4. Application of the CF Model Alone and via Monte Carlo Simulation
- –
- The accumulated 210Pbex deposits under horizon (i) (Bq·m−2) were computed as follows: .
- –
- Uncertainty u(A(37)): . This pattern continued towards the top.
- –
- A(0) = 1682 ± 117 Bq·m−2—reserve 210Pbex, on the basis of which we determined its flux to the sediment surface to be 52 ± 4 Bq·m−2·year−1.
- –
- The age of CF was determined via the expression. The extension of uncertainty was performed with care (see [29]).
- –
- The expression for the uncertainty of age was defined as follows:
- –
- To calculate the calendar year T(i), we subtracted the age of the CF from the sampling date.
- –
- MAR (r(i), kg·m−2·year−1) was determined via the formula , and its uncertainty was . MAR was shown in Figure 6.
- –
- SAR (s(i), cm·year−1) was computed using the bulk density of dry sediment ρ, as . SAR is shown in Figure 6.
- –
3.3.5. Application of the IP-CRS Model
- A.
- Limiting the depth of the section of the peat section subject to leaching (zk).
- B.
- Solving a system of integro-differential equations
- C.
- Determine the quantity of 210Pbxs removed from each layer of the washout area
- D.
- Determining the total amount of 210Pbxs
- E.
- Determining the additional 210Pbxs for each layer
- F.
- Determination of corrected 210Pbxs volumetric activities
- G.
- Applying the CRS model to the corrected profile
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yakovlev, E.; Spirov, R.; Druzhinin, S.; Ocheretenko, A.; Druzhinina, A.; Mishchenko, E.; Zhukovskaya, E. Atmospheric fallout of radionuclides in peat bogs in the Western segment of the Russian arctic. Environ. Sci. Pollut. Res. 2021, 28, 25460–25478. [Google Scholar] [CrossRef]
- Ndiaya, A.; Bentaleb, I.; Favier, C.; Fourel, F.; Sebag, D.; Fall, M.; Giresse, P.; Diouf, B. Reconstruction of the holocene climate and environmental changes of Niayes peat bog in northern coast of Senegal (NW Africa) based on stable isotopes and charcoals analysis. Quatern. Sci. Rev. 2022, 289, 107609. [Google Scholar] [CrossRef]
- Magiera, T.; Szuszkiewicz, M.; Michczyński, A.; Chróst, L.; Szuszkiewicz, M. Peat bogs as archives of local ore mining and smelting activities over the centuries: A case study of Miasteczko Śląskie (Upper Silesia, Poland). Catena 2021, 198, 105063. [Google Scholar] [CrossRef]
- Appleby, P.; Oldfield, F. The calculation of lead-210 dates assuming a constant rate of supply of unsupported 210Pb to the sediment. Catena 1978, 5, 1–8. [Google Scholar] [CrossRef]
- Goldberg, E.D. Geochronology with 210Pb Radioactive Dating Proceedings of a Symposium; International Atomic Energy Agency: Vienna, Austria, 1963; pp. 21–131. [Google Scholar]
- Fiałkiewicz-Kozieł, B.; Łokas, E.; Gałka, M.; Kołaczek, P.; De Vleeschouwer, F.; Le Roux, G.; Smieja-Król, B. Influence of transboundary transport of trace elements on mountain peat geochemistry (Sudetes, Central Europe). Quatern. Sci. Rev. 2020, 230, 106162. [Google Scholar] [CrossRef]
- Ali, A.; Ghaleb, B.; Garneau, M.; Asnong, H.; Loisel, J. Recent peat accumulation rates in minerotrophic peatlands of the Bay James region, Eastern Canada, inferred by 210Pb and 137Cs radiometric techniques. Appl. Radiat. Isot. 2008, 66, 1350–1358. [Google Scholar] [CrossRef] [PubMed]
- Fiałkiewicz-Kozieł, B.; Kolaczek, P.; Piotrowska, N.; Michczynski, A.; Lokas, E.; Wachniew, P.; Woszczyk, M.; Sensula, B. High-resolution age-depth model of a peat bog in Poland as an important basis for paleoenvironmental studies. Radiocarbon 2014, 56, 109–125. [Google Scholar] [CrossRef]
- Zhao, X.; Hou, X.; Zhang, D.; Yang, Y.; Huang, Z.; Liu, Q. Records of iodine isotopes (129I, 127I) in the Barkol peat bog from northwest China and their sources, transport and preservation. Chemsphere 2021, 279, 130531. [Google Scholar] [CrossRef]
- Cwanek, A.; Łokas, E.; Mitchell, E.A.D.; Mazei, Y.; Gaca, P.; Milton, J.A. Temporal variability of Pu signatures in a 210Pb-dated Sphagnum peat profile from the Northern Ural, Russian Federation. Chemosphere 2021, 281, 130962. [Google Scholar] [CrossRef]
- Byzova, N.M.; Preminina, Y.K. Geography of the Arkhangelsk Region; Sport Akadem Press: Moscow, Russia, 2001. [Google Scholar]
- Evzerov, V.Y. Peat deposits of the Murmansk region. Bull. VSU Ser. Geol. 2012, 2, 153–157. [Google Scholar]
- Levesque, M.; Maruun, S.P.; Dinel, H. Admixing organic overlays and mineral sublayers of shallow peat soils for improving soil productivity. Can. J. Soil Sci. 1988, 68, 775–786. [Google Scholar] [CrossRef]
- Noskova, M.G. Field Atlas of Sphagnum Mosses in the Taiga Zone of European Russia; Aquarius: Tula, Russia, 2016. [Google Scholar]
- GOST 27784-88; Soils, Methods for Determination of Ash Content in Peat and Peat-Containing Soil Horizons, 1988. Standards Publishing House: Moscow, Russia, 1988.
- GOST 28268-89; Soils, Methods of Determination of Moisture, Maximum Hygroscopic Moisture and Moisture of Steady Plant Fading, 1990. Standards Publishing House: Moscow, Russia, 2006.
- Yakovlev, E.Y.; Orlov, A.S.; Kudryavtseva, A.A.; Zykov, S.B. Estimation of Physicochemical Parameters and Vertical Migration of Atmospheric Radionuclides in a Raised Peat Bog in the Arctic Zone of Russia. Appl. Sci. 2022, 12, 10870. [Google Scholar] [CrossRef]
- MVI Recommendation: MN 3421-2010; Method for Performing Measurements on a Gamma Spectrometer. Belarusian State Institute of Metrology, BelGIM: Minsk, Russia, 2010.
- Bahur, A.E.; Manuilova, L.I.; Zueva, D.M.; Ovsyannikova, T.M.; Trukhina, T. The Method for Measuring the Specific Activity of Polonium-210 (210Po) and Lead-210 (210Pb) in Samples of Soils, Soils, Bottom Sediments, Rocks and Building Materials Based on Them by α-β Radiometric Method with Radiochemical Preparation; VIMS: Moscow, Russia, 2013. [Google Scholar]
- Olid, C.; Diego, D.; Garcia-Orellana, J.; Martínez Cortizas, A.; Klaminder, J. Modeling the downward transport of 210Pb in Peatlands: Initial Penetration-Constant Rate of Supply (IP-CRS) model. Sci. Total Environ. 2016, 541, 1222–1231. [Google Scholar] [CrossRef]
- Sanchez-Cabeza, J.; Ruiz-Fernández, A. 210Pb sediment radiochronology: An integrated formulation and classification of dating models. Geochim. Cosmochim. Acta 2012, 82, 183–200. [Google Scholar] [CrossRef]
- Sanchez-Cabeza, J.A.; Ruiz-Fernandez, A.N.; Ontiveros-Cuadras, J.F.; Perez Bernal, L.H.; Olid, C. Monte Carlo uncertainty calculation of 210Pb chronologies and accumulation rates of sediments and peat bogs. Quat. Geochronol. 2014, 23, 80–93. [Google Scholar] [CrossRef]
- Mroz, T.; Łokas, E.; Kocurek, J.; Gasiorek, M. Atmospheric fallout radionuclides in peatland from Southern Poland. J. Environ. Radioact. 2017, 175–176, 25–33. [Google Scholar] [CrossRef]
- Schleich, B.N.; Degering, D.; Unterricker, S. Natural and artificial radionuclides in forest and bog soils: Tracers for migration processes and soil development. Radiochim. Acta 2000, 88, 803–808. [Google Scholar] [CrossRef]
- Krishnaswamy, S.; Lal, D.; Martin, J.; Meybeck, M. Geochronology of lake sediments. Earth Planet. Sci. Lett. 1971, 11, 407–414. [Google Scholar] [CrossRef]
- Crozaz, G.; Picciotto, E.; De Breuck, W. Antarctic snow chronology with 210Pb. J. Geophys. Res. 1964, 69, 2597–2604. [Google Scholar] [CrossRef]
- Pennington, W.; Cambray, R.S.; Eakins, J.D.; Harkness, D.D. Radionuclide dating of the recent sediments of Blelham Tarn. Freshw. Biol. 1976, 6, 317–331. [Google Scholar] [CrossRef]
- Appleby, P.G.; Oldfield, F. The assessment of 210Pb data from sites with varying sediment accumulation rates. Hydrobiologia 1983, 103, 29–35. [Google Scholar] [CrossRef]
- Appleby, P.G. Chronostratigraphic techniques in recent sediments. In Tracking Environmental Change Using Lake Sediments; Basin Analysis, Coring and Chronological Techniques; Last, W.M., Smol, J.P., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; Volume 1, pp. 171–201. [Google Scholar]
- Paatero, J.; Jaakkola, T.; Kulmala, S. Lichen (sp. Cladonia) as a deposition indicator for transuranium elements investigated with the Chernobyl fallout. J. Environ. Radioact. 1998, 38, 223–247. [Google Scholar] [CrossRef]
- Vaasma, T.; Karu, H.; Kiisk, M.; Pensa, M.; Isakar, K.; Realo, E.; Alliksaar, T.; Traczyk, H.A. Pb-210 and fly ash particles in ombrotrophic peat bogs as indicators of industrial emissions. J. Environ. Radioact. 2017, 174, 78–86. [Google Scholar] [CrossRef] [PubMed]


| Sample Code | zi, cm | mi, g | 210Pbtot, Bk·kg−1 | 137Cs, Bk·kg−1 | ||
|---|---|---|---|---|---|---|
| x ± Δ | x ± Δ | |||||
| ISNO-1 0-3 | 1.5 | 141.18 | 310.7 | 34.1 | 38.8 | 4.6 |
| ISNO-1 3-5 | 4.0 | 72.40 | 211.1 | 50.6 | 45.6 | 9.1 |
| ISNO-1 5-7 | 6.0 | 106.03 | 168.4 | 21.9 | 31.2 | 4.1 |
| ISNO-1 7-9 | 8.0 | 81.19 | 155.3 | 35.7 | 15.5 | 4.3 |
| ISNO-1 9-11 | 10.0 | 124.67 | 168.5 | 21.9 | 16.4 | 2.3 |
| ISNO-1 11-13 | 12.0 | 83.95 | 158.0 | 20.5 | 19.8 | 3.0 |
| ISNO-1 13-15 | 14.0 | 99.77 | 155.0 | 26.3 | 19.8 | 3.5 |
| ISNO-1 15-17 | 16.0 | 108.92 | 131.0 | 20.9 | 27.5 | 3.8 |
| ISNO-1 17-19 | 18.0 | 99.31 | 180.8 | 20.3 | 43.4 | 7.4 |
| ISNO-1 19-21 | 20.0 | 96.26 | 243.9 | 73.1 | 45.5 | 6.8 |
| ISNO-1 21-23 | 22.0 | 90.26 | 72.7 | 28.8 | 37.8 | 6.4 |
| ISNO-1 23-25 | 24.0 | 78.44 | 77.9 | 38.9 | 21.1 | 4.4 |
| ISNO-1 25-27 | 26.0 | 68.70 | 44.4 | 26.2 | 13.3 | 4.0 |
| ISNO-1 27-29 | 28.0 | 72.24 | 34.3 | 13.7 | 9.9 | 2.2 |
| ISNO-1 29-31 | 30.0 | 96.57 | 26.5 | 15.9 | 4.6 | 2.3 |
| ISNO-1 31-33 | 32.0 | 85.96 | 28.8 | 11.5 | 4.9 | 3.4 |
| ISNO-1 33-35 | 34.0 | 82.87 | 26.5 | 15.9 | 4.3 | 1.3 |
| ISNO-1 35-37 | 36.0 | 78.64 | 26.3 | 10.5 | 4.3 | 1.7 |
| ISNO-1 37-39 | 38.0 | 75.98 | 26.4 | 10.5 | 3.9 | 1.6 |
| ISNO-1 39-41 | 40.0 | 92.25 | 26.5 | 10.6 | 3.2 | 1.6 |
| ISNO-1 41-43 | 42.0 | 72.76 | 26.3 | 10.5 | 3.3 | 1.6 |
| ISNO-1 43-45 | 44.0 | 50.42 | 26.2 | 10.4 | 5.1 | 2.0 |
| ISNO-1 45-47 | 46.0 | 55.68 | 26.2 | 10.5 | 3.9 | 1.5 |
| ISNO-1 47-49 | 48.0 | 40.39 | 26.3 | 10.5 | 3.7 | 2.6 |
| z(i), cm | ln(Ci) | t(i), Year | u(t(i)), Year | Year (A.D.) | ur(l) | ur(C0) | ur(Ci) | t(i) (Year) | u(t(i)), Year | Δt (Year) | u(Δt) | s (cm·Year−1) | u(s) | r (g cm−2 Year−1) | u(r) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.00 | ||||||||||||||
| 1.5 | 5.65 | −4.1 | 3.8 | 2025 | −0.0007 | 0.005 | 0.12 | 2.81 | 4.79 | 1.07 | 1.82 | 0.05 | 0.08 | ||
| 2.81 | 4.79 | ||||||||||||||
| 4.0 | 5.22 | 9.7 | 8.8 | 2011 | 0.0016 | 0.005 | 0.27 | 11.12 | 6.95 | 0.18 | 0.11 | 0.01 | 0.00 | ||
| 13.93 | 5.04 | ||||||||||||||
| 6.0 | 4.96 | 18.1 | 4.9 | 2002 | 0.0031 | 0.005 | 0.15 | 5.76 | 7.15 | 0.35 | 0.43 | 0.02 | 0.02 | ||
| 19.70 | 5.08 | ||||||||||||||
| 8.0 | 4.86 | 21.2 | 8.9 | 1999 | 0.0036 | 0.005 | 0.28 | −0.01 | 7.18 | −177.38 | 112,976.25 | −6.85 | 4364.19 | ||
| 19.68 | 5.08 | ||||||||||||||
| 10.0 | 4.96 | 18.1 | 4.9 | 2002 | 0.0031 | 0.005 | 0.15 | −0.33 | 6.17 | −6.02 | 112.03 | −0.36 | 6.65 | ||
| 19.35 | 3.51 | ||||||||||||||
| 12.0 | 4.88 | 20.6 | 5.0 | 2000 | 0.0035 | 0.005 | 0.16 | 1.60 | 5.41 | 1.25 | 4.24 | 0.05 | 0.17 | ||
| 20.95 | 4.12 | ||||||||||||||
| 14.0 | 4.86 | 21.3 | 6.6 | 1999 | 0.0036 | 0.005 | 0.20 | 3.68 | 6.16 | 0.54 | 0.91 | 0.03 | 0.04 | ||
| 24.63 | 4.58 | ||||||||||||||
| 16.0 | 4.65 | 27.9 | 6.4 | 1993 | 0.0047 | 0.005 | 0.20 | −2.93 | 5.97 | −0.68 | 1.39 | −0.04 | 0.07 | ||
| 21.70 | 3.83 | ||||||||||||||
| 18.0 | 5.04 | 15.5 | 4.2 | 2005 | 0.0026 | 0.005 | 0.13 | −11.73 | 6.94 | −0.17 | 0.10 | −0.01 | 0.00 | ||
| 9.97 | 5.78 | ||||||||||||||
| 20.0 | 5.38 | 4.5 | 10.8 | 2016 | 0.0008 | 0.005 | 0.34 | 19.27 | 12.70 | 0.10 | 0.07 | 0.00 | 0.00 | ||
| 29.25 | 11.31 | ||||||||||||||
| 22.0 | 3.84 | 54.0 | 19.9 | 1967 | 0.0091 | 0.005 | 0.62 | 23.06 | 19.30 | 0.09 | 0.07 | 0.00 | 0.00 | ||
| 52.31 | 15.64 | ||||||||||||||
| 24.0 | 3.94 | 50.6 | 24.1 | 1970 | 0.0085 | 0.005 | 0.75 | 15.06 | 30.42 | 0.13 | 0.27 | 0.00 | 0.01 | ||
| 67.37 | 26.09 | ||||||||||||||
| 26.0 | 2.90 | 84.1 | 46.3 | 1936 | 0.0142 | 0.005 | 1.44 | 29.78 | 44.24 | 0.07 | 0.10 | 0.00 | 0.00 | ||
| 97.15 | 35.73 | ||||||||||||||
| 28.0 | 2.09 | 110.2 | 54.5 | 1910 | 0.0185 | 0.005 | 1.70 | 67.69 | 957.18 | 0.03 | 0.42 | 0.00 | 0.01 | ||
| 164.84 | 956.51 | ||||||||||||||
| 30.0 | −1.32 | 219.5 | 1912.3 | 1801 | 0.0369 | 0.005 | 59.63 | 18.36 | 1354.35 | 0.11 | 8.03 | 0.01 | 0.37 | ||
| 183.20 | 958.82 | ||||||||||||||
| 32.0 | 0.94 | 146.9 | 143.7 | 1874 | 0.0247 | 0.005 | 4.48 | 0.00 | 1355.98 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 183.20 | 958.82 | ||||||||||||||
| 34.0 | −1.32 | 219.5 | 1912.3 | 1801 | 0.0369 | 0.005 | 59.63 | 58.54 | 2865.72 | 0.03 | 1.67 | 0.00 | 0.07 | ||
| 241.74 | 2700.56 | ||||||||||||||
| 36.0 | −2.71 | 264.0 | 5051.3 | 1757 | 0.0444 | 0.005 | 157.50 | 7.54 | 3833.08 | 0.27 | 134.96 | 0.01 | 5.05 | ||
| 249.28 | 2720.20 | ||||||||||||||
| 38.0 | −1.79 | 234.6 | 2020.5 | 1786 | 0.0395 | 0.005 | 63.00 | −22.23 | 2970.92 | −0.09 | 12.02 | 0.00 | 0.43 | ||
| 227.05 | 1194.54 | ||||||||||||||
| 40.0 | −1.32 | 219.5 | 1274.8 | 1801 | 0.0369 | 0.005 | 39.75 | 14.69 | 2865.67 | 0.14 | 26.55 | 0.01 | 1.17 | ||
| 241.74 | 2604.83 | ||||||||||||||
| 42.0 | −2.71 | 264.0 | 5051.3 | 1757 | 0.0444 | 0.005 | 157.50 | 44.46 | 3628.22 | 0.04 | 0.00 | 0.00 | 0.13 | ||
| 286.20 | 2525.64 |
| z(i), cm | m(i), g cm−2 | ln(Ci) |
|---|---|---|
| 1.50 | 0.07 | 5.65 |
| 4.00 | 0.17 | 5.22 |
| 6.00 | 0.25 | 4.96 |
| 8.00 | 0.34 | 4.86 |
| 10.00 | 0.44 | 4.96 |
| 12.00 | 0.54 | 4.88 |
| 14.00 | 0.63 | 4.86 |
| 16.00 | 0.73 | 4.65 |
| 18.00 | 0.83 | 5.04 |
| 20.00 | 0.92 | 5.38 |
| 22.00 | 1.01 | 3.84 |
| 24.00 | 1.09 | 3.94 |
| 26.00 | 1.16 | 2.90 |
| 28.00 | 1.22 | 2.09 |
| 30.00 | 1.31 | −1.32 |
| 32.00 | 1.39 | 0.94 |
| 34.00 | 1.47 | −1.32 |
| 36.00 | 1.55 | −2.71 |
| 38.00 | 1.62 | −1.79 |
| 40.00 | 1.70 | −1.32 |
| 42.00 | 1.78 | −2.71 |
| z(i), cm | zi, cm | ΔAi, Bq·m−2 | u(ΔAi) | A(i), Bq·m−2 | u(A(i)) | t(i), Year | u(t(i)), Year | Year (A.D.) | Δt | u(Δt) | r(i), kg m3 | u(r(i)) | ρ(i), g m−3 | u(ρ(i)) | s(i), cm Year−1 | u(s(i)) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1680 | 115 | 0.0 | 0.0 | 2021 | |||||||||||
| 1.50 | 382 | 46 | 8.28 | 1.06 | 0.02 | 0.00 | 0.04 | 0.00 | 0.36 | 0.07 | ||||||
| 3 | 1298 | 106 | 8.3 | 1.1 | 2012 | |||||||||||
| 4.00 | 127 | 35 | 3.31 | 1.74 | 0.02 | 0.01 | 0.03 | 0.00 | 0.60 | 0.36 | ||||||
| 5 | 1170 | 100 | 11.6 | 1.4 | 2009 | |||||||||||
| 6.00 | 143 | 22 | 4.19 | 2.17 | 0.02 | 0.01 | 0.05 | 0.00 | 0.48 | 0.26 | ||||||
| 7 | 1027 | 98 | 15.8 | 1.7 | 2005 | |||||||||||
| 8.00 | 100 | 28 | 3.28 | 2.57 | 0.02 | 0.02 | 0.04 | 0.00 | 0.61 | 0.51 | ||||||
| 9 | 927 | 94 | 19.1 | 1.9 | 2002 | |||||||||||
| 10.00 | 169 | 26 | 6.45 | 3.17 | 0.02 | 0.01 | 0.06 | 0.00 | 0.31 | 0.16 | ||||||
| 11 | 758 | 90 | 25.5 | 2.5 | 1995 | |||||||||||
| 12.00 | 105 | 16 | 4.79 | 3.92 | 0.02 | 0.01 | 0.04 | 0.00 | 0.42 | 0.35 | ||||||
| 13 | 653 | 88 | 30.3 | 3.0 | 1990 | |||||||||||
| 14.00 | 103 | 21 | 5.50 | 4.76 | 0.01 | 0.01 | 0.04 | 0.00 | 0.36 | 0.33 | ||||||
| 15 | 550 | 86 | 35.8 | 3.7 | 1985 | |||||||||||
| 16.00 | 109 | 22 | 7.05 | 5.98 | 0.01 | 0.01 | 0.05 | 0.00 | 0.28 | 0,25 | ||||||
| 17 | 442 | 83 | 42.8 | 4.7 | 1978 | |||||||||||
| 18.00 | 146 | 19 | 12.88 | 8.78 | 0.01 | 0.01 | 0.05 | 0.00 | 0.16 | 0.11 | ||||||
| 19 | 296 | 81 | 55.7 | 7.4 | 1965 | |||||||||||
| 20.00 | 199 | 67 | 36.01 | 16.19 | 0.00 | 0.00 | 0.05 | 0.00 | 0.06 | 0,03 | ||||||
| 21 | 96 | 45 | 91.7 | 14.4 | 1929 | |||||||||||
| 22.00 | 40 | 25 | 17.20 | 25.48 | 0.00 | 0.01 | 0.04 | 0.00 | 0.12 | 0.19 | ||||||
| 23 | 56 | 38 | 108.9 | 21.0 | 1912 | |||||||||||
| 24.00 | 39 | 29 | 37.13 | 48.67 | 0.00 | 0.00 | 0.04 | 0.00 | 0.05 | 0.09 | ||||||
| 25 | 18 | 24 | 146.1 | 43.9 | 1875 | |||||||||||
| 26.00 | 12 | 17 | 35.77 | 105.54 | 0.00 | 0.01 | 0.03 | 0.00 | 0.06 | 0.20 | ||||||
| 27 | 6 | 17 | 181.8 | 96.0 | 1839 | |||||||||||
| 28.00 | 6 | 9 | 101.43 | 1914.38 | 0.00 | 0.01 | 0.03 | 0.00 | 0.02 | 0.38 | ||||||
| 29 | 0 | 15 | 283.3 | 1912.0 | 1737 | |||||||||||
| 30.00 | 0 | 15 | ||||||||||||||
| 31 | 0 | 0 |
| z(i), cm | ΔAi, Bk·m−2 | u, ΔAi | A(i), Bk·m−2 | u(A(i)) | t(i), Year | u(t(i)), Year | Year (A.D.) | r(i), g·cm−2·Year−1 | u(r(i)) | ρi, g·cm−3 | u(ρi) | ρ(i), g·cm−3 | u(ρ(i)) | s(i), cm·Year−1 | u(s(i)) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1682 | 117 | 0 | 0 | 2021 | 0.02 | 0 | 0.04 | 0 | 0.48 | 0.01 | ||||
| 382 | 46 | 0.04 | 0 | ||||||||||||
| 3 | 1300 | 108 | 8.3 | 1.1 | 2012 | 0.02 | 0 | 0.04 | 0 | 0.44 | 0.02 | ||||
| 127 | 35 | 0.03 | 0 | ||||||||||||
| 5 | 1173 | 102 | 11.6 | 1.4 | 2009 | 0.02 | 0 | 0.04 | 0 | 0.53 | 0.01 | ||||
| 143 | 22 | 0.05 | 0 | ||||||||||||
| 7 | 1029 | 100 | 15.8 | 1.7 | 2005 | 0.02 | 0 | 0.04 | 0 | 0.53 | 0.02 | ||||
| 100 | 28 | 0.04 | 0 | ||||||||||||
| 9 | 930 | 96 | 19.0 | 2.0 | 2002 | 0.02 | 0 | 0.05 | 0 | 0.44 | 0.01 | ||||
| 169 | 26 | 0.06 | 0 | ||||||||||||
| 11 | 761 | 92 | 25.4 | 2.5 | 1995 | 0.02 | 0 | 0.05 | 0 | 0.35 | 0.01 | ||||
| 105 | 16 | 0.04 | 0 | ||||||||||||
| 13 | 656 | 91 | 30.2 | 3.1 | 1990 | 0.02 | 0 | 0.04 | 0 | 0.36 | 0.02 | ||||
| 103 | 21 | 0,05 | 0 | ||||||||||||
| 15 | 553 | 88 | 35.7 | 3.8 | 1985 | 0.01 | 0 | 0.05 | 0 | 0.30 | 0.02 | ||||
| 109 | 22 | 0.05 | 0 | ||||||||||||
| 17 | 444 | 86 | 42.7 | 4.8 | 1978 | 0.01 | 0 | 0.05 | 0 | 0.22 | 0.03 | ||||
| 146 | 19 | 0.05 | 0 | ||||||||||||
| 19 | 298 | 84 | 55.5 | 7.6 | 1965 | 0 | 0 | 0.05 | 0 | 0.11 | 0.03 | ||||
| 199 | 67 | 0.05 | 0 | ||||||||||||
| 21 | 99 | 50 | 90.9 | 15.4 | 1930 | 0 | 0 | 0.04 | 0 | 0.05 | 0.02 | ||||
| 40 | 25 | 0.04 | 0 | ||||||||||||
| 23 | 59 | 43 | 107.5 | 22.9 | 1913 | 0 | 0 | 0.04 | 0 | 0.09 | 0.02 | ||||
| 39 | 29 | 0.04 | 0 | ||||||||||||
| 25 | 20 | 32 | 141.5 | 50.4 | 1879 | 0 | 0 | 0.04 | 0 | 0.05 | 0.02 | ||||
| 12 | 17 | 0.03 | 0 | ||||||||||||
| 27 | 9 | 27 | 169.6 | 103.0 | 1851 | 0 | 0.01 | 0.03 | 0 | 0.06 | 0.02 | ||||
| 6 | 9 | 0.03 | 0 | ||||||||||||
| 29 | 3 | 26 | 203.4 | 279.0 | 1817 | 0 | 0.02 | 0.04 | 0 | 0.06 | 0.02 | ||||
| 0 | 15 | 0.05 | 0 | ||||||||||||
| 31 | 3 | 21 | 206.2 | 250.7 | 1814 | 0.01 | 0.06 | 0.04 | 0 | 0.14 | 0.02 | ||||
| 2 | 9 | 0.04 | 0 | ||||||||||||
| 33 | 1 | 19 | 253.8 | 993.8 | 1767 | 0 | 0.04 | 0.04 | 0 | 0.03 | 0.02 | ||||
| 0 | 13 | 0.04 | 0 | ||||||||||||
| 35 | 0 | 14 | 267.3 | 1137.6 | 1753 | 0.01 | 0.51 | 0.04 | 0 | 0.20 | 0.02 | ||||
| 0 | 8 | 0.04 | 0 | ||||||||||||
| 37 | 0.35 | 12 | 271.5 | 1086.0 | 1749 | 0.01 | 0.68 | 0.04 | 0 | 0.26 | 0.03 | ||||
| 0 | 8 | 0.04 | 0 | ||||||||||||
| 39 | 0.23 | 9 | 284.8 | 1274.7 | 1736 | 0 | 0.18 | 0.04 | 0 | 0.08 | 0.02 | ||||
| 0 | 9 | 0.04 | 0 | ||||||||||||
| 41 | 0 | 0 |
| Layer, cm | Depth, cm | Bulk Density, g·cm−3 | 210Pb Original, Bk·kg−1 | 210Pb Corrected | D, cm−3·Year−1 | w, cm·Year−1 | ri, Year−1 | fi | Dates from Original 210Pb, Model CRS, Years | Dates from Corrected 210Pb, Model IP-CRS, Years | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bk·m−2 | Bk·kg−1 | ||||||||||
| 0–3 | 3 | 0.0448 | 310.75 ± 34.18 | 411.0 ± 45.12 | 305.6 ± 33.60 | 0.100 | 0.288 | 0.100 | 2021 | 2021 | |
| 3–5 | 2 | 0.0345 | 211.16 ± 50.68 | 228.0 ± 54.72 | 330.6 ± 79.34 | 2014 | 2012 | ||||
| 5–7 | 2 | 0.0505 | 168.39 ± 21.89 | 190.0 ± 24.70 | 188.1 ± 24.45 | 0.100 | 2011 | 2006 | |||
| 7–9 | 2 | 0.0387 | 155.35 ± 35.73 | 158.0 ± 36.34 | 204.3 ± 46.98 | 2008 | 2000 | ||||
| 9–11 | 2 | 0.0594 | 168.49 ± 21.90 | 132.0 ± 15.84 | 111.1 ± 13.33 | 0.100 | 2005 | 1994 | |||
| 11–13 | 2 | 0.0400 | 158.02 ± 20.54 | 110.0 ± 14.30 | 137.5 ± 17.87 | 2000 | 1988 | ||||
| 13–15 | 2 | 0.0475 | 155.02 ± 26.35 | 92.0 ± 26.35 | 96.8 ± 22.26 | 0.100 | 1996 | 1982 | |||
| 15–17 | 2 | 0.0519 | 131.06 ± 20.97 | 76.0 ± 20.96 | 73.2 ± 11.71 | 0.100 | 1991 | 1976 | |||
| 17–19 | 2 | 0.0473 | 180.80 ± 20.32 | 64.0 ± 11.23 | 67.6 ± 11.49 | 0.100 | 1986 | 1970 | |||
| 19–21 | 2 | 0.0458 | 243.93 ± 73.18 | 54.0 ± 21.6 | 58.9 ± 17.67 | 0.100 | 1978 | 1964 | |||
| 21–23 | 2 | 0.0430 | 72.20 ± 28.88 | 44.0 ± 17.6 | 51.1 ± 20.44 | 0.173 | 1962 | 1958 | |||
| 23–25 | 2 | 0.0374 | 77.89 ± 38.94 | 38.0 ± 19.0 | 50.8 ± 25.40 | 0.162 | 1956 | 1951 | |||
| 25–27 | 2 | 0.0327 | 44.42 ± 26.65 | 30.0 ± 18.0 | 45.8 ± 27.48 | 0.081 | 1949 | 1945 | |||
| 27–29 | 2 | 0.0344 | 34.34 ± 13.74 | 26.0 ± 10.4 | 37.7 ± 15.08 | 0.066 | 1945 | 1938 | |||
| 29–31 | 2 | 0.0460 | 26.54 ± 15.92 | 11.0 ± 6.6 | 23.9 ± 14.34 | 0.068 | 1941 | 1932 | |||
| 31–33 | 2 | 0.0409 | 28.80 ± 11.52 | 18.0 ± 10.8 | 21.9 ± 13.14 | 0.065 | 1937 | 1924 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakovlev, E.; Kudryavtseva, A.; Orlov, A. Comparison of 210Pb Age Models of Peat Cores Derived from the Arkhangelsk Region. Appl. Sci. 2023, 13, 10486. https://doi.org/10.3390/app131810486
Yakovlev E, Kudryavtseva A, Orlov A. Comparison of 210Pb Age Models of Peat Cores Derived from the Arkhangelsk Region. Applied Sciences. 2023; 13(18):10486. https://doi.org/10.3390/app131810486
Chicago/Turabian StyleYakovlev, Evgeny, Alina Kudryavtseva, and Aleksandr Orlov. 2023. "Comparison of 210Pb Age Models of Peat Cores Derived from the Arkhangelsk Region" Applied Sciences 13, no. 18: 10486. https://doi.org/10.3390/app131810486
APA StyleYakovlev, E., Kudryavtseva, A., & Orlov, A. (2023). Comparison of 210Pb Age Models of Peat Cores Derived from the Arkhangelsk Region. Applied Sciences, 13(18), 10486. https://doi.org/10.3390/app131810486






