A Numerical Simulation Study on DC Positive Corona Discharge Characteristics at the Conductor’s Tip Defect
Abstract
:1. Introduction
2. Hybrid Numerical Model
2.1. Microscopic Chemical Reactions
2.2. Governing Equations of the Numerical Model
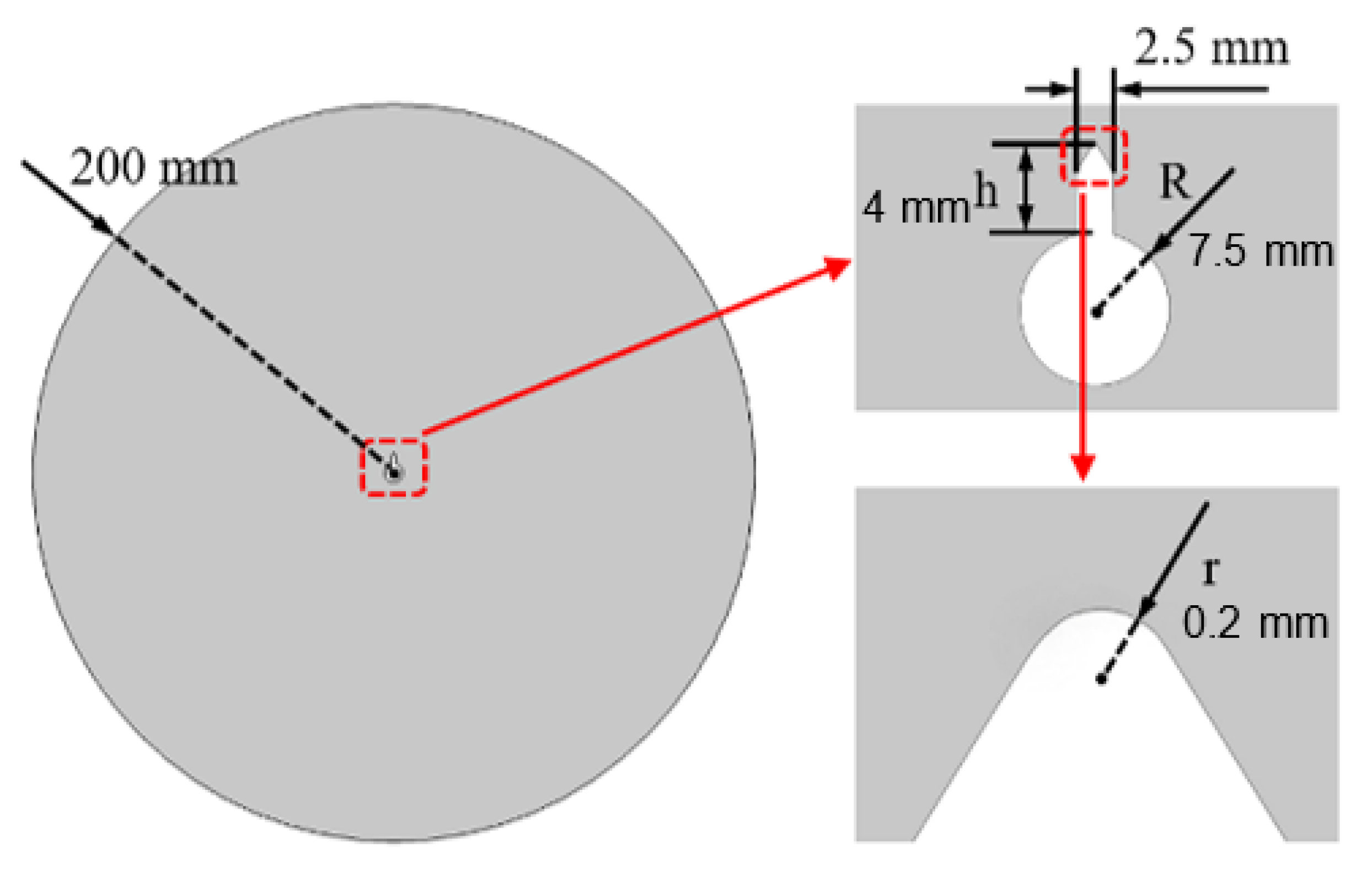
2.3. Boundary Conditions and Initial Values
3. Test and Verification
3.1. Corona Cage Test System
3.2. The Method of Obtaining Discharge Current and Judging Corona Inception
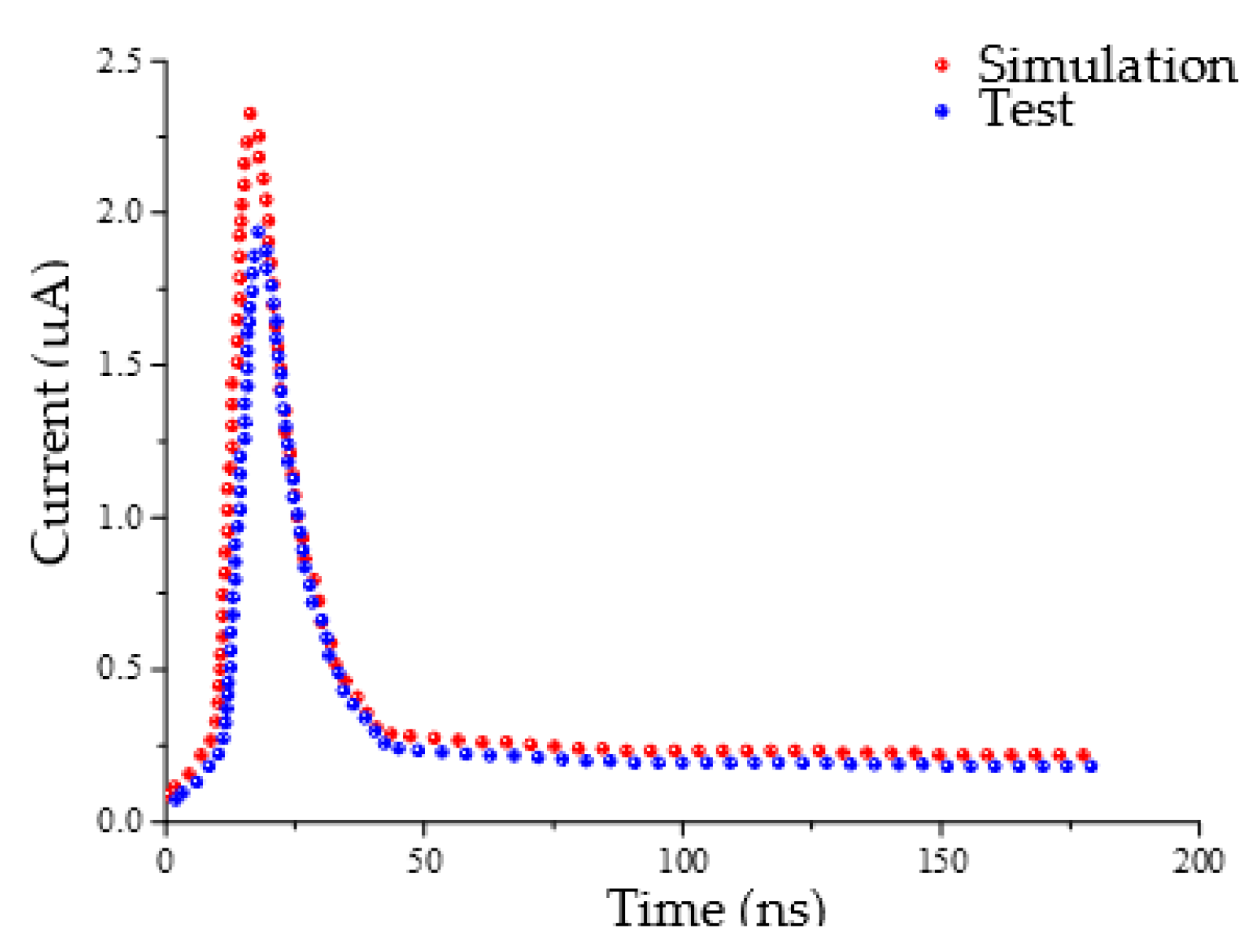
3.3. Comparison of Experimental and Simulation Results
4. Simulation Results and Discussion
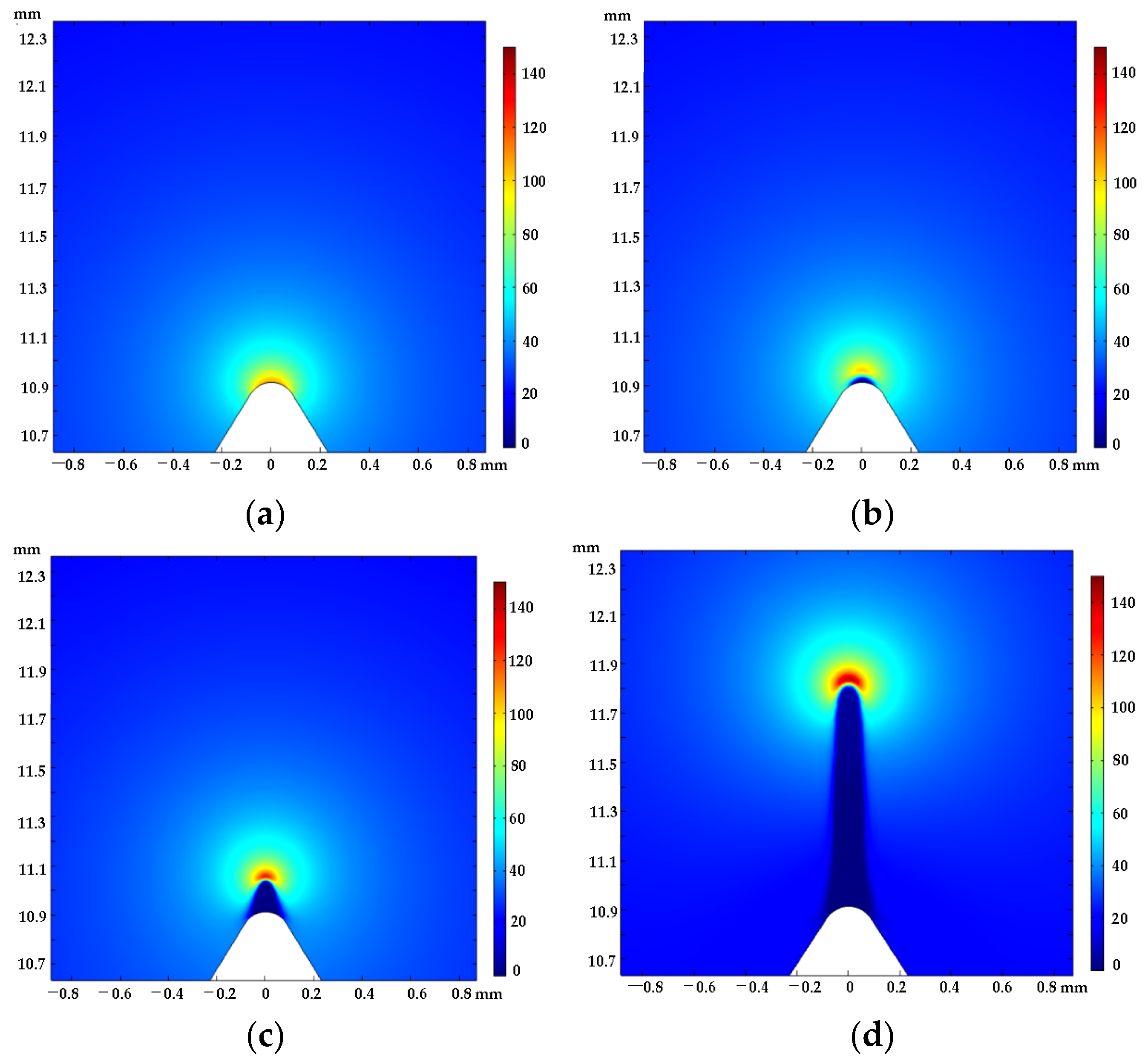
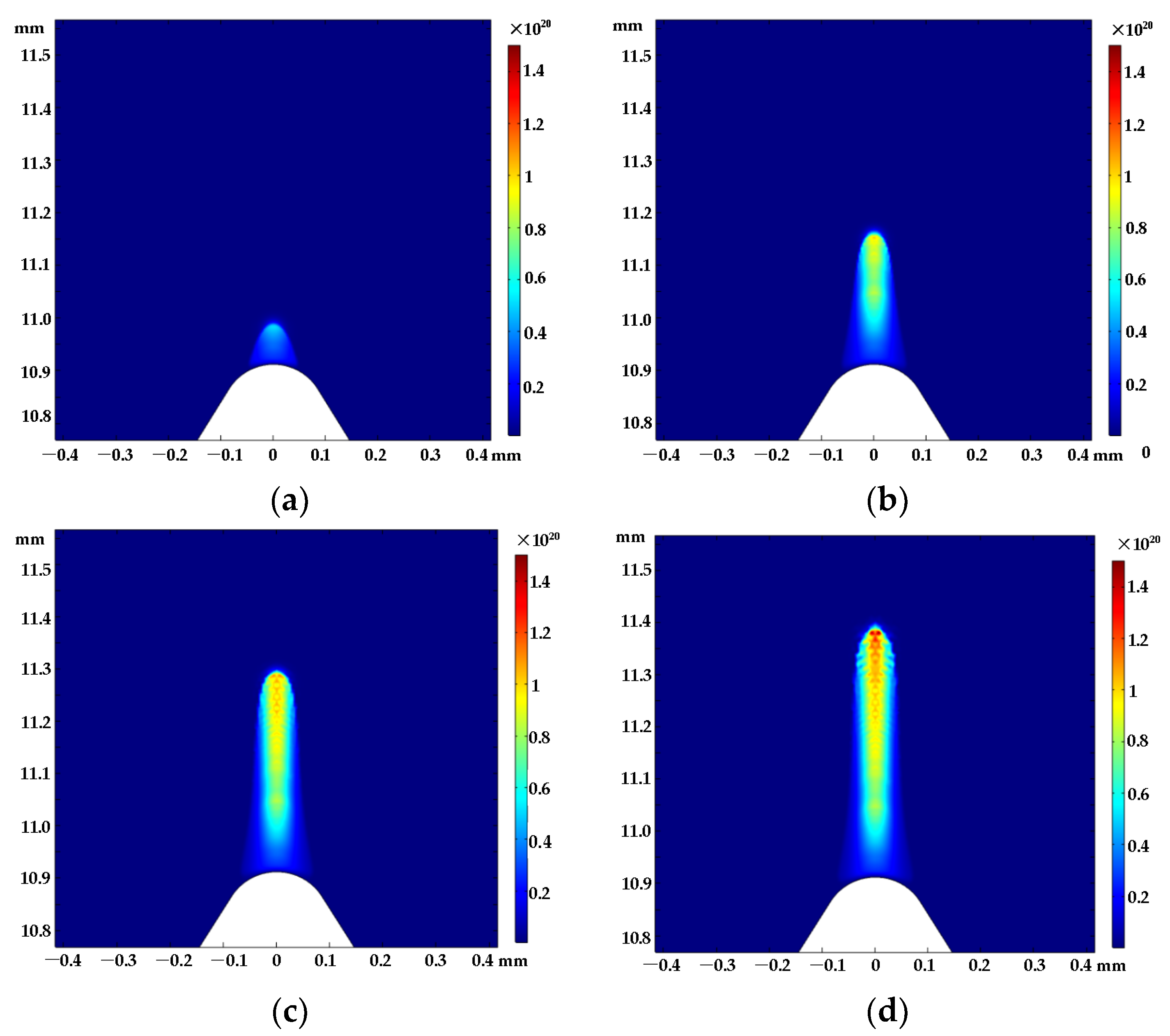
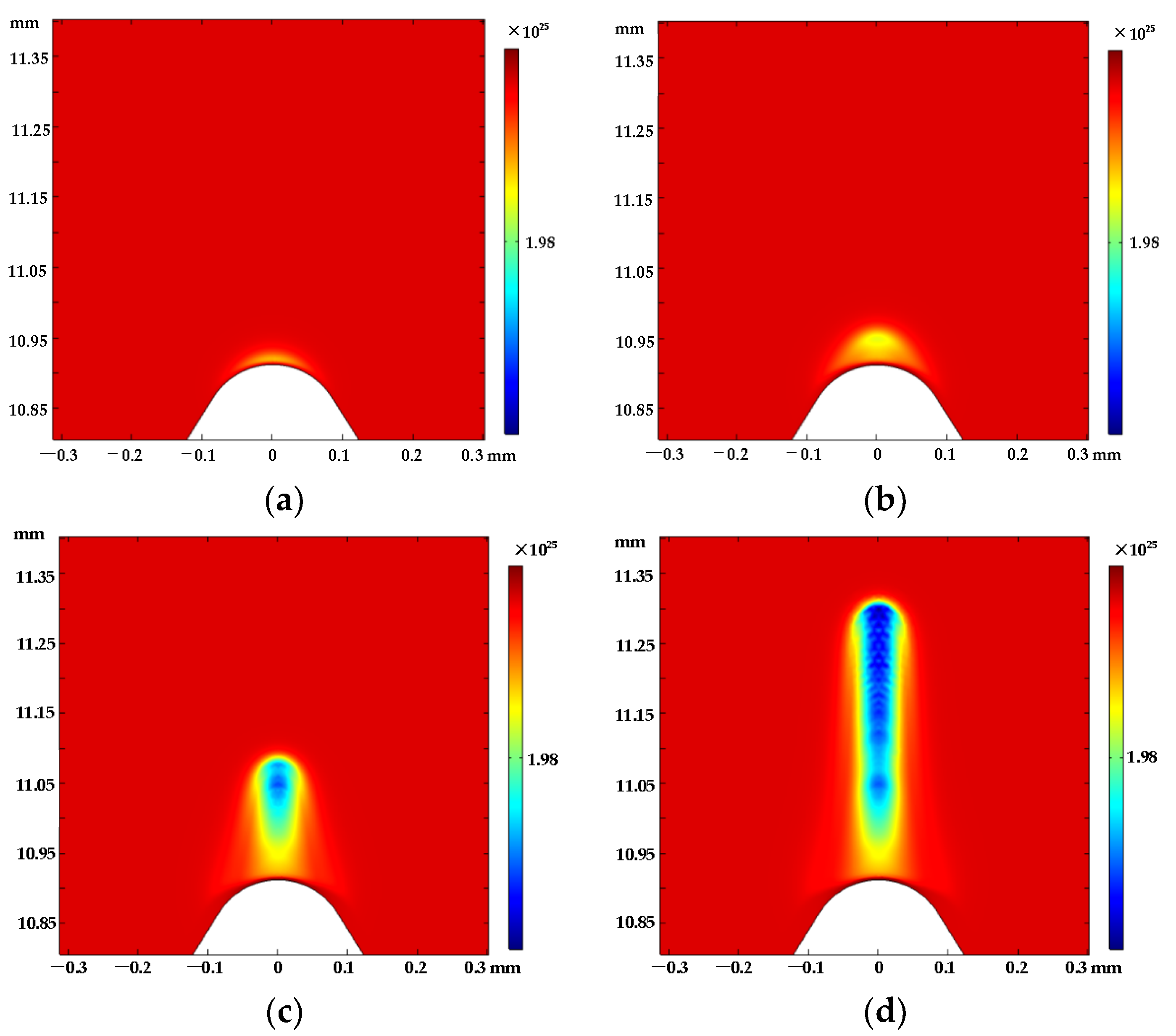
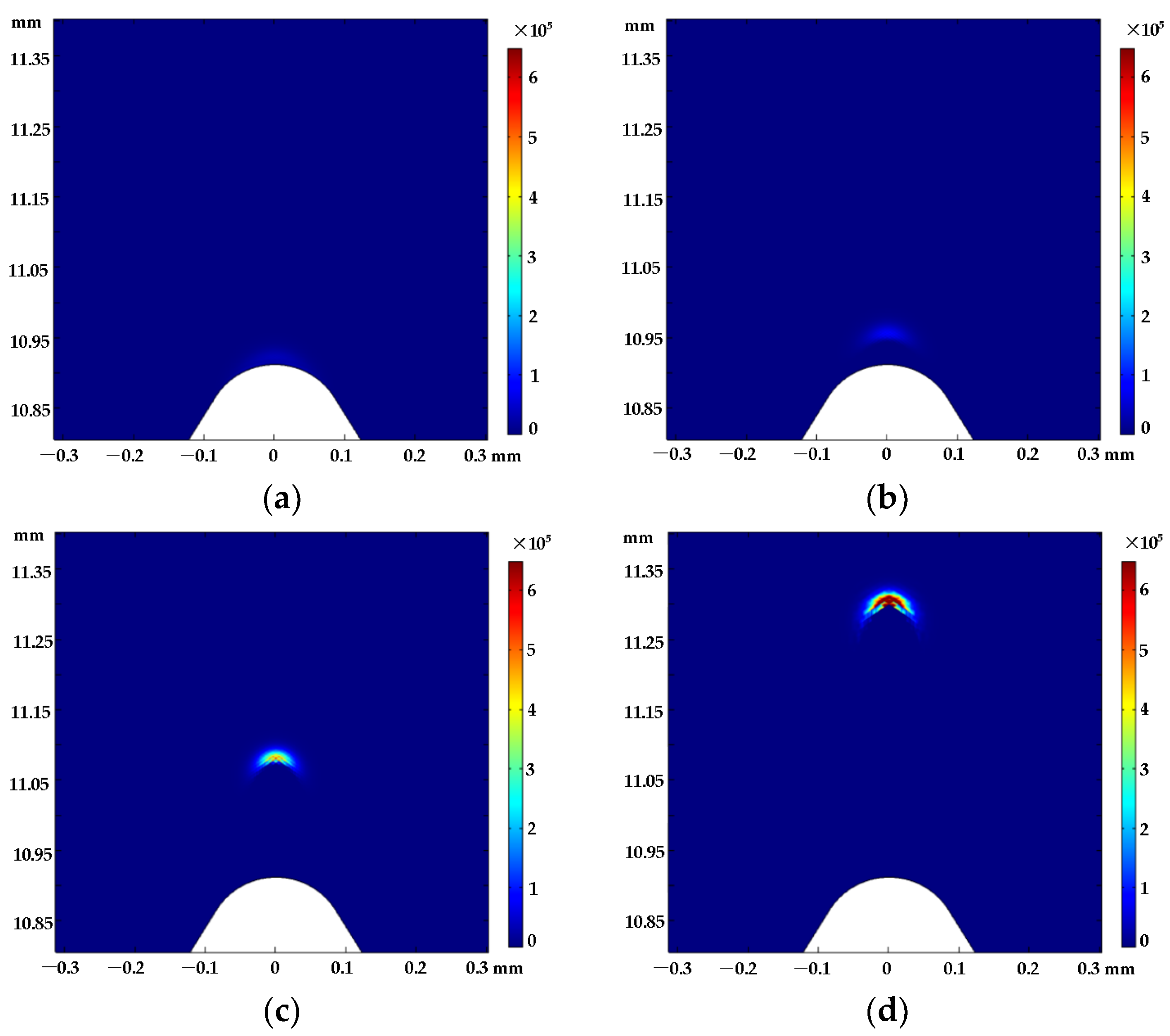
4.1. Microscopic Process of Corona Discharge
4.2. Simulation Results of Corona Characteristics under Different Factors
5. Conclusions
- (1)
- Through experimental research, the rationality of the model is verified. Compared with the experimental results, the maximum error of the corona inception voltage under different pressures is less than 0.2%. For comparison of discharge current, it is shown that the discharge current exhibits pulse characteristics: its rise time is about 10 ns and its decay time is about 300–500 ns and the current amplitude is between 2.0 μA and 2.5 μA. In general, the results in the test and simulation are consistent;
- (2)
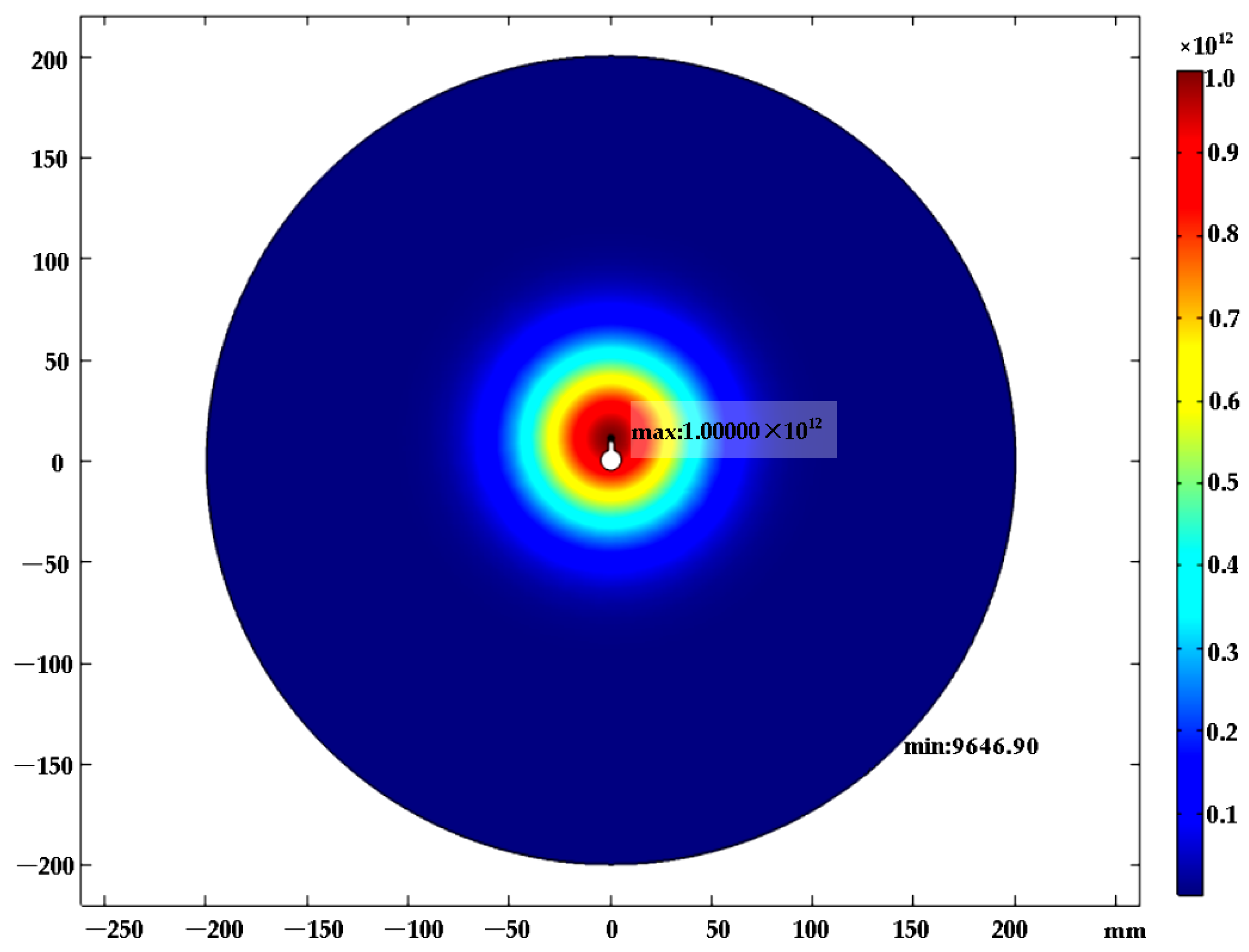
- Based on the hybrid numerical model of fluid-chemical reactions, in the process of positive corona discharge developing from the wire’s tip defect to the cathode, the evolution of streamer morphology can be observed intuitively, and the density variation of space particles and the distribution of the electric field can be obtained. There are some representative results: the field strength reaches a peak value (92.1 kV/cm) within 1.2798 ns at the beginning of discharge and the maximum electron density of the streamer head in one discharge is about 1 × 1020 m−3;
- (3)
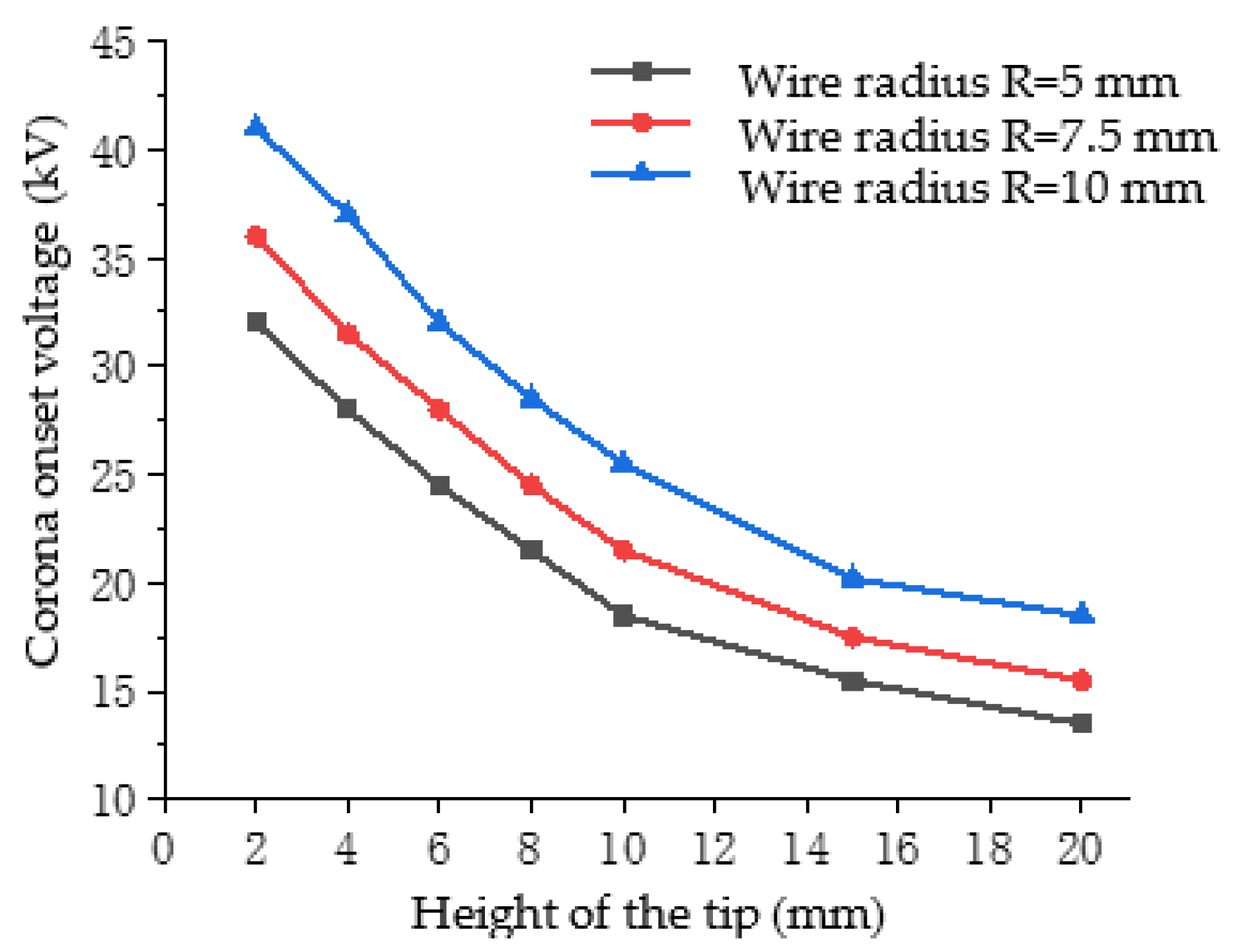
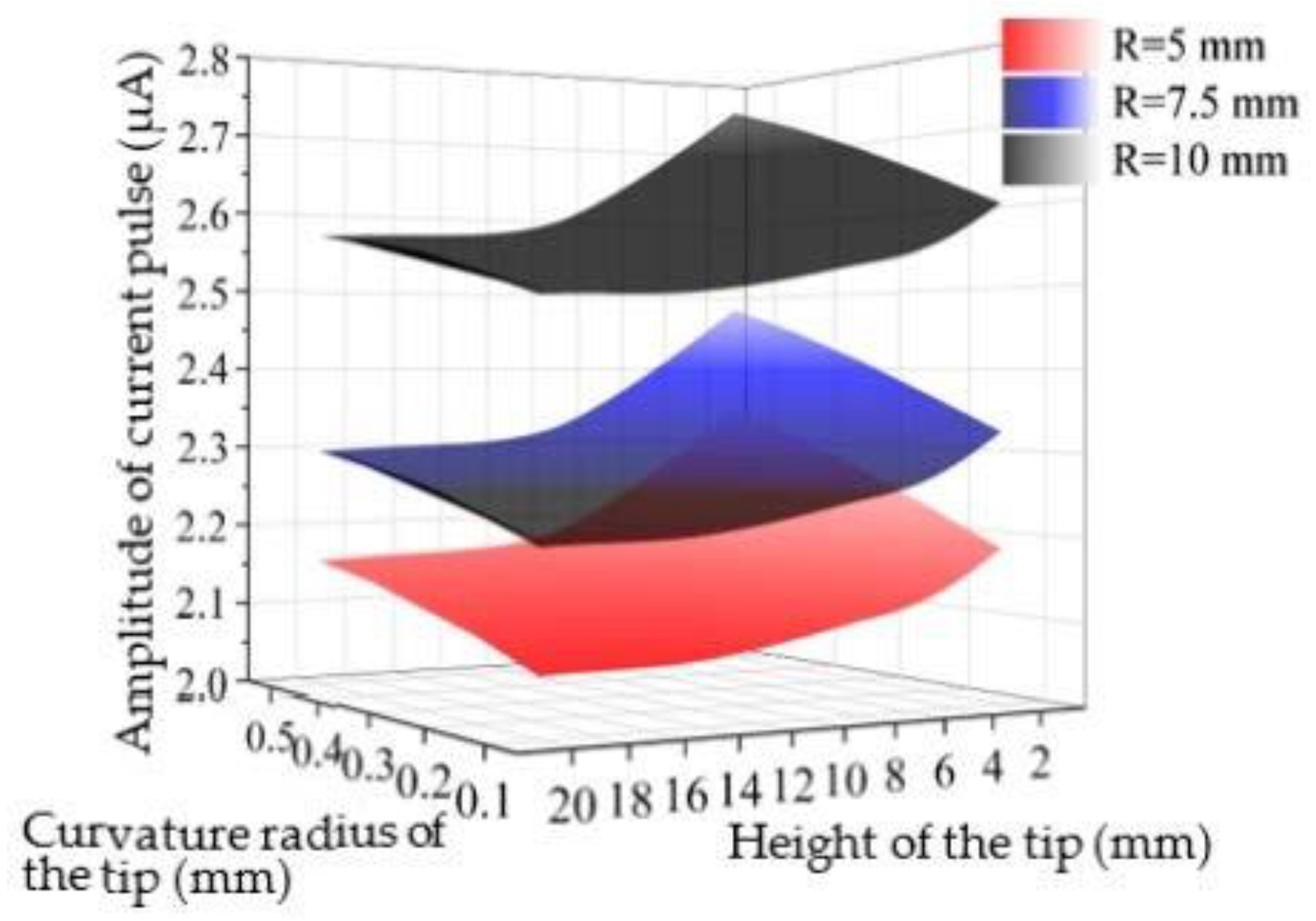
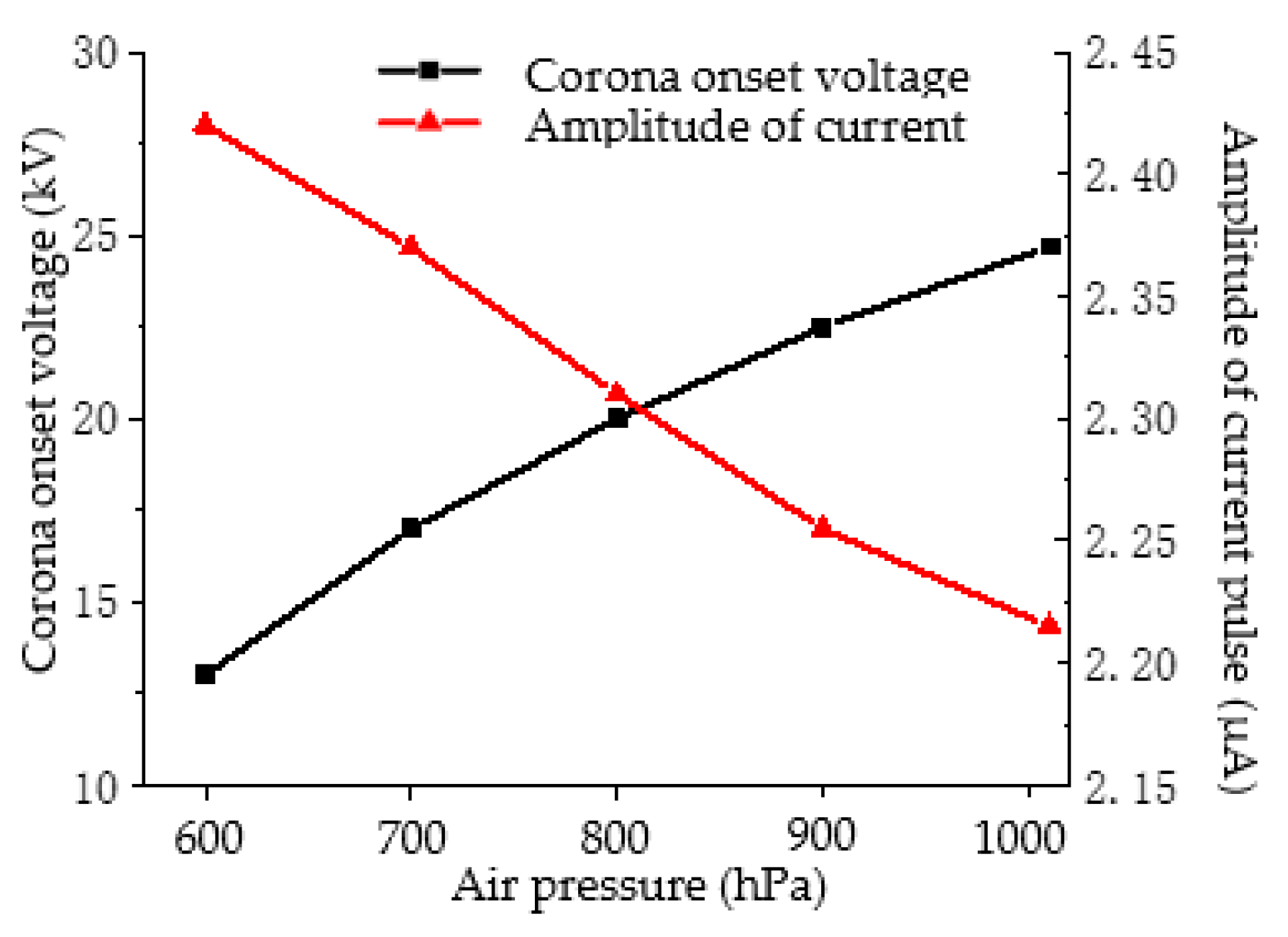
- The simulation results show that, considering the geometry of conductor tip defects, the corona inception voltage decreases with an increase of tip height and decreases in tip curvature radius and conductor radius and the amplitude of the current pulse increases with increases in wire radius and tip curvature radius and a decrease in tip height. As for air pressure ascending from 600 hPa to 1013 hPa, the corona inception voltage obtained by simulation has an increase of 81.5% and the amplitude of current pulse has a drop of 9.1%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yi, Y.; Wang, Y.; Wang, L. Conductor surface conditions effects on audible noise spectrum characteristics of positive corona discharge. IEEE Trans. Dielectr. Electr. 2016, 23, 1872–1878. [Google Scholar] [CrossRef]
- Liu, H.; Liao, R.; Zhao, X.; Lin, Y. The effect of air pressure on the surface electric field intensity characteristics under negative DC corona discharge in a corona cage. Int. J. Electr. Power Energy Syst. 2019, 113, 244–250. [Google Scholar] [CrossRef]
- Ren, X.; Jiang, X.; Yang, G.; Huang, Y.; Wu, J.; Yang, Z. Effect of environmental parameters on streamer discharge in short air gap between rod and plate. Energies 2022, 15, 817. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Bazelyan, E.M. Temperature and density effects on the properties of a long positive streamer in air. J. Phys. D Appl. Phys. 1996, 29, 2873. [Google Scholar] [CrossRef]
- Pancheshnyi, S.; Nudnova, M.; Starikovskii, A. Development of a cathode-directed streamer discharge in air at different pressures: Experiment and comparison with direct numerical simulation. Phys. Rev. E 2005, 71, 016407. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, P. Effect of relative humidity on electron distribution and ozone production by DC coronas in air. IEEE Trans. Plasma Sci. 2005, 33, 808–812. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Liao, R.; Zhao, X.; Hao, J.; He, G. Effect of relative humidity on the surface electric field intensity characteristics under DC voltage in a corona cage. IEEE Trans. Dielectr. Electr. 2021, 28, 3. [Google Scholar] [CrossRef]
- Li, H.; Zhu, J.; Yang, W.; Zhang, X.; Wang, D.; Zhu, J.; Bian, X. Humidity effects on the ground-level resultant electric field of positive DC conductors. Plasma Sci. Technol. 2019, 21, 074001. [Google Scholar] [CrossRef]
- Pfeiffer, M.; Franck, C.M. Impact of conductor surface type and rain intensity on HVDC corona losses. IEEE Trans. Power Deliv. 2015, 30, 2284–2292. [Google Scholar] [CrossRef]
- Bian, X.; Wang, L.; Liu, Y.; Yang, Y.; Guan, Z. High altitude effect on corona inception voltages of DC power transmission conductors based on the mobile corona cage. IEEE Trans. Power Deliv. 2013, 28, 1971–1973. [Google Scholar] [CrossRef]
- Lekganyane, M.J.; Ijumba, N.M.; Britten, A.C. Corona audible noise measurements in a small indoor corona cage under HVDC voltages. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Font, A.; Solak, Y.T.; Ilhan, S. DC corona characteristics derived from corona cage tests and simulations. IEEE Trans. Dielectr. Electr. 2019, 26, 1867–1875. [Google Scholar] [CrossRef]
- Xu, M.; Tan, Z.; Li, K. Modified peek formula for calculating positive DC Corona inception electric field under variable humidity. IEEE Trans. Dielectr. Electr. 2012, 19, 1377–1382. [Google Scholar] [CrossRef]
- Fu, Y.; He, M.; Chen, C.; Wang, C.; Zhang, Z. Effects of rod radius and voltage on streamer discharge in a short air gap. Plasma Sci. Technol. 2023, 25, 085401. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, X.; Deng, Z.; Lan, L.; Zhan, H.; Pei, X.; Chen, J.; Yuan, Y.; Wen, X. Kinetic study of key species and reactions of atmospheric pressure pulsed corona discharge in humid air. Plasma Sci. Technol. 2022, 24, 172–186. [Google Scholar] [CrossRef]
- Van Gaens, W.; Bogaerts, A. Corrigendum: Kinetic modelling for an atmospheric pressure argon plasma jet in humid air. J. Phys. D Appl. Phys. 2014, 47, 079502. [Google Scholar] [CrossRef]
- Van Gaens, W.; Bogaerts, A. Reaction pathways of biomedically active species in an Ar plasma jet. Plasma Sources Sci. Technol. 2014, 23, 035015. [Google Scholar] [CrossRef]
- Wang, W.; Snoeckx, R.; Zhang, X.; Cha, M.S.; Bogaerts, A. Modeling plasma-based CO2 and CH4 conversion in mixtures with N2, O2, and H2O: The bigger plasma chemistry picture. J. Phys. Chem. C 2018, 122, 8704–8723. [Google Scholar] [CrossRef]
- Liu, D.; Sun, B.; Iza, F.; Xu, D.; Wang, X.; Rong, M.; Kong, M.G. Main species and chemical pathways in cold atmospheric-pressure Ar + H2O plasmas. Plasma Sources Sci. Technol. 2017, 26, 045009. [Google Scholar] [CrossRef]
- Wu, F.; Liao, R.; Yang, L. Numerical simulation of trichel pulse characteristics in bar-plate DC negative corona discharge. Acta Phys. Sin. 2013, 62, 348–357. [Google Scholar] [CrossRef]
- Wu, F.; Liao, R.; Wang, K.; Yang, L.; Grzybowski, S. Numerical simulation of the characteristics of heavy particles in bar-plate DC positive corona discharge based on a hybrid model. IEEE Trans. Plasma Sci. 2014, 42, 868–878. [Google Scholar] [CrossRef]
- Saifutdinov, A.I.; Fairushin, I.I.; Kashapov, N.F. Analysis of various scenarios of the behavior of voltage-current characteristics of direct-current microdischarge at atmospheric pressure. JETP Lett. 2016, 104, 180–185. [Google Scholar] [CrossRef]
- Feng, N.; Ma, T.; Chen, C.; Yao, B.; Gao, W. Simulation and study of DC corona discharge characteristics of bar-plate gap. Energies 2022, 15, 6431. [Google Scholar] [CrossRef]
- Sarrette, J.P.; Eichwald, O.; Marchal, F.; Ducasse, O.; Yousfi, M. Electro-hydrodynamics and kinetic modeling of dry and humid air flows activated by corona discharges. Plasma Sci. Technol. 2016, 18, 469–472. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, Q.; Dong, Z. Kinetic study on non-thermal volumetric plasma decay in the early afterglow of air discharge generated by a short pulse microwave or laser. J. Appl. Phys. 2016, 120, 083302. [Google Scholar] [CrossRef]
- Jiang, M.; Li, Y.; Wang, H. 3D PIC-MCC simulation of corona discharge in needle-plate electrode with external circuit. Plasma Sources Sci. Technol. 2020, 29, 15–20. [Google Scholar] [CrossRef]
- Georghiou, G.E.; Papadakis, A.P.; Morrow, R.; Metaxas, A.C. Numerical modelling of atmospheric pressure gas discharges leading to plasma production. J. Phys. D Appl. Phys. 2005, 38, 303–328. [Google Scholar] [CrossRef]
- Pancheshnyi, S.; Biagi, S.; Bordage, M.C.; Hagelaar, G.J.M.; Morgan, W.L.; Phelps, A.V.; Pitchford, L.C. The LXCat project: Electron scattering cross sections and swarm parameters for low temperature plasma modeling. Chem. Phys. 2012, 398, 148–153. [Google Scholar] [CrossRef]
- Gas Discharge Plasma Database (GPLAS). Available online: http://plasma-data.net/ (accessed on 15 February 2023). (In Chinese).
- Farouk, T.; Farouk, B.; Gutsol, A.; Fridman, A. Atmospheric pressure methane–hydrogen dc micro-glow discharge for thin film deposition. J. Phys. D Appl. Phys. 2008, 41, 175202. [Google Scholar] [CrossRef]
- Li, C.; Ebert, U.; Hundsdorfer, W. Spatially hybrid computations for streamer discharges with generic features of pulled fronts: I. Planar fronts. J. Comput. Phys. 2010, 229, 200–220. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- He, W.; Liu, X.; Yang, F. Numerical simulation of direct current glow discharge in air with experimental validation. Jpn. J. Appl. Phys. 2012, 51, 026001. [Google Scholar] [CrossRef]
- Chang, J.-S.; Lawless, P.A.; Yamamoto, T. Corona discharge processes. IEEE Trans. Plasma Sci. 1997, 19, 1152–1166. [Google Scholar] [CrossRef]
- Giao, T.; Jordan, J. Modes of corona discharges in air. IEEE Trans. Power Appar. Syst. 1968, 5, 1207–1215. [Google Scholar] [CrossRef]
- Zogning, C.; Lobry, J.; Moiny, F. Comparison between positive and negative corona discharges by hydrodynamic plasma simulations. In Proceedings of the 2020 International Symposium on Electrical Insulating Materials (ISEIM), Tokyo, Japan, 13–17 September 2020; pp. 552–560. [Google Scholar]





| Equations | Rates |
|---|---|
| Elastic collision | |
| Impact ionization | |
| Charge transfer between particles | |
| Recombination Reaction | |
| Neutral reaction | |
| Electron attachment | |
| Surface Reaction | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Mai, J.; Wang, L. A Numerical Simulation Study on DC Positive Corona Discharge Characteristics at the Conductor’s Tip Defect. Appl. Sci. 2023, 13, 10472. https://doi.org/10.3390/app131810472
Wang S, Mai J, Wang L. A Numerical Simulation Study on DC Positive Corona Discharge Characteristics at the Conductor’s Tip Defect. Applied Sciences. 2023; 13(18):10472. https://doi.org/10.3390/app131810472
Chicago/Turabian StyleWang, Shenghui, Jiamin Mai, and Lihong Wang. 2023. "A Numerical Simulation Study on DC Positive Corona Discharge Characteristics at the Conductor’s Tip Defect" Applied Sciences 13, no. 18: 10472. https://doi.org/10.3390/app131810472
APA StyleWang, S., Mai, J., & Wang, L. (2023). A Numerical Simulation Study on DC Positive Corona Discharge Characteristics at the Conductor’s Tip Defect. Applied Sciences, 13(18), 10472. https://doi.org/10.3390/app131810472






