2D-Unitary ESPRIT Based Multi-Target Joint Range and Velocity Estimation Algorithm for FMCW Radar
Abstract
:1. Introduction
2. Signal Model and Principle of the Range and Velocity Estimation
2.1. Signal Model
2.2. Principle of the Range and Velocity Estimation
3. 2D-Unitary ESPRIT Based Joint Range and Velocity Estimation Algorithm of Multiple Targets
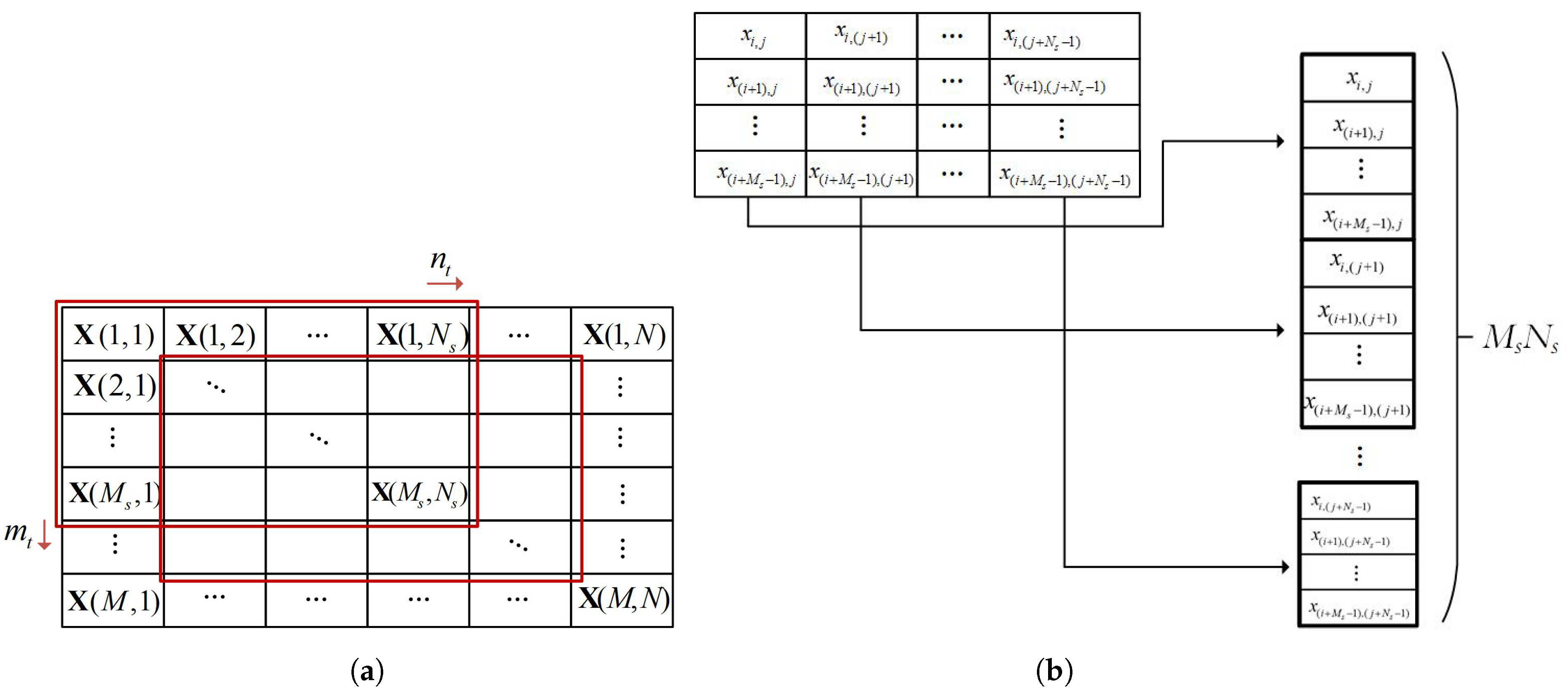
3.1. 2D Virtual Array Construction Using 2D-Spatial Smoothing Preprtocessing
3.2. 2D-Unitary ESPRIT Algorithm for Joint Range and Velocity Estimation
| Algorithm 1: 2D-Unitary ESPRIT based joint range and velocity estimation algorithm. | |
| Input : Discrete IF signal ; and . | |
| Output: Range-velocity estimates of D targets. | |
| 1 | Using 2D-spatial smoothing preprocessing, the signal matrix |
| in (13) is reconstructed into a matrix in (20); | |
| 2 | Compute the signal matrix in (37), calculate the covariance matrix in (38), and perform EVD of to obtain the signal subspace ; |
| 3 | Compute , , , , , , , ; |
| 4 | Calculate , in (39) and (40); |
| 5 | Calculate the largest D eigenvalues of the complex matrix , where ; |
| 6 | Calculate the range-Doppler angular frequency estimates: |
| , , where ; | |
| 7 | The paired and are calculated from and according to (14) and (15); |
| 8 | and are calculated using (11) and (12). |
4. Simulations and Analysis
4.1. Performance Metrics and Parameter Settings
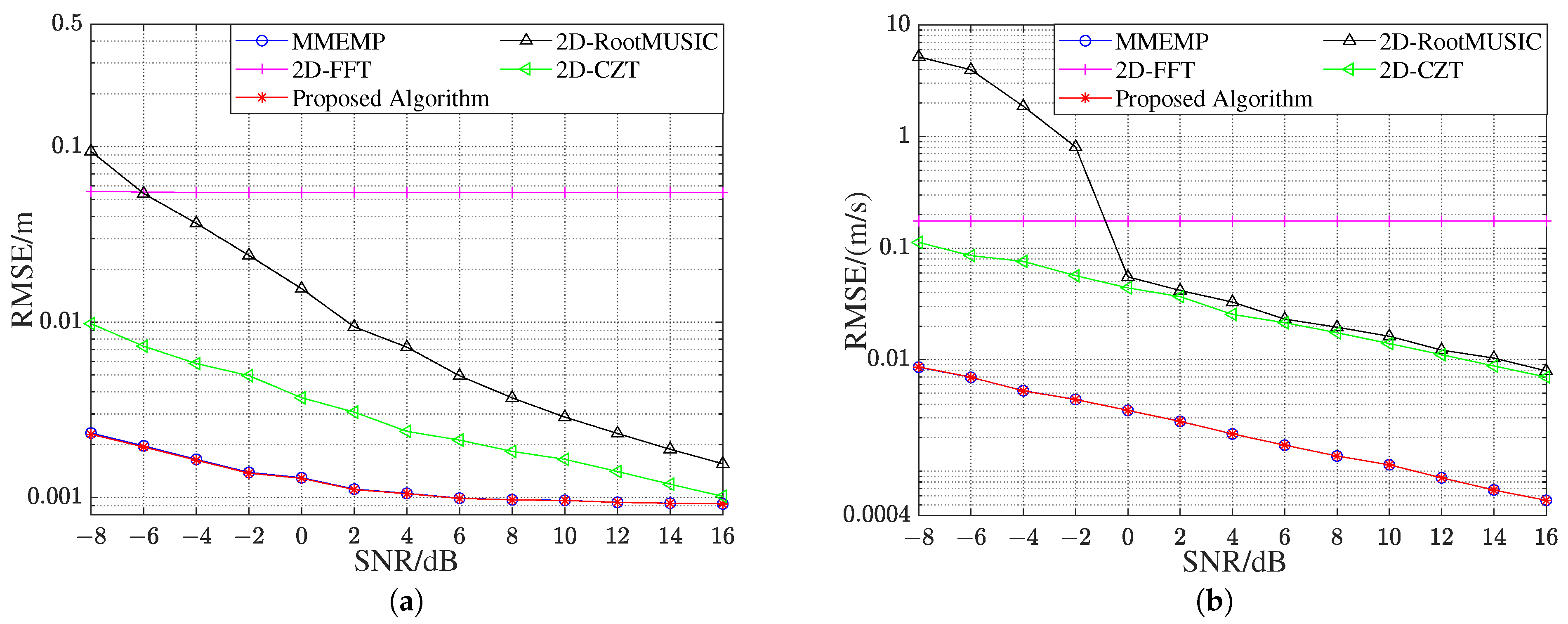
4.2. Comparison of Estimation Accuracy in the Single-Target Scenario
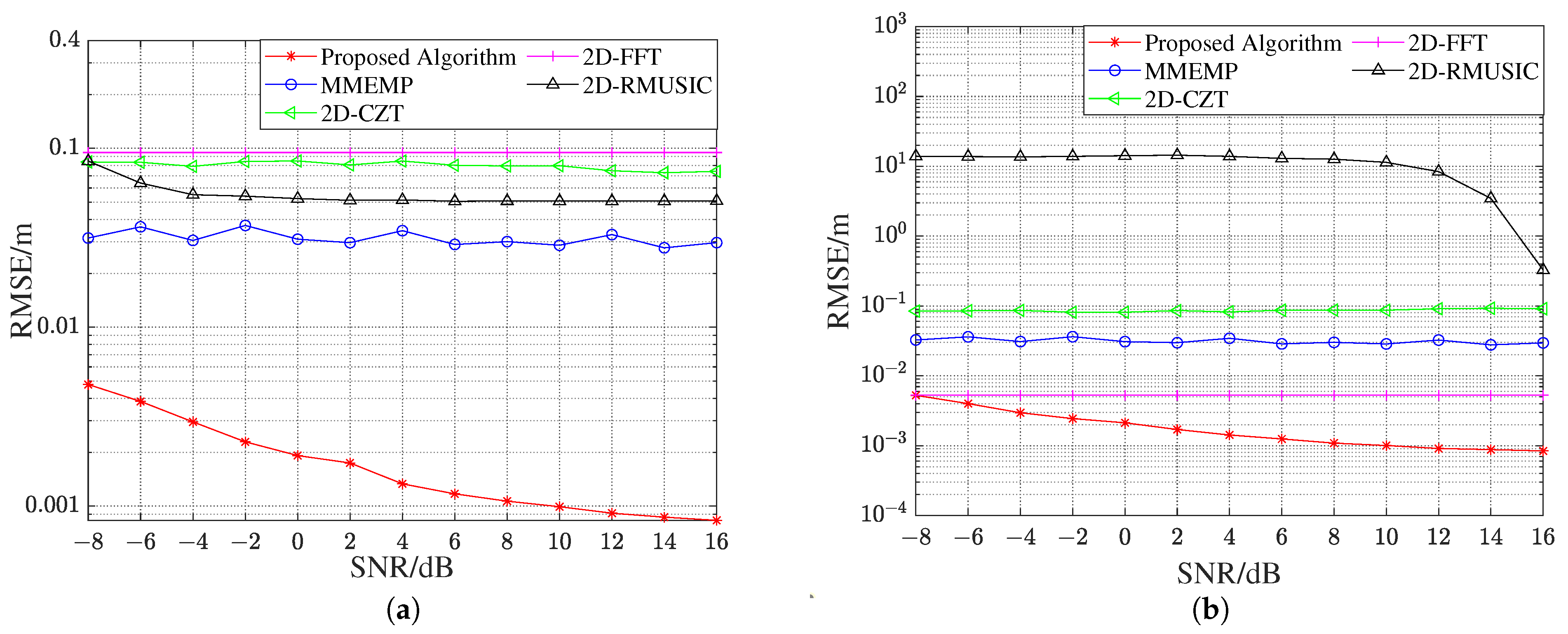
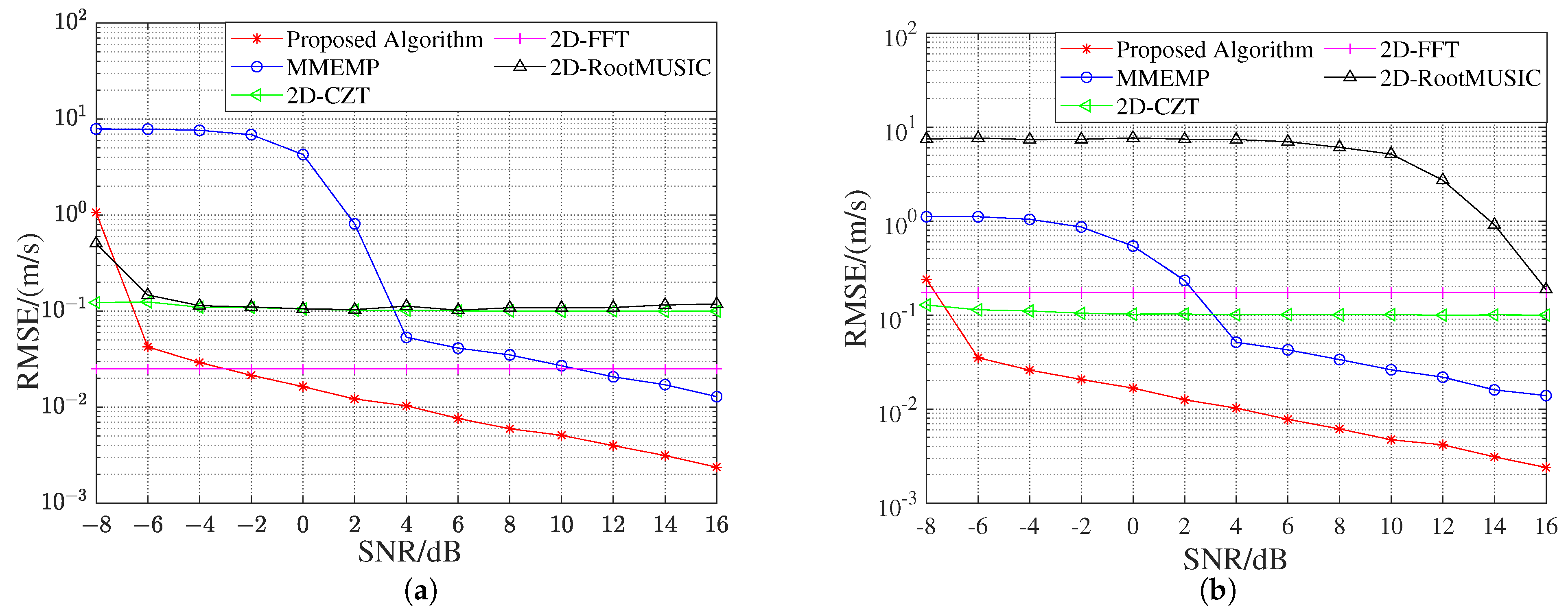
4.3. Resolution Comparison in the Multi-Target Scenario
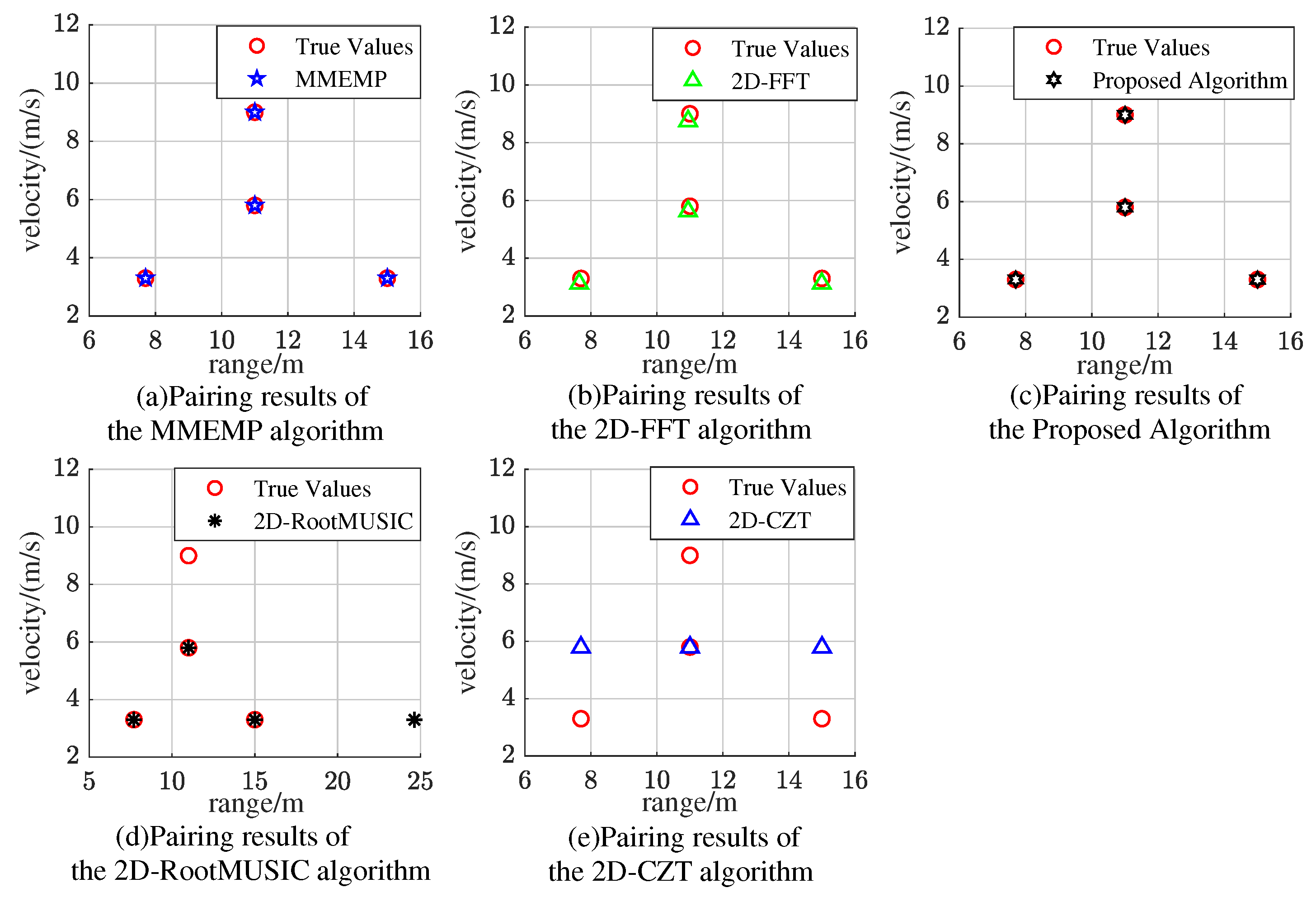
4.4. Range-Velocity Pairing Correctness Comparison in Multi-Target Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, Y.; Zhou, S. Analysis of ADAS Application and Scheme of 77G Millimeter Wave Radar. Automot. Dig. 2020, 3, 15–23. [Google Scholar] [CrossRef]
- Wang, R.; Wu, J.; Xu, H. A Review of Research and Application of Perception System Simulation for Autonomous Vehicles. J. Syst. Simul. 2022, 34, 2507–2521. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W.; Rao, Y.; Huang, Y.; Guan, J.; Dong, Y. Progress and prospects of radar target detection and recognition technology for flying birds and unmanned aerial vehicles. J. Radars 2020, 9, 803–827. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, R.; Zhou, D.; Yang, W.; Huang, Z.; Qi, H. Research on multi-target recognition and measurement algorithm of automobile collision avoidance radar. Acta Metrol. Sin. 2017, 38, 106–111. [Google Scholar]
- Mutschler, M.A.; Scharf, P.A.; Rippl, P.; Gessler, T.; Walter, T.; Waldschmidt, C. River surface analysis and characterization using FMCW radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2493–2502. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Chen, K. Advances in frequency modulated continuous wave lidar technology. Vac. Electron. Technol. 2019, 341, 18–26+40. [Google Scholar] [CrossRef]
- Song, M.; Lim, J.; Shin, D.J. The velocity and range detection using the 2D-FFT scheme for automotive radars. In Proceedings of the 2014 4th IEEE International Conference on Network Infrastructure and Digital Content, Piscataway, NJ, USA, 19–21 September 2014; pp. 507–510. [Google Scholar]
- Sun, B.; Shen, T.; Jia, L.; Li, H.; Cui, X.; Chen, Y. Dynamic Threshold Calculation for Millimeter Wave Radar Based on Environmental Noise. Laser Optoelectron. Prog. 2021, 58, 0328002–328002287. [Google Scholar]
- Rife, D.C.; Vincent, G. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones. Bell Syst. Tech. J. 1970, 49, 197–228. [Google Scholar] [CrossRef]
- Ye, M.; Liu, H.; Zhao, Y.; Sun, Z.; Hu, B. Design and hardware implementation of modified Rife algorithm for FMCW LiDAR. Infrared Laser Eng. 2022, 51, 20220222. [Google Scholar]
- Ma, L.; Jia, H.; Liu, S.; Khan, I.U. Low-complexity Doppler compensation algorithm for underwater acoustic OFDM systems with nonuniform Doppler shifts. IEEE Commun. Lett. 2020, 24, 2051–2054. [Google Scholar] [CrossRef]
- Niu, W.; Zhang, A.; Pan, L.; Li, S.; Wang, Z. A high-accuracy measuring method of beam center velocity in continuous wave radar. Chin. Space Sci. Technol. 2022, 42, 61. [Google Scholar]
- Chen, T.; Cui, R.; Guo, L. Improved Algorithm for MUSIC Applicable to Single Snapshots. J. Jilin Univ. 2018, 48, 952–956. [Google Scholar] [CrossRef]
- Kintz, A.L.; Gupta, I.J. A Modified MUSIC Algorithm for Direction of Arrival Estimation in the Presence of Antenna Array Manifold Mismatch. IEEE Trans. Antennas Propag. 2016, 64, 4836–4847. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Lemma, A.N.; Van der Veen, A.J.; Deprettere, E.F. Multiresolution ESPRIT algorithm. IEEE Trans. Signal Process. 1999, 47, 1722–1726. [Google Scholar] [CrossRef]
- Yuan, T.; Ge, J.; Zheng, Q. A Method for Improving the Accuracy of Target Detection in Continuous Wave Radar. Radar Sci. Technol. 2020, 18, 124–128. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, T.; Xu, Z.; Shi, J.; Sun, L. A Novel Method for Multi-Moving Target Detection in LFMCW Radar. Radar Sci. Technol. 2018, 16, 411–415. [Google Scholar]
- Wang, X.; Zhong, Q.; Yan, H.; Zhang, D. An improved MUSIC algorithm for two dimensional direction of arrival estimation. J. Electron. Inf. Technol. 2019, 41, 2137–2142. [Google Scholar]
- Zhang, H.; Tong, Q. Two-dimensional Root-MUSIC Direction Estimation Based on an L-shaped Array. Electron. Sci. Technol. 2015, 28, 11–13. [Google Scholar] [CrossRef]
- Rouquette, S.; Najim, M. Estimation of frequencies and damping factors by two-dimensional ESPRIT type methods. IEEE Trans. Signal Process. 2001, 49, 237–245. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, S.; Xi, Z.; Ge, Q.; Zong, B. GTD model parameters estimation and rcs reconstruction based on the improved LS-ESPRIT algorithm. J. Electron. Inf. Technol. 2020, 42, 2493–2499. [Google Scholar]
- Chen, F.J.; Fung, C.C.; Kok, C.W.; Kwong, S. Estimation of two-dimensional frequencies using modified matrix pencil method. IEEE Trans. Signal Process. 2007, 55, 718–724. [Google Scholar] [CrossRef]
- Sun, Y.; Fei, T.; Pohl, N. A high-resolution framework for range-Doppler frequency estimation in automotive radar systems. IEEE Sens. J. 2019, 19, 11346–11358. [Google Scholar] [CrossRef]
- Hua, Y. Estimating two-dimensional frequencies by matrix enhancement and matrix pencil. IEEE Trans. Signal Process. 1992, 40, 2267–2280. [Google Scholar] [CrossRef]
- Chen, Y.M. On spatial smoothing for two-dimensional direction-of-arrival estimation of coherent signals. IEEE Trans. Signal Process. 1997, 45, 1689–1696. [Google Scholar] [CrossRef]
- Kim, B.S.; Jin, Y.; Lee, J.; Kim, S. FMCW Radar Estimation Algorithm with High Resolution and Low Complexity Based on Reduced Search Area. Sensors 2022, 22, 1202. [Google Scholar] [CrossRef]
- Chintagunta, S. Joint 2D-DOA estimation of coherent targets using EV sensors in MIMO radar. Signal Process. 2022, 201, 108715. [Google Scholar] [CrossRef]
- Qiu, S.; Ma, X.; Zhang, R.; Han, Y.; Sheng, W. A dual-resolution unitary ESPRIT method for DOA estimation based on sparse co-prime MIMO radar. Signal Process. 2023, 202, 108753. [Google Scholar] [CrossRef]
- Li, Y. Research on Multi-Dimensional Parameter Joint Estimation Algorithm Based on FMCW Radar; Chongqing University of Posts and Telecommunications: Chongqing, China, 2020. [Google Scholar]
- Zoltowski, M.; Haardt, M.; Mathews, C. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT. IEEE Trans. Signal Process. 1996, 44, 316–328. [Google Scholar] [CrossRef]
- Xu, H.; Wang, D.; Ba, B.; Cui, W.; Zhang, Y. Direction-of-arrival estimation for both uncorrelated and coherent signals in coprime array. IEEE Access 2019, 7, 18590–18600. [Google Scholar] [CrossRef]
- Haardt, M.; Zoltowski, M.D.; Mathews, C.P.; Nossek, J. 2D unitary ESPRIT for efficient 2D parameter estimation. In Proceedings of the 1995 International Conference on Acoustics, Speech, and Signal Processing, Detroit, MI, USA, 9–12 May 1995; Volume 3, pp. 2096–2099. [Google Scholar]





| Parameters | Values |
|---|---|
| Sampling rate kHz | 813.16 |
| Sampling points N | 256 |
| Number of linear frequency modulation M | 32 |
| Carrier frequency /GHz | 23.8 |
| Bandwidth B/MHz | 200.47055 |
| Linear FM period /ms | 0.31482 |
| Speed of electromagnetic waves (km/s) | 299,709 |
| Fast time domain spatial smoothing length | 128 |
| Slow time domain spatial smoothing length | 16 |
| Preset R0/m and v0/(m/s) | RMSE of R0/m and v0/(m/s) | ||||
|---|---|---|---|---|---|
| 2D-FFT | 2D-CZT | 2D-RootMUSIC | MMEMP | Proposed | |
| Algorithm | |||||
| = 22 m | 0.322100 | 0.004764 | 0.015790 | 0.001526 | 0.001526 |
| = 2 m/s | 0.437500 | 0.016009 | 0.022567 | 0.002876 | 0.002872 |
| = 90 m | 0.298346 | 0.008075 | 0.008887 | 0.001655 | 0.001656 |
| = 20 m/s | 0.312500 | 0.024992 | 0.021406 | 0.003242 | 0.003240 |
| = 32 m | 0.143093 | 0.005348 | 0.010997 | 0.000681 | 0.000678 |
| = −5 m/s | 0.312500 | 0.040518 | 0.058606 | 0.002764 | 0.002762 |
| = 78 m | 0.258566 | 0.006998 | 0.015488 | 0.001759 | 0.001761 |
| = −13 m/s | 0.500000 | 0.020319 | 0.022531 | 0.002142 | 0.002136 |
| Preset R0/m and v0/(m/s) | RMSE of R0/m and v0/(m/s) | ||||
|---|---|---|---|---|---|
| 2D-FFT | 2D-CZT | 2D-RootMUSIC | MMEMP | Proposed | |
| Algorithm | |||||
| = 22 m | 0.322100 | 0.026561 | 0.685941 | 0.018371 | 0.018137 |
| = 2 m/s | 0.437500 | 0.233469 | 3.55283 | 0.043890 | 0.043179 |
| = 90 m | 0.334004 | 0.049870 | 0.753553 | 0.015121 | 0.015405 |
| = 20 m/s | 0.312500 | 0.203403 | 18.63478 | 0.019307 | 0.019125 |
| = 32 m | 0.143093 | 0.066198 | 1.16336 | 0.013487 | 0.013138 |
| = −5 m/s | 0.312500 | 0.437058 | 12.319505 | 0.008981 | 0.008957 |
| = 78 m | 0.258566 | 0.053769 | 0.468652 | 0.018281 | 0.017876 |
| = −13 m/s | 0.500000 | 0.558930 | 15.504426 | 0.028887 | 0.028395 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, D.; Yi, H.; Zhang, W.; Xu, H. 2D-Unitary ESPRIT Based Multi-Target Joint Range and Velocity Estimation Algorithm for FMCW Radar. Appl. Sci. 2023, 13, 10448. https://doi.org/10.3390/app131810448
Wen D, Yi H, Zhang W, Xu H. 2D-Unitary ESPRIT Based Multi-Target Joint Range and Velocity Estimation Algorithm for FMCW Radar. Applied Sciences. 2023; 13(18):10448. https://doi.org/10.3390/app131810448
Chicago/Turabian StyleWen, Dan, Huiyue Yi, Wuxiong Zhang, and Hui Xu. 2023. "2D-Unitary ESPRIT Based Multi-Target Joint Range and Velocity Estimation Algorithm for FMCW Radar" Applied Sciences 13, no. 18: 10448. https://doi.org/10.3390/app131810448
APA StyleWen, D., Yi, H., Zhang, W., & Xu, H. (2023). 2D-Unitary ESPRIT Based Multi-Target Joint Range and Velocity Estimation Algorithm for FMCW Radar. Applied Sciences, 13(18), 10448. https://doi.org/10.3390/app131810448





