Dynamic Analysis of Train–Bridge Coupling System for a Long-Span Railway Suspension Bridge Subjected to Strike–Slip Fault
Abstract
:1. Introduction
2. Train–Bridge System under Earthquake
3. Numerical Analysis
3.1. Configurations of HSRDTSTSB
3.2. Bridge and Track Model
3.3. Train and Wheel–Rail Contact Model
3.4. Rail Irregularity
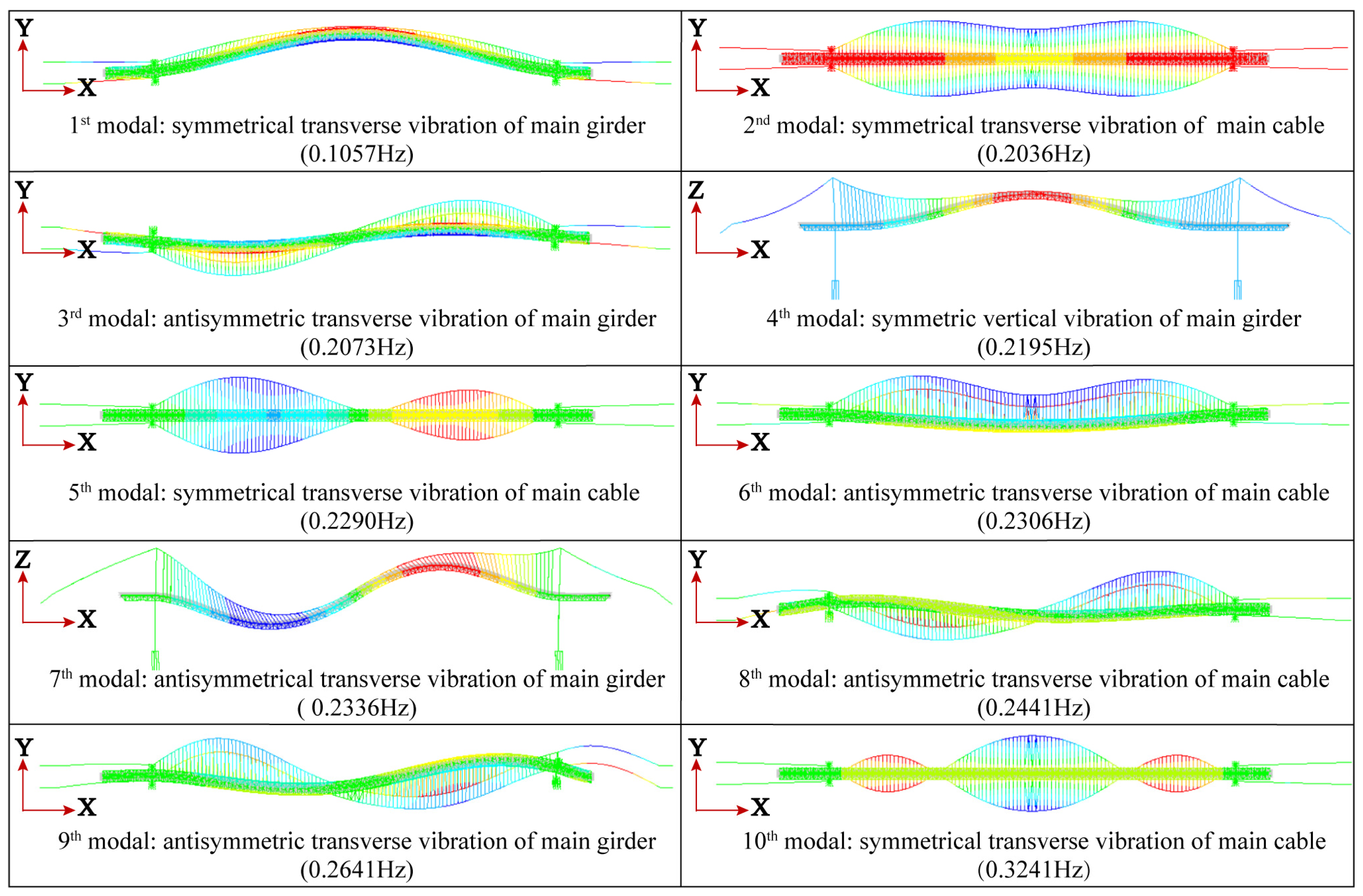
3.5. Vibration Characteristics
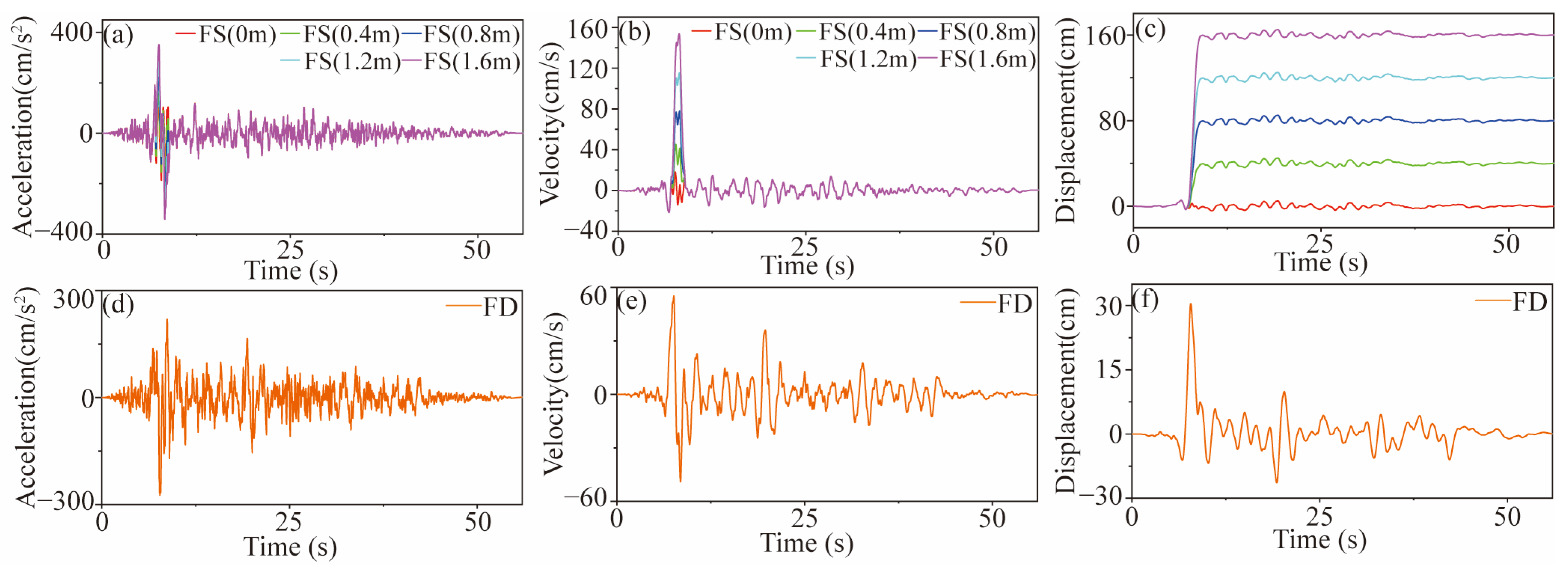
3.6. Generation of Ground Motions on Both Sides of a Strike–Slip Fault
4. Results and Discussion
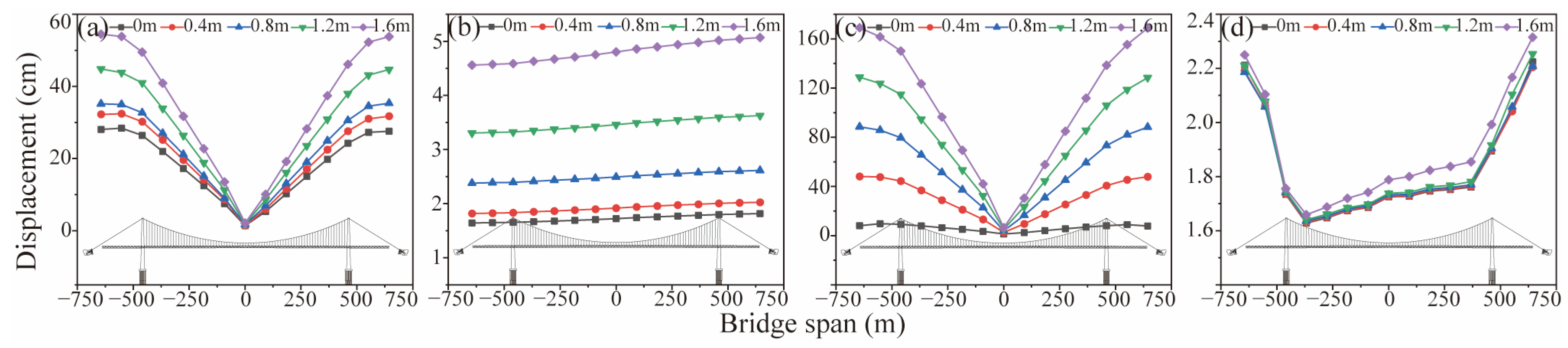
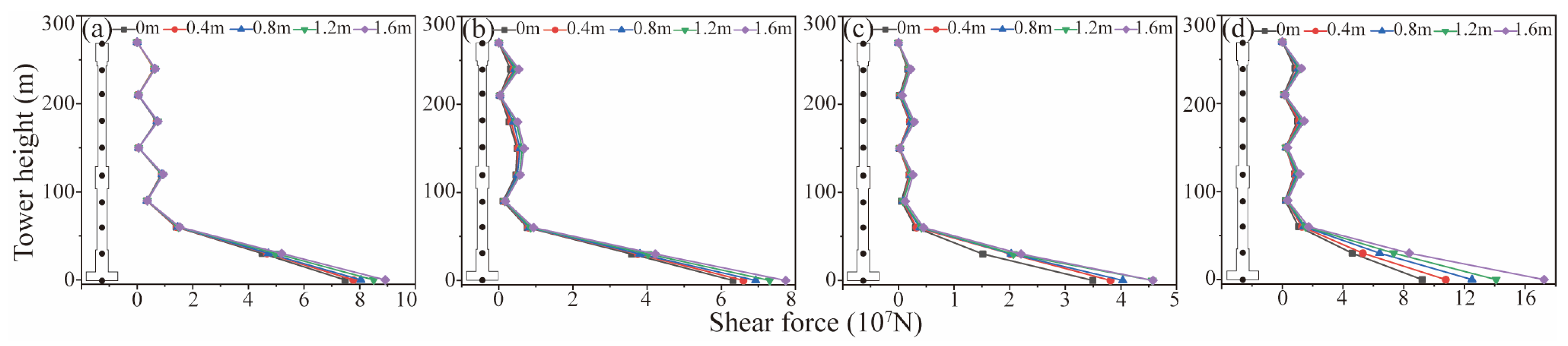
4.1. Dynamic Response of Bridge
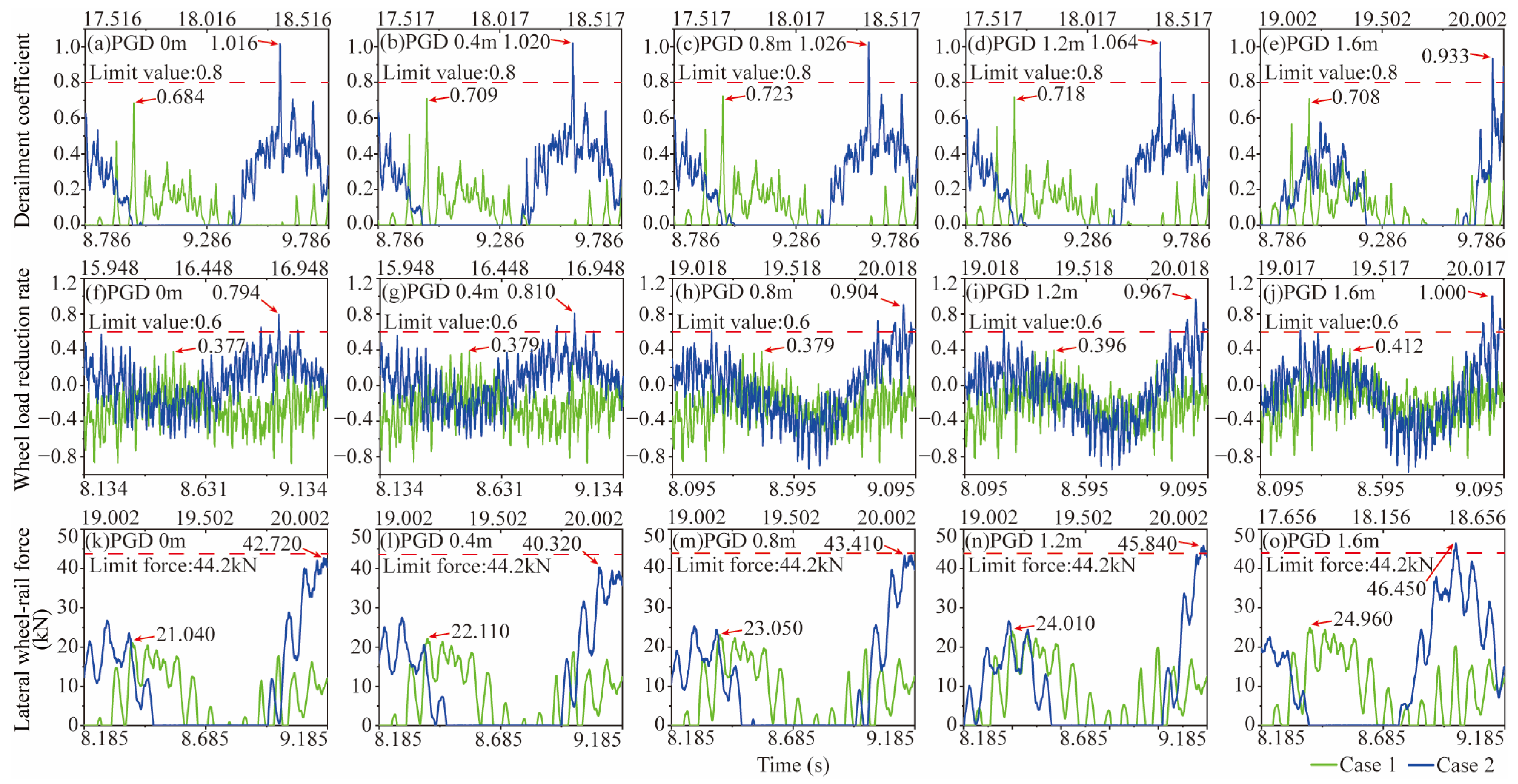
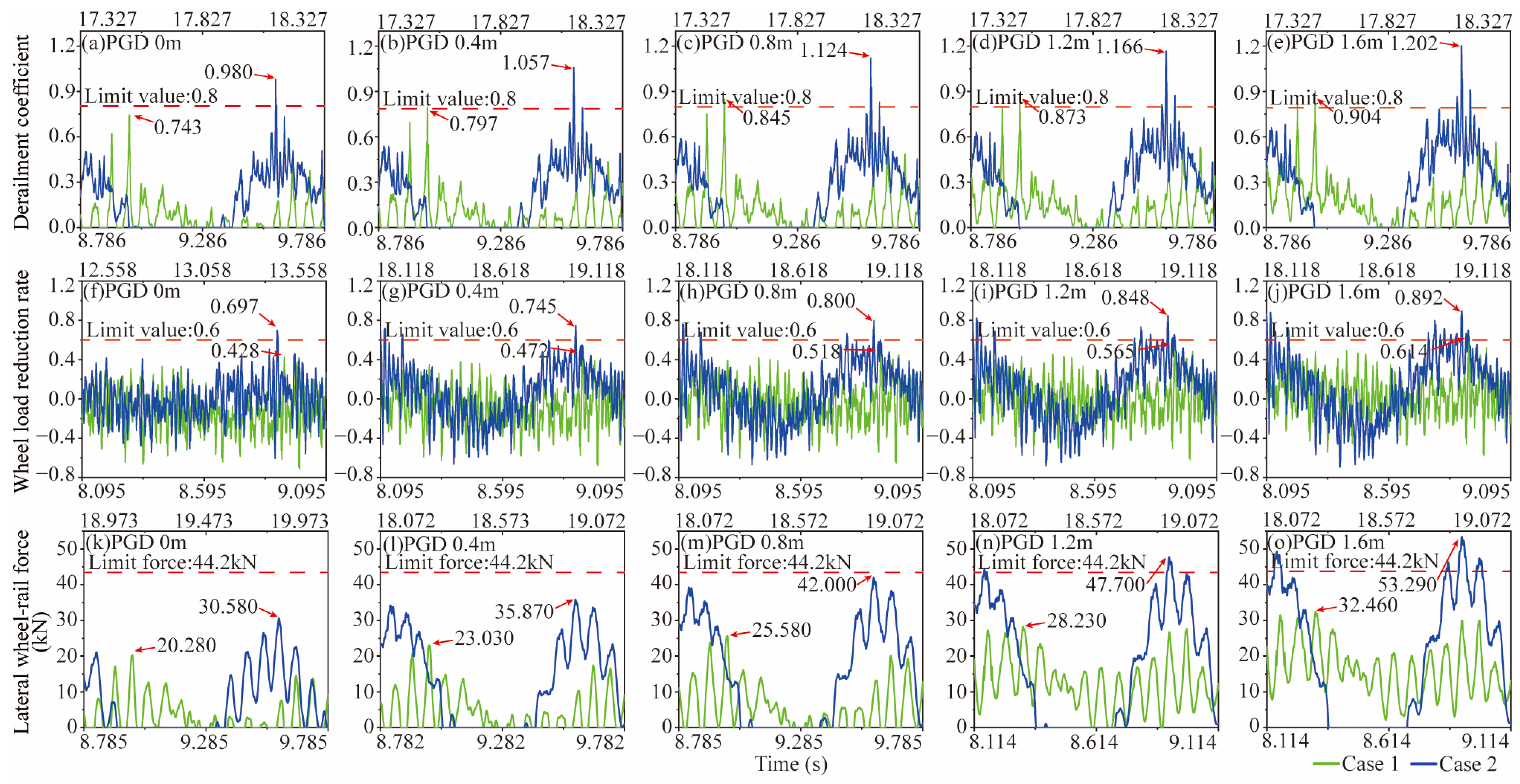
4.2. Dynamic Response of Train
5. Conclusions
- (1)
- For long-span suspension bridges crossing left-lateral strike–slip faults, it is crucial to emphasize the substantial impact of the fling-step effect on PGRD, leading to amplified bridge responses. This effect is particularly pronounced in the transverse response at FCA = 90° and significantly influences the longitudinal response at lower FCA values. Consequently, PGRD plays a pivotal role in seismic bridge responses, with a direct correlation between the magnitude of the response and PGRD.
- (2)
- It is imperative to underscore the critical consequences of lateral seismic motion during fault dislocation, which profoundly affects the dynamic parameters of trains. In contrast, the influence of longitudinal seismic motion on the derailment coefficient is relatively minor. However, as seismic motion persists, longitudinal ground motion can lead to vertical displacements in the main beam, potentially causing the wheel-load-reduction rate to surpass permissible limits.
- (3)
- Within the context of strike–slip faults, it is worth noting that PGRD resulting from fault slips is predominantly governed by the low-frequency components of seismic waves, accounting for approximately 70% of its impact on train dynamic parameters. This underscores the necessity for trains to traverse large-span bridges before PGRD reaches its full formation to significantly mitigate dynamic indicators.
- (4)
- Continuing to emphasize the importance of timing, if trains persist in traversing the bridge after the complete formation of PGRD, they will encounter a compounded effect. This effect combines additional track irregularities induced by PGRD with the high-frequency components of seismic waves, resulting in a progressive escalation of dynamic parameters that may ultimately breach established safety limits.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, T.; Yuan, X.; Zhong, J.; Yuan, W. Near-fault pulse seismic ductility spectra for bridge columns based on machine learning. Soil Dyn. Earthq. Eng. 2023, 164, 107582. [Google Scholar] [CrossRef]
- Chen, X.; Xiang, N.; Li, J.; Guan, Z. Influence of near-fault pulse-like motion characteristics on seismic performance of tall pier bridges with fragility analysis. J. Earthq. Eng. 2020, 26, 2001–2022. [Google Scholar] [CrossRef]
- Ucak, A.; Mavroeidis, G.P.; Tsopelas, P. Behavior of a seismically isolated bridge crossing a fault rupture zone. Soil Dyn. Earthq. Eng. 2014, 57, 164–178. [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Wang, J.; Zhang, J. Effects of fault rupture on seismic responses of fault-crossing simply-supported highway bridges. Eng. Struct. 2020, 206, 110104. [Google Scholar] [CrossRef]
- Gu, Y.; Guo, J.; Dang, X.; Yuan, W. Seismic performance of a cable-stayed bridge crossing strike-slip faults. Structures 2022, 35, 289–302. [Google Scholar] [CrossRef]
- Lin, Y.; Zong, Z.; Bi, K.; Hao, H.; Lin, J.; Chen, Y. Experimental and numerical studies of the seismic behavior of a steel-concrete composite rigid-frame bridge subjected to the surface rupture at a thrust fault. Eng. Struct. 2020, 205, 110105. [Google Scholar] [CrossRef]
- Yang, S.; Mavroeidis, G.P.; Tsopelas, P. Seismic response study of ordinary and isolated bridges crossing strike-slip fault rupture zones. Earthq. Eng. Struct. Dyn. 2021, 50, 2841–2862. [Google Scholar] [CrossRef]
- Cong, Z.E.; Hui, J.I.; Lei, H.U.; Hui, G.U.; Xin-yi, M.A.; Guang-song, S.O. Nonlinear seismic response characteristics of fault-crossing single-tower cable-stayed bridge. China J. Highw. Transp. 2021, 34, 230–245. [Google Scholar]
- Gong, W.; Zhu, Z.; Wang, K.; Yang, W.; Bai, Y.; Ren, J. A real-time co-simulation solution for train–track–bridge interaction. J. Vib. Control 2021, 27, 1606–1616. [Google Scholar] [CrossRef]
- Zhang, N.; Tian, Y.; Xia, H. A Train-Bridge Dynamic Interaction Analysis Method and Its Experimental Validation. Engineering 2016, 2, 528–536. [Google Scholar] [CrossRef]
- Jiang, L.; Peng, K.; Yu, J.; Zhou, W.; Zuo, Y. The influence of trains on the seismic response of simply-supported beam bridges with different pier heights expressed through an impact factor. Bull. Earthq. Eng. 2022, 20, 2795–2814. [Google Scholar] [CrossRef]
- Jin, Z.; Liu, W.; Pei, S. Probabilistic evaluation of railway vehicle’s safety on bridges under random earthquake and track irregularity excitations. Eng. Struct. 2022, 266, 114527. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Xiang, P.; Jiang, L.; Lai, Z. Safety and comfort assessment of a train passing over an earthquake-damaged bridge based on a probability model. Struct. Infrastruct. Eng. 2023, 19, 525–536. [Google Scholar] [CrossRef]
- Hu, Z.; Wei, B.; Jiang, L.; Li, S.; Min, H. Track structural damage index for high-speed railway girder bridges considering residual deformations due to earthquake. Bull. Earthq. Eng. 2022, 20, 6587–6609. [Google Scholar] [CrossRef]
- Zeng, Z.P.; Zhao, Y.G.; Xu, W.T.; Yu, Z.W.; Chen, L.K.; Lou, P. Random vibration analysis of train–bridge under track irregularities and traveling seismic waves using train–slab track–bridge interaction model. J. Sound Vib. 2015, 342, 22–43. [Google Scholar] [CrossRef]
- Zhu, D.Y.; Zhang, Y.H.; Kennedy, D.; Williams, F.W. Stochastic vibration of the vehicle-bridge system subject to non-uniform ground motions. Veh. Syst. Dyn. 2014, 52, 410–428. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, H.; De Roeck, G. Dynamic analysis of a train-bridge system under multi-support seismic excitations. J. Mech. Sci. Technol. 2010, 24, 2181–2188. [Google Scholar] [CrossRef]
- Xia, H.; Han, Y.; Zhang, N.; Guo, W. Dynamic analysis of train–bridge system subjected to non-uniform seismic excitations. Earthq. Eng. Struct. Dyn. 2006, 35, 1563–1579. [Google Scholar] [CrossRef]
- Gao, X.; Duan, P.; Qian, H. Dynamic Response Analysis of Long-Span Continuous Bridge Considering the Effect of Train Speeds and Earthquakes. Int. J. Struct. Stab. Dyn. 2020, 20, 2040013. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Ouyang, H. Influence of Random Multi-Point Seismic Excitations on the Safety Performance of a Train Running on a Long-Span Bridge. Int. J. Struct. Stab. Dyn. 2020, 20, 2050054. [Google Scholar] [CrossRef]
- Ma, C.; Choi, D. Stochastic dynamic analysis of the train-track-bridge system under tridirectional spatially correlated ground motions. Soil Dyn. Earthq. Eng. 2022, 160, 107324. [Google Scholar] [CrossRef]
- Gong, W.; Zhu, Z.; Liu, Y.; Liu, R.; Tang, Y.; Jiang, L. Running safety assessment of a train traversing a three-tower cable-stayed bridge under spatially varying ground motion. Railw. Eng. Sci. 2020, 28, 184–198. [Google Scholar] [CrossRef]
- Qiao, H.; Dai, Z.; Du, X.; Wang, C.; Long, P.; Jiao, C. Parametric study of topographic effect on train-bridge interaction of a continuous rigid frame bridge during earthquakes. Bull. Earthq. Eng. 2023, 21, 125–149. [Google Scholar] [CrossRef]
- Qiao, H.; Du, X.; Xia, H.; De Roeck, G.; Lombaert, G.; Long, P. The effect of local topography on the seismic response of a coupled train-bridge system. Struct. Eng. Mech. 2019, 69, 177–191. [Google Scholar]
- Chen, L.K.; Jiang, L.Z.; Qin, H.X.; Zhang, N.; Ling, L.; Zhang, Q.H.; Li, Q.; Cao, D.F. Nonlinear seismic assessment of isolated high-speed railway bridge subjected to near-fault earthquake scenarios. Struct. Infrastruct. Eng. 2019, 15, 1529–1547. [Google Scholar] [CrossRef]
- Chen, L.K.; Kurtulus, A.; Dong, Y.F.; Taciroglu, E.; Jiang, L.Z. Velocity pulse effects of near-fault earthquakes on a high-speed railway vehicle-ballastless track-benchmark bridge system. Veh. Syst. Dyn. 2022, 60, 2963–2987. [Google Scholar] [CrossRef]
- Zhou, T.; Jiang, L.; Xiang, P.; Liu, X. Effects of near-fault pulse-type ground motion on train–track–bridge coupled system with nonlinear supports. Nonlinear Dyn. 2023, 111, 6213–6238. [Google Scholar] [CrossRef]
- Yu, J.; Jiang, L.; Zhou, W.; Liu, X.; Lai, Z.; Feng, Y. Study on the dynamic response correction factor of a coupled high-speed train-track-bridge system under near-fault earthquakes. Mech. Based Des. Struct. Mach. 2022, 50, 3303–3321. [Google Scholar] [CrossRef]
- Jiang, H.; Zeng, C.; Peng, Q.; Li, X.; Ma, X.Y.; Song, G.S. Running safety and seismic optimization of a fault-crossing simply-supported girder bridge for high-speed railways based on a train-track-bridge coupling system. J. Cent. South Univ. 2022, 29, 2449–2466. [Google Scholar] [CrossRef]
- LS-DYNA. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2021. [Google Scholar]
- Wanming, Z.; He, X. Train-Track-Bridge Dynamic Interaction: Theory and Engineering Appliction; Science Press: Beijing, China, 2011. [Google Scholar]
- Shen, Y.; Li, J.; Freddi, F.; Igarashi, A.; Zhou, J. Numerical investigation of transverse steel damper (TSD) seismic system for suspension bridges considering pounding between girder and towers. Soil Dyn. Earthq. Eng. 2022, 155, 107203. [Google Scholar] [CrossRef]
- Li, R.; Yuan, X.; Yuan, W.; Dang, X.; Shen, G. Seismic analysis of half-through steel truss arch bridge considering superstructure. Struct. Eng. Mech. 2016, 59, 387–401. [Google Scholar] [CrossRef]
- Ying, W.; Ouyang, Z.; Ke, J.; Han, T. Study on the eccentricity between the ballast track and supporting bridge under the action of moving trains. J. Railw. Sci. Eng. 2021, 18, 2552–2560. (In Chinese) [Google Scholar]
- Wang, W.; Zhang, Y.; Ouyang, H. An iterative method for solving the dynamic response of railway vehicle-track coupled systems based on prediction of wheel-rail forces. Eng. Struct. 2017, 151, 297–311. [Google Scholar] [CrossRef]
- De Pater, D.A.; Kalker, J.J. On the rolling contact of two elastic bodies in the presence of dry friction. Wear 1968, 11, 303. [Google Scholar]
- Lei, X.; Wang, J. Dynamic analysis of the train and slab track coupling system with finite elements in a moving frame of reference. J. Vib. Control 2014, 20, 1301–1317. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, C.; Hsu, C. Derailment and Dynamic Analysis of Tilting Railway Vehicles Moving Over Irregular Tracks Under Environment Forces. Int. J. Struct. Stab. Dyn. 2017, 17, 1750098. [Google Scholar] [CrossRef]
- ICE Technology Assignment for Inter-City Express Train; Munich Research Center of German Federal Railway: Heidelberg, Germany, 1993.
- Kim, H.M.; Craig, R.R., Jr. Application of unsymmetric block Lanczos vectors in system identification. J. Vib. Control 1992, 7, 227–241. [Google Scholar]
- Abrahamson, N.A. Velocity Pulses in Near-Fault Ground Motions. In Proceedings of the UC Berkeley—CUREE Symposium in Honor of Ray Clough and Joseph Penzien, Berkeley, CA, USA, 9–11 May 2002; UC Berkeley: Consortium of Universities for Research in Earthquake Engineering: Berkeley, CA, USA, 2002. [Google Scholar]
- Thráinsson, H.; Kiremidjian, A.S. Simulation of digital earthquake accelerograms using the inverse discrete Fourier transform. Earthq. Eng. Struct. Dyn. 2002, 31, 2023–2048. [Google Scholar] [CrossRef]
- Jia, H.; Lan, X.; Zheng, S.; Li, L.P.; Liu, C.Q. Assessment on required separation length between adjacent bridge segments to avoid pounding. Soil Dyn. Earthq. Eng. 2019, 120, 398–407. [Google Scholar] [CrossRef]
- TB10621-2014; Code for Design of High-Speed Railway. China Railway Press: Beijing, China, 2015. (In Chinese)
- 95J01-L; High-Speed Test Train Power Car Strength and Dynamic Performance Specifications. China Railway Press: Beijing, China, 2014. (In Chinese)
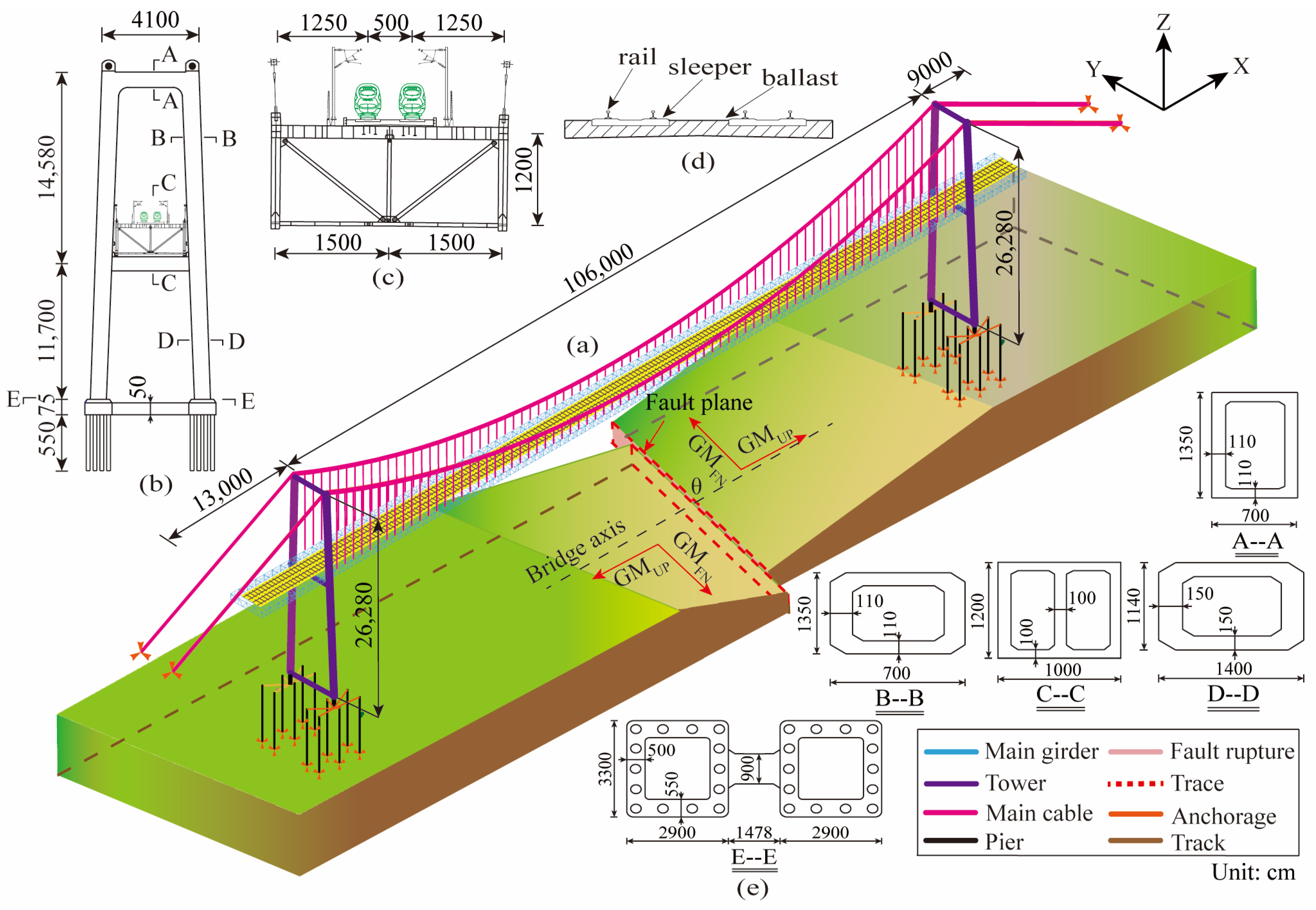
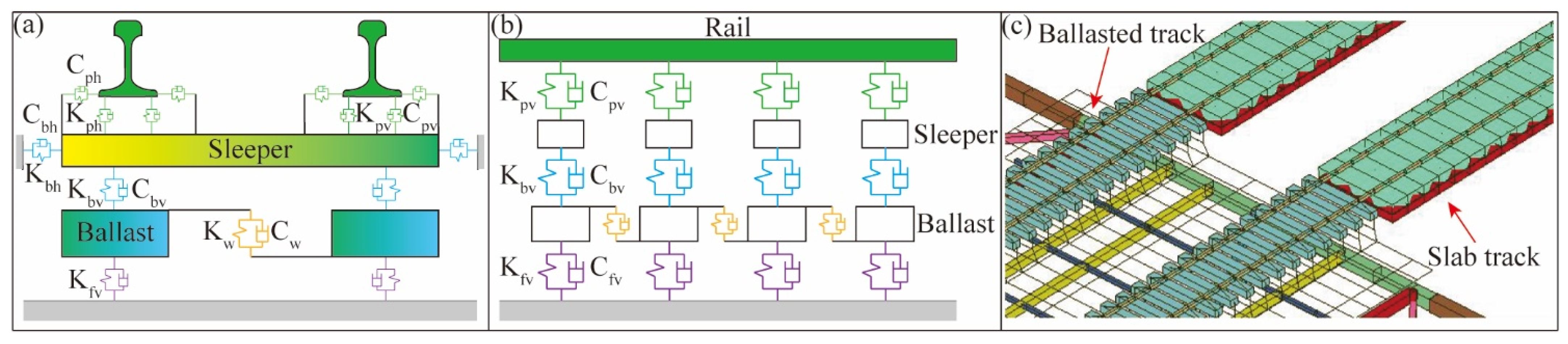
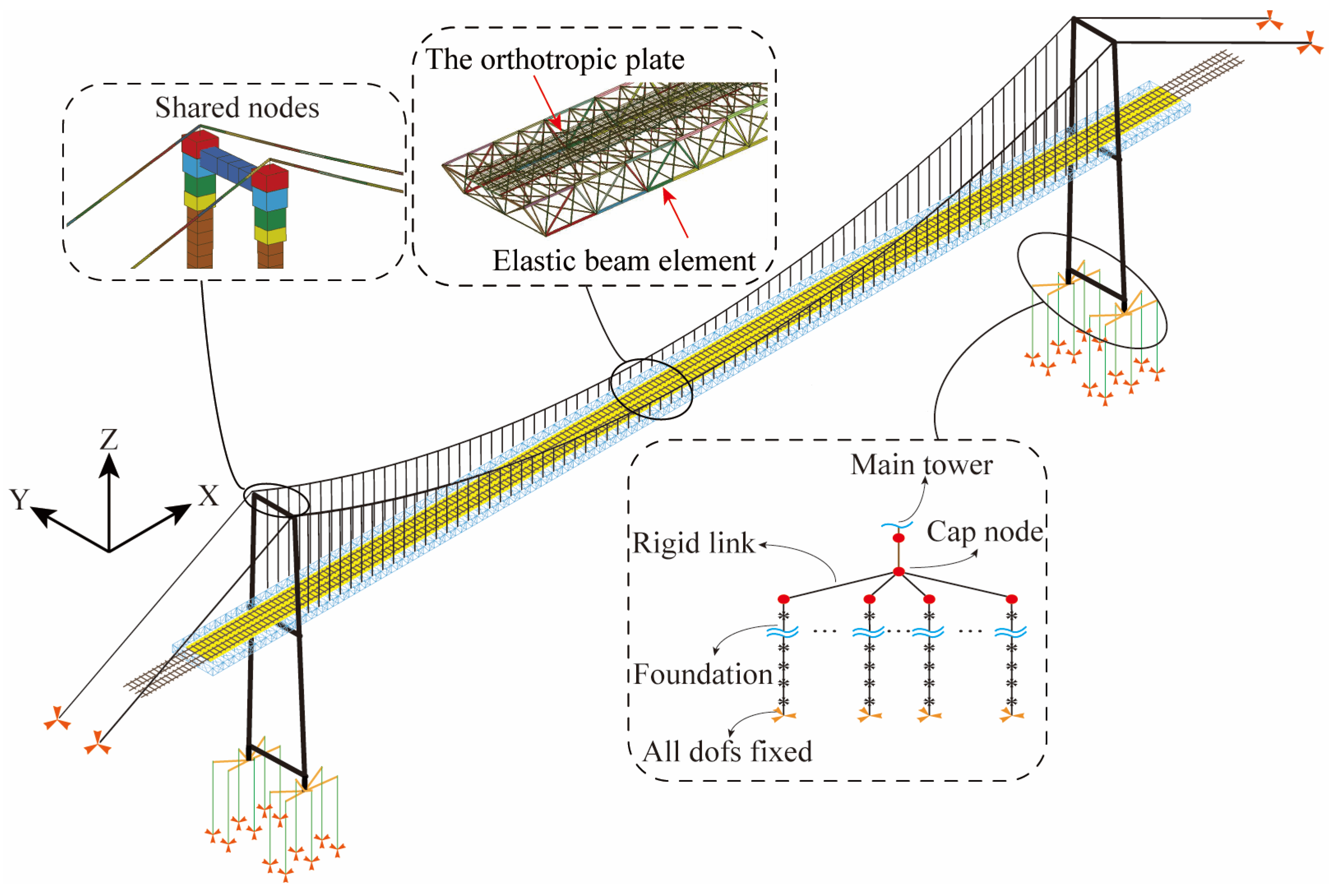
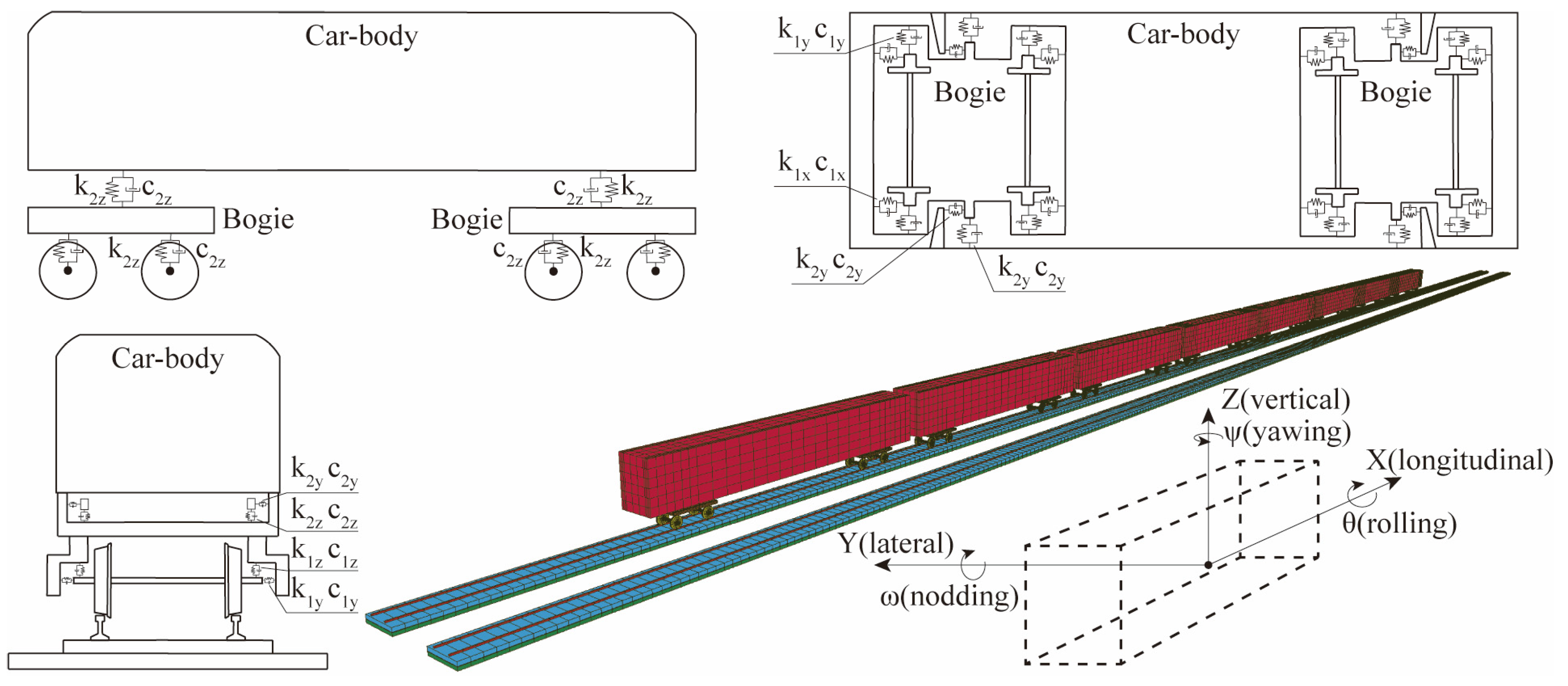




| LS-DYNA Model | Component | Parameter | Value |
|---|---|---|---|
| * MAT_ELASTIC (MAT_001) | Main girder/Rail | Young’s modulus | 210 GPa |
| Poisson’s ratio | 0.3 | ||
| Mass density | 7850 | ||
| Main tower | Young’s modulus | 34.5 GPa | |
| Poisson’s ratio | 0.2 | ||
| Mass density | 2420 | ||
| Cushion cap | Young’s modulus | 33.5 GPa | |
| Poisson’s ratio | 0.2 | ||
| Mass density | 2410 | ||
| Foundation | Young’s modulus | 31.5 GPa | |
| Poisson’s ratio | 0.2 | ||
| Mass density | 2390 | ||
| * MAT_CABLE_DISCRETE_BEAM (MAT_071) | Main cable | Young’s modulus | 200 GPa |
| Mass density | 8500 | ||
| Sling | Young’s modulus | 200 GPa | |
| Mass density | 8400 | ||
| * MAT_LINEAR_ELASTIC_DISCRETE _BEAM (MAT_066) | Track | Transversal stiffness of the fastener | |
| Transversal damper of the fastener | |||
| Vertical stiffness of the fastener | |||
| Vertical damper of the fastener | |||
| Transversal stiffness of the sleeper-ballast | |||
| Transversal damper of the sleeper-ballast | |||
| Vertical stiffness of the sleeper-ballast | |||
| Vertical damper of the sleeper-ballast | |||
| Stiffness of adjacent ballast | |||
| Damper of adjacent ballast | |||
| Vertical stiffness of the ballast-bridge | |||
| Vertical damper of the ballast-bridge |
| Location | Data | Station | Rupture Distance (km) | Component | PGA (cm/s2) | PGV (cm/s) | PGD (cm) | |
|---|---|---|---|---|---|---|---|---|
| Landers, CA, USA | 28 June 1992 | 7.2 | LUC | 1.1 | FN 206° | 702.5 | 64.8 | 64.5 |
| FP 296° | 672.8 | 141.4 | 258.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Kang, W.; Yang, J.; Dai, S.; Zheng, S.; Jia, H. Dynamic Analysis of Train–Bridge Coupling System for a Long-Span Railway Suspension Bridge Subjected to Strike–Slip Fault. Appl. Sci. 2023, 13, 10422. https://doi.org/10.3390/app131810422
Chen S, Kang W, Yang J, Dai S, Zheng S, Jia H. Dynamic Analysis of Train–Bridge Coupling System for a Long-Span Railway Suspension Bridge Subjected to Strike–Slip Fault. Applied Sciences. 2023; 13(18):10422. https://doi.org/10.3390/app131810422
Chicago/Turabian StyleChen, Sijie, Wei Kang, Jian Yang, Shengyong Dai, Shixiong Zheng, and Hongyu Jia. 2023. "Dynamic Analysis of Train–Bridge Coupling System for a Long-Span Railway Suspension Bridge Subjected to Strike–Slip Fault" Applied Sciences 13, no. 18: 10422. https://doi.org/10.3390/app131810422
APA StyleChen, S., Kang, W., Yang, J., Dai, S., Zheng, S., & Jia, H. (2023). Dynamic Analysis of Train–Bridge Coupling System for a Long-Span Railway Suspension Bridge Subjected to Strike–Slip Fault. Applied Sciences, 13(18), 10422. https://doi.org/10.3390/app131810422







