Weighted Group Sparse Regularized Tensor Decomposition for Hyperspectral Image Denoising
Abstract
:1. Introduction
- (1)
- Utilizing the global spatial and spectral correlation among hyperspectral images, the tensor ring decomposition technique is employed to segregate unpolluted hyperspectral images from raw observations that have been tainted with intricate noise.
- (2)
- Due to the fact that the gradient components in smooth areas of hyperspectral images typically exhibit a complete absence (a value of zero) in the spectral dimension, the gradient components in edge regions demonstrate non-zero values. Hence, to address this discrepancy, we incorporate a regularization term, with the group sparsity weighted, into the framework of tensor ring decomposition. It can explore the group structure of spatially differential images along the spectral dimension.
- (3)
- A symmetric alternating direction method multiplier is employed to solve the model of the low-rank tensor ring decomposition with regularization on weighted group sparsity. To enhance the efficiency of this method, a proximity point operator is incorporated. Through numerical experiments, it has been determined that this approach outperforms other commonly utilized methods in terms of both quantitative evaluation and visual comparison.
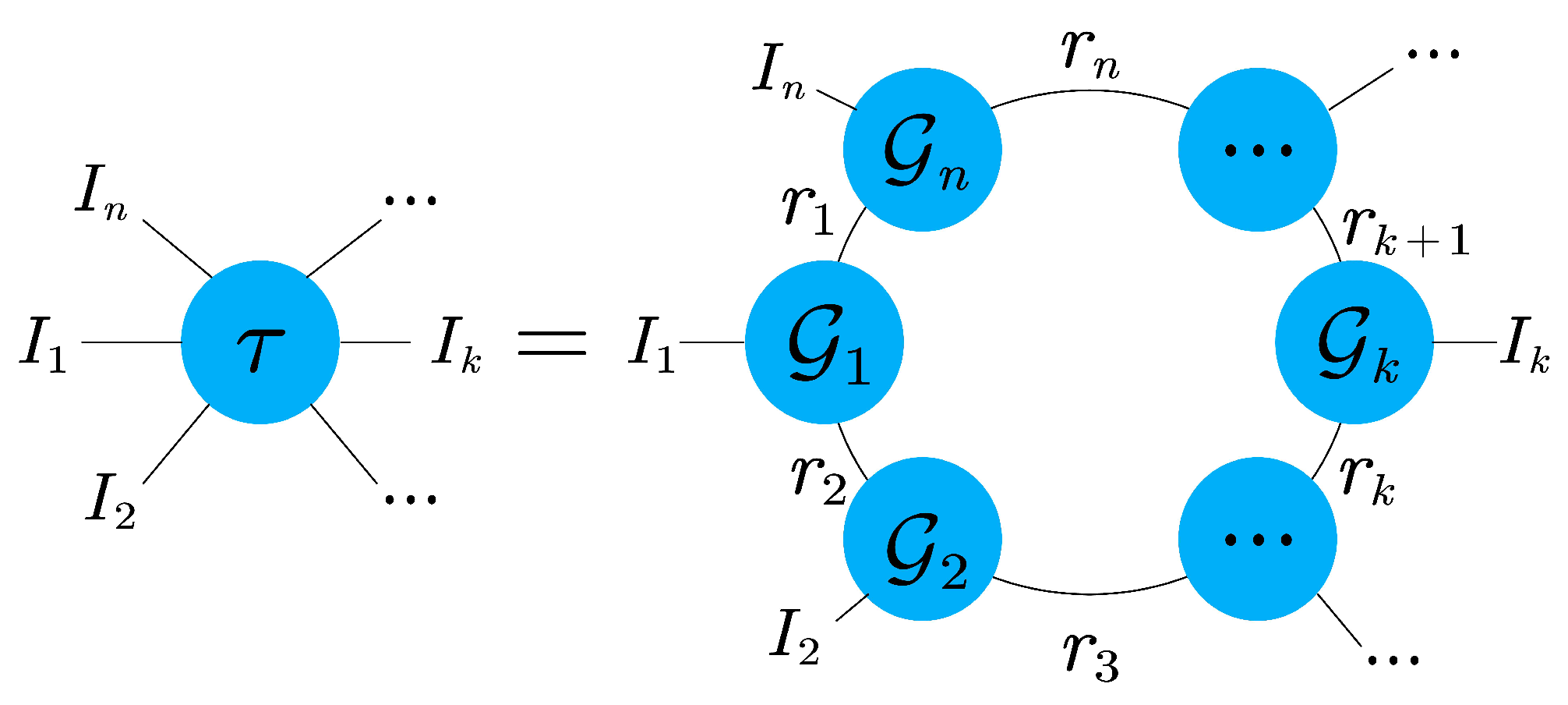
2. Notations and Tensor Ring
2.1. Notations
2.2. Tensor Ring
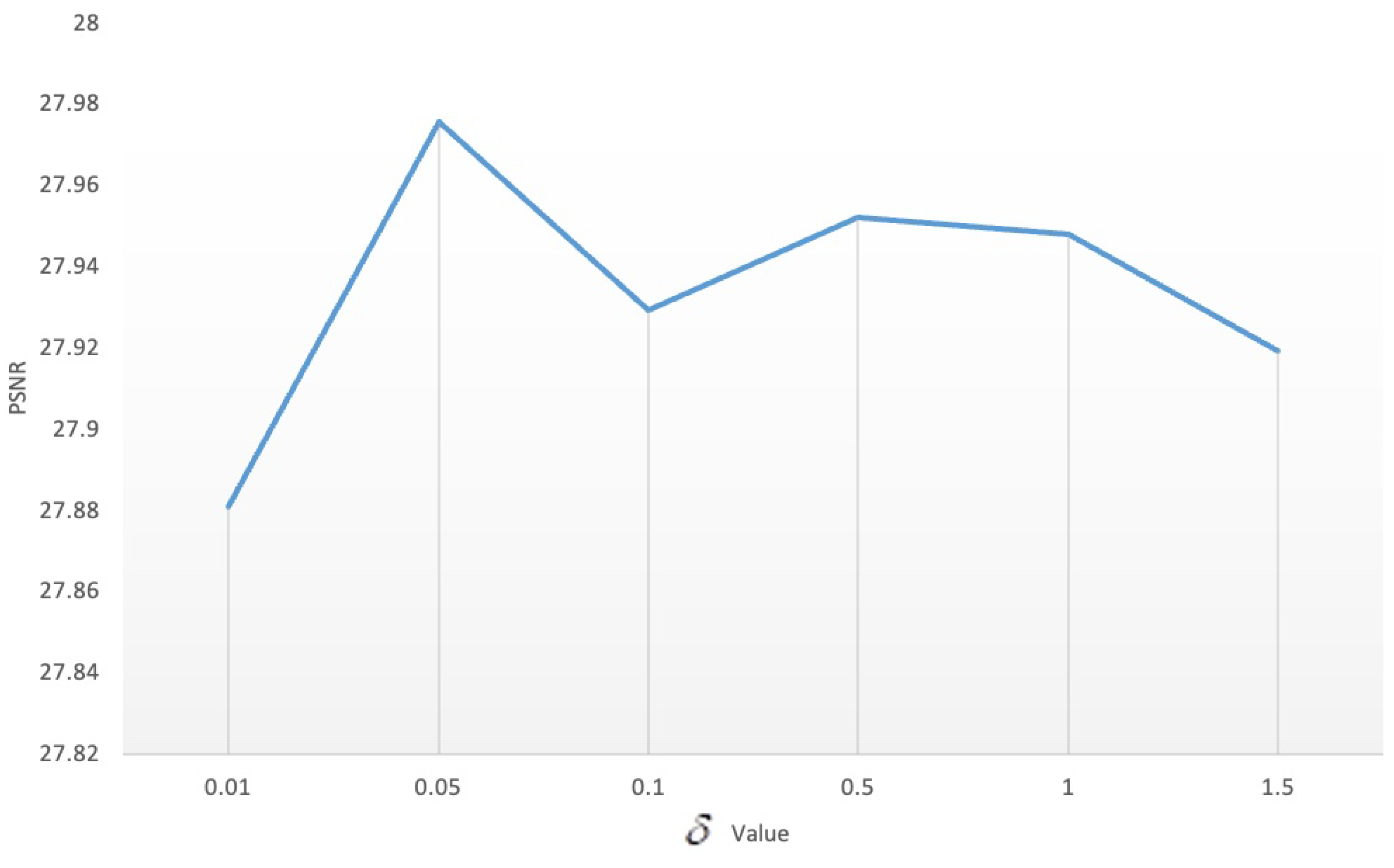
3. Proposed Method
| Algorithm 1 ADMM for HSI Denoising. |
|
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Name |
| FLIS | The Flying Laboratory of Imaging Systems |
| HSI | Hyperspectral Imaging |
| CP | Canonical Polyadic |
| t-SVD | Tensor Singular-Value Decomposition |
| LRTDGS | A Weighted Group Sparsity-Regularized Low-Rank Tensor Decomposition Mode |
| GCS | Global Correlation Across Spectrum |
| NLR-CPTD | A Nonlocal Low-Rank Regularized CP Tensor Decomposition Method |
| WSN-LRMA | Weighted Schatten -Norm Low-Rank Matrix Approximation |
| TR | Tensor Ring |
| TV | Total Variational |
| LRTV | Total Variational Regularized Low-Rank Matrix Decomposition |
| SSTV | Spectral–Spatial Total Variational Regularization |
| LLRSSTV | The Spatial–Spectral Total Variance Regularized Local Low-Rank Matrix Recovery Method |
| LRMR | Patchwise Low-Rank Matrix Approximation |
| TLR-SSTV | Spatial–Spectral Total Variation Regularized Local Low-Rank Tensor Recovery Model |
| FFT | Fast Fourier Transform |
| PSNR-HVS | The Peak Signal-to-Noise Ratio Based On the Characteristics of the Human Visual System |
| MSSIM | Mean Structural Similarity Index Measure |
| ERGAS | Erreur Relative Globale Adimensionnelle Desynthse |
References
- Stuart, M.B.; McGonigle, A.J.S.; Willmott, J.R. Hyperspectral Imaging in Environmental Monitoring: A Review of Recent Developments and Technological Advances in Compact Field Deployable Systems. Sensors 2019, 19, 3071. [Google Scholar] [CrossRef]
- Hanuš, J.; Slezák, L.; Fabiánek, T.; Fajmon, L.; Hanousek, T.; Janoutová, R.; Kopkáně, D.; Novotný, J.; Pavelka, K.; Pikl, M.; et al. Flying Laboratory of Imaging Systems: Fusion of Airborne Hyperspectral and Laser Scanning for Ecosystem Research. Remote Sens. 2023, 15, 3130. [Google Scholar] [CrossRef]
- Schodlok, M.C.; Frei1, M.; Segl, K. Implications of new hyperspectral satellites for raw materials exploration. Miner. Econ. 2022, 35, 495–502. [Google Scholar] [CrossRef]
- Avola, G.; Matese, A.; Riggi, E. Precision Agriculture Using Hyperspectral Images. Remote Sens. 2023, 15, 1917. [Google Scholar] [CrossRef]
- Moncholi-Estornell, A.; Cendrero-Mateo, M.P.; Antala, M.; Cogliati, S.; Moreno, J.; Van Wittenberghe, S. Enhancing Solar-Induced Fluorescence Interpretation: Quantifying Fractional Sunlit Vegetation Cover Using Linear Spectral Unmixing. Remote Sens. 2023, 15, 4274. [Google Scholar] [CrossRef]
- Naß, A.; van Gasselt, S. A Cartographic Perspective on the Planetary Geologic Mapping Investigation of Ceres. Remote Sens. 2023, 15, 4209. [Google Scholar] [CrossRef]
- Sharma, S.R.; Singh, B.; Kaur, M. A hybrid encryption model for the hyperspectral images: Application to hyperspectral medical images. Multimed. Tools Appl. 2023. [Google Scholar] [CrossRef]
- Bedini, E. The use of hyperspectral remote sensing for mineral exploration: A review. J. Hyperspectral Remote Sens. 2017, 7, 189–211. [Google Scholar] [CrossRef]
- Haagsma, M.; Hagerty, C.H.; Kroese, D.R.; Selker, J.S. Detection of soil-borne wheat mosaic virus using hyperspectral imaging: From lab to field scans and from hyperspectral to multispectral data. Precis. Agric. 2023, 24, 1030–1048. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Measurement of Total Dissolved Solids and Total Suspended Solids in Water Systems: A Review of the Issues, Conventional, and Remote Sensing Techniques. Remote Sens. 2023, 15, 3534. [Google Scholar] [CrossRef]
- Renard, N.; Bourennane, S.; Blanc-Talon, J. Denoising and dimensionality reduction using multilinear tools for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2008, 5, 138–142. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.Z.; Zhao, X.L. Destriping of multispectral remote sensing image using low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4950–4967. [Google Scholar] [CrossRef]
- Liu, X.; Bourennane, S.; Fossati, C. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3717–3724. [Google Scholar] [CrossRef]
- Guo, X.; Huang, X.; Zhang, L.; Zhang, L. Hyperspectral image noise reduction based on rank-1 tensor decomposition. ISPRS J. Photogramm. Remote Sens. 2013, 83, 50–63. [Google Scholar] [CrossRef]
- Fan, H.; Li, C.; Guo, Y.; Kuang, G.; Ma, J. Spatial Cspectral total variation regularized low-rank tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6196–6213. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.Z. Hyperspectral Image Restoration Using Weighted Group Sparsity-Regularized Low-Rank Tensor Decomposition. IEEE Trans. Cybern. 2020, 50, 3556–3570. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Meng, D.; Leung, Y.; Zhao, X.-L. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1227–1243. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C. Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5174–5189. [Google Scholar] [CrossRef]
- Xie, Y.; Qu, Y.; Tao, D.; Wu, W.; Yuan, Q.; Zhang, W. Hyperspectral Image Restoration via Iteratively Regularized Weighted Schatten p-Norm Minimization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4642–4659. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhou, G.; Xie, S.; Zhang, L.; Cichocki, A. Tensor Ring Decomposition. arXiv 2016, arXiv:1606.05535. [Google Scholar] [CrossRef]
- Zhao, Q.; Sugiyama, M.; Yuan, L.; Cichocki, A. Learning Efficient Tensor Representations with Ring-structured Networks. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar]
- Wang, W.; Aggarwal, V.; Aeron, S. Efficient low rank tensor ring completion. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- He, W.; Yokoya, N.; Yuan, L.; Zhao, Q. Remote Sensing Image Reconstruction Using Tensor Ring Completion and Total Variation. IEEE Trans. Geoence Remote Sens. 2019, 57, 8998–9009. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, H.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Using Local Low-Rank Matrix Recovery and Global Spatial-CSpectral Total Variation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1–17. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Hyperspectral Images. Available online: https://engineering.purdue.edu/~biehl/MultiSpec/hyperspectral.html (accessed on 3 July 2023).
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Zeng, H.; Xie, X.; Cui, H.; Yin, H.; Ning, J. Hyperspectral Image Restoration via Global L1-2 Spatial-Spectral Total Variation Regularized Local Low-Rank Tensor Recovery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3309–3325. [Google Scholar] [CrossRef]
- Valizadeh, S.; Nasiopoulos, P.; Ward, R. Perceptual rate distortion optimization of 3D–HEVC using PSNR-HVS. Multimed. Tools Appl. 2018, 77, 22985–23008. [Google Scholar] [CrossRef]







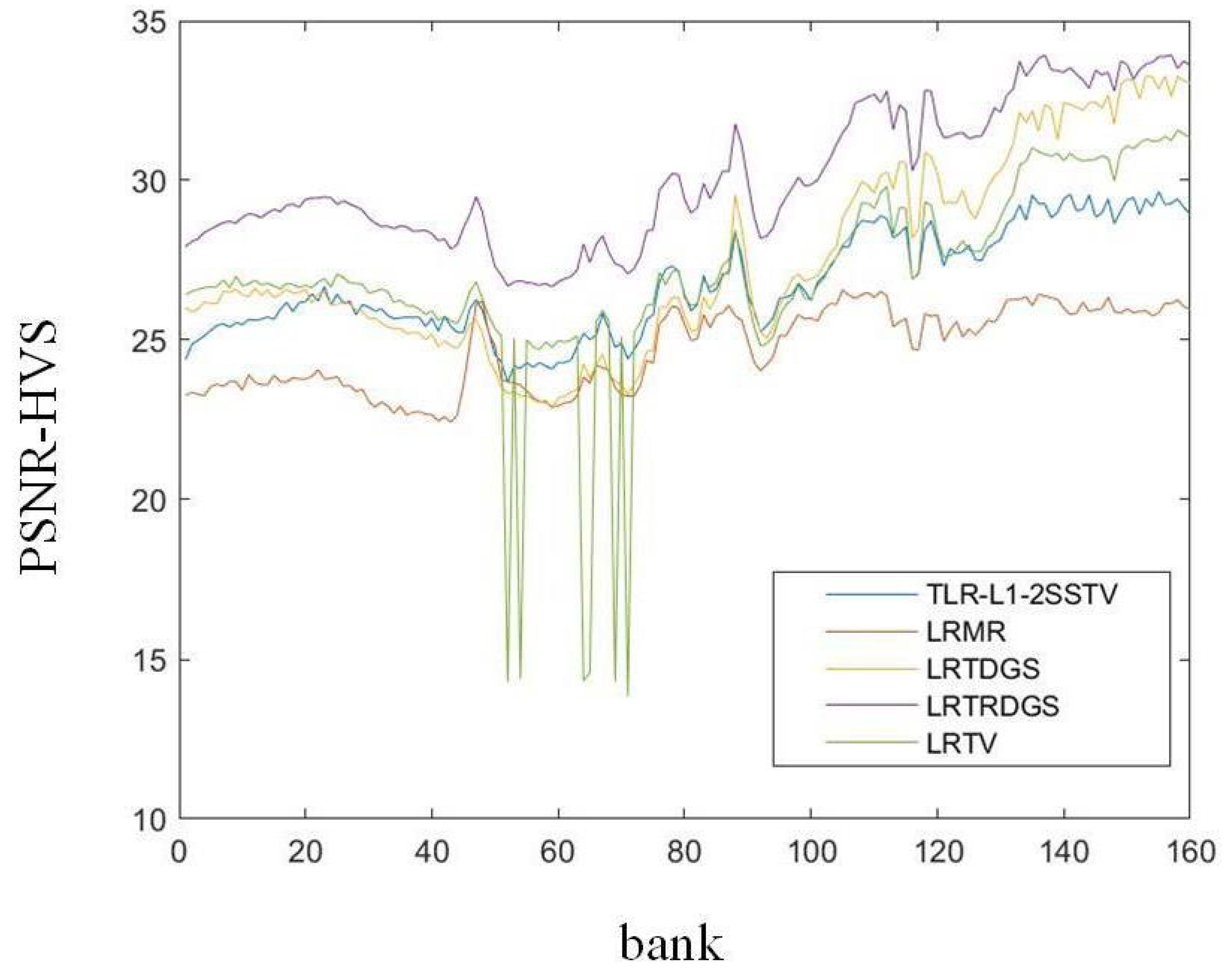
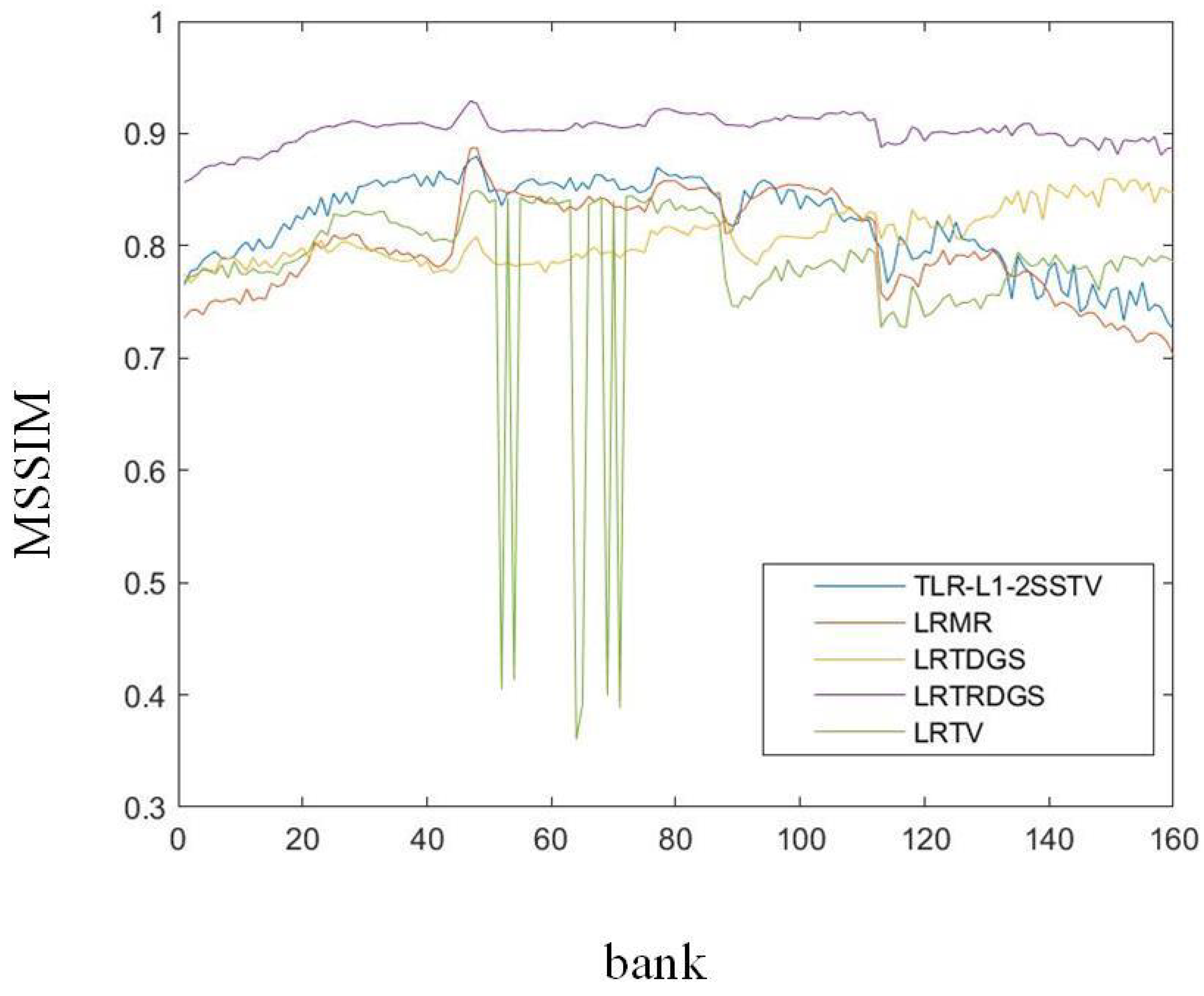


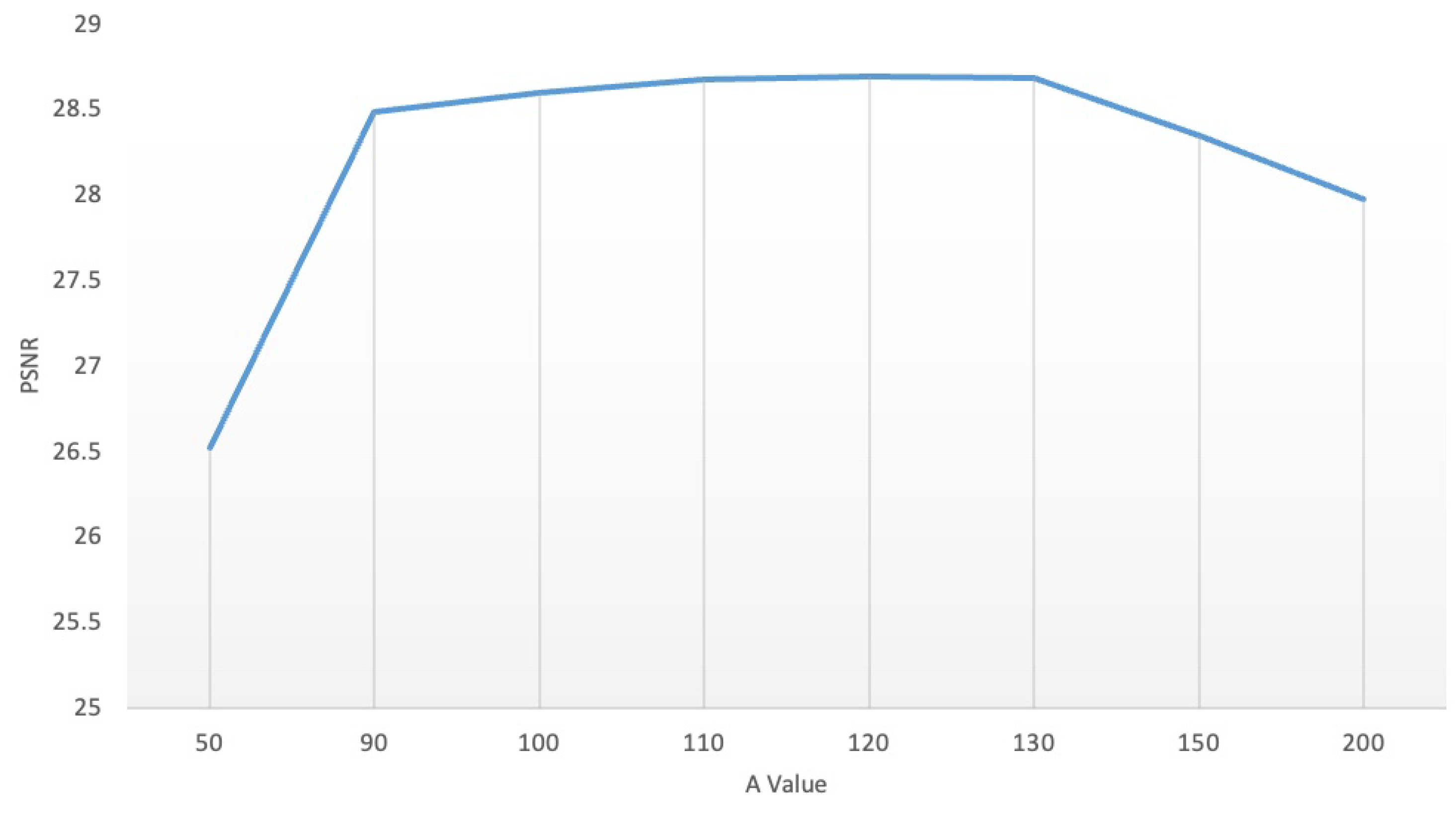
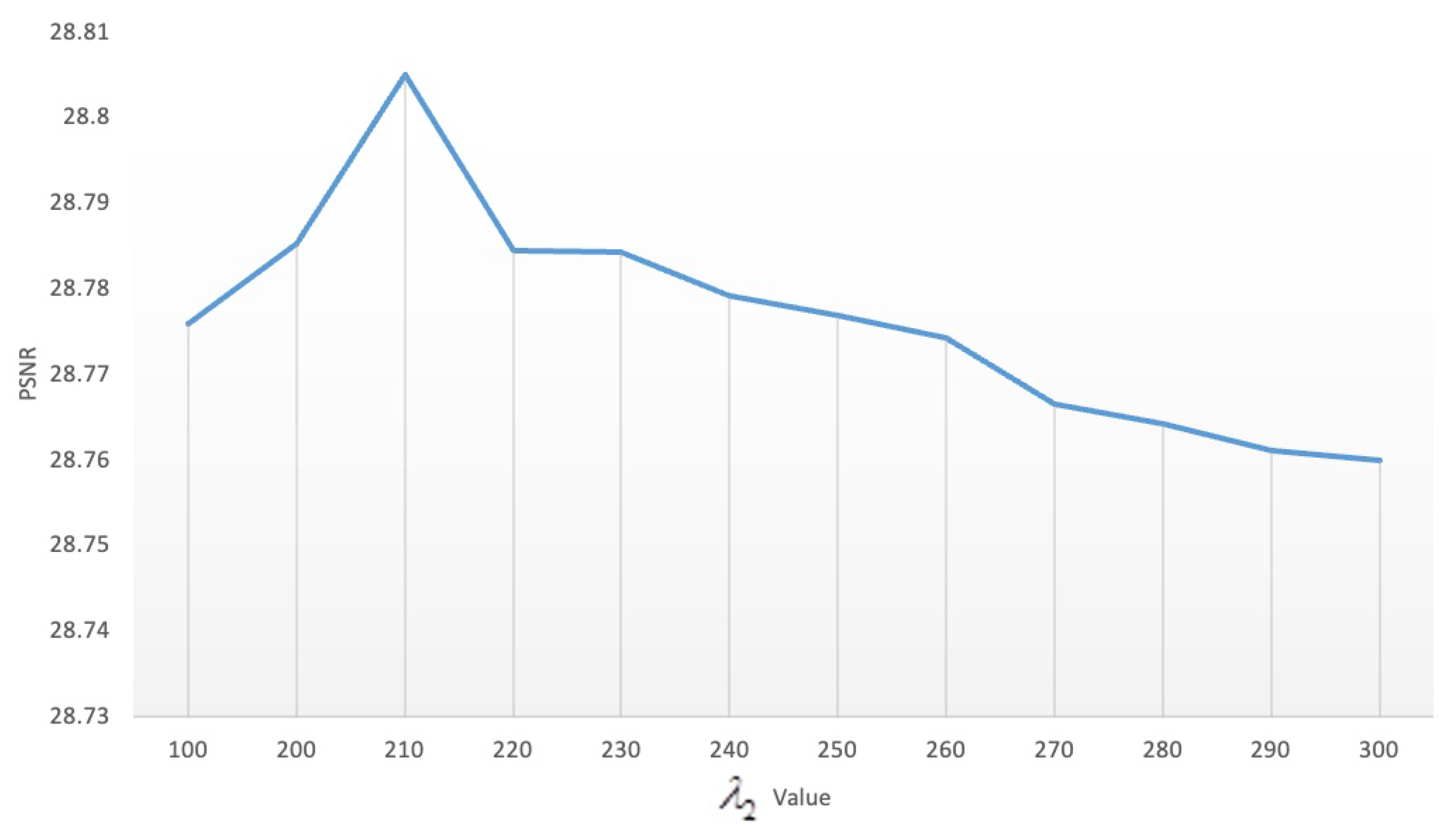
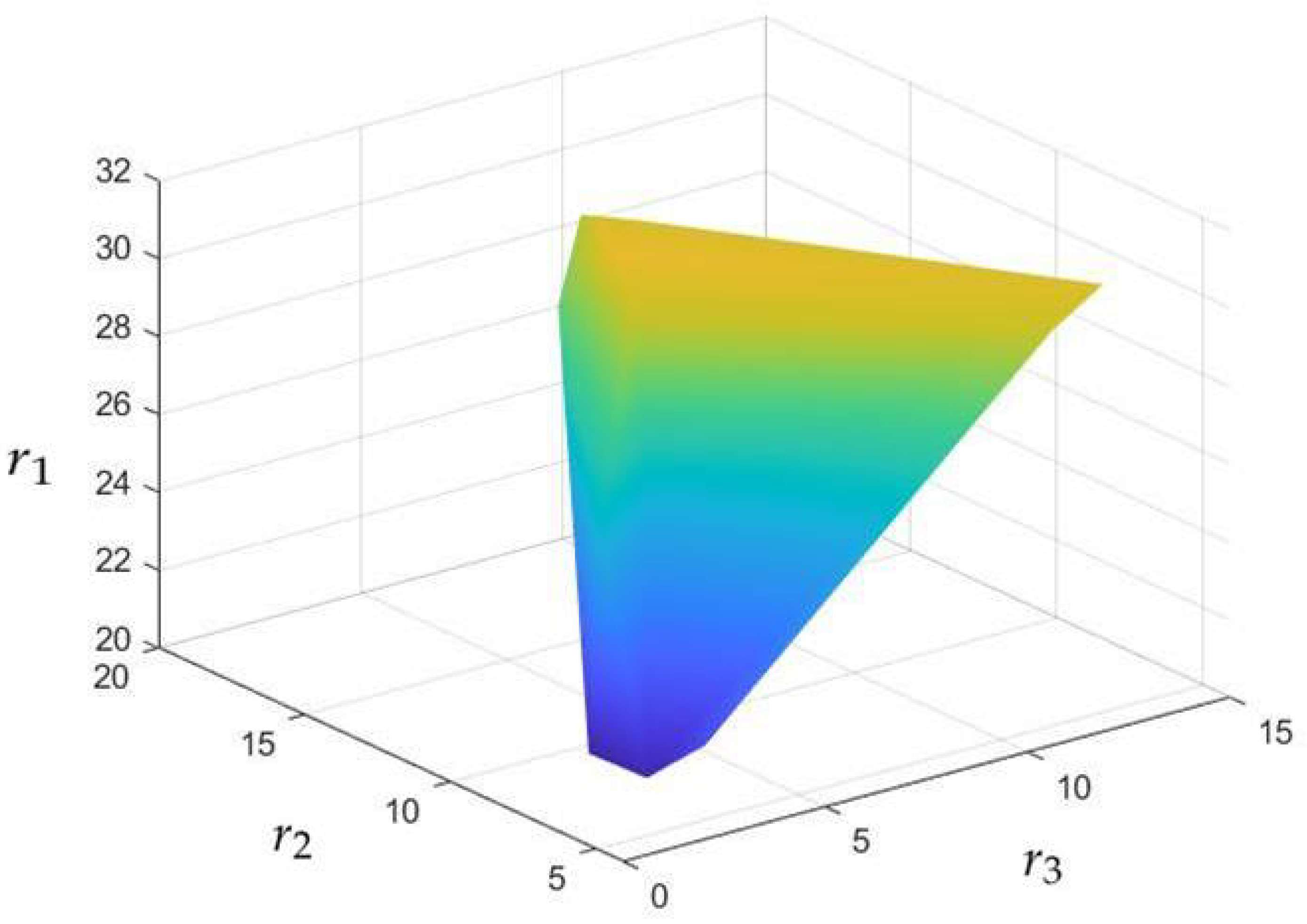

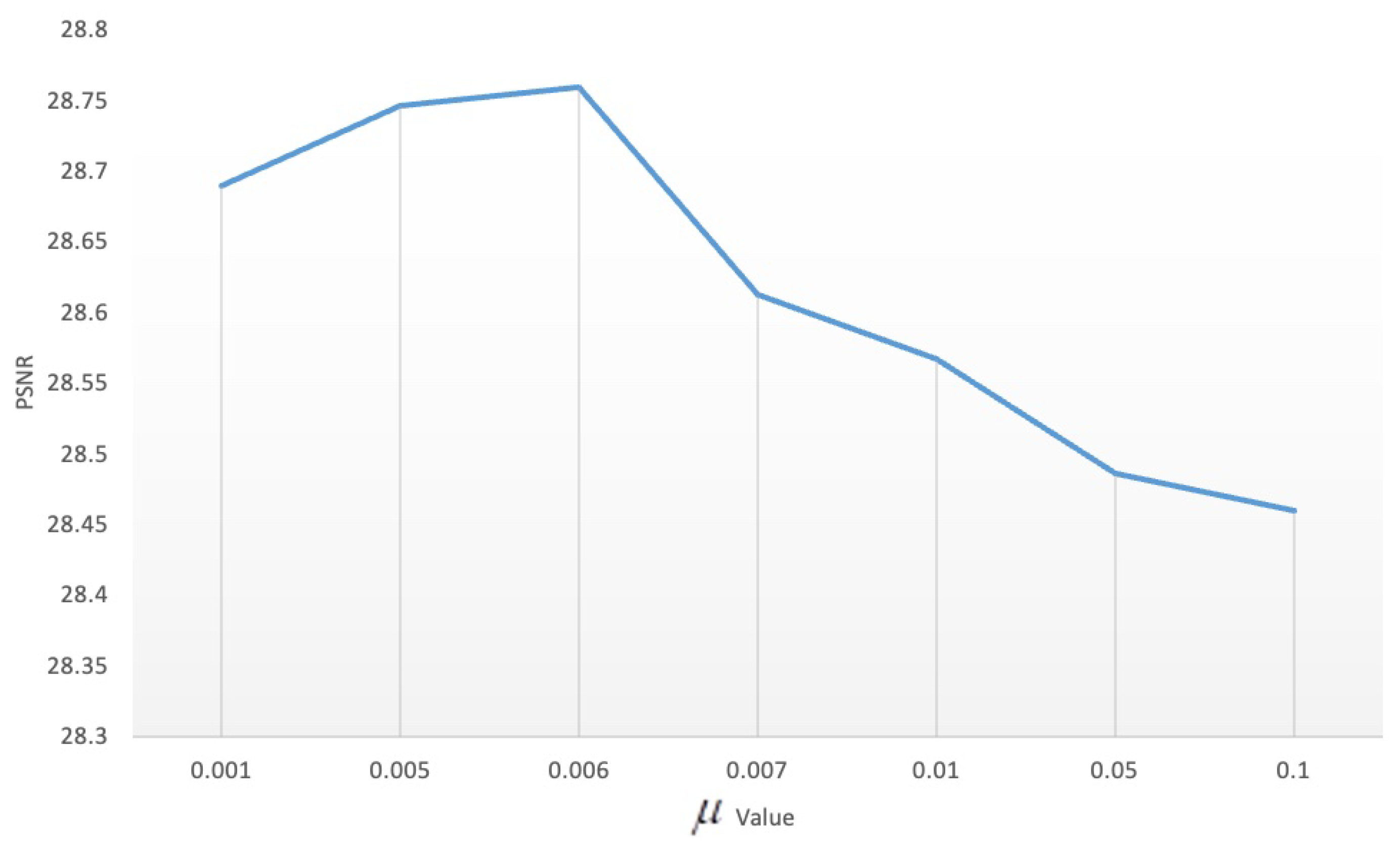
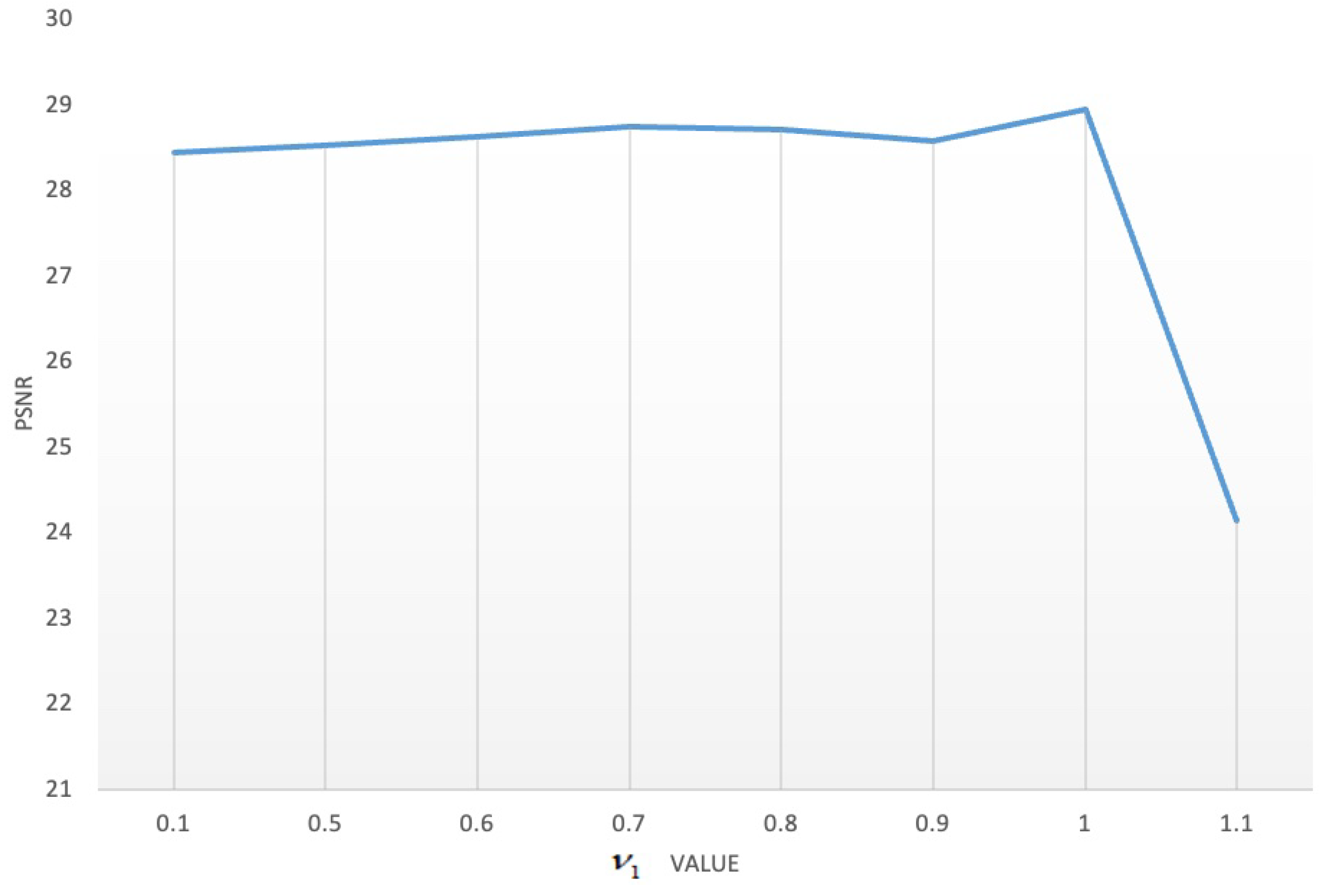


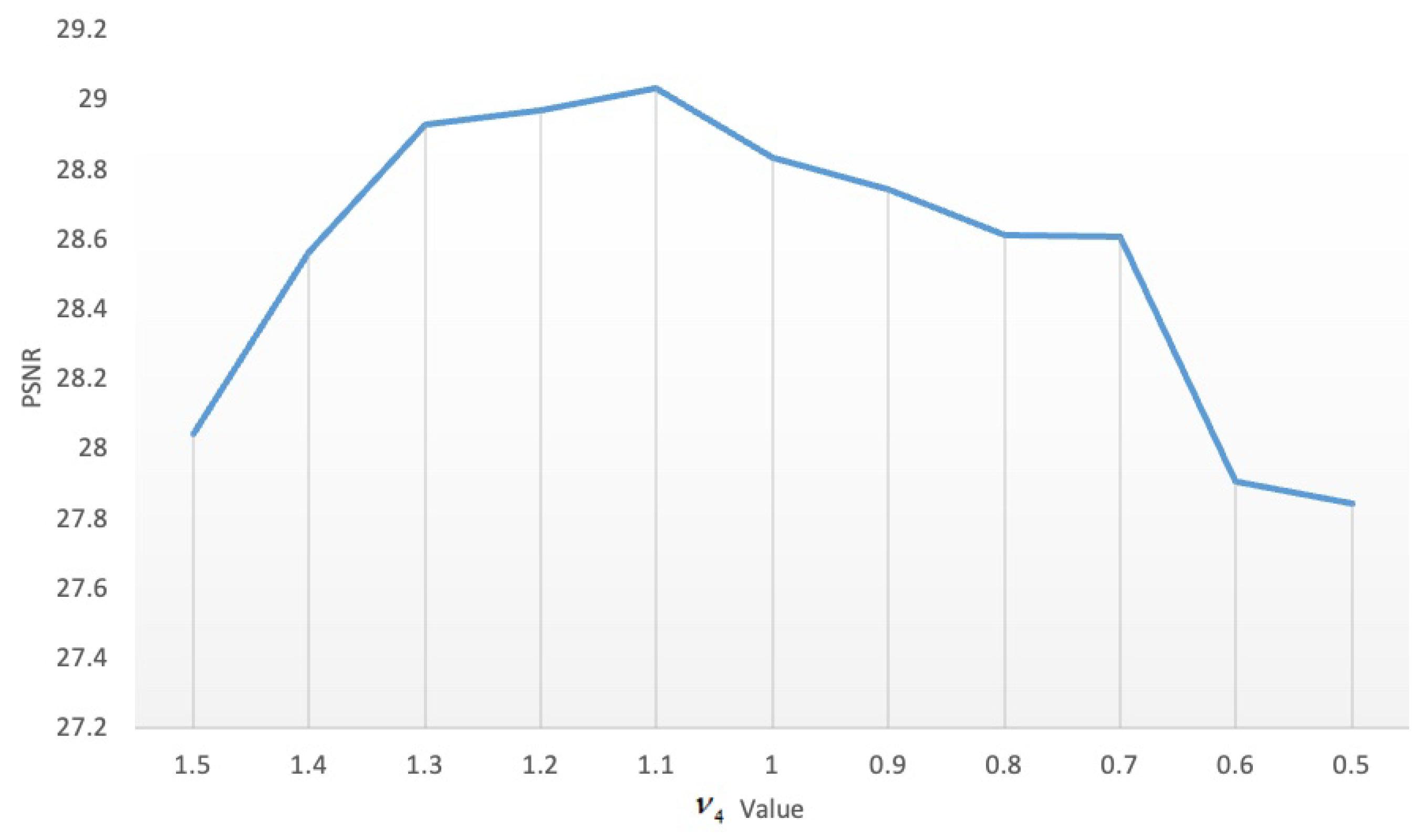

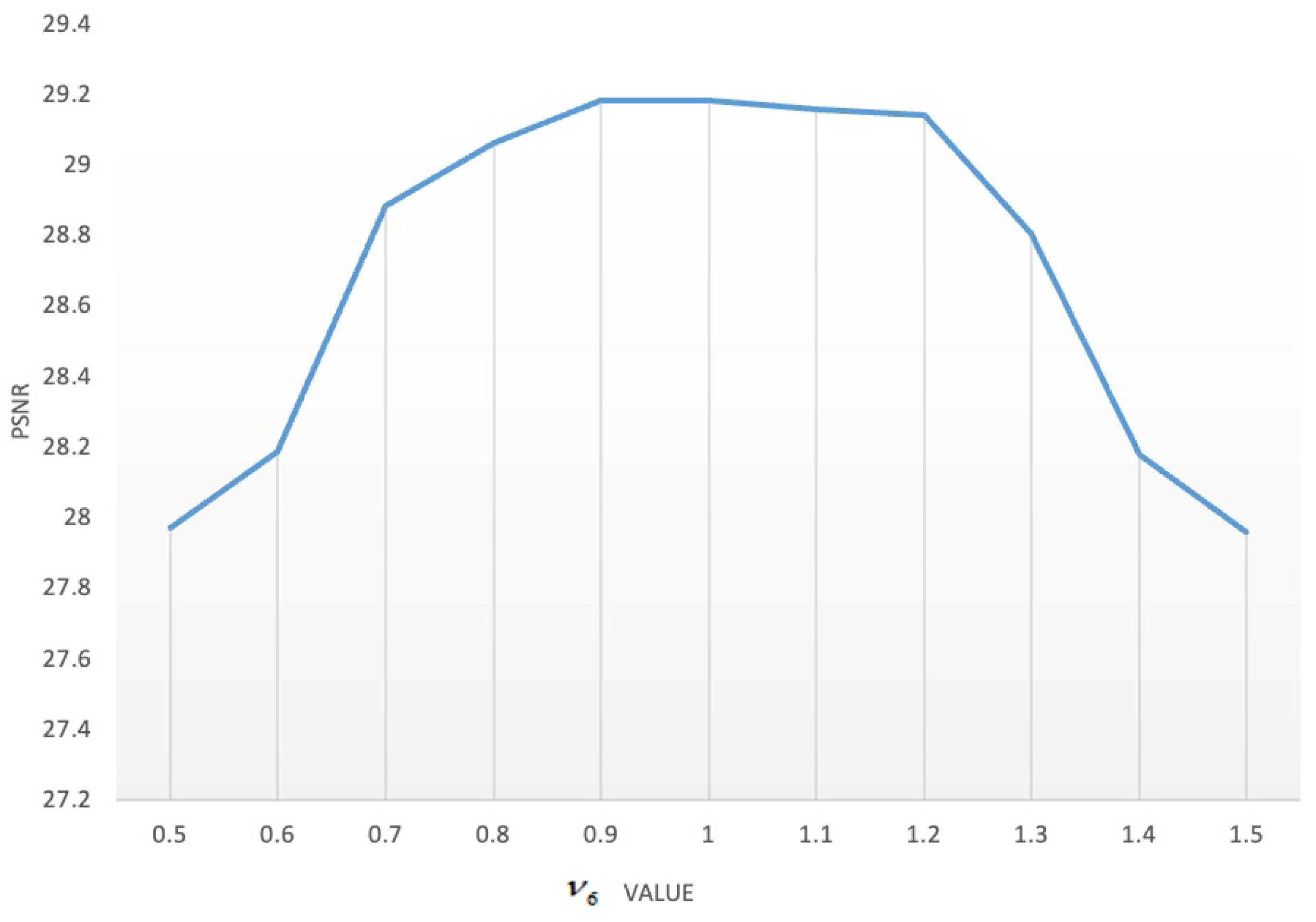
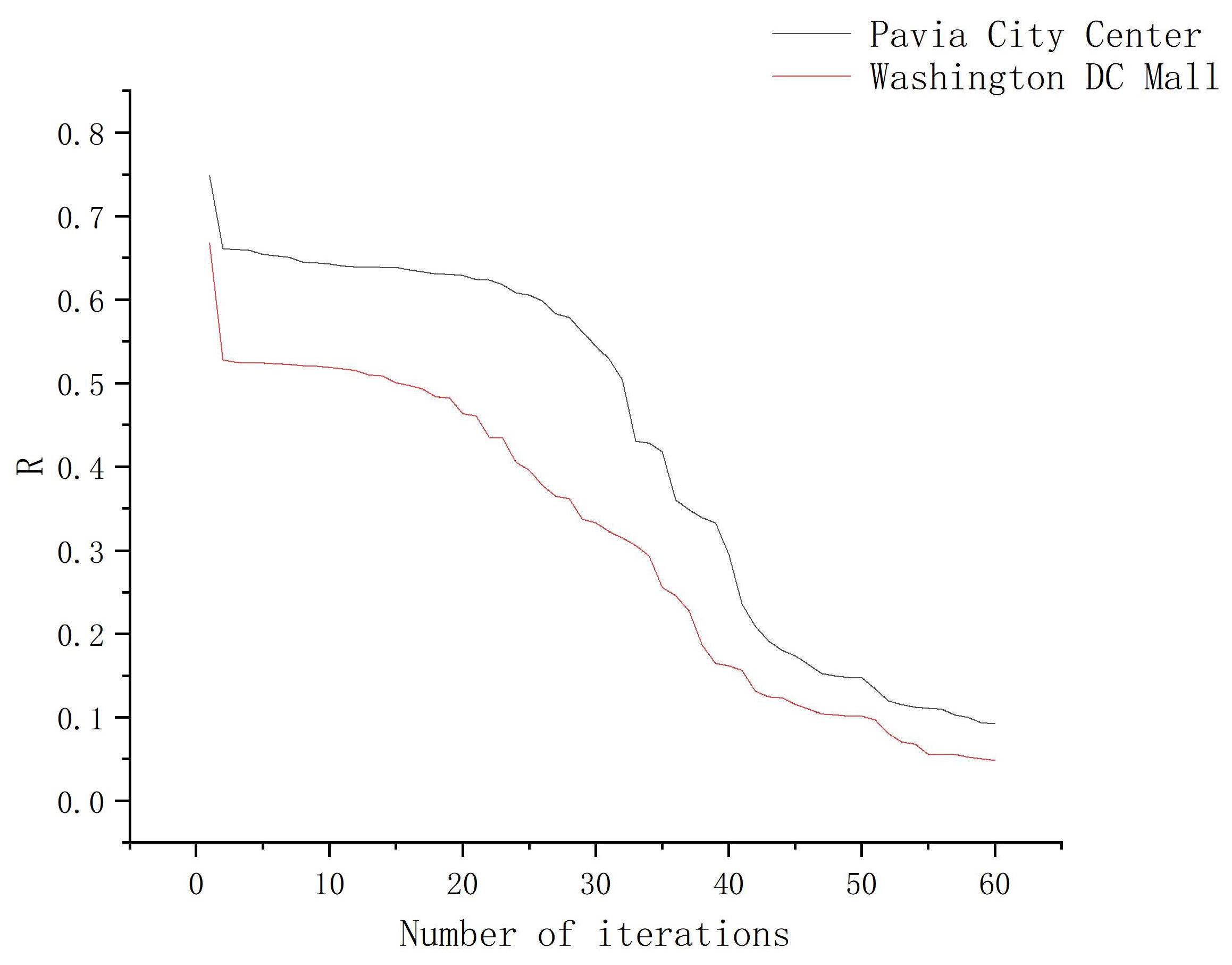
| Case | Noise Level | Indicators | Noise | LRTV | LRMR | LRTDGS | TLR-SSTV | LRTRDGS |
|---|---|---|---|---|---|---|---|---|
| Case 1-1 | PSNR-HVS | 13.9932 | 28.7625 | 29.1682 | 26.9825 | 27.7324 | 29.8258 | |
| MSSIM | 0.1733 | 0.7904 | 0.8469 | 0.7195 | 0.8438 | 0.8471 | ||
| ERGAS | 665.9520 | 168.4686 | 117.701 | 150.0049 | 148.9314 | 108.9523 | ||
| time (s) | 117.272 | 99.203 | 72.022 | 88.274 | 100.32 | |||
| Case 1-2 | PSNR-HVS | 7.9962 | 24.8261 | 24.3712 | 24.9912 | 24.6279 | 25.7813 | |
| MSSIM | 0.0510 | 0.6418 | 0.6469 | 0.6003 | 0.6834 | 0.6887 | ||
| ERGAS | 1332.676 | 331.8135 | 206.591 | 188.9809 | 217.5825 | 178.4174 | ||
| time (s) | 122.123 | 101.691 | 84.024 | 91.271 | 110.276 | |||
| Case 2-1 | +Deadline | PSNR-HVS | 10.7621 | 26.1072 | 26.4181 | 25.5719 | 27.4619 | 27.5891 |
| MSSIM | 0.0871 | 0.6982 | 0.7445 | 0.6435 | 0.8401 | 0.8416 | ||
| ERGAS | 999.3376 | 233.1479 | 163.708 | 182.5346 | 155.4789 | 152.6477 | ||
| time (s) | 119.718 | 100.178 | 81.651 | 87.874 | 103.782 | |||
| Case 2-2 | +Deadline | PSNR-HVS | 7.9963 | 23.9574 | 24.3571 | 24.7893 | 23.9965 | 24.9979 |
| MSSIM | 0.0505 | 0.6202 | 0.6477 | 0.5918 | 0.6736 | 0.6762 | ||
| ERGAS | 1330.449 | 348.6010 | 208.053 | 201.1706 | 230.4959 | 190.4651 | ||
| time (s) | 124.267 | 104.781 | 86.983 | 91.784 | 113.926 | |||
| Case 3-1 | + | PSNR-HVS | 9.1271 | 25.2875 | 24.3688 | 25.2870 | 25.2769 | 25.9945 |
| MSSIM | 0.0640 | 0.6658 | 0.6700 | 0.6207 | 0.7212 | 0.7223 | ||
| ERGAS | 1169.856 | 276.2930 | 202.819 | 184.5704 | 200.0335 | 166.8273 | ||
| time (s) | 98.962 | 119.267 | 74.232 | 85.127 | 103.261 | |||
| Case 3-2 | + | PSNR-HVS | 6.9612 | 22.9659 | 22.4892 | 23.7926 | 23.8920 | 23.9864 |
| MSSIM | 0.0362 | 0.5578 | 0.5565 | 0.5448 | 0.6130 | 0.6188 | ||
| ERGAS | 1526.545 | 351.0957 | 257.677 | 216.6734 | 247.5929 | 215.5840 | ||
| time (s) | 97.122 | 116.968 | 78.197 | 85.969 | 101.206 | |||
| Case 4-1 | + +Deadline | PSNR-HVS | 7.2871 | 23.3789 | 23.9865 | 24.8547 | 23.6794 | 24.2688 |
| MSSIM | 0.0404 | 0.5800 | 0.5887 | 0.5598 | 0.6042 | 0.6277 | ||
| ERGAS | 1462.063 | 359.3642 | 232.914 | 211.6882 | 253.7716 | 208.3434 | ||
| time (s) | 100.271 | 120.861 | 81.994 | 89.275 | 111.788 | |||
| Case 4-2 | + +Deadline | PSNR-HVS | 10.1122 | 25.9769 | 25.0153 | 25.1878 | 24.9962 | 25.9014 |
| MSSIM | 0.0685 | 0.6798 | 0.6880 | 0.6200 | 0.7242 | 0.7350 | ||
| ERGAS | 1128.251 | 269.8426 | 189.770 | 191.0023 | 205.3501 | 174.1756 | ||
| time (s) | 99.882 | 117.962 | 80.997 | 87.291 | 108.782 | |||
| Case 5-1 | + +Deadline | PSNR-HVS | 11.5786 | 26.8971 | 26.2788 | 26.0165 | 26.8961 | 26.9987 |
| MSSIM | 0.1003 | 0.7242 | 0.7498 | 0.6700 | 0.8258 | 0.8666 | ||
| ERGAS | 942.5571 | 264.2848 | 162.700 | 170.5190 | 165.8885 | 154.6694 | ||
| time (s) | 100.978 | 118.653 | 82.878 | 87.998 | 109.004 | |||
| Case 5-2 | + +Deadline | PSNR-HVS | 6.8768 | 23.6871 | 23.0902 | 24.8910 | 23.8760 | 24.6891 |
| MSSIM | 0.0373 | 0.5704 | 0.5776 | 0.5545 | 0.6139 | 0.6391 | ||
| ERGAS | 1551.881 | 381.8465 | 236.612 | 212.0504 | 250.6892 | 199.8251 | ||
| time (s) | 100.101 | 118.433 | 84.903 | 88.022 | 110.057 |
| Case | Noise Level | Indicators | Noise | LRTV | LRMR | LRTDGS | TLR-SSTV | LRTRDGS |
|---|---|---|---|---|---|---|---|---|
| Case 1-1 | PSNR-HVS | 14.0163 | 27.901 | 29.7813 | 28.082 | 27.9870 | 30.8762 | |
| MSSIM | 0.2560 | 0.8160 | 0.9046 | 0.8233 | 0.8928 | 0.9120 | ||
| ERGAS | 751.882 | 162.6289 | 120.4509 | 145.6978 | 151.9219 | 105.1567 | ||
| time (s) | 65.903 | 125.355 | 101.05 | 168.771 | 129.875 | |||
| Case 1-2 | PSNR-HVS | 8.0724 | 24.8962 | 24.9809 | 25.8565 | 21.6804 | 26.8577 | |
| MSSIM | 0.0885 | 0.6706 | 0.7563 | 0.7345 | 0.4456 | 0.8046 | ||
| ERGAS | 1503.76 | 265.8668 | 211.9395 | 188.3212 | 314.1924 | 168.3608 | ||
| time (s) | 68.384 | 129.074 | 116.272 | 171.283 | 134.115 | |||
| Case 2-1 | +Deadline | PSNR-HVS | 14.0758 | 27.9572 | 29.6927 | 28.0184 | 26.9483 | 30.0078 |
| MSSIM | 0.2543 | 0.8121 | 0.9031 | 0.8234 | 0.8689 | 0.8996 | ||
| ERGAS | 753.640 | 159.1033 | 122.6426 | 146.1582 | 167.6949 | 120.0915 | ||
| time (s) | 66.282 | 118.784 | 110.709 | 165.203 | 130.673 | |||
| Case 2-2 | +Deadline | PSNR-HVS | 8.0034 | 24.9894 | 24.8892 | 25.8762 | 24.0708 | 26.9950 |
| MSSIM | 0.0880 | 0.6662 | 0.7556 | 0.7393 | 0.7898 | 0.7987 | ||
| ERGAS | 1503.85 | 258.5927 | 213.5223 | 190.8474 | 212.9540 | 181.1324 | ||
| time (s) | 63.228 | 112.783 | 106.889 | 159.995 | 127.257 | |||
| Case 3-1 | + | PSNR-HVS | 11.9947 | 27.7842 | 25.0749 | 27.9302 | 27.8404 | 30.7730 |
| MSSIM | 0.1701 | 0.7808 | 0.7993 | 0.8056 | 0.8755 | 0.9012 | ||
| ERGAS | 1047.90 | 175.0467 | 213.6028 | 153.4816 | 161.8219 | 112.6899 | ||
| time (s) | 65.893 | 116.291 | 109.680 | 160.003 | 127.982 | |||
| Case 3-2 | + | PSNR-HVS | 7.9956 | 24.0949 | 21.0092 | 24.8709 | 24.0825 | 26.9904 |
| MSSIM | 0.0827 | 0.6465 | 0.6547 | 0.7162 | 0.7646 | 0.8026 | ||
| ERGAS | 1529.86 | 258.4262 | 340.4201 | 204.1038 | 230.8225 | 80.2526 | ||
| time (s) | 66.113 | 116.982 | 111.293 | 160.904 | 128.040 | |||
| Case 4-1 | + +Deadline | PSNR-HVS | 7.2837 | 23.8392 | 23.0392 | 25.1039 | 23.9029 | 25.9372 |
| MSSIM | 0.0716 | 0.6058 | 0.6908 | 0.7066 | 0.7450 | 0.7553 | ||
| ERGAS | 1672.07 | 303.2406 | 264.5094 | 207.8214 | 236.6696 | 201.1609 | ||
| time (s) | 70.284 | 119.103 | 117.739 | 165.492 | 130.265 | |||
| Case 4-2 | + +Deadline | PSNR-HVS | 8.9829 | 25.0284 | 18.9271 | 26.0174 | 25.0172 | 26.8740 |
| MSSIM | 0.0849 | 0.6982 | 0.6003 | 0.7508 | 0.8120 | 0.8245 | ||
| ERGAS | 1472.33 | 241.7256 | 449.2673 | 185.5257 | 204.7093 | 174.2441 | ||
| time (s) | 69.027 | 118.685 | 115.336 | 162.870 | 128.278 | |||
| Case 5-1 | + +Deadline | PSNR-HVS | 7.7944 | 23.8902 | 21.9080 | 24.9823 | 23.9802 | 25.6890 |
| MSSIM | 0.0780 | 0.6163 | 0.6715 | 0.7083 | 0.7525 | 0.7677 | ||
| ERGAS | 1584.39 | 307.9037 | 301.3547 | 208.4486 | 236.4430 | 198.0863 | ||
| time (s) | 73.282 | 125.394 | 117.003 | 166.682 | 131.082 | |||
| Case 5-2 | + +Deadline | PSNR-HVS | 8.5902 | 24.6823 | 19.9322 | 25.8948 | 24.7839 | 26.7735 |
| MSSIM | 0.0860 | 0.6667 | 0.6278 | 0.7293 | 0.7847 | 0.8052 | ||
| ERGAS | 1494.11 | 271.4693 | 392.7230 | 198.8723 | 222.9171 | 184.1283 | ||
| time (s) | 71.942 | 123.463 | 110.228 | 160.382 | 129.735 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhu, Z.; Liu, Y.; Zhang, B. Weighted Group Sparse Regularized Tensor Decomposition for Hyperspectral Image Denoising. Appl. Sci. 2023, 13, 10363. https://doi.org/10.3390/app131810363
Wang S, Zhu Z, Liu Y, Zhang B. Weighted Group Sparse Regularized Tensor Decomposition for Hyperspectral Image Denoising. Applied Sciences. 2023; 13(18):10363. https://doi.org/10.3390/app131810363
Chicago/Turabian StyleWang, Shuo, Zhibin Zhu, Yufeng Liu, and Benxin Zhang. 2023. "Weighted Group Sparse Regularized Tensor Decomposition for Hyperspectral Image Denoising" Applied Sciences 13, no. 18: 10363. https://doi.org/10.3390/app131810363
APA StyleWang, S., Zhu, Z., Liu, Y., & Zhang, B. (2023). Weighted Group Sparse Regularized Tensor Decomposition for Hyperspectral Image Denoising. Applied Sciences, 13(18), 10363. https://doi.org/10.3390/app131810363






