Optimizing Design and Operational Parameters for Enhanced Mixing and Hydrodynamics in Bubbling Fluidized Bed Gasifiers: An Experimental and CFD-Based Approach
Abstract
:1. Introduction
2. Experimental Setup
3. Materials and Methods
3.1. Fluidized Bed Material Characteristics
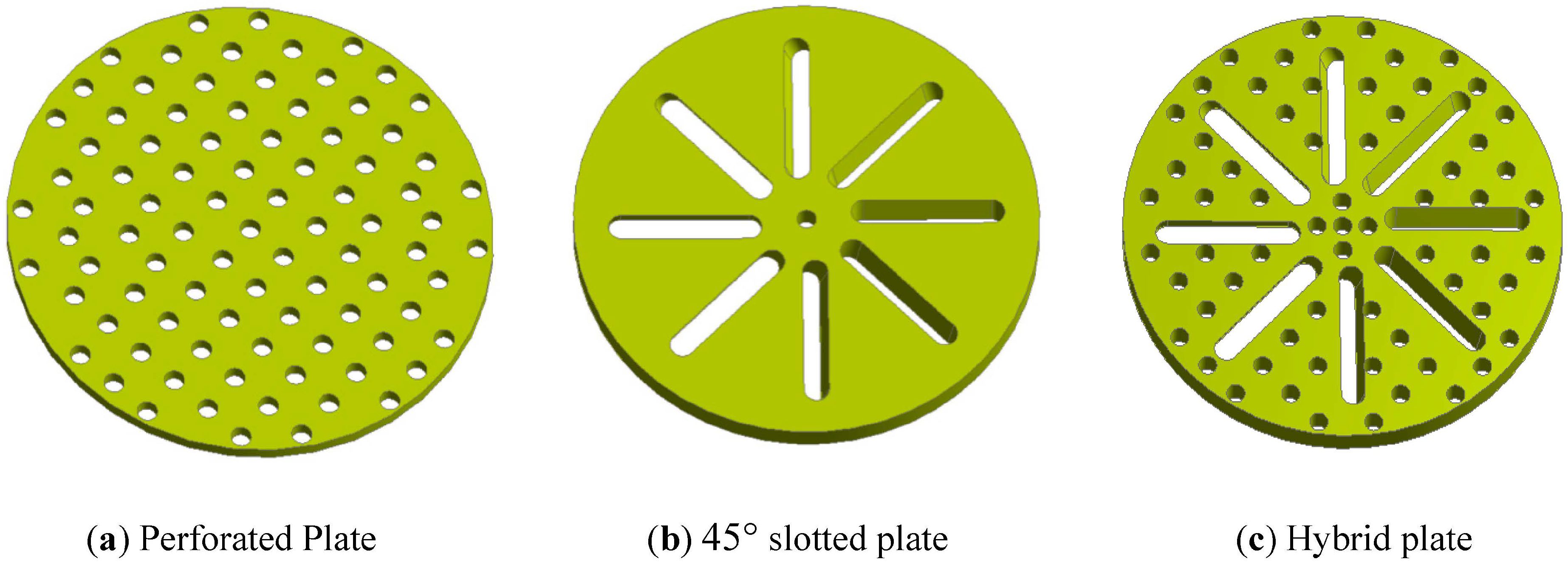
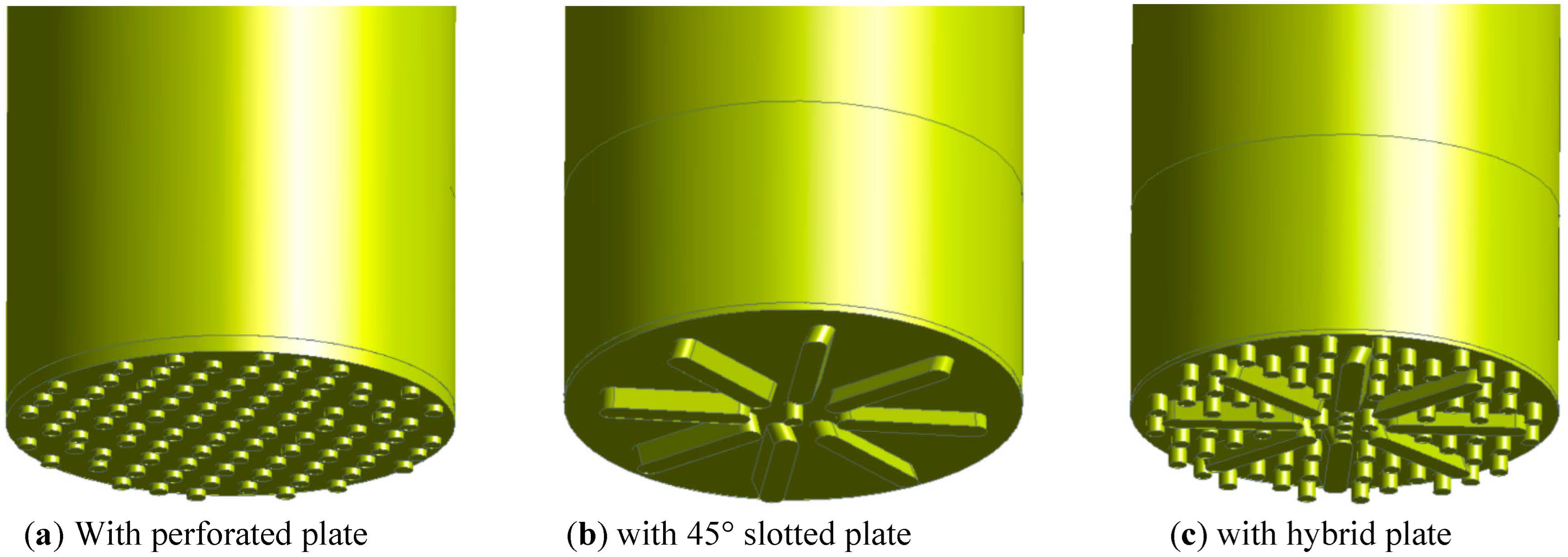
3.2. Geometry of Distributor Plates
3.3. Experimental Scheme
3.4. Experimental Procedure
4. Experimental Results and Discussion
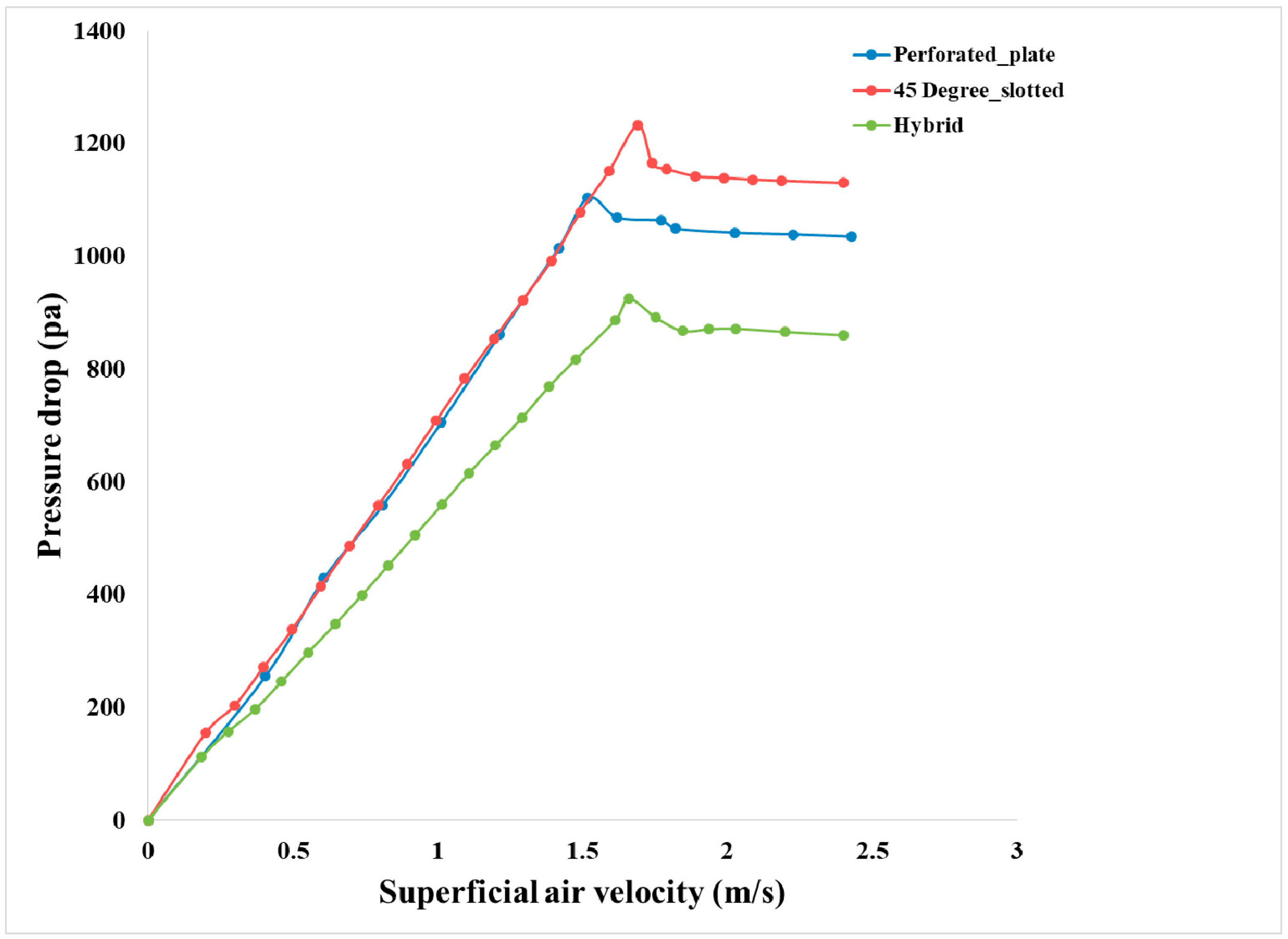
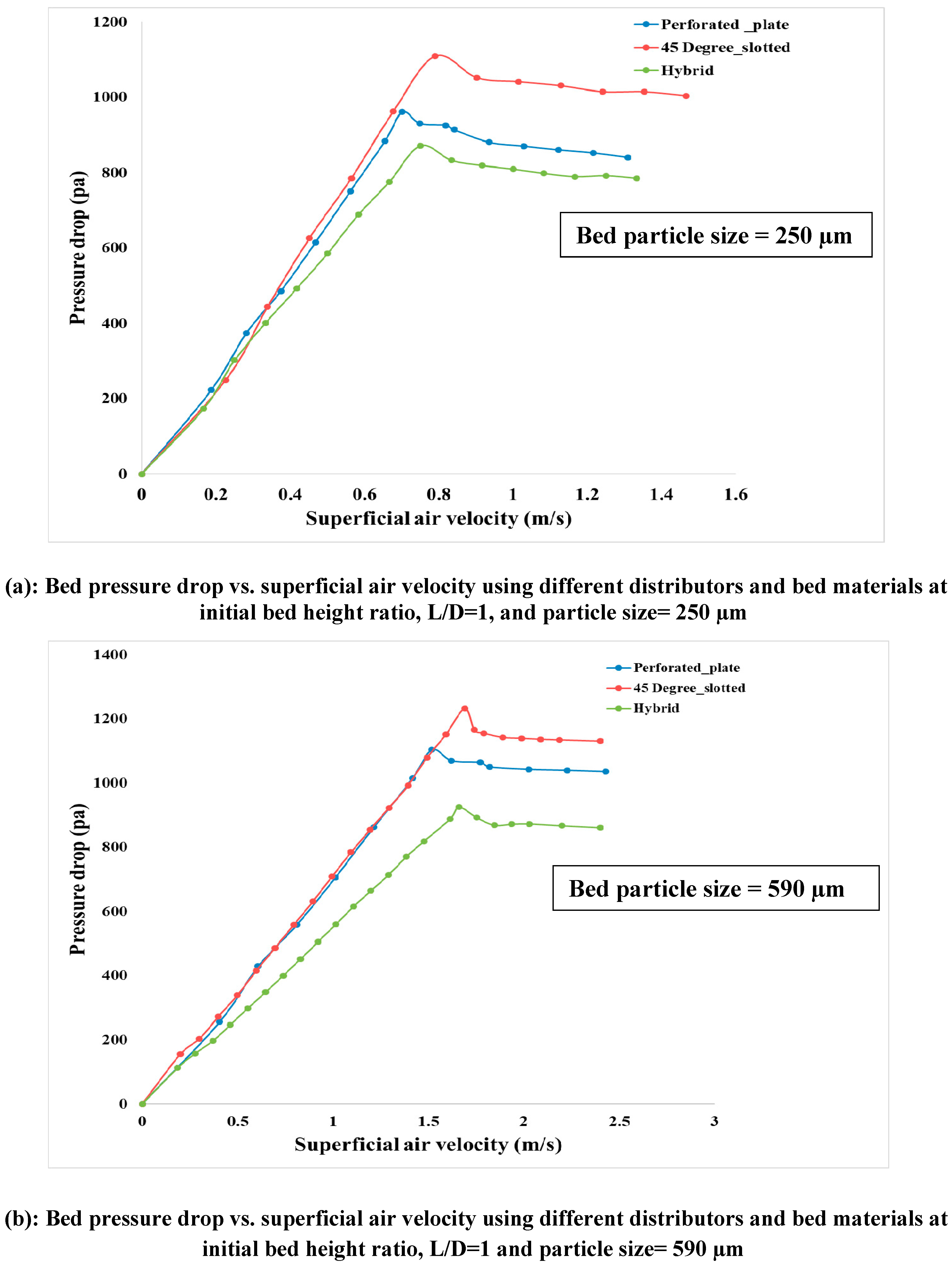
4.1. Sensitivity Analysis for Different Distributor Plates
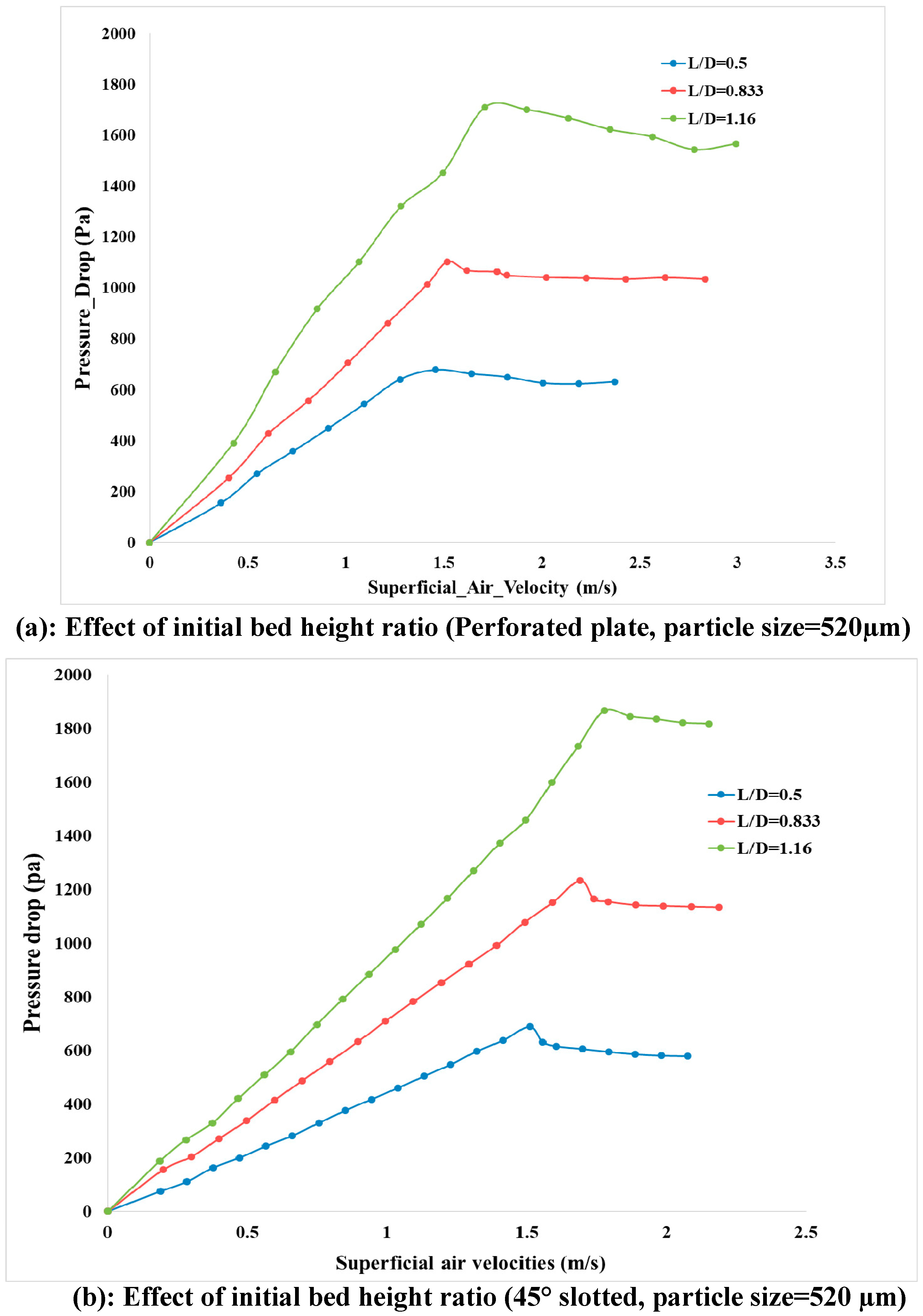
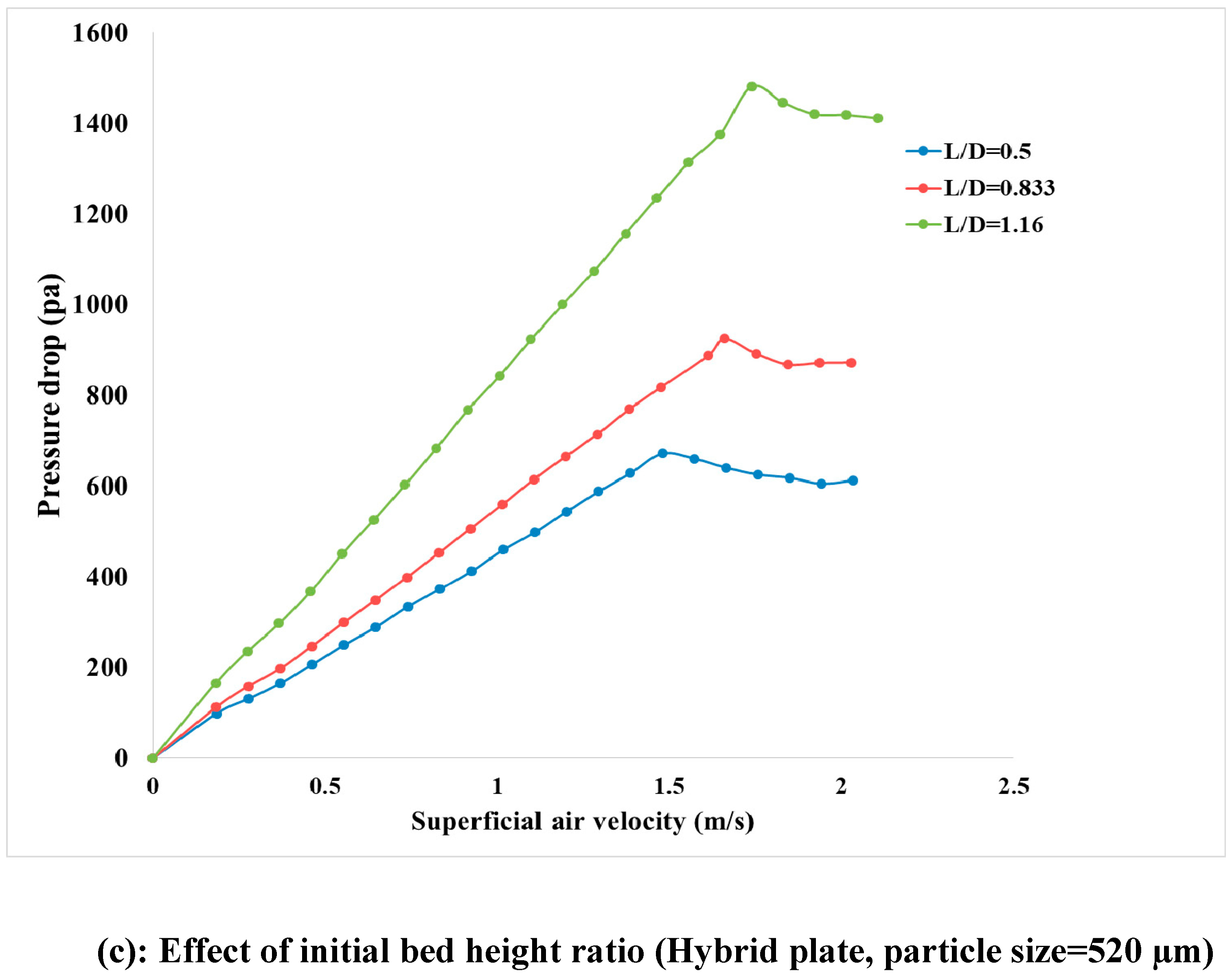
4.2. Effect of Initial Bed Height
4.3. Effect of Bed Particle Size
4.4. Bubble Dynamics
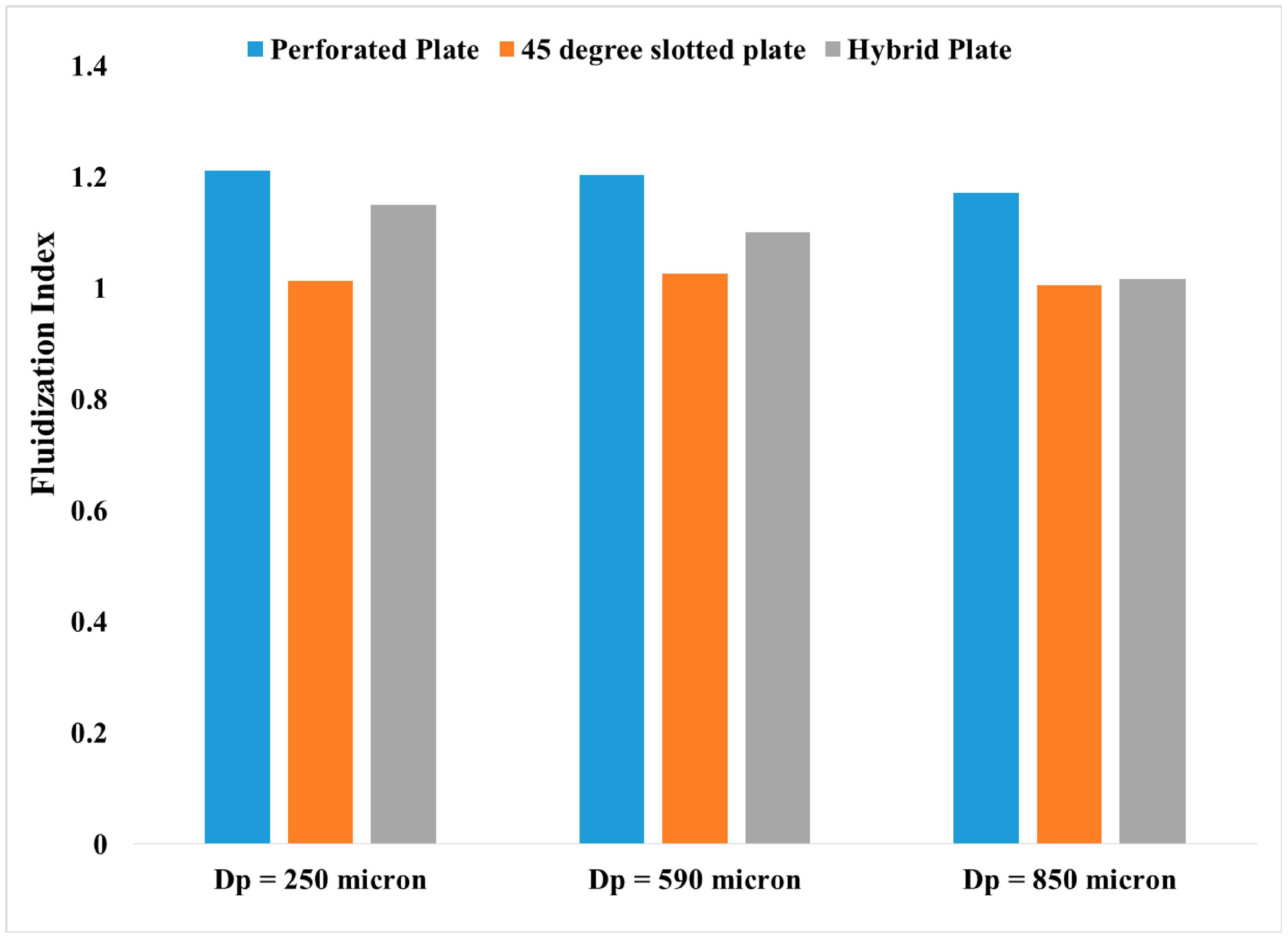
4.4.1. Fluidization Index (F.I.)
4.4.2. Bubble Rise Dynamics for Novel Hybrid Plate Distributor
4.5. Initial Bed Height Rise Ratio and Average Bed Fluctuations
5. Computational Analysis
5.1. Computational Model
5.1.1. Governing Equations
5.1.2. Turbulence Model
5.1.3. Computational Methodology
5.1.4. Initial and Boundary Conditions
5.2. Geometry
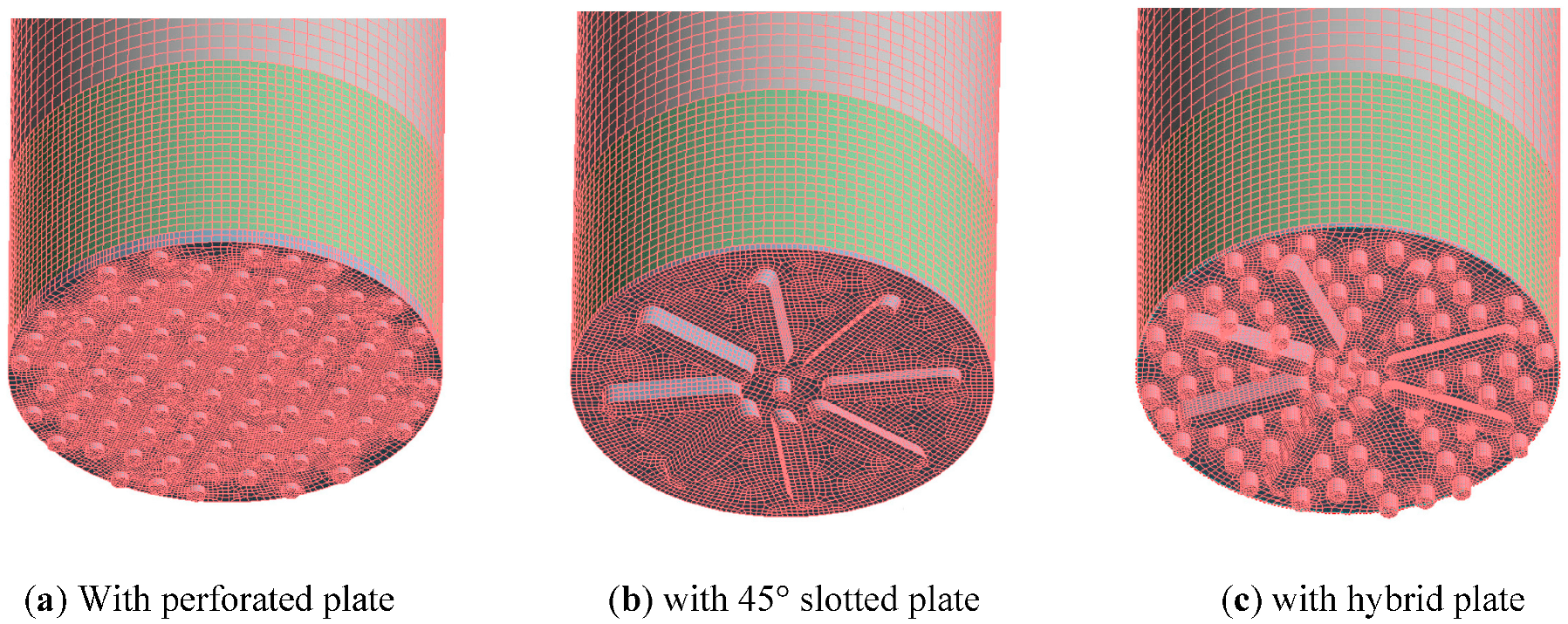
5.3. Computational Mesh Generation
5.4. Grid Independence Study
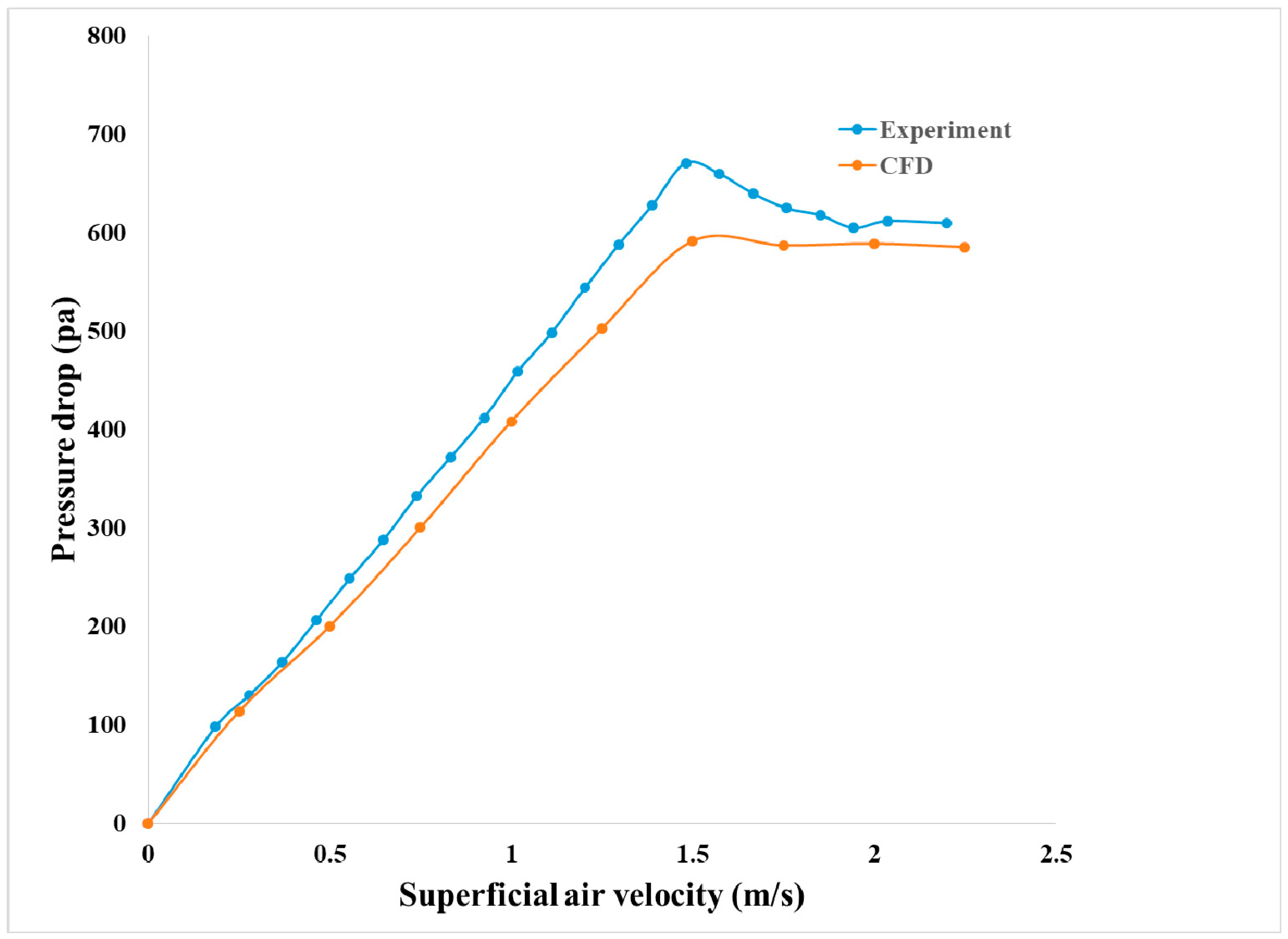
5.4.1. CFD Model Validation
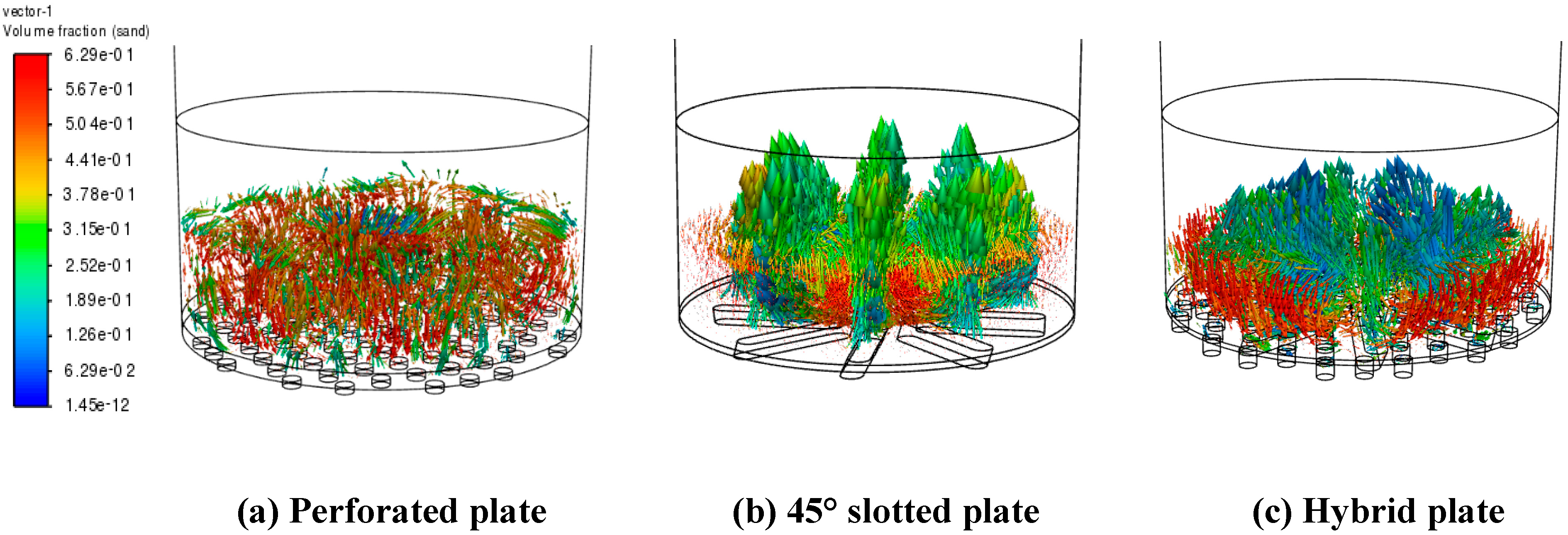
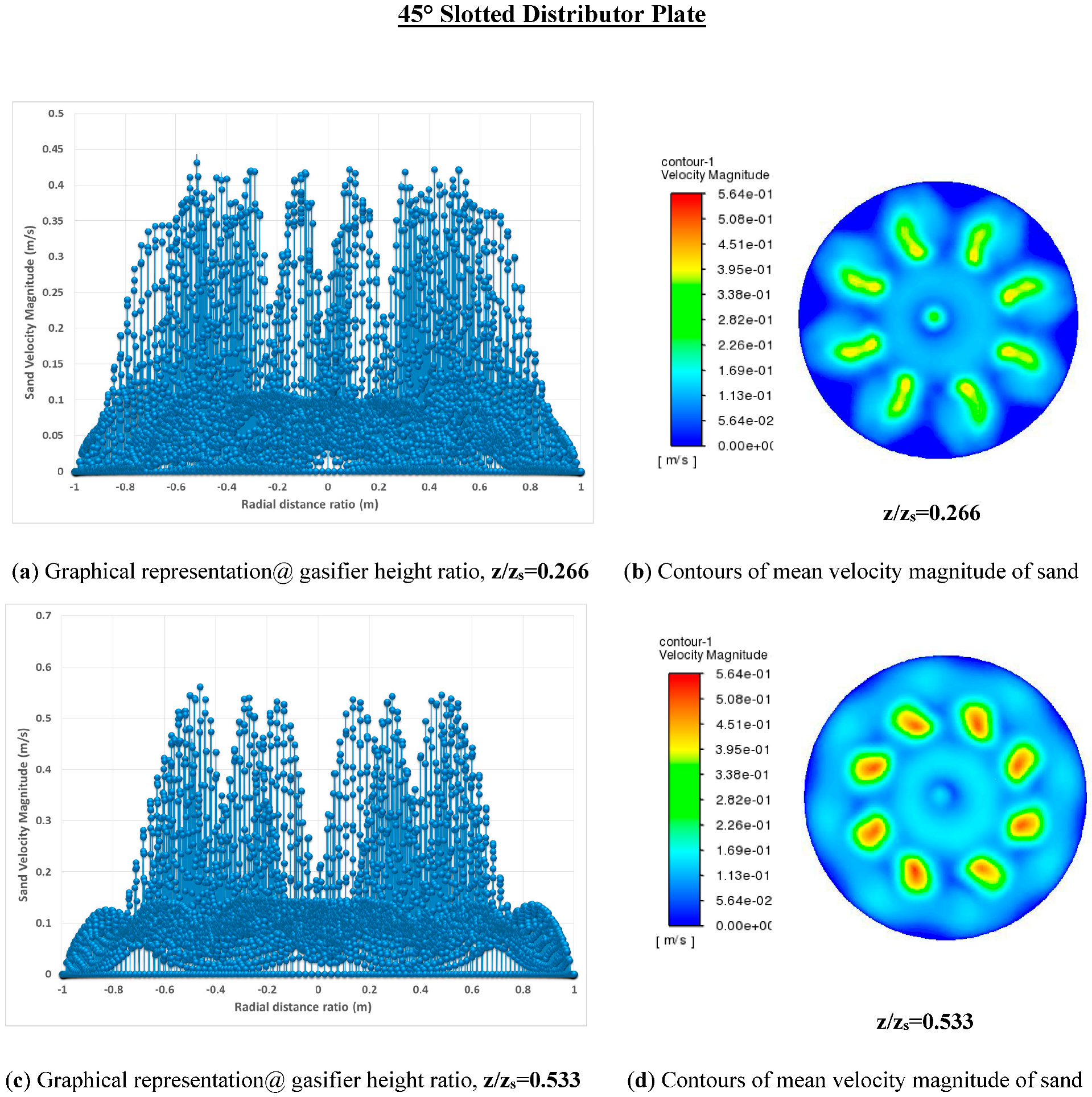
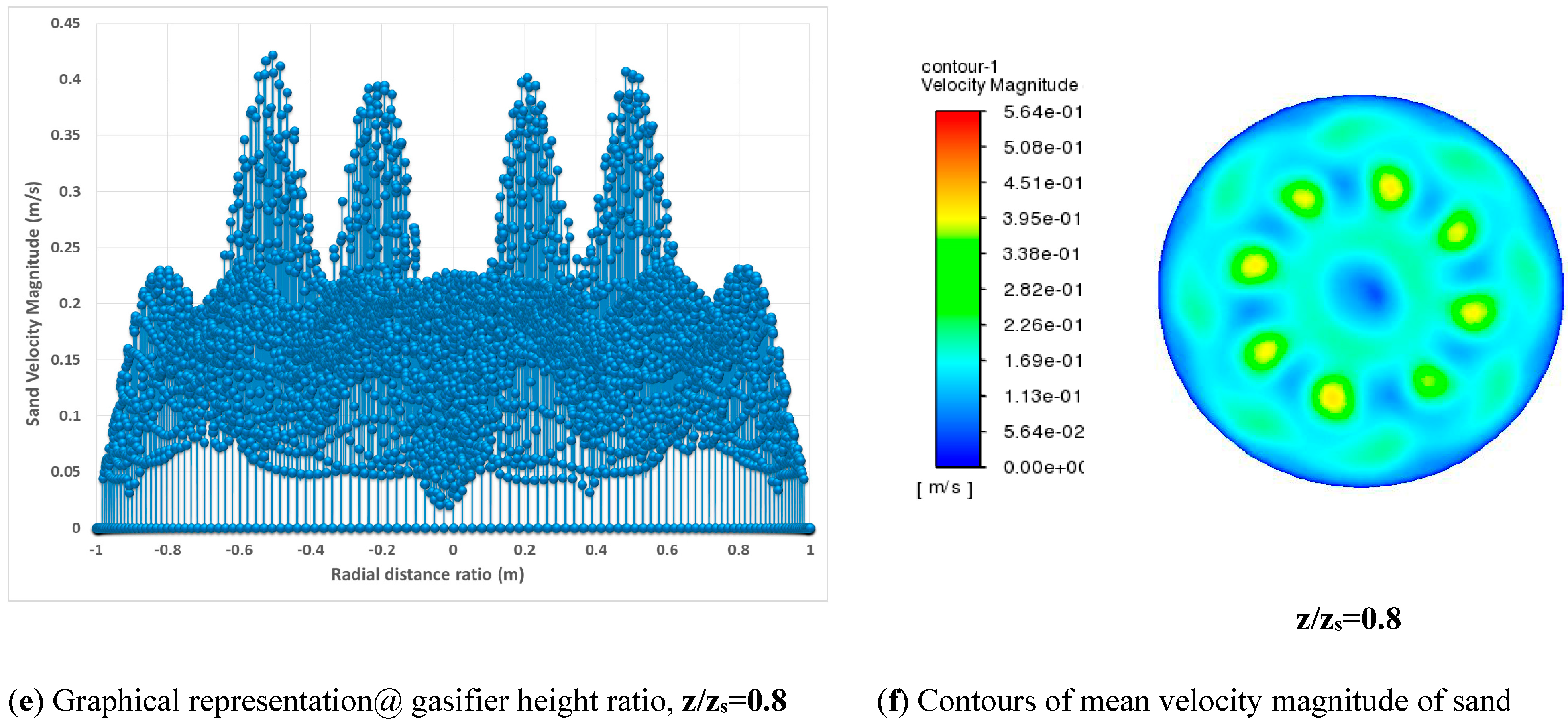
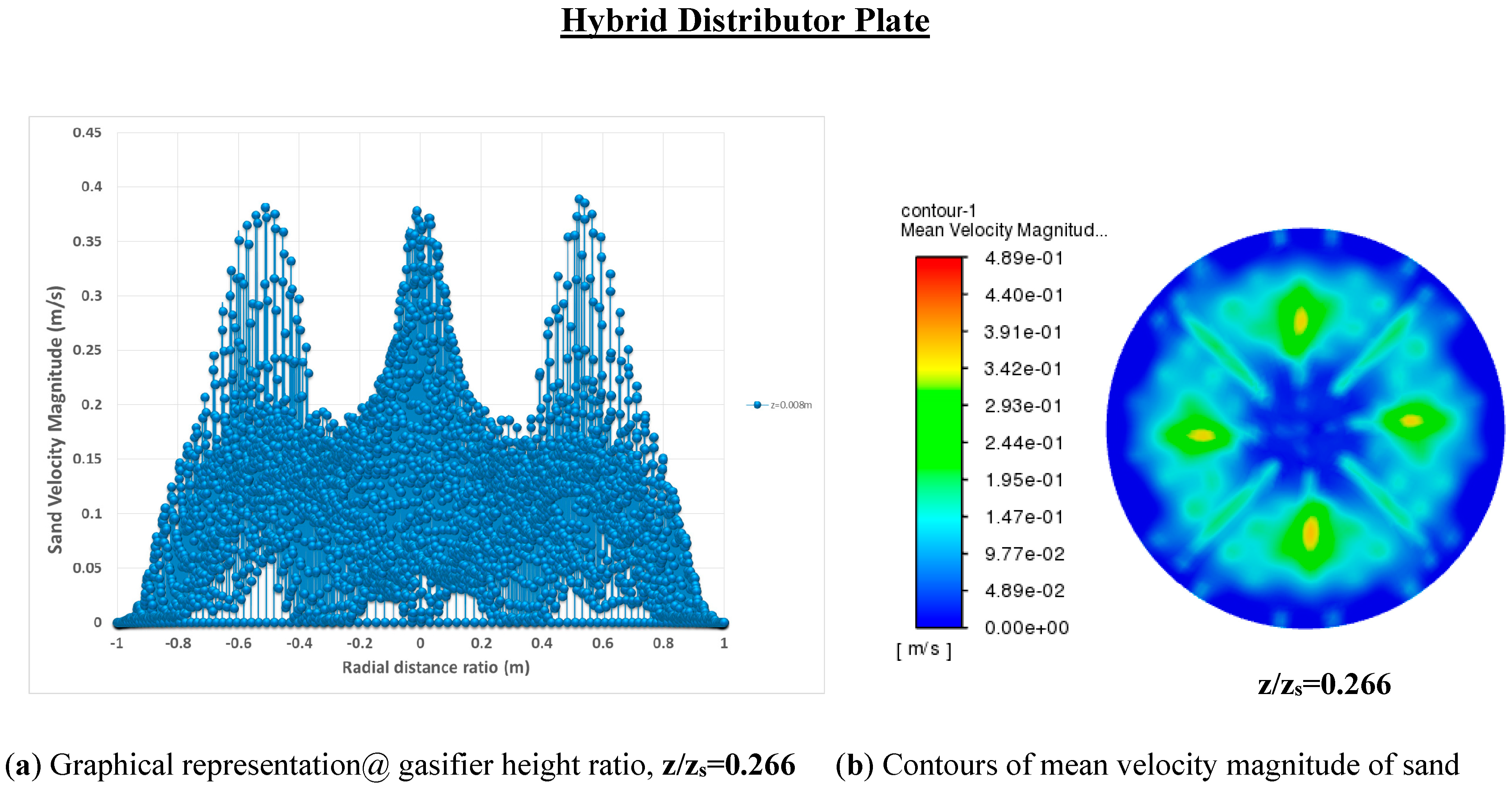
5.4.2. Inside Flow Pattern with Different Distributor Plates
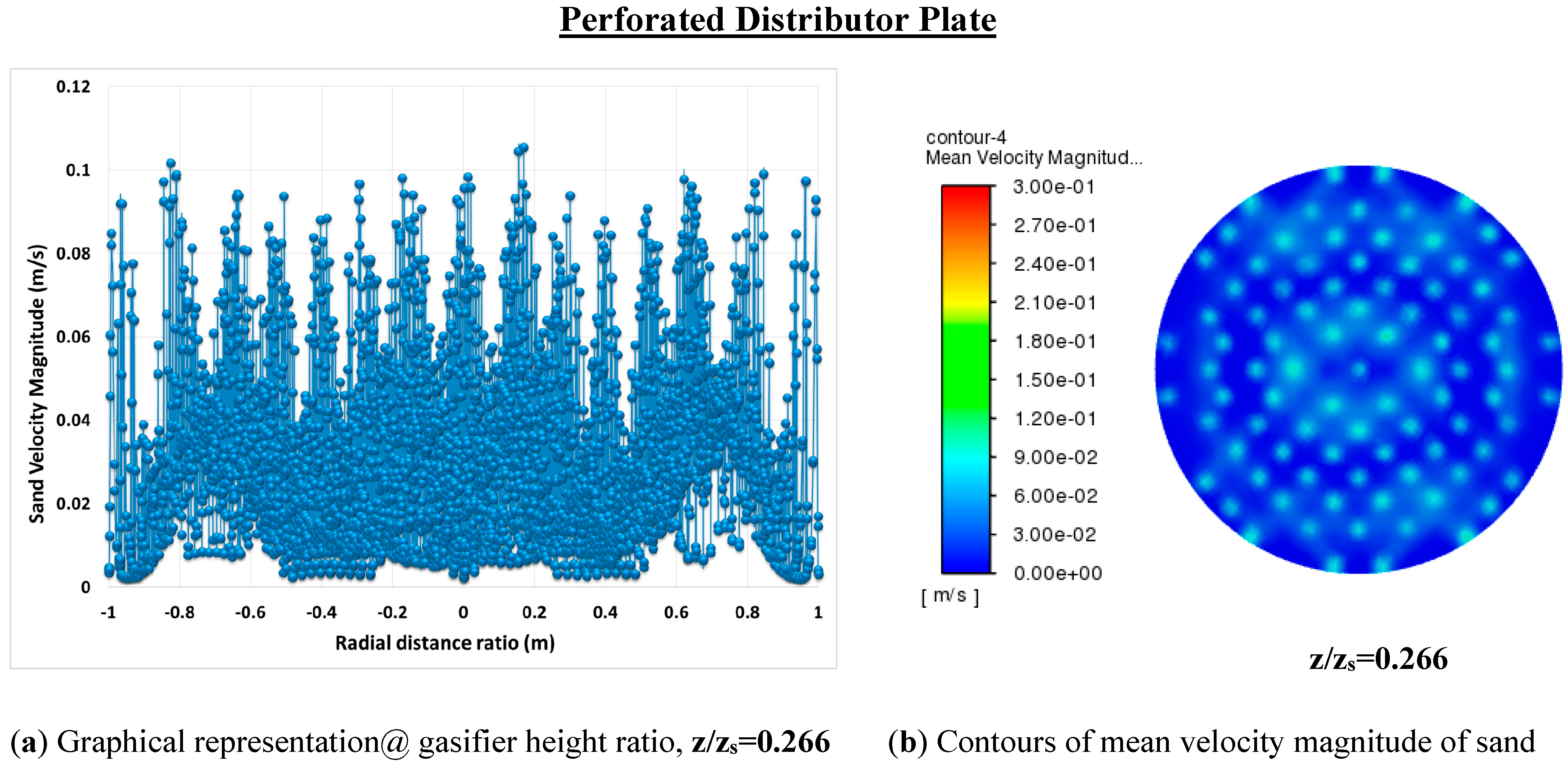
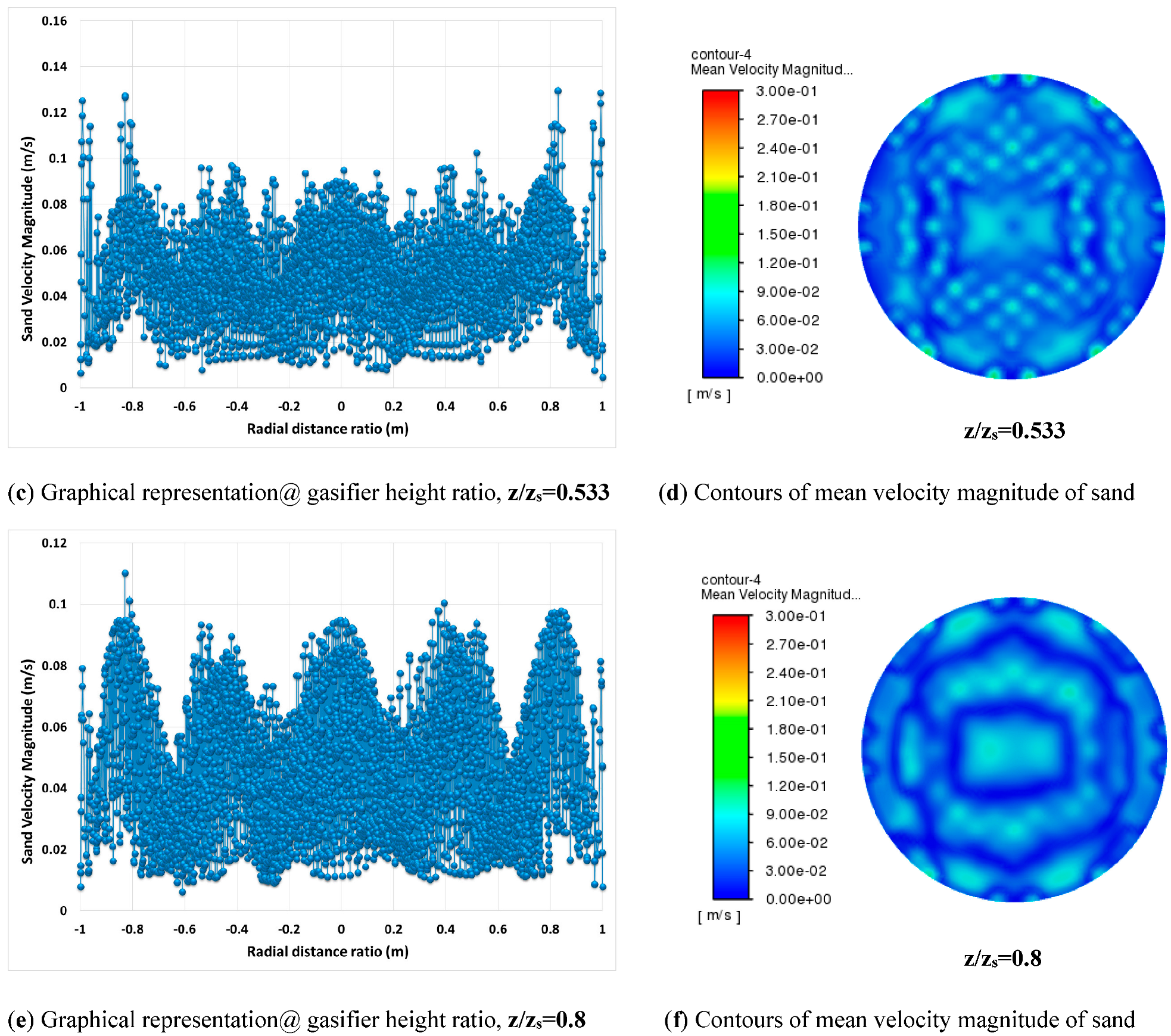
5.4.3. Velocity Distribution of Solid Particles within a Fluidized Zone of a Gasifier
5.5. Conclusions and Recommendations
- The perforated distributor plate exhibits the lowest minimum fluidization velocity compared to the other two.
- Pressure drop is found to be maximum for a 45° slotted plate.
- The hybrid plate shows the lowest pressure drop due to its highest open area ratio. Also, using this plate, minimum fluidization velocity remains between perforated and 45° slotted plate cases.
- Furthermore, a lower portion swirling flow is observed in a 45° slotted plate for better lateral mixing of particles. The initial Bed height rise ratio is also highest for a 45° slotted plate and lowest for a perforated distributor plate due to many smaller-sized bubbles initially rupturing the bed surface.
- It is also revealed that the bubble rise velocity ratio (F.I.) is highest for a perforated distributor plate, whereas it becomes lowest for a 45° slotted plate.
- The 45° slotted plate improves inside mixing and lateral flow in the fluidized bed’s lower portion.
- The hybrid plate improves mixing by combining smaller holes with 45° slots.
- For applications requiring critical lower portion solid mixing and dead zone removal, a 45° slotted plate is recommended.
- The hybrid plate suits various operational conditions and improves gasifier operational efficiency.
- Table 7 of the article summarizes the conclusions on the hydrodynamics of bubbling fluidized bed gasifiers, detailing the findings and recommendations for various operational and geometric parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Volume fraction gas phase [-] | |
| Volume fraction solid phase [-] | |
| Volume fraction of all ‘m’ phases [-] | |
| Gas viscosity [kg m−1 s−1] | |
| Density of solid [kg m−3] | |
| Density of gas [kg m−3] | |
| Shear solid viscosity [kg m−1 s−1] | |
| Solid bulk viscosity [kg m−1 s−1] | |
| CD | Drag coefficient of phases [-] |
| Exchange coefficient of gas solid phases [-] | |
| Solid-phase strain tensor [-] | |
| Gas-phase strain tensor [-] | |
| Solid phase velocity [m s−1] | |
| Gas phase velocity [m s−1] | |
| I | Unity tensor [-] |
| ds | Diameter of solid particles [m] |
| d0 | Diameter of holes of distributor [m] |
| Ls | Length of slot of distributor [m] |
| Ws | Width of slot [m] |
| u0 | Superficial Gas velocity [m s−1] |
| L | Initial bed height [m] |
| D○ | Diameter of Gasifier |
| ϕ | Open area ratio of distributor plate [-] |
| FD | Drag force [kg m s−2] |
| CD | Drag coefficient [-] |
| D | Diameter of distributor plate [m] |
| Umf,b | Minimum bubble rise velocity [m s−1] |
| Umf,f | Final minimum fluidization velocity [m s−1] |
| F.I | Fluidization index [-] |
References
- Salatino, P.; Solimene, R. Mixing and segregation in fluidized bed thermochemical conversion of biomass. Powder Technol. 2017, 316, 29–40. [Google Scholar] [CrossRef]
- Sánchez-Prieto, J.; Hernández-Jiménez, F.; Garcia-Gutierrez, L.M.; Soria-Verdugo, A. Experimental study on the characteristic mixing time of solids and its link with the lateral dispersion coefficient in bubbling fluidized beds. Chem. Eng. J. 2017, 307, 113–121. [Google Scholar] [CrossRef]
- Garcia-Gutierrez, L.; Soria-Verdugo, A.; Ruiz-Rivas, U. Optimization of the feeding ports location in a fluidized bed combustor based on Monte Carlo simulations of fuel particles motion. Fuel 2015, 141, 82–92. [Google Scholar] [CrossRef]
- Niklasson, F.; Thunman, H.; Johnsson, F.; Leckner, B. Estimation of solids mixing in a fluidized-bed combustor. Ind. Eng. Chem. Res. 2002, 41, 4663–4673. [Google Scholar] [CrossRef]
- Basu, P. Combustion and Gasification in Fluidized Beds; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Li, Y.; Rong, J.; Zhang, K.; Fan, X. Impact of solid and gas flow patterns on solid mixing in bubbling fluidized beds. Chem. Eng. Res. Des. 2018, 132, 1037–1053. [Google Scholar] [CrossRef]
- Askarishahi, M.; Salehi, M.-S.; Godini, H.R.; Wozny, G. CFD study on solids flow pattern and solids mixing characteristics in bubbling fluidized bed: Effect of fluidization velocity and bed aspect ratio. Powder Technol. 2015, 274, 379–392. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, H.; Gao, J.; Lu, J.; Wang, Y.; Wang, C. Characterization of gas–solid fluidization in fluidized beds with different particle size distributions by analyzing pressure fluctuations in wind caps. Chem. Eng. J. 2018, 352, 923–939. [Google Scholar] [CrossRef]
- Lin, C.-L.; Wey, M.-Y.; You, S.-D. The effect of particle size distribution on minimum fluidization velocity at high temperature. Powder Technol. 2002, 126, 297–301. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Zhu, X.; Huang, L.; Zhu, X. Experimental study on fluidization behaviors of walnut shell in a fluidized bed assisted by sand particles. RSC Adv. 2018, 8, 40279–40287. [Google Scholar] [CrossRef]
- Feng, D.; Chen, H.; Whiting, W.B. The effects of distributor design on fluidized-bed hydrodynamic behavior. Chem. Eng. Commun. 1985, 36, 317–332. [Google Scholar] [CrossRef]
- Padhi, R.; Dora, D.; Mohanty, Y.; Roy, G.; Sarangi, B. Prediction of bed pressure drop, fluctuation and expansion ratios for three-phase fluidization of ternary mixtures of dolomite in a conical conduit. Cogent Eng. 2016, 3, 1181821. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. CFD-DEM study of biomass gasification in a fluidized bed reactor: Effects of key operating parameters. Renew. Energy 2020, 159, 1146–1164. [Google Scholar] [CrossRef]
- Wang, S.; Luo, K.; Fan, J. CFD-DEM coupled with thermochemical sub-models for biomass gasification: Validation and sensitivity analysis. Chem. Eng. Sci. 2020, 217, 115550. [Google Scholar] [CrossRef]
- Hwang, I.S.; Sohn, J.; Do Lee, U.; Hwang, J. CFD-DEM simulation of air-blown gasification of biomass in a bubbling fluidized bed gasifier: Effects of equivalence ratio and fluidization number. Energy 2021, 219, 119533. [Google Scholar] [CrossRef]
- Chyou, Y.-P.; Chang, D.-M.; Chen, P.-C.; Chien, H.-Y.; Wu, K.-T.; Chein, R.-Y. Development of biomass gasification technology with fluidized-bed reactors for enhancing hydrogen generation: Part I, hydrodynamic characterization of dual fluidized-bed Gasifiers. Appl. Sci. 2019, 10, 2. [Google Scholar] [CrossRef]
- Hatate, Y.; Uemura, Y.; Migita, M.; Kawano, Y.; Tanaka, Y.; Ijichi, K.; King, D. Effect of Distributor on Bubble Size and Bubble Rise Velocity in the Slugging Regime of a Semi-Cylindrical Gas-Solid Fluidized Bed. Chem. Eng. Commun. 1991, 101, 39–44. [Google Scholar] [CrossRef]
- Dhrioua, M.; Hassen, W.; Kolsi, L.; Anbumalar, V.; Alsagri, A.S.; Borjini, M.N. Gas distributor and bed material effects in a cold flow model of a novel multi-stage biomass gasifier. Biomass Bioenergy 2019, 126, 14–25. [Google Scholar] [CrossRef]
- Sobrino, C.; Acosta-Iborra, A.; Santana, D.; de Vega, M. Bubble characteristics in a bubbling fluidized bed with a rotating distributor. Int. J. Multiph. Flow 2009, 35, 970–976. [Google Scholar] [CrossRef]
- Nakamura, H.; Kondo, T.; Watano, S. Improvement of particle mixing and fluidization quality in rotating fluidized bed by inclined injection of fluidizing air. Chem. Eng. Sci. 2013, 91, 70–78. [Google Scholar] [CrossRef]
- Sobrino, C.; Ellis, N.; de Vega, M. Distributor effects near the bottom region of turbulent fluidized beds. Powder Technol. 2009, 189, 25–33. [Google Scholar] [CrossRef]
- Sobrino, C.; Almendros-Ibañez, J.A.; Santana, D.; de Vega, M. Fluidization of Group B particles with a rotating distributor. Powder Technol. 2008, 181, 273–280. [Google Scholar] [CrossRef]
- Xiong, Q.; Yeganeh, M.M.; Yaghoubi, E.; Asadi, A.; Doranehgard, M.H.; Hong, K. Parametric investigation on biomass gasification in a fluidized bed gasifier and conceptual design of gasifier. Chem. Eng. Process. Process Intensif. 2018, 127, 271–291. [Google Scholar] [CrossRef]
- Yudin, A.S.M.; Anuar, S.; Oumer, A.N.J.A.P.T. Improvement on particulate mixing through inclined slotted swirling distributor in a fluidized bed: An experimental study. Adv. Powder Technol. 2016, 27, 2102–2111. [Google Scholar] [CrossRef]
- Sreenivasan, B.; Raghavan, V.R. Hydrodynamics of a swirling fluidised bed. Chem. Eng. Process. Process Intensif. 2002, 41, 99–106. [Google Scholar] [CrossRef]
- Najafi, A.F.; Mousavian, S.M.; Amini, K. Numerical investigations on swirl intensity decay rate for turbulent swirling flow in a fixed pipe. Int. J. Mech. Sci. 2011, 53, 801–811. [Google Scholar] [CrossRef]
- Eslami Afrooz, I.; Chuan Ching, D.L. Effect of novel swirl distributor plate on hydrodynamics of fluidized bed gasifier. Int. J. Eng. 2019, 32, 1358–1365. [Google Scholar]
- Ghasem, N.M.; Ang, W.L.; Hussain, M.A. Dynamics and stability of ethylene polymerization in multizone circulating reactors. Korean J. Chem. Eng. 2009, 26, 603–611. [Google Scholar] [CrossRef]
- Raza, N.; Ahsan, M.; Mehran, M.; Naqvi, S.; Ahmad, I.J.E.R. Computational Analysis of the Hydrodynamic Behavior for Different Air Distributor Designs of Fluidized Bed Gasifier. Front. Energy Res. 2021, 9, 692066. [Google Scholar] [CrossRef]
- Al-Akaishi, A.; Valera-Medina, A.; Chong, C.; Marsh, R.J.E.P. CFD analysis of the fluidised bed hydrodynamic behaviour inside an isothermal gasifier with different perforated plate distributors. Energy Procedia 2017, 142, 835–840. [Google Scholar] [CrossRef]
- Kang, P.; Hu, X.E.; Lu, Y.; Wang, K.; Zhang, R.; Han, L.; Yuan, H.; Chen, H.; Luo, X.; Zhou, Y.J. Modeling and Optimization for Gas Distribution Patterns on Biomass Gasification Performance of a Bubbling Spout Fluidized Bed. Energy Fuels 2020, 34, 1750–1763. [Google Scholar] [CrossRef]
- Bakhurji, A.; Bi, X.; Grace, J.R. Hydrodynamics and solids mixing in fluidized beds with inclined-hole distributors. Particuology 2019, 43, 19–28. [Google Scholar] [CrossRef]
- Yohana, E.; Muchammad; Tauviqirrahman, M.; Sayekti, A.A.; Choi, K.-H.; Paramita, V. Effect of particle size and bed height on the characteristic of a fluidized bed dryer. Cogent Eng. 2020, 7, 1738185. [Google Scholar] [CrossRef]
- Hamzehei, M. CFD modeling and simulation of hydrodynamics in a fluidized bed dryer with experimental validation. Int. Sch. Res. Not. 2011, 2011, 131087. [Google Scholar] [CrossRef]
- Russell, A.; Schmelzer, J.; Müller, P.; Krüger, M.; Tomas, J. Mechanical properties and failure probability of compact agglomerates. Powder Technol. 2015, 286, 546–556. [Google Scholar] [CrossRef]
- Timsina, R.; Thapa, R.K.; Moldestad, B.M.E.; Eikeland, M.S. Effect of particle size on flow behavior in fluidized beds. Int. J. Energy Prod. Manag. 2019, 4, 287–297. [Google Scholar] [CrossRef]
- Bandara, J.; Eikeland, M.S.; Moldestad, B.M.E. Analyzing the effects of particle density, size, size distribution and shape for minimum fluidization velocity with Eulerian-Lagrangian CFD simulation. Linkop. Electron. Conf. Proc. 2017, 138, 60–65. [Google Scholar] [CrossRef]
- Abrahamsen, A.R.; Geldart, D. Behaviour of gas-fluidized beds of fine powders part I. Homogeneous expansion. Powder Technol. 1980, 26, 35–46. [Google Scholar] [CrossRef]
- Ram, D.K. The determination of minimum bubbling velocity, minimum fluidization velocity and fluidization index of fine powders (hematite) using gas-solid tapered beds. Int. J. Sci. Res. 2013, 2, 287–293. [Google Scholar]
- Guenther, C.; Syamlal, M.; Shadle, L.; Ludlow, C. A numerical investigation of an industrial scale gas–solids CFB. Circ. Fluid. Bed Technol. VII 2002, 73, 483–488. [Google Scholar]
- Andrews IV, A.T.; Loezos, P.N.; Sundaresan, S. Coarse-grid simulation of gas-particle flows in vertical risers. Ind. Eng. Chem. Res. 2005, 44, 6022–6037. [Google Scholar] [CrossRef]
- Shukrie, A.; Anuar, S.; Oumer, A.N. Air distributor designs for fluidized bed combustors: A review. Eng. Technol. Appl. Sci. Res. 2016, 6, 1029–1034. [Google Scholar] [CrossRef]












| Bed Material | Galdert Classification | Average Particle Diameter (µm) | Bulk Density (kg/m3) | Particle Density (kg/m3) | Void Fraction (%) |
|---|---|---|---|---|---|
| Sand 1 | Type B | 250 | 1234 | 2420 | 51 |
| Sand 2 | Type B | 590 | 1330 | 2510 | 53 |
| Sand 3 | Type B | 850 | 1424 | 2590 | 55 |
| Distributor Type | Diameter of the Plate, D (m) | The Thickness of the Plate, t (m) | Diameter of Holes, d0 (m) | Length of Slot, l (m) | Width of Slot, W (m) | Open Area Ratio γ (%) | Number of Holes/Slots |
|---|---|---|---|---|---|---|---|
| Perforated | 0.125 | 0.008 | 0.005 | - | - | 14.25 | 89 (holes) |
| 45° degree | 0.125 | 0.008 | - | 0.03 | 0.0065 | 13.99 | 8 (Slots) |
| Hybrid | 0.125 | 0.008 | 0.005 | 0.03 | 0.0065 | 25.55 | 89 + 8 (holes + slots) |
| Number of Plates = 3 Perforated Plate, 45° Slotted Plate, Hybrid Plate (Perforated + Slotted) | ||||
|---|---|---|---|---|
| Operational Variables | ||||
| Input Variables | Output Variables | |||
| Geometric Variables Three designs of Distributor Plates.
| Superficial Air Velocities | 1.5*Umf | 3.0*Umf |
|
| Initial bed Height Ratio (L/D)/bed aspect ratio | 0.5, 0.833, 1.16 | 0.5, 0.833, 1.16 | ||
| Particle Size (µm) | 250, 590, 850 | 250, 590, 850 | ||
| Particle Size µm | Density of Particles (kg/m3) | Perforated Plate F.I. (Umf,b/Umf,f) | 45° Plate F.I. (Umf,b/Umf,f) | Novel Hybrid Plate F.I. (Umf,b/Umf,f) |
|---|---|---|---|---|
| 250 | 2590 | 1.211 | 1.013 | 1.151 |
| 590 | 2510 | 1.203 | 1.026 | 1.101 |
| 850 | 2420 | 1.172 | 1.005 | 1.017 |
| Properties of Gas and Particle Flow | Parameter Values |
|---|---|
| Mean Particle diameter (µm) | 250, 590, 850 |
| Density of sand (kg/m3) | 2590, 2510, 2420 |
| Density of air (kg/m3) | 1.225 |
| Multiphase model | Eulerian-Eulerian |
| Superficial gas velocity (m/s) | 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4.0, 4.5 |
| Restitution coefficient | 0.90 |
| Packing limit of solids | 0.63 |
| Drag model for gas-solid flows | Syamlal-Obrien |
| Solution methodology | Pressure velocity coupling |
| Mesh Generated | Grid Size (Number of Cells) | Pressure Drop (CFD) (Pa)@ Superficial Velocity (m/s) [1.5Umf] | Pressure Drop (Experiment) (Pa) | Maximum Solid Volume Fraction L/D = 0.4 |
|---|---|---|---|---|
| Light | 4.0 × 105 | 902 | 1120 | 0.38 |
| Medium | 1.2 × 106 | 1052 | 0.51 | |
| Heavy | 2.0 × 106 | 1071 | 0.58 |
| Operational Parameters | Geometric Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Static Distributor Plates | |||||||||
| Perforated | 45° Slotted | Novel Hybrid Plate | |||||||
| Pros | Cons/Limitation | Remarks | Pros | Cons/Limitation | Remarks | Pros | Cons/Limitation | Remarks | |
| Pressure drop, Minimum fluidization velocity, Bed aspect ratio, Bubble rise velocity, bed height rise, superficial gas velocity. | Uniform distribution of particles at the mid and upper section of fluidization zone, lower minimum fluidization velocity. | Moderate to high Pressure drop, probability of dead zones at the lower bed zones, the possibility of de-fluidization phenomena. | Due to dominant axial velocity component the chances of solid particles elutriation are higher at higher flow rates. | Lower portion swirling flow for better mixing of solid particles. Limit the chances of de-fluidization, lower average bed fluctuations. | Higher Pressure drop due to higher open area ratio and angular flow of gas solid flow towards periphery of gasifier, higher minimum fluidization velocity. | Due to initial tangential and radial component of flow the solid particles move towards periphery tend to lose more energy of fluidizing medium. | Wide range of initial bed height can be possible from low to high, Lower pressure drop, moderate minimum fluidization velocity, moderate bed height rise, long range particle size inclusion for fluidization, both axial and swirling flow motion. | Elutriation of particles can happen at higher flow rates. | Due to hybrid openings of plate, both axial and tangential velocity of flow resulted in moderate bed height rise. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, N.; Mehdi, R.; Ahsan, M.; Mehran, M.T.; Naqvi, S.R.; Uddin, E. Optimizing Design and Operational Parameters for Enhanced Mixing and Hydrodynamics in Bubbling Fluidized Bed Gasifiers: An Experimental and CFD-Based Approach. Appl. Sci. 2023, 13, 9317. https://doi.org/10.3390/app13169317
Raza N, Mehdi R, Ahsan M, Mehran MT, Naqvi SR, Uddin E. Optimizing Design and Operational Parameters for Enhanced Mixing and Hydrodynamics in Bubbling Fluidized Bed Gasifiers: An Experimental and CFD-Based Approach. Applied Sciences. 2023; 13(16):9317. https://doi.org/10.3390/app13169317
Chicago/Turabian StyleRaza, Naveed, Rifat Mehdi, Muhammad Ahsan, Muhammad Taqi Mehran, Salman Raza Naqvi, and Emad Uddin. 2023. "Optimizing Design and Operational Parameters for Enhanced Mixing and Hydrodynamics in Bubbling Fluidized Bed Gasifiers: An Experimental and CFD-Based Approach" Applied Sciences 13, no. 16: 9317. https://doi.org/10.3390/app13169317
APA StyleRaza, N., Mehdi, R., Ahsan, M., Mehran, M. T., Naqvi, S. R., & Uddin, E. (2023). Optimizing Design and Operational Parameters for Enhanced Mixing and Hydrodynamics in Bubbling Fluidized Bed Gasifiers: An Experimental and CFD-Based Approach. Applied Sciences, 13(16), 9317. https://doi.org/10.3390/app13169317








