UAV-Assisted Caching Strategy Based on Content Cache Pricing in Vehicular Networks

Abstract

A UAV-assisted caching strategy considering content cache pricing in vehicular networks is proposed to address the problem of high communication load and high backhaul link overhead in vehicular networks. Consider a traffic scenario consisting of a content provider (CP), a network operator (NO), and multiple mobile users, where the NO has a set of cache-enabled roadside units (RSUs) and an unmanned aerial vehicle (UAV). The CP leases some popular contents to the NO for its benefit and the NO places this leased content in its RSU’s local cache to save expensive backhaul transmission overhead and latency. However, both NO and CP are selfish and their interests conflict with each other because they have opposing expectations for content pricing. In order to take into account the interests of both, this paper defines the utilities of CP and MNO and uses the Stackelberg game framework to model the competition between the two entities, where CP acts as a leader and sets the rental price of the content and NO acts as a follower responding to CP’s actions. An iteration-based dynamic programming algorithm is also designed to find the Stackelberg equilibrium. Meanwhile, a caching-capable UAV is introduced into the vehicular network and, based on this, a Dijkstra-based path planning algorithm is designed to further increase the total utility of NO by optimizing the trajectory of the UAV. The simulation results show that the strategy in this paper can reasonably allocate the benefits of CP and NO, reduce the average request delay, and increase the utility of NO; for example, we reduced the request latency for vehicle users by 27% and increased the total utility of NO by 13%.

1. Introduction

With the rapid development of vehicular networks, more and more in-vehicle applications are enriching the functions of vehicles, such as intelligent transportation, in-vehicle entertainment, in-vehicle office, road safety, and driverless applications. Vehicles need to obtain a variety of information from the outside world, such as traffic information, entertainment information, and real-time news, in order to provide users with a better driving experience. However, the number of vehicles is increasing dramatically and the information that users want to obtain is becoming more and more diverse, which leads to a dramatic increase in the communication load of the vehicular network. In addition, due to the high-speed mobility of vehicles, the topology of the vehicular network changes rapidly, making the communication links of vehicles easily interrupted, which leads to a degradation of the user’s quality of experience. In order to reduce the workload of vehicular networks and improve the communication quality of the networks, caching techniques have been introduced in vehicular networks.

Caching technology in vehicular networks is to cache content at various nodes such as RSUs and vehicles at the edge of the network, so that vehicles can receive the demanded content directly from surrounding nodes, thus effectively reducing the communication distance for requesting vehicles to receive content and reducing the traffic load on content servers and networks. The more common caching strategies currently applied in in-vehicle networks can be categorized into non-cooperative caching [1,2] and cooperative caching [3,4,5,6], which reduce the impact of vehicle mobility on the in-vehicle network and improve the quality of service.

However, the above studies only determine the caching strategy from the perspective of the caching node, aiming at reducing the traffic load on the network or enhancing the user’s quality of experience, and do not consider the overhead caused by caching as well as the benefits gained. In order to reduce request latency and save overhead, NO often chooses to rent some contents from remote CP at a cost and cache them on the network’s edge devices, so a reasonable rental price and caching decision will benefit both the NO and the CP.

Most of the current papers that study the caching problem from an economic perspective do not utilize flexible air mobile caching devices for assistance, such as UAVs. Vehicle users in the vehicular network have high-speed mobility and have a short contact time with the cache nodes with fixed positions on the ground; the introduction of UAVs with caching function in the vehicular network can effectively solve this problem and reduce the average request latency of vehicle users.

In summary, existing caching strategies in in-vehicle networks do not simultaneously consider the overhead, revenue, or air resources utilization in the delivery process, so this paper designs a UAV-assisted caching strategy based on content cache pricing in vehicular networks. Specifically, we consider a traffic scenario consisting of a CP, an NO, and multiple mobile subscribers. The CP rents some popular content to the NO for profit, while the NO puts these contents into its RSU’s local cache to save on costly backhaul transmission overhead and latency. However, CP and NO are both selfish and their interests conflict with each other because they have opposite expectations on content pricing. Therefore, we model the competition between the VP and MNO as a Stackelberg game to jointly maximize the profits of the VP and MNO. Meanwhile, a UAV with caching capability is utilized to further reduce the request latency and increase the utility of the NO. The innovative points of this paper are as follows:

(1) A UAV-assisted vehicular network caching model considering the economic relationship between CP and NO is constructed. CP leases some popular contents to NO for benefits and NO caches these leased contents in RSU to save expensive backhaul transmission overhead and latency. The utility of CP and NO is defined by analyzing the benefit relationship between CP, NO, and vehicle users.

(2) The competing interests of CP and NO are modeled using the Stackelberg game model, where CP is the leader and NO is the follower. An iteration-based dynamic programming algorithm is designed to find the Stackelberg equilibrium point to obtain the optimal caching decision for the RSU and content rental price.

(3) A UAV with caching function is introduced into the vehicular network, which caches the contents already leased by the RSUs. A Dijkstra-based path planning algorithm is designed to further increase the total utility of the NO and improve the quality of service by optimizing the trajectory of the UAV.

The next sections of this paper are organized as follows: Section 2 reviews the related works in the literature; Section 3 gives the system model and contents delivery decision and establishes the optimization problem; Section 4 designs the joint optimization algorithm for the caching decision of the RSU and the trajectory of the UAV; Section 5 gives the simulation results of the algorithm and analyzes them; Section 6 concludes the whole paper.

2. Related Work

In terms of caching strategies, the undifferentiated caching strategy proposed by [1] means that the content is cached at each network node through which it passes. The caching with probability strategy proposed by [2] means that a network node caches the content that passes through that node with some fixed probability. These non-cooperative caching strategies make the content have a high redundancy in the network, resulting in a wastage of caching resources. In cooperative caching strategies, multiple nodes in the network cooperate with each other to effectively reduce the redundancy of content in the network. The authors of [3] identified and formulated the problem of maximizing the average cache hit rate considering the time-varying topology of the network, vehicle mobility, user preferences, and the limited cache capacity of the RSU. A cache update policy based on learning automata is designed to determine the appropriate content to be cached in the RSU. The authors of [4] proposed a file partitioning and grouping scheme in a distributed coding cache system that designs a static single-server system for heterogeneous file transfers. The authors of [5] designed a collaborative edge caching scheme based on location and popular content and proposed an optimal collaborative content layout for macro base stations and RSUs to reduce transmission latency and service cost. Ref. [6] proposed an active caching scheme for parked vehicles that uses parked vehicles to cache data in advance at appropriate times and locations so that users can receive the data as they pass by.

In order to study the issue of caching from an economic perspective, the authors of [7] considered a concave pricing mechanism where CPs are charged through a concave price function of the time that content is cached in the CP cache. The proposed concave pricing mechanism is analyzed theoretically and provides a solution for CPs to optimally choose the length of time to stay in the ISP cache. The authors of [8] considered transcoding between different versions of video and the base station considered the energy consumption value when caching video clips; then, based on the different uses of caching, base station computational resources, and backhaul links by the in-vehicle users, they proposed a network resource pricing algorithm to improve the flexibility of the utilization of in-vehicle network resources. Ref. [9] focused on the complex relationship between competition and cooperation among multiple CPs and solved a non-cooperative game model based on game theory to study the interaction between caching and pricing strategies of ICN entities. By establishing the optimal utility function of each entity, the optimal cache share of ISP (internet service provider) and the optimal pricing of ISP and CP are obtained. The authors of [10] proposed a joint video pricing and cache placement strategy by considering the heterogeneity of video file sizes and the classical law of demand in the field of economics, maximizing the profit of both CP and NO in the case of non-cooperative base station caching and cooperative base station caching. The authors of [11] focused on caching and transaction models for vehicular networks and proposed a generic cache valuation and online pricing framework to achieve the goals of incentive compatibility, personal rationality, privacy preservation, computational efficiency, and utility maximization.

In terms of utilizing UAVs, the authors of [12] optimized the caching and computational resource allocation of the network by optimizing the trajectory and flight altitude of the UAVs. In [13], an active caching scheme was designed in which UAVs were dispatched to provide content delivery services to vehicular users in a specific area. Ref. [14] considered content delivery in terrestrial networks for low earth orbit (LEO) satellites and cache-assisted UAV communications. The minimum achievable throughput per ground user (GU) is maximized by co-optimizing cache placement, UAV resource allocation, and trajectory with limited cache capacity and flight time. The authors of [15] considered a scenario where infrastructure is rendered unusable due to a disaster situation and use UAVs to service vehicles in the affected area to meet the quality of service for users. The authors of [16] used UAVs to help with infrastructure operations. Since deploying multiple UAVs incurs greater costs, the number of UAVs dispatched is optimized to provide coverage of specific areas. In [17], the authors investigated communication with multiple UAVs with an onboard network and proposed an efficient collaborative UAV sensing and sending protocol. Ref. [18] proposed a joint optimization problem for UAV deployment and content placement to minimize the average request latency and proposed a Q-learning algorithm to solve the content placement problem. In [19], the authors proposed a UAV network that transmits data from the vehicle to the core network, where one UAV serves the vehicle and the others are used to relay the data, saving energy by limiting the maneuverability of the UAVs in a certain area.

3. System Model

The system model is shown in Figure 1. The system includes a CP, an NO, and multiple mobile onboard users; the NO has a set of cache-enabled RSUs and a cache-enabled UAV, where the coverage of the RSUs is $C_R$ and the coverage of the UAV is $C_U$, $C_R>C_U$. The CP rents some of the contents to the NO and the NO caches this rented content in the RSUs to save the expensive transmission cost. The roads in the city are two-way lanes with lanes appearing in pairs and there are two road sections, each of length $L$. An RSU is deployed next to each road section, which can provide services to vehicles on that road section, with the RSU on the left road section denoted as $R_l$ and the RSU on the right road section denoted as $R_r$. A UAV with caching capabilities is deployed over the road sections to assist the RSUs in providing services to vehicle users.

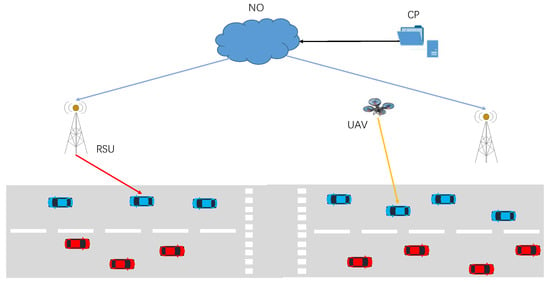
Figure 1. A content caching system comprising a CP and an MNO with cache-enabled RSUs and vehicular users.

3.1. Traffic Model

In a dense urban vehicle environment, vehicles at the same moment tend to travel at similar speeds. However, as time changes, changes in traffic conditions will affect the number of vehicles on the lane; for example, changes in traffic lights will lead to changes in vehicle density. In this paper, we assume that there exists a set of continuous time periods set, denoted as $T=\left\{T_1,\cdots ,T_x,\cdots ,T_X\right\}$, and the vehicles in each time period travel at the same uniform speed and the vehicle users in different time periods travel at different speeds. Use $\left\{n_1^l,\cdots ,n_x^l,\cdots ,n_X^l\right\}$ and $\left\{n_1^r,\cdots ,n_x^r,\cdots ,n_X^r\right\}$ to denote the number of vehicles entering the roadway from the left and right, respectively, at each time period. Then, the total number of vehicle users coming in from the left side of the roadway is $N_l={\displaystyle \sum _{x=1}^X{n}_x^l}$ and the total number of vehicle users coming in from the right side of the roadway is $N_r={\displaystyle \sum _{x=1}^X{n}_x^r}$.

For the movement of the UAV, the road is divided into several rectangular blocks and the side length of each rectangular block is the coverage diameter of the UAV. Taking each time period Tx as a trajectory optimization cycle, the UAV stays in a block during a trajectory optimization cycle to serve the vehicle users in that block and selects an adjacent block at the end of the current trajectory optimization cycle to fly to that block in the next cycle, i.e., whenever the vehicle density changes, the UAV’s position also changes. Choosing different flight trajectories results in different gains and time delays. It is worth noting that the caching decision of frequent node replacement will incur a large overhead, so the optimization of caching decision is a long-time optimization, while the UAV has mobility and needs to plan the flight trajectory for each time slot for it, which is a short-time optimization; the relationship between the two is shown in Figure 2.

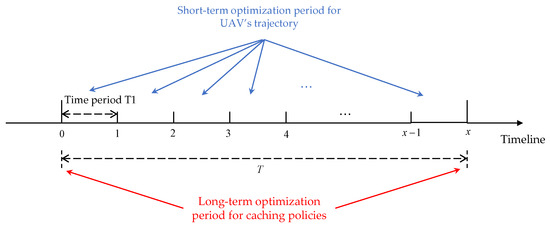
Figure 2. The relationship between the long-term optimization period of the caching policies and the short-term optimization period of the UAV’s trajectory.

3.2. Content Request Model

Assume that there is a total of $I$ contents, each of equal size, all of $s$. The set of contents is denoted as $F=\left\{F_1,\cdots ,F_i,\cdots ,F_I\right\}$. Due to the unstable topology of the in-vehicle network, the vehicle user transmission link may be interrupted, resulting in content acquisition failure. In order to ensure the success rate of content transmission, this paper divides the content into a number of equal-sized content blocks and, if the communication link is broken during transmission, the content blocks that have not been transmitted will be discarded and need to be transmitted again after the link is re-established.

The probability of a file being requested is positively correlated with the file popularity ranking; the probability of the file with the highest popularity ranking being requested can be expressed as [20]

$$P{R}_{\tau }=\frac{{\tau }^{-\gamma }}{{\displaystyle \sum _{f=1}^F{f}^{{}^{-\gamma }}}},\tau \in [1,F]$$

(1)

where $\gamma$ denotes the exponential constant of the Zipf distribution; the larger $\gamma$ is, the more the user’s requests are concentrated in the top ranked files in terms of popularity; $\tau$ denotes the ranking of the files in the file library. It is assumed that each vehicle user will request content according to popularity before driving off the first road; the request time follows a uniform distribution. The content request indicator variable is denoted by $r{e}_{n,i}^t$, and $r{e}_{n,i}^t=1$ indicates that $v_n$ has requested $f_i$ at the moment $t$, otherwise $r{e}_{n,i}^t=0$.

3.3. Caching Model and Content Delivery Strategy

In the scenario of this paper, the NO leases some contents from the CP and caches them in the RSUs and pays a fee to the CP, while the UAV caches the leased content from the RSUs without paying an additional fee. The set of $R_m$-caching decision indicator variables is denoted by $Y_m^R=\left\{y_{m,1}^R,\cdots y_{m,i}^R,\cdots ,y_{m,I_m}^R\right\}$, where $y_{m,i}^R$ is the caching indicator variable of $R_m$ for content $f_i$, $m\in \left\{l,r\right\}$ and $y_{m,i}^R=1$ if $R_m$ caches content $f_i$, otherwise $y_{m,i}^R=0$. The UAV will select the content with high popularity from the content rented by the NO to cache. If the node caches the content requested by the vehicle user it is a cache hit, otherwise it is a cache miss.

This paper involves both caching nodes, RSU and UAV, and the UAV only caches content leased by the RSU. Thus, for each content there are three caching cases: not cached by any caching node, cached only by RSU, and cached by both RSU and UAV. If the content is not cached by any node, the user of the vehicle requesting it will be on hold until it leaves the road. Then, the user will receive the content from the CP via the RSU relay. If the content is only cached by the RSU, the vehicle user obtains the content via the RSU. If the content is cached by both the RSU and the UAV, the vehicle user requesting it receives the content from the UAV first, as the transmission speed of the UAV is greater than that of the RSU. This situation is more complex and the delivery process can be divided into three cases as shown in Figure 3. Taking the delivery decision for content $f_i$ as an example, the analysis is as follows:

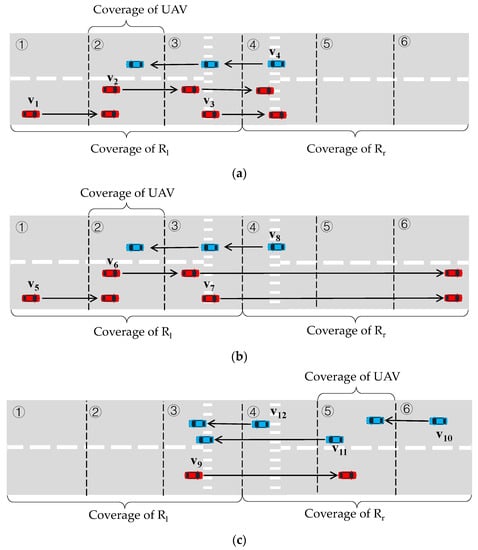
Figure 3. Content delivery process when both UAV and RSU cache content f_i. (a) Both RSUs and UAVs cached f_i; (b) the UAV and one RSU cache f_i, the other does not, and the UAV stays in the section where f_i is cached; (c) the UAV and one RSU cache f_i, the other does not, and the UAV stays in the section where f_i is not cached.

For the case where both RSUs and the UAV have cached $f_i$, take the example of a UAV staying on the road section where $R_l$ is located, as shown in Figure 3a. When a vehicle drives in from the $R_l$ side of the road section, if the vehicle user requests $f_i$ when it is not in the UAV coverage range, such as $V_1$, the user will first obtain $f_i$ from $R_l$ and, if it is still not obtained when driving into the UAV coverage range (rectangle block ②), it will continue to obtain $f_i$ from the UAV. If the vehicle user requests $f_i$ while within the coverage of the UAV, e.g., $V_2$, the user will first obtain $f_i$ from the UAV and, if it is still not fully obtained when driving out of the UAV coverage, the remainder will continue to be obtained from $R_l$, and, if it is still not fully obtained when driving out of the $R_l$ section, it will continue to obtain $f_i$ from $R_r$. If the vehicle user requests $f_i$ after driving through the coverage area of the UAV, e.g., $V_3$, it first obtains $f_i$ from $R_l$ and continues to obtain $f_i$ from $R_r$ if it is still not fully acquired when driving out of the section where $R_l$ is located. When a vehicle drives in from the $R_r$-side section, as in $V_4$, it first acquires f from $R_r$, continues to acquire $f_i$ from $R_l$ if it has not yet fully acquired the content and is not in the coverage area of the UAV when it drives out of the $R_r$ section, and continues to acquire $f_i$ from the UAV if it has not yet fully acquired it when it drives into the coverage area of the UAV. The delivery process is the same when the UAV stays in the section where $R_r$ is located.

For the case where the UAV and one RSU caches $f_i$ and the other RSU does not, the UAV stays on the road section where the RSU that caches $f_i$ is located. Take the case where $R_l$ caches $f_i$, $R_r$ is not cached, and the UAV stays on the $R_l$ side, as shown in Figure 3b. When a vehicle drives in from the $R_r$ side of the roadway, if the vehicle user sends a request when it is not in the coverage range of the UAV, e.g., $V_5$, the user will first obtain $f_i$ from $R_l$ and continue to obtain $f_i$ from the UAV if the content is still not fully obtained when it drives into the coverage range of the UAV. If the vehicle user sends a request within the coverage area of the UAV, e.g., $V_6$, it will first obtain $f_i$ from the UAV, then continue to obtain $f_i$ from $R_r$ if the content is still not fully available when driving out of the UAV’s coverage area. If the content is still not fully available when driving out of the section where $R_r$ is located, it will enter a wait state until it has driven the entire section and then obtain the content from the CP. If the vehicle user requests $f_i$ after driving through the UAV coverage, e.g., $V_7$, it first obtains content from $R_l$ and, if it still does not fully obtain $f_i$ when it leaves the section where $R_l$ is, it enters a wait state until it leaves the $R_r$ section and obtains $f_i$ from the CP. When the vehicle enters from the $R_r$ side of the road, e.g., $V_8$, it sends a request and then enters a wait state until it enters the $R_l$ section and starts to obtain $f_i$ from $R_l$; if it still has not fully obtained the content when it enters the UAV coverage, it continues to obtain it from the UAV.

For the case where the UAV and one RSU caches $f_i$ and the other does not, the UAV stays on the road section where the RSU that does not cache the content is located. Take the example of $R_l$ caching $f_i$, $R_r$ not caching, and the UAV staying on the $R_r$ side, as shown in Figure 3c. When a vehicle drives in from the $R_r$ side of the roadway, as in $V_9$, it first acquires content from $R_l$ and, if it does not fully acquire content when driving out of the $R_l$ roadway, it continues to acquire $f_i$ from the UAV. When the vehicle is approaching from the $R_r$-side section, if the vehicle user sends a request when it is not in the coverage area of the UAV, e.g., $V_{10}$, it enters a wait state until it is in the coverage area and obtains $f_i$ from the UAV. If the vehicle user sends a request, e.g., $V_{11}$, while in the coverage area of the UAV, it first obtains $f_i$ from the UAV and, if the content is still not fully obtained when driving out of the coverage area of the UAV, it enters the wait state until it drives into the $R_r$ side section and obtains $f_i$ from the $R_r$. If the vehicle user sends a request, e.g., $V_{12}$, after driving through the coverage area of the UAV, it enters the wait state until it drives into the $R_r$ side section and obtains $f_i$ from the $R_r$.

3.4. Communication Model and Latency Analysis

This section analyses the communication model and latency for the vehicle user. When the vehicle user is at position $l$, the rate at which the roadside unit $R_m$, $m\in \left\{l,r\right\}$, transmits content to the vehicle user v is expressed as

$$R_{m,n}^{\mathit{RV}}\left(l\right)=B{\mathit{log}}_2\left(1+\frac{P_m{G}_{m,n}\left(l\right)}{{\sigma }^2}\right)$$

(2)

where $P_m$ is the transmit power of $R_m$; $G_{m,n}\left(l\right)$ denotes the channel gain between $R_m$ and $v_n$ for the vehicle user at position $l$; $l\in \left(0,2l\right)$, $G_{m,n}\left(l\right)=\chi \cdot d_{m,n}{\left(l\right)}^{-\delta }$, $d_{m,n}\left(l\right)$ is the distance between $R_m$ and $v_n$; $B$ is the channel bandwidth.

For communication between UAVs and vehicle users, this paper considers a probability-based air-to-ground communication model consisting of two communication channels: a line-of-sight channel and a non-line-of-sight channel. The probability of line-of-sight transmission is

$$P_{LoS}=\frac{1}{1+{\beta }_1\exp \left[-{\beta }_2\left(\theta -{\beta }_1\right)\right]}$$

(3)

The probability of non-line-of-sight transmission is $P_{NLoS}=1-P_{LoS}$, where $\theta$ denotes the elevation angle from the UAV to the vehicle user and ${\beta }_1$ and ${\beta }_2$ are constant parameters influenced by environmental factors. The path loss between the UAV and its associated vehicle user can be expressed as

$$\{\begin{array}{l}{L}_{Los}={\eta }_{LoS}{\left(\frac{4\pi f_c}{c}\right)}^2{d}_{u,n}{\left(l\right)}^2\\ L_{NLos}={\eta }_{NLoS}{\left(\frac{4\pi f_c}{c}\right)}^2{d}_{u,n}{\left(l\right)}^2\end{array}$$

(4)

where ${\eta }_{LoS}$ and ${\eta }_{\mathrm{NLos}}$ are the attenuation factors corresponding to the line-of-sight and non-line-of-sight links, $f_c$ is the carrier frequency, $c$ denotes the speed of light, and $d_{u,n}\left(l\right)$ denotes the distance between the UAV and the vehicle user $v_n$. Therefore, we can obtain the average path loss of the UAV-to-vehicle user link as

$$\overline{L}=P_{Los}{L}_{Los}+P_{NLos}{L}_{NLos}$$

(5)

The content transmission rate from the UAV to the vehicle user $v_n$ at moment $t$ can be obtained as

$$R_{u,n}^{UV}\left(l\right)=B\cdot {\mathit{log}}_2\left(1+\frac{P_U}{\overline{L}\cdot d_{u,n}\left(l\right)\cdot {\sigma }^2\cdot B}\right)$$

(6)

where $B$ denotes the bandwidth, $P_U$ denotes the transmitted power of the UAV, and ${\sigma }^2$ denotes the Gaussian white noise variance at the receiver.

The request delay for the vehicle user consists of a waiting delay $d_w$ and a transmission delay $d_t$ with each cache node, where the waiting time is the time the vehicle user travels without a cache node transmitting content for it before the content is fully available; the transmission delay needs to be calculated based on the transmission speed. Assuming that the length of each time slot is $t$ and the size of the content to be transmitted is $S_s$, which is an integer multiple of the content block size $s$, and that the transmission link is broken at position $L_{break}$, the calculation of the transmission delay is shown in Figure 4. Suppose the current time slot is the $q$ th time slot after starting transmission, at this time, the vehicle user’s position is $l_q=l+t\cdot v\cdot q$, the amount of data that can be transmitted by this time slot is $s_t\left(l_q\right)=t\cdot R\left(l_q\right)$, the size of the data that has not been transmitted is $s_r\left(l_q\right)=S-{\displaystyle \sum _{j=1}^{q-1}t\cdot R\left(l_j\right)}$. If $s_r\left(l_q\right){>s}_T\left(l_q\right)$, it means that the current time slot cannot complete the content delivery and the next time slot will continue the transmission. Otherwise, the current time slot can complete content delivery; the time used for data transmission in this time slot is $\frac{s_r\left(l_q\right)}{R\left(l_q\right)}$. The content transmission ends at this time slot and the transmission delay of the vehicle user at this cache node can be expressed as

$$d_t={\displaystyle \sum _{j=1}^{q-1}t+\frac{s_r\left(l_q\right)}{R\left(l_q\right)}}$$

(7)

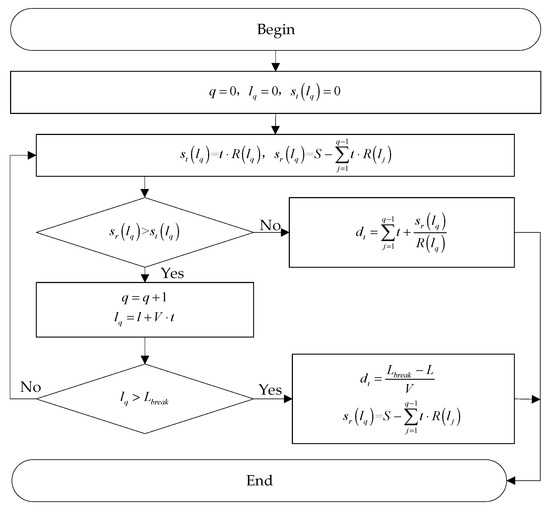
Figure 4. Content transfer process.

If the transmission link is broken or switched during transmission, i.e., the vehicle position exceeds $L_{break}$, the content blocks that have not completed transmission will be discarded. The size of the completed content of the transmission is $s_t=s\cdot floor\left(\frac{s_t}{s}\right)$, where $\mathit{floor}$ is a downward rounding function, then the size of the uncompleted content of the transmission is $s_r=S-s_t$. The user will continue to acquire the remaining content blocks at the next cache node. The transmission delay of the vehicle user at that cache node can be expressed as

$$d_t=\frac{L_{break}-L}{V}$$

(8)

In summary, in conjunction with the content delivery policy in Section 3.3, the request latency can be calculated for each vehicle user.

3.5. Price Model

In this paper, we use the revenue sharing contract model from the literature [10], where each RSU in the NO pays a fee $a$ to the CP for caching a content and a vehicle user pays a fee $b$ for acquiring a content from the NO. For the benefits received from the vehicle user, the CP and NO will split the benefits proportionally according to how the vehicle acquires the content. If the NO caches the content requested by the user and completes delivery of the content before it drives off the entire road, it will split the benefits with the CP in proportion ${\theta }_1$, i.e., the benefits of size ${\theta }_1\cdot b$ belong to the NO and the remaining benefits belong to the CP. If the NO does not complete delivery before the vehicle user drives off, it will need to acquire the content from the CP and then forward it to the vehicle user, splitting the benefits in proportion ${\theta }_2$, ${\theta }_1>{\theta }_2$.

4. RSU Caching Strategy Considering Content Cache Pricing

In this paper, we consider the utilities of both CP and NO. For the NO, we consider not only its economic utility, but also its time cost. In this section, we optimize the utility of the network and the request latency of the vehicle users in two ways. First, the utility formulas of CP and NO are analyzed by considering CP and NO as merchants and customers and content as a commodity. Second, the competition between them is modeled using the Stackelberg game framework to optimize the utility of both by changing the pricing of the content and the caching decision of the RSU. It is worth noting that the UAV caches the content already leased by the RSU without paying a fee to the CP and the effect of the UAV is not considered at this stage for now. Finally, when the rental price and the caching decision of RSU are determined, the utility of NO is further improved by optimizing the trajectory of UAV to further reduce the request latency of vehicle users and further improve the utility of NO.

4.1. Stackelberg Game for Joint Pricing and Cache Decision Optimization

Profit maximization of CP and profit maximization of NO are two conflicting optimization objectives. Assume that both CP and NO are selfish and intend to maximize their own revenues. Obviously, CP wants to increase the rental price in order to generate more revenue from the rental content. However, this will increase the rental cost and lead to a decrease in the benefit to the NO and thus a decrease in the amount of content rented by the RSU, which in turn may lead to a decrease in the total utility of the CP. To achieve a balance between the two competitions, game theory is an effective way to achieve their generally accepted prices and optimal cache placement strategies.

4.1.1. Utility Function

The total utility $U^{MNO}$ of the NO is determined by the benefit $W^{MNO}$ obtained from the vehicle user and the average delay $D^{ave}$ of content delivery. The utility of the CP consists of the rent obtained from the NO and the benefit obtained from the vehicle user. Different caching decisions and vehicle request locations yield different utilities; this section defines the utility functions for CP and NO.

Suppose that a vehicle drives at a uniform speed $V_m$ on a roadway covered by $R_m$. If the vehicle user has complete access to the content through $R_m$ only, it must have at least a distance of length $K_m$ to drive within the coverage of $R_m$; $K_m\le L$, $K_m$ is denoted as

$$K_m=\frac{S}{R}\cdot V_m$$

(9)

If the vehicle user obtains the content only through $R_m$, it needs to send the request within the first $L-K_m$ distance after entering the $R_m$ section. Since the time when a vehicle user sends a request obeys a uniform distribution, the probability that any vehicle user can obtain the content $f_i$ completely from $R_m$ is

$$P_m=1-\frac{K_m}{L}$$

(10)

Since requests for content are independent, the total utility can be split into the sum of the utilities of all content in the cache. Taking content $f_i$ as an example, when both RSUs cache content $f_i$, i.e., $y_{l,i}=1$ and $y_{r,i}=1$, the user of the vehicle requesting $f_i$ must be able to obtain the content completely before driving out of the entire roadway. The benefit $w_{i,[1,1]}^{MNO}$ and the average request delay obtained by the NO by caching f are

$$w_{i,[1,1]}^{MNO}=\left(N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot {\theta }_1\cdot b-2a$$

(11)

$$d_{i,[1,1]}^{ave}=\frac{1}{L}{\displaystyle {\int }_0^L{D}_i\left(l\right)}dl$$

(12)

The utility gained by the CP $u_{i,[1,1]}^{\mathit{CP}}$ is:

$$u_{i,[1,1]}^{\mathit{CP}}=\left(N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot \left(1-{\theta }_1\right)\cdot b+2\cdot a$$

(13)

where $D_i\left(l\right)$ represents the transmission delay when the vehicle user requests content $f_i$ after entering the section $l$ meters, which can be calculated according to the method in Section 3.4.

When $R_l$ caches $f_i$ and $R_r$ does not, i.e., $y_{l,i}=1$ and $y_{r,i}=0$, the benefits and request delays brought by vehicle users driving in from different directions are different. For the vehicles driving in from the $R_l$ section, only the requests sent within the first $L-K_l$ meters can receive the content through RSU only, otherwise the vehicle users cannot receive the $f_i$ completely when driving out of the $R_l$ section and enter the waiting state until they drive out of the whole section and receive the content from the CP through NO forwarding. Since vehicle users will only send requests within the first section they drive into, vehicles that drive in from the $R_r$ section and request $f_i$ will definitely receive the content. They send the request and enter the wait state until they drive into the $R_l$ section and receive the content from $R_l$. In summary, the benefit $w_{i,[1,0]}^{MNO}$ and the average request delay $d_{[1,0]}^{ave}$ obtained by the NO through cache $f_i$ in this case are

$$w_{i,[1,0]}^{MNO}=\left(P_l\cdot N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot {\theta }_1\cdot b+\left(1-P_l\right)\cdot N_l\cdot P{R}_{l,i}\cdot {\theta }_2\cdot b-a$$

(14)

$$d_{i,[1,0]}^{ave}=\frac{1}{L}\cdot \left[{\displaystyle {\int }_0^{K_m}{D}_i\left(l\right)}dl+{\displaystyle {\int }_{K_m}^L\frac{2\cdot L-l}{V}}dl\right]\cdot \frac{N_l}{N_l+N_r}+\frac{1}{L}\cdot \left[{\displaystyle {\int }_0^L\frac{L-l}{V}}dl+D_i\left(0\right)\right]\cdot \frac{N_r}{N_l+N_r}$$

(15)

The utility obtained by CP is:

$$u_{i,[1,0]}^{\mathit{CP}}=\left(P_l\cdot N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot \left(1-{\theta }_1\right)\cdot b+\left(1-P_l\right)\cdot N_l\cdot P{R}_{l,i}\cdot \left(1-{\theta }_2\right)\cdot b+a$$

(16)

When $R_l$ did not cache $f_i$ and $R_r$ cached $f_i$, i.e., $y_{l,i}=0$ and $y_{r,i}=1$, similar to the above analysis, the benefit $w_{i,[0,1]}^{MNO}$ and the average request delay $d_{[0,1]}^{ave}$ obtained by NO by caching $f_i$ are denoted as

$$w_{i,[0,1]}^{MNO}=\left(N_l\cdot P{R}_{l,i}+P_r\cdot N_r\cdot P{R}_{r,i}\right)\cdot {\theta }_1\cdot b+\left(1-P_r\right)\cdot N_r\cdot P{R}_{r,i}\cdot {\theta }_2\cdot b-a$$

(17)

$$d_{i,[0,1]}^{ave}=\frac{1}{L}\cdot \left[{\displaystyle {\int }_0^L\frac{L-l}{V}}dl+D_i\left(0\right)\right]\cdot \frac{N_l}{N_l+N_r}+\frac{1}{L}\cdot \left[{\displaystyle {\int }_0^{K_m}{D}_i\left(l\right)}dl+{\displaystyle {\int }_{K_m}^L\frac{2\cdot L-l}{V}}dl\right]\cdot \frac{N_r}{N_l+N_r}$$

(18)

The utility $u_{i,[0,1]}^{\mathit{CP}}$ obtained by the CP is the same as $u_{i,[1,0]}^{\mathit{FP}}$ above, denoted as

$$u_{i,[0,1]}^{\mathit{CP}}=\left(N_l\cdot P{R}_{l,i}+P_r\cdot N_r\cdot P{R}_{r,i}\right)\cdot \left(1-{\theta }_1\right)\cdot b+\left(1-P_r\right)\cdot N_r\cdot P{R}_{r,i}\cdot \left(1-{\theta }_2\right)\cdot b+a$$

(19)

When neither $R_l$ nor $R_r$ caches $f_i$, i.e., $y_{l,i}=0$ and $y_{r,i}=0$, the vehicle will obtain the content from the CP as it drives the entire roadway. The benefit $w_{i,[0,0]}^{MNO}$ and the average request delay $d_{[0,0]}^{ave}$ obtained by the NO by caching $f_i$ are denoted as

$$w_{i,[0,0]}^{MNO}=\left(N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot {\theta }_2\cdot b$$

(20)

$$d_{i,[0,0]}^{ave}=\frac{1}{L}{\displaystyle {\int }_0^L\frac{2\cdot L-l}{V}}dl$$

(21)

The utility $u_{i,[1,1]}^{\mathit{CP}}$ obtained by CP is:

$$u_{i,[0,0]}^{\mathit{CP}}=\left(N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot \left(1-{\theta }_2\right)\cdot b$$

(22)

Through the above analysis, the benefit obtained by NO through cache $f_i$ can be expressed as

$$w_i^{MNO}=w_{i,[1,1]}^{MNO}\cdot y_{l,i}\cdot y_{r,i}+w_{i,[1,0]}^{MNO}\cdot y_{l,i}\cdot \left(1-y_{r,i}\right)+w_{i,[0,1]}^{MNO}\cdot \left(1-y_{l,i}\right)\cdot y_{r,i}+w_{i,[0,0]}^{MNO}\cdot \left(1-y_{l,i}\right)\cdot \left(1-y_{r,i}\right)$$

(23)

The average request latency of vehicle users for content $f_i$ is expressed as

$$d_i^{ave}=d_{i,[1,1]}^{ave}\cdot y_{l,i}\cdot y_{r,i}+d_{i,[1,0]}^{ave}\cdot y_{l,i}\cdot \left(1-y_{r,i}\right)+d_{i,[0,1]}^{ave}\cdot \left(1-y_{l,i}\right)\cdot y_{r,i}+d_{i,[0,0]}^{ave}\cdot \left(1-y_{l,i}\right)\cdot \left(1-y_{r,i}\right)$$

(24)

Thus, the utility obtained by NO through cache f is expressed as

$$u_i^{MNO}=w_i^{MNO}+\gamma \cdot \left(d_i^{\max }-d_i^{ave}\right)$$

(25)

where r is a weighting factor for benefit and delay and q is a constant used to make the trend of delay the same as that of benefit. The utility of CP for content f is expressed as

$$u_i^{\mathit{CP}}=u_{i,[0,0]}^{\mathit{CP}}\cdot y_{l,i}\cdot y_{r,i}+u_{i,[0,0]}^{\mathit{CP}}\cdot y_{l,i}\cdot \left(1-y_{r,i}\right)+u_{i,[0,0]}^{\mathit{CP}}\cdot \left(1-y_{l,i}\right)\cdot y_{r,i}+u_{i,[0,0]}^{\mathit{CP}}\cdot \left(1-y_{l,i}\right)\cdot \left(1-y_{r,i}\right)$$

(26)

4.1.2. Stackelberg Game Model

In this paper, the competitive relationship between the CP and the NO is modeled as a Stackelberg game, where the CP acts as a leader and the NO acts as a follower in response to the CP’s actions. More specifically, CP first gives the rental price $a$ and informs NO about it. The NO determines the amount of content it rents for each RSU and the optimal cache placement policy that maximizes its utility based on the lease price $a$, the expected number of content requests, and the average content request probability. Thus, the Stackelberg game consists of two subproblems: the problem of how the leader (CP) determines the lease price to maximize its utility and the problem of how the follower (NO) conducts caching to maximize its utility.

(1) The utility maximization problem of CP

$$\begin{array}{l}P1.1:\underset{a}{\max }{U}^{\mathit{CP}}={\displaystyle \sum _{i=1}^I{u}_i^{\mathit{CP}}}\\ \hspace{1em}\hspace{1em}s.t.\hspace{1em}\hspace{1em}\left(C1\right)0\le a\le a_{\max }\\ \hspace{1em}\hspace{1em}\hspace{1em}\left(C2\right)y^R\in \left(0,1\right)\\ \end{array}$$

(27)

where constraint (C1) indicates that the lease price does not exceed the maximum unit price set by the market and (C2) indicates that the cache decision indicator variable of the RSU takes the value of 0 or 1.

(2) The utility maximization problem of NO

$$\begin{array}{l}P1.2:\underset{Y^R}{\max }{U}^{MNO}={\displaystyle \sum _i^I{u}_i^{MNO}}\\ \hspace{1em}\hspace{1em}s.t.\hspace{1em}\left(C2\right)y^R\in \left(0,1\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\left(C3\right){\displaystyle \sum _{i=1}^I{y}_{m,i}^{R}s}\le CR,m\in \left\{l,r\right\}\end{array}$$

(28)

where constraint (C3) indicates that the cached content data size cannot exceed the maximum cache capacity.

The utility of the leader and the followers is optimal when the Stackelberg game reaches the equilibrium point; the lease price and cache decision corresponding to the equilibrium point are the optimal values. If any entity deviates from the equilibrium point, its own benefit will be reduced. According to the definition in [7], the equilibrium point of the Stackelberg game in this paper is defined as:

Let $a*$ denote the optimal solution of the utility maximization problem $P1.1$ for CP and $Y^R*$ denote the optimal solution of the utility maximization problem for NO given the optimal lease price $a*$. For any $\left(a,Y^R\right)$ in the feasible region, if the following conditions are satisfied:

$$U^{\mathit{CP}}\left(a*,Y^R*\right)\ge U^{\mathit{CP}}\left(a,Y^R*\right)$$

(29)

$$U^{MNO}\left(a*,Y^R*\right)\ge U^{MNO}\left(a*,Y^R\right)$$

(30)

then $\left(a*,Y^R*\right)$ is the equilibrium point of the proposed Stackelberg countermeasure.

4.1.3. Iterative-Based Dynamic Programming Algorithm

For problem $P1.2$, with constant lease price $a$, it can be viewed as a backpack problem, where two RSUs with limited capacity are equivalent to two backpacks with different benefits obtained by placing content into different backpacks. The content caching decision is optimized according to the cache capacity and the utility obtained by each content in different RSUs so as to maximize the utility. However, this problem is different from the traditional knapsack problem in that, first, there are multiple knapsacks (two RSUs) and, second, the content cache obtains different benefits in different RSUs and the caching situation of two RSUs for the same content affects the mutual utility. That is, if the utility obtained by NO is $u_l$ when only $R_l$ caches content $f_i$ and $u_r$ when only $R_r$ caches, but the total benefit obtained when both RSUs cache $f_i$ is not equal to $u_l+u_r$. Therefore, this paper designs a dynamic programming-based cache optimization algorithm to solve this problem.

The core idea of the dynamic programming algorithm is to decompose the original backpack problem into a set of smaller backpack problems and find the relationship between the optimal solution of the original backpack problem and the optimal solution of the smaller backpack problems. Following this idea, we use a three-dimensional array ${\mathit{DP}}_{C_l^R,C_l^R,I}$ to store the solutions of these smaller backpack problems. The three-dimensional array is defined as

$$d{b}_{cl,cr,i}=\{\begin{array}{l}d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}, if{c}_l<s, c_r<s\\ \max \left[d{b}_{cl-1,cr,i-1}+u_{i,[1,0]}^{MNO},d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}\right], if{c}_l\ge s, c_r<s\\ \max \left[d{b}_{cl,cr-1,i-1}+u_{i,[0,1]}^{MNO},d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}\right], {if c}_l<s, c_r\ge s\\ \max \left[d{b}_{cl-1,cr,i-1}+u_{i,[1,0]}^{MNO},d{b}_{cl,cr-1,i-1}+u_{i,[0,1]}^{MNO},d{b}_{cl-1,cr-1,i-1}+u_{i,[1,1]}^{MNO},d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}\right], {if c}_l\ge s, c_r\ge s\end{array}$$

(31)

where $d{b}_{cl,cr,i}\in {\mathit{DP}}_{C_l^R,C_l^R,I}$ denotes the maximum utility when the cache capacity of $R_l$ is $c_l$ and the cache capacity of $R_r$ is $c_r$ and the subscript of the cacheable content is between 0 and $i$. Initially, $d{b}_{cl,cr,0}=0$, $d{b}_{1,0,0}=u_{1,\left[1,0\right]}^{MNO}$, and $d{b}_{0,1,0}=u_{1,\left[0,1\right]}^{MNO}$, which can be calculated recursively based on the optimal solution to some smaller backpacking problem. Equation (31) determines the caching decision of NO for content $f_i$. Meanwhile, this paper uses $Y^R=\left[Y_i^l,Y_i^r\right]$ to record the caching of RSU, where $Y_i^l$ and $Y_i^r$ denote the set of caching decisions of $R_l$ and $R_r$ for $i$ contents, respectively. The specific procedure is shown in Algorithm 1.

Algorithm 1: Dynamic programming algorithm

1. $d{b}_{1,0,0}=u_{1,\left[1,0\right]}^{MNO};d{b}_{0,1,0}=u_{1,\left[0,1\right]}^{MNO}$

2. For $c_l=0$ to $C_l$ do:

3.    For $c_r=0$ to $C_r$ do:

4.        $d{b}_{cl,cr,0}=0$

5.    end for

6. end for

7. For $c_l=0$ to $C_l$ do:

8.    For $c_r=0$ to $C_r$ do:

9.        For $i=1$ to $I$ do:

10.          Calculate $U_i=\left[u_{i,[1,0]}^{MNO},u_{i,[0,1]}^{MNO},u_{i,[1,1]}^{MNO},u_{i,[0,0]}^{MNO}\right]$ according to Equation (25)

11.          If $c_l\ge s$$\mathrm{and} c_r\ge s$:

12.              $d{b}_{cl,cr,i}=\max \left[d{b}_{cl-1,cr,i-1}+u_{i,[1,0]}^{MNO},d{b}_{cl,cr-1,i-1}+u_{i,[0,1]}^{MNO},d{b}_{cl-1,cr-1,i-1}+u_{i,[1,1]}^{MNO},d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}\right]$

13.               If $d{b}_{cl,cr,i}$$=d{b}_{cl-1,cr,i-1}+u_{i,[1,0]}^{MNO}$$: y_i^l=1;y_i^r=0$

14.               Else if $d{b}_{cl,cr,i}$$=d{b}_{cl,cr-1,i-1}+u_{i,[0,1]}^{MNO}$$: y_i^l=0;y_i^r=1$

15.               Else if $d{b}_{cl,cr,i}$$=d{b}_{cl-1,cr-1,i-1}+u_{i,[1,1]}^{MNO}$$:y_i^l=1;y_i^r=1$

16.               Else: $y_i^l=0;y_i^r=0$

17.               End if

18.          Else if $c_l\ge s$:

19.               If $d{b}_{cl-1,cr,i-1}+u_{i,[1,0]}^{MNO}\text{>}d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}$:

20.                 $d{b}_{cl,cr,i}=d{b}_{cl-1,cr,i-1}+u_{i,[1,0]}^{MNO};y_i^l=1;y_i^r=0$

21.               Else:

22.                 $d{b}_{cl,cr,i}=d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO};y_i^l=0;y_i^r=0$

23.               End if

24.          Else if $c_r\ge s$:

25.               If $d{b}_{cl,cr-1,i-1}+u_{i,[0,1]}^{MNO}\text{>}d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO}$:

26.                 $d{b}_{cl,cr,i}=d{b}_{cl,cr-1,i-1}+u_{i,[0,1]}^{MNO};y_i^l=0;y_i^r=1$

27.               Else:

28.                 $d{b}_{cl,cr,i}=d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO};y_i^l=0;y_i^r=0$

29.               End if

30.          Else:

31.               $d{b}_{cl,cr,i}=d{b}_{cl,cr,i-1}+u_{i,[0,0]}^{MNO};y_i^l=0;y_i^r=0$

32.          End if

33.        End for

34.    End for

35. End for

36. $U^{MNO}*=d{b}_{C_l^R,C_l^R,I}$; $Y^R*=\left[Y_a^l,Y_a^r\right]$

Based on Algorithm 1, an iterative-based dynamic programming algorithm is designed in this paper to find the equilibrium point of all Stackelberg games; the specific process is shown in Algorithm 2. Algorithm 2 involves an iterative interaction between the CP and the NO. As the leader, the CP first initializes the lease price $a$ to 0 and then starts the game. In the process of the game, the NO obtains the optimal content caching decision and the corresponding maximum utility at the current rental price by Algorithm 1 based on the content popularity and the local cache space. After that, the CP calculates its own utility based on the caching decision made by the NO and then increases the rental price $a$ slightly by $\mathrm{\Delta }a$ and iterates to repeat the above interaction.

Algorithm 2: Iterative-based dynamic programming algorithm

1. $a=0$ 2. While $a\le a_{\max }$ 3.   Calculate the maximum utility $W_a^{MNO}$ of NO when the lease price is $a$ by Algorithm 1. 4.   Calculate the maximum utility $W_a^{\mathit{CP}}$ of CP when the lease price is $a$ according to Equation (26). 5.   $a=a+\mathrm{\Delta }a$ 6. The lease price $a*$ that maximizes $W_a^{\mathit{CP}}$ is the final lease price 7. The utility of NO is $W_a^{MNO}$ and the cache decision is $\mathit{Cach}{e}_{a*}$.

4.2. Trajectory Optimization of UAV

After determining the rental price of the content and the caching decision of the RSU, the utility of the CP is determined, but the utility of the NO can be further enhanced by optimizing the trajectory of the UAV. The optimization problem can be expressed as follows:

$$\begin{array}{l}P2:\underset{G}{\max }{U}^{MNO}\\ \hspace{1em}\hspace{1em}s.t.\hspace{1em}\left(C4\right)0\le V^U\le V_{\max }^U\\ \hspace{1em}\hspace{1em}\hspace{1em}\left(C5\right){\displaystyle \sum _{i=1}^I{y}_i^{U}s}\le CU\\ \hspace{1em}\hspace{1em}\hspace{1em}\left(C6\right)y^U\in \left(0,1\right)\end{array}$$

(32)

where G denotes the trajectory of the UAV, constraint (C4) is a constraint on the flight speed of the UAV, (C5) indicates that the size of the UAV’s cached content data cannot exceed the maximum cache capacity, and (C6) indicates that the UAV’s cache decision indicator variable takes the value of 0 or 1.

In this paper, we assume that the road is divided into $Z$ small road segments and the length of each segment is the coverage diameter of the UAV with $Z=\frac{2L}{C^U}$. The UAV stays directly above the center of a block during a trajectory optimization cycle $T_x$ to serve the vehicle users within that block and selects an adjacent block at the end of the current trajectory optimization cycle to serve the vehicles within that block during the next trajectory optimization cycle $T_{z+1}$. The starting and ending points of the UAV are the same and fixed to facilitate the charging of the UAV. For the optimization period $T_x$, if given the UAV location, the request delay $d_i\left(l\right)$ of the vehicle user who makes a request at location $l$ when the UAV caches content $f_i$ can be calculated based on the analysis of the content delivery policy and content request delay in Section 3.4 and Section 3.5; the average request delay of the user who requests $f_i$ at this time is

$$d_i^{U,ave}=\frac{1}{L}\cdot {\displaystyle {\int }_0^L{d}_i\left(l\right)}$$

(33)

According to the analysis in Section 4.1.1, the average request delay $d_i^{ave}$ for $f_i$ when the UAV is not caching $f_i$ at this time can be calculated, so the delay saved by the UAV when slowing down $f_i$ can be expressed as

$$d_i^{save}=\left(N_l\cdot P{R}_{l,i}+N_r\cdot P{R}_{r,i}\right)\cdot \left(d_i^{ave}-d_i^{U,ave}\right)$$

(34)

Also, the introduction of a UAV can further increase the benefit of NO. When the UAV and one RSU caches $f_i$ and another RSU does not and the UAV stays on the roadway where the RSU that caches $f_i$ is located, with $R_l$ caching $f_i$ and $R_r$ not caching, and the UAV stays on the $R_l$ side, for example, the probability of obtaining the content increases to $P_U$ for the user of the vehicle that drives in from the $R_l$ side. When the UAV and one RSU caches $f_i$ and the other does not and the UAV stays on the roadway where the RSU that does not cache content $f_i$ is located, taking the example that $R_l$ caches $f_i$, $R_r$ does not, and the UAV stays on the $R_r$ side, the probability of obtaining content increases to 1 for the user of the vehicle approaching from the $R_l$ side. Thus, the benefit that caching $f_i$ can bring to the NO is

$$w_i^{save}=\{\begin{array}{l}\left(P_U-P\right)\cdot N_l\cdot P{R}_i\cdot c\cdot y_{l,i}\cdot \left(1-y_{r,i}\right)+\left(1-P\right)\cdot N_r\cdot P{R}_i\cdot c\cdot \left(1-y_{l,i}\right)\cdot y_{r,i},\mathit{If} \mathit{the} \mathit{UAV} \mathit{stays} \mathit{on} \mathit{the} R_l \mathit{side}\\ \left(1-P\right)\cdot N_l\cdot P{R}_i\cdot c\cdot y_{l,i}\cdot \left(1-y_{r,i}\right)+\left(P_U-P\right)\cdot N_r\cdot P{R}_i\cdot c\cdot \left(1-y_{l,i}\right)\cdot y_{r,i},\mathit{If} \mathit{the} \mathit{UAV} \mathit{stays} \mathit{on} \mathit{the} R_r \mathit{side}.\end{array}$$

(35)

So, the problem can be simplified as follows:

$$\begin{array}{l}P3:\underset{G}{\max }{U}^{save}={\displaystyle \sum _i^I\left(w_i^{save}+\gamma \cdot d_i^{save}\right)}\cdot y_i^U\\ \hspace{1em}\hspace{1em}s.t.\hspace{1em}\left(C4\right)0\le V^U\le V_{\max }^U\\ \hspace{1em}\hspace{1em}\hspace{1em}\left(C5\right){\displaystyle \sum _{i=1}^I{y}_i^{U}s}\le CU\\ \hspace{1em}\hspace{1em}\hspace{1em}\left(C6\right)y^U\in \left(0,1\right)\end{array}$$

(36)

The UAV caches the contents of the RSU lease according to the prevalence, so the utility saved when the UAV is on each road block in different trajectory optimization cycles can be calculated; the utility saved when the UAV stays on road block $L_x$ in optimization cycle $T_x$ is denoted by $u_{x,z}^{save}$. At this point, $P3$ can be regarded as a shortest path problem and the UAV trajectory is regarded as a directed graph, as shown in Figure 5, where the point $\left(x,z\right)$ indicates that the UAV stays on the rectangular block $L_z$ during the optimization period $T_x$. The edge connecting the two points indicates the path of the UAV and $u_{x,z}^{save}$ is used as the weight of the edge.

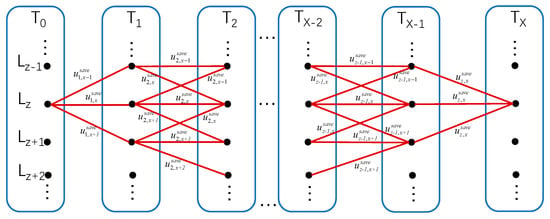
Figure 5. Directed graph of UAV trajectory.

This problem can be solved by Dijkstra’s algorithm, which has the main feature of starting from the starting point and using the strategy of greedy algorithm, traversing to the nearest neighboring point of the starting point that has not been visited each time until it is extended to the ending point. The details are shown in Algorithm 3. First, the starting point $L_{begin}$ and the ending point $L_{\mathit{end}}$ are given, $L_{begin}=L_{\mathit{end}}$, and a directed graph is drawn. Initially, the starting point is marked and the distance is recorded as 0, i.e., $L_{begin}=L_{\mathit{end}}$. All points except the starting point are unmarked and the distance to the starting point is recorded as positive infinity, i.e., ${\mathit{dis}}_{0,\left(T_0,L_{begin}\right)}=\infty$. Next, iteration is performed. The point just added is denoted as $pt$, its set of neighboring points is denoted as $p{t}_{\mathit{nei}}$, and the distance ${\mathit{dis}}_{\mathit{pt},p}$ of neighboring point $p$ passing through $pt$ to the starting point is calculated, $p\in p{t}_{\mathit{nei}}$, where the value of ${\mathit{dis}}_{\mathit{pt},p}$ is the weight of $pt$ to $p{t}_{\mathit{nei}}$ plus the distance of $pt$ to the starting point. If ${\mathit{dis}}_{\mathit{pt},p}$ is less than the distance ${\mathit{dis}}_{0,p}$ to the starting point recorded by $p$, update ${\mathit{dis}}_{0,p}$ to the value of ${\mathit{dis}}_{\mathit{pt},p}$. After the distance update, the closest point from the unmarked point to the starting point is selected, marked, and included in the set of optimal paths. Repeat the last two steps until the update to the end point to achieve the final path and the saved utility.

Algorithm 3: Dijkstra-based path planning algorithm

1. $L_{\min }=L_{z-1}, L_{\max }=L_{z+1}, fla{g}_{\left(T_x,l_p\right)}=1$ 2. For $x=1$ to $X$: 3.     For $z=1$ to $Z$: 4.         ${\mathit{dis}}_{0,\left(T_x,l_z\right)}=\infty ,fla{g}_{\left(T_x,l_z\right)}=0$ 5.     end for 6. end for 7. $pt=\left(T_0,L_{begin}\right), {\mathit{dis}}_{0,pt}{=\mathit{dis}}_{0,\left(T_0,L_{begin}\right)}=0, fla{g}_{\left(T_0,L_{begin}\right)}=1$ 8. While Presence of untagged nodes. 9.     For $p$ in $p{t}_{nei}$: 10.       ${\mathit{dis}}_p={\mathit{dis}}_{0,pt}+u_p^{save}$ 11.       If ${\mathit{dis}}_p<{\mathit{dis}}_{0,p}$ 12.          ${\mathit{dis}}_{0,p}={\mathit{dis}}_p$ 13.       End if 14.     end for 15.     Select the closest point to the starting point from the unmarked points, denoted as $pt$ 16.     $fla{g}_{pt}=1$, add $pt$ to the trajectory $G$ of the UAV

In summary, the complexity of the algorithm used for this strategy is $o\left(C_l\cdot C_r\cdot I\right)$. The algorithm can accurately find the optimal RSU caching strategy and UAV flight trajectory, but the complexity is high and the computing time is long, which is suitable for scenarios with smaller contents and higher requirements for accuracy.

5. Analysis of Simulation Results

In order to evaluate the performance of the proposed algorithm, we use python to simulate the algorithm and compare it with the caching strategy in the literature [10]. The path loss index is $\alpha =4$, the channel fading gain is $\chi ={10}^{-2}$, the channel width is $B=1.1 \mathit{MHZ}$, the power of Gaussian noise is $P_n=-110 dBm$, and other simulation parameters are shown in Table 1.

Table 1. Simulation parameters.

Parameter	Value
The number of contents	50
Cache capacity of RSU	10
Cache capacity of UAV	5
The parameter of Zipf distribution	0.7
The transmission power of RSU (mW)	2000
The transmission power of UAV (mW)	200
The communication radius of RSU (m)	300
The communication radius of UAV (m)	100
The length of lane (m)	600
The fee $b$ paid by the vehicle user	1
$\mathrm{Benefit} \mathrm{sharing} \mathrm{ratio} {\theta }_1$	0.9
$\mathrm{Benefit} \mathrm{sharing} \mathrm{ratio} {\theta }_2$	0.5

Figure 6 gives the variation of utility with different total number of contents, where the total utility of the NO is determined by both the benefits of the NO and the average delay of the vehicle users. From Figure 6a–d, it can be seen that, as the total number of contents increases, the total utility of the CP and the total utility of the NO decrease, the benefit of the NO increases, and the average request delay increases. This is because the cache capacity of the RSUs and the UAV is fixed and the larger the total amount of content, the smaller the percentage of content cached, the smaller the probability of vehicles receiving content through cache nodes and the larger the content request latency. The total utility of NO is determined by the benefits of NO and the average request latency; thus, as the total amount of content increases, the total utility of NO decreases, which leads to a lower demand for content by NO during the game, so that the rental price of content decreases and the total utility of CP decreases. Compared with the strategy in [10], the benefit of CP for the strategy in this paper is slightly lower than that of [10]; all other performances are better than that of the strategy in [10]. This is because the policy in [10] does not chunk the content, so if the content is not fully available when the vehicle user drives out of the coverage of the cache node, it needs to be re-downloaded at the next cache node, which leads to a lower probability of successful delivery. Moreover, the policy in [10] does not apply UAV, which leads to an increase in delay, a decrease in the benefit of the NO, and a decrease in the utility of the NO. Since the benefits of CP and NO are fixed, the utility of CP is slightly greater than that of this paper. The performance of this paper is better compared to the caching-by-popularity strategy. This is because the dynamic programming algorithm applied in this paper can optimize both the content rental price and the caching decision of RSUs to obtain better performance compared with caching by popularity.

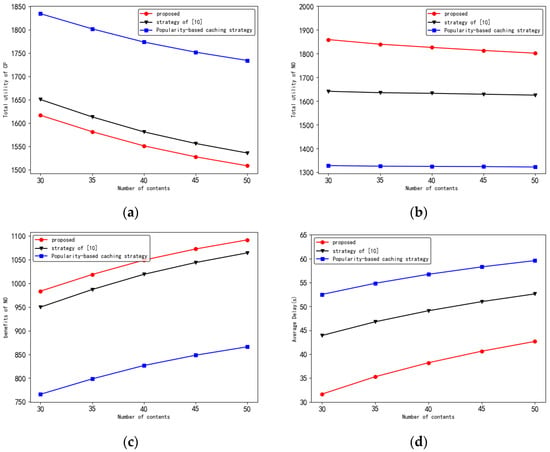
Figure 6. Performance versus total content. (a) Total utility of CP in relation to the total number of contents; (b) total utility of NO in relation to the total number of contents; (c) relationship between the benefit of NO and the total number of contents; (d) relationship between average delay and total number of contents.

Figure 7 gives the relationship between the performance of this paper’s strategy and the Zipf distribution parameter for different total number of contents. From Figure 7b–d, it can be seen that the average delay decreases with the increase in Zipf distribution parameters when the total number of contents is constant and the benefit and total utility of NO increases with the increase in Zipf distribution parameters. This is because, as the Zipf distribution parameter increases, the requests of vehicle users become more and more concentrated on the content with high popularity, so the cache hit rate increases, the request latency of vehicles becomes smaller, and the success rate of vehicles to successfully obtain the content becomes larger. As the cache hit rate increases, the benefit and total utility of NO increases. From Figure 7a, the average delay decreases as the Zipf distribution parameter increases when the total number of contents is constant. This is because, as the Zipf distribution parameter increases, the request rate of vehicle users for content with low popularity decreases, which will lead to a lower degree of demand for these contents by NO, so the content rental price decreases and the total utility of CP decreases accordingly.

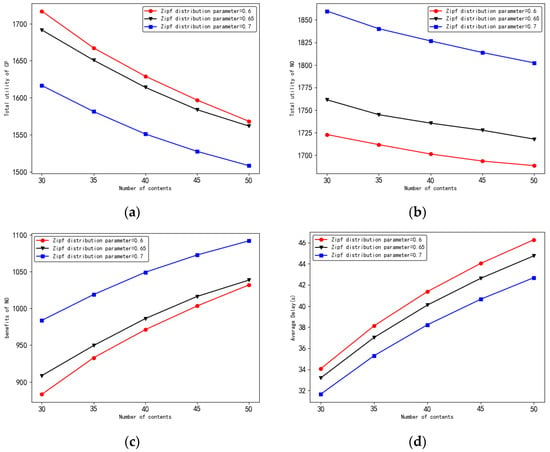
Figure 7. Performance versus Zipf distribution parameters. (a) Relationship between the total utility of CP and the Zipf distribution parameter; (b) relationship between the total utility of NO and the Zipf distribution parameter; (c) relationship between the benefit of NO and the Zipf distribution parameter; (d) relationship between the average delay and the Zipf distribution parameter.

Figure 8 gives the relationship between the performance of this paper’s strategy and the vehicle speed for different total number of contents. From Figure 8a–d, it can be seen that the average delay decreases with the increase in vehicle speed, the benefit and total utility of NO increases with the increase in vehicle speed, and the total benefit of CP decreases with the increase in vehicle speed. This is because, as vehicle speed increases, the time vehicle users spend traveling on the roadway becomes shorter, the maximum waiting delay becomes shorter, and the average delay decreases. As the vehicle travel speed increases, the contact time between the vehicle and each cache node decreases, and the success rate of content delivery decreases, so the degree of demand for content by NO decreases and the content rental price decreases, resulting in a decrease in the total utility of CP and an increase in the benefits and total utility of NO.

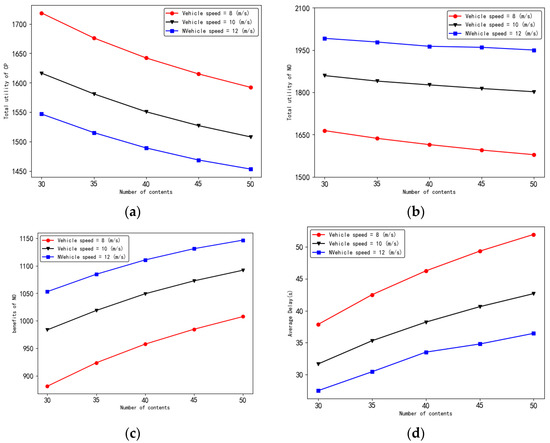
Figure 8. Performance versus vehicle speed. (a) Relationship between the total utility of CP and the vehicle speed; (b) relationship between the total utility of NO and the vehicle speed; (c) relationship between the benefit of NO and the vehicle speed; (d) relationship between the average delay and the vehicle speed.

Figure 9 gives the relationship between the performance of this paper’s strategy and the communication radius of RSU for different total number of contents. From Figure 9a–d, it can be seen that the average delay, the benefit, and the total utility of NO decreases with the increase in the communication radius of RSU and the total benefit of CP increases with the increase in the communication radius of RSU. This is because, as the communication radius of the RSU increases, the success rate of the vehicle user in obtaining content from the RSU increases; then, the average request delay of the vehicle user decreases. At the same time, the demand of NO for content becomes larger and the content rental price increases; then, the total utility of CP increases and the benefit of NO decreases. The total utility of NO is determined by both the delay and the benefit of NO and, combined, it decreases slightly with the increase in RSU communication radius.

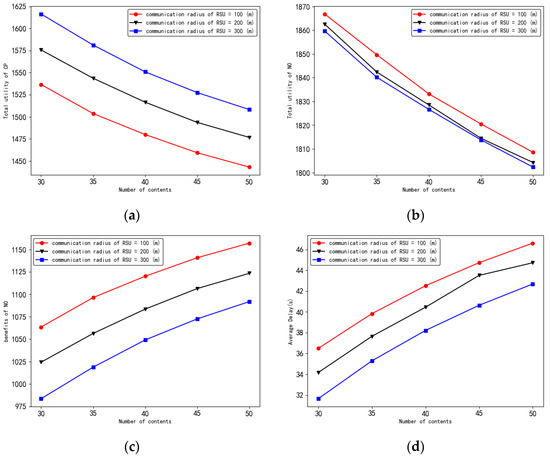
Figure 9. Performance versus communication radius of RSU. (a) Relationship between the total utility of CP and the communication radius of RSU; (b) relationship between the total utility of NO and the communication radius of RSU; (c) relationship between the benefit of NO and the communication radius of RSU; (d) relationship between the average delay and the communication radius of RSU.

6. Conclusions

In this paper, we investigated a UAV-assisted caching strategy based on content cache pricing in vehicular networks. In a traffic scenario consisting of CP, NO, and multiple vehicle users, the CP leases some popular content to the NO for benefits and the NO caches this leased content in RSUs to save expensive backhaul transmission overhead and latency. We analyzed the content delivery process and benefit exchanges between CP, NO, and vehicle users and defined the utilities of CP and NO. Then, the competition between CP and NO was modeled using the Stackelberg game framework and an iteration-based dynamic planning algorithm was designed to find the Stackelberg equilibrium by optimizing the caching decisions of RSUs and the rental prices of contents. Finally, a cache-capable UAV was introduced into the onboard network to cache the content already leased by the NO and a Dijkstra-based path planning algorithm was designed to further increase the total utility of the NO and improve the service quality by optimizing the trajectory of the UAV. The simulation results show that the strategy in this paper can have a reasonable distribution of the benefits of CP and NO, reduce the average request latency, and increase the utility of NO. Compared with [10], the strategy in this paper reduces the total benefit of CP by 2% and increases the total utility of NO by 13% where the benefit of NO is increased by 3% and the request delay is reduced by 27%.

However, there are still several issues in this paper. For example, we assumed that the communication environment was secure and did not consider the possible problems of eavesdropping and information leakage in practice. In our future work, we will further study the information encryption technology in this scenario to further guarantee the security of communication.