Stability and Periodic Motions for a System Coupled with an Encapsulated Nonsmooth Dynamic Vibration Absorber

Abstract

The dynamic vibration absorber (DVA) is widely used in engineering models with complex vibration modes. The research on the stability and periodic motions of the DVA model plays an important role in revealing its complex vibration modes and energy transfer. The aim of this paper is to study the stability and periodic motions of a two-degrees-of-freedom system coupled with an encapsulated nonsmooth dynamic vibration absorber under low-frequency forced excitation. Based on the slow–fast method, the model is transformed into a six-dimensional piecewise smooth system coupling two time scales. The existence and stability of the admissible equilibrium points for the model are discussed under different parameter conditions. Based on the first integrals, the Melnikov vector function of the nonsmooth dynamic vibration absorber model is calculated. The existence and number of periodic orbits bifurcated from a family of periodic orbits under different parameters are discussed. The phase diagram configuration of periodic orbits is given based on numerical simulation. The results obtained in this paper offer a new perspective for vibration analysis and parameter control for nonsmooth dynamic vibration absorbers.

1. Introduction

There is increasing interest in dissipating the undesired vibration passively fueled by the requirement of civil engineering [1], mechanical systems [2] and so on. The dynamic vibration absorber [3] is a key device that helps to mitigate the vibration, and there are growing efforts in designing its structure to achieve better performance. The early dynamic vibration absorber was a linear vibration control device [4]. The introduction of nonlinearity caused the dynamic vibration absorber to mitigate vibration in a wider frequency band compared to the linear DVA [5]. The nonsmooth dynamic vibration absorber originated from the idea of using stops in the vibration absorber in [6], subsequently developed by Natsiavas [7], Pun [8] and many other scholars.

The nonsmooth dynamic vibration absorber has received considerable attention from researchers due to its excellent performance, such as mitigating the vibration and absorbing energy [9,10,11] efficiently. Several types of models, including models with piecewise smooth stiffness or damping [12,13,14,15,16,17] and vibro-impact [18], have been designed. For the single-degree-of-freedom primary system coupled with a nonsmooth DVA, Weiss et al. [12] designed a nonsmooth DVA considering the effects of gravity and the activation of the nonlinear absorber. The efficiency of nonsmooth absorbers can be verified using numerical and experimental methods. Yao et al. [13] proposed a new nonlinear energy sink (NES) composed of multiple piecewise linear stiffness. The vibration-suppression effects were investigated by numerical simulations and experiments. Chen et al. [14] developed a piecewise NES with descending stiffness and investigated its effect on the vibration suppression. They discovered that this type of NES could remove the stable higher branch efficiently. Li et al. [15] studied the energy harvesting and targeted energy transfer (TET) of a piecewise linear NES through numerical simulation. Geng and Ding [16] proposed an enhanced NES with piecewise linear stiffness and considered the influence of the stiffness and the gap displacement on the vibration absorption. For a two-degrees-of-freedom primary system coupled with a nonsmooth DVA, Geng and Ding [17] designed an encapsulated NES to control two resonance modes. With the aid of a harmonic balance method and experimental methods, the vibration control under different parameters of the NES was investigated. Fang et al. [18] discussed the vibration suppression and modal energy transfer for a vibro-impact nonlinear energy sink model.

Low-frequency forced excitation, referred to as a slow-varying parameter due to its frequency being much lower than the natural frequency of the system, is crucial to analyze the periodic motions and other dynamical behaviors of DVAs [19]. Regarding the dynamic behavior of oscillator systems, in [20] and [21] the authors focused on the dynamical motion for two classes of three-degrees-of-freedom (DOF) auto-parametric systems. Abohamer et al. [22] analyzed the dynamical motion of a new three-degrees-of-freedom nonlinear damped dynamical system. Amer et al. [23] investigated the planar motion of a dynamical model with a two-degrees-of-freedom dynamical tuned absorber system under a harmonic excitation moment. For the stability and bifurcation of DVAs, Lelkes et al. [24] investigated the stability and bifurcation of equilibrium points for a piecewise linear aeroelastic system for the cases of adding a vibration absorber to the system and not adding a vibration absorber, respectively. Wang et al. [25] studied the vibration reduction effect of a Van der Pol oscillator coupled with the nonlinear energy sink under low-frequency forced excitation, which was described using a four-dimensional nonlinear smooth system. The results obtained by the finite element method are consistent with the numerical simulation results. To our knowledge, few studies have considered the stability of a two-degrees-of-freedom system coupled with an encapsulated nonsmooth DVA.

For periodic motions of a nonsmooth DVA, Lee et al. [26] explored the periodic orbit, saddle-node bifurcation and TET of a vibro-impact NES using bifurcation diagrams, frequency–energy plots and Poincaré maps. Starosvetsky and Gendelman [27] investigated the vibration absorption for a nonlinear energy sink model with piecewise quadratic damping. Interesting results obtained were that undesirable periodic regimes could be eliminated by coupling the NES with a properly tuned piecewise quadratic damping. Savadkoohi and Lamarque [28] studied the complex dynamical behaviors of coupled Dahl-type and nonsmooth systems at a fast time scale and a slow time scale. Al-Shudeifat and Saeed [29] analyzed the periodic motion and frequency energy plots for a two-degrees-of-freedom system coupled with a piecewise smooth nonlinear energy sink. Geng et al. [30] proposed a ground-limited NES with a piecewise spring. Based on the harmonic balance method, an analytical solution of NES was studied considering the approximate function of a piecewise smooth function. Hong et al. [31] studied the vibration behaviors of a vibro-impact system with an elastic stop and analyzed its stability of the periodic solution using Floquet theory. There are few studies on analyzing the periodic solutions of the nonsmooth DVA model using the Melnikov method and it remains to be studied.

Motivated by this, the stability and periodic motions of the two-degrees-of-freedom primary system coupled with an encapsulated nonsmooth DVA modeled by a six-dimensional piecewise smooth system are studied. The key contributions of this paper are as follows.

• The fast–slow analysis method is introduced to study the stability of the equilibrium point of the nonsmooth dynamic vibration absorber model. The existence and stability of the admissible equilibrium points of an encapsulated DVA model with piecewise smooth properties are discussed in different parameter regions. The asymptotical stable and unstable regions of an admissible equilibrium point for a nonsmooth DVA model under different parameter conditions are obtained, which provides theoretical guidance for the design of a nonsmooth DVA structure.
• Few studies have focused on the bifurcation and number of periodic solutions of a three-degrees-of-freedom nonsmooth DVA model. In this paper, the expression of a Melnikov vector function suitable for studying the bifurcation of periodic orbits of six-dimensional piecewise smooth systems is given, and it is applied to study the existence and number of periodic solutions of an encapsulated DVA model.
• The relationship figure is introduced to provide guidance for estimating the number of periodic orbits. The existence and number of periodic solutions under different parameter conditions are given, and the geometric description is given.

This paper is arranged as follows: In Section 2, the model and its governing equation are proposed. In Section 3, the existence and stability of admissible equilibrium points are discussed. In Section 4, the Melnikov function is calculated and the existence and number of periodic orbits are discussed. The phase configurations of periodic orbits are presented with a numerical simulation.

2. System Description

In this section, the two-degrees-of-freedom system with an encapsulated nonsmooth dynamic vibration absorber under low-frequency excitation is proposed based on the NES model established by Geng and Ding [17], which is modeled using the six-dimensional piecewise smooth system and shown in Figure 1.

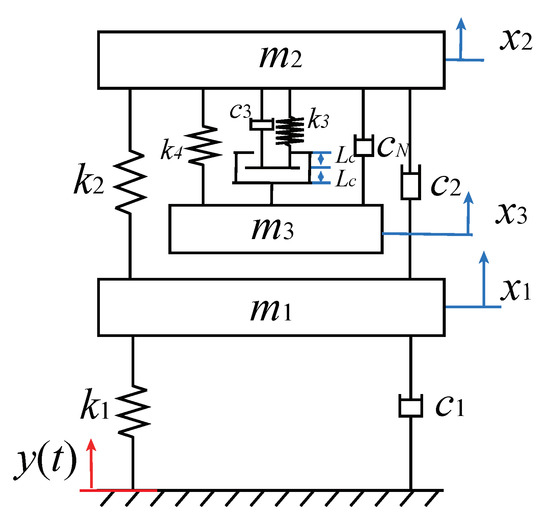
Figure 1. The nonsmooth dynamic vibration absorber model.

Figure 1 depicts a two-degrees-of-freedom primary system coupled with an encapsulated nonsmooth dynamic vibration absorber. The external excitation is $y\left(t\right)$ acting on the base. Compared with Reference [17], the difference is that the model uses linear springs. The piecewise stiffness and piecewise damper of the system are constructed by using the gap. According to Newton’s second law, the governing equation is described as

$$\begin{array}{cc}\hfill & m_1{\ddot{x}}_1+c_1\left({\dot{x}}_1-\dot{y}\right)+k_1\left(x_1-y\right)=c_2\left({\dot{x}}_2-{\dot{x}}_1\right)+k_2\left(x_2-x_1\right),\hfill \\ \hfill & m_2{\ddot{x}}_2+c_2\left({\dot{x}}_2-{\dot{x}}_1\right)+k_2\left(x_2-x_1\right)=c_N\left({\dot{x}}_3-{\dot{x}}_2\right)+k_4\left(x_3-x_2\right)+g\left(x_3-x_2\right)+h\left({\dot{x}}_3-{\dot{x}}_2\right),\hfill \\ \hfill & m_3{\ddot{x}}_3+c_N\left({\dot{x}}_3-{\dot{x}}_2\right)+k_4\left(x_3-x_2\right)+g\left(x_3-x_2\right)+h\left({\dot{x}}_3-{\dot{x}}_2\right)=0,\hfill \end{array}$$

(1)

where · is the derivation of t. $x_1,x_2,x_3$ and $m_1,m_2,m_3$ are displacements and masses of the two-degrees-of-freedom system and attached mass. $c_1,c_2,c_3,c_N$ are the damping coefficients and $k_1,k_2,k_3,k_4$ are the stiffness coefficients. $y\left(t\right)=asin\left(\omega t\right)$ is the external excitation and $L_c$ is the gap displacement. The piecewise elastic restoring force is

$$\begin{array}{c}\hfill g\left(x_3-x_2\right)=\left\{\begin{array}{cc}{k}_3\left(x_3-x_2-L_c\right),& x_3-x_2>L_c\\ 0,& -L_c\le x_3-x_2\le L_c\\ k_3\left(x_3-x_2+L_c\right),& x_3-x_2<-L_c\end{array},\right.\end{array}$$

and the piecewise damping force is

$$\begin{array}{c}\hfill h\left({\dot{x}}_3-{\dot{x}}_2\right)=\left\{\begin{array}{cc}{c}_3\left({\dot{x}}_3-{\dot{x}}_2\right),& x_3-x_2>L_c\\ 0,& -L_c\le x_3-x_2\le L_c\\ c_3\left({\dot{x}}_3-{\dot{x}}_2\right),& x_3-x_2<-L_c\end{array}.\right.\end{array}$$

The following dimensionless parameters are used:

$$\begin{array}{c}\hfill {\rho }_1=\frac{m_2}{m_1},{\rho }_2=\frac{m_3}{m_2},{\omega }_1=\sqrt{\frac{k_1}{m_1}},{\omega }_2=\sqrt{\frac{k_2}{m_2}},{\omega }_3=\sqrt{\frac{k_3}{m_3}},{\zeta }_1=\frac{c_1}{2m_1{\omega }_3},{\zeta }_2=\frac{c_2}{2m_1{\omega }_3},\\ \hfill {\zeta }_3=\frac{c_2}{2m_2{\omega }_3},{\zeta }_4=\frac{c_N}{2m_2{\omega }_3},{\zeta }_5=\frac{c_3}{2m_2{\omega }_3},{\zeta }_6=\frac{c_N}{2m_3{\omega }_3},{\zeta }_7=\frac{c_3}{2m_3{\omega }_3},{\nu }_1=\frac{{\omega }_2}{{\omega }_3},{\nu }_2=\frac{{\omega }_1}{{\omega }_3},v=\frac{k_4}{k_3},\\ \hfill u=\frac{k_4}{k_2},{\overline{x}}_1=\frac{x_1}{D},{\overline{x}}_2=\frac{x_2}{D},{\overline{x}}_3=\frac{x_3}{D},L=\frac{L_c}{D},\overline{t}={\omega }_{3}t,w_1=\frac{a}{D}sin\frac{\omega }{{\omega }_3}\overline{t},w_2=\frac{a\omega }{D{\omega }_3}cos\frac{\omega }{{\omega }_3}\overline{t}.\end{array}$$

For convenience, the over bar of $\overline{t}$ is dropped. The dimensionless equations of system (1) are shown as follows.

$$\begin{array}{cc}\hfill & {\ddot{\overline{x}}}_1+2{\zeta }_1\left({\dot{\overline{x}}}_1-w_2\right)+{\nu }_2^2\left({\overline{x}}_1-w_1\right)=2{\zeta }_2\left({\dot{\overline{x}}}_2-{\dot{\overline{x}}}_1\right)+{\nu }_1^2{\rho }_1\left({\overline{x}}_2-{\overline{x}}_1\right),\hfill \\ \hfill & {\ddot{\overline{x}}}_2+2{\zeta }_3\left({\dot{\overline{x}}}_2-{\dot{\overline{x}}}_1\right)+{\nu }_1^2\left({\overline{x}}_2-{\overline{x}}_1\right)=2{\zeta }_4\left({\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2\right)+u{\nu }_1^2\left({\overline{x}}_3-{\overline{x}}_2\right)\hfill \\ \hfill & +{\rho }_2\tilde{g}\left({\overline{x}}_3-{\overline{x}}_2\right)+2{\zeta }_5\tilde{h}\left({\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2\right),\hfill \\ \hfill & {\ddot{\overline{x}}}_3+2{\zeta }_6\left({\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2\right)+v\left({\overline{x}}_3-{\overline{x}}_2\right)+\tilde{g}\left({\overline{x}}_3-{\overline{x}}_2\right)+2{\zeta }_7\tilde{h}\left({\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2\right)=0.\hfill \end{array}$$

(2)

where

$$\begin{array}{c}\hfill \tilde{g}\left({\overline{x}}_3-{\overline{x}}_2\right)=\left\{\begin{array}{cc}{\overline{x}}_3-{\overline{x}}_2-L,& {\overline{x}}_3-{\overline{x}}_2>L\\ 0,& -L\le {\overline{x}}_3-{\overline{x}}_2\le L,\\ {\overline{x}}_3-{\overline{x}}_2+L,& {\overline{x}}_3-{\overline{x}}_2<-L\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \tilde{h}\left({\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2\right)=\left\{\begin{array}{cc}{\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2,& {\overline{x}}_3-{\overline{x}}_2>L\\ 0,& -L\le {\overline{x}}_3-{\overline{x}}_2\le L.\\ {\dot{\overline{x}}}_3-{\dot{\overline{x}}}_2,& {\overline{x}}_3-{\overline{x}}_2<-L\end{array}\right.\end{array}$$

When $\omega <<{\omega }_3$, system (1) is a fast system coupled with a slow-varying parameter, using the slow–fast method. Fast subsystem (2) is a generalized autonomous system.

3. Stability of Equilibrium Points

In this section, the existence and stability of the admissible equilibrium points for the model are discussed under different parameter conditions. Firstly, when ${\overline{x}}_3-{\overline{x}}_2>L$, the r-subsystem is shown as

$$\begin{array}{cc}\hfill {\ddot{\overline{x}}}_1=& -\left({\nu }_2^2+{\nu }_1^2{\rho }_1\right){\overline{x}}_1-\left(2{\zeta }_1+2{\zeta }_2\right){\dot{\overline{x}}}_1+{\nu }_1^2{\rho }_1{\overline{x}}_2+2{\zeta }_2{\dot{\overline{x}}}_2+2{\zeta }_1{w}_2+{\nu }_2^2{w}_1,\hfill \\ \hfill {\ddot{\overline{x}}}_2=& {\nu }_1^2{\overline{x}}_1+2{\zeta }_3{\dot{\overline{x}}}_1-\left({\nu }_1^2+{\rho }_2+u{\nu }_1^2\right){\overline{x}}_2-\left(2{\zeta }_3+2{\zeta }_4+2{\zeta }_5\right){\dot{\overline{x}}}_2+\left({\rho }_2+u{\nu }_1^2\right){\overline{x}}_3\hfill \\ \hfill & +\left(2{\zeta }_4+2{\zeta }_5\right){\dot{\overline{x}}}_3-{\rho }_{2}L,\hfill \\ \hfill {\ddot{\overline{x}}}_3=& \left(1+v\right){\overline{x}}_2+\left(2{\zeta }_6+2{\zeta }_7\right){\dot{\overline{x}}}_2-\left(1+v\right){\overline{x}}_3-\left(2{\zeta }_6+2{\zeta }_7\right){\dot{\overline{x}}}_3+L.\hfill \end{array}$$

(3a)

The c-subsystem is shown as

$$\begin{array}{cc}\hfill & {\ddot{\overline{x}}}_1=-\left({\nu }_2^2+{\nu }_1^2{\rho }_1\right){\overline{x}}_1-\left(2{\zeta }_1+2{\zeta }_2\right){\dot{\overline{x}}}_1+{\nu }_1^2{\rho }_1{\overline{x}}_2+2{\zeta }_2{\dot{\overline{x}}}_2+2{\zeta }_1{w}_2+{\nu }_2^2{w}_1,\hfill \\ \hfill & {\ddot{\overline{x}}}_2={\nu }_1^2{\overline{x}}_1+2{\zeta }_3{\dot{\overline{x}}}_1-\left({\nu }_1^2+u{\nu }_1^2\right){\overline{x}}_2-\left(2{\zeta }_3+2{\zeta }_4\right){\dot{\overline{x}}}_2+u{\nu }_1^2{\overline{x}}_3+2{\zeta }_4{\dot{\overline{x}}}_3,\hfill \\ \hfill & {\ddot{\overline{x}}}_3=v{\overline{x}}_2+2{\zeta }_6{\dot{\overline{x}}}_2-v{\overline{x}}_3-2{\zeta }_6{\dot{\overline{x}}}_3.\hfill \end{array}$$

(3b)

The l-subsystem is shown as

$$\begin{array}{cc}\hfill {\ddot{\overline{x}}}_1=& -\left({\nu }_2^2+{\nu }_1^2{\rho }_1\right){\overline{x}}_1-\left(2{\zeta }_1+2{\zeta }_2\right){\dot{\overline{x}}}_1+{\nu }_1^2{\rho }_1{\overline{x}}_2+2{\zeta }_2{\dot{\overline{x}}}_2+2{\zeta }_1{w}_2+{\nu }_2^2{w}_1,\hfill \\ \hfill {\ddot{\overline{x}}}_2=& {\nu }_1^2{\overline{x}}_1+2{\zeta }_3{\dot{\overline{x}}}_1-\left({\nu }_1^2+{\rho }_2+u{\nu }_1^2\right){\overline{x}}_2-\left(2{\zeta }_3+2{\zeta }_4+2{\zeta }_5\right){\dot{\overline{x}}}_2+\left({\rho }_2+u{\nu }_1^2\right){\overline{x}}_3\hfill \\ \hfill & +\left(2{\zeta }_4+2{\zeta }_5\right){\dot{\overline{x}}}_3+{\rho }_{2}L,\hfill \\ \hfill {\ddot{\overline{x}}}_3=& \left(1+v\right){\overline{x}}_2+\left(2{\zeta }_6+2{\zeta }_7\right){\dot{\overline{x}}}_2-\left(1+v\right){\overline{x}}_3-\left(2{\zeta }_6+2{\zeta }_7\right){\dot{\overline{x}}}_3-L.\hfill \end{array}$$

(3c)

Introducing the state vector $\mathit{y}={(y_1,y_2,y_3,y_4,y_5,y_6)}^{\mathrm{T}}={({\overline{x}}_1,{\dot{\overline{x}}}_1,{\overline{x}}_2,{\dot{\overline{x}}}_2,{\overline{x}}_3,{\dot{\overline{x}}}_3)}^{\mathrm{T}}$, system (2) could be transformed into

$$\begin{array}{cc}\hfill & \dot{\mathit{y}}={\mathit{A}}_r\mathit{y}+{\mathit{b}}_r,\mathit{y}\in D_r,\hfill \\ \hfill & \dot{\mathit{y}}={\mathit{A}}_c\mathit{y}+{\mathit{b}}_c,\mathit{y}\in {\mathrm{\Pi }}^{+}\cup D_c\cup {\mathrm{\Pi }}^{-},\hfill \\ \hfill & \dot{\mathit{y}}={\mathit{A}}_l\mathit{y}+{\mathit{b}}_l,\mathit{y}\in D_l,\hfill \\ \hfill \end{array}$$

(4)

where

$$\begin{array}{cc}\hfill {\mathit{A}}_r=& {\mathit{A}}_l={\partial }_{1,2}^{6,6}\left(1\right)+{\partial }_{2,1}^{6,6}\left(-{\nu }_2^2-{\nu }_1^2{\rho }_1\right)+{\partial }_{2,2}^{6,6}\left(-2{\zeta }_1-2{\zeta }_2\right)+{\partial }_{2,3}^{6,6}\left({\nu }_1^2{\rho }_1\right)+{\partial }_{2,4}^{6,6}\left(2{\zeta }_2\right)\hfill \\ \hfill & +{\partial }_{3,4}^{6,6}\left(1\right)+{\partial }_{4,1}^{6,6}\left({\nu }_1^2\right)+{\partial }_{4,2}^{6,6}\left(2{\zeta }_3\right)+{\partial }_{4,3}^{6,6}\left(-{\nu }_1^2-{\rho }_2-u{\nu }_1^2\right)+{\partial }_{4,4}^{6,6}\left(-2{\zeta }_3-2{\zeta }_4-2{\zeta }_5\right)\hfill \\ \hfill & +{\partial }_{4,5}^{6,6}\left({\rho }_2+u{\nu }_1^2\right)+{\partial }_{4,6}^{6,6}\left(2{\zeta }_4+2{\zeta }_5\right)+{\partial }_{5,6}^{6,6}\left(1\right)+{\partial }_{6,3}^{6,6}\left(1+v\right)+{\partial }_{6,4}^{6,6}\left(2{\zeta }_6+2{\zeta }_7\right)\hfill \\ \hfill & +{\partial }_{6,5}^{6,6}\left(-1-v\right)+{\partial }_{6,6}^{6,6}\left(-2{\zeta }_6-2{\zeta }_7\right),\hfill \\ \hfill {\mathit{A}}_c=& {\partial }_{1,2}^{6,6}\left(1\right)+{\partial }_{2,1}^{6,6}\left(-{\nu }_2^2-{\nu }_1^2{\rho }_1\right)+{\partial }_{2,2}^{6,6}\left(-2{\zeta }_1-2{\zeta }_2\right)+{\partial }_{2,3}^{6,6}\left({\nu }_1^2{\rho }_1\right)+{\partial }_{2,4}^{6,6}\left(2{\zeta }_2\right)\hfill \\ \hfill & +{\partial }_{3,4}^{6,6}\left(1\right)+{\partial }_{4,1}^{6,6}\left({\nu }_1^2\right)+{\partial }_{4,2}^{6,6}\left(2{\zeta }_3\right)+{\partial }_{4,3}^{6,6}\left(-{\nu }_1^2-u{\nu }_1^2\right)+{\partial }_{4,4}^{6,6}\left(-2{\zeta }_3-2{\zeta }_4\right)\hfill \\ \hfill & +{\partial }_{4,5}^{6,6}\left(u{\nu }_1^2\right)+{\partial }_{4,6}^{6,6}\left(2{\zeta }_4\right)+{\partial }_{5,6}^{6,6}\left(1\right)+{\partial }_{6,3}^{6,6}\left(v\right)+{\partial }_{6,4}^{6,6}\left(2{\zeta }_6\right)+{\partial }_{6,5}^{6,6}\left(-v\right)\hfill \\ \hfill & +{\partial }_{6,6}^{6,6}\left(-2{\zeta }_6\right),\hfill \\ \hfill {\mathit{b}}_r=& {\partial }_{2,1}^{6,1}\left(2{\zeta }_1{w}_2+{\nu }_2^2{w}_1\right)+{\partial }_{4,1}^{6,1}\left(-{\rho }_{2}L\right)+{\partial }_{6,1}^{6,1}\left(L\right),\hfill \\ \hfill {\mathit{b}}_l=& {\partial }_{2,1}^{6,1}\left(2{\zeta }_1{w}_2+{\nu }_2^2{w}_1\right)+{\partial }_{4,1}^{6,1}\left({\rho }_{2}L\right)+{\partial }_{6,1}^{6,1}(-L),\hfill \\ \hfill {\mathit{b}}_c=& {\partial }_{2,1}^{6,1}\left(2{\zeta }_1{w}_2+{\nu }_2^2{w}_1\right).\hfill \end{array}$$

${\partial }_{p,q}^{m,n}\left(\mathit{M}\right)$ is termed as a matrix, in which the $(p,q)$-th block is $\mathit{M}$ and the other blocks are zero matrices [32]. The regions and switching manifolds of system (4) are described as

$$\begin{array}{cc}\hfill & D_r=\left\{\mathit{y}\in {\mathit{R}}^6\mid y_5-y_3>L\right\},\hfill \\ \hfill & D_c=\left\{\mathit{y}\in {\mathit{R}}^6\mid -L<y_5-y_3<L\right\},\hfill \\ \hfill & D_l=\left\{\mathit{y}\in {\mathit{R}}^6\mid y_5-y_3<-L\right\},\hfill \\ \hfill & {\mathrm{\Pi }}^{+}=\left\{\mathit{y}\in {\mathit{R}}^6\mid y_5-y_3=L\right\},\hfill \\ \hfill & {\mathrm{\Pi }}^{-}=\left\{\mathit{y}\in {\mathit{R}}^6\mid y_5-y_3=-L\right\}.\hfill \end{array}$$

3.1. Equilibrium Points

According to the definition of equilibrium points of piecewise smooth systems [33], an equilibrium point is termed an admissible equilibrium point if ${\dot{\mathit{x}}}^{\ast }={\mathit{f}}^i\left({\mathit{x}}^{\ast }\right)$ and ${\mathit{x}}^{\ast }\in D_i$. If the system satisfies ${\dot{\mathit{x}}}^{\ast }={\mathit{f}}^i\left({\mathit{x}}^{\ast }\right)$, ${\mathit{x}}^{\ast }\in D_j,i\ne j$ then it is called a virtual equilibrium point.

Firstly, the equilibrium points of system (4) are

$$\begin{array}{cc}\hfill E_c=& \frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}\left({\partial }_{1,1}^{6,1}\left(1\right)+{\partial }_{3,1}^{6,1}\left(1\right)+{\partial }_{5,1}^{6,1}\left(1\right)\right),\hfill \\ \hfill E_r=& {\partial }_{1,1}^{6,1}\left(\frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}-\frac{{\rho }_1{\rho }_{2}L}{{\nu }_2^2}+\frac{{\rho }_{1}L\left(u{\nu }_1^2+{\rho }_2\right)}{{\nu }_2^2\left(v+1\right)}\right)\hfill \\ \hfill & +{\partial }_{3,1}^{6,1}\left(\frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}-\frac{\left({\rho }_1{\nu }_1^2+{\nu }_2^2\right){\rho }_{2}L}{{\nu }_1^2{\nu }_2^2}+\frac{\left({\rho }_1{\nu }_1^2+{\nu }_2^2\right)\left(u{\nu }_1^2+{\rho }_2\right)L}{{\nu }_1^2{\nu }_2^2\left(v+1\right)}\right)\hfill \\ \hfill & +{\partial }_{5,1}^{6,1}\left(\frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}-\frac{\left({\rho }_1{\nu }_1^2+{\nu }_2^2\right){\rho }_{2}L}{{\nu }_1^2{\nu }_2^2}+\frac{L}{{\nu }_1^2{\nu }_2^2\left(v+1\right)}\right.\hfill \\ \hfill & \left.·\left({\rho }_{1}u{\nu }_1^4+u{\nu }_1^2{\nu }_2^2+{\rho }_1{\rho }_2{\nu }_1^2+{\nu }_1^2{\nu }_2^2+{\rho }_2{\nu }_2^2\right)\right),\hfill \\ \hfill E_l=& {\partial }_{1,1}^{6,1}\left(\frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}+\frac{{\rho }_1{\rho }_{2}L}{{\nu }_2^2}-\frac{{\rho }_{1}L\left(u{\nu }_1^2+{\rho }_2\right)}{{\nu }_2^2\left(v+1\right)}\right)\hfill \\ \hfill & +{\partial }_{3,1}^{6,1}\left(\frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}+\frac{\left({\rho }_1{\nu }_1^2+{\nu }_2^2\right){\rho }_{2}L}{{\nu }_1^2{\nu }_2^2}-\frac{\left({\rho }_1{\nu }_1^2+{\nu }_2^2\right)\left(u{\nu }_1^2+{\rho }_2\right)L}{{\nu }_1^2{\nu }_2^2\left(v+1\right)}\right).\hfill \\ \hfill & +{\partial }_{5,1}^{6,1}\left(\frac{{\nu }_2^2{w}_1+2w_2{\zeta }_1}{{\nu }_2^2}+\frac{\left({\rho }_1{\nu }_1^2+{\nu }_2^2\right){\rho }_{2}L}{{\nu }_1^2{\nu }_2^2}-\frac{L}{{\nu }_1^2{\nu }_2^2\left(v+1\right)}\right.\hfill \\ \hfill & \left.·\left({\rho }_{1}u{\nu }_1^4+u{\nu }_1^2{\nu }_2^2+{\rho }_1{\rho }_2{\nu }_1^2+{\nu }_1^2{\nu }_2^2+{\rho }_2{\nu }_2^2\right)\right).\hfill \end{array}$$

Then, the existence of the admissible equilibrium point is discussed under different conditions of v.

Case 1: $v>0$

• $E_c$ is always an admissible equilibrium point;
• $E_r$ is always a virtual equilibrium point, because $\frac{L}{v+1}<L$;
• $E_l$ is always a virtual equilibrium point, because $-\frac{L}{v+1}>-L$.

Case 2: $v=0$

• $E_c$ is always an admissible equilibrium point;
• $E_r$ is always a boundary equilibrium point, because $v=0$;
• $E_l$ is always a boundary equilibrium point, because $v=0$.

Case 3: $v<0$

• $E_c$ is always an admissible equilibrium point;
• $E_r$ is always an admissible equilibrium point, because $\frac{L}{v+1}>L$;
• $E_l$ is always a boundary equilibrium point, because $-\frac{L}{v+1}<-L$.

Next, the stability of an admissible equilibrium point $E_c$ is discussed when $v>0$.

3.2. Stability

From (4), the characteristic equation is shown as follows,

$$\begin{array}{c}\hfill {\lambda }^6+a_1{\lambda }^5+a_2{\lambda }^4+a_3{\lambda }^3+a_4{\lambda }^2+a_5\lambda +a_6=0,\end{array}$$

(5)

where

$$\begin{array}{cc}\hfill a_1=& 2{\zeta }_1+2{\zeta }_2+2{\zeta }_3+2{\zeta }_4+2{\zeta }_6,\hfill \\ \hfill a_2=& v+{\nu }_1^2+u{\nu }_1^2+{\nu }_2^2+4{\zeta }_1{\zeta }_3+4{\zeta }_1{\zeta }_4+4{\zeta }_2{\zeta }_4+4{\zeta }_1{\zeta }_6+4{\zeta }_2{\zeta }_6+4{\zeta }_3{\zeta }_6+{\nu }_1^2{\rho }_1,\hfill \\ \hfill a_3=& 2v{\zeta }_1+2{\nu }_1^2{\zeta }_1+2u{\nu }_1^2{\zeta }_1+2v{\zeta }_2+2u{\nu }_1^2{\zeta }_2+2v{\zeta }_3+2{\nu }_2^2{\zeta }_3+2{\nu }_2^2{\zeta }_4+2{\nu }_1^2{\zeta }_6+2{\nu }_2^2{\zeta }_6\hfill \\ \hfill & +8{\zeta }_1{\zeta }_3{\zeta }_6+2{\nu }_1^2{\zeta }_4{\rho }_1+2{\nu }_1^2{\zeta }_6{\rho }_1,\hfill \\ \hfill a_4=& v{\nu }_1^2+v{\nu }_2^2+{\nu }_1^2{\nu }_2^2+u{\nu }_1^2{\nu }_2^2+4v{\zeta }_1{\zeta }_3+4{\nu }_1^2{\zeta }_1{\zeta }_6+4{\nu }_2^2{\zeta }_3{\zeta }_6+v{\nu }_1^2{\rho }_1+u{\nu }_1^4{\rho }_1,\hfill \\ \hfill a_5=& 2v{\nu }_1^2{\zeta }_1+2v{\nu }_2^2{\zeta }_3+2{\nu }_1^2{\nu }_2^2{\zeta }_6,\hfill \\ \hfill a_6=& v{\nu }_1^2{\nu }_2^2,\hfill \\ \hfill {\Delta }_1=& a_1,{\Delta }_3=\left|\begin{array}{ccc}{a}_1& a_3& a_5\\ 1& a_2& a_4\\ 0& a_1& a_3\end{array}\right|,{\Delta }_5=\left|\begin{array}{ccccc}{a}_1& a_3& a_5& 0& 0\\ 1& a_2& a_4& a_6& 0\\ 0& a_1& a_3& a_5& 0\\ 0& 1& a_2& a_4& a_6\\ 0& 0& a_1& a_3& a_5\end{array}\right|.\hfill \end{array}$$

The parameters of a DVA play an important role in its design and application. According to the Liénard–Chipart criterion [24], the conditions that Equation (5) has negative real parts are $a_2>0,a_4>0,a_6>0,a_1>0,{\Delta }_3>0,{\Delta }_5>0$. The asymptotically stable and unstable regions of $E_c$ are discussed under

$$\begin{array}{c}\hfill P_{ar1}=(v,{\rho }_1,{\rho }_2,u,{\zeta }_1,{\zeta }_5,{\zeta }_6,{\zeta }_7)=(2,0.2,0.01,1,1,0,0,0.1).\end{array}$$

According to the conditions $a_2>0,a_4>0,a_6>0,a_1>0,{\Delta }_3>0,{\Delta }_5>0$, the asymptotically stable and unstable regions of $E_c$ under $P_{ar1}$ in the two-dimensional parameter space $({\nu }_1,{\nu }_2)$ are shown in Figure 2.

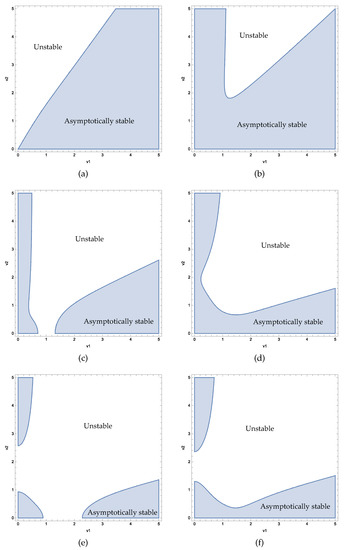
Figure 2. The asymptotically stable and unstable regions of $E_c$: (a) $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(0.1,0,0)$. (b) $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(0.1,0.1,0.2)$. (c) $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(0.5,0.1,0.8)$. (d) $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(2,1,2)$. (e) $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(2,1,5)$. (f) $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(2,1,3).$

Figure 2 shows that the asymptotically stable and unstable regions of $E_c$ have different distributions for different ${\zeta }_2,{\zeta }_3,{\zeta }_4$ values, providing theoretical guidance for the parameter design of a DVA. The relationship between the system parameters ${\nu }_1$ and ${\nu }_2$ can be obtained, which is drawn with the stability conditions. As can be seen in Figure 2a, when the parameter ${\nu }_1$ increases, the critical value of the parameter ${\nu }_2$ also increases gradually. When the system is in the shadow part of the region, the equilibrium point is asymptotically stable.

The vibration reduction effect of system (1) with and without the nonsmooth DVA in the asymptotically stable and unstable regions under $({\zeta }_2,{\zeta }_3,{\zeta }_4)=(0.1,0,0)$ when $y\left(t\right)=0.5sin\left(0.1t\right)$ is shown in Figure 3.

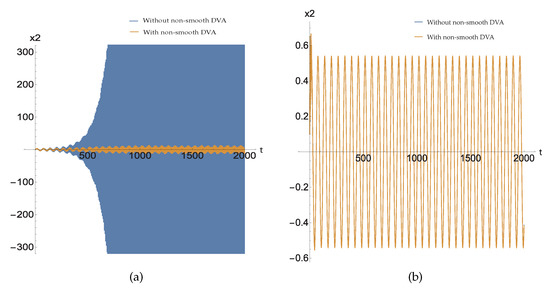
Figure 3. The vibration reduction effect in the unstable and asymptotically stable regions: (a) $({\nu }_1,{\nu }_2)=(1,2.5)$. (b) $({\nu }_1,{\nu }_2)=(2,1)$.

Figure 3a shows that the vibration is reduced in the unstable region. Figure 3b shows the vibration of the mass $m_2$ with nonsmooth DVA and without nonsmooth DVA in the asymptotically stable region.

The asymptotically stable regions of $E_c$ could be visualized in the 3D parameter space $({\nu }_1,{\nu }_2,u)$ for different ${\zeta }_2,{\zeta }_4,{\zeta }_6$ values under the following condition, which is shown in Figure 4.

$$\begin{array}{c}\hfill P_{ar2}=(v,{\rho }_1,{\rho }_2,{\zeta }_1,{\zeta }_3,{\zeta }_5,{\zeta }_7)=(1,1,0.1,2,0,0,0.1).\end{array}$$

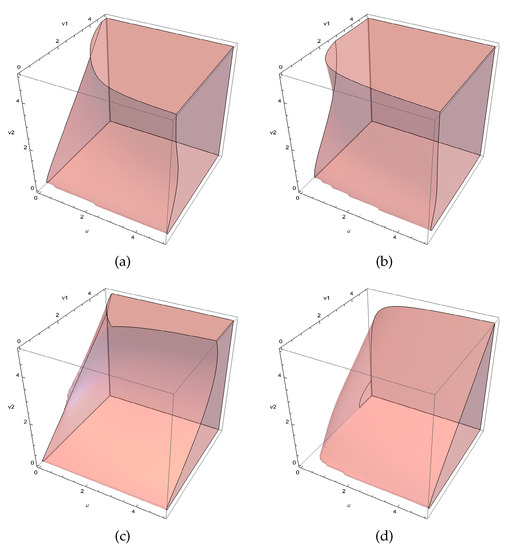
Figure 4. The asymptotically stable regions of $E_c$: (a) $({\zeta }_2,{\zeta }_4,{\zeta }_6)=(3,1.5,5)$. (b) $({\zeta }_2,{\zeta }_4,{\zeta }_6)=(2,2,2)$. (c) $({\zeta }_2,{\zeta }_4,{\zeta }_6)=(5,0,0.1)$. (d) $({\zeta }_2,{\zeta }_4,{\zeta }_6)=(2,0.2,0)$.

4. Bifurcation of Periodic Orbits

In this section, we explore the existence and number of periodic orbits for a nonsmooth DVA model based on the Melnikov method. Let ${\overline{x}}_4={\overline{x}}_3-{\overline{x}}_2,{\overline{x}}_5={\overline{x}}_2-{\overline{x}}_1$, and system (2) is transformed into

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\ddot{\overline{x}}}_4=& -\tilde{g}\left({\overline{x}}_4\right)-(v+u{\nu }_1^2){\overline{x}}_4-{\rho }_2\tilde{g}\left({\overline{x}}_4\right)-\left(2{\zeta }_4+2{\zeta }_6\right){\dot{\overline{x}}}_4-\left(2{\zeta }_5+2{\zeta }_7\right)\tilde{h}\left({\dot{\overline{x}}}_4\right)\hfill \\ \hfill & +{\nu }_1^2{\overline{x}}_5+2{\zeta }_3{\dot{\overline{x}}}_5,\hfill \\ \hfill {\ddot{\overline{x}}}_5=& {\rho }_2\tilde{g}\left({\overline{x}}_4\right)+u{\nu }_1^2{\overline{x}}_4+2{\zeta }_5\tilde{h}\left({\dot{\overline{x}}}_4\right)+2{\zeta }_4{\dot{\overline{x}}}_4-\left({\nu }_1^2+{\rho }_1{\nu }_1^2\right){\overline{x}}_5-\left(2{\zeta }_2+2{\zeta }_3\right){\dot{\overline{x}}}_5\hfill \\ \hfill & +{\nu }_2^2{\overline{x}}_1+2{\zeta }_1{\dot{\overline{x}}}_1-\left({\nu }_2^2{w}_1+2{\zeta }_1{w}_2\right),\hfill \\ \hfill {\ddot{\overline{x}}}_1=& {\rho }_1{\nu }_1^2{\overline{x}}_5+2{\zeta }_2{\dot{\overline{x}}}_5-{\nu }_2^2{\overline{x}}_1-2{\zeta }_1{\dot{\overline{x}}}_1+\left({\nu }_2^2{w}_1+2{\zeta }_1{w}_2\right),\hfill \end{array}\end{array}$$

(6)

where

$$\begin{array}{c}\hfill \tilde{g}\left({\overline{x}}_4\right)=\left\{\begin{array}{cc}{\overline{x}}_4-L,& {\overline{x}}_4>L\\ 0,& -L\le {\overline{x}}_4\le L,\\ {\overline{x}}_4+L,& {\overline{x}}_4<-L\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \tilde{h}\left({\dot{\overline{x}}}_4\right)=\left\{\begin{array}{cc}{\dot{\overline{x}}}_4,& {\overline{x}}_4>L\\ 0,& -L\le {\overline{x}}_4\le L.\\ {\dot{\overline{x}}}_4,& {\overline{x}}_4<-L\end{array}\right.\end{array}$$

System (6) is transformed into the following form:

$$\begin{array}{cc}\hfill & {\ddot{\overline{x}}}_4=-\tilde{g}\left({\overline{x}}_4\right)-p_1{\overline{x}}_4-p_2\tilde{g}\left({\overline{x}}_4\right)-p_3{\dot{\overline{x}}}_4-p_4\tilde{h}\left({\dot{\overline{x}}}_4\right)+p_5{\overline{x}}_5+p_6{\dot{\overline{x}}}_5,\hfill \\ \hfill & {\ddot{\overline{x}}}_5=e_1\tilde{g}\left({\overline{x}}_4\right)+e_2{\overline{x}}_4+e_3\tilde{h}\left({\dot{\overline{x}}}_4\right)+e_4{\dot{\overline{x}}}_4-e_5{\overline{x}}_5-e_6{\dot{\overline{x}}}_5+e_7{\overline{x}}_1+e_8{\dot{\overline{x}}}_1-e_9,\hfill \\ \hfill & {\ddot{\overline{x}}}_1=q_1{\overline{x}}_5+q_2{\dot{\overline{x}}}_5-q_3{\overline{x}}_1-q_4{\dot{\overline{x}}}_1+q_5,\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill & p_1=v+u{\nu }_1^2,p_2={\rho }_2,p_3=2{\zeta }_4+2{\zeta }_6,p_4=2{\zeta }_5+2{\zeta }_7,p_5={\nu }_1^2,p_6=2{\zeta }_3,\hfill \\ \hfill & e_1={\rho }_2,e_2=u{\nu }_1^2,e_3=2{\zeta }_5,e_4=2{\zeta }_4,e_5={\nu }_1^2+{\rho }_1{\nu }_1^2,e_6=2{\zeta }_2+2{\zeta }_3,e_7={\nu }_2^2,\hfill \\ \hfill & e_8=2{\zeta }_1,e_9={\nu }_2^2{w}_1+2{\zeta }_1{w}_2,q_1={\rho }_1{\nu }_1^2,q_2=2{\zeta }_2,q_3={\nu }_2^2,q_4=2{\zeta }_1,q_5={\nu }_2^2{w}_1+2{\zeta }_1{w}_2.\hfill \end{array}$$

The following scales transformation is introduced.

$$\begin{array}{cc}\hfill & p_k\to \epsilon p_k,e_i\to {\epsilon }^2{e}_i,q_j\to {\epsilon }^2{q}_j,e_6\to \epsilon e_6,e_8\to \epsilon e_8,q_2\to \epsilon q_2,q_4\to \epsilon q_4,k=1,\cdots ,5,\hfill \\ \hfill & \left\{i\in N^{+}\mid i\le 9,i\ne 6,8\right\},\left\{j\in N^{+}\mid j\le 5,j\ne 2,4\right\}.\hfill \end{array}$$

And let ${\dot{\overline{x}}}_4=z_1,{\dot{\overline{x}}}_5=\epsilon z_2,{\dot{\overline{x}}}_1=\epsilon z_3,y_1={\overline{x}}_4,y_2=z_1,y_3={\overline{x}}_5,y_4=z_2,y_5={\overline{x}}_1,y_6=z_3.$ System (7) is transformed into

$$\begin{array}{cc}\hfill & {\dot{y}}_1=y_2\hfill \\ \hfill & {\dot{y}}_2=-\widehat{g}\left(y_1\right)+\epsilon \left(-p_1{y}_1-p_2\widehat{g}\left(y_1\right)-p_3{y}_2-p_4\widehat{h}\left(y_2\right)+p_5{y}_3+p_6{y}_4\right)\hfill \\ \hfill & {\dot{y}}_3=\epsilon y_4\hfill \\ \hfill & {\dot{y}}_4=\epsilon (e_1\widehat{g}\left(y_1\right)+e_2{y}_1+e_3\widehat{h}\left(y_2\right)+e_4{y}_2-e_5{y}_3-e_6{y}_4+e_7{y}_5+e_8{y}_6-e_9)\hfill \\ \hfill & {\dot{y}}_5=\epsilon y_6\hfill \\ \hfill & {\dot{y}}_6=\epsilon (q_1{y}_3+q_2{y}_4-q_3{y}_5-q_4{y}_6+q_5)\hfill \end{array}$$

(8)

where

$$\begin{array}{cc}\hfill & \widehat{g}\left(y_1\right)=\left\{\begin{array}{cc}{y}_1-L,& y_1>L\\ 0,& -L\le y_1\le L\\ y_1+L,& y_1<-L\end{array},\widehat{h}\left(y_2\right)=\left\{\begin{array}{cc}{y}_2,& y_1>L\\ 0,& -L\le y_1\le L.\\ y_2,& y_1<-L\end{array}\right.\right.\hfill \end{array}$$

4.1. Melnikov Function

We investigate the number and parameter control of periodic orbits for an encapsulated DVA model. Using the r-subsystem of (8), let

$$\begin{array}{cc}\hfill & P_1^r=0,\hfill \\ \hfill & P_2^r=-p_1{y}_1-p_2(y_1-L)-p_3{y}_2-p_4{y}_2+p_5{y}_3+p_6{y}_4,\hfill \\ \hfill & Q_1^r=y_4,\hfill \\ \hfill & Q_2^r=e_1(y_1-L)+e_2{y}_1+e_3{y}_2+e_4{y}_2-e_5{y}_3-e_6{y}_4+e_7{y}_5+e_8{y}_6-e_9,\hfill \\ \hfill & Q_3^r=y_6,\hfill \\ \hfill & Q_4^r=q_1{y}_3+q_2{y}_4-q_3{y}_5-q_4{y}_6+q_5.\hfill \end{array}$$

Using the c-subsystem of (8), let

$$\begin{array}{cc}\hfill & P_1^c=0,\hfill \\ \hfill & P_2^c=-p_1{y}_1-p_3{y}_2+p_5{y}_3+p_6{y}_4,\hfill \\ \hfill & Q_1^c=y_4,\hfill \\ \hfill & Q_2^c=e_2{y}_1+e_4{y}_2-e_5{y}_3-e_6{y}_4+e_7{y}_5+e_8{y}_6-e_9,\hfill \\ \hfill & Q_3^c=y_6,\hfill \\ \hfill & Q_4^c=q_1{y}_3+q_2{y}_4-q_3{y}_5-q_4{y}_6+q_5.\hfill \end{array}$$

Using the l-subsystem of (8), let

$$\begin{array}{cc}\hfill & P_1^l=0,\hfill \\ \hfill & P_2^l=-p_1{y}_1-p_2(y_1+L)-p_3{y}_2-p_4{y}_2+p_5{y}_3+p_6{y}_4,\hfill \\ \hfill & Q_1^l=y_4,\hfill \\ \hfill & Q_2^l=e_1(y_1+L)+e_2{y}_1+e_3{y}_2+e_4{y}_2-e_5{y}_3-e_6{y}_4+e_7{y}_5+e_8{y}_6-e_9,\hfill \\ \hfill & Q_3^l=y_6,\hfill \\ \hfill & Q_4^l=q_1{y}_3+q_2{y}_4-q_3{y}_5-q_4{y}_6+q_5.\hfill \end{array}$$

First of all, the first integrals of the unperturbed subsystems defined in $D_i$ are

$$\begin{array}{cc}\hfill & {\mathit{H}}^r=(\frac{1}{2}{y}_2^2+\frac{1}{2}{(y_1^{}-L)}^2,y_3,y_4,y_5,y_6),\hfill \\ \hfill & {\mathit{H}}^c=(\frac{1}{2}{y}_2^2,y_3,y_4,y_5,y_6),\hfill \\ \hfill & {\mathit{H}}^l=(\frac{1}{2}{y}_2^2+\frac{1}{2}{(y_1^{}+L)}^2,y_3,y_4,y_5,y_6).\hfill \end{array}$$

Next, we will discuss the bifurcation problem of the periodic orbits of system (8) when $h_1>0$, and obtain its orbits $L_{h_1,\widehat{h}}^w(w=1,\cdots ,4)$ as

$$\begin{array}{cc}\hfill & {\Gamma }_{h_1,\widehat{h}}^1:y_1^{}=\sqrt{2h_1-y_2^2}+L,-\sqrt{2h_1}\le y_2\le \sqrt{2h_1},\hfill \\ \hfill & {\Gamma }_{h_1,\widehat{h}}^2:y_2^{}=-\sqrt{2h_1},-L\le y_1\le L,\hfill \\ \hfill & {\Gamma }_{h_1,\widehat{h}}^3:y_1^{}=-\sqrt{2h_1-y_2^2}-L,-\sqrt{2h_1}\le y_2\le \sqrt{2h_1},\hfill \\ \hfill & {\Gamma }_{h_1,\widehat{h}}^4:y_2^{}=\sqrt{2h_1},-L\le y_1\le L.\hfill \end{array}$$

The coordinates of the intersection points are

$$\begin{array}{c}\hfill A_1^{\ast }=(L,\sqrt{2h_1}),A_2^{\ast }=(L,-\sqrt{2h_1}),A_3^{\ast }=(-L,-\sqrt{2h_1}),A_4^{\ast }=(-L,\sqrt{2h_1}).\end{array}$$

According to [34], the Melnikov vector function of six-dimensional piecewise smooth systems could be obtained as follows, in which the unperturbed systems are functions independent of $y_3,y_4,y_5,y_6$.

$$\begin{array}{cc}\hfill \mathit{M}(h,\mu )& ={\partial }_{1,1}^{5,1}(\sum _{w=1}^4{N}_{w1}\left(h\right)\left(M_{1w1}(h,\mu )\right)+\sum _{u=2}^5{\partial }_{u,1}^{5,1}(\sum _{w=1}^4{M}_{wu}(h,\mu ))\hfill \\ \hfill & =\sum _{\beta =1}^5{\partial }_{\beta ,1}^{5,1}\left(M_{\beta }(h,\mu )\right),\hfill \end{array}$$

(9)

where

$$\begin{array}{cc}\hfill & M_{111}(h,\mu )={\int }_{{\Gamma }_{h_1,\widehat{h}}^1}{P}_2^r\mathrm{d}{y}_1-P_1^r\mathrm{d}{y}_2,\hfill \\ \hfill & M_{1\alpha 1}(h,\mu )={\int }_{{\Gamma }_{h_1,\widehat{h}}^{\alpha }}{P}_2^c\mathrm{d}{y}_1-P_1^c\mathrm{d}{y}_2,\hfill \\ \hfill & M_{131}(h,\mu )={\int }_{{\Gamma }_{h_1,\widehat{h}}^3}{P}_2^l\mathrm{d}{y}_1-P_1^l\mathrm{d}{y}_2,\hfill \\ \hfill & M_{1u}(h,\mu )={\int }_{{\Gamma }_{h_1,\widehat{h}}^1}{Q}_{u-1}^r\mathrm{d}t,\hfill \\ \hfill & M_{\alpha u}(h,\mu )={\int }_{{\Gamma }_{h_1,\widehat{h}}^{\alpha }}{Q}_{u-1}^c\mathrm{d}t,\alpha =2,4,u=2,\cdots ,5,\hfill \\ \hfill & M_{3u}(h,\mu )={\int }_{{\Gamma }_{h_1,\widehat{h}}^3}{Q}_{u-1}^l\mathrm{d}t,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & N_{11}\left(h\right)=1,N_{21}\left(h\right)=\frac{H_{y_2}^l\left(A_3\left(h\right)\right)}{H_{y_2}^c\left(A_3\left(h\right)\right)}\frac{H_{y_2}^c\left(A_4\left(h\right)\right)}{H_{y_2}^l\left(A_4\left(h\right)\right)}\frac{H_{y_2}^r\left(A_1\left(h\right)\right)}{H_{y_2}^c\left(A_1\left(h\right)\right)},\hfill \\ \hfill & N_{31}\left(h\right)=\frac{H_{y_2}^c\left(A_4\left(h\right)\right)}{H_{y_2}^l\left(A_4\left(h\right)\right)}\frac{H_{y_2}^r\left(A_1\left(h\right)\right)}{H_{y_2}^c\left(A_1\left(h\right)\right)},N_{41}\left(h\right)=\frac{H_{y_2}^r\left(A_1\left(h\right)\right)}{H_{y_2}^c\left(A_1\left(h\right)\right)}.\hfill \end{array}$$

According to its first integrals form, the following polar coordinate transformation is introduced for the r-subsystem:

$$\begin{array}{c}\hfill {\Gamma }_{h,\widehat{h}}^1:y_1=\sqrt{2h_1}sin\left(t\right)+L,y_2=\sqrt{2h_1}cos\left(t\right),y_3=h_2,y_4=h_3,y_5=h_4,y_6=h_5.\end{array}$$

From (9), the first component of its Melnikov vector function is shown as the following form by means of Maple.

$$\begin{array}{cc}\hfill M_{111}\left(h\right)=& {\int }_{{\Gamma }_{h,\widehat{h}}^1}{P}_2^r\mathrm{d}{y}_1-P_1^r\mathrm{d}{y}_2\hfill \\ \hfill =& {\int }_{\beta }^{-\beta }\sqrt{2h_1}cos\left(t\right)[-p_1\left(\sqrt{2h_1}sin\left(t\right)+L\right)-p_2\sqrt{2h_1}sin\left(t\right)-p_3\sqrt{2h_1}cos\left(t\right)\hfill \\ \hfill & -p_4\sqrt{2h_1}cos\left(t\right)+p_5{h}_2+p_6{h}_3]dt\hfill \\ \hfill =& 2h_1{p}_{3}sin\left(\beta \right)cos\left(\beta \right)+2h_1{p}_{4}sin\left(\beta \right)cos\left(\beta \right)+2h_1{p}_3\beta +2h_1{p}_4\beta \hfill \\ \hfill & +2\sqrt{2h_1}Lsin\left(\beta \right)p_1-2\sqrt{2h_1}sin\left(\beta \right)h_2{p}_5-2\sqrt{2h_1}sin\left(\beta \right)h_3{p}_6.\hfill \end{array}$$

where $\beta =arcsin\frac{\sqrt{2h_1}}{\sqrt{L^2+2h_1}},sin\beta =\frac{\sqrt{2h_1}}{\sqrt{L^2+2h_1}},cos\beta =\frac{L}{\sqrt{L^2+2h_1}}$. Introduce the polar coordinate transformation for the l-subsystem

$$\begin{array}{c}\hfill {\Gamma }_{h,\widehat{h}}^3:y_1=\sqrt{2h_1}sin\left(t\right)-L,y_2=\sqrt{2h_1}cos\left(t\right),y_3=h_2,y_4=h_3,y_5=h_4,y_6=h_5.\end{array}$$

Then

$$\begin{array}{cc}\hfill M_{131}\left(h\right)=& {\int }_{{\Gamma }_{h,\widehat{h}}^3}{P}_2^l\mathrm{d}{y}_1-P_1^l\mathrm{d}{y}_2\hfill \\ \hfill =& {\int }_{\beta -\pi }^{-\pi -\beta }\sqrt{2h_1}cos\left(t\right)[-p_1\left(\sqrt{2h_1}sin\left(t\right)-L\right)-p_2\sqrt{2h_1}sin\left(t\right)\hfill \\ \hfill & -p_3\sqrt{2h_1}cos\left(t\right)-p_4\sqrt{2h_1}cos\left(t\right)+p_5{h}_2+p_6{h}_3]\mathrm{d}t\hfill \\ \hfill =& 2h_1{p}_{3}sin\left(\beta \right)cos\left(\beta \right)+2h_1{p}_{4}sin\left(\beta \right)cos\left(\beta \right)+2h_1{p}_3\beta +2h_1{p}_4\beta \hfill \\ \hfill & +2\sqrt{2h_1}Lsin\left(\beta \right)p_1+2\sqrt{2h_1}sin\left(\beta \right)h_2{p}_5+2\sqrt{2h_1}sin\left(\beta \right)h_3{p}_6.\hfill \end{array}$$

Note that the differential at both sides of the formula $H_1^r=\frac{1}{2}{y}_2^2+\frac{1}{2}{(y_1-L)}^2=h_1$ can be obtained

$$y_2\mathrm{d}{y}_2=-(y_1-L)\mathrm{d}{y}_1.$$

(10)

Consider system (8) and obtain

$$\frac{\mathrm{d}{y}_1}{\mathrm{d}t}=y_2.$$

(11)

Substitute (10) and (11) into $M_{12}\left(h\right)$ and obtain

$$\begin{array}{c}\hfill M_{12}\left(h\right)={\int }_{{\Gamma }_{h,\widehat{h}}^1}{Q}_1^r\mathrm{d}t={\int }_{\sqrt{2h_1}}^{-\sqrt{2h_1}}\left(-\frac{h_3}{\sqrt{2h_1-y_2^2}}\right)\mathrm{d}{y}_2=h_3\pi .\end{array}$$

Similarly, we can obtain

$$\begin{array}{c}\hfill M_{22}\left(h\right)={\int }_{{\Gamma }_{h,\widehat{h}}^2}{Q}_1^c\mathrm{d}t={\int }_L^{-L}\left(-\frac{h_3}{\sqrt{2h_1}}\right)\mathrm{d}{y}_1=\frac{\sqrt{2}{h}_{3}L}{\sqrt{h_1}},\end{array}$$

$$\begin{array}{c}\hfill M_{32}\left(h\right)={\int }_{{\Gamma }_{h,\widehat{h}}^3}{Q}_1^l\mathrm{d}t={\int }_{-\sqrt{2h_1}}^{\sqrt{2h_1}}\left(\frac{h_3}{\sqrt{2h_1-y_2^2}}\right)\mathrm{d}{y}_2=h_3\pi ,\end{array}$$

$$\begin{array}{c}\hfill M_{42}\left(h\right)={\int }_{{\Gamma }_{h,\widehat{h}}^4}{Q}_1^c\mathrm{d}t={\int }_{-L}^L\left(\frac{h_3}{\sqrt{2h_1}}\right)\mathrm{d}{y}_1=\frac{\sqrt{2}{h}_{3}L}{\sqrt{h_1}}.\end{array}$$

With the same procedure, it is easy to obtain each component of $M_3\left(h\right),M_4\left(h\right),M_5\left(h\right)$. According to (9), the first-order Melnikov functions are

$$\begin{array}{cc}\hfill M_1\left(h\right)=& 4h_1{p}_{3}sin\left(\beta \right)cos\left(\beta \right)+4h_1{p}_{4}sin\left(\beta \right)cos\left(\beta \right)+4h_1{p}_3\beta +4h_1{p}_4\beta \hfill \\ \hfill & +4\sqrt{2h_1}Lsin\left(\beta \right)p_1-4p_3\sqrt{2h_1}L,\hfill \\ \hfill M_2\left(h\right)=& 2h_3\pi +\frac{2\sqrt{2}{h}_{3}L}{\sqrt{h_1}},\hfill \\ \hfill M_3\left(h\right)=& -\frac{2}{\sqrt{h_1}}(\sqrt{2}{e}_{5}L{h}_2+\sqrt{2}{e}_{6}L{h}_3-\sqrt{2}{e}_{7}L{h}_4-\sqrt{2}{e}_{8}L{h}_5+\pi \sqrt{h_1}{e}_5{h}_2\hfill \\ \hfill & +\pi \sqrt{h_1}{e}_6{h}_3-\pi \sqrt{h_1}{e}_7{h}_4-\pi \sqrt{h_1}{e}_8{h}_5+L\sqrt{2}{e}_9+\pi \sqrt{h_1}{e}_9),\hfill \\ \hfill M_4\left(h\right)=& 2h_5\pi +\frac{2\sqrt{2}{h}_{5}L}{\sqrt{h_1}},\hfill \\ \hfill M_5\left(h\right)=& \frac{2}{\sqrt{h_1}}\left(\sqrt{2}L+\pi \sqrt{h_1}\right)\left(q_1{h}_2+q_2{h}_3-q_3{h}_4-q_4{h}_5-q_5\right).\hfill \end{array}$$

(12)

From $M_2\left(h\right)=0,M_4\left(h\right)=0$ and $L,h_1>0$, we obtain $h_3=0,h_5=0$.

From $M_5\left(h\right)=0$, we obtain $h_2=\frac{q_3{h}_4+q_5}{q_1},q_1\ne 0$.

From $M_3\left(h\right)=0$, we obtain $h_4=-\frac{e_5{q}_5+e_9{q}_1}{e_5{q}_3-e_7{q}_1}$.

Then $h_2=-\frac{e_7{q}_5+e_9{q}_3}{e_5{q}_3-e_7{q}_1}$.

Therefore, we discuss the number and parameter according to the zeros of $M_1\left(h\right)=0$ under the following condition

$$\begin{array}{cc}\hfill P_{ar3}=& (u,{\nu }_1,{\nu }_2,{\rho }_1,{\rho }_2,{\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4,{\zeta }_5,{\zeta }_6,{\zeta }_7,w_1,w_2)\hfill \\ \hfill =& (1,1,2,1,0.1,0.5,1,2,1.5,2,8,10,0.01,0.02).\hfill \end{array}$$

According to the first equation of (12), the relationship between $p_1,L,h_1$ is obtained, which is depicted in Figure 5.

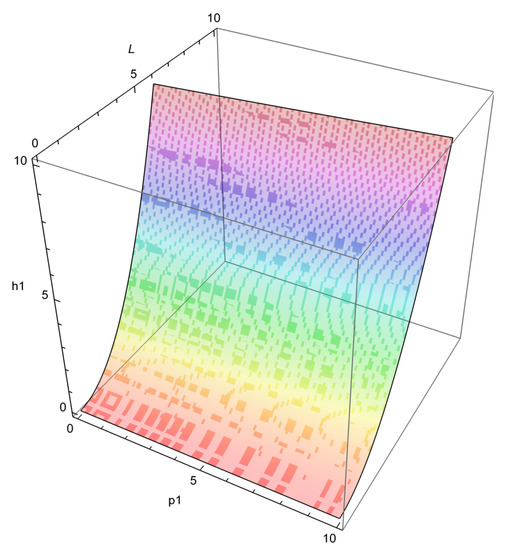
Figure 5. The relationship between $p_1,L,h_1$ of system (8).

The surface in the figure is an isosurface with $M_1\left(h\right)=0$. The number of periodic orbits could be discussed in different regions of $(p_1,L)$ according to Figure 5.

4.2. Numerical Simulation

When $(p_1,L)=(2,1.8)$, equation $M_1\left(h\right)=0$ has four real solutions and the determinant of the Jacobian matrix does not equal zero. The phase configurations of the periodic orbits of system (8) projected on $(y_1,y_2,y_3),(y_1,y_2,y_4),(y_1,y_2,y_5)$ and $(y_1,y_2)$ are depicted in Figure 6.

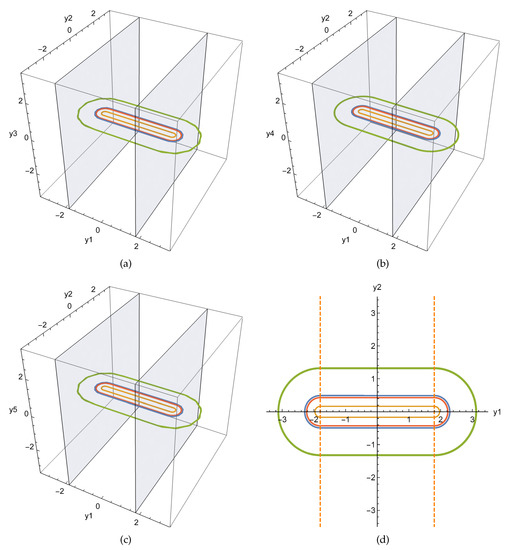
Figure 6. Periodic orbits of system (8): (a) $(y_1,y_2,y_3)$-space; (b) $(y_1,y_2,y_4)$-space; (c) $(y_1,y_2,y_5)$-space; (d) $(y_1,y_2)$-plane.

When $(p_1,L)=(3,1.5)$, equation $M_1\left(h\right)=0$ has two real roots and the determinants of the Jacobian matrix at the solutions are not equal to zero. The phase diagram configurations of system (8) are shown in Figure 7.

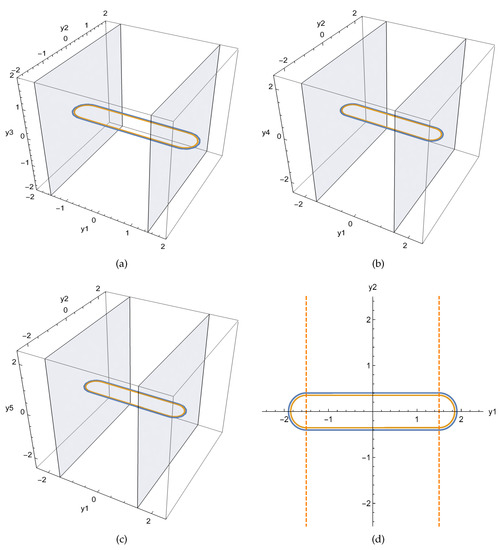
Figure 7. Periodic orbits of system (8): (a) $(y_1,y_2,y_3)$-space; (b) $(y_1,y_2,y_4)$-space; (c) $(y_1,y_2,y_5)$-space; (d) $(y_1,y_2)$-plane.

We selected L and $p_1$ as free variables, and the number of periodic orbits under parameter $P_{ar3}$ is discussed, which is as shown in Table 1.

Table 1. The number of periodic orbits with parameter L and $p_1$.

L	${\mathit{p}}_1$	The Number of Periodic Solutions
2	50	8
1	2	4
1.5	18	3
2.5	32	3
3	72	8

According to the Melnikov function obtained, the excitation parameter affects the position of periodic orbits under the following condition:

$$\begin{array}{cc}\hfill P_{ar4}=& (u,{\nu }_1,{\nu }_2,{\rho }_1,{\rho }_2,{\zeta }_1,{\zeta }_2,{\zeta }_3,{\zeta }_4,{\zeta }_5,{\zeta }_6,{\zeta }_7,w_1,w_2)\hfill \\ \hfill =& (1,1,2,1,0.1,0.5,1,2,1.5,2,8,10,0.05,0.06).\hfill \end{array}$$

When $(p_1,L)=(2,1.8)$, equation $M_1\left(h\right)=0$ has four real roots and the determinants of the Jacobian matrix at the solutions are not equal to zero. As the parameters $w_1$ and $w_2$ are varied, so is the position of the periodic orbits. The phase diagram configurations of system (8) are shown in Figure 8.

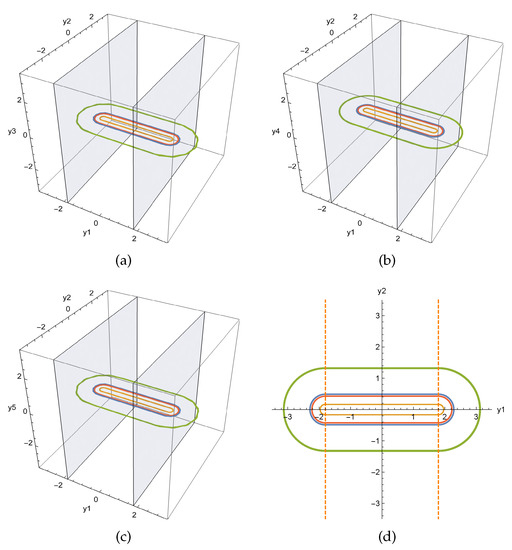
Figure 8. Periodic orbits of system (8): (a) $(y_1,y_2,y_3)$-space; (b) $(y_1,y_2,y_4)$-space; (c) $(y_1,y_2,y_5)$-space; (d) $(y_1,y_2)$-plane.

When $(p_1,L)=(11.52,0.8)$, equation $M_1\left(h\right)=0$ has six real roots and the determinants of the Jacobian matrix at the solutions are not equal to zero. The configurations of systems (8) are shown in Figure 9.

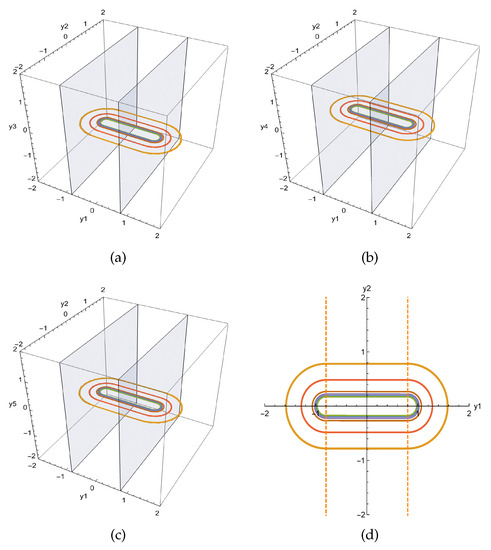
Figure 9. Periodic orbits of system (8): (a) $(y_1,y_2,y_3)$-space; (b) $(y_1,y_2,y_4)$-space; (c) $(y_1,y_2,y_5)$-space; (d) $(y_1,y_2)$-plane.

5. Conclusions

It is essential to study the periodic motions of a nonsmooth dynamic vibration absorber under low-frequency forced excitation, because its periodic motions are closely intertwined with energy transfer and vibration analysis. In this paper, the existence and stability of the admissible equilibrium point of a nonsmooth DVA are studied. The stability mechanism of the system under different parameters is clarified. The existence of the admissible equilibrium point is illustrated when the model has different stiffness characteristics. By selecting parameters in the asymptotically and unstable regions of the admissible equilibrium point and comparing their vibration control characteristics, it is shown that the nonsmooth DVA has a certain vibration reduction effect in both asymptotically and unstable regions, and the vibration reduction effect is better in the unstable parameter region.

The bifurcation of periodic orbits for a two-degrees-of-freedom system with an encapsulated nonsmooth dynamic vibration absorber means that it can be transformed into a six-dimensional piecewise smooth system. Based on the first integrals, the Melnikov function and the condition of bifurcation of periodic orbits are obtained. With the aid of the Melnikov function, the relationship between $p_1,L,h_1$ is presented, which provides guidance for estimating the number of periodic orbits. Under the different regions of $(p_1,L)$, the number and position of periodic orbits for the nonsmooth dynamic vibration absorber system are investigated. There exist two, three, four, six, and eight periodic orbits in the nonsmooth DVA model. It is found that the gap parameter L and $p_1,p_3,p_4$ affect the number of periodic orbits. The low-frequency forced excitation considered as a slowly varying parameter plays an essential role in the influence of the position of periodic orbits. The phase configurations of periodic orbits are depicted with numerical simulation under different regions of parameters. It offers a theoretical direction for parameter control for a nonsmooth dynamic vibration absorber. Future work will address the analysis of the energy transfer of the nonsmooth dynamic vibration absorber and the validation of theoretical results.