Abstract
Structured grid-based sparse matrix-vector multiplication and Gauss–Seidel iterations are very important kernel functions in scientific and engineering computations, both of which are memory intensive and bandwidth-limited. GPDSP is a general purpose digital signal processor, which is a very significant embedded processor that has been introduced into high-performance computing. In this paper, we designed various optimization methods, which included a blocking method to improve data locality and increase memory access efficiency, a multicolor reordering method to develop Gauss–Seidel fine-grained parallelism, a data partitioning method designed for GPDSP memory structures, and a double buffering method to overlap computation and access memory on structured grid-based SpMV and Gauss–Seidel iterations for GPDSP. At last, we combined the above optimization methods to design a multicore vectorization algorithm. We tested the matrices generated with structured grids of different sizes on the GPDSP platform and obtained speedups of up to 41× and 47× compared to the unoptimized SpMV and Gauss–Seidel iterations, with maximum bandwidth efficiencies of 72% and 81%, respectively. The experiment results show that our algorithms could fully utilize the external memory bandwidth. We also implemented the commonly used mixed precision algorithm on the GPDSP and obtained speedups of 1.60× and 1.45× for the SpMV and Gauss–Seidel iterations, respectively.
1. Introduction
Numerical computations based on structured grids play an important role in scientific research and industrial applications. The commonly used finite element method, finite difference method, and finite volume method are all computed on grids. Sparse matrix-vector multiplication (SpMV) and Gauss–Seidel iterations are very important kernel functions [1] that have a significant impact on performance in practical applications. Both functions are memory-intensive and require indirect memory access by an index.
All Krylov subspace methods require calls to SpMV functions, and Gauss–Seidel iterations are commonly used as smoothing operators and as the bottom solver in multigrid solvers. The original Gaussian–Seidel iteration has very limited parallelism because of its strict dependencies. It is possible to break its dependencies and develop fine-grained parallelism by multicolor reordering [2]. Gauss–Seidel fine-grained parallel algorithms are usually closely related to the processor architecture. A two-level blocked Gauss–Seidel algorithm was used on the SW26010-Pro processor [2]. A Gauss–Seidel algorithm with 8-color block reordering was applied to the SW26010 [3]. The red–black reordering Gauss–Seidel algorithm was designed for the CPU–MIC architecture on the Tianhe-2 supercomputer [4]. The K supercomputer is a homogeneous architecture, and the performance of the Gauss–Seidel algorithm for 8-color point reordering and 4-color row reordering was compared [5].
Currently, the computing performance of high-performance supercomputers has reached the E-level. The power consumption and heat dissipation are important factors affecting supercomputers. The general purpose digital signal processor (GPDSP) is a very important embedded processor. It has the advantage of ultra-low power consumption due to its very long instruction words and on-chip temporary memory [6]. GPDSPs that have been introduced for high-performance computing include TI’s C66X series [7,8] and Phytium’s Matrix series [9,10,11,12,13].
The Matrix-DSP is a GPDSP developed by Phytium, which can be used either as an accelerator with a CPU or as a processor alone. It has a complex architecture containing multilevel memory structures and multilevel parallel components, which can implement instruction-level parallelism, vectorized parallelism, and multicore parallelism. It is difficult to fully exploit the performance of the Matrix-DSP by simply transplanting existing algorithms designed for single-core processors [12]. Zhao et al. mapped the Winograd algorithm for accelerating convolutional neural networks onto the Matrix-DSP [14]. Z. Liu et al. designed a multicore vectorization GEMM for the Matrix-DSP [12]. Yang et al. evaluated the efficiency of a DCNN on the Matrix-DSP [15]. Due to the novelty of the Matrix-DSP processor, memory-intensive programs are still underdeveloped, and there are no public papers on sparse matrix computation for the Matrix-DSP yet available.
In this paper, we designed multi-core vector algorithms based on structured grid SpMV and Gauss–Seidel iterations for the Matrix-DSP and evaluated our algorithms on the Matrix-DSP platform. The main contributions are as follows:
(1) We improved the data locality and indirect memory access speed by blocking, using a multicolor reordering method to develop the fine-grained parallelism of the Gauss–Seidel algorithm, and dividing the data finely according to the memory structure of the Matrix-DSP.
(2) In terms of the data transfer, we used a double-buffered DMA scheme, which overlaps the computation and transfer time. We also implemented general mixed-precision algorithms, which reduced the memory access.
(3) We tested various grid cases on the Matrix-DSP, and the experimental results show that our improved algorithms could fully exploit the bandwidth efficiency of the Matrix-DSP, wherein they reached 72% and 81% of the theoretical bandwidth, respectively. Compared with the unoptimized methods, the SpMV and Gauss–Seidel iterations achieved 41× and 47× speedup outcomes, respectively. Our mixed-precision work further improved the performance by 1.60× and 1.45×, respecitvely.
2. Background
2.1. Structured Grid-Based Sparse Matrix
In the finite element method, finite difference method, and finite volume method, it is necessary to discretize the computational space by using grids. Several discrete formats of partial differential equations in structured meshes are listed in the following figures: Figure 1a shows the 5-point difference format for the 2D Poisson equation, (b) describes the 27-point difference format for the discretized 3D heat diffusion equation in HPCG [1], and (c) shows the 33-edge discretized format of the 3D Maxwell equation based on vector finite elements [16,17,18]. The sparse matrix generated by the structured grid is characterized by the fact that the matrix rows inside the grid have fixed nonzero elements, while the matrix rows on the boundaries have fewer nonzero elements. The number of nonzero elements per row can be expressed as follows:
where denotes the number of points or edges associated with itself, and denotes the number of degrees of freedom (DOF) possessed on one point or edge.
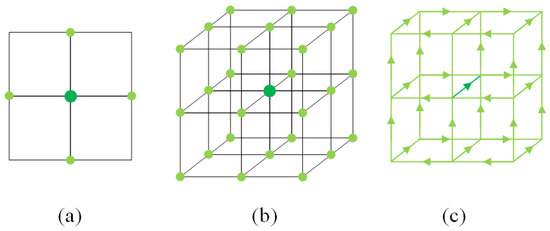
Figure 1.
Discrete format of partial differential equations in a structured grid. (a) represents 5-point format, (b) represents 27-point format and (c) represents 33-point format.
For example, the simulation of 3D mantle convection is equivalent to solving a system of partial differential equations for the conservation of dimensionless mass, momentum, and energy. When using the finite element method to solve the partial differential equations, we can first derive the equivalent equation system by integrating the Galerkin weak form. Then, we use a structured mesh to discretize the solution domain, and Figure 2 shows the distribution of the field values on the mesh. The velocity field is attached to the nodes, with components, and the pressure field is attached to the cell centers. By performing element integration, sparse matrix assembly, and using the arbitrariness of the weight function, we transform the problem into solving a linear system. When using the Uazwa algorithm and the multigrid solver to solve, it is necessary to use the Gauss–Seidel and SpMV functions; the detailed derivation and the solution can be referred to in the paper by [19].
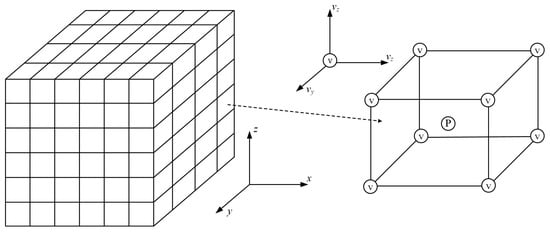
Figure 2.
3D mantle convection finite-element-structured grid partitioning (velocity field attached to nodes, and pressure field is attached to cell center).
The coefficient matrix K of the velocity v conforms to the description of Equation (1): entails the velocity components in three directions, means that the matrix row corresponding to a point is associated with 27 nodes, and can be obtained.
2.2. Ellpack–Itpack Format
The Ellpack–Itpack [20] (ELL) format is an efficient storage format for vector processor architectures. It is well suited for storing coefficient matrices generated from structured grids, since the matrix rows have the same number of nonzero elements, except for the boundary points. The matrix generated by a structured grid in the case of a 5-point discrete format is given in Figure 3. In the ELL format, two arrays store the elements and column indices in column order, where indicates the matrix row number, and indicates the maximum number of nonzero elements per row.
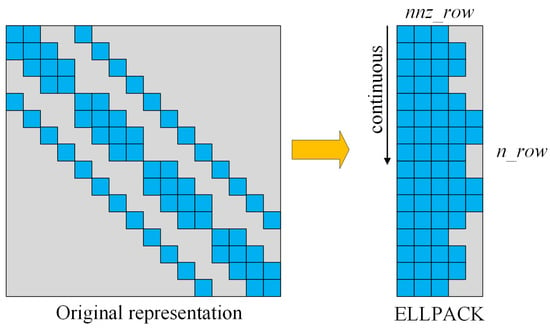
Figure 3.
ELL format based on 5-point discrete format on a grid.
Algorithms 1 and 2 describe the unoptimized SpMV and Gauss–Seidel algorithms using the ELL format to store matrices. The arrays K, idx, x, ax, F, and diag store the matrix elements, column indices, the vector to be multiplied, the output of the matrix-vector multiplication, the right-hand term, and the matrix diagonal elements, respectively. It can be seen that SpMV has good data parallelism and can be simply developed for multicore vectorization. However, the Gauss–Seidel algorithm has a strong dependence on the update of x. At each iteration through the outer loop, can only be calculated after is finished, and the outer loop of Algorithm 2 (Line 1) can only be computed serially.
| Algorithm 1 Unoptimized SpMV algorithm using ELL format to store matrices |
|
| Algorithm 2 Unoptimized Gauss-Seidel algorithm using ELL format to store matrices |
|
3. Overview of the Matrix-DSP
The Matrix-DSP integrates 24 DSP cores with a peak double precision performance of 4.608 TFLOPS per second at 2.0 GHz. The Matrix-DSP uses the very long instruction word (VLIW), which can launch five scalar instructions and six vector instructions simultaneously, for a total of eleven instructions. The overall architecture of the Matrix-DSP, shown in Figure 4, consists of a scalar processing unit (SPU) for scalar computation and flow control, as well as a vector processing unit (VPU) for vector computation. The VPU consists of 16 64-bit vector processing elements (VPEs) that support vector computation with a total length of 1024 bits. Each VPE consists of six functional components, including three floating point multiply accumulators (FMAC), two vector load/store units, and one bit process (BP). The SPU and VPU can exchange data through the scalar-vector-shared register (SVR), which supports broadcasting data from scalar registers to vector registers.
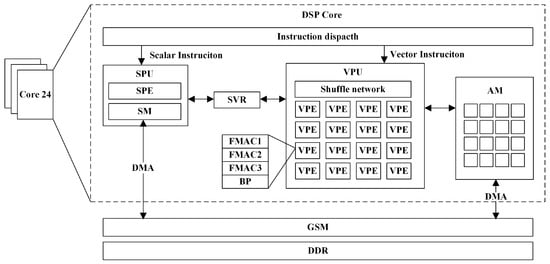
Figure 4.
Matrix-DSP architecture.
The Matrix-DSP [9,10,11,12,13] has a multi-level memory architecture with one 64 KB scalar memory (SM) for scalar access and one 768 KB array memory (AM) for vector access on each DSP core. All 24 cores share a 6 MB of global shared memory (GSM), which provides up to 307 GB/s of on-chip read and write bandwidth, as well as supports up to 128 GB of external shared memory. The Matrix-DSP integrates a direct memory access (DMA) engine, which enables fast data transfer between different memory structures(SM, AM, GSM, and external memory). The DMA provides the point-to-point transfer instruction DMA_p2p, which can transfer contiguous memory data with a fixed offset, as well as the indirect indexed address transfer instruction DMA_SG, which can transfer data from the GSM or external memory through an index array. The 24 DSP cores can only exchange and share data through the GSM or external memory. The external memory used for the Matrix-DSP in this paper is a dual-channel DDR4 with a theoretical bandwidth of 42.6 GB/s.
4. SpMV and Gauss–Seidel on Matrix-DSP
In this section, we analyzed the Matrix-DSP architecture, optimized structured grid-based SpMV, and Gauss–Seidel algorithm by multiple methods.
4.1. Blocking Method
Both the SpMV and Gauss–Seidel algorithms require repeatedly addressing the vector by an index, and the number of repetitions depends on the discrete format. The speed of indirect addressing seriously affects the computational performance; thus, we designed a blocking method to increase the data locality. As shown in the right of Figure 5, the overall grid is divided into grid blocks of equal size, and the address space of the vector of any block is within the block and its buffer layer. Figure 6 and Figure 7 describe the data division and the data transfer direction for the two functions, respectively. As shown in the lower right of Figure 6 and Figure 7, the local vector Local_x of block_0, which needs to be repeatedly addressed, is first put into the GSM, which can provide a higher bandwidth than the external memory. The Local_x of block_0 consists of a Vector_x of block_0 and a Buffer_x of block_0, which is indexed by the Buffer_idx of block_0. The memory size of the Local_x cannot exceed the GSM memory, as shown in Equation (2).
Theoretically, the higher the GSM memory usage, the higher the performance that is obtained. In addition, the blocking algorithm allows each block to have the same local index Local_idx, so there is no need to store the array of the global column index idx.
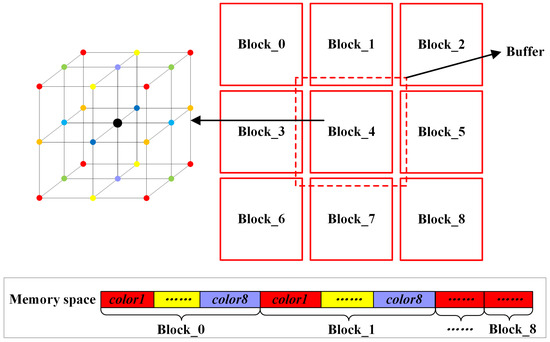
Figure 5.
Blocking method and multicolor reordering method.
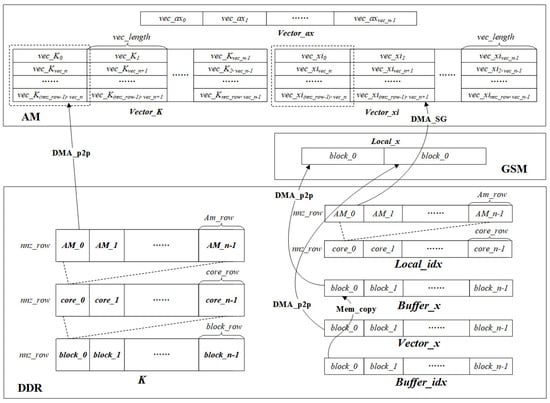
Figure 6.
Description of SpMV data division and transmission.
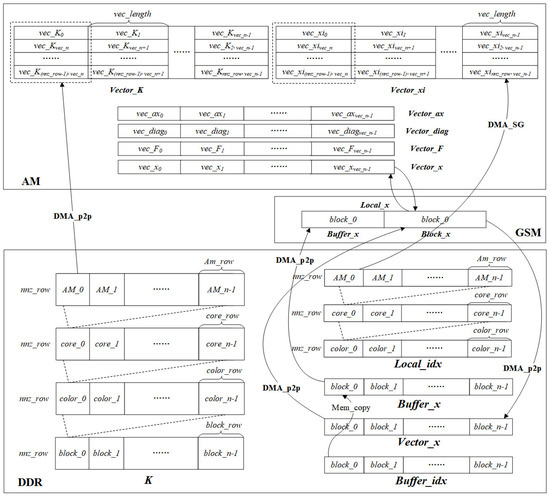
Figure 7.
Description of Gauss–Seidel data division and transmission.
4.2. Multicolor Reordering Method
In a structured grid, a matrix row is represented as a DOF on a node or an edge, and the data dependency between matrix rows in the Gauss–Seidel algorithm is represented as the neighboring relationship between the DOF. We performed a multicolor reordering method, which is commonly used in developing Gauss–Seidel fine-grained parallelism on the blocked grid.
An example of multicolor reordering based on a 27-point discrete format is given on the left of Figure 5 [5]. The grid points in the 3D space are divided into eight colors, and the adjacent nodes of any node have different colors from the node itself. After reordering, the nodes of are numbered first, then the nodes of are numbered and so on until . In this way, there is no data dependency between points of the same color during calculation, and they can be calculated in parallel, thus transforming the dependency between nodes into the dependency between colors. At the same time, in order to ensure the continuity of memory space access, the matrix rows corresponding to points with the same color are arranged continuously, as shown in Figure 5 below.
The overall calculation order is shown in the data arrangement order in Figure 5 below. First, calculate to in ; then, calculate color1 to color8 in until all the blocks are calculated.
4.3. Data Division Method
The SpMV of the block and the Gauss–Seidel of the same color within the block are completely data independent and suitable for data parallelism. Considering that each row of the matrix has the same number of nonzero elements with no load imbalance, the matrix is partitioned by a one-dimensional static method. As shown at the bottom of Figure 6 and Figure 7, the matrix K and Local_idx are equally distributed to each DSP core that is used. In the SpMV, , and in the Gauss–Seidel, , where denotes the number of DSP cores used, denotes the number of matrix rows assigned to one DSP core, denotes the number of matrix rows in one block, and denotes the number of matrix rows of one color in one block. Specifically, row ID of is assigned to the , while row ID of is assigned to the , and so on.
However, the AM space has a capacity of only 768 KB, and it may not be possible to calculate matrix rows at once, so the needs to be further divided. We define the as the maximum number of matrix rows that the AM space can calculate at one time, and we define the as the number of loops that need to be calculated, which can be calculated as . Specifically in the SpMV, the AM space needs to store the product vector Vector_ax of size , the coefficient matrix vector Vector_K, and the index addressing vector Vector_xi of size . The Gauss–Seidel additionally needs to store the iteration vector Vector_x, the right-hand term vector Vector_F, and the diagonal element vector Vector_diag of size . Therefore, the SpMV needs to satisfy the ≤ 768 KB, and the Gauss–Seidel needs to satisfy the ≤ 768 KB. Theoretically, the higher the utilization of the AM memory, the lower the consumption of DMA transfers, and the higher the utilization of the bandwidth.
In AM space, data are stored as vectors, where denotes the vector length that an SIMD instruction can calculate, which can be computed by , and denotes the number of vectors in the , which can be computed by . Therefore, the also needs to satisfy the condition to be a multiple of .
As shown in Figure 6 and Figure 7, in each AM loop, the Vector_K of length is transferred from the DDR to the AM through the DMA_p2p, and the Vector_xi of length is transferred from the GSM to the AM through the DMA_SG. For the Gauss–Seidel, it is additionally necessary to transfer the Vector_diag, the Vector_F, and the Vector_x of length to the AM. After completing the data transfer, the SpMV and Gauss–Seidel are performed. Finally, the Vector_ax and Vector_x are returned to the DDR and GSM, respectively.
4.4. DMA Double Buffering Method
The Matrix-DSP accelerator supports transferring data and computation simultaneously, so we designed the DMA double-buffering method in the AM space to overlap the computation and transfer. Figure 8 and Figure 9a,b describe the flow of the conventional memory access calculation and the flow of the double buffer memory access calculation, respectively. We created two buffers for the Vector_K, Vector_xi, Vector_ax in the SpMV and for the Vector_K, Vector_xi, Vector_diag, Vector_F, Vector_x in the Gauss–Seidel. Therefore, all computation time, except the last one, can be overlapped by the transfer time. In both algorithms, the DMA memory access time accounts for a large proportion, and the calculation time accounts for a small proportion, so the performance improvement is limited.
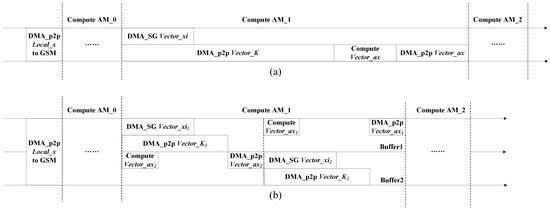
Figure 8.
Description of SpMV DMA double buffering. (a) denotes the original data transfer computation flow and (b) denotes the double-buffer data transfer computation flow.
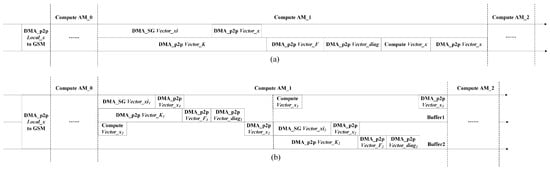
Figure 9.
Description of Gauss–Seidel DMA double buffering. (a) denotes the original data transfer computation flow and (b) denotes the double-buffer data transfer computation flow.
4.5. Multicore Vectorization Algorithm
Combining the above optimization methods, the final multicore vectorization algorithms can be obtained as shown in Algorithms 3 and 4. Both algorithms compute blocks sequentially (Line 1 in Algorithms 3 and 4), and the first steps are generating the Local_x and transferring it to the the GSM (Lines 2–4 in Algorithms 3 and 4). In the SpMV, each DSP core computes subblocks in parallel, and double-buffering is performed in the AM loop (Lines 6–17 in Algorithm 3). Then, the Vector_K and Vector_xi are transferred into the AM (Lines 8–9 in Algorithm 3) for vector computation (Lines 10–15 in Algorithm 3). Finally, the computation output of the Vector_ax is returned to the DDR (Line 16 in Algorithm 3). In Gauss–Seidel, all DSP cores are computed in parallel for one color (Lines 5–24 in Algorithm 4). In each AM loop with double buffering, the Vector_x, Vector_K, Vector_xi, Vector_diag, and Vector_F are transferred into the AM (Lines 9–13 in Algorithm 4); then, vector iteration is performed (Lines 14–21 in Algorithm 4), and, finally, the updated Vector_x is transferred back to the GSM (Line 22 in Algorithm 4). When all colors have been completed, the Vector_x from the GSM is transferred back to the DDR for updating (Line 25 in Algorithm 4).
| Algorithm 3 Optimized SpMV on Matrix-DSP |
|
| Algorithm 4 Optimized Gauss-Seidel on Matrix-DSP |
|
4.6. Mixed Precision Algorithm
Mixed precision is a method that can effectively improve the computational speed, and its main idea is to use low precision in the computation-intensive part while maintaining the final computational accuracy. We implemented a conventional mixed-precision function on the Matrix-DSP that stores the coefficient matrix in a float type while using a double type for computation. This function has been used in some open-source software and papers [21,22]. The specific process is as follows: First, the generated coefficient matrix is stored in the external memory in a float type. Second, the matrix elements are transferred to the AM through the DMA. Third, the VPU reads the data from the AM using a high half-word read instruction. Fourth, the high 32-bit float in the vector register is converted to a 64-bit double in the vector register by the high half-word precision enhancement instruction. Finally, the computation of the SpMV and Gauss–Seidel iterations are performed, and the results are transferred back to the external memory in a double type.
5. Experimental Evaluation
The Matrix-DSP supports two programming modes, which are the assembly mode and C mode. Assembly programming has the advantage of being manually pipelined, but the workload is high. Computation-intensive programs rely on good assembly programs to obtain high performance. The C programming model involves a relatively low workload. However, for access-intensive programs, the percentage of computation time is low and is masked by double buffering, so the C language mode can achieve a similarly high performance. Therefore, we chose the C programming mode.
We chose the sparse matrices, which are from a 27-point discrete format with three DOFs at each point, for the test. The tests are performed on three scale grids: , , and . The scale grid can put the vector x in the GSM without blocking, while the block sizes of the other two grids are , and the memory of in the GSM is 3.390 MB. Some other parameters can be obtained by the formula in Section 4.3: , , and . Figure 10 depicts the results of the optimized SpMV and Gauss–Seidel. The peak performance of the SpMV without any optimization was only 0.128 Gflops/s, 0.128 Gflops/s, and 0.126 Gflops/s on , , and grids, respectively, and 0.127 Gflops/s, 0.128 Gflops/s, and 0.127 Gflops/s for the Gauss–Seidel, respectively.
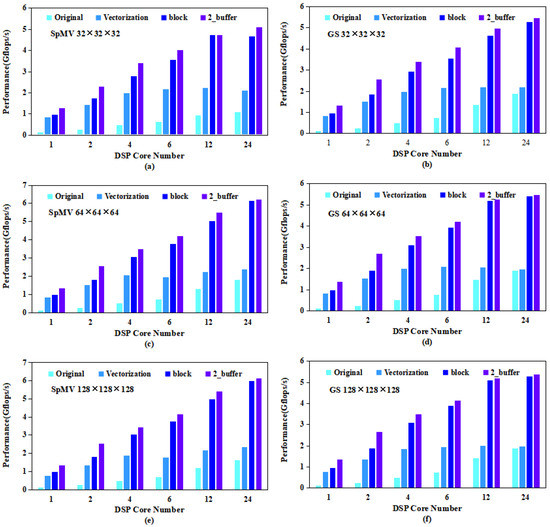
Figure 10.
SpMV and Gauss–Seidel performance test results ((a,c,e) describe the SpMV performance on , , and grid, respectively; (b,d,f) describe the Gauss–Seidel performance on , , and grid, respectively).
After multicore acceleration, the performances of the SpMV, which reached 1.88 Gflops/s, 1.91 Gflops/s, and 1.88 Gflops/s, respectively, were improved by about 14× for all three grids. As for the Gauss–Seidel, the peak performance was improved by 8.5× on the small-scale grid and about 13× on other larger-scale grids, thus reaching 1.08 Gflops/s, 1.78 Gflops/s, and 1.64 Gflops/s, respectively.
Vectorization optimizations on the SpMV and Gauss–Seidel share common properties in that the smaller the cores used, the higher the FLOPS percentage increase, and the performance plateaus when the core number exceeds six. This is mainly because the computational performance grows linearly with the number of DSP cores, but the bandwidth of the DDR has reached the bottleneck early. The performance results on three different scale grids were 2.18 Gflops/s, 1.96 Gflops/s, and 1.95 Gflops/s for the SpMV, respectively, and 2.11 Gflops/s, 2.37 Gflops/s and 2.33 Gflops/s for the Gauss-Seidel, respectively.
The blocking method makes efficient use of the high bandwidth features of the GSM. It can be seen from Figure 10 that the performance improvement of the blocking method for the two functions became more obvious as the number of DSP cores increased. This is mainly because, when the number of DSP cores is large, the DDR memory bandwidth allocated to each DSP core is limited, thus making the advantage of the GSM’s high bandwidth very remarkable. On three scale grids, from small to large, the SpMV achieved 2.41×, 2.75×, and 2.70× in speedups, respectively, with FLOPSs of 5.26 Gflops/s, 5.41 Gflops/s, and 5.27 Gflops/s, respectively. The Gauss–Seidel achieved 2.21×, 2.58×, and 2.56× in speedups, respectively, with FLOPSs of 4.67 Gflops/s, 6.13 Gflops/s, and 6.00 Gflops/s, respectively.
As shown in Figure 10, the performance improvement from the double buffering was very small, with neither the Gauss–Seidel nor the SpMV improving by more than 2%. However, when only 1–2 DSP cores were used, the double buffering could result in performance increases of 30–40%. This is because when the number of DSP cores is small, each DSP core is allocated with a higher DDR bandwidth and higher computation ratio. If the Matrix-DSP can be equipped with a higher bandwidth external memory, the effect of double buffering will be more significant. In summary, the optimized algorithms obtained a total of 41× and 47× in speedups, respectively, compared to the unoptimized algorithms.
Bandwidth efficiency is another important evaluation standard and is defined as , where is the bandwidth efficiency, is the valid bandwidth, and is the theoretical bandwidth. The total accessed memory of the SpMV is defined as , and for the Gauss–Seidel, it is defined as . As shown in Figure 11, the bandwidth efficiency increased with the number of DSP cores, which can be explained by the fact that the bandwidth of indirect access to the GSM through the DMA_SG increased with the number of DSP cores. The bandwidth efficiencies of the SpMV on the three grids were all around 72%, and the Gauss–Seidel had an efficiency of 67% on the small-scale grid and about 81% on the other two grids. It is worth mentioning that the bandwidth efficiency of using the DMA to transfer the contiguous memory data was 85%.
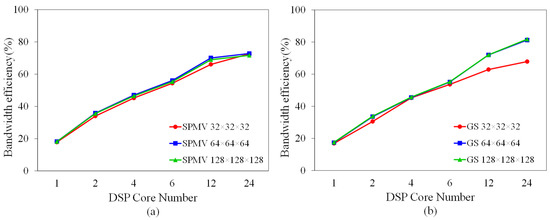
Figure 11.
The bandwidth efficiency test results of SpMV and Gauss–Seidel. (a) denotes the bandwidth test result of SpMV and (b) denotes the bandwidth test result of Gauss–Seidel.
Figure 12 shows the test results of the mixed-precision algorithms in subSection 4.6. Both the SpMV and Gauss–Seidel achieves speedups of about 1.2× on the grid. On the other two scale grids, the FLOPS speedups were about 1.6× for the SpMV and 1.45× for the Gauss–Seidel, and all the FLOPSs were around 8.9 Gflops/s.
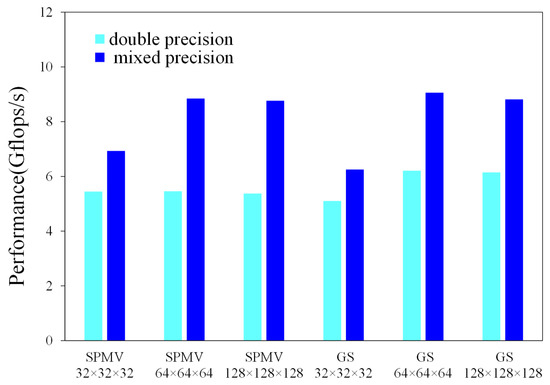
Figure 12.
Performance of SpMV and Gauss–Seidel with the mixed-precision algorithms.
6. Conclusions
The SpMV and Gauss–Seidel based on the structured grid are widely used in scientific computing and engineering, and they usually account for a large percentage of the computation time. In this paper, we used the ELL format to store the sparse matrices from structured grids and proposed the optimized SpMV and Gauss–Seidel algorithms for GPDSP architecture. Compared to the unoptimized algorithms, the optimized SpMV and Gauss–Seidel obtained speedups of 41× and 47×, respectively. Finally, the mixed-precision algorithms were implemented to reduce memory access, thus resulting in a further improvement in the FLOPS. In the next step of the work, we plan to conduct research on irregular sparse matrices and implement commonly used sparse matrix kernel functions, such as the SpMV, SpMM, SpGEMM, etc., on the Matrix-DSP architecture.
Author Contributions
Conceptualization, Q.W. and J.L.; methodology, Y.W.; software, Y.W., X.Z. and Q.Z.; investigation, Y.W.; data curation, Y.W. and X.Z.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W.; funding acquisition, J.L., Q.W. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2021YFB0300101), the National Natural Science Foundation of China (Grant No. 61902413, No. 62002365, No. 12102468 and No. 12002380), and the National University of Defense Technology Foundation (No. ZK21-02, No. ZK20-52).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dongarra, J.; Heroux, M.A.; Luszczek, P. High-performance conjugate-gradient benchmark: A new metric for ranking high-performance computing systems. Int. J. High Perform. Comput. Appl. 2016, 30, 3–10. [Google Scholar] [CrossRef]
- Zhu, Q.; Luo, H.; Yang, C.; Ding, M.; Yin, W.; Yuan, X. Enabling and scaling the HPCG benchmark on the newest generation Sunway supercomputer with 42 million heterogeneous cores. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MI, USA, 14–19 November 2021; pp. 1–13. [Google Scholar]
- Ao, Y.; Yang, C.; Liu, F.; Yin, W.; Jiang, L.; Sun, Q. Performance optimization of the HPCG benchmark on the Sunway TaihuLight supercomputer. ACM Trans. Archit. Code Optim. TACO 2018, 15, 1–20. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Liu, F.; Zhang, X.; Lu, Y.; Du, Y.; Yang, C.; Xie, M.; Liao, X. 623 Tflop/s HPCG run on Tianhe-2: Leveraging millions of hybrid cores. Int. J. High Perform. Comput. Appl. 2016, 30, 39–54. [Google Scholar] [CrossRef]
- Kumahata, K.; Minami, K.; Maruyama, N. High-performance conjugate gradient performance improvement on the K computer. Int. J. High Perform. Comput. Appl. 2016, 30, 55–70. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Liu, C.; Liu, S.; Lei, Y.; Zhang, J.; Zhang, Y.; Gu, Y. Advancing DSP into HPC, AI, and beyond: Challenges, mechanisms, and future directions. CCF Trans. High Perform. Comput. 2021, 3, 114–125. [Google Scholar] [CrossRef]
- Ali, M.; Stotzer, E.; Igual, F.D.; van de Geijn, R.A. Level-3 BLAS on the TI C6678 multi-core DSP. In Proceedings of the 2012 IEEE 24th International Symposium on Computer Architecture and High Performance Computing, New York, NY, USA, 24–26 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 179–186. [Google Scholar]
- Igual, F.D.; Ali, M.; Friedmann, A.; Stotzer, E.; Wentz, T.; van de Geijn, R.A. Unleashing the high-performance and low-power of multi-core DSPs for general-purpose HPC. In Proceedings of the SC’12: International Conference on High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–11. [Google Scholar]
- Yin, S.; Wang, Q.; Hao, R.; Zhou, T.; Mei, S.; Liu, J. Optimizing Irregular-Shaped Matrix-Matrix Multiplication on Multi-Core DSPs. In Proceedings of the 2022 IEEE International Conference on Cluster Computing (CLUSTER), Heidelberg, Germany, 6–9 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 451–461. [Google Scholar]
- Pei, X.; Wang, Q.; Liao, L.; Li, R.; Mei, S.; Liu, J.; Pang, Z. Optimizing parallel matrix transpose algorithm on multi-core digital signal processors. J. Natl. Univ. Def. Technol. 2023, 45, 57–66. [Google Scholar]
- Wang, Q.; Pei, X.; Liao, L.; Wang, H.; Li, R.; Mei, S.; Li, D. Evaluating matrix multiplication-based convolution algorithm on multi-core digital signal processors. J. Natl. Univ. Def. Technol. 2023, 45, 86–94. [Google Scholar]
- Liu, Z.; Tian, X. Vectorization of Matrix Multiplication for Multi-Core Vector Processors. Chin. J. Comput. 2018, 41, 2251–2264. [Google Scholar]
- Gan, X.; Hu, Y.; Liu, J.; Chi, L.; Xu, H.; Gong, C.; Li, S.; Yan, Y. Customizing the HPL for China accelerator. Sci. China Inf. Sci. 2018, 61, 1–11. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, J.; Chen, X. Vectorized winograd’s algorithm for convolution neural networks. In Proceedings of the 2021 IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), New York City, NY, USA, 30 September–3 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 715–722. [Google Scholar]
- Yang, C.; Chen, S.; Wang, Y.; Zhang, J. The evaluation of DCNN on vector-SIMD DSP. IEEE Access 2019, 7, 22301–22309. [Google Scholar] [CrossRef]
- Jin, J.-M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ren, Z.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite element approach for plane wave 3-D electromagnetic modelling. Geophys. J. Int. 2013, 194, 700–718. [Google Scholar] [CrossRef]
- Li, C.; Wan, W.; Song, W. An Improved Nodal Finite-Element Method for Magnetotelluric Modeling. IEEE J. Multiscale Multiphys. Comput. Tech. 2020, 5, 265–272. [Google Scholar] [CrossRef]
- Zhong, S.; Yuen, D.A.; Moresi, L.N. Numerical methods for mantle convection. Treatise Geophys. 2007, 7, 227–252. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Zhong, S. Constraints on thermochemical convection of the mantle from plume heat flux, plume excess temperature, and upper mantle temperature. J. Geophys. Res. Solid Earth 2006, 111, B4. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. Int. Workshop Coupled Methods Numer. Dyn. 2007, 1000, 1–20. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).