Abstract
The train basic resistance characteristic is crucial for ATO performance. However, this characteristic is slow time-varying with wheel rail wear and fast time-varying with weather conditions. The parameters of train basic resistance are difficult to measure directly, usually only a set of empirical parameters can be obtained through repeated experiments. These factors result in an inconsistency between the model parameters in the ATO controller and the actual train basic resistance parameters (TBRP), leading to a decrease in the effectiveness of the model-based controller. Therefore, this paper proposes an indirect TBRP identification method based on speed trajectory fitting to improve the effectiveness of the TBRP for model-based ATO controllers. Firstly, the original TBRP identification problem is transformed into an optimization problem, which is to minimize the deviation between the actual speed trajectory and the model-calculated one. Then, the Newton’s method is used to accelerate the search for the best set of TBRPs with minimum deviation. Finally, case studies are used to verify the effectiveness of the proposed method.
1. Introduction
Automatic Train Operation (ATO) technology plays a key role in the Intelligent Railway System, which executes the control of automatic train operation process and determines the quality of train operation [1]. The train basic resistance is an important component of train dynamics, which consists of axle bearing friction, rolling, and sliding friction between wheels and rails, impact resistance and air resistance. Its value accuracy affects the control performance of ATO system, but itself is affected by train formation, geometry, weight, wheel rail, climatic conditions, train running speed [2], etc. These factors have complex high-order coupling characteristics, making it difficult to directly calculate accurate resistance value using mechanism models. As a consequence, TBRPs are usually measured under experimental conditions to obtain a set of empirical parameters [3]. However, due to environmental conditions, such as wind speed, weather, air humidity, altitude, and air pressure, as well as the body wear and replacement of vehicle components, the TBRP change both fast and slowly over time. This leads to a deviation between the empirical parameters and the actual parameters, which may cause severe overshoot and oscillation of the model-based controller. In addition, basic resistance measurement techniques based on sensors are difficult to develop and costly. In response to this issue, researchers mainly approach it from two aspects: Basic resistance modeling and TBRPs identification.
The first basic resistance formula was determined by Davis [4], as shown in Equation (1):
where v is running speed of train. The parameters a, b, c are resistance characteristic parameters. a is related to wheel rolling friction and bearing friction, b is related to wheel rail sliding friction, c is related to air resistance. Parameters a, b, c can be confirmed in the official train parameter specification when vehicle category has been determined. Subsequently, Stanley [5] built models for freight train and rolling resistance, and proposed introducing suspension resistance in the Davis formula. Xue [6] analyzed the influence of air pressure and temperature change on the basic resistance of locomotive and vehicle operation by studying the data of the Sichuan-Tibet Railway. Kang [7] analyzed the composition of high-speed train basic resistance and its relationship with train weight, achieving the decoupling of air resistance and other resistances.
The above research has achieved significant results in basic resistance modeling. However, the high-order and complex basic resistance models are not suitable for the design of some linear controllers. The ever-changing operating environment and vehicle mechanical wear still cause basic resistance uncertainty. These factors led to some identification methods being proposed.
One of the identification methods is the basic resistance characteristics identification method [8,9,10,11,12]. This method uses speed differences to calculate acceleration, then obtain the calculated basic resistance by Newton’s second law. The objective function is to minimize the deviation between the characteristic curve of a set of TBRPs and the calculated basic resistance, as shown in Equation (2):
where Y is the calculated basic resistance, θ is basic resistance parameters, Φ = [1, v, v2] is the input-output data information vector, Θ is the definition domain of θ. The objective function is greatly affected by the accuracy and precision of data acquisition. When data shaping or high amplitude sporadic noise exists, the error of basic resistance is large. In terms of algorithm design, researchers have proposed least squares method [8,9], heuristic algorithm [10,11], and the multi-innovation theory-based identification algorithm [12] to solve the problems of this method, but issues with computational efficiency and stability still exist. On the other hand, researchers consider model inconsistency as a disturbance and use adaptive control strategies to address parameter uncertainty [13,14]. These methods can handle parameter uncertainty problems, but some control accuracy and stationarity may be lost due to the need for real-time adjustment of deviation.
Faced with these problems, this paper proposes an indirect train basic resistance parameter identification method based on speed-fitting objective (TBRPI-SF). Unlike in Equation (2), the parameter identification problem of TBRPI-SF is transformed into an optimization problem, which is to find a set of basic resistance parameters that can minimize the deviation between the fitting curve obtained from the model-based calculation and the actual speed trajectory curve. The Newton’s method is used to find the optimal TBRP adjustment direction. In addition, this paper discusses the boundary constraints and local solution problems of this algorithm. Finally, cases are set to verify the effectiveness and stability of this algorithm.
2. Train Dynamics Modeling
The objective function of BRPI-SF in this paper is to minimize the deviation between the fitting curve and the actual operating curve. The fitting curve is calculated using the traction calculation method based on train operation data and the train dynamics model.
The state of the train is affected by train weight, traction or braking force, basic resistance and additional resistance during operation. Considering the uneven additional resistance caused by different positions of each vehicle, this paper establishes the multi-mass train model, and its schematic diagram is shown in Figure 1.
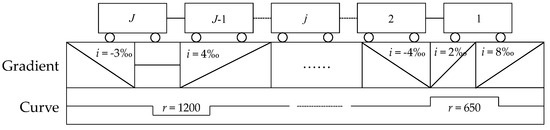
Figure 1.
Schematic diagram of the multi-mass train model.
According to Newton’s second law, the dynamic functions are described as:
where v is running speed (m/s) of train, t is running time (s), s is train position (m). M is train mass (t), γ is the rotating mass coefficient. F represents the train control force (kN), with positive and negative indicating traction and braking forces, respectively. W0(θ,v) is train basic resistance (kN). According to Davis formula, W0(θ,v) can be expressed as a univariate quadratic equation with train running speed as a variable, as shown in Equation (4):
where w0(θ,v) represents unit basic resistance (N/kN). g is the gravity coefficient, taken as 9.81 (N/kg or m/s2). θ = [a, b, c], a, b, and c are basic resistance parameters. G(s) represents the additional resistance (kN), which is affected by the train operation position s, and its calculation formula is written as follows:
where wi and wr represent unit additional resistance (N/kN) of gradient and curve. mj is the mass (t) of j-th car. sj is the position of the j-th car’s centroid. i(sj) means the gradient thousand fraction at position sj. r(sj) means the curve radius (m) at position sj. α is usually 600.
To facilitate analysis, train speed v and running time t are expressed as functions with train position s as independent variables, using Equation (3) to get:
With the changes in speed and position, the combined force acting on the train will also change. Therefore, the train operation process is a complicated non-uniform motion, which cannot be solved directly by Equation (6). The traction calculation method divides the train operation process into some stages through discretization and assumes that combined force acting remains constant within each stage. Therefore, the train acceleration remains unchanged within a single stage and is considered constant acceleration operation.
The train operation process is divided into I stages. In the i-th stage, the train start position is si-1. End position is si. Force is Fi-1. Initial speed is vi-1, which is obtained in (i-1)-th stage. We can obtain vi by combining Equations (4)–(6), which is shown in Equation (7):
where is the calculation speed under parameter θ. Therefore, based on train position and control force data, we can obtain the fitting curves v under a set of θ, where .
Figure 2 illustrates the fitting curves under three sets of TBRPs. We can see that accurate parameters θ1 can better reproduce the train operation process. Incorrect parameters, like θ2 and θ3, cause serious deviation from the fitting curve. It will lead to the unenforceability of the optimization curve and a decrease in controller control accuracy.
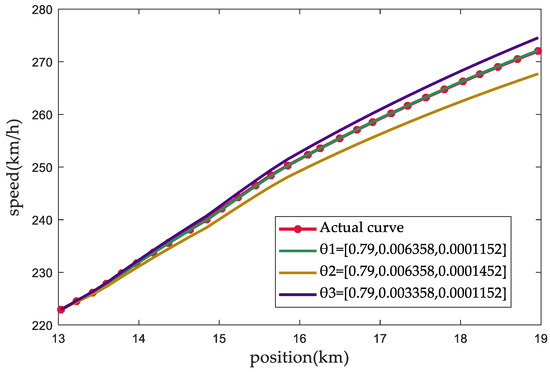
Figure 2.
The fitting curves under three sets of TBRPs.
3. Algorithm
3.1. Objective Function
From a modeling perspective, if the parameters can make the train operation process calculated by the train dynamics model closer to the real value, it will be considered more accurate. Therefore, the objective of TBRPI-SF is to obtain the best set of TBRPs. After selecting them for traction calculation, the square mean of speed error between the fitting position speed curve and the actual position speed curve is the smallest.
Train operation data is obtained through two methods: Timed and event-triggered. Divide the train operation process into I stages using the acquisition interval of operation data. The operation data can be organized into: , where , they are the control force, position, and speed information in the actual train operation data. Let , , the fitting curves v for this set of operational data under a set of basic resistance parameters θ is obtained by Equation (7).
The accuracy of the parameter is assessed using the mean square error between the fitted curve and the actual curve, which is expressed as:
As a result, the optimization problem of BRPI-SF can be described as:
where, Θ is the definition domain of θ. Each basic resistance parameter has a corresponding physical significance. Therefore, there exists a boundary Θ = [θmin,θmax] that satisfies θmin < θ < θmax. From Equation (9), it can be seen that BRPI-SF is a constraint estimation problem.
In summarize, the main steps of the parameter identification method proposed in this paper are: (1) Configure train formation and line information, set train operation data, (2) establish the train dynamics model to obtain fitted curves for any set of basic parameters, (3) optimize to find the best set of TBRP.
For this optimization problem, heuristic algorithms are easy to apply to solve, but their solving efficiency is relatively low. In order to meet the requirement of high efficiency when this method is applied to the train controller, this paper uses the Newton’s method to solve this problem.
3.2. Newton’s Method
The Newton’s method is an algorithm that uses a derivative to calculate the fastest descent direction of the function value. The updated formula for the Newton’s method is:
where θn and θn+1 are the parameters of the n-th and (n+1)-th iteration period. is the Hessian matrix of the f(θ). is the gradient of the f(θ).
Derive the composition of and :
Calculate the derivative of Equation (8):
where is the gradient of the i-th stage’s calculated speed in n-th iteration period. The composition of and is:
According to Equation (7), we can obtain :
where . When i = 1, , so .
Similarly, we can obtain and :
As a result, can be calculated iteratively by combining Equations (11)–(15).
Furthermore, we derive the Hessian matrix and calculate the derivative of Equation (11):
The composition of and is:
According to Equation (13), we can obtain :
where . When i = 1, , so .
Similarly, we can obtain , , , and :
As a result, can be calculated iteratively by combining Equations (13)–(23).
3.3. Boundary Constraints and Local Solution Problems
The Newton’s method is generally used to solve unconstrained optimization problems, but the TBRPI-SF problem has a limited range of parameters. On the other hand, the TBRPI-SF problem is a non-convex problem with multiple local optimal solutions. Therefore, the algorithm proposed in this paper needs to be improved to solve these issues.
For the boundary constraint problem of BRPI-SF, this paper adopts a step size adjustment method based on the Wolfe criterion:
When , find a step size α (0 < α < 1), which meet:
where c1 and c2 are constants, and 0 < c1 < c2 < 1. Starting from α = 1, we search for α that satisfies Equation (24) and . The parameters update formula in this iteration period is . Wolfe criterion preserves the descent direction of the optimal gradient and makes function value drop sufficiently under the constraint conditions.
The ending criterion of this algorithm is:
where ε1 is maximum acceptable deviation, as the stop condition for this algorithm.
For non-convex problem, does not mean that the optimal solution has been found. Therefore, when and Equation (25) is not satisfied, it means falling into local optima. Where means the minimum acceptable update distance in one iteration period. We expect the algorithm to jump out of the local solution and start searching again now. At this time, a parameter random updated method is used to search for a parameter that satisfies , where is a parameter limitation, reducing the possibility of re-entering local solutions.
In summary, the proposed basic resistance parameter identification based on the Newton’s method is shown as Algorithm 1:
| Algorithm 1: Basic resistance parameter identification based on the Newton’s method | |
| 1. | Initialize train formation information, including number of vehicles J, length lj, and weight mj of each vehicle. |
| 2. | Set train operation data, including control force and actual speed and position . |
| 3. | Initialize line information, including gradient i(s) and curve r(s) at each position s. |
| 4. | Initialize basic resistance parameters θ1 and calculate f(θ1). |
| 5. | for episode = 1,…n,…N do |
| 6. | Use θn to calculate the calculated speed vn. |
| 7. | Calculate the coefficient kn, pn, qn, un. |
| 8. | Calculate the gradient and . |
| 9. | Calculate the and . |
| 10. | Determine if . If so, update parameters as Equation (10). If not, find α based on the Wolfe criterion and update parameters as . |
| 11. | Calculate and determine if . If so, end for. If not, randomly search for a set of parameters . |
| 12. | End for |
4. Case Analysis
4.1. Simulation Setting
This paper selects the Wuhan-Guangzhou high-speed railway as the simulation line, with a main line length of 1069 kilometers. Sample train operation data form the train monitoring device. These operation data include train position, speed, traction, and braking force. The train parameters are shown in Table 1.

Table 1.
Train parameters.
Some parameters setting of the Newton’s method are shown in Table 2. The range of basic resistance parameters is set to match the characteristics of the actual high-speed train. The value of c1 is chosen to easier to facilitate the identification of an appropriate step size α. The value of c2 is chosen to achieve faster convergence. As for ε1, its value depends on the magnitude of data disturbance, and a generally suitable value is considered to be 0.05.

Table 2.
Parameters setting of the Newton’s method.
4.2. Case Studies
4.2.1. Effectiveness Test without Disturbance
Firstly, to verify the effectiveness of this method under no disturbance, we created four sets of simulation data with different TBRPs. The actual basic resistance parameter values are shown in Table 3. This method was used to identify the TBRPs with random initial parameters. The acceptable deviation ε1 was adjusted to 10−5. The four identification results are recorded in Table 3. In the case of no data disturbance, the TBRPs obtained by this method were basically the same as the actual values. In these four identification processes, the minimum number of iterations was 4 and the maximum was 7. The mean square errors in each case were very small and met the acceptable deviation ε1, which proves the effectiveness of the parameters and this method. The same conclusion can be drawn from Figure 3, where the fitting curve calculated by the identified parameters is consistent with the actual curve.

Table 3.
Parameter identification results for four cases.
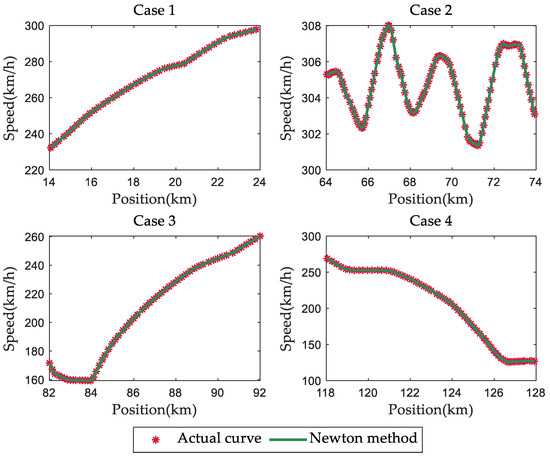
Figure 3.
Comparison between fitted curves and actual curves for four cases.
4.2.2. Effectiveness Test under Random Disturbance
Secondly, we set up a set of simulation data and introduced white noise acquisition disturbances into the velocity data. The basic resistance parameter of the simulation data is set to θ = [0.79, 0.0229, 0.001493]. Using the Newton’s method to identify the TBRPs of the data. The acceptable deviation ε1 is adjusted to 0.05. Compare the curve calculated from the Newton’s method with the actual curve and obtain Figure 4a. The results verify that the basic resistance parameter obtained from the Newton’s method are accurate and can effectively reproduce the operation process of the train. The simulation results in Figure 4b shows that the standard deviation between the fitted curve and the actual curve was reduced from 904 to 0.033 within 5 iterations. The computational efficiency of the algorithm is pretty good. From Figure 4c, we can see the process of TBRPs changing with iterations. The final parameter is [0.483, 0.0273, 0.001492]. Compared to the actual parameters, the parameter c is the same, but error in parameter a and b. These errors are considered normal because of the existence of random disturbance. Actually, the unit basic resistance corresponding to the two sets of parameters is basically consistent in the speed domain [270, 305] (km/h), as shown in Figure 4d.
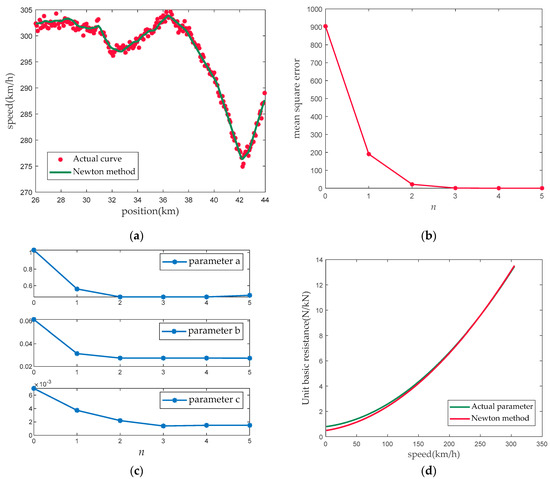
Figure 4.
Parameter identification results. (a) Comparison between fitted curves and actual curves, (b) standard deviation changes with iteration, (c) TBRPs with iteration, (d) comparison between actual parameter characteristics and parameter characteristics obtained by Newton’s method.
4.2.3. Online Identification Test
Finally, we set up a set of simulation experiments on the TBRPs changing with the position of the line. This simulation simulates the scenarios of reduced friction caused by smooth track after rain and increased air resistance caused by increased external wind speed. The simulation conditions of TBRPs in different sections are shown in Table 4. We introduced random disturbances in the last two sections. In this simulation process, the TBRPs of the current section were identified online based on real-time operation data generated by the train. The sampling interval was 100 m, and the data capacity I was 20.

Table 4.
The simulation conditions of TBRPs in different sections.
Figure 5 illustrates the results of this simulation. The identification algorithm accurately predicted the basic resistance values of most positions, but significant deviations exist in the positions of parameter switching. Similar to the previous simulation case, in the section of no data disturbance, the TBRPs obtained by this method are basically the same as the actual values, but in the section of existing data disturbance, the identification results of parameter c are relatively close to the actual situation, and deviations exist in the identification results parameters b and c.
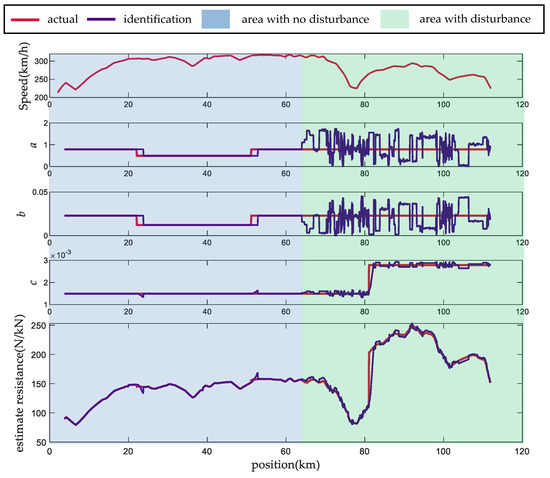
Figure 5.
Results of this simulation on the TBRPs changing with the position.
4.2.4. Summary
In summary, the TBRPs identification method based on the Newton’s method can find more accurate TBRP to improve the accuracy of traction calculation. The above cases prove the effectiveness of the algorithm under the condition of disturbance or not. The algorithm can find the optimal solution within several generations, which is short enough for designing periodicity real-time identification to use in the train controller.
5. Conclusions
This paper proposes an indirect TBRP identification method based on speed trajectory fitting. We transform the original TBRP identification problem into an optimization problem, which is to minimize the deviation between the actual speed trajectory and the model calculated one. By deducing the gradient and Hessian matrix of the objective function, the Newton’s method is used to determine the optimal updating direction of the TBRPs. This paper discusses the boundary constraints and local solution problems of this algorithm and solves them by Wolfe criterion and random movement. Finally, simulation cases are set up to verify its effectiveness. The results show that this method can accurately identify the TBRPs under the condition without disturbance and obtain the accurate basic train resistance under the condition with random disturbance. In the online identification test, this method accurately predicted the basic resistance value of most sections. This parameter identification method can be embedded into the train control equipment to realize the online identification, so as to improve the performance of train controller.
Author Contributions
Conceptualization, F.X. and T.L.; methodology, T.L.; software, F.X.; validation, F.X., T.L. and P.S.; data curation, F.X.; writing—original draft preparation, F.X. and T.L.; writing—review and editing, F.X., T.L. and P.S.; visualization, T.L.; supervision, F.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Open Project Funding of State Key Laboratory for Traction and Control System of EMU and Locomotive, China Academy of Railway Sciences Corporation Limited (Contract No. 2022YJ294), by project K2021J048 supported by CR.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation data can be downloaded at: https://www.researchgate.net/publication/372656434_Simulation_data_An_indirect_identification_method_for_train_basic_resistance_parameters (accessed on 20 May 2023). It involves the reported data in Figure 2 and the simulation data in Chapter 4.
Acknowledgments
The author thanks the anonymous reviewers for their constructive comments and the editor for handling the paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Huang, W.Y.; Yang, N.Q. Ponderation on railway train basic resistance. China Railw. Sci. 2000, 21, 44–57. [Google Scholar]
- Yu, Z.D.; Chen, D.W. Modeling and system identification of the braking system of urban rail vehicles. J. China Railw. Soc. 2011, 33, 37–40. [Google Scholar]
- Tian, H.Q. Study on the characteristics of train air resistance under wind environment. China Railw. Sci. 2008, 29, 108–112. [Google Scholar]
- Lukaszewicz, P. A simple method to determine train running resistance from full-scale measurements. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 331–337. [Google Scholar] [CrossRef]
- Stanley, A.B.; Richard, A.U.; James, P.R. The interpretation of train rolling resistance from fundamental mechanics. IEEE Trans. Ind. Appl. 1983, IA-19, 802–817. [Google Scholar]
- Xue, Y.H.; Ding, J.J.; Wang, L.J.; Li, Y.; Chen, K. Research on the basic resistance of locomotives and rolling stocks in Sichuan-Tibet Railway. Electr. Drive Locomot. 2021, 10, 67–72. [Google Scholar]
- Kang, X.; Zeng, Y.; Zhang, B. Measurement method for the air resistance of highspeed train. China Railw. Sci. 2012, 33, 54–59. [Google Scholar]
- Xie, G.; Zhang, D.; Hei, X.H.; Qian, F.C.; Cao, B.G.; Sei, T.; Hiroshi, M. Online identification method of time - varying parameters for Longitudinal dynamics model of high-speed train. J. Traffic Transp. Eng. 2017, 17, 71–81. [Google Scholar]
- Wang, W. Parameter Identification and Its Application in Urban Train Control Model. Master’s Thesis, Beijing Jiaotong University, Beijing, China, July 2018. [Google Scholar]
- Hansen, H.S.; Nawaz, M.U.; Olsson, N. Using operational data to estimate the running resistance of trains. Estimation of the resistance in a set of Norwegian tunnels. J. Rail Transp. Plan. Manag. 2017, 7, 62–76. [Google Scholar] [CrossRef]
- Lei, Y.; Zeng, Q.; Zhu, T.M. Train basic resistance identification and its online update algorithm. J. Inf. Comput. Sci. 2015, 12, 4161–4171. [Google Scholar] [CrossRef]
- Liu, X.Y.; Ning, B.; Xun, J.; Wang, C.; Xiao, X.; Liu, T. Parameter identification of train basic resistance using multi-innovation theory. IFAC-Paper 2018, 51, 637–642. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, L.L.; Yang, H.; Zhang, J.H. Adaptive error compensation control for high-speed train based on characteristic model. J. East China Jiaotong Univ. 2023, 40, 77–86. [Google Scholar]
- Shi, W.S. Research on automatic train operation base on model-free adaptive control. J. China Railw. Soc. 2016, 38, 72–77. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).