Anomalies in Infrared Outgoing Longwave Radiation Data before the Yangbi Ms6.4 and Luding Ms6.8 Earthquakes Based on Time Series Forecasting Models
Abstract
1. Introduction
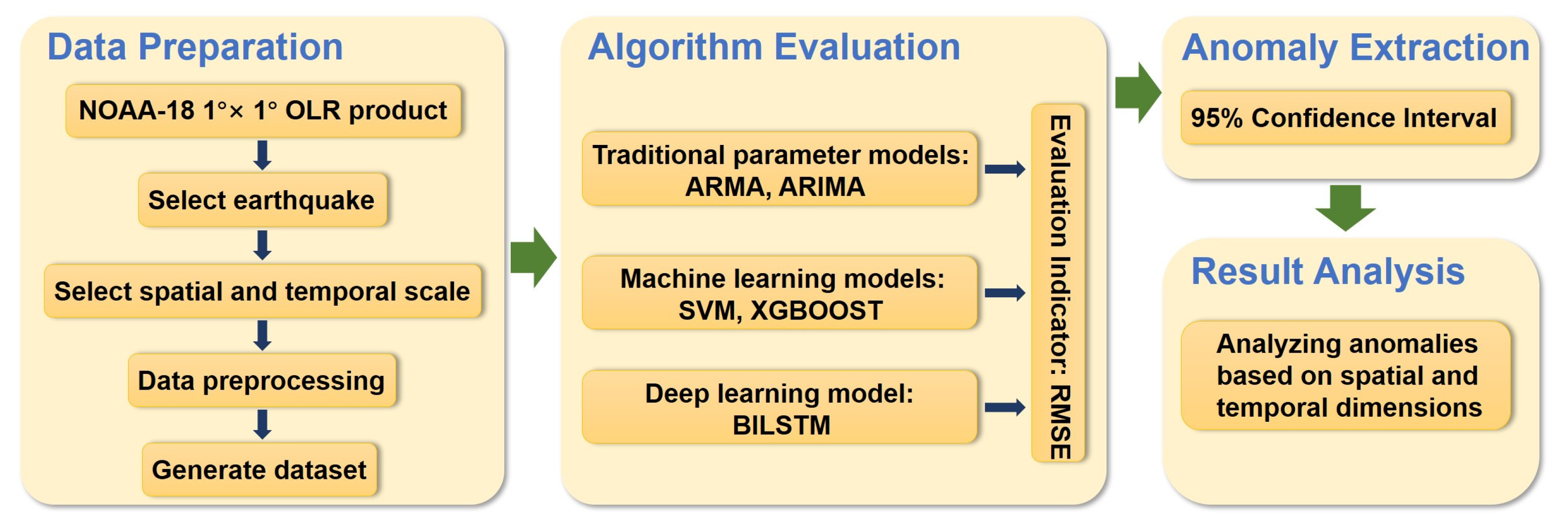
2. Data
2.1. HIRS OLR Data
2.2. Data Processing
3. Methods
3.1. Time Series Forecasting Models
3.1.1. ARMA/ARIMA
3.1.2. SVM
3.1.3. XGBoost
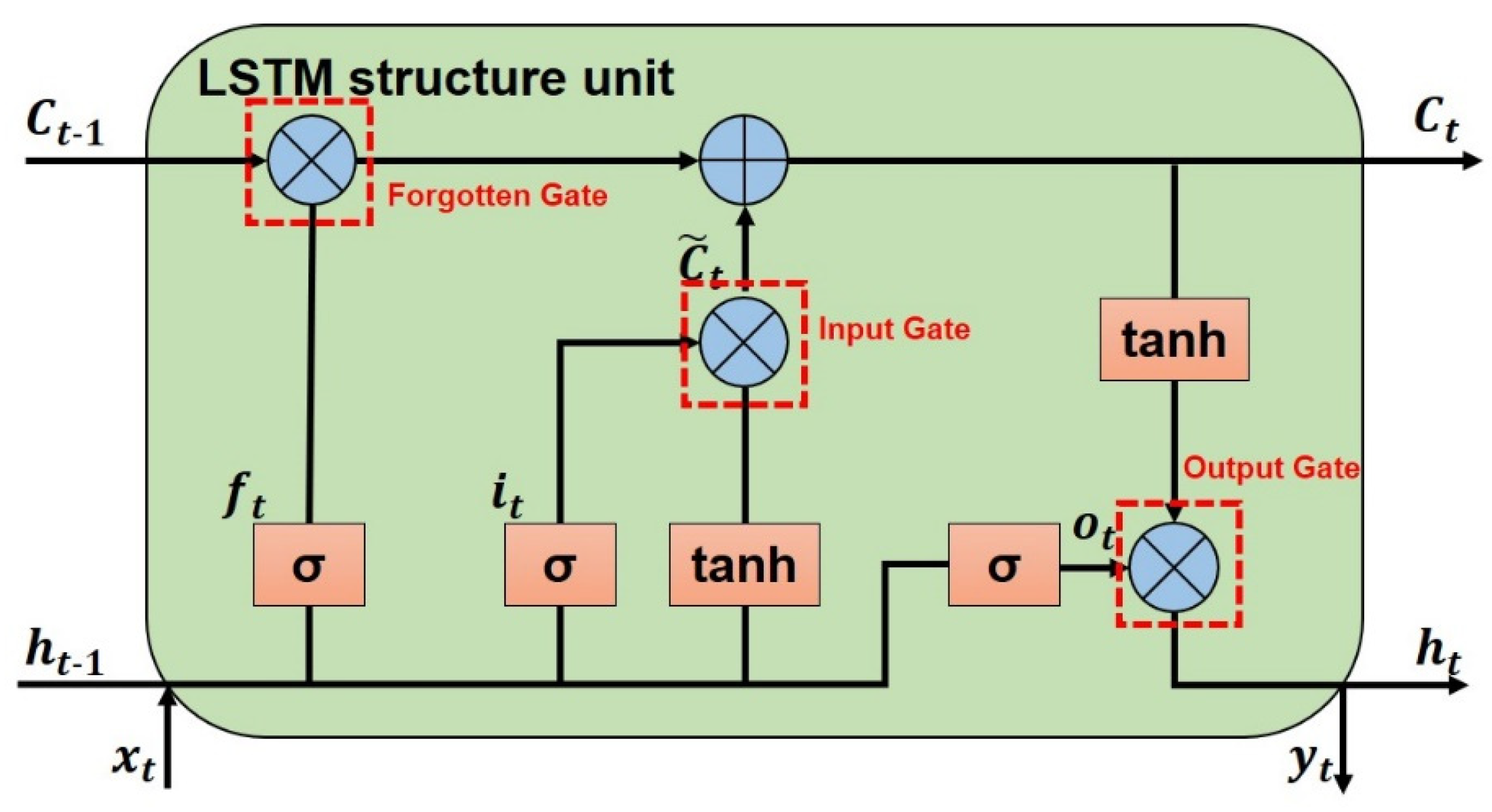
3.1.4. BILSTM
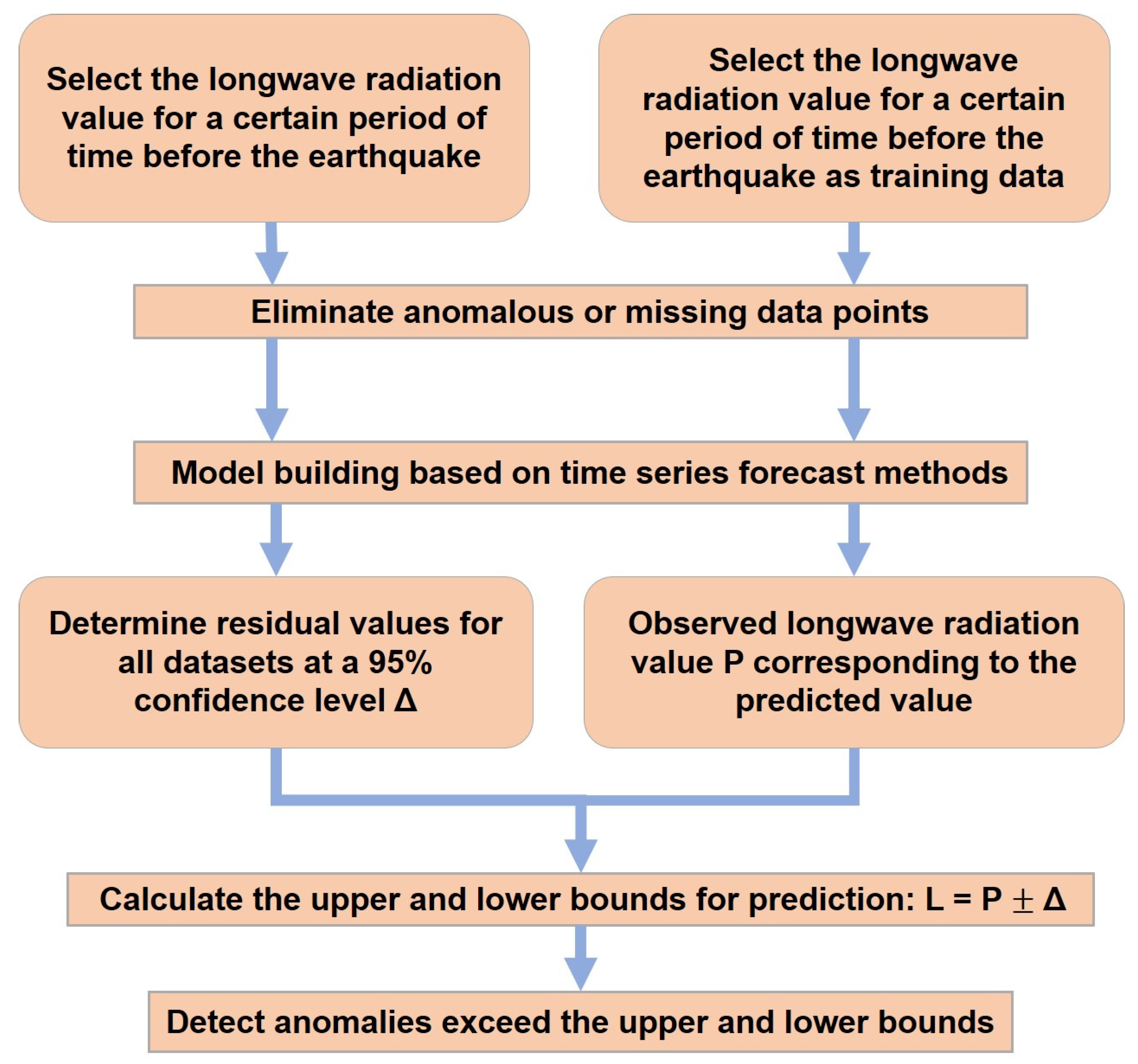
3.2. Anomaly Assessment Method
4. Results
4.1. Analysis of Algorithm Evaluation Results
4.2. Analysis of Anomaly Results of Earthquake Cases
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gornyy, V.; Sal’man, A.; Tronin, A.; Shilin, B. Outgoing terrestrial infrared radiation as an indicator of seismic activity. Dokl. Akad. Nauk USSR 1988, 301, 67–69. (In Russian) [Google Scholar]
- Lu, X.; Meng, Q.; Gu, X.; Zhang, X.; Xie, T.; Geng, F. Thermal infrared anomalies associated with multi-year earthquakes in the Tibet region based on China’s FY-2E satellite data. Adv. Space Res. 2016, 58, 989–1001. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Q. A statistical analysis of TIR anomalies extracted by RSTs in relation to an earthquake in the Sichuan area using MODIS LST data. Nat. Hazards Earth Syst. Sci. 2019, 19, 535–549. [Google Scholar] [CrossRef]
- Xiong, P.; Shen, X.H.; Bi, Y.X.; Kang, C.L.; Chen, L.Z.; Jing, F.; Chen, Y. Study of outgoing longwave radiation anomalies associated with Haiti earthquake. Nat. Hazards Earth Syst. Sci. 2010, 10, 2169–2178. [Google Scholar] [CrossRef]
- Kong, X.; Bi, Y.; Glass, D.H. Detecting seismic anomalies in outgoing long-wave radiation data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 649–660. [Google Scholar] [CrossRef]
- Mahmood, I.; Iqbal, M.F.; Shahzad, M.I.; Qaiser, S. Investigation of atmospheric anomalies associated with Kashmir and Awaran Earthquakes. J. Atmos. Sol.-Terr. Phys. 2017, 154, 75–85. [Google Scholar] [CrossRef]
- Natarajan, V.; Philipoff, P.; Sreedharan, V.W.; Venkatachalapathy, H. Observation of pre-earthquake thermal signatures using geostationary satellites: Implications for earthquake forecasting. J. Appl. Remote Sens. 2016, 10, 46004. [Google Scholar] [CrossRef]
- Prakash, R.; Srivastava, H. Diurnal variations of outgoing long wave radiation (OLR) vis a vis 4 January, 2016 Manipur earthquake (Mw: 6.7): An earthquake precursor? Mausam 2017, 68, 475–486. [Google Scholar] [CrossRef]
- Sun, K.; Shan, X.-J.; Ouzounov, D.; Shen, X.-H.; Jing, F. Analyzing long wave radiation data associated with the 2015 Nepal earthquakes based on Multi-orbit satellite observations. Chin. J. Geophys. 2017, 60, 3457–3465. [Google Scholar]
- Ouzounov, D.; Liu, D.; Chunli, K.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from IR satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Ohring, G.; Gruber, A. Satellite radiation observations and climate theory. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 25, pp. 237–304. [Google Scholar]
- Yang, H.M.; Pan, Z.S.; Wei, B.; Of, S. Review of Time Series Prediction Methods. Comput. Sci. 2019, 46, 21–28. [Google Scholar]
- Saqib, M.; Senturk, E.; Sahu, S.A.; Adil, M.A. Ionospheric anomalies detection using autoregressive integrated moving average (ARIMA) model as an earthquake precursor. Acta Geophys. 2021, 69, 1493–1507. [Google Scholar] [CrossRef]
- Saqib, M.; Senturk, E.; Sahu, S.A.; Adil, M.A. Comparisons of autoregressive integrated moving average (ARIMA) and long short term memory (LSTM) network models for ionospheric anomalies detection: A study on Haiti (M-w=7.0) earthquake. Acta Geod. Geophys. 2022, 57, 195–213. [Google Scholar] [CrossRef]
- Senturk, E.; Saqib, M.; Adil, M.A. A Multi-Network based Hybrid LSTM model for ionospheric anomaly detection: A case study of the M-w 7.8 Nepal earthquake. Adv. Space Res. 2022, 70, 440–455. [Google Scholar] [CrossRef]
- Yue, Y.; Koivula, H.; Bilker-Koivula, M.; Chen, Y.; Chen, F.; Chen, G. TEC Anomalies Detection for Qinghai and Yunnan Earthquakes on 21 May 2021. Remote Sens. 2022, 14, 4152. [Google Scholar] [CrossRef]
- Xiong, P.; Zhai, D.; Long, C.; Zhou, H.; Zhang, X.; Shen, X. Long short-term memory neural network for ionospheric total electron content forecasting over China. Space Weather. 2021, 19, e2020SW002706. [Google Scholar] [CrossRef]
- Mohammed, D.H.K.; Kulahci, F.; Muhammed, A. Determination of possible responses of Radon-222, magnetic effects, and total electron content to earthquakes on the North Anatolian Fault Zone, Turkiye: An ARIMA and Monte Carlo Simulation. Nat. Hazards 2021, 108, 2493–2512. [Google Scholar] [CrossRef]
- Mir, A.A.; Celebi, F.V.; Alsolai, H.; Qureshi, S.A.; Rafique, M.; Alzahrani, J.S.; Mahgoub, H.; Hamza, M.A. Anomalies Prediction in Radon Time Series for Earthquake Likelihood Using Machine Learning-Based Ensemble Model. IEEE Access 2022, 10, 37984–37999. [Google Scholar] [CrossRef]
- Feng, X.; Zhong, J.; Yan, R.; Zhou, Z.; Tian, L.; Zhao, J.; Yuan, Z. Groundwater radon precursor anomalies identification by EMD-LSTM model. Water 2022, 14, 69. [Google Scholar] [CrossRef]
- Roebeling, R.; Schulz, J.; Hewison, T.; Theodore, B. Inter-calibration of METEOSAT IR and WV channels using HIRS. AIP Conf. Proc. 2013, 1531, 288–291. [Google Scholar]
- Turner, E.C.; Tett, S.F. Using longwave HIRS radiances to test climate models. Clim. Dyn. 2014, 43, 1103–1127. [Google Scholar] [CrossRef]
- Zhai, D.; Zhang, X.; Xiong, P. Detecting thermal anomalies of earthquake process within outgoing longwave radiation using time series forecasting models. Ann. Geophys. 2020, 63, PA548. [Google Scholar] [CrossRef]
- Ellingson, R.G.; Yanuk, D.J.; Lee, H.-T.; Gruber, A. A technique for estimating outgoing longwave radiation from HIRS radiance observations. J. Atmos. Ocean. Technol. 1989, 6, 706–711. [Google Scholar] [CrossRef]
- Lee, H.-T.; Ellingson, R.G. HIRS OLR climate data record–production and validation updates. AIP Conf. Proc. 2013, 1531, 420–423. [Google Scholar]
- Chen, Q.F.; Zheng, D.L.; Che, S. Earthquake Cases in China (1992–1994); Seismological Press: Beijng, China, 2002. [Google Scholar]
- Chen, Q.F.; Zheng, D.L.; Liu, G.P.; Li, M. Earthquake Cases in China (1995–1996); Seismological Press: Beijing, China, 2002. [Google Scholar]
- Jiang, H.K.; Fu, H.; Yang, M.L.; Ma, H.S. Earthquake Cases in China (2003–2006); Seismological Press: Beijing, China, 2014. [Google Scholar]
- Jing, F.; Shen, X.; Kang, C.; Meng, Q.; Xiong, P. Anomalies of outgoing longwave radiation before some medium to large earthquakes. Earthquake 2009, 29, 117–122. [Google Scholar]
- Feng, J.; Xuhui, S.; Hui, W.; Chunli, K.; Pan, X. Infrared characteristics analysis of the 2015 Nepal M S 8.1 earthquake. Acta Seismol. Sin. 2016, 38, 429–437. [Google Scholar]
- Song, D.; Zang, L.; Shan, X.; Yuan, Y.; Cui, J.; Shao, H.; Shen, C.; Shi, H. A study on the algorithm for extracting earthquake thermal infrared anomalies based on the yearly trend of LST. Seismol. Geol. 2016, 38, 680–695. [Google Scholar]
- He, S.; Zhou, Q.; Liu, Z. Seismogenic Structure of the 2021 Yangbi, Yunnan MS6.4 Earthquake and Earthquake Risk Analysis in the Epicenter Area. J. Seismol. Res. 2021, 44, 380–390. [Google Scholar]
- Fan, X.; Wang, X.; Dai, L.; Fang, C.; Deng, Y.; Zou, C.; Tang, M.; Wei, Z.; Dou, X.; Zhang, J. Characteristics and spatial distribution pattern of M S 6.8 Luding earthquake occurred on September 5, 2022. J. Eng. Geol. 2022, 30, 1504–1516. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Kumar, U.; Jain, V. ARIMA forecasting of ambient air pollutants (O 3, NO, NO 2 and CO). Stoch. Environ. Res. Risk Assess. 2010, 24, 751–760. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 3. [Google Scholar]
- Zhang, H.; Zhang, S.; Wang, P.; Qin, Y.; Wang, H. Forecasting of particulate matter time series using wavelet analysis and wavelet-ARMA/ARIMA model in Taiyuan, China. J. Air Waste Manag. Assoc. 2017, 67, 776–788. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Chen, B.-J.; Chang, M.-W. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- LI, H.; ZHU, Y. Xgboost algorithm optimization based on gradient distribution harmonized strategy. J. Comput. Appl. 2020, 40, 1633. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yan, X.; Shi, Z.; Wang, G.; Zhang, H.; Bi, E. Detection of possible hydrological precursor anomalies using long short-term memory: A case study of the 1996 Lijiang earthquake. J. Hydrol. 2021, 599, 126369. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, S.; Li, Q.; Li, Y.; Li, J.; Yang, Y. A new method for heart rate prediction based on LSTM-BiLSTM-Att. Measurement 2023, 207, 112384. [Google Scholar] [CrossRef]
- Yu, H.Z.; Zhu, Q.Y. A probabilistic approach for earthquake potential evaluation based on the load/unload response ratio method. Concurr. Comput. Pract. Exp. 2010, 22, 1520–1533. [Google Scholar] [CrossRef]
- Alam, A.; Wang, N.; Zhao, G.; Barkat, A. Implication of radon monitoring for earthquake surveillance using statistical techniques: A case study of Wenchuan earthquake. Geofluids 2020, 2020, 2429165. [Google Scholar] [CrossRef]
- Yin, J.; Song, Z.; Xue, Y.; Liu, J.; Zhang, G.; Zhu, Y. Analysis on global huge earthquake activity. Acta Seismol. Sin. 2012, 34, 191–201. [Google Scholar]
- Kutoglu, S.H.; Ghasempour, F.; Sekertekin, A. Investigation of Possible MODIS AOD Anomalies as Earthquake Precursors for Global Earthquakes. Adv. Space Res. 2021, 68, 3531–3545. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, X.; Wu, F.; Chen, Y. A New Method for Detection of Pre-Earthquake Ionospheric Anomalies. Chin. J. Geophys. 2013, 56, 213–222. [Google Scholar]
- Xiong, P.; Tong, L.; Zhang, K.; Shen, X.; Battiston, R.; Ouzounov, D.; Iuppa, R.; Crookes, D.; Long, C.; Zhou, H. Towards advancing the earthquake forecasting by machine learning of satellite data. Sci. Total Environ. 2021, 771, 145256. [Google Scholar] [CrossRef]
- Xie, T.; Kang, C.L.; Ma, W.Y. Thermal infrared brightness temperature anomalies associated with the Yushu (China) Ms = 7.1 earthquake on 14 April 2010. Nat. Hazards Earth Syst. Sci. 2013, 13, 1105–1111. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, Y.; Guo, X.; Qin, M.; Ning, Y.-L.; Gao, J. Thermal infrared and long-wave radiation anomalies of Yushu MS 7.1 earthquake. Prog. Geophys. 2013, 28, 2444–2452. [Google Scholar]
- Zhang, X.; Zhang, Y.; Guo, X.; Wei, C.; Zhang, L. Analysis of thermal infrared anomaly in the Nepal MS8.1 earthquake. Earth Sci. Front. 2017, 24, 227–233. [Google Scholar]
- Tramutoli, V. Robust AVHRR Techniques (RAT) for environmental monitoring: Theory and applications. In Earth Surface Remote Sensing II; SPIE: Bellingham, WA, USA, 1998; pp. 101–113. [Google Scholar]
- Pulinets, S.; Ouzounov, D.; Karelin, A.; Davidenko, D. Lithosphere-atmosphere-ionosphere-magnetosphere coupling-a concept for pre-earthquake signals generation. In Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; American Geophysical Union: Washington, DC, USA, 2018; pp. 77–98. [Google Scholar]
- Parrot, M.; Tramutoli, V.; Liu, T.J.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena associated with large earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 197–225. [Google Scholar] [CrossRef]
- Conti, L.; Picozza, P.; Sotgiu, A. A critical review of ground based observations of earthquake precursors. Front. Earth Sci. 2021, 9, 676766. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Jiang, C.; Zhao, Z.; Zhang, Y.; Ma, Z. Analysis of Pre-Earthquake Ionospheric Anomalies in the Japanese Region Based on DEMETER Satellite Data. Universe 2023, 9, 229. [Google Scholar] [CrossRef]
- Fu, C.-C.; Lee, L.-C.; Ouzounov, D.; Jan, J.-C. Earth’s outgoing longwave radiation variability prior to M≥ 6.0 earthquakes in the Taiwan area during 2009–2019. Front. Earth Sci. 2020, 8, 364. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, M.; Gong, C.; Wang, L. Ionosphere abnormalities before the 2017 MS7. 0 Jiuzhai Valley earthquake. J. Guilin Univ. Technol. 2020, 40, 372–378. [Google Scholar]
- Du, X.; Zhang, X. Ionospheric Disturbances Possibly Associated with Yangbi Ms6. 4 and Maduo Ms7. 4 Earthquakes in China from China Seismo Electromagnetic Satellite. Atmosphere 2022, 13, 438. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, X.; Du, X. Analysis of Ionospheric Perturbations Possibly Related to Yangbi Ms6. 4 and Maduo Ms7. 4 Earthquakes on 21 May 2021 in China Using GPS TEC and GIM TEC Data. Atmosphere 2022, 13, 1725. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A. Spatial transformer networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; Volume 28. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
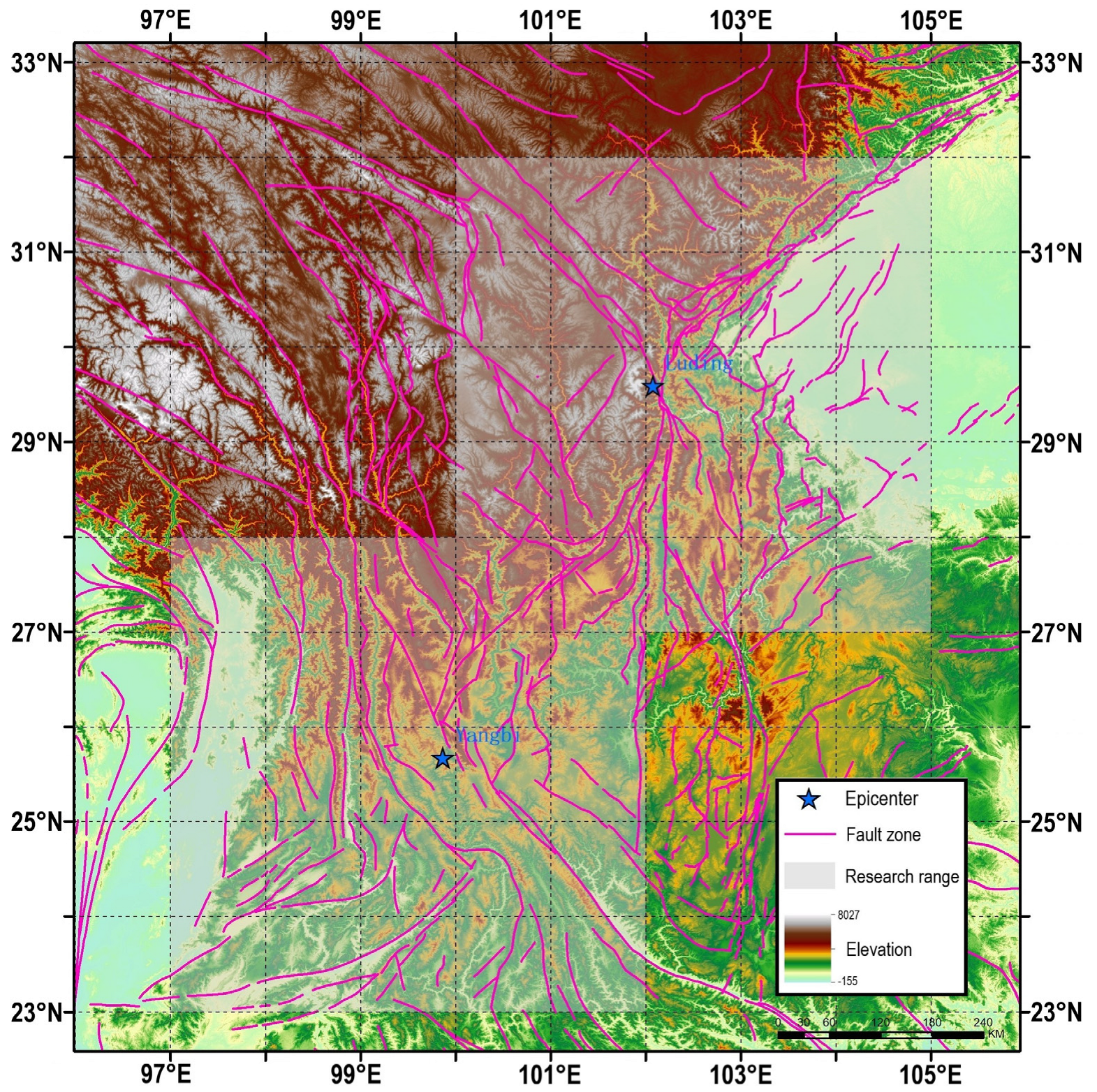
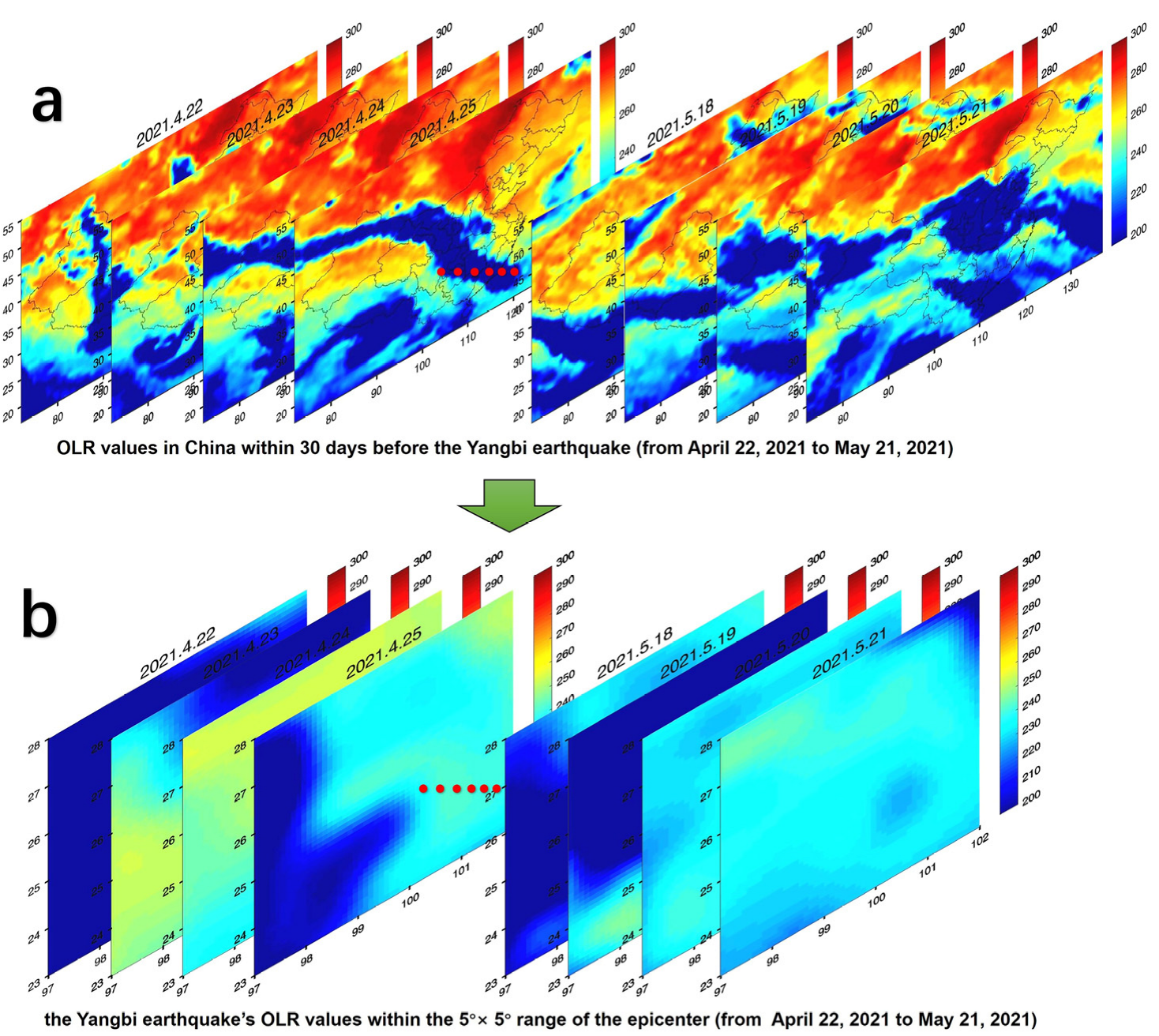


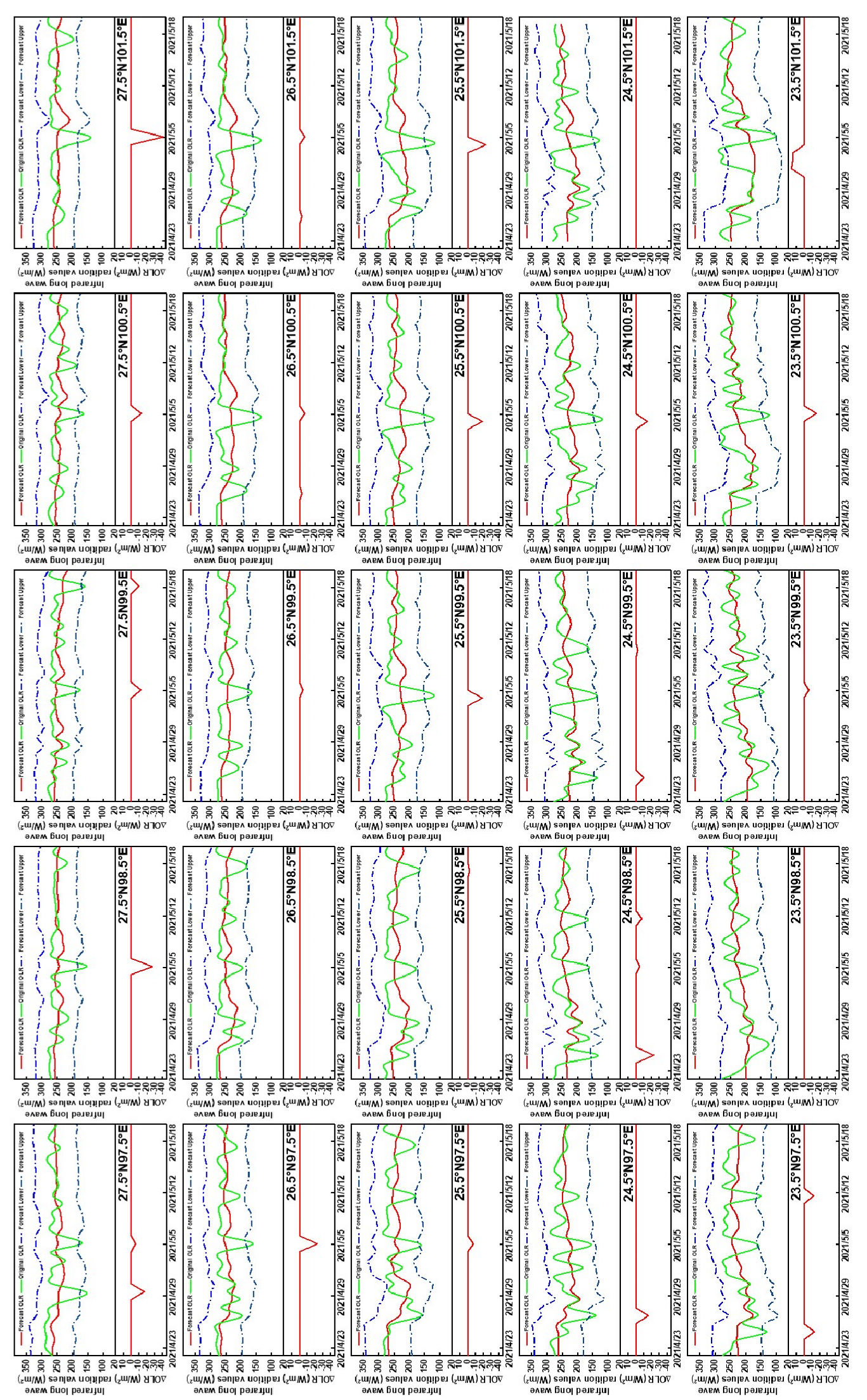

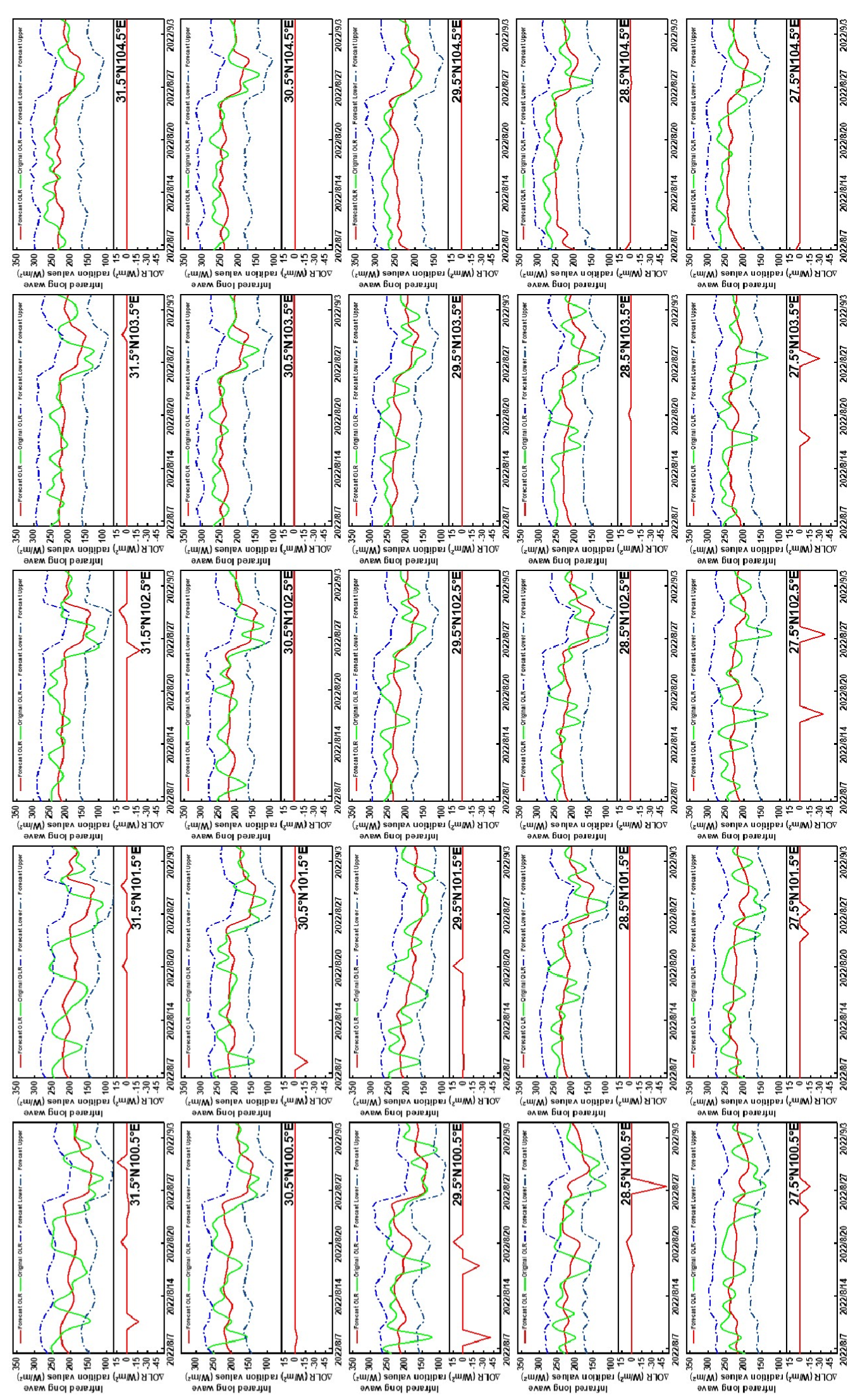

| Time (UTC + 8) | Longitude/° E | Latitude /° N | Depth/KM | Magnitude/MS | Location |
|---|---|---|---|---|---|
| 21 May 2021 21:48 | 99.87 | 25.67 | 8 | 6.4 | Yangbi County, Yunnan Province |
| 5 September 2022 12:52 | 102.08 | 29.59 | 16 | 6.8 | Luding County, Sichuan Province |
| BILSTM | 5 Days | 10 Days | 15 Days | 20 Days | 25 Days | 30 Days |
|---|---|---|---|---|---|---|
| 23.5° N 97.5° E | 35.8714 | 44.4602 | 40.7788 | 44.0537 | 41.95 | 44.4664 |
| 23.5° N 98.5° E | 21.17 | 24.7485 | 26.7656 | 33.1445 | 33.2425 | 39.824 |
| 23.5° N 99.5° E | 24.1076 | 24.4975 | 30.2064 | 37.9868 | 37.9291 | 42.8743 |
| 23.5° N 100.5° E | 16.7314 | 18.9341 | 23.4452 | 42.1087 | 43.1239 | 41.4841 |
| 23.5° N 101.5° E | 31.0999 | 27.5695 | 31.9941 | 50.9161 | 49.8469 | 47.2746 |
| 24.5° N 97.5° E | 9.9734 | 24.9584 | 26.6236 | 33.5992 | 38.2924 | 36.2921 |
| 24.5° N 98.5° E | 13.3886 | 34.8646 | 35.2853 | 38.5706 | 37.172 | 40.8611 |
| 24.5° N 99.5° E | 15.065 | 25.6253 | 34.2971 | 40.8797 | 38.0604 | 40.7207 |
| 24.5° N 100.5° E | 15.0526 | 24.6202 | 27.0864 | 41.9177 | 42.5833 | 41.4012 |
| 24.5° N 101.5° E | 22.1425 | 26.9378 | 29.9275 | 44.0822 | 44.73 | 42.7893 |
| 25.5° N 97.5° E | 42.6918 | 41.4088 | 38.9593 | 40.4864 | 43.8695 | 41.0631 |
| 25.5° N 98.5° E | 48.6846 | 39.9932 | 37.4426 | 39.5021 | 40.3489 | 41.4182 |
| 25.5° N 99.5° E | 22.459 | 22.2276 | 29.1774 | 42.9795 | 39.9472 | 38.9058 |
| 25.5° N 100.5° E | 22.459 | 22.2276 | 29.1774 | 42.9795 | 39.9472 | 38.9058 |
| 25.5° N 101.5° E | 23.2545 | 22.5681 | 30.5917 | 43.7706 | 44.0704 | 41.7547 |
| 26.5° N 97.5° E | 25.8453 | 26.5048 | 25.9652 | 32.772 | 33.1736 | 31.2204 |
| 26.5° N 98.5° E | 42.6866 | 34.406 | 31.3593 | 31.8476 | 34.0241 | 32.3093 |
| 26.5° N 99.5° E | 24.1937 | 25.337 | 25.5326 | 32.002 | 31.4707 | 30.8233 |
| 26.5° N 100.5° E | 12.9577 | 13.9075 | 25.1652 | 38.3288 | 37.1007 | 36.8696 |
| 26.5° N 101.5° E | 16.4933 | 19.1507 | 25.8206 | 38.2982 | 38.8576 | 37.6009 |
| 27.5° N 97.5° E | 16.3102 | 14.6956 | 19.9246 | 26.974 | 34.2035 | 32.8196 |
| 27.5° N 98.5° E | 16.2189 | 13.5482 | 18.7207 | 28.0452 | 27.5518 | 26.2956 |
| 27.5° N 99.5° E | 42.1547 | 32.8008 | 29.7843 | 31.8504 | 30.7415 | 28.9882 |
| 27.5° N 100.5° E | 22.2848 | 30.6576 | 29.3146 | 32.4005 | 30.3714 | 29.3901 |
| 27.5° N 101.5° E | 35.9955 | 31.3212 | 31.2098 | 38.7217 | 35.2332 | 33.7072 |
| Total RMSE | 619.292 | 667.9708 | 734.5553 | 948.2177 | 947.8418 | 940.0596 |
| 5 Days | 10 Days | 15 Days | 20 Days | 25 Days | 30 Days | |
|---|---|---|---|---|---|---|
| ARMA | 625.0028 | 647.0955 | 835.6342 | 871.0932 | 882.8587 | 941.6699 |
| ARIMA | 718.1327 | 738.4042 | 2060.7494 | 1034.0422 | 1542.7989 | 928.8650 |
| SVM | 775.9093 | 784.3109 | 806.0665 | 1025.3715 | 1034.8680 | 1026.3374 |
| XGBoost | 640.0953 | 670.1815 | 773.8258 | 930.6856 | 964.0494 | 946.3818 |
| BILSTM | 619.2920 | 667.9708 | 734.5553 | 948.2177 | 947.8418 | 940.0596 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Sun, K.; Zhang, J. Anomalies in Infrared Outgoing Longwave Radiation Data before the Yangbi Ms6.4 and Luding Ms6.8 Earthquakes Based on Time Series Forecasting Models. Appl. Sci. 2023, 13, 8572. https://doi.org/10.3390/app13158572
Zhu J, Sun K, Zhang J. Anomalies in Infrared Outgoing Longwave Radiation Data before the Yangbi Ms6.4 and Luding Ms6.8 Earthquakes Based on Time Series Forecasting Models. Applied Sciences. 2023; 13(15):8572. https://doi.org/10.3390/app13158572
Chicago/Turabian StyleZhu, Junqing, Ke Sun, and Jingye Zhang. 2023. "Anomalies in Infrared Outgoing Longwave Radiation Data before the Yangbi Ms6.4 and Luding Ms6.8 Earthquakes Based on Time Series Forecasting Models" Applied Sciences 13, no. 15: 8572. https://doi.org/10.3390/app13158572
APA StyleZhu, J., Sun, K., & Zhang, J. (2023). Anomalies in Infrared Outgoing Longwave Radiation Data before the Yangbi Ms6.4 and Luding Ms6.8 Earthquakes Based on Time Series Forecasting Models. Applied Sciences, 13(15), 8572. https://doi.org/10.3390/app13158572





