Solving Panel Block Assembly Line Scheduling Problem via a Novel Deep Reinforcement Learning Approach
Abstract
1. Introduction
- (1)
- We introduce an end-to-end reinforcement learning approach to learn scheduling rules, overcoming limitations such as poor model generalization. This method can effectively solve instances of any scale without the need for retraining;
- (2)
- We present an MDP model for the panel block assembly line scheduling problem, providing a comprehensive definition of states, actions, and rewards within this MDP framework. The algorithms utilized for model training are also elaborated upon;
- (3)
- We propose a graph embedding method that employs disjunctive graphs to represent the state information of the panel block assembly line. This approach directly extracts scheduling features from the disjunctive graph, marking the first instance of combining DRL with disjunctive graphs to address the scheduling problem in shipbuilding’s panel block assembly lines.
2. Literature Review
2.1. Solving Scheduling Problem via Heuristics
2.2. Solving Scheduling Problem via Metaheuristics
2.3. Solving Scheduling Problem via Reinforcement Learning
2.4. Research Gap
3. Preliminaries
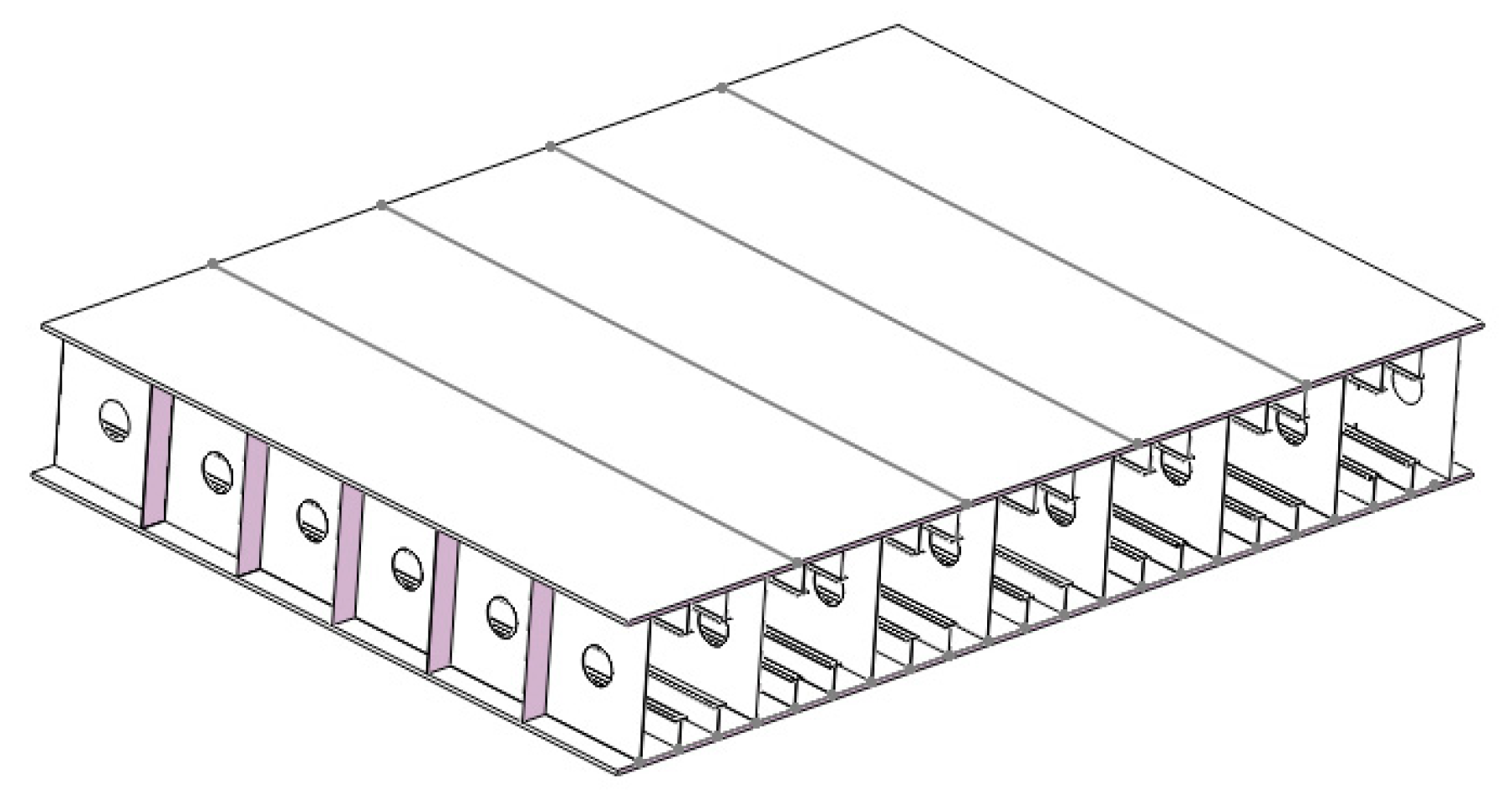
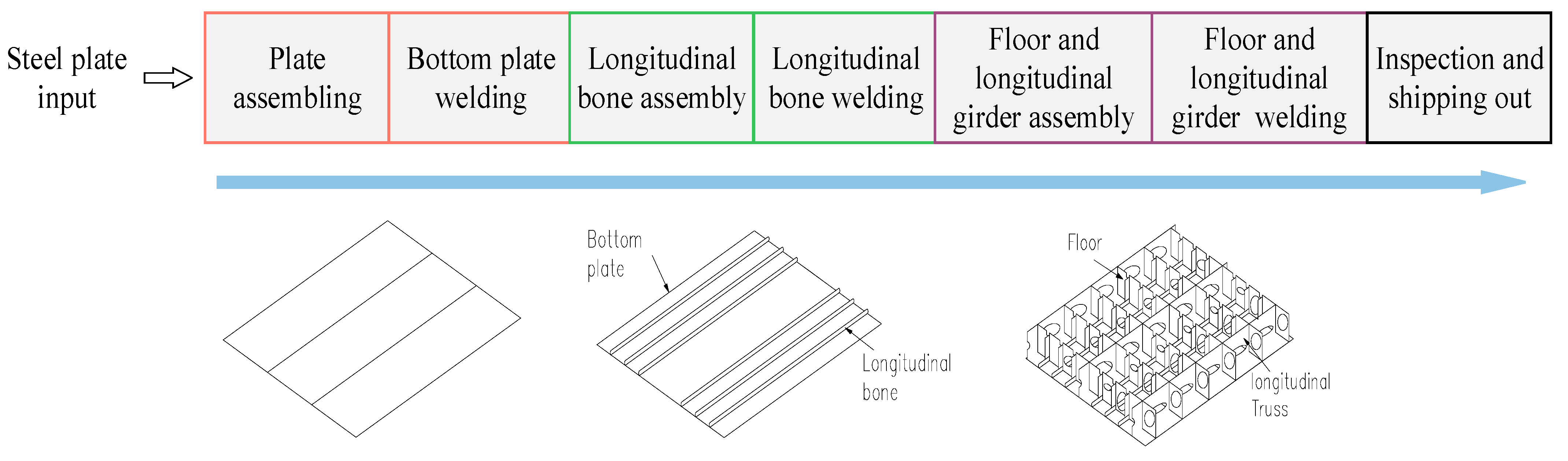
3.1. Description of Scheduling Problem
3.1.1. Symbolic Representation
3.1.2. Problem Description
3.2. Reinforcement Learning
3.3. Disjunctive Graph
4. Methods
4.1. MDP Model
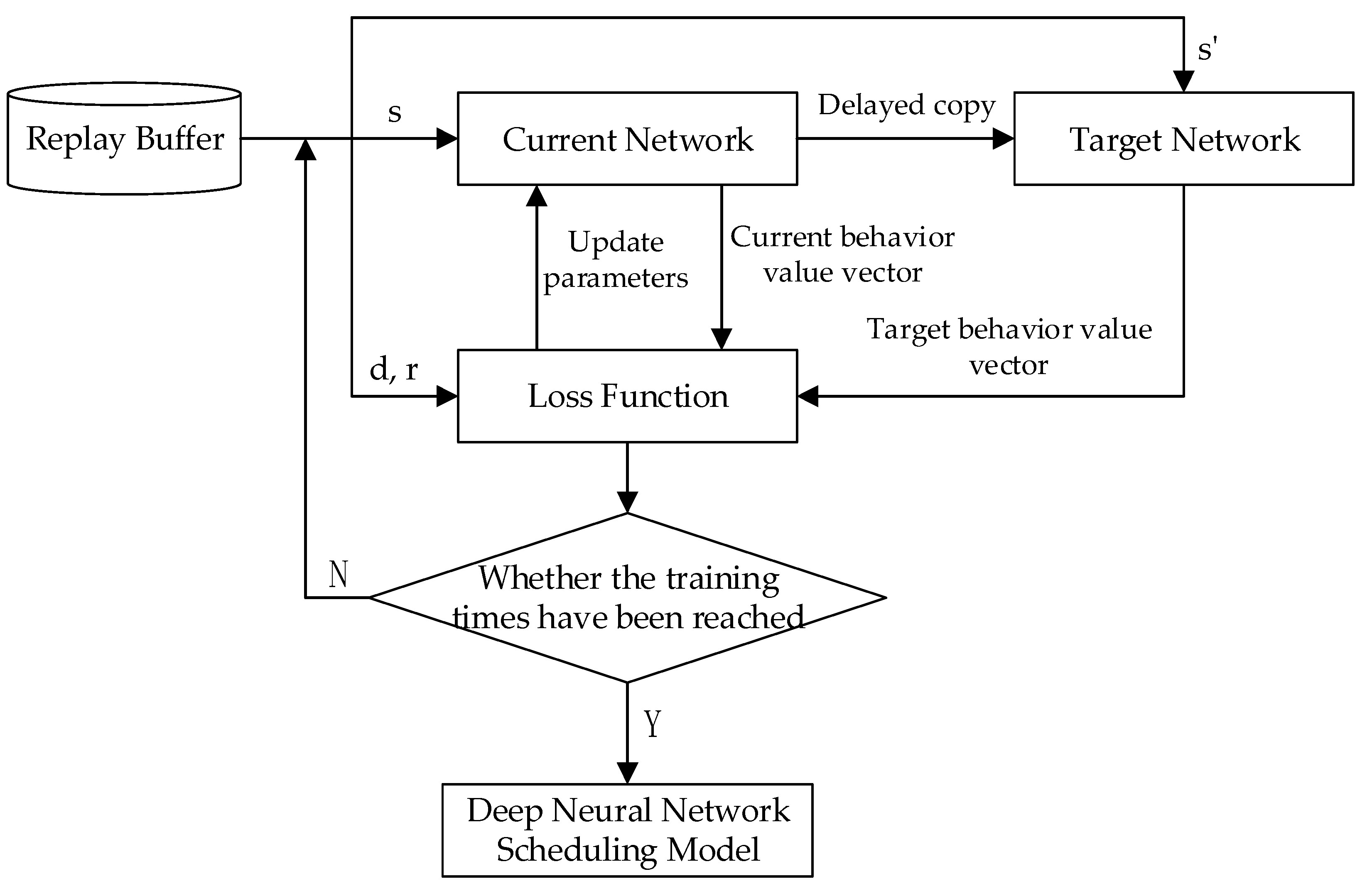
4.2. Learning Algorithm
| Algorithm 1. PPO Algorithm for training our model |
| Input: update epoch k; PPO steps M; number of actors to compute reward and perform update N; actor network ; behavior actor network trainable parameters of actor network ; trainable parameters of behavior actor network critic network ; trainable parameters of critic network ; clipping ratio ; policy loss coefficient ; value function loss coefficient ; entropy loss coefficient 1 Initialization: initialize parameter sets of , and ; 2 for m = 1, , M, do; 3 Pick N independent scheduling instances from distribution D; 4 for n=1, N, do; 5 for t=0,1,2,, do 6 sample based on ; 7 Receive reward and next state ; 8 = ; = 9 if is terminal then 10 break; 11 end 12 end 13 14 15 16 17 end 18 for k = 1, 2, , K do; 19 update actor and critic parameters by Adam optimizer 20 21 end 22 23 end 24 Output: Trained parameter set of |
5. Computational Experiment
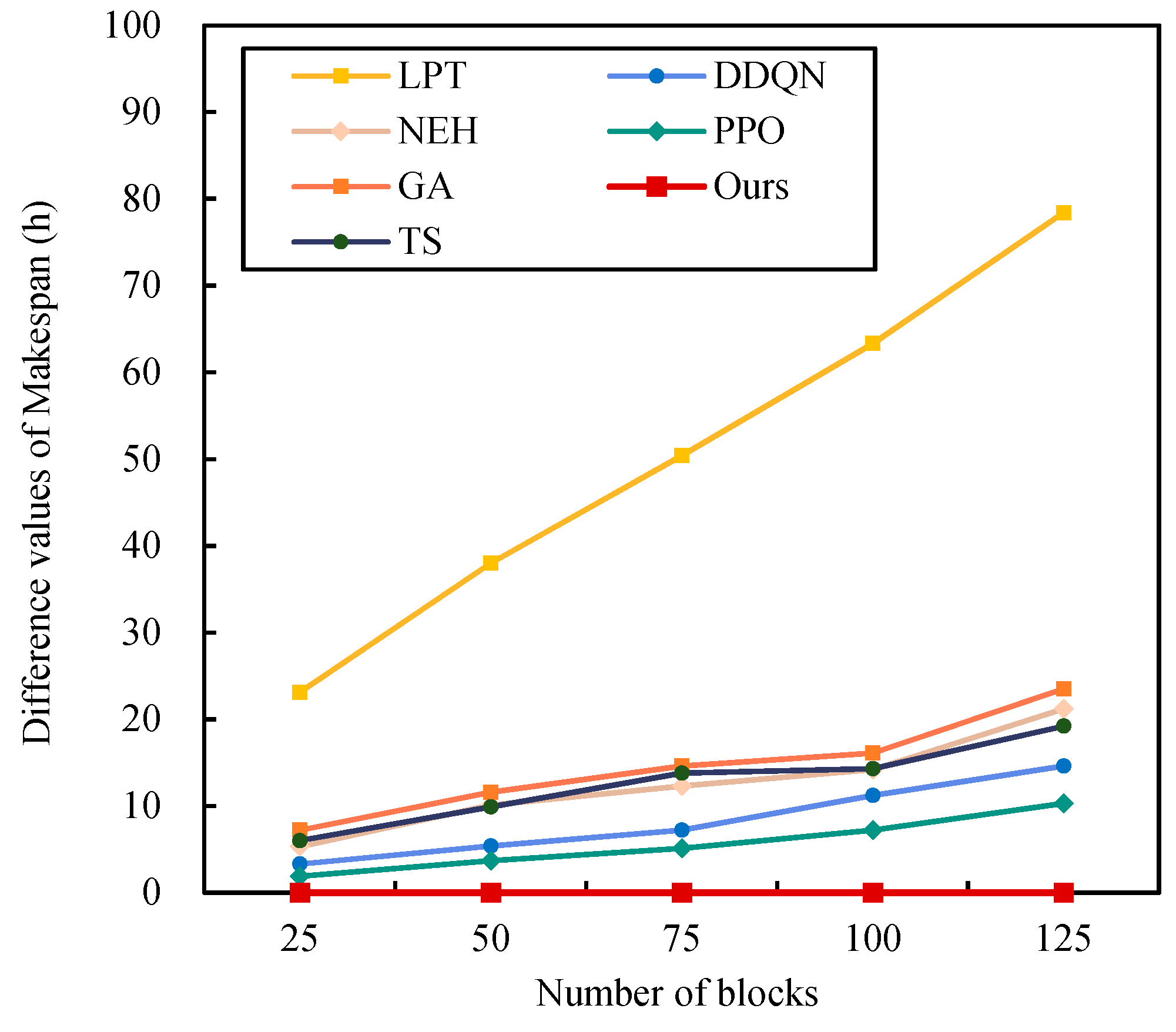
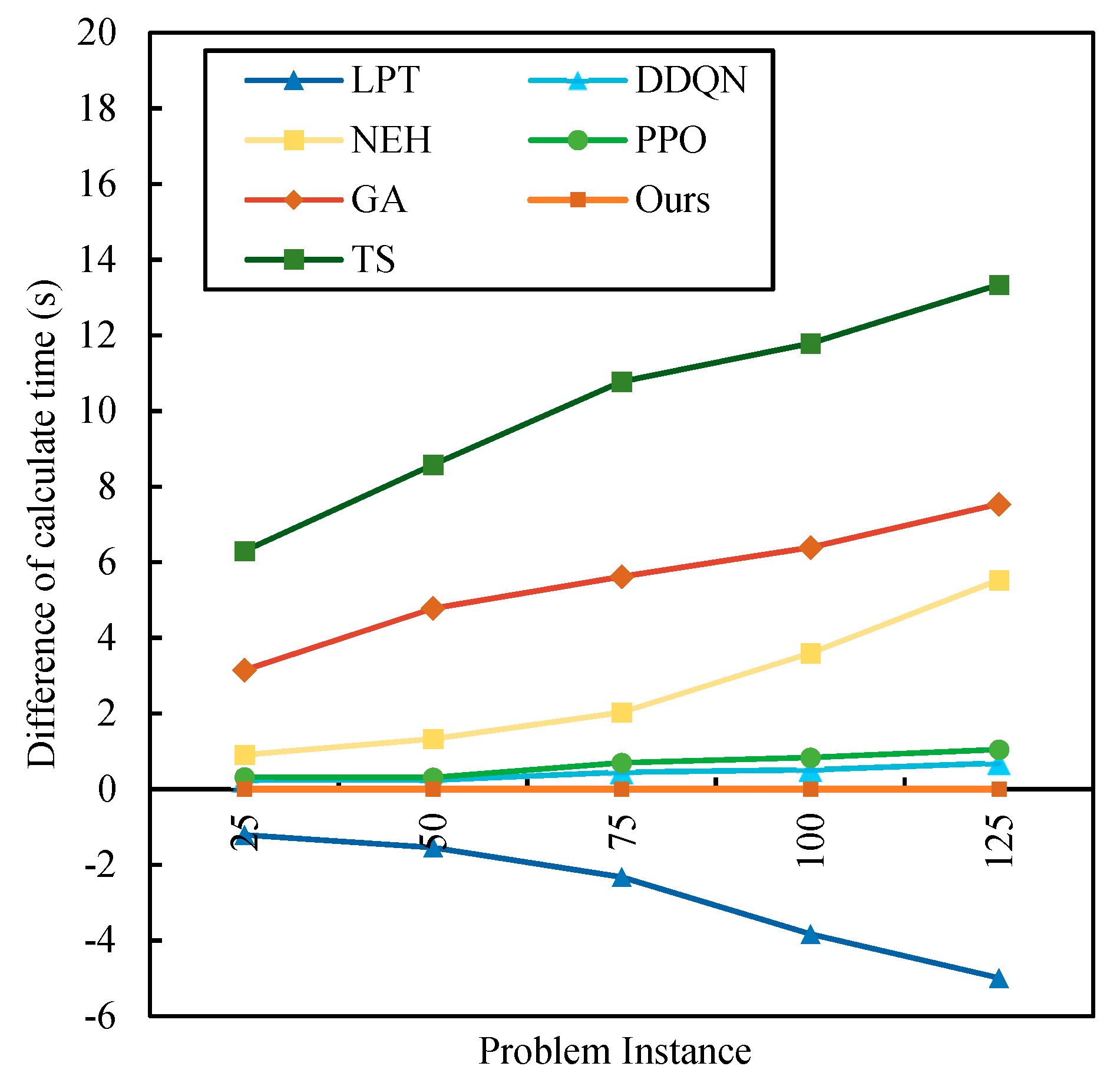
5.1. Computational Results of the Panel Block Assembly Line
5.2. Computational Results of Benchmark Instances
5.3. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. LPT
Appendix A.2. NEH
Appendix A.3. Genetic Algorithm (GA)
Appendix A.4. Tabu Search Algorithm (TS)
Appendix A.5. DDQN
Appendix A.6. PPO
References
- Shao, K.; Zhu, Y.H.; Zhao, D.B. StarCraft micromanagement with reinforcement learning and curriculum transfer learning. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 73–84. [Google Scholar] [CrossRef]
- Guo, H.N.; Li, S.H.; Qi, K.Y.; Guo, Y.; Xu, Z.W. Learning automata based competition scheme to train deep neural networks. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 151–158. [Google Scholar] [CrossRef]
- Cai, Q.; Jing, X.; Chen, Y.; Liu, J.; Kang, C.; Li, B. Online Monitoring of Ship Block Construction Equipment Based on the Internet of Things and Public Cloud: Take the Intelligent Tire Frame as an Example. KSII Trans. Internet Inf. Syst. 2021, 15, 3970–3990. [Google Scholar]
- Salazar-Domínguez, C.M.; Hernández-Hernández, j.; Rosas-Huerta, E.D.; Iturbe-Rosas, G.E.; Herrera-May, A.L. Structural Analysis of a Barge Midship Section Considering the Still Water and Wave Load Effects. J. Mar. Sci. Eng. 2021, 9, 99. [Google Scholar] [CrossRef]
- Hoosen, M.; Chalfant, J.S. Subdivision Blocks and Component Placement in Early-Stage Ship Design. In Proceedings of the 2021 IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA, 4–6 August 2021. [Google Scholar]
- Son, Y.B.; Nam, J.H. Creation of hierarchical structure for computerized ship block model based on interconnection relationship of structural members and shipyard environment. Int. J. Nav. Arch. Ocean 2022, 14, 100455. [Google Scholar] [CrossRef]
- Zheng, Y.Q.; Mo, G.F.; Zhang, J. Blocking flowline scheduling of panel block in shipbuilding. Comput. Integr. Manuf. Syst. 2016, 22, 2305–2314. [Google Scholar]
- Woo, J.H.; Oh, D. Development of simulation framework for shipbuilding. Int. J. Comput. Integ. M 2018, 31, 210–227. [Google Scholar] [CrossRef]
- Lee, Y.G.; Ju, S.H.; Woo, J.H. Simulation-based planning system for shipbuilding. Int. J. Comput. Integr. Manuf. 2020, 33, 626–641. [Google Scholar] [CrossRef]
- Kwak, D.H.; Woo, J.H.; Park, J.G. Analysis of master plan and procurement plan of shipbuilding based on queuing theory with variability. J. Korean Inst. Ind. Eng. 2020, 46, 673–682. [Google Scholar]
- Yang, Z.; Liu, C. A hybrid multi-objective gray wolf optimization algorithm for a fuzzy blocking flow shop scheduling problem. Adv. Mech. Eng. 2018, 10, 2072045641. [Google Scholar] [CrossRef]
- Ko, D. A Study on the Saving Method of Plate Jigs in Hull Block Butt Welding. IOP conference series. Mater. Sci. Eng. 2017, 269, 12089. [Google Scholar]
- Kafali, M.; Aydin, N.; Genç, Y.; Çelebi, U.B. A two-stage stochastic model for workforce capacity requirement in shipbuilding. J. Mar. Eng. Technol. 2022, 21, 146–158. [Google Scholar] [CrossRef]
- Guo, H.; Li, J.; Yang, B.; Mao, X.; Zhou, Q. Green scheduling optimization of ship plane block flow line considering carbon emission and noise. Comput. Ind. Eng. 2020, 148, 106680. [Google Scholar] [CrossRef]
- Kolich, D.; Storch, R.L.; Fafandjel, N. Lean Methodology to Transform Shipbuilding Panel Assembly. J. Ship Prod. Des. 2017, 33, 317–326. [Google Scholar] [CrossRef]
- Luo, S. Dynamic Scheduling for Flexible Job Shop with New Job Insertions by Deep Reinforcement Learning. Appl. Soft. Comput. 2020, 91, 106208. [Google Scholar] [CrossRef]
- Ohn, S.; Filip, W.; Prafulla, D.; Alec, R.; Oleg, K. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Fernandez-Viagas, V.; Rubén, R.; Jose, M.F. A New Vision of Approximate Methods for the Permutation Flowshop to Minimise Makespan: State of the Art and Computational Evaluation. Eur. J. Oper. Res. 2017, 257, 707–721. [Google Scholar] [CrossRef]
- Hall, N.G.; Sriskandarajah, C. A survey of machine scheduling problems with blocking and no-wait in process. Oper. Res. 1996, 44, 510–525. [Google Scholar] [CrossRef]
- Oliveira, A.; Gordo, J.M. Lean Tools Applied to a Shipbuilding Panel Line Assembling Process. Brodogradnja 2018, 69, 53–64. [Google Scholar] [CrossRef]
- Ryu, H.; Kang, S.; Lee, K. Numerical Analysis and Experiments of Butt Welding Deformations for Panel Block Assembly. Appl. Sci. 2020, 10, 1669. [Google Scholar] [CrossRef]
- Johnson, S.M. Optimal two- and three-stage production schedules with setup times included. Nav. Res. Logist. Q. 1954, 1, 61–67. [Google Scholar] [CrossRef]
- Palmer, D.S. Sequencing Jobs Through a Multi-Stage Process in the Minimum Total Time—A Quick Method of Obtaining a Near Optimum. J. Oper. Res. Soc. 2017, 16, 101–107. [Google Scholar] [CrossRef]
- Gupta, J. A Functional Heuristic Algorithm for the Flowshop Scheduling Problem. J. Oper. Res. Soc. 1971, 22, 39–47. [Google Scholar] [CrossRef]
- Singh, H.; Oberoi, J.S.; Singh, D. The taxonomy of dynamic multi-objective optimization of heuristics algorithms in flow shop scheduling problems: A systematic literature review. Int. J. Ind. Eng.-Theory Appl. Pract. 2020, 27, 429–462. [Google Scholar]
- Framinan, J.M.; Leisten, J. A review and classification of heuristics for permutation flow-shop scheduling with makespan objective. J. Oper. Res. Soc. 2004, 55, 1243–1255. [Google Scholar] [CrossRef]
- Hsu, C.Y.; Chann, C.P.; Hui, C.M. A link age miningin block-based evolutionary algorithm for permutation flowshop scheduling problem. Comput. Ind. Eng. 2015, 83, 159–171. [Google Scholar] [CrossRef]
- Lin, Q.; Gao, L.; Li, X.; Zhang, C. A hybrid back tracking search algorithm for permutation flow-shop scheduling problem. Comput. Ind. Eng. 2015, 85, 437–446. [Google Scholar] [CrossRef]
- Karabulut, K. A hybrid iterated greedy algorithm for total tardiness minimization in permutation flowshops. Comput. Ind. Eng. 2016, 98, 300–307. [Google Scholar] [CrossRef]
- Deb, S.; Tian, Z.; Fong, S.; Tang, R.; Wong, R.; Dey, N. Solving permutation flow-shop scheduling problem by rhinoceros search algorithm. Soft Comput. 2018, 22, 6025–6034. [Google Scholar] [CrossRef]
- De Fátima, M.M.; Ribeiro, M.H.D.M.; Silva R, G. Discrete differential evolution metaheuristics for permutation flow shop scheduling problems. Comput. Ind. Eng. 2022, 166, 107956. [Google Scholar]
- Liu, C.L.; Chang, C.C.; Tseng, C.J. Actor-critic deep reinforcement learning for solving job shop scheduling problems. IEEE Access 2020, 8, 71752–71762. [Google Scholar] [CrossRef]
- Waschneck, B.; Reichstaller, A.; Belzner, L. Optimization of global production scheduling with deep reinforcement learning. Procedia CIRP 2018, 72, 1264–1269. [Google Scholar] [CrossRef]
- Lin, C.C.; Deng, D.J.; Chih, Y.L. Smart manufacturing scheduling with edge computing using multiclass deep Q network. IEEE Trans. Ind. Inform. 2019, 15, 4276–4284. [Google Scholar] [CrossRef]
- Park, J.; Chun, J.; Kim, S.H. Learning to schedule job-shop problems: Representation and policy learning using graph neural network and reinforcement learning. Int. J. Prod. Res. 2021, 59, 3360–3377. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Z.; Wang, J. Intelligent decision-making of scheduling for dynamic permutation flowshop via deep reinforcement learning. Sensors 2021, 21, 1019. [Google Scholar] [CrossRef]
- Pan, R.; Dong, X.; Han, S. Solving permutation flowshop problem with deep reinforcement learning. In Proceedings of the Prognostics and Health Management Conference (PHM-Besançon), Besançon, France, 4–7 May 2020; pp. 349–353. [Google Scholar]
- Yang, S.L.; Xu, Z.G. The Distributed Assembly Permutation Flow shop Scheduling Problem with Flexible Assembly and Batch Delivery. Int. J. Prod. Res. 2021, 59, 4053–4071. [Google Scholar] [CrossRef]
- Ramírez, J.; Yu, W.; Perrusquía, A. Model-free reinforcement learning from expert demonstrations: A survey. Artifcial Intell. Rev. 2022, 55, 3213–3241. [Google Scholar] [CrossRef]
- Błażewicz, J.; Pesch, E.; Sterna, M. The disjunctive graph machine representation of the job shop scheduling problem. Eur. J. Oper. Res. 2000, 127, 317–331. [Google Scholar] [CrossRef]
- Chen, R.; Li, W.; Yang, H. A Deep Reinforcement Learning Framework Based on an Attention Mechanism and Disjunctive Graph Embedding for the Job Shop Scheduling Problem. IEEE Trans. Ind. Inform. 2022, 19, 1322–1331. [Google Scholar] [CrossRef]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Zhou, J.; Cui, G.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. arXiv 2018, arXiv:1812.08434. [Google Scholar] [CrossRef]
- Lv, M.; Hong, Z.; Chen, L.; Chen, T.; Zhu, T.; Ji, S. Temporal multi-graph convolutional network for traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3337–3348. [Google Scholar] [CrossRef]
- Taillard, E.D. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]



| Notation | Description |
|---|---|
| n | The number of blocks |
| m | The number of workstations |
| B | The set of blocks |
| S | The set of workstations |
| i | The number of blocks in set B |
| j | The process number of block i |
| The i-th block | |
| The j-th workstation | |
| The operation of block on workstation | |
| The processing time of block on workstation | |
| The processing sequence of blocks | |
| The maximum completion time | |
| The completion time of block on workstation |
| Workstation | Block Number | |||||
|---|---|---|---|---|---|---|
| Block1 | Block2 | Block3 | Block4 | Block5 | Block6 | |
| Plate assembling | 2.7 h | 3.0 h | 3.0 h | 3.0 h | 3.0 h | 2.7 h |
| Bottom plate welding | 4.6 h | 4.8 h | 4.8 h | 4.5 h | 4.5 h | 4.6 h |
| Longitudinal bone assembly | 2.6 h | 2.4 h | 2.4 h | 2.5 h | 2.5 h | 2.6 h |
| Longitudinal bone welding | 3.3 h | 3.0 h | 3.0 h | 3.4 h | 3.4 h | 3.3 h |
| Ribbed longitudinal Truss assembly | 3.8 h | 3.5 h | 3.5 h | 3.6 h | 3.6 h | 3.8 h |
| Ribbed longitudinal Truss welding | 5.8 h | 5.4 h | 5.4 h | 5.8 h | 5.8 h | 5.8 h |
| Inspection and shipping out | 2.5 h | 3.2 h | 3.2 h | 2.5 h | 2.5 h | 2.5 h |
| Hyperparameter | Value |
|---|---|
| Batch size | 128 |
| Learning rate | |
| Learning rate decay factor | 0.98 |
| Learning rate decay step | 3000 |
| Optimizer | Adam |
| The clipping parameter | 0.2 |
| The policy loss coefficient | 2 |
| Number of Blocks | Heuristic | Metaheuristic | Reinforcement Learning | Ours | |||
|---|---|---|---|---|---|---|---|
| LPT | NEH | GA | TS | DDQN | PPO | ||
| 25 | 180.5 | 162.7 | 164.6 | 163.4 | 160.7 | 159.3 | 157.4 |
| 50 | 327.7 | 299.8 | 301.3 | 299.6 | 295.1 | 293.4 | 289.7 |
| 75 | 457.5 | 419.4 | 421.7 | 420.9 | 414.3 | 412.2 | 407.1 |
| 100 | 613.7 | 564.6 | 566.5 | 564.7 | 561.6 | 557.6 | 550.4 |
| 125 | 753.3 | 696.1 | 698.4 | 694.1 | 689.5 | 685.2 | 674.9 |
| Number of Blocks | Heuristic | Metaheuristic | Reinforcement Learning | Ours | |||
|---|---|---|---|---|---|---|---|
| LPT | NEH | GA | TS | DDQN | PPO | ||
| 25 | 23.1 | 5.3 | 7.2 | 6 | 3.3 | 1.9 | 0 |
| 50 | 38 | 10.1 | 11.6 | 9.9 | 5.4 | 3.7 | 0 |
| 75 | 50.4 | 12.3 | 14.6 | 13.8 | 7.2 | 5.1 | 0 |
| 100 | 63.3 | 14.2 | 16.1 | 14.3 | 11.2 | 7.2 | 0 |
| 125 | 78.4 | 21.2 | 23.5 | 19.2 | 14.6 | 10.3 | 0 |
| Number of Blocks | Heuristic | Metaheuristic | Reinforcement Learning | Ours | |||
|---|---|---|---|---|---|---|---|
| LPT | NEH | GA | TS | DDQN | PPO | ||
| 25 | 0.00 | 2.12 | 4.36 | 7.51 | 1.45 | 1.53 | 1.21 |
| 50 | 0.00 | 2.87 | 6.32 | 10.12 | 1.78 | 1.85 | 1.54 |
| 75 | 0.00 | 4.35 | 7.94 | 13.10 | 2.77 | 3.02 | 2.32 |
| 100 | 0.00 | 7.43 | 10.22 | 15.62 | 4.34 | 4.67 | 3.83 |
| 125 | 0.00 | 10.52 | 12.53 | 18.33 | 5.68 | 6.04 | 4.99 |
| Number of Blocks | Heuristic | Metaheuristic | Reinforcement Learning | Ours | |||
|---|---|---|---|---|---|---|---|
| LPT | NEH | GA | TS | DDQN | PPO | ||
| 25 | −1.21 | 0.91 | 3.15 | 6.30 | 0.24 | 0.32 | 0 |
| 50 | −1.54 | 1.33 | 4.78 | 8.58 | 0.24 | 0.31 | 0 |
| 75 | −2.32 | 2.03 | 5.62 | 10.78 | 0.45 | 0.70 | 0 |
| 100 | −3.83 | 3.60 | 6.39 | 11.79 | 0.51 | 0.84 | 0 |
| 125 | −4.99 | 5.53 | 7.54 | 13.34 | 0.69 | 1.05 | 0 |
| Problem Instance | Size | Heuristic | Metaheuristic | Reinforcement Learning | Ours | |||
|---|---|---|---|---|---|---|---|---|
| LPT | NEH | GA | TS | DDQN | PPO | |||
| Ta010 | 20 × 5 | 1213.4 | 1108 | 1108 | 1108 | 1108 | 1108 | 1108 |
| Ta020 | 20 × 10 | 1701 | 1689.7 | 1693 | 1691.3 | 1657.7 | 1646.3 | 1640.2 |
| Ta030 | 20 × 20 | 2305.2 | 2286.1 | 2278.4 | 2259.8 | 2263.0 | 2256.5 | 2247.4 |
| Ta040 | 50 × 5 | 2901.6 | 2884.5 | 2881.6 | 2875 | 2879.1 | 2874.8 | 2861.8 |
| Ta050 | 50 × 10 | 3198 | 3175.4 | 3171.5 | 3162.6 | 3168.3 | 3159.5 | 3145.1 |
| Ta060 | 50 × 20 | 3971.6 | 3951.8 | 3954 | 3946.5 | 3931.4 | 3903.4 | 3887.4 |
| Ta070 | 100 × 5 | 5560 | 5483.2 | 5479.1 | 5451.5 | 5452.5 | 5429.7 | 5396.2 |
| Ta080 | 100 × 10 | 6089.7 | 6004 | 5996.4 | 5989.1 | 5983.0 | 5971.8 | 5949 |
| Ta090 | 100 × 20 | 6705.9 | 6670.8 | 6658.5 | 6649.4 | 6652.3 | 6649.4 | 6627 |
| Problem Instance | Size | Heuristic | Metaheuristic | Reinforcement Learning | Ours | |||
|---|---|---|---|---|---|---|---|---|
| LPT | NEH | GA | TS | DDQN | PPO | |||
| Ta010 | 20 × 5 | 0 | 1.73 | 3.75 | 7.14 | 0.70 | 0.79 | 0.72 |
| Ta020 | 20 × 10 | 0 | 2.14 | 4.26 | 7.58 | 1.19 | 1.35 | 1.14 |
| Ta030 | 20 × 20 | 0 | 2.47 | 5.74 | 9.77 | 1.39 | 1.52 | 1.31 |
| Ta040 | 50 × 5 | 0 | 2.61 | 6.22 | 10.26 | 1.41 | 1.58 | 1.35 |
| Ta050 | 50 × 10 | 0 | 4.21 | 7.69 | 12.91 | 2.64 | 2.95 | 2.38 |
| Ta060 | 50 × 20 | 0 | 6.72 | 8.94 | 14.59 | 4.62 | 5.35 | 3.42 |
| Ta070 | 100 × 5 | 0 | 7.33 | 9.59 | 15.14 | 5.44 | 6.28 | 3.74 |
| Ta080 | 100 × 10 | 0 | 10.87 | 12.94 | 17.93 | 7.65 | 9.32 | 4.47 |
| Ta090 | 100 × 20 | 0 | 12.95 | 15.47 | 19.66 | 8.60 | 10.67 | 6.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Luo, L.; He, Y.; Fan, Z.; Ji, S. Solving Panel Block Assembly Line Scheduling Problem via a Novel Deep Reinforcement Learning Approach. Appl. Sci. 2023, 13, 8483. https://doi.org/10.3390/app13148483
Zhou T, Luo L, He Y, Fan Z, Ji S. Solving Panel Block Assembly Line Scheduling Problem via a Novel Deep Reinforcement Learning Approach. Applied Sciences. 2023; 13(14):8483. https://doi.org/10.3390/app13148483
Chicago/Turabian StyleZhou, Tao, Liang Luo, Yuanxin He, Zhiwei Fan, and Shengchen Ji. 2023. "Solving Panel Block Assembly Line Scheduling Problem via a Novel Deep Reinforcement Learning Approach" Applied Sciences 13, no. 14: 8483. https://doi.org/10.3390/app13148483
APA StyleZhou, T., Luo, L., He, Y., Fan, Z., & Ji, S. (2023). Solving Panel Block Assembly Line Scheduling Problem via a Novel Deep Reinforcement Learning Approach. Applied Sciences, 13(14), 8483. https://doi.org/10.3390/app13148483





