Estimation of Methane Gas Production in Turkey Using Machine Learning Methods

Abstract

Methane gas emission into the atmosphere is rising due to the use of fossil-based resources in post-industrial energy use, as well as the increase in food demand and organic wastes that comes with an increasing human population. For this reason, methane gas, which is among the greenhouse gases, is seen as an important cause of climate change along with carbon dioxide. The aim of this study was to predict, using machine learning, the emission of methane gas, which has a greater effect on the warming of the atmosphere than other greenhouse gases. Methane gas estimation in Turkey was carried out using machine learning methods. The R² metric was calculated as logistic regression (LR) 94.9%, artificial neural networks (ANNs) 93.6%, and support vector regression (SVR) 92.3%. All three machine learning methods used in the study were close to ideal statistical criteria. LR had the least error and highest prediction success, followed by ANNs and then SVR. The models provided successful results, which will be useful in the formulation of policies in terms of animal production (especially cattle production) and the disposal of organic human wastes, which are thought to be the main causes of methane gas emission.

1. Introduction

In order to ensure the continuity of living things in the world, there must be suitable climatic conditions and sufficient water resources. Although the world’s climate has always been in a state of change, this change gained rapid momentum in today’s world due to the activities of human beings, especially after the Industrial Revolution. Although its effects and consequences vary from region to region, the threat of climate change concerns all humanity. The first international step in this context is known as the United Nations Framework Convention on Climate Change, formed in 1992 [1,2,3,4].

One of the most important factors affecting climate change is the increase in emissions of natural greenhouse gases such as methane (CH₄), carbon dioxide (CO₂), and diazo monoxide (N₂O), which cannot be prevented due to continuing human activities. In order to reduce global warming by 1.5°, an emission reduction of 45 per cent is required. From 2022 to 2023, this rate was found to be 1%. It was determined that the increase in methane gas emissions is very high, and 52 of 198 countries have not reported this under the United Nations Framework Convention on Climate Change [5].

When the literature was examined, many studies were found to focus on greenhouse gas and carbon dioxide emissions. However, methane gas, which plays a major role in global warming, is less well studied. In order to reach the target reduction of 1.5° in 2050, methane gas emissions, which are 27 times more effective than carbon dioxide in causing global warming, must be urgently taken under control [6,7].

The motivation of this study was to provide a guiding scientific approach in the formulation of policies necessary to control methane gas production by estimating its production. For this purpose, Turkey, which has both agricultural and industrial activities, and has not been able to reduce the use of coal in energy production to the desired level, was selected as a sample country for the study. The data set covering the years 1990–2020 was used in the study. When designing the model, the variables affecting the emission of methane gas, and the contributions of these variables to methane emission, were formed around three main categories: agricultural activities, fossil energy sources, and wastes. In the architecture of the model, the general variables of population and gross domestic product, which are considered highly influential to the above three categories, were added to the model. With these models, created using machine learning methods, Turkey’s methane gas production was predicted with an average success rate of 93.6%. This study will create a vision for countries to reduce emissions by predicting methane gas. It is also expected to be a guide in the road map that Turkey will follow for emission reduction at COP 28, to be held in Dubai on 30 November 2023. The study is expected to contribute to the literature due to the lack of studies on methane gas.

In the first part of the study, the importance and purpose of the research are emphasized. In the second part, similar studies in the literature are reviewed. Next, the characteristics of the data set and methodology are given and the design and results of the models are discussed. The results of the models are analyzed according to three different statistical methods and compared graphically. Finally, the contribution of the study’s results to the literature are described.

When the literature was examined, it was seen that most studies were situated within the framework of greenhouse gas and carbon dioxide emissions. By considering the effect of methane gas emissions on global warming, this study identified a gap in the literature. Table 1 shows the systematic literature review.

Table 1. Systematic literature review.

Author Details	Topic	Input/Output Variables	Machine Learning Technique	Conclusion
(Oertel et al., 2016) [8]	Greenhouse gas emission and parameters affecting the emission process	Input: Literature review was conducted. Output: According to the result of the literature review, it was revealed that 300 mg CO2 leads to a global annual net soil emission of ≥350 Pg CO2e.	The study is based on a literature review.	The author discussed the parameters related to soil emission (by reviewing the literature).
(Garip and Oktay, 2018) [9]	Estimation of carbon dioxide emissions	Input: Oil, natural gas, coal, hydropower, renewable energy. Output: In the CO2 forecasts between 2004 and 2014, it was observed that the forecasts were successful in the first years and the success in the forecasts decreased in the last two years.	Random Forest Regression Support Vector Regression	It was observed that support vector machines gave better results than the random forest regression method.
(Baareh, 2013) [10]	Estimation of carbon dioxide emissions	Inputs: Oil, natural gas, coal, primary energy consumption. Output: Data from 1982 to 2000 were used and found to have high predictive ability.	Artificial neural network	The artificial neural network model was found to have high forecasting ability.
(Kalra et al., 2020) [11]	Measurement of the relationship between global temperature and greenhouse gas concentration	Input: Carbon dioxide, nitrous oxide, methane. Output: In the 65 years of global temperature data between 1850 and 2016, they found that CO2 increased to the maximum in the global temperature increase.	Linear regression Decision tree regression Random forest regression Artificial neural networks	It was observed that the best performance was obtained from the artificial neural network method.
(Hamrani et al., 2020) [12]	Estimation of greenhouse gas emissions	Input: Carbon dioxide and nitrous oxide. Output: In the 5-year period from 2012 to 2017, the LSTM model was found to give the most accurate performance.	Classical regression Shallow learning Deep learning	It was observed that the best performance was obtained from the LSTM model.
(Saha et al., 2021) [13]	Estimation of agricultural nitrous oxide emissions	Input: Nitrous oxide. Output: 1576 daily observations over a 6-year period from 2002 to 2014 were used. The random forest regression model was able to predict nitrous oxide data in two different fields.	Random forest regression	It was found that the random forest regression model can improve nitrous oxide flux predictions with limited data.
(Gholami et al., 2020) [14]	Using machine learning for dust emission sensitization in Iran	Inputs: Land use, lithology, digital elevation, vegetation cover, wind speed, rainfall, bulk density, organic matter, electrical conductivity, texture, soil texture, exchangeable sodium content and calcium carbonate content, soil property. Output: The analysis of these 14 inputs revealed that there was no multicollinearity between the inputs. CForest was found to make the best prediction.	XGBoost Cubist BMARS ANFIS Cforest Elasticnet	It was observed that CForest algorithm made the best prediction.
(Şişeci Çeşmeli and Pençe, 2020) [15]	Greenhouse gas estimation for Turkey using machine learning algorithms	Input: Greenhouse gases data set for 1967–2017 (as time series). Output: Tested with time series and 10-fold cross-validation, the LTSM model was the most successful and estimated 15.67 billion tons of greenhouse gas emissions prospectively.	Poisson regression Linear regression Artificial neural networks Adaptive network based fuzzy inference system (ANFIS) LSTM	It was observed that LSTM made the best estimation.
(Gümüştekin Aydın and Aydoğdu, 2022) [16]	Carbon dioxide emission estimation of Turkey and EU countries using machine learning algorithms	Input: Consumption of “total population, solid fossil fuel, natural gas, oil, solar energy, biogas, primary solid biofuel, renewable municipal waste, geothermal energy and hydropower” from 2000 to 2019. Output: It was observed that the amount of CO2 decreased in EU countries and the amount of CO2 increased exponentially in Turkey.	Support vector machines Decision tree modelling Artificial neural networks	It was seen that the support vector machines method made the best prediction.
(Abbasi et al., 2021) [17]	Estimation of carbon dioxide emissions through machine learning algorithms	Inputs: Soil moisture, temperature, organic matter, total carbon, nitrogen, air temperature, solar radiation, rainfall, pan evaporation. Output: Soil temperature, organic matter, carbon, nitrogen, air temperature, radiation and pan evaporation were found to be highly correlated parameters.	Support vector machines Random forest regression Least absolute shrinkage selection Feed forward neural network Radial basis functional neural network Extreme learning machine	It was observed that the random forest regression method made the best prediction.
(Kerimov and Chernyshev, 2022) [18]	Estimation of greenhouse gas emissions through machine learning algorithms	A research study was conducted to define the model structure.	Decision tree Random forest regression Deep neural networks	The study compared the advantages and disadvantages of the techniques.
(Saleh et al., 2016) [19]	Estimation of carbon dioxide emissions using support vector machines	Input: Electric power and coal Output: The support vector machines method was used by trial and error. The results showed that the RMSE value was 0.004, but the aim was to obtain a value lower than this.	Support vector machines	In the study, it was concluded that the RMSE value was higher than expected. It was predicted that a lower value would lead to a higher prediction and a higher prediction would provide information about CO2 emission.
(Jiang et al., 2023) [20]	Estimation of greenhouse gas emissions in paddy fields in China through machine learning algorithms	Input: 3-year data set from 2009 to 2011. Output: The stacking model improved R2 and reduced RMSE.	Linear regression Random forest regression Nearest neighbor regression Gradient boosting regression Stacking group	It was found that the stacking model was the best prediction method, and the linear regression model was the worst prediction method.

2. Materials and Methods

In this study, three different machine learning methods, logistic regression, artificial neural networks, and support vector regression, were used to predict methane gas production in Turkey. Models with eleven independent variables were designed to predict the dependent variable methane gas. The data were reduced to 0–1 using the min-max normalization technique. Cross-validation was used to increase the success of the study. R², MAE, and MSE statistical metrics were used to determine the success and error of the models.

2.1. Data Set

Turkey, which has both agricultural and industrial activities and cannot reduce coal use in energy production to the desired level, was selected as a sample country. Data covering the annual period between 1990 and 2020 were used. The data set was created from the data obtained from the Turkish Statistical Institute (TUIK) database. The data set consisted of 372 data in total. While designing the model in the study, the variables affecting the emission of methane gas and the contribution of these variables to methane emission were formed around three main categories. The first and most important factor influencing methane gas emission is the agricultural activity of a country. The largest methane gas emission resulting from agricultural activities is caused by enteric fermentation. Enteric fermentation is the digestion of food by microorganisms in the digestive system of cattle. As a result of this process, methane gas is formed as a by-product. For this reason, the number of cattle in Turkey was determined as the input variable for red meat production in the model. Another agricultural activity that causes methane gas emissions is paddy cultivation. During the cultivation process of paddy, a large amount of water must be kept on the field surface for a long time. As a result, the organic materials in the soil remain in an oxygen-free environment and cause methane gas emission. Considering this situation in paddy cultivation, the surface area of cultivated paddy fields was added to the model. The last methane gas emission factor, which was accepted as an input variable in the category of agricultural activities, is the burning of biomass in agricultural areas. As a result of this combustion, methane gas is released to the atmosphere from the organic residues in these areas. The size of agricultural surface area and agricultural greenhouse gas emissions were, therefore, included in the model. The second main category of causative factors for methane gas emissions is the production and utilization processes of coal and natural gas, which are fossil energy sources. During the production (including enrichment), storage, and distribution phases of natural gas, methane gas, which is the main component of this gas, is released and causes emissions. At the same time, methane emissions occur during the extraction of coal, another fossil-based fuel (especially in closed underground mines). The share of these two fossil fuels in total energy production was added to the model as a variable. Since these two fossil fuels are used especially in manufacturing and heavy industry, the industrial production index was also added to the model. The third main factor category in the formation of methane gas emission is waste. Especially in landfill areas, where domestic wastes accumulate, there is a high rate of organic waste, which increases methane gas emission. For this reason, greenhouse gas emissions of wastes were also added to the model. The general variables of population and gross domestic product of the country, which are considered to affect all three main categories of emission causes, were also added to the model. The model is shown in Table 2.

Table 2. Input/Output variables.

Output Variable	Input Variables
Methane Gas Emissions (tons)	Agricultural Activities	Number of Cattle (pcs)
		Red Meat Production (tons)
		Agricultural Area (hectare)
		Agricultural Greenhouse Gas Emissions (tons)
		Paddy Production (hectare)
	Energy	Share of Coal in Total Energy Production (%)
		Share of Natural Gas in Total Energy Production (%)
		Industrial Production Index (2003 = 100)
	Waste	Waste Greenhouse Gas Emission (tons)
	General	Population (Number of People)
		GDP ($)

In designing machine learning models, the properties of the independent variables are important. The average, maximum, minimum, and standard deviation (SD) of the data used in the model are given in Table 3.

Table 3. Characteristics of independent variables.

	Average	Maximum	Minimum	SD
Methane gas	48,868,492	63,988,980	40,945,943	7,131,161
Population	68,251,387	83,614,362	53,921,758	9,039,080
GDP	506,221,633,744	957,783,020,853	130,690,172,297	301,529,901,430
Coal share in electricity	30.72	37.20	22.80	4.05
Natural gas share in electricity	33.88	49.70	14.60	12.25
Industrial production index	70.59	144.69	33.13	34.52
Number of cattle	12,580,168	18,157,971	9,901,458	2,275,392
Agricultural area	39,389,935	42,033,000	37,716,000	1,160,451
Agriculture greenhouse gas emission	48,621,599	73,155,372	37,607,794	9,063,809
Waste greenhouse gas emission	15,132,177	17,786,989	11,080,826	2,168,268
Cattle meat production	614,882	1,341,445	303,120	313,293
Paddy production area	82,125	126,419	40,400	29,149

2.2. Machine Learning

Machine learning is basically an algorithm-based approach to obtain information used for data classification and prediction. Machine learning is a scientific field of study used to develop various algorithms, modelling, and techniques to enable computers to learn like humans. It deals with learning methods and the performance of these methods by applying mathematical and statistical operations on data and making inferences from predictions [21,22]. Different mathematical and statistical methods are used to reach the solution. They are divided into two groups, supervised learning and unsupervised learning. Each method should be chosen according to the data set used in machine learning. In supervised learning, data are labelled, classified, and dependent and independent variables are used together. In unsupervised learning, the data set has independent variables but no dependent variables. The data set is unlabeled, and the problem and its results are not known beforehand [23].

2.2.1. Logistic Regression

Logistic regression is used in classification problems to predict the outcomes of categorical dependent variables depending on one or more pre-indicator variables. It is a regression method that helps to make classifications and predictions. Logistic regression analysis is a method that calculates the estimated values of the dependent variable as probabilities and allows classification in accordance with probability rules [24].

There are three basic methods in logistic regression: binary, ordinal, and nominal. Binary logistic regression is a logistic regression analysis with dependent variables containing two possible answers. Ordinal logistic regression is where the dependent variables have an ordinal scale and at least three categories. In nominal logistic regression, the dependent variable has a nominal scale and at least three categories [25].

Odds ratio is used in logistic regression. Odds ratio (OR) is the ratio of the probability of success or occurrence “P” to the probability of failure or non-occurrence “1-P”. Odds values take values within the range (0, +∞). If two separate odds ratios are compared, the odds ratio is obtained. The odds ratio (OR) cannot be negative according to the formula and can be a value between 0 and infinity. When OR = 1, it can be said that the factor of interest (according to the reference) has no effect on increasing or decreasing the probability of the situation under investigation. When OR < 1, the factor of interest (according to the reference) has a decreasing effect on the probability of the situation under investigation. When OR > 1, the factor of interest (according to the reference) has an increasing effect on the probability of the investigated situation [26].

2.2.2. Artificial Neural Networks

Artificial neural networks (ANNs) are a machine learning technique that imitates the learning method of the human brain and performs functions such as learning, remembering, and generating new data from the data obtained using generalization methods. ANNs are synthetic systems that mimic biological neural networks. As in the human biological structure, the aim is to train machines to learn through artificial neural networks and to make decisions with what they have learned. Artificial neural networks can be trained and adapted to be self-organized, self-learning, and self-evaluating to model the learning structure of the human brain [27].

ANNs are mathematical models consisting of many neurons connected to each other by weights. The network consists of input, intermediate (hidden), and output layers. Each input is multiplied by a connection weight. After the neurons weigh the input information, they sum it linearly and the threshold converts this information into output information by processing it in a linear or non-linear function. Other neurons connected to the cell receive this output as input information [28].

ANNs can also be classified structurally. ANNs are categorized into two main groups, feed-forward networks and feedback networks, in terms of the structure of the connections between neurons, depending on the direction of information flow. In feed-forward networks, the flow of information from input to output layer through the intermediate layer proceeds in only one direction. They consist of an input, hidden, and output layer. Information flow on the network proceeds from the input layer to the output layer. In other words, neurons are fed one after the other. In feedback artificial neural networks, the information flows from the output of any neuron to its input. In this type of network structure, feedback connections are in question [29].

2.2.3. Support Vector Regression

Support vector machines (SVMs) are a supervised learning algorithm used for both classification and regression analyses. The algorithm was developed by Vladimir Vapnik [30]. It can be used for continuous dependent variables and categorical variables. It is a supervised learning method that analyzes data, recognizes models and patterns, and is used in classification and regression analysis. Using the training data, it produces a mapping function between input and output. SVMs are high dimensional and distributed. Unlike classical models, the parameters are not predefined, and their number varies according to the training data. By keeping the error value in the training data constant, the confidence interval is minimized [31].

The line dividing the data set into two is called the hyperplane. It creates one or more hyperplanes in multidimensional space. Although it is possible to draw infinite hyperplanes, it is important to determine the optimal hyperplane, in other words, the most appropriate hyperplane. The distance between the hyperplane and the nearest data point in the data set is called the margin. The aim is to select a hyperplane with the highest margin between the hyperplane and a point in the data set. This is to increase the chances of correctly classifying new data. There should be no data points within the separated region [32].

A data set may often contain a set of data that cannot be linearly separated. In this case, in order to classify the data set, it is necessary to pass the data from a two-dimensional view to a three-dimensional view. This process is called the two-dimensional process. It takes a low dimensional input field and transforms it into a higher dimensional field. Maximizing the distances between the nearest data point and the hyperplane helps to determine the correct hyperplane. This is called the margin distance. Another important reason for choosing a high margin hyperplane is robustness. If we choose a low margin hyperplane, the probability of misclassification will be high [33].

3. Results and Discussion

In this study, three different methods, namely, logistic regression, artificial neural network, and support vector regression, were used to predict methane gas in Turkey. The study system is shown in Figure 1.

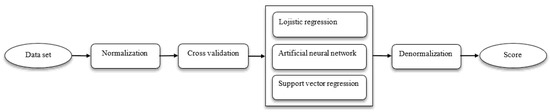
Figure 1. Working system.

Eleven independent variables were used to predict methane gas, which was the dependent variable of the study. The independent variables were Turkey’s population, GDP, coal share in electricity, number of cattle, natural gas share in electricity, industrial production index, agriculture greenhouse gas emission, agricultural area, waste greenhouse gas emission, cattle meat production, and paddy production area. For each independent variable, there were thirty-one annual data between 1990 and 2020.

The min-max method was used for normalization in the study. A linear transformation was performed on the original data. In this normalization, the relationships between the original data values were preserved, and the largest and smallest values in a group of data were considered [34]. All other data were normalized according to these values. This method is a scaling technique where the data are rescaled to be between 0 and 1. The result of having a limited range between 0 and 1 in this process is that it suppresses the effect of outliers and allows for smaller standard deviations [35].

Cross-validation measures the success of the model by creating validation clusters from the data set. Testing with a single data set may not be sufficient. For this reason, it is very important to perform k-fold cross-validation, that is, to create more than one machine learning model from a single data set, to check these models with different test sets, and to average the accuracy of all of them. The data set was clustered according to the k-layer cross-validation applied as training and test data. When ten layers of cross-validation were applied to the data, nine parts were used to develop the model and the remaining one part was used to test the model. This process was repeated 10 times. Each time, it took a different validation set as the test set and used the remaining 9 sets to improve the model [36,37].

The coefficient of determination (R²) is a statistical measure that examines how differences in one variable can be explained by differences in a second variable when predicting the outcome of a particular event. In other words, the coefficient of determination is a statistical metric that measures how well a statistical model predicts an outcome. This coefficient assesses how strong the linear relationship between two variables is. The outcome is represented by the dependent variable of the model. The lowest value of R² is 0 and the highest value is 1. It is the proportion of variance in the dependent variable that is explained by the model [38,39]. The R² is shown in Equation (1):

$${\mathrm{R}}^2=1-\frac{\mathrm{U}\mathrm{n}\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d}\mathrm{V}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{V}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}$$

(1)

The MAE (mean absolute error) is a statistical metric that measures the average magnitude of errors in a set of predictions without considering their direction. It is calculated by taking the absolute difference between the predicted values and the actual values and averaging it across the data set. MAE only measures the magnitude of errors and is not concerned with their direction. The lower the MAE, the higher the accuracy of a model [40,41]. The MAE formula is shown in Equation (2):

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}\sum _{i=1}^n\left|e_i\right|$$

(2)

The MSE (mean squared error) is a model evaluation metric often used in regression models. MSE is equal to the mean squared difference between predicted values and actual values. Since MSE squares the error, it causes large errors to be clearly highlighted. MSE is a metric that ranges from 0 to infinity and values closer to zero are considered better. For MSE values calculated for the same data set, the lower the MSE value, the more accurate the model [42,43]. The MSE is shown in Equation (3):

$$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{n}\sum _{\mathrm{i}=1}^n{e}_i^2$$

(3)

where n is the number of datapoints and e is the error value.

Three different machine learning techniques were used in this study: logistic regression, artificial neural networks, and support vector regression.

In the artificial neural network method, a feedback model consisting of eleven input neurons and one output neuron was developed. As a result of trial-and-error methods, two hidden layers were used, as this gave the most successful result. There were three neurons in each hidden layer. The model is shown in Figure 2.

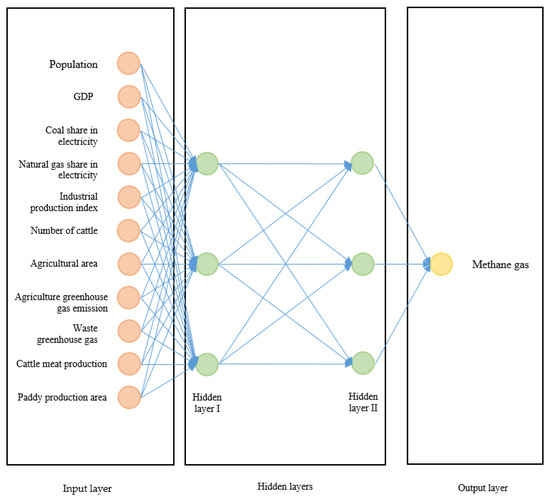
Figure 2. ANN model.

After testing various functions for the activation function, the sigmoid function was preferred because it gave the most successful result. One of the parameters that has an effect on the success of the model in artificial neural networks is learning. The feedback learning algorithm was used in this study, and 100 iterations were performed. Figure 3 shows that the error curve decreased non-linearly. In the figure, the x-axisshows the number of iterations, and the y-axisshows the error. The scale of the x-axiswas between 1 and 100 and the y-axiswas between 0 and 5. The error curve stabilized between the 50th and 62th iteration and reached the ideal value.

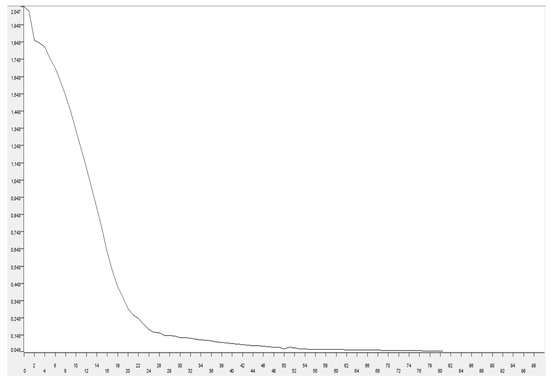
Figure 3. Error plot for ANN.

The maximum likelihood method was used to estimate the parameters for the logistic regression model. In this study, the log likelihood value was −51.022 as a result of 100 iterations. Nonlinear SVR was preferred in the method where support vector regression was used. As a result of the tests for the kernel function, it was decided to use the radial basis function (RBF). The overlapping penalty value of the model was chosen as 10 and the RBF sigma value was chosen as 0.5.

The evaluation of regression models is given in Table 4.

Table 4. Evaluation of models.

	Logistic Regression	Artificial Neural Network	Support Vector Regression
R2	0.949	0.936	0.923
MAE	0.052	0.053	0.065
MSE	0.005	0.006	0.009

Figure 4 shows the coefficient of determination (R²) graphs. R² shows the rate of explanation of independent variables. In other words, it refers to the variance ratio of the dependent variable explained by the independent variables. Here, zero indicates that the model has 0% explanatory power, and one indicates that the model has 100% explanatory power and that the independent variables are strong in explaining the dependent variable and provide a linear curve [38,39]. R² was 94.9% for logistic regression, 93.6% for artificial neural networks, and 92.3% for support vector regression. These results show that the ideal values were met.

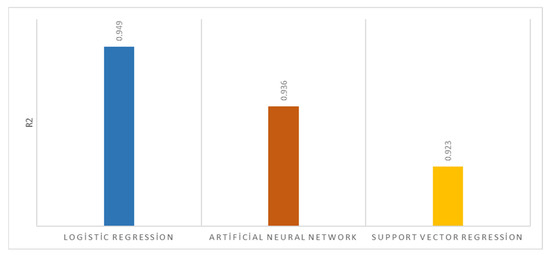
Figure 4. R² evaluation.

The mean absolute error (MAE) graphs are presented in Figure 5. MAE is calculated by averaging the absolute values of the prediction errors. It is often preferred for determining the error values of models because it can be easily interpreted. The MAE value can vary from 0 to ∞. The lower the MAE value, the lower the error value of the model [40,41]. The MAE metric gives the magnitude of the error as a quantity. In the study, it was seen that the MAE was 0.052 for logistic regression, 0.053 for artificial neural networks, and 0.065 for support vector regression. The MAE was considered to be successful in all three models.

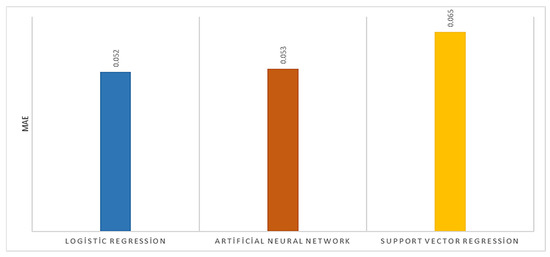
Figure 5. MAE evaluation.

Figure 6 shows the mean squared error (MSE) graphs. MSE is a statistical metric that evaluates the error of machine learning methods. MSE is equal to the mean squared difference between predicted values and actual values. MSE is often used in regression models. Because MSE squares the error, it causes major errors to be clearly highlighted. MSE is a metric that ranges from 0 to infinity, and values close to zero are considered better [42,43]. It was seen that the MSE was 0.005 for logistic regression, 0.006 for artificial neural networks, and 0.009 for support vector regression. The error rate of the models was found to be low and acceptable.

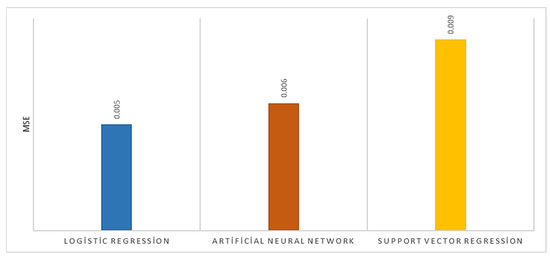
Figure 6. MSE evaluation.

According to the error and success evaluation, the order of the models in terms of their success is logistic regression, then artificial neural network and, finally, support vector regression. Figure 7 shows the scatter plots of the models.

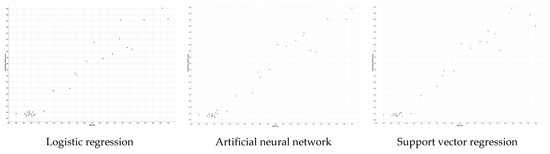
Figure 7. Scatter plot of methods.

Figure 5 shows the scatter plot of the machine learning models used for methane gas prediction. The x-axisin the figure shows the actual values and the y-axisshows the predicted values. The scales of the x and y axes were between 0 and 1. In all three models, there was a positive correlation between the methane gas value and the predicted results. Moreover, this link was quite strong. As the value of one of the variables increased, the other increased and the points clustered near the line. Figure 8 shows the line plots of the models.

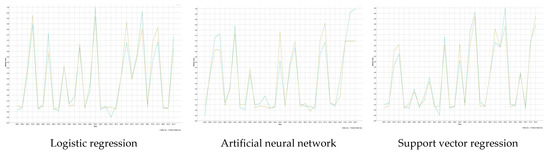
Figure 8. Line plot of machine learning models.

Figure 8 shows the relationship between actual and predicted values. The x-axis in the figure shows the years and the y-axisshows the actual and predicted values. The x-axisscale covered the period between 1990 and 2020; the y-axiscovered the period between 0 and 1. The relationship was strong for all three models. When the figures were analyzed in detail, it was seen that the model with the strongest relationship was logistic regression, followed by artificial neural network and support vector regression.

The boundaries of the study were contained to countries that have coal mines and continue to produce energy from coal, and support cattle breeding and paddy production. In this respect, the model may need to be modified in order to be applied in continental European countries with serious regulations on coal production and very limited paddy production.

4. Conclusions

The aim of this study was to use machine learning to predict the emission of methane gas, which has a greater effect on the warming of the atmosphere than other greenhouse gases. The differentiating aspect of this study from other studies in the literature is that greenhouse gas emission studies have so far either predicted greenhouse gas emissions in general or focused on carbon dioxide emissions. However, the atmospheric heating potential of methane gas is higher than other greenhouse gases. This study was also unique in its use of not only technical data but also economic and environmental factors, which were accepted as variables in the design of the model.

In the study, three different machine learning techniques were applied to find the best machine learning technique. The aim was to provide preliminary information for researchers that the machine learning technique works successfully, so they can use this model in the future. In terms of the usability of the model and the accessibility of the data set, it was thought to be a guiding study, especially in making decisions to prevent methane gas and in the creation of sustainable policies. In particular, the model provided statistically very useful and successful results that can be used in the formulation of policies in terms of animal production (especially cattle production) and the disposal of organic human waste, which is considered to be the main cause of methane gas emission.

The results revealed that the methane gas emission variables used in the study can be considered as variables for future greenhouse gas emission estimation studies.

In this study, methane gas production in Turkey was successfully estimated using machine learning methods. Three different supervised machine learning methods—logistic regression, artificial neural networks, and support vector regression—were used in the study. To analyze and evaluate these methods, R², MAE, and MSE metrics were calculated. R² was found to be 94.9% for logistic regression, 93.6% for artificial neural networks, and 92.3% for support vector regression. These results show that the ideal values were met. MSE was 0.052 for logistic regression, 0.053 for artificial neural networks, and 0.065 for support vector regression. MAE was considered successful in all three models. MSE was 0.005 for logistic regression, 0.006 for artificial neural networks, and 0.009 for support vector regression. The error rate of the models was found to be low and acceptable. According to the results of the analyses, it can be seen that the success of all three models was high, and the error was within the acceptable range. The model was also more successful than that of similar studies. According to the statistical metrics, logistic regression, artificial neural networks, and support vector regression were all successful models, with the least error obtained with logistic regression, for methane gas production forecasting in Turkey.