Spin–Orbital Transformation in a Tight Focus of an Optical Vortex with Circular Polarization
Abstract
1. Introduction
2. The Denseness of Lengthwise Projections of the SAM and OAM
3. The Total Lengthwise OAM and SAM Averaged over the Cross-Section of the Beam
4. The SOC upon the Light Focusing
5. Transformation of the Longitudinal Energy Flux into the Transverse Energy Flux
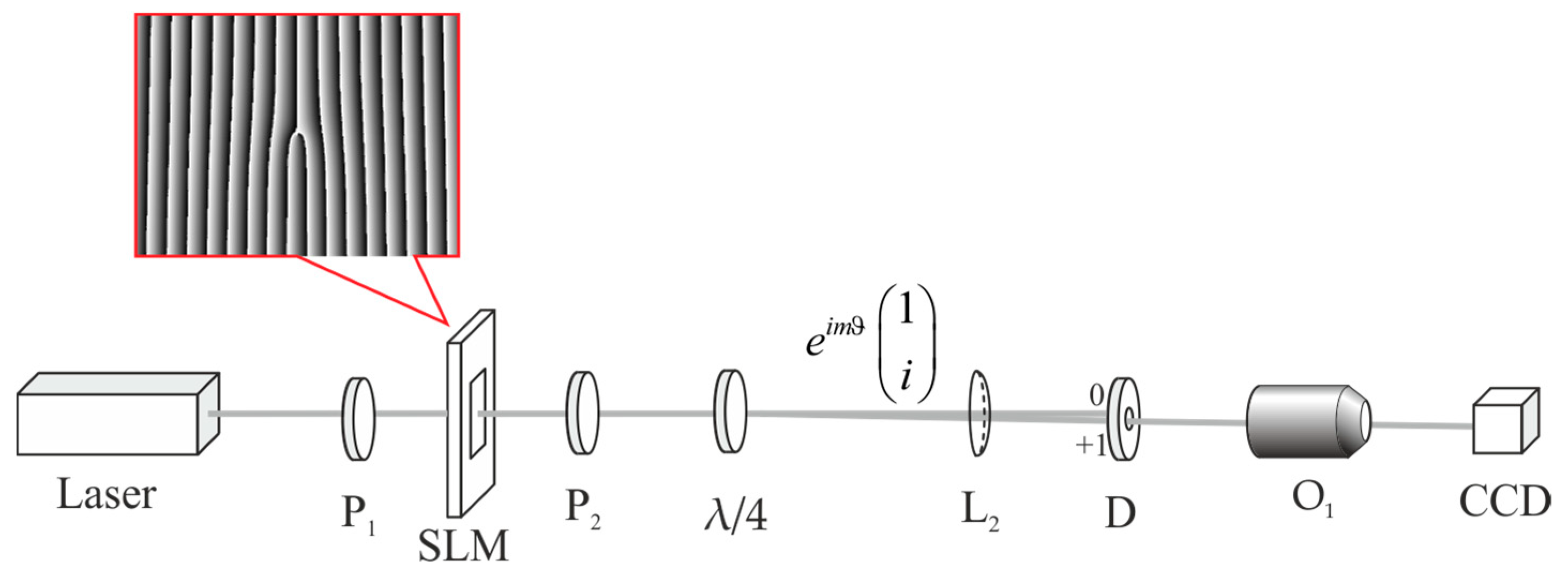
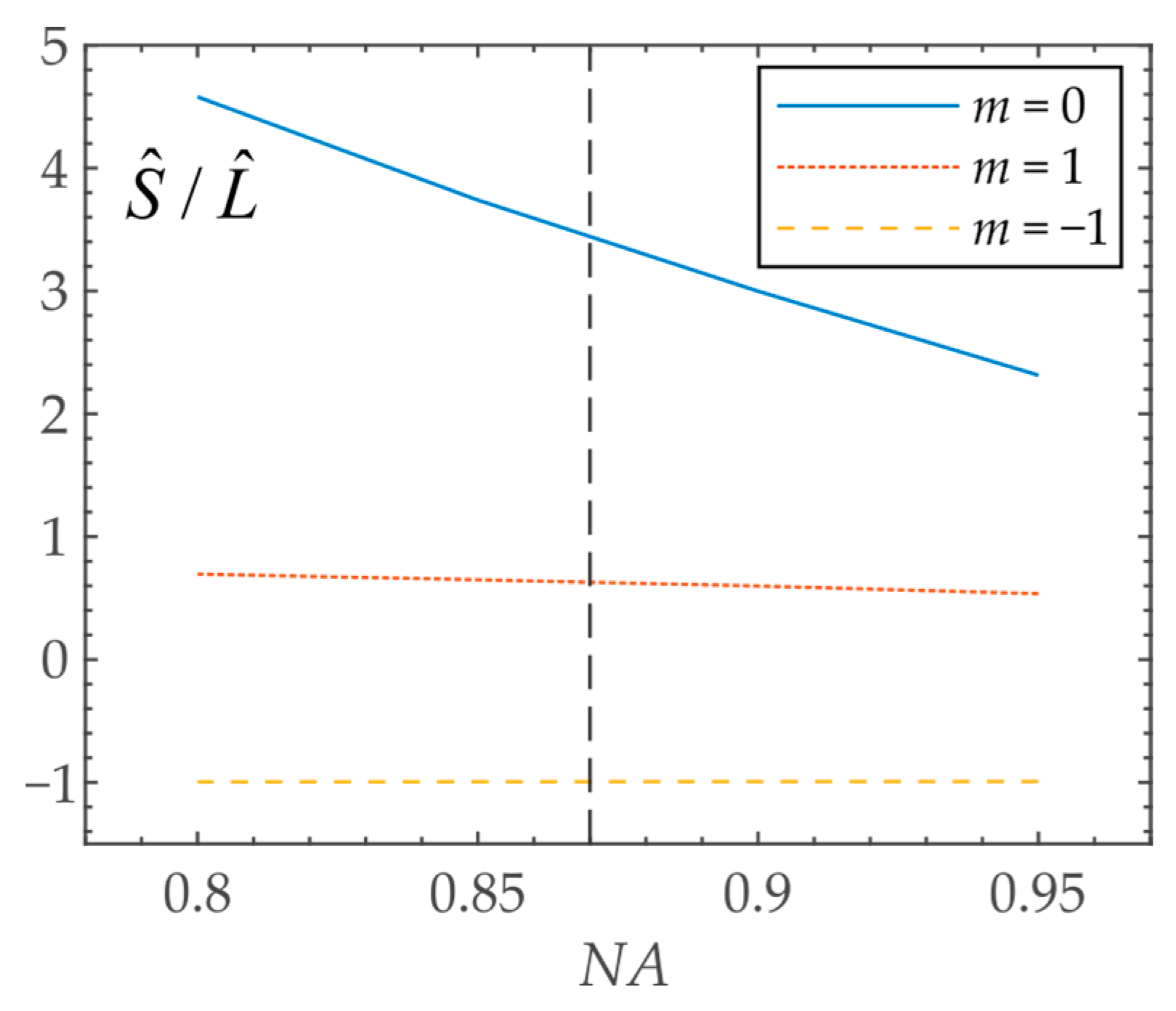
6. Separate Measurement of the OAM and SAM in the Focus
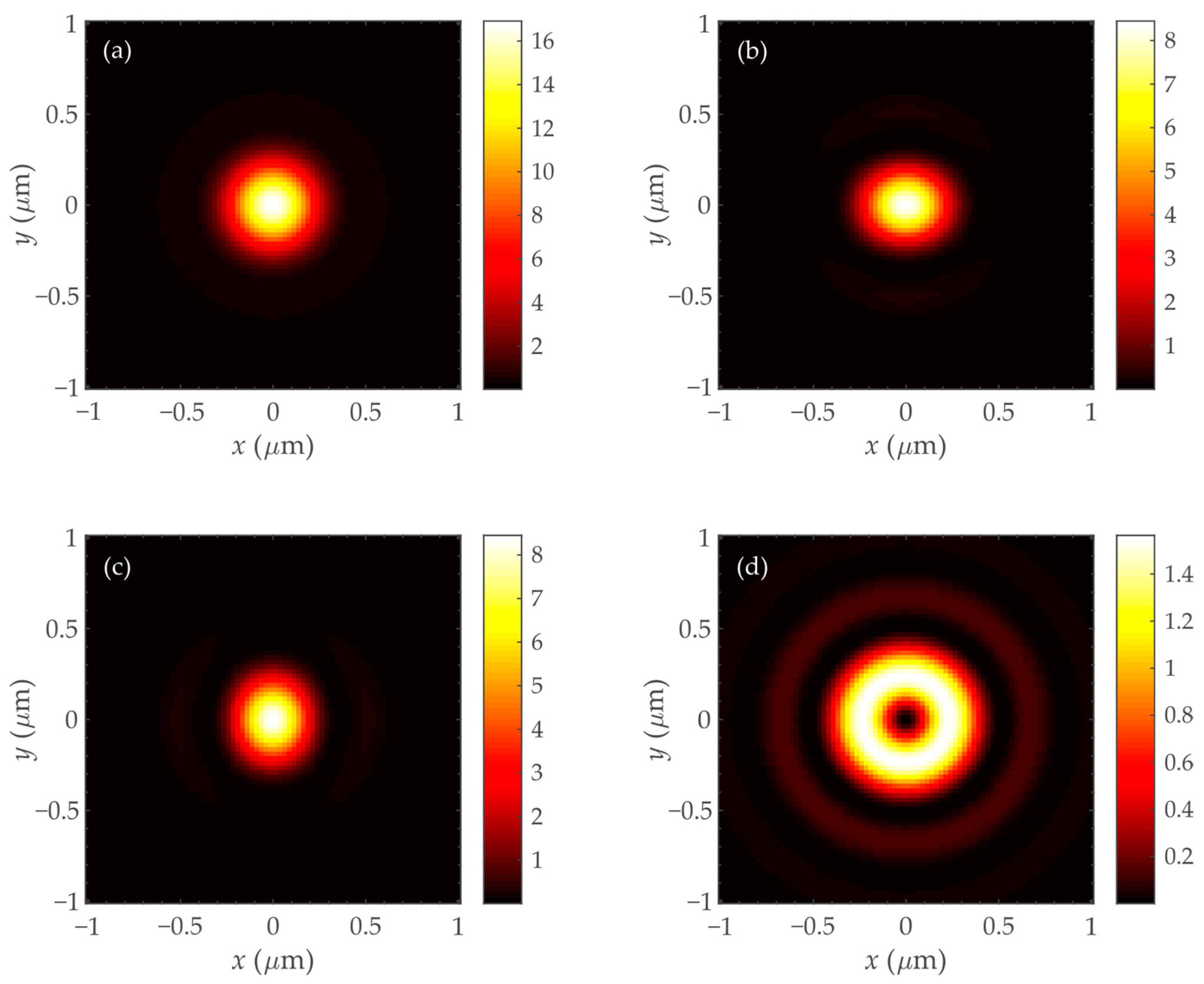
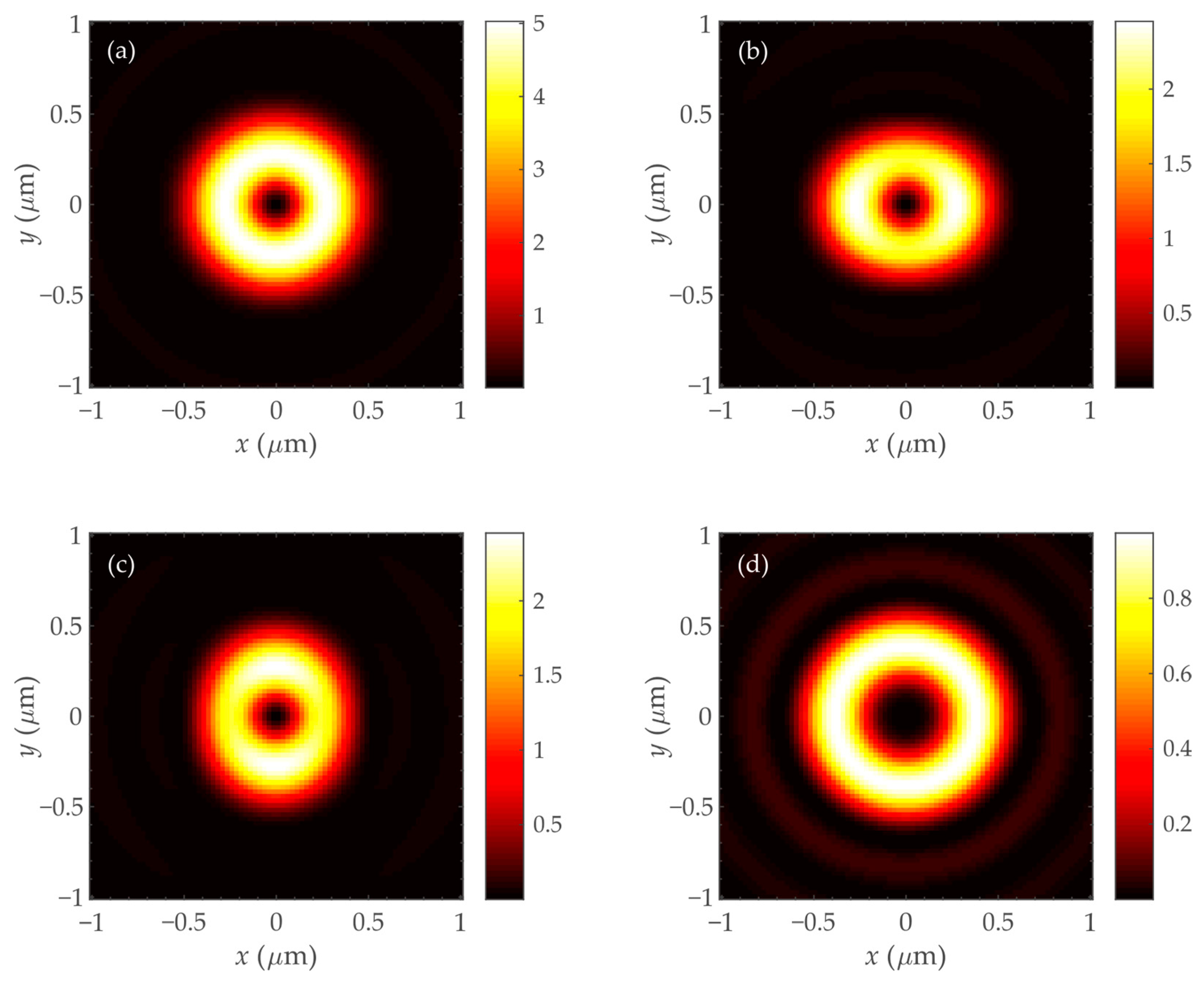
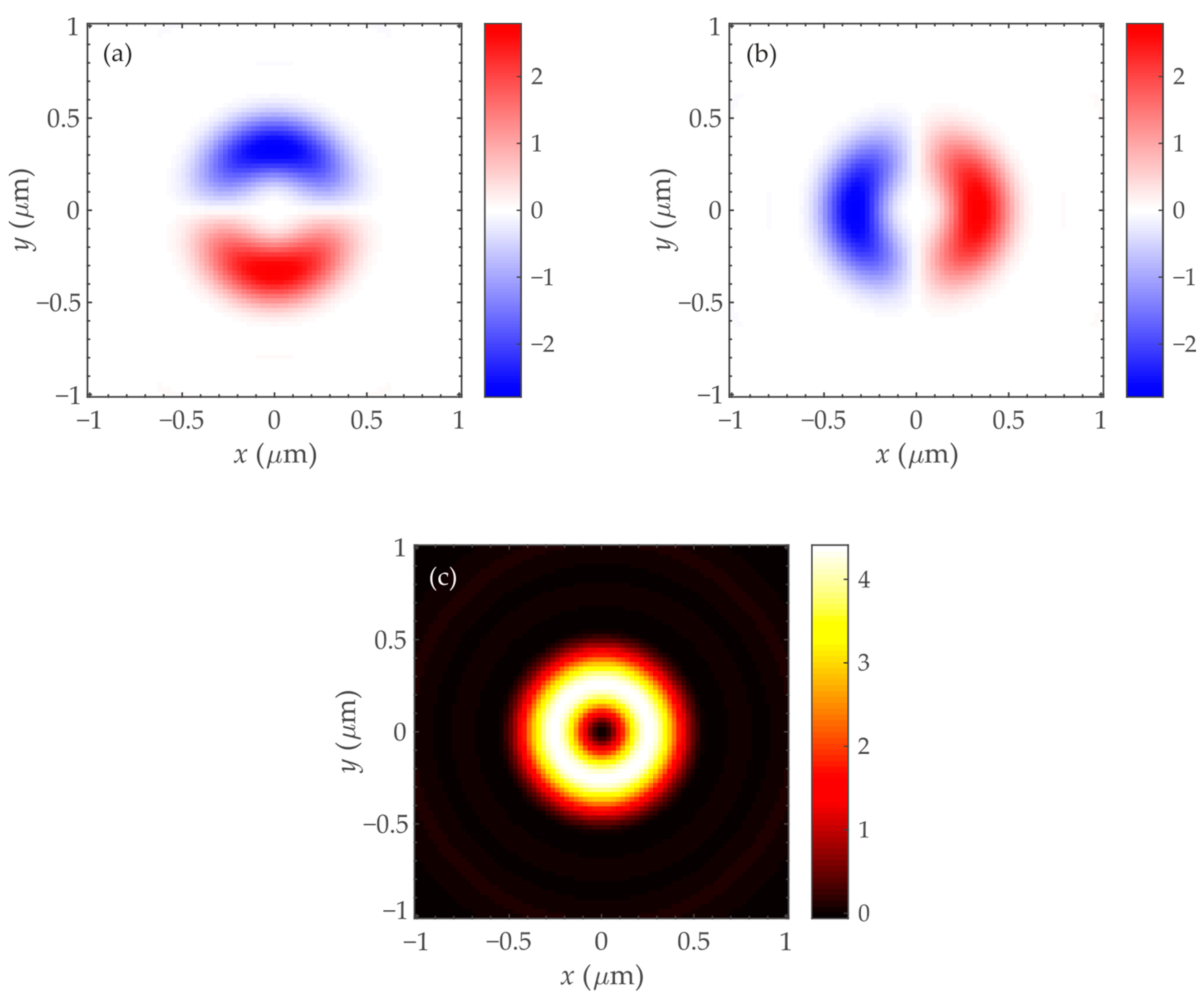
7. Simulation Results
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bliokh, K.; Rodríguez-Fortuño, F.; Nori, F.; Zayats, A.V. Spin–orbit interactions of light. Nat. Photon. 2015, 9, 796–808. [Google Scholar] [CrossRef]
- Bliokh, K.Y. Geometrical Optics of Beams with Vortices: Berry Phase and Orbital Angular Momentum Hall Effect. Phys. Rev. Lett. 2006, 97, 043901. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Bliokh, Y.P. Topological spin transport of photons: The optical Magnus effect and Berry phase. Phys. Lett. A 2004, 333, 181–186. [Google Scholar] [CrossRef]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Bliokh, Y.P. Conservation of angular momentum, transverse shift, and spin Hall effect in reflection and refraction of an electromagnetic wave packet. Phys. Rev. Lett. 2006, 96, 073903. [Google Scholar] [CrossRef]
- Bokor, N.; Iketaki, Y.; Watanabe, T.; Fujii, M. Investigation of polarization effects for high-numerical-aperture first-order Laguerre–Gaussian beams by 2D scanning with a single fluorescent microbead. Opt. Express 2005, 13, 10440–10447. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A.; Zaitsev, V.D. Spin Hall Effect before and after the Focus of a High-Order Cylindrical Vector Beam. Appl. Sci. 2022, 12, 12218. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kozlova, E.S.; Butt, M.A. High-Order Orbital and Spin Hall Effects at the Tight Focus of Laser Beams. Photonics 2022, 9, 970. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V. Spin Hall Effect of Double-Index Cylindrical Vector Beams in a Tight Focus. Micromachines 2023, 14, 494. [Google Scholar] [CrossRef]
- Zhao, Y.; Edgar, J.S.; Jeffries, G.D.M.; McGloin, D.; Chiu, D.T. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef]
- Dogariu, A.; Schwartz, C. Conservation of angular momentum of light in single scattering. Opt. Express 2006, 14, 8425–8433. [Google Scholar] [CrossRef] [PubMed]
- Haefner, D.; Sukhov, S.; Dogariu, A. Spin Hall effect of light in spherical geometry. Phys. Rev. Lett. 2009, 102, 123903. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Ostrovskaya, E.A.; Alonso, M.A.; Rodríguez-Herrera, O.G.; Lara, D.; Dainty, C. Spin-to-orbit angular momentum conversion in focusing, scattering, and imaging systems. Opt. Express 2011, 19, 26132–26149. [Google Scholar] [CrossRef] [PubMed]
- Baranova, N.B.; Savchenko, A.Y.; Zel’dovich, B.Y. Transverse shift of a focal spot due to switching of the sign of circular-polarization. JETP Lett. 1994, 59, 232–234. [Google Scholar]
- Zel’dovich, B.Y.; Kundikova, N.D.; Rogacheva, L.F. Observed transverse shift of a focal spot upon a change in the sign of circular polarization. JETP Lett. 1994, 59, 766–769. [Google Scholar]
- Darsht, M.Y.; Zel’dovich, B.Y.; Kataevskaya, I.V.; Kundikova, N.D. Formation of an isolated wavefront dislocation. JETP Lett. 1995, 80, 817–821. [Google Scholar]
- Brasselet, E.; Izdebskaya, Y.; Shvedov, V.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Dynamics of optical spin-orbit coupling in uniaxial crystals. Opt. Lett. 2009, 34, 1021–1023. [Google Scholar] [CrossRef]
- Berry, M.V.; Jeffrey, M.R.; Mansuripur, M. Orbital and spin angular momentum in conical diffraction. J. Opt. A 2005, 7, 685–690. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef]
- Biener, G.; Niv, A.; Kleiner, V.; Hasman, E. Formation of helical beams by use of Pancharatnam–Berry phase optical elements. Opt. Lett. 2002, 27, 1875–1877. [Google Scholar] [CrossRef]
- Marrucci, L.; Manzo, C.; Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006, 96, 163905. [Google Scholar] [CrossRef] [PubMed]
- Kruk, S.S.; Decker, M.; Staude, I.; Schlecht, S.; Greppmair, M.; Neshev, D.N.; Kivshar, Y.S. Spin-polarized photon emission by resonant multipolar nanoantennas. ACS Photon. 2014, 1, 1218–1223. [Google Scholar] [CrossRef]
- Vuong, L.T.; Adam, A.J.L.; Brok, J.M.; Planken, P.C.M.; Urbach, H.P. Electromagnetic spin-orbit interactions via scattering of subwavelength apertures. Phys. Rev. Lett. 2010, 104, 083903. [Google Scholar] [CrossRef]
- Gong, S.-H.; Alpeggiani, F.; Sciacca, B.; Garnett, E.C.; Kuipers, L. Nanoscale chiral valley-photon interface through optical spin-orbit coupling. Science 2018, 359, 443–447. [Google Scholar] [CrossRef] [PubMed]
- Ni, J.; Liu, S.; Chen, Y.; Hu, G.; Hu, Y.; Chen, W.; Li, J.; Chu, J.; Qiu, C.-W.; Wu, D. Direct Observation of Spin–Orbit Interaction of Light via Chiroptical Responses. Nano Lett. 2022, 22, 9013–9019. [Google Scholar] [CrossRef]
- Dai, H.; Yuan, L.; Yin, C.; Cao, Z.; Chen, X. Direct Visualizing the Spin Hall Effect of Light via Ultrahigh-Order Modes. Phys. Rev. Lett. 2020, 124, 053902. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Smirnova, D.; Nori, F. Quantum spin Hall effect of light. Science 2015, 348, 1448–1451. [Google Scholar] [CrossRef]
- Wenhao, X.; Yichang, S.; Hailu, L. Spin-orbit interaction of light. Chin. J. Quantum Electron. 2022, 39, 159–181. [Google Scholar]
- Zhang, W.; Wang, Y.; Xu, D.; Luo, H. Spin-orbit interaction of light: When twisted light meets twisted metasurfaces. Phys. Rev. A 2023, 107, 043502. [Google Scholar] [CrossRef]
- Aiello, A.; Lindlein, N.; Marquardt, C.; Leuchs, G. Transverse Angular Momentum and Geometric Spin Hall Effect of Light. Phys. Rev. Lett. 2009, 103, 100401. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Liu, S.; Zhao, J. Unveiling the photonic spin Hall effect of freely propagating fan-shaped cylindrical vector vortex beams. Opt. Lett. 2015, 40, 4444–4447. [Google Scholar] [CrossRef] [PubMed]
- Ling, X.; Yi, X.; Zhou, X.; Liu, Y.; Shu, W.; Luo, H.; Wen, S. Realization of tunable spin-dependent splitting in intrinsic photonic spin Hall effect. Appl. Phys. Lett. 2014, 105, 151101. [Google Scholar] [CrossRef]
- Mardonov, S.; Sherman, E.Y.; Muga, J.G.; Wang, H.W.; Ban, Y.; Chen, X. Collapse of spin-orbit-coupled Bose-Einstein condensates. Phys. Rev. A 2015, 91, 043604. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Nalimov, A.G.; Stafeev, S.S. Exploiting the circular polarization of light to obtain a spiral energy flow at the subwavelength focus. J. Opt. Soc. Am. B 2019, 36, 2850–2855. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc. R. Soc. A 1959, 253, 358–379. [Google Scholar]
- Kotlyar, V.V.; Kovalev, A.A.; Telegin, A.M. Angular and Orbital Angular Momenta in the Tight Focus of a Circularly Polarized Optical Vortex. Photonics 2023, 10, 160. [Google Scholar] [CrossRef]
- Bliokh, K.; Bekshaev, A.; Nori, F. Extraordinary momentum and spin in evanescent waves. Nat. Commun. 2014, 5, 3300. [Google Scholar] [CrossRef]
- Arzola, A.V.; Chvátal, L.; Jákl, P.; Zemnek, P. Spin to orbital light momentum conversion visualized by particle trajectory. Sci. Rep. 2019, 9, 4127. [Google Scholar] [CrossRef]
- Chandravati, P. Numerical study of spin–orbit interaction of light in nonparaxial focusing of Gaussian beams. Optik 2021, 228, 166199. [Google Scholar]
- Wang, Q.; Tu, C.; He, H.; Xia, Z.; Hou, X.; Li, Y.; Wang, H. Local angular momentum induced dual orbital effect. APL Photonics 2022, 7, 086102. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotlyar, V.V.; Stafeev, S.S.; Zaitsev, V.D.; Telegin, A.M.; Kozlova, E.S. Spin–Orbital Transformation in a Tight Focus of an Optical Vortex with Circular Polarization. Appl. Sci. 2023, 13, 8361. https://doi.org/10.3390/app13148361
Kotlyar VV, Stafeev SS, Zaitsev VD, Telegin AM, Kozlova ES. Spin–Orbital Transformation in a Tight Focus of an Optical Vortex with Circular Polarization. Applied Sciences. 2023; 13(14):8361. https://doi.org/10.3390/app13148361
Chicago/Turabian StyleKotlyar, Victor V., Sergey S. Stafeev, Vladislav D. Zaitsev, Alexey M. Telegin, and Elena S. Kozlova. 2023. "Spin–Orbital Transformation in a Tight Focus of an Optical Vortex with Circular Polarization" Applied Sciences 13, no. 14: 8361. https://doi.org/10.3390/app13148361
APA StyleKotlyar, V. V., Stafeev, S. S., Zaitsev, V. D., Telegin, A. M., & Kozlova, E. S. (2023). Spin–Orbital Transformation in a Tight Focus of an Optical Vortex with Circular Polarization. Applied Sciences, 13(14), 8361. https://doi.org/10.3390/app13148361






