The Machine-Learning-Based Prediction of the Punching Shear Capacity of Reinforced Concrete Flat Slabs: An Advanced M5P Model Tree Approach
Abstract
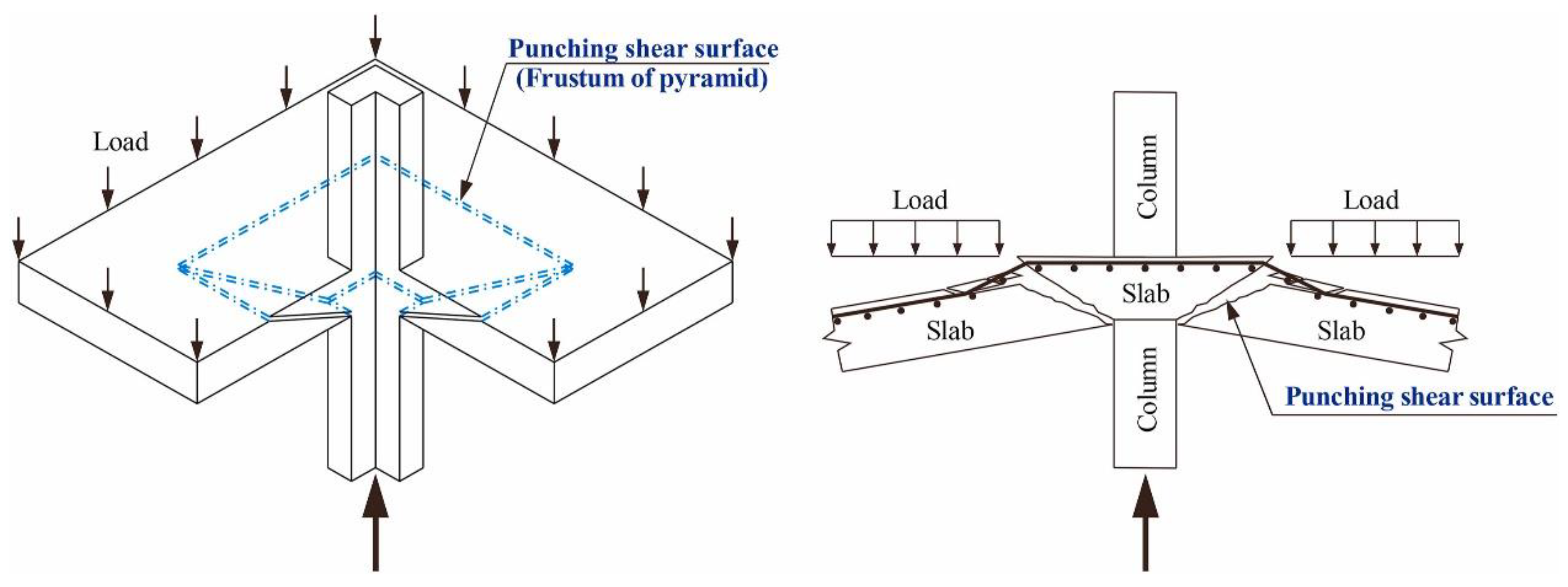
1. Introduction
2. Literature Review
3. Materials and Methods
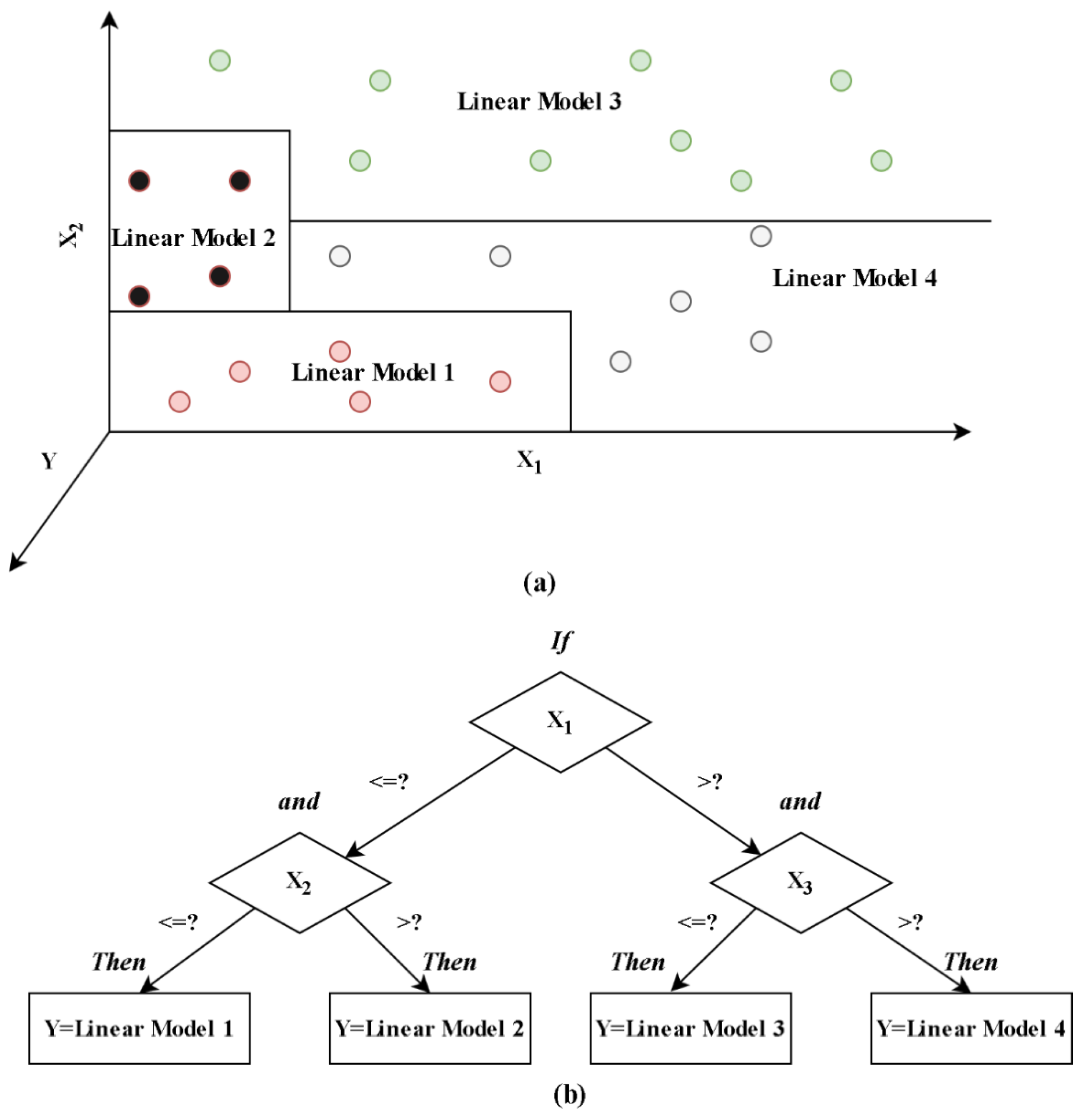
3.1. M5P Model Tree Techniques
3.2. Data Collection and Pre-Processing
4. Model Results
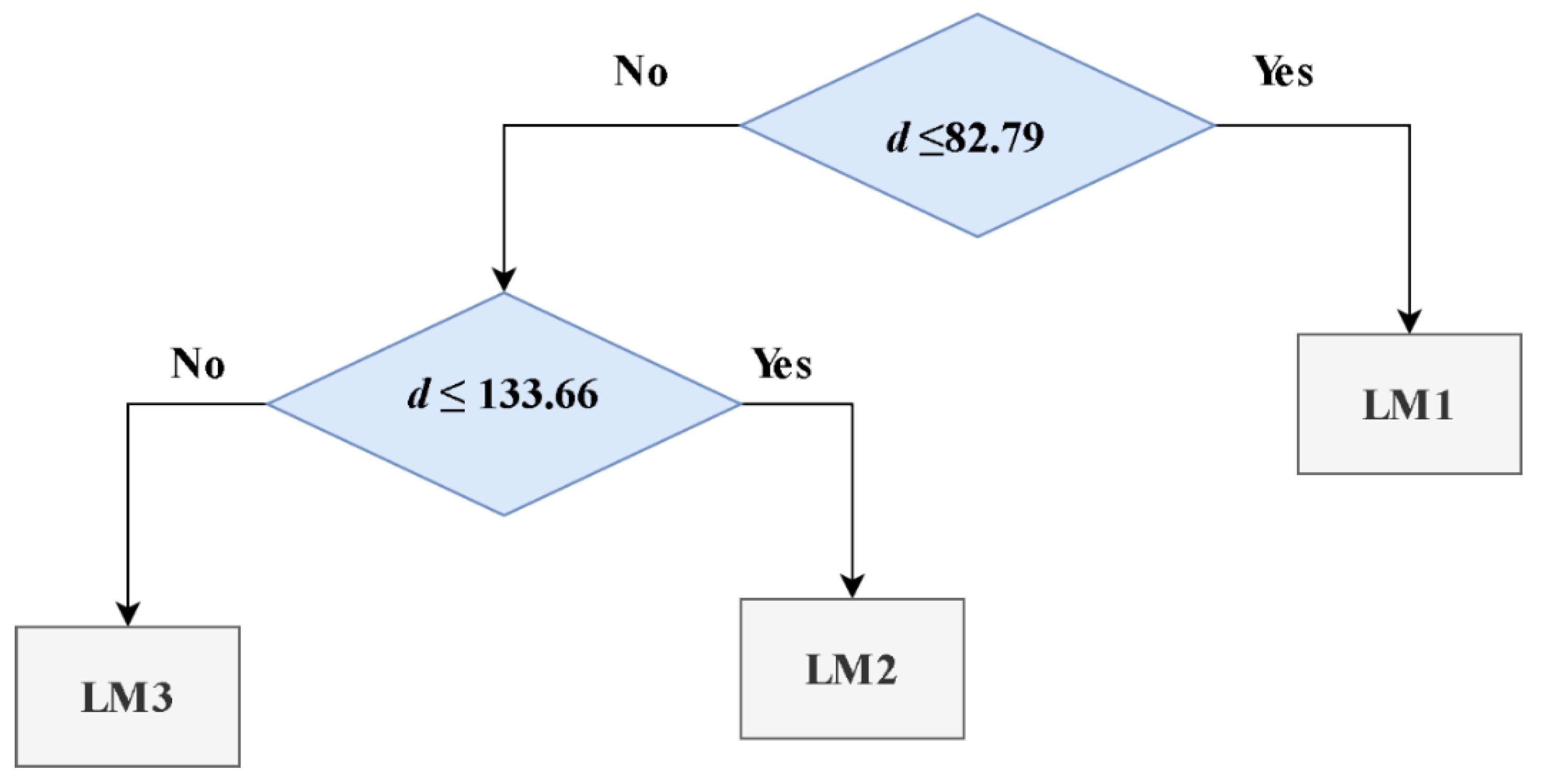
4.1. M5P-Derived Models
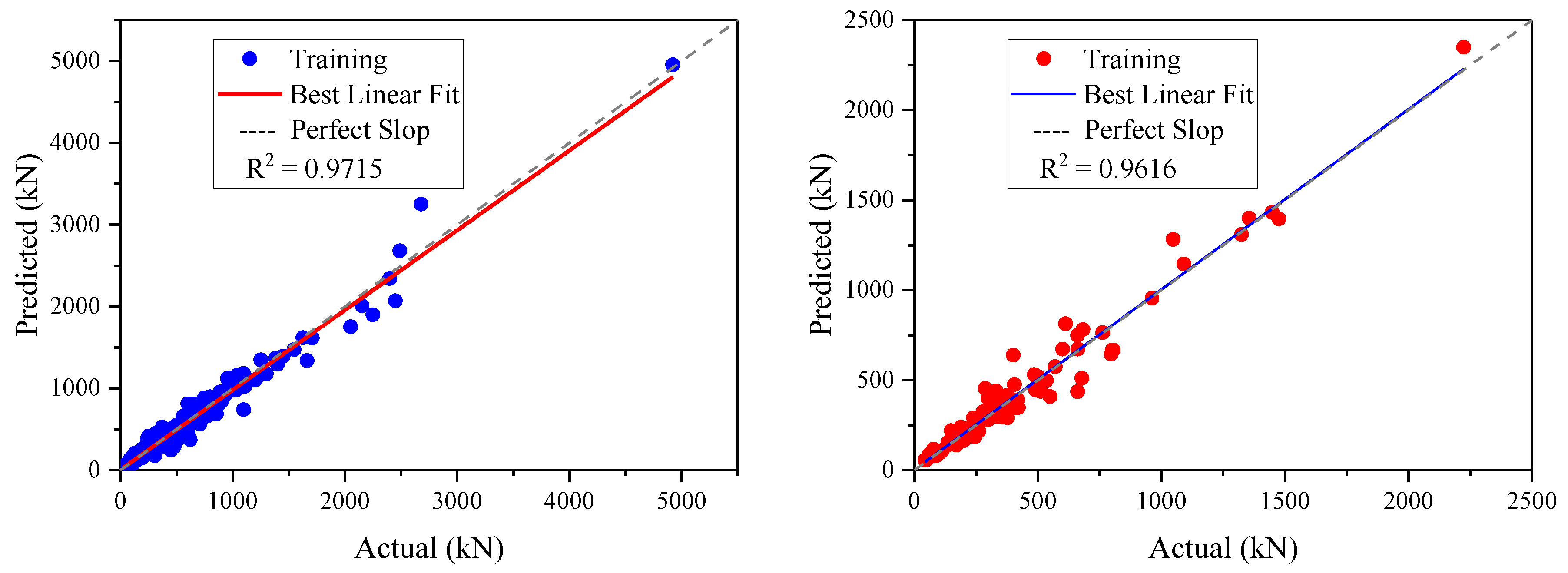
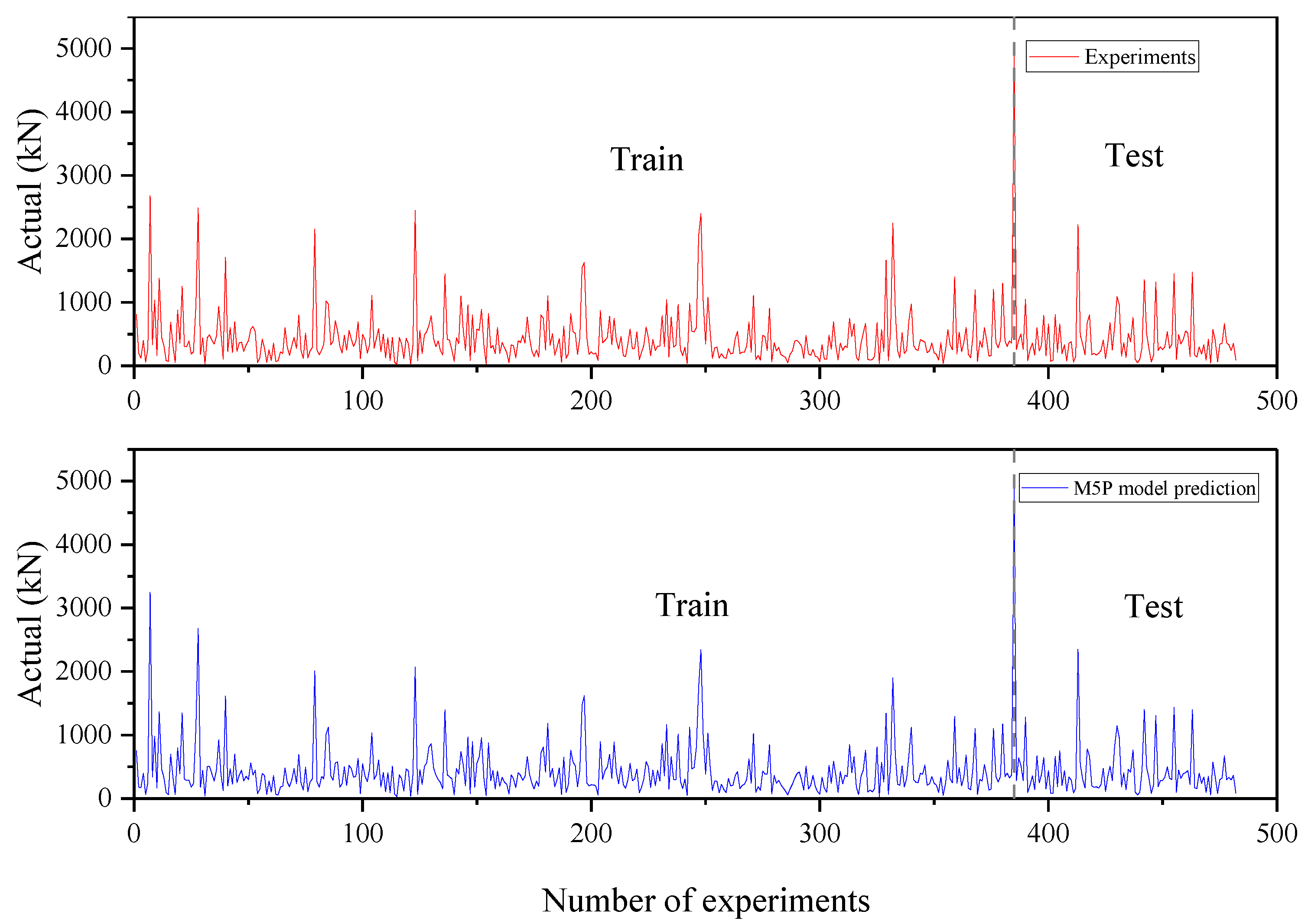
4.2. Performance Analysis
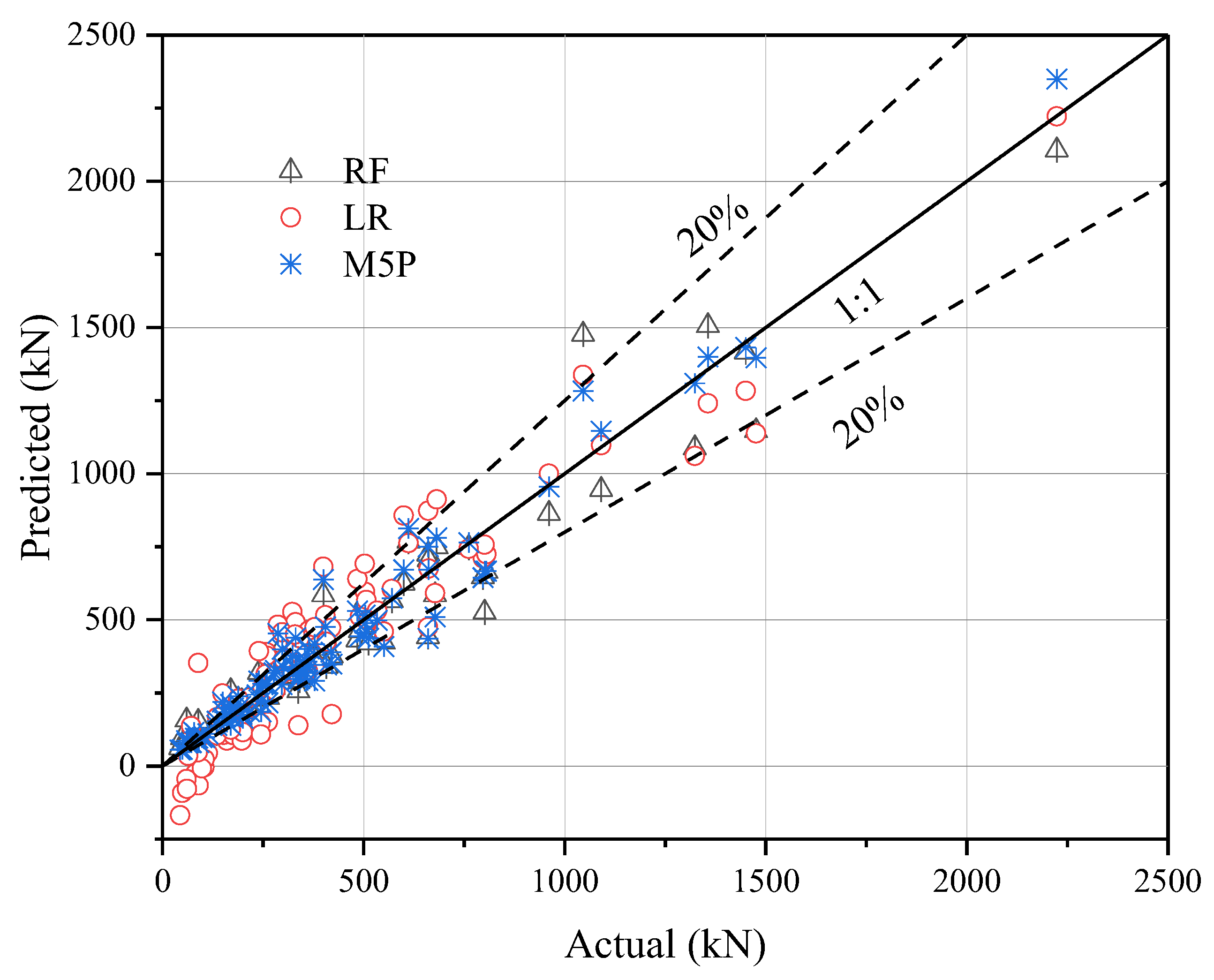
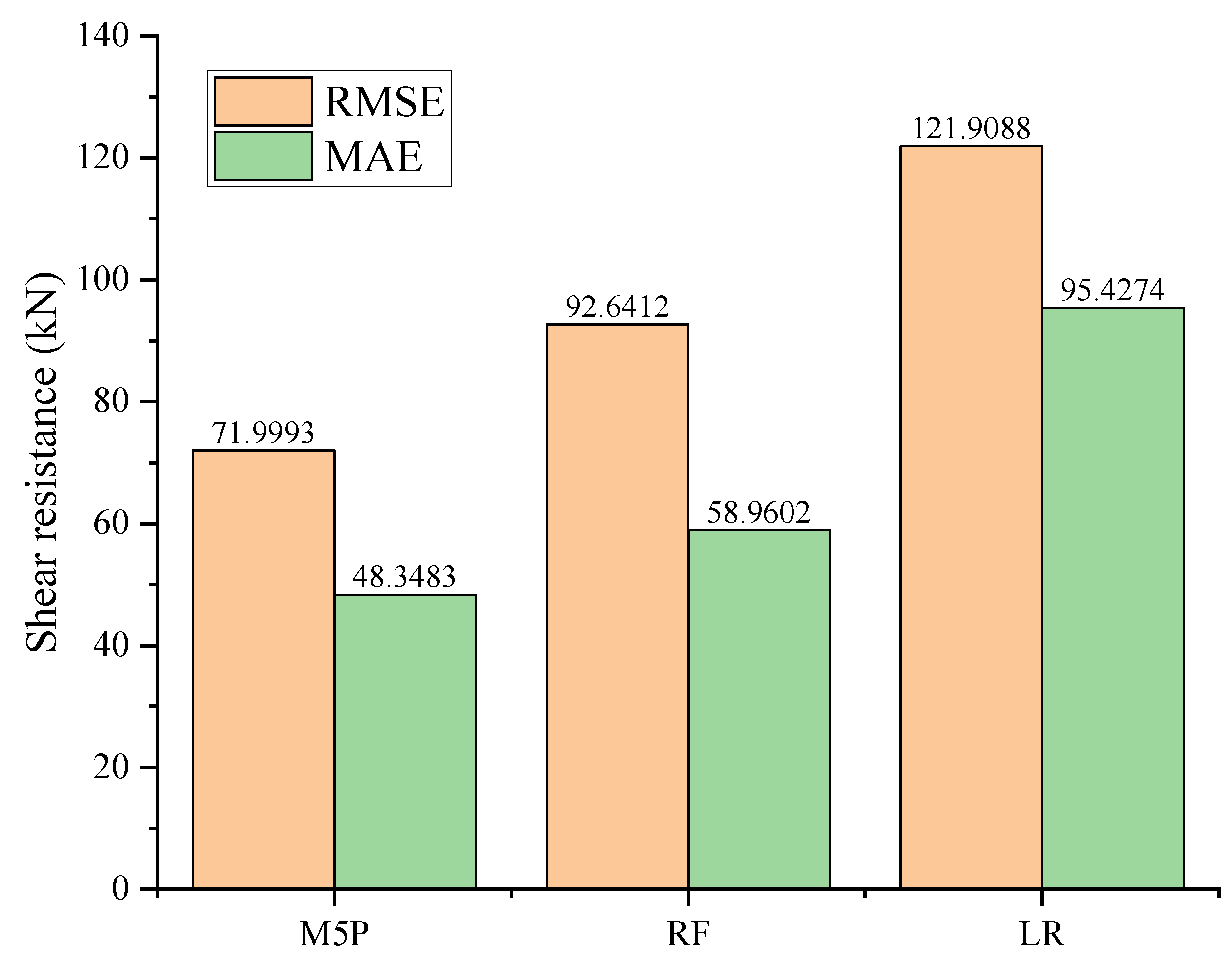
4.3. Comparative Evaluation of the Newly Formulated M5P Model and Various Other Machine Learning Models
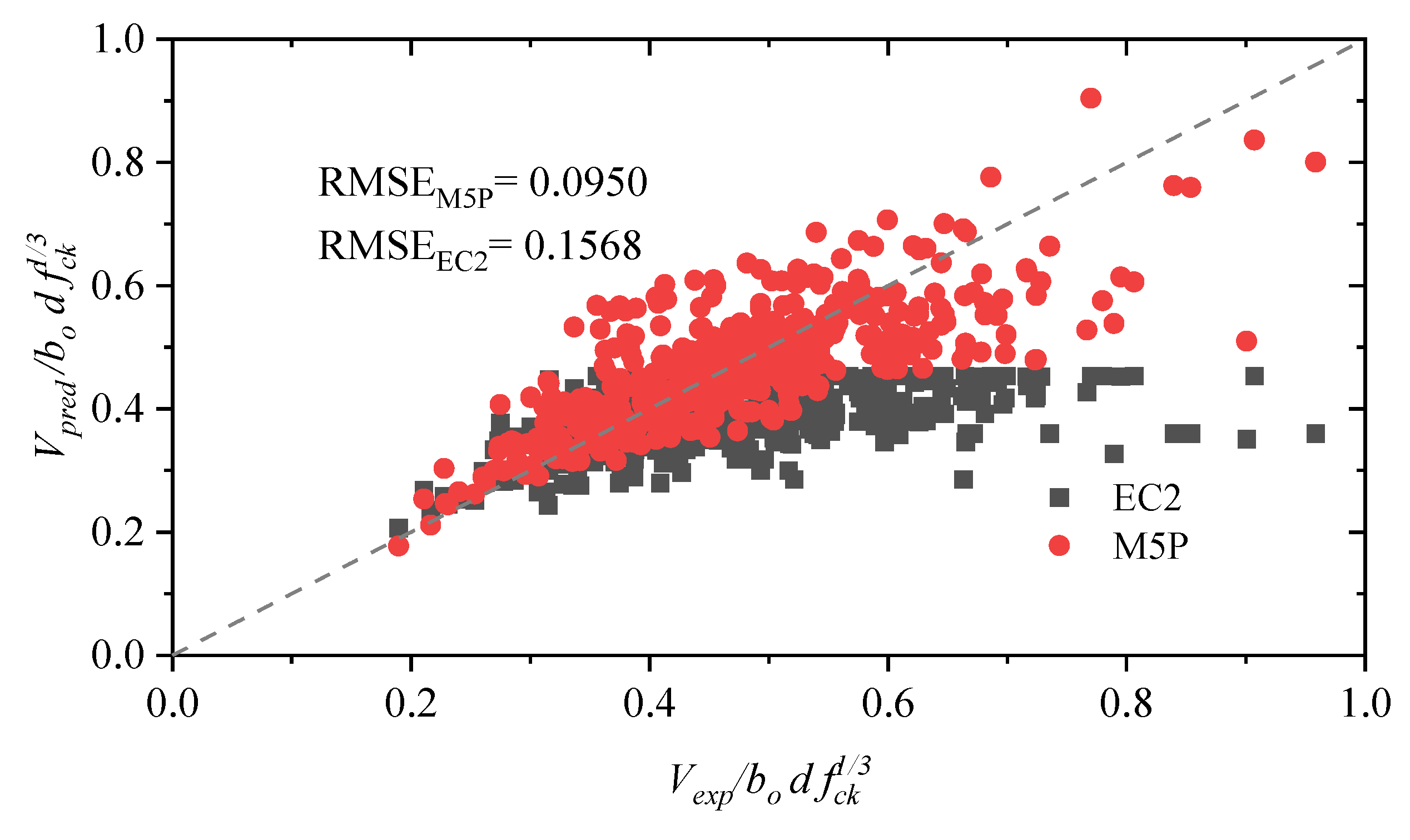
4.4. Design Code and Empirical Formulas
4.5. Comparison with Previously Developed Models
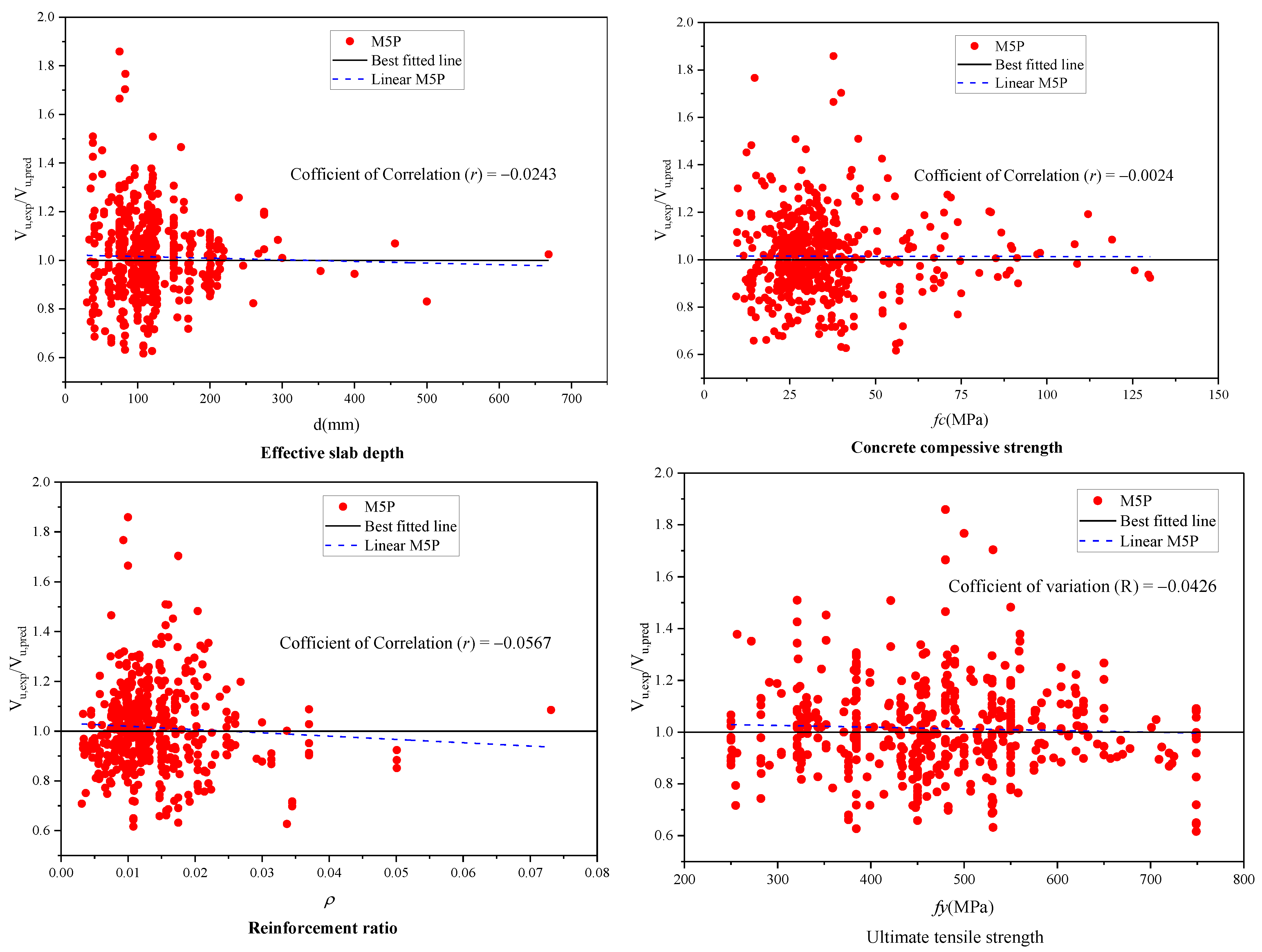
4.6. Model Error Susceptibility to Input Variables
4.7. Parametric and Sensitivity Analyses
5. Conclusions
- The M5P algorithm outperformed existing models and design codes, providing more accurate predictions for the punching shear strength. This improved accuracy could lead to more efficient designs and increased safety in RC structures.
- The effective depth of the slab (d) was identified as the most significant factor affecting the punching shear strength, which is consistent with previous studies and engineering experience.
- The M5P model demonstrated a high level of accuracy, with a low correlation between input design variables and model error. This is an essential characteristic for an ideal predictive model, as it ensures that the predictions are not significantly influenced by irrelevant factors.
- The sensitivity analysis indicated that the effective depth of the slab (d) had the most significant impact on the model performance, while the yield strength of reinforcement (fy) had the least impact. This information can be used to prioritize design considerations and improve the overall efficiency of the design process.
- The dataset used for the development and validation of the M5P model was limited in size and scope, which may affect the generalizability of the results. Future research could benefit from larger and more diverse datasets, including slabs with different reinforcement configurations and materials.
- This study focused on the prediction of punching shear capacity without considering other failure modes or serviceability requirements. This may limit the model applicability in certain scenarios, where additional factors need to be taken into account.
- The M5P model does not directly account for the influence of construction quality, environmental conditions, or long-term deterioration on the punching shear capacity. These factors may have significant impacts on the performance of RC flat slabs and should be considered in future research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mangalathu, S.; Shin, H.; Choi, E.; Jeon, J.-S. Explainable machine learning models for punching shear strength estimation of flat slabs without transverse reinforcement. J. Build. Eng. 2021, 39, 102300. [Google Scholar] [CrossRef]
- Theodorakopoulos, D.; Swamy, R. Ultimate punching shear strength analysis of slab–column connections. Cem. Concr. Compos. 2002, 24, 509–521. [Google Scholar] [CrossRef]
- Elshafey, A.A.; Rizk, E.; Marzouk, H.; Haddara, M.R. Prediction of punching shear strength of two-way slabs. Eng. Struct. 2011, 33, 1742–1753. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Alsayed, S.H. Prediction of punching shear strength of HSC interior slab-column connections. KSCE J. Civ. Eng. 2013, 17, 473–485. [Google Scholar] [CrossRef]
- Standards, B. Structural Use of Concrete: Part 1: Code of Practice for Design and Construction; British Standards Institution: London, UK, 2007. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute: Detroit, MI, USA, 2019. [Google Scholar]
- En, B. 1-1. Eurocode 2: Design of Concrete Structures–Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- Elstner, R.C.; Hognestad, E. Shearing strength of reinforced concrete slabs. J. Proc. 1956, 53, 29–58. [Google Scholar]
- Bažant, Z.P.; Cao, Z. Size effect in punching shear failure of slabs. ACI Struct. J. 1987, 84, 44–53. [Google Scholar]
- Al-Abdaly, N.M.; Al-Taai, S.R.; Imran, H.; Ibrahim, M. Development of prediction model of steel fiber-reinforced concrete compressive strength using random forest algorithm combined with hyperparameter tuning and k-fold cross-validation. East. Eur. J. Enterp. Technol. 2021, 5, 113. [Google Scholar] [CrossRef]
- Alhakeem, Z.M.; Jebur, Y.M.; Henedy, S.N.; Imran, H.; Bernardo, L.F.; Hussein, H.M. Prediction of Ecofriendly Concrete Compressive Strength Using Gradient Boosting Regression Tree Combined with GridSearchCV Hyperparameter-Optimization Techniques. Materials 2022, 15, 7432. [Google Scholar] [CrossRef]
- Faridmehr, I.; Nehdi, M.; Baghban, M.H. Novel informational bat-ANN model for predicting punching shear of RC flat slabs without shear reinforcement. Eng. Struct. 2022, 256, 114030. [Google Scholar] [CrossRef]
- Henedy, S.N.; Naser, A.H.; Imran, H.; Bernardo, L.F.; Teixeira, M.M.; Al-Khafaji, Z. Development of Prediction Models for the Torsion Capacity of Reinforced Concrete Beams Using M5P and Nonlinear Regression Models. J. Compos. Sci. 2022, 6, 366. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Truong, G.T.; Shin, M. Development of extreme gradient boosting model for prediction of punching shear resistance of r/c interior slabs. Eng. Struct. 2021, 235, 112067. [Google Scholar] [CrossRef]
- Shatnawi, A.; Alkassar, H.M.; Al-Abdaly, N.M.; Al-Hamdany, E.A.; Bernardo, L.F.A.; Imran, H. Shear Strength Prediction of Slender Steel Fiber Reinforced Concrete Beams Using a Gradient Boosting Regression Tree Method. Buildings 2022, 12, 550. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, L.; Liang, S. Explainable machine learning-based model for failure mode identification of RC flat slabs without transverse reinforcement. Eng. Fail. Anal. 2022, 141, 106647. [Google Scholar] [CrossRef]
- Silva Júnior, F.E.S.d.; Gomes, W.J.d.S. Machine learning models to predict the punching shear strength of reinforced concrete flat slabs. Rev. IBRACON Estrut. Mater. 2023, 16, e16405. [Google Scholar]
- Fiore, A.; Marano, G.C.; Laucelli, D.; Monaco, P. Evolutionary modeling to evaluate the shear behavior of circular reinforced concrete columns. Adv. Civ. Eng. 2014, 2014, 684256. [Google Scholar] [CrossRef]
- Liang, S.; Shen, Y.; Gao, X.; Cai, Y.; Fei, Z. Symbolic machine learning improved MCFT model for punching shear resistance of FRP-reinforced concrete slabs. J. Build. Eng. 2023, 69, 106257. [Google Scholar] [CrossRef]
- Marasco, S.; Fiore, A.; Greco, R.; Cimellaro, G.P.; Marano, G.C. Evolutionary polynomial regression algorithm enhanced with a robust formulation: Application to shear strength prediction of RC beams without stirrups. J. Comput. Civ. Eng. 2021, 35, 04021017. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y. Prediction and feature analysis of punching shear strength of two-way reinforced concrete slabs using optimized machine learning algorithm and Shapley additive explanations. Mech. Adv. Mater. Struct. 2023, 30, 3086–3096. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Tasmania, Australia, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Weka. Weka 3: Data Mining Software in Java; University of Waikato: Hamilton, New Zealand, 2011; Volume 19, p. 52. Available online: https://www.cms.waikato.ac.nz/ml/weka/ (accessed on 20 June 2021).
- Wang, Y.; Witten, I.H. Induction of Model Trees for Predicting Continuous Classes; University of Waikato: Hamilton, New Zealand, 1996. [Google Scholar]
- Bhattacharya, B.; Price, R.; Solomatine, D. Machine learning approach to modeling sediment transport. J. Hydraul. Eng. 2007, 133, 440–450. [Google Scholar] [CrossRef]
- Frank, I.E.; Todeschini, R. The Data Analysis Handbook; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Chetchotisak, P.; Ruengpim, P.; Chetchotsak, D.; Yindeesuk, S. Punching shear strengths of RC slab-column connections: Prediction and reliability. KSCE J. Civ. Eng. 2018, 22, 3066–3076. [Google Scholar] [CrossRef]
- Olalusi, O.B.; Spyridis, P. Uncertainty modelling and analysis of the concrete edge breakout resistance of single anchors in shear. Eng. Struct. 2020, 222, 111112. [Google Scholar] [CrossRef]
- Franzblau, A.N. A Primer of Statistics for Non-Statisticians; American Psychological Association: Washington, DC, USA, 1958. [Google Scholar]
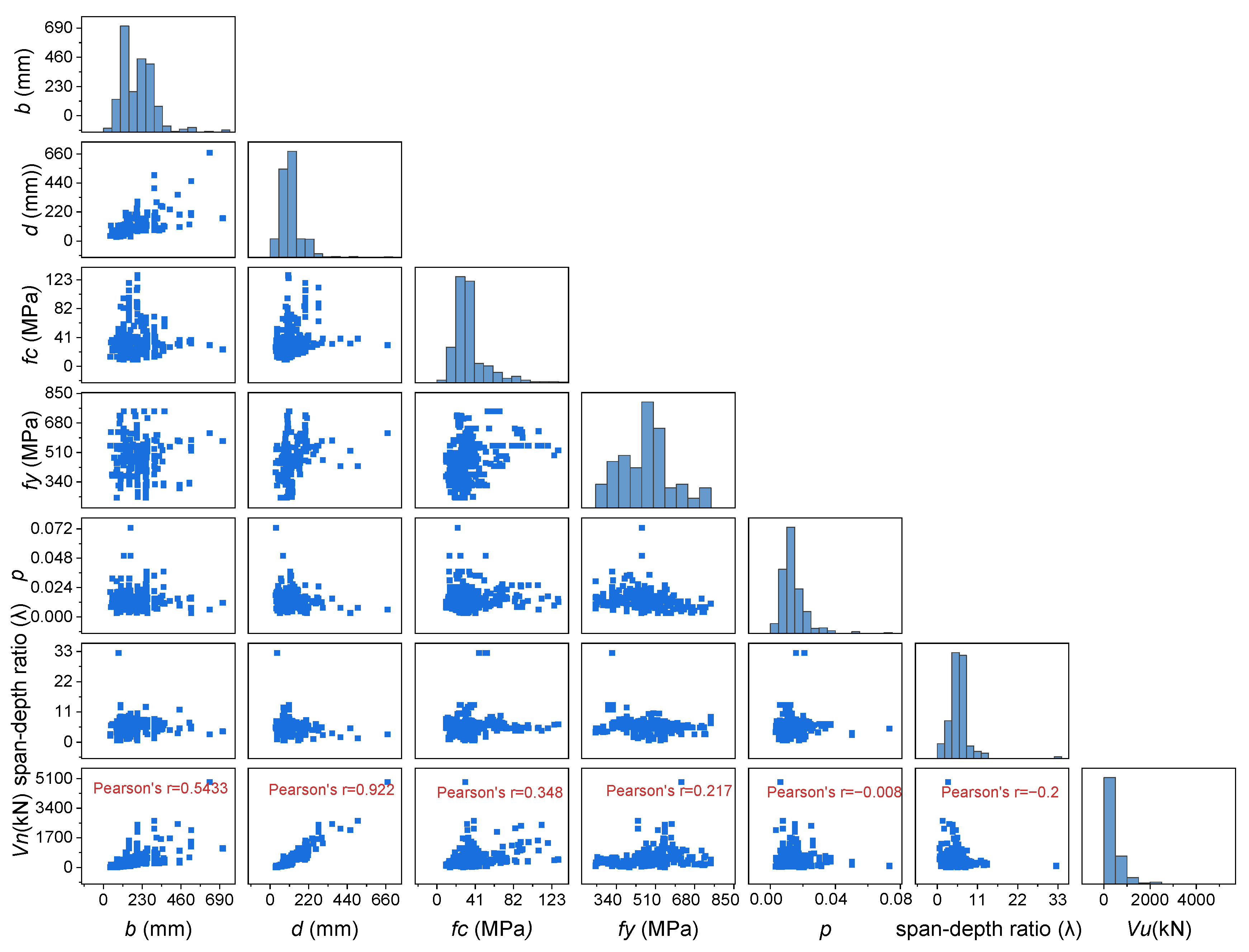
| Data Category | Statistics | b (mm) * | d (mm) * | fc (MPa) * | fy (MPa) * | ρ * | λ * | Vu (kN) * |
|---|---|---|---|---|---|---|---|---|
| Training data | Median | 196.350 | 112.500 | 31.900 | 468.000 | 0.012 | 5.952 | 324.000 |
| Mean | 192.689 | 117.989 | 35.696 | 475.082 | 0.013 | 5.972 | 441.046 | |
| Minimum | 40.055 | 29.970 | 9.401 | 250.000 | 0.003 | 0.612 | 24.000 | |
| Maximum | 707.644 | 668.500 | 130.100 | 749.000 | 0.050 | 32.507 | 4915.000 | |
| Standard deviation | 99.133 | 62.842 | 19.641 | 112.799 | 0.007 | 3.170 | 456.952 | |
| Testing data | Median | 200.000 | 100.000 | 29.546 | 453.600 | 0.013 | 5.685 | 330.000 |
| Mean | 193.885 | 111.895 | 33.209 | 453.680 | 0.015 | 5.910 | 406.104 | |
| Minimum | 51.000 | 33.166 | 11.771 | 250.000 | 0.003 | 1.000 | 44.000 | |
| Maximum | 520.000 | 400.000 | 98.000 | 749.000 | 0.073 | 13.551 | 2224.000 | |
| Standard deviation | 90.321 | 55.409 | 14.841 | 109.773 | 0.009 | 2.144 | 361.110 |
| Statistics | RMSE | R | R2 | MAE |
|---|---|---|---|---|
| Training | 77.1034 | 0.9857 | 0.9716 | 47.9516 |
| Testing | 71.9993 | 0.9806 | 0.9616 | 48.3483 |
| Total | 76.1038 | 0.9849 | 0.9700 | 48.0491 |
| Folds | Performance Measures | ||
|---|---|---|---|
| MAE (MPa) | R2 | RMSE (MPa) | |
| 66.2896 | 0.9430 | 100.1055 | Fold 1 |
| 51.2254 | 0.9581 | 83.0453 | Fold 2 |
| 38.7523 | 0.9465 | 56.0006 | Fold 3 |
| 57.7699 | 0.9410 | 89.9521 | Fold 4 |
| 62.5797 | 0.9697 | 125.1674 | Fold 5 |
| 55.3234 | 0.9517 | 90.8542 | Average |
| 10.8431 | 0.0121 | 25.1970 | SD |
| Parameters | M5P | RF | LR |
|---|---|---|---|
| RMSE | 71.9993 | 92.6412 | 121.9088 |
| R2 | 0.9616 | 0.9339 | 0.8930 |
| MAE | 48.3483 | 58.9602 | 95.4274 |
| Predicted Model | RMSE | MAE | R2 | Statistical Properties of Vactual/VM5P | ||||
|---|---|---|---|---|---|---|---|---|
| μΩ | SD | COVΩ % | Min | Max | ||||
| ACI 318-19 [6] | 181.7370 | 118.6216 | 0.8803 | 1.4486 | 0.4225 | 29.1678 | 0.5641 | 4.2303 |
| BS 8110-97 [5] | 169.9748 | 112.9098 | 0.9595 | 1.3571 | 0.3319 | 24.4572 | 0.7472 | 4.1163 |
| Eurocode 2 (EC2) [7] | 105.8192 | 71.4915 | 0.9571 | 1.2459 | 0.3368 | 27.0321 | 0.7057 | 3.9481 |
| Elshafey et al. [3] | 122.1256 | 72.7415 | 0.9392 | 1.0526 | 0.2811 | 26.7070 | 0.4951 | 3.3695 |
| Elsanadedy et al. [4] | 108.3236 | 68.2791 | 0.9503 | 1.0894 | 0.2935 | 26.9456 | 0.4587 | 3.2054 |
| Chetchotisak et al. [27] | 100.7650 | 59.1147 | 0.9579 | 0.9874 | 0.2416 | 24.4647 | 0.5431 | 3.0663 |
| M5P in this study | 76.3815 | 48.1163 | 0.9700 | 1.0147 | 0.1705 | 16.8060 | 0.6161 | 1.8585 |
| Excluded Variables | Input Variables | Training Set | Testing Set | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| None | (b)(d)(fc)(fy)(ρ)(λ) | 0.9857 | 77.1034 | 47.9516 | 0.9806 | 71.9993 | 48.3483 |
| (b) | (d)(fc)(fy)(ρ)(λ) | 0.9404 (−4.59%) | 116.3163 (+50.9%) | 64.0720 (+33.6%) | 0.9222 (−5.95%) | 108.6096 (+50.85%) | 68.4123 (+41.6%) |
| (d) | (b)(fc)(fy)(ρ)(λ) | 0.6676 (−32.28%) | 271.8977 (+252.7%) | 125.1944 (+161.1%) | 0.5988 (−38.91%) | 228.9639 (+218.0%) | 136.6226 (+182.5%) |
| (fc) | (b)(d)(fy)(ρ)(λ) | 0.9171 (−6.96%) | 140.4382 (+82.2%) | 72.2165 (+50.6%) | 0.9383 (+4.31%) | 93.0885 (+29.3%) | 60.4217 (+25.0%) |
| (fy) | (b)(d)(fc)(ρ)(λ) | 0.9673 (−1.87%) | 82.8514 (+7.45%) | 48.3227 (+0.77%) | 0.9592 (−2.18%) | 75.5153 (+4.88%) | 49.3749 (+2.12%) |
| (ρ) | (b)(d)(fc)(fy)(λ) | 0.9017 (−8.52%) | 152.1536 (+97.4%) | 78.1118 (+62.9%) | 0.9052 (−7.69%) | 113.9448 (+58.3%) | 70.9103 (+46.7%) |
| (λ) | (b)(d)(fc)(fy)(ρ) | 0.9698 (−1.61%) | 79.5789 (+3.22%) | 48.8820 (+1.94%) | 0.9456 (−3.57%) | 84.1065 (+16.8%) | 55.4452 (+14.7%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdallah, M.H.; Thoeny, Z.A.; Henedy, S.N.; Al-Abdaly, N.M.; Imran, H.; Bernardo, L.F.A.; Al-Khafaji, Z. The Machine-Learning-Based Prediction of the Punching Shear Capacity of Reinforced Concrete Flat Slabs: An Advanced M5P Model Tree Approach. Appl. Sci. 2023, 13, 8325. https://doi.org/10.3390/app13148325
Abdallah MH, Thoeny ZA, Henedy SN, Al-Abdaly NM, Imran H, Bernardo LFA, Al-Khafaji Z. The Machine-Learning-Based Prediction of the Punching Shear Capacity of Reinforced Concrete Flat Slabs: An Advanced M5P Model Tree Approach. Applied Sciences. 2023; 13(14):8325. https://doi.org/10.3390/app13148325
Chicago/Turabian StyleAbdallah, Marwa Hameed, Zainab Abdulrdha Thoeny, Sadiq N. Henedy, Nadia Moneem Al-Abdaly, Hamza Imran, Luís Filipe Almeida Bernardo, and Zainab Al-Khafaji. 2023. "The Machine-Learning-Based Prediction of the Punching Shear Capacity of Reinforced Concrete Flat Slabs: An Advanced M5P Model Tree Approach" Applied Sciences 13, no. 14: 8325. https://doi.org/10.3390/app13148325
APA StyleAbdallah, M. H., Thoeny, Z. A., Henedy, S. N., Al-Abdaly, N. M., Imran, H., Bernardo, L. F. A., & Al-Khafaji, Z. (2023). The Machine-Learning-Based Prediction of the Punching Shear Capacity of Reinforced Concrete Flat Slabs: An Advanced M5P Model Tree Approach. Applied Sciences, 13(14), 8325. https://doi.org/10.3390/app13148325







