Life Cycle Cost Model for Life Support Systems of Crewed Autonomous Transport for Deep Space Habitation

Abstract

Intelligent transport systems are used in various transport systems, among which a special place is occupied by crewed autonomous transport systems such as space stations for deep space habitation. These objects have a complex and critical requirement for life support systems (LSSs) to maintain safe and habitable conditions for the crew in the isolated environment. This paper explores the different architectural options for life support systems (LSSs) in autonomous transport systems, specifically focusing on space stations. Three alternative LSS architectures are discussed: Open LSS (OLSS), Closed LSS (CLSS), and Mixed LSS (MLSS). Each architecture has its own advantages and disadvantages. OLSS relies on external resource delivery, reducing initial costs but increasing dependence on resupply missions. CLSS operates autonomously, generating resources onboard, but has higher initial costs and technological complexity. MLSS combines external delivery and onboard generation, providing flexibility and adaptability. The material emphasizes the importance of cost-effectiveness analysis at the early stages of design and identifies the boundary values of mission duration that determine the most effective LSS architecture choice. The material highlights the significance of striking the right balance between cost and performance to develop intelligent ecosystems of LSS for space stations and other autonomous transport systems.

1. Introduction

Currently, the active development of spacecrafts is reaching a new level, which is characterized by an ever-increasing interest in long-term manned stations and the study of the possibility of creating habitable space settlement complexes on space objects closest to the Earth, such as the Moon and Mars:

-

One of the most prominent examples of long-term crewed autonomous transport systems are space stations, like the International Space Station (ISS). The ISS has been continually inhabited since November 2000, serving as a home wherein astronauts perform research to help us understand the effects of long-term space travel on the human body [1,2].

-

National Aeronautics and Space Administration (NASA) and other space agencies are developing autonomous rovers for use on Mars. An example of this is the Mars 2020 Perseverance mission, which aims to seek signs of ancient life and collect samples of rock and regolith (broken rock and soil) for a possible return to Earth [3].

-

Some organizations propose the development of autonomous habitats on the Moon as part of plans for human exploration and settlement of the lunar surface. For instance, NASA’s Artemis program aims to land “the first woman and the next man” on the Moon by 2024, with the intent of establishing a sustainable human presence by 2027 [4].

-

The European Space Agency (ESA) has the Lunar Pathfinder mission, aiming to provide communication services for other lunar missions. They are also part of the larger NASA-led Artemis program, contributing various elements like the European Service Module for the Orion spacecraft [5].

-

ESA is a part of the ExoMars program, working with Roscosmos to search for signs of life on Mars. Their Trace Gas Orbiter is currently in orbit around Mars, studying its atmosphere [6].

-

Some private companies, like SpaceX, are proposing the development of lunar space stations for use as a staging area for human missions to the Moon and beyond. SpaceX’s Starship, designed to carry up to 100 people, is intended to eventually serve as a transport system for crewed missions to destinations such as the Moon and Mars [5,6,7].

-

The Japan Aerospace Exploration Agency (JAXA) has also expressed interest in lunar missions, primarily through robotic explorers. They are planning a series of lunar landers and rovers for the coming years, such as the Smart Lander for Investigating Moon (SLIM) and the more ambitious Human Lunar Systems [8].

-

For Mars, JAXA’s efforts have so far been focused on smaller missions and contributing to international missions. For example, JAXA’s MELOS (Mars Exploration with Lander-Orbiter Synergy) mission is aimed at investigating the Martian environment for the conditions that may have supported life [9].

-

The Indian Space Research Organisation (ISRO) has also made strides in lunar exploration with their Chandrayaan series of lunar scientific missions. Chandrayaan-2, launched in 2019, aimed to soft-land a rover on the lunar south pole, although the landing was not successful [10].

-

ISRO is planning its first mission to Mars called Mangalyaan-2, following the successful insertion of the Mars Orbiter Mission (MOM, or Mangalyaan-1) into the Mars orbit in 2014 [11].

China has been very active in the space domain, rapidly developing its space program over the last two decades:

-

China’s National Space Administration (CNSA) has been expanding its capabilities in satellite technology, space exploration, and human spaceflight. CNSA launched its first manned mission, Shenzhou 5, in 2003, making China the third country to independently send humans into space [12].

-

China has also been advancing its capabilities in long-term crewed missions, demonstrated by the Tiangong space stations. The Tiangong-1 and Tiangong-2 were experimental space stations launched in 2011 and 2016, respectively, wherein astronauts stayed from several days to weeks. These missions served as crucial stepping stones toward establishing a large, modular space station similar to the ISS [13].

-

In 2021, China launched the Tianhe core module: the first module of its planned large modular space station known as the Chinese large modular space station (or the Tiangong Space Station). With this space station, China aims to sustain long-term human presence in space, conducting scientific and technological experiments just like the ISS [14].

-

China’s lunar exploration program has also been noteworthy. The Chang’e program, named after the Chinese moon goddess, has included multiple successful robotic missions to the Moon. Notably, Chang’e 5 successfully returned lunar samples to Earth in 2020, making China the third country to accomplish such a feat, after the U.S. and the former Soviet Union [15].

-

China is also planning crewed lunar missions, potentially including the construction of a lunar base in the long term. In collaboration with Russia, China plans to construct an International Lunar Research Station (ILRS), a comprehensive scientific experiment base on the lunar surface and/or lunar orbit that will be built and utilized in multiple phases [16].

-

Regarding Mars, China’s Tianwen-1 mission successfully entered the Mars orbit in February 2021. This mission included an orbiter, a lander, and a rover, demonstrating a comprehensive approach to Martian exploration. The successful landing and operation of the Zhurong rover marked a major milestone for China’s space program [17].

As is evident, the interest in exploring the Moon and Mars is truly international, with many nations planning missions or collaborations to extend humanity’s reach and understanding of our solar system.

Space stations have a complex and critical requirement for life support systems (LSSs) to maintain a safe and habitable environment for the crew. To achieve this, an intelligent ecosystem of life support systems must be designed and developed, which integrates multiple systems and functions to sustain the crew’s life in space [18,19,20].

An intelligent ecosystem of life support systems must have several key features [21]. It must be robust and reliable, capable of functioning effectively in the extreme and harsh environment of space. The life support system must also be self-sufficient, capable of recycling and reusing resources as much as possible, such as water, air, and food, to minimize the need for resupply missions [22,23]. This requires an analysis of alternative ways to provide the crew with the necessary means of life in order to optimize their methods of delivery and generation while ensuring their availability throughout the mission.

At the same time, even at the early stages of design, arises the task of building a model that would make it possible to evaluate the economic efficiency of life support systems during the entire duration of the mission for various architectures of their construction. This article proposes one of the approaches to solve the problem of choosing the most effective architecture for the life support system, depending on the degree of autonomy and duration of the mission.

2. Related Works

Autonomous life support systems for crewed spacecraft and space stations are critical systems, providing a closed loop control of air, water, food, and waste to keep crew members alive during a mission [24].

Among the various life support resources, food production currently causes the greatest difficulty in terms of the transition to a fully autonomous mode [25]. This is due to several reasons:

-

Growing food in space requires a controlled environment with precise temperature, humidity, and light conditions. Additionally, the food must be nutrient-dense and packaged to withstand the harsh conditions of space travel.

-

Space stations have limited space for growing crops, and the plants must be grown in a confined environment, which can limit the types of crops that can be grown.

-

Growing crops requires significant energy, which must be supplied by the station’s power systems.

-

Developing bioregenerative systems, which can recycle and purify air, water, and waste to support food production is complex and requires further research and development.

The intelligent ecosystem of life support systems must be capable of autonomous operation, requiring minimal human intervention [26]. This will maximize efficiency and minimize the crew’s workload, enabling them to focus on their mission objectives and scientific experiments.

However, advances in plant biology, controlled environment agriculture, and food science are leading to the development of more efficient and effective food production systems for use in space [27].

There are some types of alternative bioregenerative life support systems that have been tested in space conditions [28]. Some examples include:

-

Micro-Ecological Life Support System (MELiSSA) that aims to provide a closed-loop system for the production of food, water, and oxygen for long-duration space missions [29]. It is the European project of circular life support system which includes a large number of recycling functions which are demonstrated on the ground (e.g., MELiSSA Pilot Plant) and in space (e.g., Artemiss).

-

BioMed-1 is a controlled environment and plant-growing system developed as part of the European Space Agency (ESA) initiatives [28].

-

Veggie is a similar BioMed-1 plant-growing system developed by NASA [30].

-

MOSPECS is a microbial life support system that uses microorganisms to produce oxygen, remove carbon dioxide, and break down waste [28].

-

Mars Oxygen In-Situ Resource Utilization (MOXIE) is a system that can use the Martian atmosphere to produce oxygen by separating carbon dioxide (CO₂) from Martian air and then decomposing CO₂ into oxygen and carbon monoxide [31].

-

In-Situ Resource Utilization (ISRU) is designed to use the local resources of the Martian ecosystem (soil, atmosphere, ice) to produce life support resources [32].

Many of these systems have been tested on the ISS and are being developed for the possibility of fully autonomous food production for deep space flights in the future [28].

To replenish the resources of the life support systems of space stations, cargo spacecrafts are used to replenish this resource. Today, these resources are delivered to space stations by cargo spacecrafts, such as the Russian Progress spacecraft, the European Automated Transfer Vehicle, and the Japanese H-II Transfer Vehicle, as well as by commercial spacecrafts, such as SpaceX’s Dragon spacecraft [33].

Completely abandoning the delivery of life support resources and switching to an autonomous mode of replenishing them at stations can be considered when the following conditions are met [34]:

-

Advanced life support technologies are developed and tested to allow for full resource recycling within the station, including air, water, and food.

-

Reliable and efficient systems for waste management, including human waste, are established.

-

The ability to produce essential resources, such as oxygen and food, through local ISRU methods.

-

Adequate storage capacity is available for excess resources and waste.

-

Robust communication and control systems are in place to monitor and maintain the life support systems.

-

A comprehensive backup system is available in case of failures or malfunctions.

The development of autonomous life support systems would significantly reduce the dependence on resupply missions and increase the sustainability of long-duration missions [35].

There are not only technological but also economic factors that play a role in the transition to full autonomy in life support systems for deep space missions:

-

Eliminating or reducing the frequency of resupply missions can significantly reduce the overall mission cost.

-

Autonomous life support systems can provide a more sustainable and self-sufficient operation, reducing the need for frequent resupply missions.

-

Reducing the reliance on resupply missions and ensuring autonomous resource replenishment can increase the safety of the crew.

-

Autonomous life support systems can enable longer missions and increase the operational capabilities of the station, leading to new scientific and exploration opportunities.

The important role of the LSS is also found in the fact that, at present, it is these systems that limit the transfer of this class transport systems to a fully autonomous mode.

However, the development and implementation of fully autonomous life support systems require significant investment in research and development, which can be a barrier to their widespread adoption. Additionally, there may be challenges in establishing the necessary infrastructure and supply chains for ISRU technologies [36]. These factors must be considered when evaluating the economic feasibility of transitioning to full autonomy in life support systems, especially for deep space missions.

The intelligent ecosystem of life support systems must also be cost-effective, considering the cost of development, production, maintenance, and replacement. The overall cost of the mission must be minimized, and the life support system must be designed to minimize the impact on the budget while maintaining the required performance.

The decision on the architecture of life support systems must be made at the early stages of their creation, evaluating their effectiveness in terms of cost, reliability, and sustainability [37]. For this purpose, it is advisable to apply life cycle costing models that estimate the costs associated with various components of the system, including the costs of development, production, operation, and maintenance [38,39,40].

In Table 1 is an overview of some common life cycle cost (LCC) models often used in assessing complex, long-term technical systems and their brief description, advantages, and disadvantages.

Table 1. Description of life cycle cost models.

Model, References	Description	Advantages	Disadvantages
Advanced Missions Cost Model (AMCM) [41,42,43]	AMCM is developed by NASA’s Jet Propulsion Laboratory. It focuses on estimating costs for planetary science missions but can be adjusted for other mission types. It uses parametric cost estimating relationships based on historical mission data.	Tailored to space mission costs, covering a wide range of mission types.	It is heavily based on historical mission data, which may not fully account for advances in technology or unique mission parameters.
NASA-Air Force Cost Model (NAFCOM) [44,45,46]	NAFCOM is a cost estimation model used for predicting the cost of space hardware. It uses regression analysis of historical data to develop cost estimating relationships.	Useful for predicting the cost of spacecraft and launch vehicles, including subsystems.	Relies on historical data, which may not reflect current trends or advancements. Also, it may not account for new, unique, or highly innovative designs.
Spacecraft/Vehicle Level Cost Model (SVLCM) [47,48,49,50]	SVLCM is designed to estimate the costs associated with spacecraft or vehicle design and development. It is based on a database of past spacecraft and vehicle programs.	It can estimate costs at different stages of a project, from preliminary design to launch.	It is limited by the accuracy and relevance of its historical database. New technology or unique requirements may not be adequately represented.
Project Cost Estimating Capability (PCEC) [51,52,53]	PCEC is a parametric cost estimating tool developed by NASA for human and robotic space exploration missions. It uses cost estimating relationships based on historical NASA and commercial space project data.	It includes a risk analysis capability and can produce estimates in a short time frame.	As with other historical-data-based models, it may not fully account for new technologies, novel mission designs, or rapidly changing industry trends.
Parametric Estimating Relationships (PERs) [54,55,56]	PERs model costs based on relationships between system characteristics (parameters) and historical costs.	Effective for early stage design when details are not fully known.	Can be less accurate as it relies on historical data, which may not always reflect future scenarios.
Engineering Cost Modeling (ECM) [57,58,59]	ECM uses engineering calculations to estimate the costs of individual system components.	High precision if component-level information is available.	Requires a significant amount of detailed information and expert knowledge.
Activity-Based Costing (ABC) [60,61,62]	ABC estimates costs by looking at the resources consumed by activities in each process.	Very detailed and accurate cost breakdown.	Requires in-depth knowledge of processes and resources used.
System Dynamics Cost Modeling (SDCM) [63,64,65]	SDCM is a method for understanding the behavior of complex systems over time.	Considers interactions and feedback within the system, giving a holistic view.	Requires extensive knowledge of the system dynamics.
Design-To-Cost (DTC) [66,67,68]	DTC is a management strategy and methodology to determine and manage the optimal balance between operational capabilities and life cycle costs.	Ensures cost-effectiveness and affordability from the start.	May limit innovation and performance as cost becomes a primary design constraint.

The use of life cycle costing models in the early stages of design makes it possible, on the one hand, to ensure that investments are reliable and pay off in the long term, and on the other hand, to identify all potential design problems at an early stage before they become more serious, resulting in cost savings and improved overall productivity.

This paper proposes a model for determining the boundary conditions of economic efficiency for various options for building intelligent life support systems for manned autonomous vehicles.

3. Materials and Methods

The life cycle cost (LCC) of any system includes both the initial investment costs for development and production, and the operating costs over the life of the system. When building an LCC model, it is necessary to consider the interdependence of all factors, in which changes in one factor can have a significant impact on the overall LCC of the system. Applied to non-life support systems, this LCC model can be used to calculate combinations of autonomous systems with both fully renewable resources and delivery by cargo spacecrafts, as well as to evaluate trade-offs between different life support systems in terms of cost and sustainability.

In the LCC model of life support systems for autonomous transport systems with crews, it is necessary to take into account various functional components:

-

The complexity of the life support system, including the number and variety of components, can have a significant impact on the cost of the system.

-

The degree of autonomy of the system, including the number and complexity of automated functions, can also affect the cost of the system.

-

The technology and materials used in the life support system can impact its cost, particularly if cutting-edge or specialized technologies are required.

-

The scale of production, including the number of units to be produced and the level of investment required for production, can also impact the cost of the system.

-

Development costs, including the cost of design, engineering, testing, and certification, can have a significant impact on the overall cost of the system.

-

The ongoing costs of maintenance and operation, including spare parts, repairs, and replacement, should also be considered in the cost model.

-

The duration of the mission, including the length of time the life support system will be in operation, can also impact the cost of the system.

Let us consider one of the approaches to the construction of this LCC model, taking into account most of these factors. Table 2 shows the main notation used in constructing the model equations.

Table 2. Notations used in the model.

Notations	Parameters
$T_m$	- Autonomous vehicle mission time
$\gamma$	- Volume of life support resources (LSRs) consumption by the crew for 1 day
$s_1$	- Cost of LSRs consumed by crew members in one day
$\mathsf{\Omega }={\mathsf{\Omega }}_A+{\mathsf{\Omega }}_{\overline{A}}$	- LSS architecture that fully meets the needs of the LSRs crew
${\mathsf{\Omega }}_A$	- On-board component of the LSS architecture, autonomously meeting the needs of the LSRs crew on the vehicle through their reproduction
${\mathsf{\Omega }}_{\overline{A}}$	- A component of the LSS architecture, the resources generated which must be replenished externally.
$\eta ={\mathsf{\Omega }}_A/\mathsf{\Omega }$	- Degree of autonomy of LSS
$C_{\mathsf{\Sigma }}\left(\mathsf{\Omega },t\right)$	- LSS Life Cycle Cost
$C_{\eta }\left(\mathsf{\Omega },t\right)$	- Cost of development and production of LSS architecture with a degree of autonomy $\eta$
$C_r\left(\mathsf{\Omega },t\right)$	- The cost of delivery of external LSRs not generated on board the transport system of the autonomous component of the LSS architecture during the mission
$C_m\left(\mathsf{\Omega },t\right)$	- Cost of consumed external LSRs per mission
${\tau }_{\eta }$	- The time after which it is required to replenish the LSRs with the degree of autonomy of the $\eta$
$u$	- Number of freight transport flights during the delivery mission and replenished on the autonomous transport system
$c_1$	- The cost of one flight of a cargo spacecraft
$z_0$	- Maximum value of LSRs delivered by one cargo spacecraft (CS)
$c_0$	- Cost of a fully autonomous LSS

The assessment of the efficiency of the life support systems (LSSs) for the mentioned autonomous transport system is based on the evaluation of the total cost throughout its life cycle:

$$C\left(\mathsf{\Omega },t\right)=C_{\eta }\left(\mathsf{\Omega },t\right)+C_r\left(\mathsf{\Omega },t\right)+C_m\left(\mathsf{\Omega },t\right)$$

(1)

We frame the challenge of designing the architecture for the life support system in an autonomous transport system as the development of an LSS with an optimal architecture, denoted as ${\mathsf{\Omega }}_{opt}$. The objective is to minimize the total cost incurred over the mission duration $T_m$:

$$C\left({\mathsf{\Omega }}_{opt},t\right)=min\left\{\left(C\left(\mathsf{\Omega },t\right)|t=T_m\right)\right\}$$

(2)

There are three alternative LSS architectures for the examined ecosystem:

-

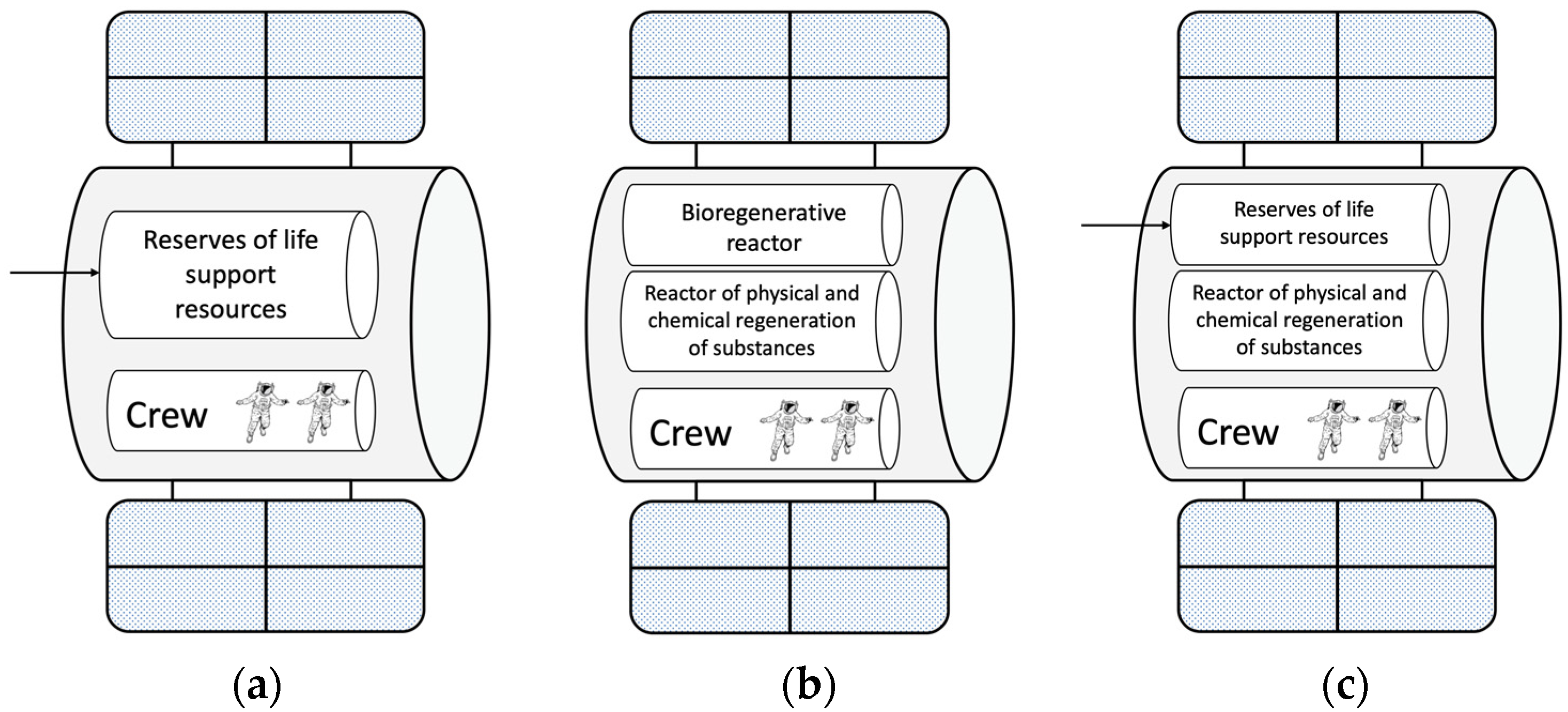
Open LSS (OLSS). It is a completely non-autonomous life support system in which all resources are provided from the outside through delivery by means of cargo carriers. LCC of non-autonomous life support system (Figure 1a): $C_1\left(\mathsf{\Omega },t\right){|}_{\eta =0}$.

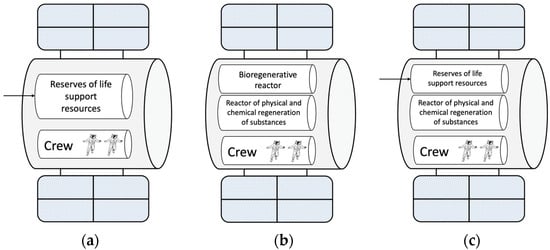Figure 1. Alternative LSS architectures: (a)—Open LSS, (b)—Closed LSS, (c)—Mixed LSS.

-

Closed LSS (CLSS). The life support system is fully autonomous, in which all resources are generated on board the transport system and do not require external support. LCC of autonomous life support system (Figure 1b): $C_2\left(\mathsf{\Omega },t\right){|}_{\eta =1}$.

-

Mixed LSS (MLSS). It is a mixed-type life support system, in which part of the life support resources are generated on board an autonomous transport system, and part of them are delivered from the outside by freight transport. LCC of mixed system (Figure 1c): $C_3\left(\mathsf{\Omega },t\right){|}_{0<\eta <1}$.

4. Results

The model of the dependence of the LSS cost on the degree of autonomy is important at the early steps of LSS concept design for crewed autonomous transport for deep space habitation still in the beginning of mission development. This could help to identify trends and patterns in the data and make predictions about the cost of life support systems with different levels of autonomy. This type of model can be used to make predictions about the cost of life support systems with different levels of autonomy and to determine the optimal level of autonomy that balances cost and performance.

Each alternative architecture—OLSS, CLSS, and MLSS—offers unique advantages and disadvantages (Table 3). The choice of architecture depends on mission objectives, resource availability, budget constraints, and the desired level of autonomy and self-sufficiency.

Table 3. Advantages and disadvantages of different alternative LSS architectures.

Life Support System Architecture	Advantages	Disadvantages
Open LSS	OLSS relies on external delivery of resources, reducing the need for complex onboard resource generation and recycling systems. This leads to lower initial development costs. OLSS does not require sophisticated resource recycling and regeneration systems, simplifying the overall system design. OLSS adapts to changes in resource requirements or technological advancements through external resupply missions.	The main drawback of OLSS is its reliance on external cargo carriers for resource delivery. This dependence on resupply missions introduces logistical challenges, including cost, scheduling, and the risk of potential disruptions or delays. OLSS lacks full autonomy in resource generation and recycling, relying on external sources for critical resources. This limits the system’s ability to operate independently for extended periods. The frequent delivery of resources through resupply missions has an environmental impact due to increased launch activities and waste generated from disposable containers.
Closed LSS	CLSS operates independently, generating and recycling all necessary resources onboard. This provides greater self-sufficiency and reduces dependence on external resupply missions. CLSS is well-suited for long-duration missions, as it can sustain the crew’s needs for extended periods without relying on external resources. CLSS minimizes the need for frequent resupply missions, resulting in reduced environmental impact from launch activities and waste generation.	The need for complex resource generation and recycling systems for full autonomy results in higher initial development costs for CLSS. The complexity of advanced technology and reliable systems in CLSS increases the risk of failures or malfunctions. The inability to adapt to changes in mission requirements or evolving technologies without significant redesign and reengineering is a limitation of CLSS.
Mixed LSS	MLSS combines the advantages of both OLSS and CLSS by allowing for a mix of external resource delivery and onboard resource generation. This provides flexibility and adaptability to varying mission requirements. MLSS reduces the dependence on external resources by incorporating autonomous resource generation capabilities, mitigating the risks associated with relying solely on resupply missions. MLSS offers a balance between the lower initial development costs of OLSS and the higher self-sufficiency of CLSS, making it a potentially cost-effective option.	MLSS increases technical challenges and system complexity due to the need for both external resource management and onboard resource generation systems. The integration of external resource delivery and onboard resource generation systems in MLSS requires careful coordination for seamless operation and resource management. The partial reliance of MLSS on external resource delivery limits its ability to operate independently for extended durations.

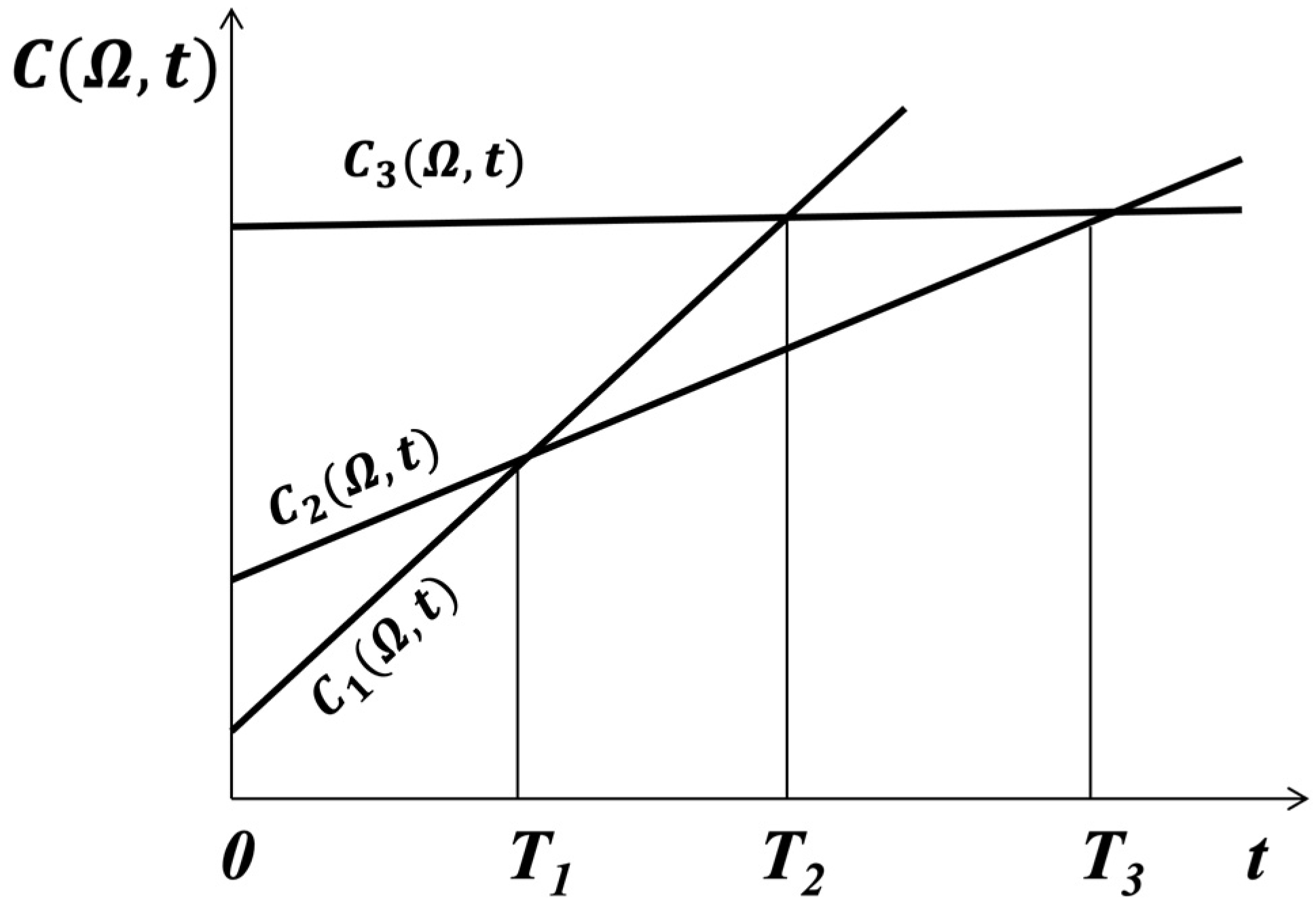
To select the most effective solution, we will use the dependence of the cost of the life cycle of the LCC on the duration of the mission and its chosen architecture (Figure 2).

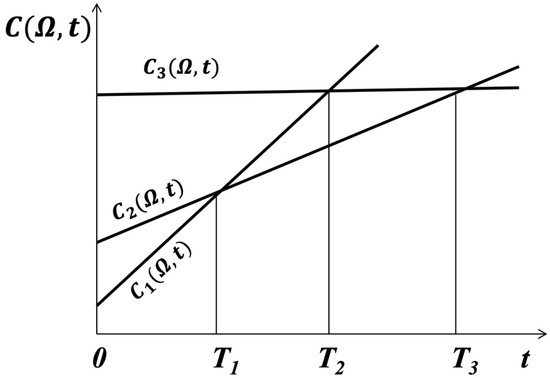
Figure 2. The function of the dependence of the cost of the life cycle of LSS on time.

The cost graphs $C\left(\mathsf{\Omega },t\right)$ exhibit a relationship of specific life support system architecture denoted as $C_1\left(\mathsf{\Omega },t\right)$—for OLSS, $C_2\left(\mathsf{\Omega },t\right)$—for MLSS, and $C_3\left(\mathsf{\Omega },t\right)$—for CLSS. The initial value of each line corresponds to the design and production cost, and the slope of these lines is correlated with specific operating costs associated with each architecture.

The search for optimal solutions in practice should be solved in the field of alternative pairs of LSS architectures:

• For an OLSS–MLSS pair, the boundary condition is the point $T_1$. When the condition $T_m<T_1$ is met, a completely non-autonomous life support system would be more efficient in terms of life cycle cost. If the condition $T_m>T_1$ is met, a mixed-type life support system would be more efficient in terms of life cycle cost.
• For a CLSS–MLSS pair, the boundary condition is the point $T_3$. When the condition $T_1<T_m<T_3$ is met, a mixed-type life support system would be more efficient in terms of life cycle cost. If the condition $T_m>T_3$ is met, a fully autonomous life support system will be more efficient in terms of life cycle cost.

In the class of OLSS–CLSS systems, the search for a solution from a practical point of view does not make sense, because the transition from a completely non-autonomous to a fully autonomous life support system without an intermediate consideration of the mixed system is impossible. Therefore, determining the value of $T_2$ from a practical point of view is of no interest.

To determine mission duration boundary values $T_1$ and $T_3$, which determine the decision-making on the choice of the most effective LSS architecture, we determine the cost of the LSS life cycle for each of the alternative architectures.

4.1. Fully Autonomous Life Support System $\left(\eta =1\right)$

With a fully autonomous LSS architecture, all LSRs are generated on board the autonomous transport system and do not need to be replenished externally.

$$\begin{gathered} C_r\left(\mathsf{\Omega },t\right)=0, \\ {C}_m\left(\mathsf{\Omega },t\right)=0, \\ C\left(\mathsf{\Omega },t\right){|}_{\eta =1}=C_{\eta }\left(\mathsf{\Omega },t\right)+C_r\left(\mathsf{\Omega },t\right)+C_m\left(\mathsf{\Omega },t\right)=C_{\eta }\left(\mathsf{\Omega },t\right)=c_0 \end{gathered}$$

(3)

4.2. Completely Non-Autonomous Life Support System $\left(\eta =0\right)$

In the absence of life support elements on the autonomous transport system, all life support resources should be replenished from the outside with the help of cargo vehicles.

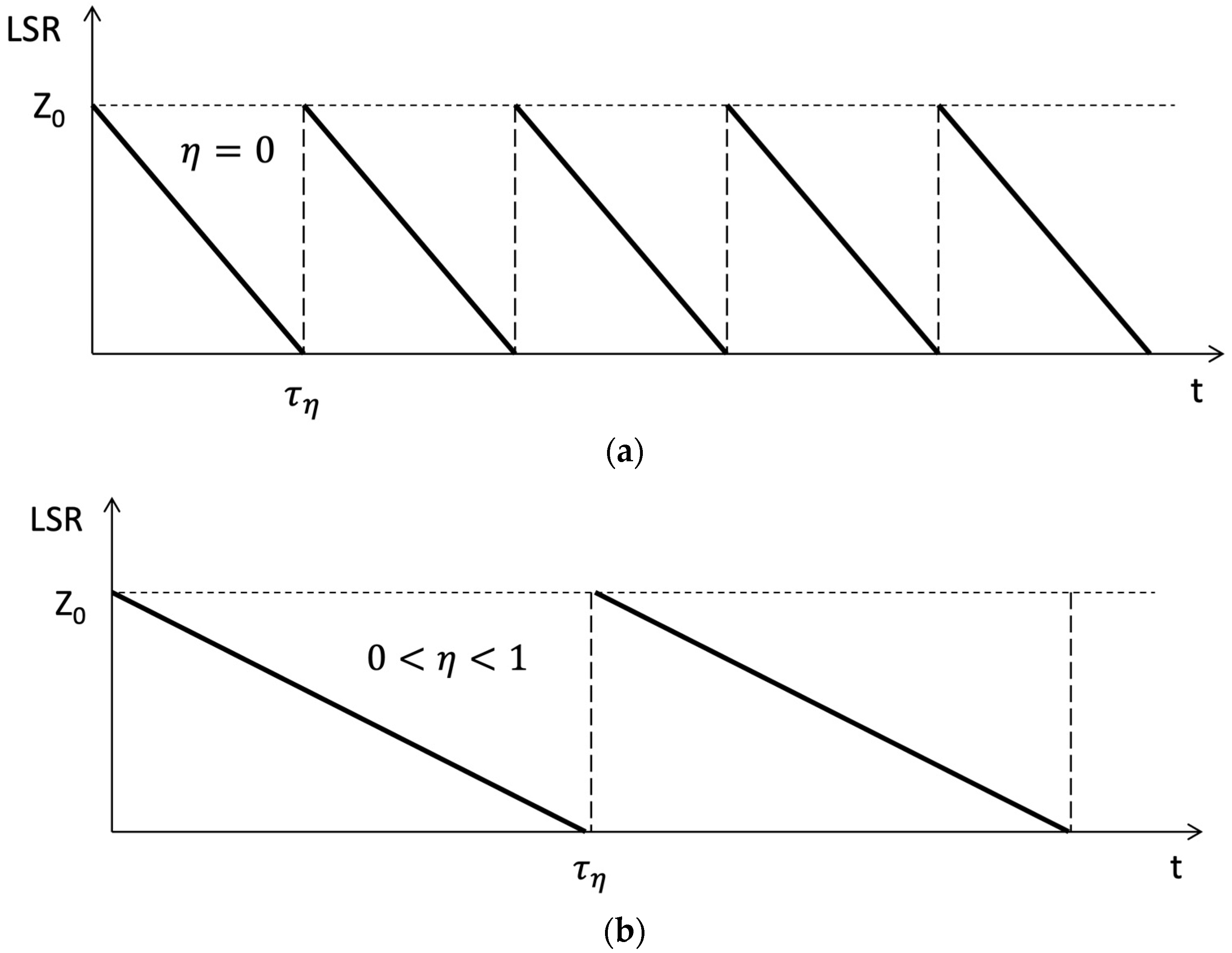
With the LSR volume of the CS, $z_0$ LSR replenishment periodicity is required over time ${\tau }_0$ (Figure 3a):

$${\tau }_0={\tau }_{\eta =0}=z_0/\gamma$$

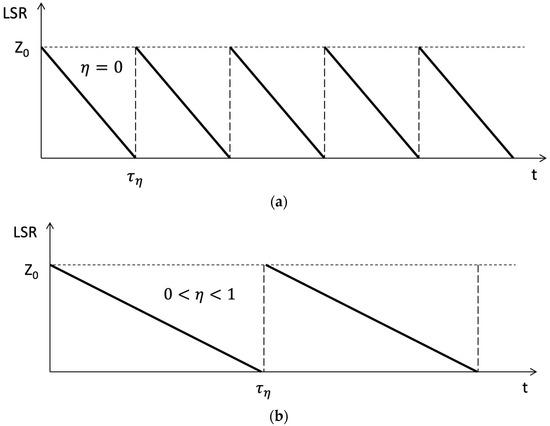
Figure 3. The function of replenishing life support system resources at different levels of LSS autonomy. (a)—for OLSS architecture, (b)—for MLSS architecture.

The maximum value of life support resources delivered by one cargo spacecraft $z_0$ is the maximum amount of essential life support resources, such as food, water, air, and other consumables, which can be transported and delivered to a space station or autonomous habitat by a single cargo spacecraft during a resupply mission.

In this case, during the mission we will need $u=T_m/\tau$ as the number of trips of a CS and the cost of shipping the life support resources will be

$$C_r\left(\mathsf{\Omega },t\right)=c_{1}u=\frac{c_1{T}_m\gamma }{Z_0}$$

(4)

The cost of the LSRs consumed by the crew during the mission will be

$$C_m\left(\mathsf{\Omega },t\right)=s_1{T}_m$$

(5)

Since with this method of providing the crew with LSR resources there are no on-board components of the LSS architecture,

$$C_{\eta }\left(\mathsf{\Omega },t\right){|}_{\eta =0}=0$$

(6)

In this case, the lifecycle cost of this LSS architecture according to expression (1) and considering (4)–(6) takes the form

$$C\left(\mathsf{\Omega },t\right){|}_{\eta =0}=T_m\left(s_1+\frac{c_1\gamma }{z_0}\right)$$

(7)

4.3. Mixed Life Support System with Partially Autonomous LSS Functions $(0<\eta <1)$

Part of the LSS is placed on board the autonomous transport system and part of the life support resources generated by it are generated on the spot and do not require replenishment by delivery by a cargo vehicle. This makes it possible to more fully use the releasing volume of the truck to deliver a larger part of the LRSs not generated on the autonomous system itself, which in this case is enough for a longer time (Figure 3b):

$${\tau }_{\eta }=\frac{z_0}{\gamma \left(1-\eta \right)}$$

At the same time, the number of flights of a cargo vehicle during the mission will be

$$u=\frac{T_m}{{\tau }_{\eta }}=\frac{T_m\gamma \left(1-\eta \right)}{z_0}$$

In this case, the cost of shipping the LSR will be

$$C_r\left(\mathsf{\Omega },t\right)=c_{1}u=\frac{c_1{T}_m\gamma \left(1-\eta \right)}{Z_0}$$

The cost of the LSRs consumed by the crew during the mission will be

$$C_m\left(\mathsf{\Omega },t\right)=s_1\left(1-\eta \right)T_m$$

The greatest difficulty in analyzing the cost of the LSS life cycle in the early stages of its creation is the determination of the cost of its architecture, which is located on an autonomous transport system. In the work [38] based on experimental data, it is shown that the specified cost is well approximated by power functions, which allows for the expression to be used to describe the cost of the LSS architecture:

$$C_{\eta }\left(\mathsf{\Omega },t\right){|}_{0<\eta <1}=c_0{\eta }^b$$

(8)

where $b$ is some coefficient, the value of which can be determined experimentally [38]. Dependence (8) is confirmed by the experimental studies given in [38].

For this LSS architecture under consideration, the cost of its life cycle based on the resulting expressions will be determined as follows:

$$C\left(\mathsf{\Omega },t\right){|}_{0<\eta <1}=C_{\eta }\left(\mathsf{\Omega },t\right)+C_r\left(\mathsf{\Omega },t\right)+C_m\left(\mathsf{\Omega },t\right)=c_0{\eta }^b+\left(1-\eta \right)T_m\left(\frac{c_1\gamma }{z_0}+s_1\right)$$

(9)

This section delineates an in-depth analysis of various life support system architectures tailored to space stations for a diverse range of missions. This analysis is conducted through the application of Formulas (3), (7) and (9), each modeling the LSS life cycle cost for a particular type of architecture.

Expression (3) lends itself to the characterization of the life cycle cost for a fully physical–chemical life support system, probing into the nuances of initial cost dependencies and system structures. Expression (7) describes the life cycle cost for a hybrid life support system, offering a comprehensive view of operational costs while encapsulating the interactions between the physical–chemical and bioregenerative components. Lastly, Equation (9) is applied to a fully bioregenerative life support system, amalgamating the concepts addressed in the previous formulas to present a holistic understanding of the life cycle cost in such a system.

The above-mentioned models give a detailed, quantitative framework for analyzing, comparing, and ultimately designing different architectures of life support systems, each catering to different types of space missions. This framework as a methodological tool enhances the decision-making process in early design stages, providing researchers with key insights to inform their design choices of future space missions.

5. Discussion

In the context of the provided Figure 2, the boundary values of the duration of missions $T_1$ and $T_3$ are critical in determining the most effective life support system architecture choice.

$T_1$ represents the mission duration below which the Open LSS architecture is deemed to be the most effective option. This boundary value is determined based on factors such as the cost and logistical feasibility of resupply missions. When the mission duration is relatively short, it may be more cost-effective and practical to rely on external resource delivery through resupply missions, rather than investing in complex onboard resource generation and recycling systems. Below $T_1$, OLSS offers advantages in terms of lower initial development costs and reduced system complexity.

The boundary value of $T_1$ can be defined by equating expression (8) to expression (9):

$$T_1=\frac{c_0{\eta }^{b-1}{z}_0}{c_1\gamma +s_1{z}_0}$$

In this case, with the duration of the mission $T_m<T_1$ from a cost-effective point of view, it is advantageous not to use a mixed LSS architecture.

$T_3$ represents the mission duration beyond which the Closed LSS architecture becomes the most effective choice. This boundary value is determined by considering factors such as the increased cost efficiency and self-sufficiency of CLSS over extended durations. CLSS, with its fully autonomous resource generation and recycling capabilities, is well-suited for long-duration missions wherein dependence on external resupply missions may become impractical or costly. Beyond $T_3$, CLSS offers advantages in terms of greater self-sufficiency, reduced reliance on external resources, and minimized environmental impact from reduced resupply missions.

The boundary value of $T_3$ can be defined by equating expression (3) to expression (9):

$$T_3=\frac{c_0{z}_0\left(1-{\eta }^b\right)}{\left(1-\eta \right)\left(c_1\gamma +s_1{z}_0\right)}$$

In this case, with the duration of the mission $T_m>T_3$ from a cost-effective point of view, it is advantageous to use a fully autonomous LSS, which ensures the production of all LSRs on board.

The range between $T_1$ and $T_3$ represents the domain wherein the Mixed LSS architecture becomes the most effective option. MLSS combines aspects of both OLSS and CLSS, offering a balance between cost-effectiveness and self-sufficiency. Within this range, the mission duration allows for a mix of external resource delivery and onboard resource generation, striking a balance based on factors such as cost, logistical feasibility, and desired level of autonomy.

Of real practical interest is the determination of the boundary value of $T_3$, because at present, as it was shown in the first sections of this article, various LSS configurations are actively used in practice, and it is interesting to compare them with architectures that provide fully autonomous generation of LSRs directly on autonomous transport systems.

The focus of this paper is on developing a conceptual cost model for life support systems in autonomous space systems at an early design stage. The goal is to propose a methodology that allows for a high-level understanding of the trade-offs between different life support system architectures, taking into account a range of factors such as mission duration and system autonomy.

However, it is important to note the inherent complexity and uncertainty involved in these models, especially at the early design stages:

• Simulating the effectiveness of the proposed model requires access to detailed data and parameters, many of which are not publicly available due to the sensitive nature of space exploration activities. Also, it is worth noting that the effectiveness of different life support systems will heavily depend on specific mission parameters, technological advancements, and even unpredictable factors like crew behavior, which can be challenging to simulate accurately.
• Defining the exact parameters and their interdependencies would require extensive data and experimental results, which are usually proprietary information of space agencies or private companies. As an open-source academic paper, this work is meant to propose a framework that can be adapted and refined based on specific mission details and as more data become available.
• Performance analysis and comparisons would necessitate access to confidential and detailed data about the actual performances of various life support systems. Also, given the novelty and variability of the systems, comparing them in a meaningful way can be challenging.
• A comprehensive analysis would require an in-depth understanding of the unique contexts and constraints of different mission scenarios, which often are not public knowledge.

While the limitations above make it challenging to include a comprehensive exploration of the proposed model, this work provides a framework for decision-making on life support system architecture. It helps to outline the factors to consider and provides a mathematical representation of the trade-offs, which are important and useful even if their component values are not exactly known.

6. Conclusions

Life support systems are critical components of crewed autonomous transport for deep space habitation and the need for life cycle cost models in the early stages of design cannot be overstated.

In this paper, three architectures of the LSS intellectual ecosystem are considered as alternatives: (1) open LSS in which all life support resources (LSRs) are provided from the outside through delivery by means of cargo carriers; (2) closed LSS in which all LSRs are generated on board the transport system and do not require external support; (3) mixed LSS in which part of the LSRs are generated on board an autonomous transport system, and part of them are delivered from the outside by freight transport.

This paper proposes a mathematical model of LSS life cycle cost that makes it possible to estimate the costs of creating and operating a LSS in the early stages of design to choose its most effective architecture, depending on the degree of autonomy.

This life cycle cost models of life support systems for autonomous transport systems at an early stage of their design are important and can be useful even though their component values are not known exactly for several reasons:

• The life cycle cost model can be used for budget planning and resource allocation, making it easier to determine project feasibility and prioritize development.
• The model can help focus efforts on areas that can have the greatest impact on the overall cost of a system and can be used to compare design options and make trade-offs between cost and performance.
• Even if the exact cost of components is not known a priori, the life cycle cost model can be updated as more information becomes available. This can help improve the accuracy of cost estimates over time, making it easier to make informed decisions.

This article defines the boundary conditions of economic efficiency for choosing various options for building intelligent architectures of the LSS ecosystem for crewed autonomous transport for deep space habitation.

The proposed life cycle cost model for life support systems can be extended to areas not related to space flights, but wherein there are similar problems and requirements. For example, the proposed approach can be adapted to the analysis of life support systems in extreme conditions, such as deep-sea exploration, Arctic stations, remote oil platforms, and others. Of course, in this case, it will be necessary to take into account additional conditions, for example, climatic ones. However, this is not difficult to achieve even within the framework of the proposed models. For example, taking into account the indicated climatic conditions is easily carried out within the framework of the same LSS models:

• Climate conditions can influence the consumption rates of resources within the life support system. For example, in Arctic environments, colder temperatures may increase energy requirements for heating, while in hot and humid climates, additional resources may be needed for cooling and ventilation. These variations in resource consumption rates can be included in the equations by adjusting the corresponding parameters.
• Climate conditions can influence the logistics and resupply planning for the life support systems. Extreme weather events or seasonal variations may affect the availability and feasibility of delivering resources. Considering these climate-related logistics challenges is possible in the proposed equations. They help optimize the architecture of life support systems according to this factor.
• Climate conditions may require specific adaptations or modifications to the life support system design. For instance, in extreme cold environments, additional insulation or heating systems may be necessary, while in hot and arid conditions, water conservation and efficient cooling technologies may be prioritized. Design solutions for adaptation to climate can be taken into account in the proposed equations by appropriately changing the value of the initial costs for the development of LSS. At the same time, the life cycle cost models of various LSS architectures do not undergo changes.

By including domain-specific variables and adjusting the model parameters accordingly, it becomes possible to estimate the cost implications and optimize the design of life support systems for these case studies. In this case, the model becomes a tool for assessing the cost and feasibility of sustainable living environments, ecologically clean communities, or self-sufficient systems. While the specific applications of the value model may vary, the underlying concepts and principles remain relevant and adaptable.