Uniform Circle Formation for Fully, Semi-, and Asynchronous Opaque Robots with Lights ^†

Abstract

In the field of robotics, a lot of theoretical models have been settled to formalize multi-agent systems and design distributed algorithms for autonomous robots. Among the most investigated problems for such systems, the study of the Uniform Circle Formation (UCF) problem earned a lot of attention for the properties of such a convenient disposition. Such a problem asks robots to move on the plane to form a regular polygon, running a deterministic and distributed algorithm by executing a sequence of look–compute–move cycles. This work aims to solve the UCF problem for a very restrictive model of robots: they are punctiform, anonymous, and indistinguishable. They are completely disoriented, i.e., they share neither the coordinate system nor chirality. Additionally, they are opaque, so collinearities can hide important data for a proper computation. To tackle these system limitations, robots are equipped with a persistent light used to communicate and store a constant amount of information. For such a robot model, this paper presents a solution for UCF for each of the three scheduling modes usually studied in the literature: fully synchronous, semi-synchronous, and asynchronous. Regarding the time complexity, the proposed algorithms use a constant number of cycles (epochs) for fully synchronous (semi-synchronous) robots, and linearly, many epochs in the worst case for asynchronous robots.

1. Introduction

The last decade has seen a major increase in the development and dissemination of distributed environments for mobile entities, e.g., sensor networks, multi-robot systems, and drone swarms, having a great impact in several different contexts. Along with the application studies in the robotics and electronics fields [1,2,3,4,5], computer science research has attempted to design theoretical models [6,7,8,9,10] which best formalize and simulate generic distributed systems, and to study efficient algorithms for some primitive tasks. Such an analytical investigation aims at providing a rigorous and universal methodology to study the collaborative strategies for mobile multi-agent systems [10,11,12,13], model peculiar real-world scenarios [14,15,16], prove and analyze the correctness of algorithmic solutions [17,18], and investigate their computational complexity [19,20,21,22,23].

Several theoretical models have been introduced for these purposes: agents, also called robots, act under several assumptions about their capabilities and about a particular scenario. Models of great importance are the ones where robots are autonomous, i.e., they work without central control, and operate through a sequence of look–compute–move cycles in which each robot (i) takes the snapshot of the system(look), (ii) executes a deterministic algorithm (compute), and (iii) travels to the computed destination (move) [9,22,23,24].

Different model assumptions are considered, affecting the computational power of robots [19,21,22,23]. Generally, robots are assumed to be point-like, anonymous (without any distinct identifiers yielding the ability to distinguish one robot from another), and oblivious (without any persistent memory). In order to consider more powerful and realistic models, the luminous robot [11,20,21,22,25,26,27] has been introduced: robots equipped with a persistent light assuming different colors. Since such a light color is preserved from one look–compute–move cycle to the next one, it can be used as a persistent constant memory and a means of communication as well.

Another step towards realistic models is to work, not with point-like (punctiform model) robots, but fat robots [13,28,29], where all robots are supposed to be solid discs with a certain radius. Moreover, robots can be transparent [13,19,30], enabling complete visibility of the system, or opaque [11,26,31].

Depending on the nature of the problem, robots can move either on the Euclidean plane, or on a graph [22,23] which can either be known in advance or not. Concerning robot activation policy, three modes are proposed in the literature: fully synchronous (fsynch), where all robots execute their cycle synchronously, semi-synchronous (ssynch), where robots in a subset execute their cycle synchronously whereas the others remain idle, and asynchronous (asynch), where each robot acts asynchronously.

Several research efforts focus on very basic classes of geometric pattern formation problems to be solved within such distributed environments [10,11,32,33]. In the Gathering problem, robots are required to meet in a certain location. Solutions to this problem are provided in [34] for asynch robots with limited visibility, in [29] for a few fat asynch robots, and in [28] for fat fsynch robots with limited visibility. In [14,15], Gathering is tackled for robots that move on a ring, coping with two fault models: with a mobile malicious agent [15] and with a stationary faulty node (black hole) [14].

The Circle Formation problem requires robots to displace upon a common circle. In [13], this problem is solved for asynchronous fat transparent robots moving freely on the plane, while in [31] asynchronous opaque robots moving on an infinite grid are considered.

In the Uniform Circle Formation (UCF) problem [26,30,35,36,37], robots are required to move to the vertices of a common regular polygon whose number of vertices—which can or cannot be known in advance—is exactly the number of robots in the system. This problem has received a lot of attention (see, e.g., [36] for a survey) for both theoretical and practical reasons. From a practical point of view, a regular layout may present several advantages for a distributed system. E.g., in a network of mobile agents, it may be convenient to regularly displace them to facilitate communications, visibility and computations. Every agent is equidistant from its neighbors and has the same view of the system: this guarantees a fair communication, where there are no evident differences in the energy spent in sending messages. Moreover, this uniform pattern allows to implement distributed algorithms which guarantee a fair load balancing among agents.

So far, swarms of transparent robots have been mainly considered in the UCF investigation. However, such a full visibility feature might not turn out to be realistic. Accordingly, obstructed visibility can represent a constraint making the model more interesting and realistic, although more difficult to manage. In such an opaque model, if three robots are collinear, the middle robot obstructs the vision of the other two. So, whenever collinearities occur, some robots may have a wrong perception of the actual global number of agents in the system and, more generally, of the configuration of the whole system itself. In this realm, the first natural problem to be tackled is Complete Visibility, where robots are required to displace on the plane so that each robot is visible to all others. Since robot opaqueness turns out to be a critical issue, some additional capabilities for robots might be considered. In particular, solutions in the literature are proposed for luminous robots. Such a well-studied functionality turns out to be a natural minimal enhancement to solve several tasks (see, e.g., [19,20,21,22,23,25]). In [38], a $\mathcal{O}(logN)$ time algorithm is given, solving Complete Visibility by using $\mathcal{O}\left(1\right)$ colors in the asynch mode. Moreover, the problem is solved with a constant amount of time and colors both for the ssynch mode [39] and for the asynch one [40]. In [16], a fault-tolerant algorithm for Complete Visibility is exhibited. Overall, a strategy for reaching a configuration where every robot can see the entire swarm can be used as a sub-routine in all those problems where robots need to count themselves (as in UCF, [26]).

Related Works and Main Contributions

This paper investigates the UCF problem for a swarm of opaque and luminous robots. Such a problem has been investigated and solved under different combinations of system assumptions in order to point out the minimal sets of features for its solution. In [35,37], the problem is solved for fat robots, but (partially) oriented. Specifically, the authors of [37] cope with transparent and fat robots, which agree on one axis of their coordinate systems, operating in the ssynch mode. The algorithm in [35] solves the UCF problem for a swarm of fat, opaque, but oriented (they share a common coordinate system) robots in the asynch mode. In [30], the authors provide a solution for transparent, disoriented, and non-rigid robots, in the asynch mode. The work in [26] exhibits an algorithm solving the UCF problem for swarms of opaque luminous robots only in the fsynch mode, featuring six cycles and a constant number of colors. In all the above-cited works, robots solve the problem without colliding.

The current paper considers robots sharing the same features as [26], and aims to improve and complete its algorithmic investigation. Specifically, all three synchronization modes are examined here; as a matter of fact, this paper provides three algorithmic solutions to solve the UCF problem by opaque luminous robots in the fsynch, ssynch, and asynch modes. In particular, the algorithm for the fsynch mode improves the one in [26] in that it uses only three instead of six cycles and a constant number of colors. The ssynch mode is solved within constant time (epochs) and a constant number of colors. Finally, the algorithmic strategies are adapted in order to obtain a solution for the asynch mode, working in linear time (epochs) in the worst case and with a constant number of colors.

2. Preliminaries

This section aims to formally introduce the distributed system (e.g., model features, robot synchronization and computation) under consideration. Such formal preliminaries are preparatory for the definition of the UCF problem, which will be given at the end of this section. Informally, the UCF problem requires a swarm of n robots with very specific features to move on the plane and form a regular n-gon, so that each robot lies on a vertex of the polygon. After the formation of such a pattern, no robot will move.

2.1. Robot Features

Consider a finite set (swarm) of punctiform computational agents, called robots, which forms a distributed system located in the Euclidean plane ${\mathbb{R}}^2$. These robots are as follows:

(i)

Anonymous and indistinguishable: they do not share any own identifier;

(ii)

Autonomous: there is no central coordinator;

(iii)

Homogeneous: they execute the same deterministic algorithm;

(iv)

Mobile: they can freely move on the plane, provided they never collide;

(v)

Undisturbed: they cannot be stopped by any adversary before reaching the computed destination (rigid model).

The robots are equipped with sensory capabilities to spot the positions of other robots. The following limitations on robots are assumed:

(i)

They do not know how many they are;

(ii)

They are disoriented: no agreement among the individual coordinate systems, nor on unit distance and chirality (roughly speaking, agreement on clockwise direction);

(iii)

They are opaque (not transparent): collinearities cause obstructed visibility.

Indeed, these latter three inabilities introduce complications in the algorithm design. E.g., due to opacity (iii) and lack of knowledge of the number of robots (i), each robot may not be able to know whether or not some robots are hidden at any given time. Moreover, the disorientation (ii) might cause robot collisions which may compromise system integrity. To deal with these adversities, robots are equipped with a light displaying a certain number of different colors they can communicate through (see, e.g., [19,20,21,22,23,25]). Such a light is the only means robots have to exchange information and represent a constant memory they can use to store some information. Except for the lights, they do not have other persistent memory.

2.2. Configuration

Let $\mathcal{R}$ be the finite set of all robots in the swarm, $\mid \mathcal{R}\mid$ being unknown to each robot. Let $Colors$ be the finite set of colors the light of each robot can assume to communicate.

Given a fixed coordinate system $\omega$ on ${\mathbb{R}}^2$, the configuration of $r\in \mathcal{R}$ at time t is defined as the pair ${\varphi }_{\omega }^t\left(r\right)=(po{s}_{\omega }^t\left(r\right),ligh{t}^t\left(r\right))$, where $po{s}_{\omega }^t\left(r\right)$ are the coordinates in ${\mathbb{R}}^2$ where r is located at time t according to $\omega$, and $ligh{t}^t\left(r\right)$ is the color in $Colors$ of the light of r in that instant. For the sake of simplicity, the lighter notation ${\varphi }^t\left(s\right)$ will be used whenever there is no ambiguity about the used coordinate system.

2.3. Visibility

For any pair of robots $r,s\in \mathcal{R}$, r sees s (formally, $r\bowtie s$) if and only if (i) either $r=s$ or (ii) there does not exist a third robot sitting on the line segment joining r and s. Let $Vi{s}^t\left(r\right)=\{s\in \mathcal{R}\mid r\bowtie sattimet\}$ be the set of all the robots visible by r at time t. It is clear that r has a complete visibility of the whole swarm $\mathcal{R}$ at time t whenever $Vi{s}^t\left(r\right)=\mathcal{R}$.

2.4. Snapshot

Let $\mathbb{A}$ be the deterministic algorithm that each robot r has to execute according to its own local coordinate system ${\omega }_r$, unit distance, and chirality. If $r\bowtie s$ at time t, then r senses only its position $po{s}_{{\omega }_r}^t\left(s\right)$, and its light $ligh{t}^t\left(s\right)$, and no other information on s. The snapshot of r at time t is defined as the set $snapsho{t}_r^t=\{{\varphi }_{{\omega }_r}^t\left(s\right)\mid s\in Vi{s}^t\left(r\right)\}$.

2.5. Cycle

Each robot r operates in look–compute–move atomic cycles. Each cycle at time t consists of these steps:

• Look: the robot r takes the instantaneous snapshot $snapsho{t}_r^t$ according to its coordinate system ${\omega }_r$.
• Compute: r runs the deterministic algorithm $\mathbb{A}$ which, by having $snapsho{t}_r^t$ as sole input, computes the destination point of r and the (possibly) new color for the light of r. Formally, $\mathbb{A}\left(snapsho{t}_r^t\right)={\varphi }_{{\omega }_r}^{t^{\prime }}\left(r\right)$, where $t^{\prime }>t$ will be the time the current cycle ends.
• Move: r sets its new color and, then, moves straight towards the destination point computed above, without being stopped (rigidity assumption). If r stays still, it performs a null movement.

2.6. Collision

The model investigated in this paper does not tolerate either multiplicity (no robot can occupy the same location of another robot at the same time) or overlapping trajectories, so that $\mathbb{A}$ has to guarantee that, for any given moving robot, its trajectory (even null) has no points in common with the trajectory of any other moving robot. Formally, an overlapping trajectory between r and s occurs when (i) r is moving from a to $a^{\prime }$, (ii) s is traveling from b to $b^{\prime }$, and (iii) $\overline{a{a}^{\prime }}$ and $\overline{b{b}^{\prime }}$ have points in common. Both multiplicity and overlapping trajectories are considered as collisions.

2.7. Synchronization

Concerning robot activation and synchronization, different modes are studied in the literature:

• In the fully synchronous mode (fsynch), time is logically subdivided into global rounds, and all robots are activated at each round. Since look–compute–move cycles are executed atomically, all robots terminate their cycle by the next round. Moreover, all robots start and finish each cycle step (look, compute, move) at the same instant.
• The semi-synchronous mode (ssynch) coincides with the fsynch mode, except that not all robots are necessarily activated at each round. However, every robot is activated an infinite number of times (fairness condition).
• In the asynchronous mode (asynch), the robots are activated independently from each other, and each robot executes its look–compute–move cycle within an unpredictable but finite amount of time. In this mode, the snapshot taken by a robot during its look phase—used to compute its final destination—may not represent the real system configuration when the robot starts moving.

For the ssynch and the asynch modes, an appropriate way to measure time is addressed by the notion of an epoch. An epoch is the amount of time within which each robot will be activated at least once. The fairness condition ensures each epoch lasts a finite time.

2.8. Computation

Let ${\mathit{C}}_t=\{{\varphi }^t\left(r\right)\mid r\in \mathcal{R}\}$ be the system configuration at time t, given a fixed coordinate system on ${\mathbb{R}}^2$. A system configuration is said to be valid if there is no multiplicity. Let $\mathcal{C}$ be the set of all the valid system configurations. Let ${\mathit{C}}_0\in \mathcal{C}$ denote the initial configuration of the system, where all robots in $\mathcal{R}$ have lights off.

In the fsynch and ssynch modes, let $⊢\subseteq {\mathcal{C}}^2$ be the relation such that ${\mathit{C}}^{\prime }⊢{\mathit{C}}^{\prime \prime }$ if and only if the configuration ${\mathit{C}}^{\prime \prime }$ is reachable from ${\mathit{C}}^{\prime }$ by executing a round, where all the activated robots simultaneously accomplish their look–compute–move cycle, without colliding. A computation on $\mathcal{R}$ is a sequence of valid configurations ${\mathit{C}}_0,\cdots ,{\mathit{C}}_t,{\mathit{C}}_{t+1},\cdots$ such that the following applies:

(i)

${\mathit{C}}_0$ is the initial configuration;

(ii)

${\mathit{C}}_t⊢{\mathit{C}}_{t+1}$ for every $t\ge 0$.

Such a computation reaches a terminal configuration${\mathit{C}}_{{\mathit{t}}_{\mathit{end}}}$ whenever ${\mathit{C}}_{{\mathit{t}}_{\mathit{end}}}={\mathit{C}}_t$ for any $t>t_{end}$.

Even if in the asynch mode a computation on $\mathcal{R}$ cannot be described by a fixed discrete time scale, the system is said to reach a terminal configuration if it achieves a system configuration that will never change in the future.

2.9. The UCF Problem

Let a fsynch, ssynch, and asynch swarm of n robots be in any given initial valid configuration ${\mathit{C}}_0$. The UCF problem asks the swarm to move from ${\mathrm{C}}_0$ to a valid terminal configuration in which robots lay on the vertices of a regular n-gon.

3. Some Notions and Results

Consider a swarm of n robots and assume all of them sit on their smallest enclosing circle (SEC). Two distinct robots $p,q$ on the SEC delimit two arcs $\stackrel{⌢}{pq}$ (clockwise and counterclockwise); p and q are adjacent whenever there is at least one of the two arcs $\stackrel{⌢}{pq}$ upon which no other robot sits. Clearly, in a robot swarm forming a regular n-gon, each pair $p,q$ of adjacent robots forms an angle $\frac{2\pi }{n}$ with the center O of the SEC, formally $\widehat{pOq}=\frac{2\pi }{n}$. Such an angle will be called the base angle of the n-gon.

Let $Colors$ be the set of the possible colors, where each color is represented by a string. Along the paper, the following name convention will be used: any given robot whose light color is a string with prefix pivot or angle is called a pivot or an angle robot, respectively. Pivot and angle robots will be set to fix the base angle, and some strategic segments within the SEC; the other robots will use these strategic segments to reach their own target positions. According to this, the following definitions are now given:

Definition 1.

For $2\le k\le n$, let $(r_1,r_2,\dots ,r_k)$ be a k-tuple of distinct robots on the SEC (centered on O). Such a tuple is called a regular k-tuple if it satisfies the following conditions:

• $\widehat{r_{i}O{r}_{i+1}}=\frac{2\pi }{n}$ for every $1\le i<k$;
• $r_i$ is a pivot or angle robot for every $1\le i\le k$;
• For odd k, just the central robot $r_{\lceil \frac{k}{2}\rceil }$ can be a pivot;
• For even $k>2$, just the two central robots $r_{\frac{k}{2}}$, $r_{\frac{k}{2}+1}$ can be pivots simultaneously.

The strategies to move the robots on the vertices of a regular n-gon (inscribed in the SEC) start by setting particular regular $\{2,3,4,5\}$-tuples. These tuples will not move for the whole computation, while the other robots will move to complete the regular n-gon.

From now on, unless otherwise stated, given two points $a,b$ on the SEC, the arc $\stackrel{⌢}{ab}$ refers to the minor arc joining a and b on the SEC.

Definition 2.

Let $r_1$ and $r_2$ be two robots on the SEC, and let $d_1$ and $d_2$ be the opposite endpoints of the diameters passing through $r_1$ and $r_2$, respectively. The overlap arcs for $r_1$ and $r_2$ are the arcs $\stackrel{⌢}{r_1{d}_2}$ and $\stackrel{⌢}{r_2{d}_1}$ (see Figure 1).

Clearly, if $r_1$ and $r_2$ sit on the endpoints of the same diameter, their overlap arcs have null length.

Theorem 1.

Let n be the number of robots lying on the SEC.

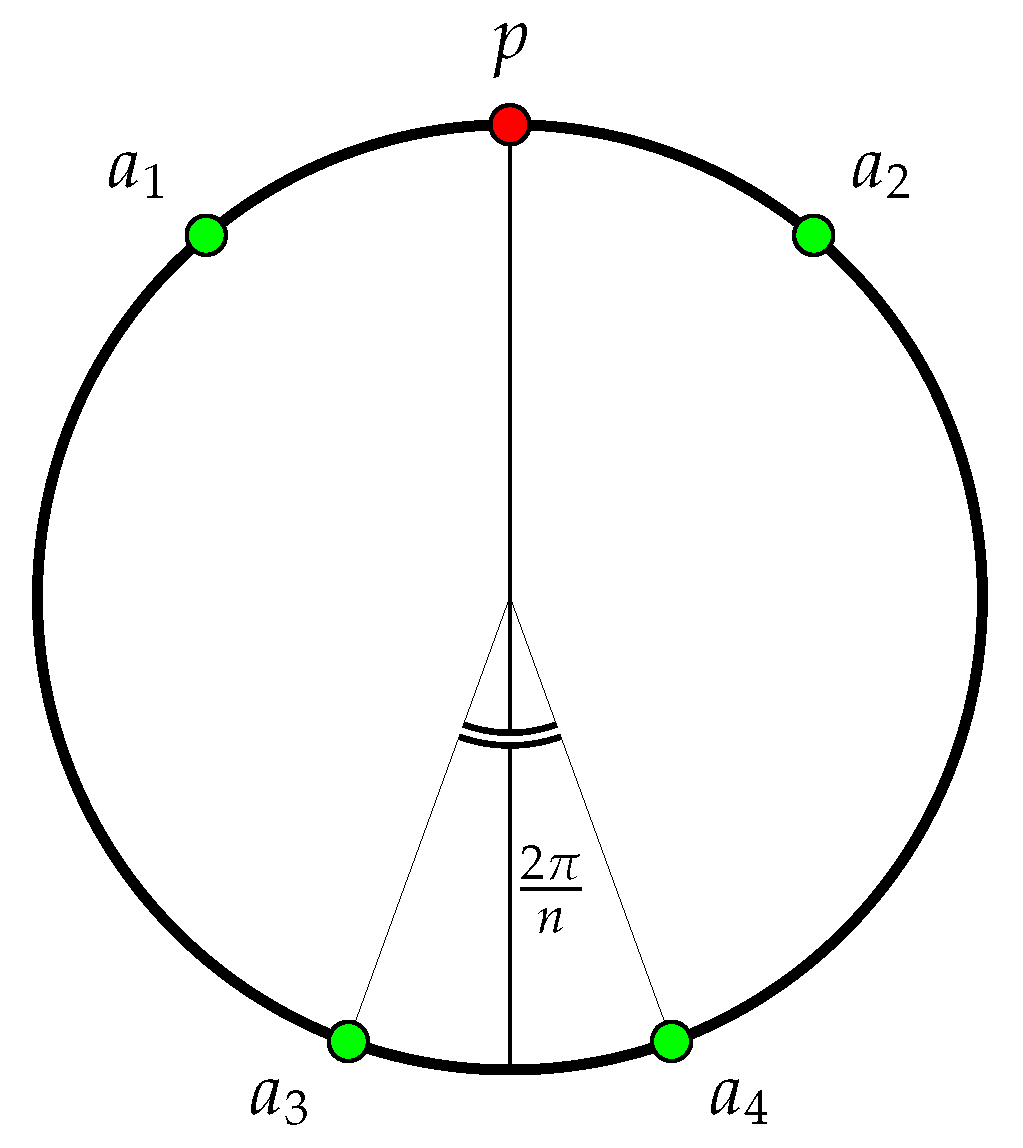
• For odd n, there exists a diameter passing through a robot and dividing the SEC into two halves, each having $\frac{n-1}{2}$ robots.
• For even n, there exists a diameter dividing the SEC into two halves such that $\left(i\right)$ either the diameter passes through just one robot and the half-SECs have $\frac{n}{2}$ and $\frac{n}{2}-1$ robots, or $\left(ii\right)$ the diameter passes through two (opposite) robots and the half-SECs have $\frac{n}{2}-1$ robots each.

Proof. 

Consider an odd n, and reason by induction on n. For $n=1$, the property follows straightforwardly. Now, assume the property holds true for an odd $n>1$, and let us prove the property for $n+2$. Let us rule out two robots, say $r_1$ and $r_2$, having minimal overlap arcs $\stackrel{⌢}{a}$ and $\stackrel{⌢}{a^{\prime }}$, so that n robots are left on the SEC. So, by the induction hypothesis, there exists a diameter D passing through a robot and dividing the SEC into two halves, each having $\frac{n-1}{2}$ robots. Notice that, by Definition 2, no robot can sit on $\stackrel{⌢}{a}$ and $\stackrel{⌢}{a^{\prime }}$, and since D passes through a robot, it clearly cannot leave $r_1$ and $r_2$ on the same half-SEC. Whence, the result follows. For even n, the proof is similar.  □

One method to find specific properties of the SEC configuration is to consider the strings composed of the adjacent angles formed by robots.

Definition 3.

Given a handedness direction (clockwise or counterclockwise), consider an arc H of the SEC, and the list $r_1\cdots r_m$ of m robots on H, so that $r_i$ and $r_{(i+1)}$ are adjacent for every $1\le i<m$ (following the given direction). Let e ($e^{\prime }$) be the endpoint of H which is adjacent to $r_1$ ($r_m$). Let ${\alpha }_i$ be the angle defined as  

$${\alpha }_i=\left\{\begin{array}{cc}\widehat{eO{r}_1}\hfill & \mathrm{if}i=0\hfill \\ {\widehat{r_{i}Or}}_{(i+1)}\hfill & \mathrm{if}i\in \{1,\cdots ,m-1\}\hfill \\ \widehat{r_{m}O{e}^{\prime }}\hfill & \mathrm{if}i=m\hfill \end{array}\right.$$

where O is the center of the SEC.

The angle-string related to the arc H is the sequence $\left({\alpha }_0\right){\alpha }_1\cdots {\alpha }_{m-1}\left({\alpha }_m\right)$ where ${\alpha }_0$ or ${\alpha }_m$ is omitted if it is a null angle (i.e., if $r_1$ or $r_m$ lies on e or $e^{\prime }$).

Note that the definition of angle-string generalizes also to the case when H coincides with the whole SEC, provided that a starting (and ending) endpoint e is fixed. Given a valid lexicographical conversion, SEC angle-strings (i.e., related to the whole SEC) or arc angle-strings (i.e., related to specific arcs) play a crucial role in locating strategic segments (diameters or chords) within the SEC.

Except for the rotational symmetry case with more than two sectors, the presented algorithms aim to split the SEC into two half-SECs through a specific diameter, called the main diameter. The main diameter is unequivocally defined by specific geometric properties of the configuration. To maintain it throughout the whole computation of the algorithm, specific robots elect themselves as pivots, move in specific positions, and light themselves with a proper pivot color. These pivots unequivocally define the main diameter even after the break of the initial geometric properties.

In the next sections, a precise explanation of the selection of the main diameter will be stated. After the election of the main diameter, one regular tuple, say $\tau$, or two opposite regular tuples, say $\tau ,{\tau }^{\prime }$, are formed to fix the main diameter until the end of the algorithm. In fact, if $\stackrel{⌢}{c}$ is the arc of the SEC covered by $\tau$, the main diameter is the diameter passing in the middle point of $\stackrel{⌢}{c}$.

Let d be the elected main diameter, in a configuration where all the robots lay on the SEC. Let b be one of the nearest robots to d but not laying on d, and let $\ell \left(b,d\right)$ be the distance from b to d. Moreover, let $\nu$ be one of the closest vertices of the regular polygon not belonging to d that has to be formed by the robot swarm.

Definition 4.

Let $d^{\prime }$ and $d^{\prime \prime }$ be the two opposite chords parallel to a main diameter d, at distance $\frac{min\{\ell (b,d),\ell (\nu ,d\left)\right\}}{2}$ from d. The segments $d^{\prime }$ and $d^{\prime \prime }$ are called the safe diameters of d (see Figure 2).

For rotational symmetries with more than two sectors, safe chords will be considered instead of safe diameters:

Definition 5.

Let $(a_1,p_1,a_2)$ and $(a_3,p_2,a_4)$ be two adjacent regular 3-tuples (i.e., without any other 3-tuple on the arcs $\stackrel{⌢}{a_2{a}_3}$ or $\stackrel{⌢}{a_1{a}_4}$), and suppose that $p_1$ and $p_2$ are not the two endpoints of the same diameter. The chord joining $p_1$ and $p_2$ is called the safe chord (see Figure 3).

Pivots and angle robots are made to move to set either the main diameter or safe chords which divide the SEC into sectors with the same amplitude and on which robots are evenly distributed. This setting can be achieved in just one round (in the fsynch mode), provided robots share a common clockwise direction in the sector they sit on:

Definition 6.

Two or more robots are said to be oriented whenever they agree on a common clockwise direction.

Angle-strings are also used to fix a global or local handedness orientation to the system. In particular, from each robot, two angle-strings start, clockwise and counterclockwise. Given a proper string conversion, groups of robots can be elected according to the lexicographical order of the $2n$ angle-strings, n being the number of the robots.

Theorem 2.

Given three oriented robots and three distinct robot-free points on the same arc of the SEC, it is always possible for the three robots to reach these points in a single round and avoid collisions.

Proof. 

Let $e_1$ and $e_2$ be the endpoints of the arc. By joining $e_1$ with $e_2$, the arc can be regarded as a circle. Such a circle consists of the three consecutive arcs delimited by the three points to be reached by the three robots. The following three cases can occur:

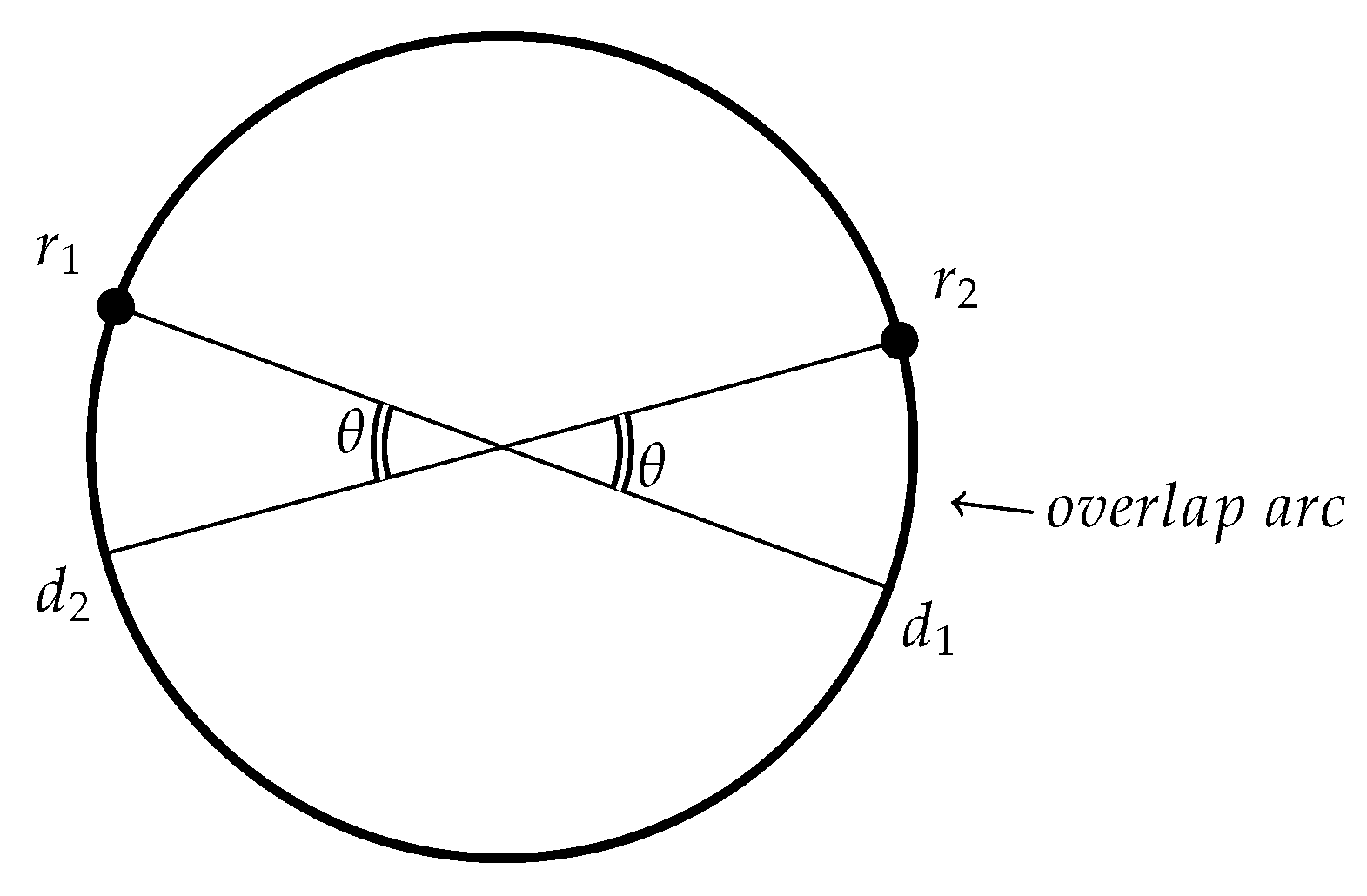
• The three robots sit on the same arc: The two external robots reach the two endpoints of the arc they sit on, traveling without collision. This enables the third robot to reach the third point without any collision as well.
• Two robots sit on one arc, and the other in another arc: As the previous case, for the two robots in the same arc. The third robot can reach the third point safely.
• One robot per each arc: By traveling according to the common orientation, robots move to their final destinations without collisions.

 □

4. Preliminary Steps

This section shows some well-known preliminary actions to be taken by the swarm, which are summarized in the following:

• To form a regular n-gon, any robot in a swarm of n robots needs to know n. This may be achieved by first solving the Complete Visibility problem, where all robots are asked from any given valid initial system configuration to reach a terminal configuration where each robot is visible to all others. At this point, n can be clearly computed at a glance. However, n cannot be stored by robots, since they are equipped with constant memory. Hence n will be somehow readily fixed in the topology of the swarm. A possible solution to Complete Visibility moves robots to the vertices of their convex hull. To this end, the algorithms in [39,40] can be used in order to solve Complete Visibility on fsynch, ssynch and asynch modes using a constant amount of time and colors.
• Next, each robot takes its snapshot (look), computes the smallest enclosing circle (SEC) e.g., by Welzl’s algorithm [41] (compute), and eventually moves radially towards the SEC (move). Clearly, such movements cannot collide, since each trajectory is radial to the same center. It might be the case that two robots (and, of course, no more than two) sit on the same radial trajectory. However, by computing distances from the two possible final destinations, they can easily choose to move in opposite directions and reach the two diametrically opposite locations. At the end of this preliminary phase, all robots lie on the SEC upon which the final regular n-gon will be formed. It is important to note that this SEC will not change along the whole execution of the algorithms. This step can be achieved in just one round/epoch, without any specific color light (i.e., they can maintain their current color).
• Let $C_H$ be the swarm configuration at this point, where all robots are vertices of a convex hull inscribed within their SEC. If $C_H$ is a perfect convex hull [42], all robots lie on the edges of the associated regular $\frac{n}{2}$-gon (called supporting polygon, SP), two robots per edge. In this case, the regular n-gon can be easily set by making robots slide along the edges of the SP until they reach the vertices of the target n-gon. Given a perfect convex hull, the SP is unique and does not change while robots are sliding on its edges (this guarantees the correctness of this strategy also in the ssynch and asynch modes). So, each activated robot takes its snapshot (look), checks whether the system configuration forms a perfect convex hull and computes the SP (compute), eventually slides along the edge until it reaches the correct vertex of the regular n-gon (move). Notice that two robots on the same edge head in opposite directions, and therefore no collision occurs. Note that a biangular configuration (a set of $n\ge 2$ robots forms a biangular configuration if robots lie on a circle C centered on O, and two non zero angles $\alpha ,\beta$ exist such that for every pair r and p of robots adjacent on C, it holds that $\widehat{rOp}\in \{\alpha ,\beta \}$ and $\alpha$ and $\beta$ alternate clockwise [42]) and a regular polygon pattern are special cases of perfect convex hull. Also in [30], the perfect convex hull and the biangular configuration are dealt with as special cases at the beginning of their algorithm.
  This possible preliminary step takes just one round/epoch, without changing the current color of the robots.

After the previous three preliminary steps, two different scenarios can occur: either the configuration is already a regular polygon or ${\mathit{C}}_{\mathit{H}}$ is not a perfect convex hull. In the first scenario, the algorithm ends. For the second scenario, the three strategies to form a regular polygon for the fsynch, ssynch, and asynch modes are now outlined.

5. The Algorithm for the Fully Synchronous Mode

Let ${\mathit{C}}_{\mathit{H}}$ be the swarm configuration at this point; without loss of generality, robot lights are assumed to have the same color.

5.1. Summary of the Algorithm

The strategy of the algorithm aims at finding and adopting regular tuples in $C_H$ as follows:

• Selects unambiguously some robots to be the pivots of the future regular tuples (see Definition 1).
• Makes some robots move to form regular tuples with the selected pivots. Indeed, these movements are not necessary if the regular tuples are already formed. Once the regular tuples are settled, the involved robots will not move anymore, thus fixing once and for all the base angle $\frac{2\pi }{n}$ of the regular n-gon to be formed.
• Makes the other robots compute their destination points (on the basis of the regular tuples) and move to form the regular polygon.

Moreover, the algorithm must deal with the following issues:

• Robots have constant memory (color lights). So, some information, such as the cardinality of the system, cannot be stored.
• Obstructed visibility can cause deadlocks and collisions in certain system configurations. To avoid them, robots will lie and move safely onto specific segments, namely safe diameters and chords (see Definitions 4 and 5). No robot will cross these safe segments.
• In the fsynch mode, an algorithm is efficient if it can fully exploit parallelism (roughly speaking, if it makes the most of the robots move simultaneously during the same round, hence leading to quick executions). Thus, the algorithm has to avoid situations yielding strictly sequential dynamics.

The next subsections show how the algorithm works, cycle by cycle.

5.2. Cycle 1: Pivot Selection and Angle Setting

From $C_H$, the algorithm starts setting the regular tuples. The algorithmic dynamic depends on the degree of symmetry of $C_H$. Three cases must be considered: asymmetry, symmetry with exactly one axis, and rotational symmetry.

Asymmetry. Consider the case of asymmetry, i.e., no symmetry axis exists in $C_H$. However, there exists at least one diameter passing through a robot and dividing the SEC into two halves, upon which robots distribute according to Theorem 1. The robot swarm must agree on one such diameter, say D, which will be the main diameter. To find D, robots agree on starting from a commonly designated robot x and following a common orientation on the SEC. The following lemma is needed to perform this task:

Lemma 1.

Starting from the configuration $C_H$ and in case of asymmetry, all robots on the SEC are able to unambiguously agree on a robot x.

Proof. 

Let r be any given robot on the SEC. It considers all possible $2n$ SEC angle-strings, and unambiguously chooses one of them, e.g., the lexicographically smallest string, which starts from just one robot, given the asymmetry of $C_H$. So, the robot x is the elected robot for any r.  □

So, let x and w be the robot and the lexicographically smallest angle-string chosen according to Lemma 1. This enables the algorithm to elect a starting robot (i.e., x) and an orientation on the SEC (i.e., the direction given by w), by which the main diameter D search can be carried on: each robot starts checking whether the diameter through x satisfies Theorem 1 and, if this is not the case, it tries with the next robot along the orientation settled by w. Clearly, this process makes the whole swarm converge on the claimed main diameter D. Let p be the position of the robot that determines D. The strategy distinguishes between having an odd or even number n of robots in the swarm.

Evenn. By Theorem 1, one or two robots may sit at the endpoints of D. In both cases, the robot at position p assumes the color pivot. Moreover, in the second case, the opposite robot on D assumes the color angle. The explanation continues discussing the first situation, since the second may be easily derived. By Theorem 1, one of the half-SEC, say $H^{+}$, has one more robot than the other, say $H^{-}$. So, a robot in $H^{+}$ needs to move to the empty endpoint $a_3$ (opposite to p) of D and assume the color angle. At the same time, two other positions $a_1$ and $a_2$ (regular polygon vertices) must be reached by two robots. These two positions correspond to the polygon vertices at the immediate left and right of p. The three robots sat at positions $a_1$, p,$a_2$ form the regular 3-tuple (see Figure 4).

So, globally, three robots must be moved: two from $H^{+}$ and one from $H^{-}$, so that both the half-SECs contain the same number of robots at the end of this round. The orientation provided by x and w is used to determine which robots in $H^{+}$ and $H^{-}$ must move to the vertices of the polygon: for instance, the last robots by such an orientation can be selected. Then, Theorem 2 ensures that the three vertices will be safely reached by the robots.

Summing up, each robot r performs the following:

• Look–Compute: r unambiguously spots the pivot position p on the main diameter. Furthermore, it computes the positions $a_1$, $a_2$, $a_3$ and the robots intended for these positions.
• Move: If r is in the pivot position p, then it does not move and sets its color as pivot. If r is intended for the position $a_1$, $a_2$, or $a_3$, it sets its color as angle and moves there. Otherwise, r does nothing.

Oddn. A single robot lies on the main diameter D, specifically at one of its endpoints, say p. Such a robot assumes the color pivot, and the formation of the regular 3-tuple around p takes place as above. Opposite to p, the regular polygon edge perpendicular to D must be formed. So, two robots will reach the endpoints $a_3$ and $a_4$ of such an edge, assuming the color angle (see Figure 5). Note that, in each half-SEC, exactly two robots move to their vertex destinations. Again, (a trivial adaptation of) Theorem 2 ensures safe robot travel.

Summing up, each robot r performs the following:

• Look–Compute: r unambiguously spots the pivot position p on the main diameter. Furthermore, it computes the positions $a_1$, $a_2$, $a_3$, $a_4$ and the robots intended for these positions.
• Move: If r is in the pivot position p, then it does not move and sets its color as pivot. If r is intended for the position $a_1$, $a_2$, $a_3$, or $a_4$, it sets its color as angle and moves there. Otherwise, r does nothing.

Symmetry with exactly one axis. Let l be the only axis of symmetry in $C_H$. Note that two or more symmetry axes yield a rotational symmetry, that is considered in the next case. The diameter of the SEC lying on l will be the main diameter. Three cases are considered: odd n, even n with two axis robots (i.e., robots on the symmetry axis), and even n with no axis robots.

Odd n. In this case, l passes through a robot, which will be the pivot p, and splits the opposite edge of the polygon. So, l divides the SEC into two symmetrical halves, each with $\frac{n-1}{2}$ robots (p excluded).

Now, the algorithm aims to create the regular 3-tuple around p, as well as to set two robots at the endpoints of the regular n-gon edge opposite to p. Therefore, two robots in each half-SEC must be moved. Even in this case, Theorem 2 ensures no crossing trajectories. However, to apply Theorem 2, an orientation is necessary; in this case, it can be trivially settled in each half-SEC as being the direction from the pivot to the other endpoint of the diameter laying on the axis l (namely, the main diameter). To determine which robots in each half-SEC must move to the vertices of the polygon, the algorithm can choose, e.g., the last robots according to such an orientation.

As in the asymmetrical case discussed above, let $a_1$ and $a_2$ be the positions of the two polygon vertices around p, while $a_3$ and $a_4$ are the positions of the two vertices of the polygon edge opposite to p (see Figure 6).

Summing up, each robot r performs the following:

• Look–Compute: r computes the axis of symmetry l (and hence the main diameter) and the positions $a_1,a_2,a_3,a_4$ of the polygon vertices.
• Move: If r is on l, it sets its color as pivot and stays still. If r is intended for the position $a_1$, $a_2$, $a_3$, or $a_4$, it sets its color as angle and moves there. Otherwise, r does nothing.

Even n with two axis robots. In this case, l passes through two opposite robots, which will be the two pivots $p_1$ and $p_2$. The diameter on l is the main diameter, as above. The axis l divides the SEC into two symmetrical halves, each with $\frac{n-2}{2}$ robots ($p_1$ and $p_2$ excluded). First of all, one of the two pivots must be selected, around which to form the regular 3-tuple. To this end, let $e_1$ and $e_2$ be the two endpoints of the diameter which is perpendicular to the axis l. Each robot computes the angle-strings $w^{\prime }$ and $w^{\prime \prime }$ obtained, respectively, by traveling from $p_1$ to $e_1$ and from $p_2$ to $e_2$. Notice that $w^{\prime }$ and $w^{\prime \prime }$ remain the same even if $e_1$ and $e_2$ are switched, due to the symmetry axis l. It is easy to see that $w^{\prime }=w^{\prime \prime }$ implies a rotational symmetry, which will be dealt with later. So, the algorithm can establish the lexicographically smallest string between $w^{\prime }$ and $w^{\prime \prime }$, say $w^{\prime }$, and choose $p_1$, from which $w^{\prime }$ starts, as the pivot around which to form the regular 3-tuple. As usual, let $a_1$ and $a_2$ be the positions of polygon vertices around $p_1$ (see Figure 7).

It is notable that the strings $w^{\prime }$ and $w^{\prime \prime }$ enable all robots to agree on a common upper and lower side of the main diameter (and of the SEC).

Summing up, each robot r performs the following:

• Look–Compute: r computes the axis of symmetry l (and hence the main diameter with the robots $p_1$ and $p_2$) and the positions $a_1$ and $a_2$ around which they will form the regular 3-tuple.
• Move: If r belongs to l, it sets its color as pivot and does not move. If r is intended for the position $a_1$ or $a_2$, it sets its color as angle and moves there. Otherwise, r does nothing.

Even n with no axis robots. In this case, l splits the SEC without passing through any robot. Let d be the main diameter laying on l, and let $d^{\prime }$ be the diameter perpendicular to d. As in the previous case, by computing the arc angle-strings delimited by the endpoints of d and the endpoints of $d^{\prime }$, robots can determine the upper (and lower) side of the SEC. So, in the upper side, robots form a regular 4-tuple, centered on l, in the positions $a_1,p_1,p_2,a_2$, while in the lower side two robots reach the two endpoints $a_3,a_4$ of the polygon edge opposite to the 4-tuple and split by l (see Figure 8).

It is evident that, in all this robot displacing, at most three robots per each half-SEC are involved. Moreover, although the whole robot swarm does not share a common orientation, each half-SEC is oriented. Furthermore, due to symmetry, the orientations in the two half-SECs are opposite. So, by Theorem 2, no collisions among moving robots arise.

Summing up, each robot r performs the following:

• Look–Compute: r computes the axis of symmetry l (and hence the main diameter) and the positions $a_1,p_1,p_2,a_2$, and $a_3,a_4$ of the vertices nearest to l in the regular n-gon. In particular, $\overline{p_1{p}_2}$ and $\overline{a_3{a}_4}$ will be the two opposite edges split by l.
• Move: If r is intended for the position $p_1$ or $p_2$, it sets its color as pivot and moves there. If r is intended for the position $a_1$, $a_2$, $a_3$, or $a_4$, it sets its color as angle and moves there. Otherwise, r does nothing.

Rotational symmetry. Let $r_0,\cdots ,r_{n-1}$ be the sequence of adjacent robots on the SEC starting from an arbitrary robot, following a fixed orientation. If the related SEC angle-string ${\alpha }_0\cdots {\alpha }_{n-1}$ can be factored into k identical factors up to rotation, then the convex hull on the SEC can be divided into k identical sectors, each being the $\frac{2\pi }{k}$-rotation of the previous one.

Let $P_i=\{r_j\mid j\equiv i mod \frac{n}{k}\}$ with $0\le i<\frac{n}{k}$ be the class of symmetry which contains k robots sharing the same relative position in the k different sectors. Clearly, from all the robots in the same class $P_i$, the same two SEC angle-strings, say $w_i$ and ${w_i}^R$, start in opposite directions. The algorithmic strategy now follows two different paths according to a particular property of the $\frac{n}{k}$ classes of symmetry, and, in particular, of their angle-strings. In fact, two scenarios can occur:

• One main class of symmetry: it is possible to unambiguously spot a unique P from which the lexicographically minimal angle-string starts.
• Two main classes of symmetry: it is possible to unambiguously spot just two classes $P_u,P_v$ from which the lexicographically minimal angle-string starts.

Notice that if more than two classes of symmetry share the same angle-string, then sectors contain sub-sectors in turn.

One main class of symmetry. In this case, it is possible to unambiguously choose a class of symmetry P (called the main class of symmetry), by suitably adapting the technique in the proof of Lemma 1. The k robots in P will be the pivots. In the case of rotational symmetry with two sectors, the diameter joining the two pivots will be the main diameter. For more than two sectors, the chords joining pivots in two consecutive sectors will be the safe chords, according to Definition 5.

Around each pivot, two angle robots must be set to form a regular 3-tuple. Thus, for each arc H delimited by consecutive pivots, two angle positions $a,a^{\prime }$ must be covered by two robots chosen within H. To unambiguously spot these two robots on H, the algorithm can elect the two robots closest to a or $a^{\prime }$. In the case of equidistance, one robot can be unambiguously elected by considering the distance from the closest pivot.

Specifically, in order to set k regular 3-tuples in this configuration, each robot r performs the following:

• Look–Compute: r computes the main class of symmetry $P=\{p_0,\cdots ,p_{k-1}\}$ and the positions $\{a_{j_1},a_{j_2}\mid j\in \{0,\cdots ,k-1\}\}$ of the vertices adjacent to the vertices in P, in the target regular n-gon. It chooses the robots intended for the angle positions.
• Move: If r belongs to P, it sets its color as pivot. If r is a robot intended for an angle position, it sets its color as angle and moves to its destination vertex. Otherwise, r does nothing.

The final robot displacement is shown in Figure 9 and Figure 10.

Two main classes of symmetry. This case occurs when there are two classes of symmetry of robots, say $P_u=\{u_0,\cdots ,u_{k-1}\}$ and $P_v=\{v_0,\cdots ,v_{k-1}\}$, that share the same minimal angle-string (here, $u_i$ and $v_i$ belong to the same rotation sector i, as shown in Figure 11).

In particular, it is not possible to select a unique class $P_i$ of robots where the minimal angle-string starts from.

The robots in $P_u\cup P_v$ will play the role of placeholders for the pivot setting. However, it is necessary to define a common method to pair consecutive placeholders. Formally, robots must consider the pairs of placeholders as $(u_i,v_i)$ or $(v_i,u_{(i+1) mod k})$ for each $0\le i<k$. The algorithm can unambiguously choose how to pair these placeholders according, for example, to the smaller central angle between consecutive placeholders (i.e., between the angles $u_i\widehat{O}{v}_i$ and $v_i\widehat{O}{u}_{(i+1) mod k}$, where O is the center of the SEC). In case of equal amplitude, they are paired using the lexicographical order on the two angle-strings between the placeholders. In fact, each placeholder forms two different angle-strings with its consecutive placeholders (otherwise the sectors contain sub-sectors in turn).

Assuming without loss of generality that the pairs are in the form $(u_i,v_i)$, the following axes can be defined:

Definition 7.

Let $\{(u_i,v_i)\mid i=0,\cdots ,k-1\}$ be the pairs of placeholders. Given a pair $\rho =(u_i,v_i)$ of placeholders, the following axes are defined:

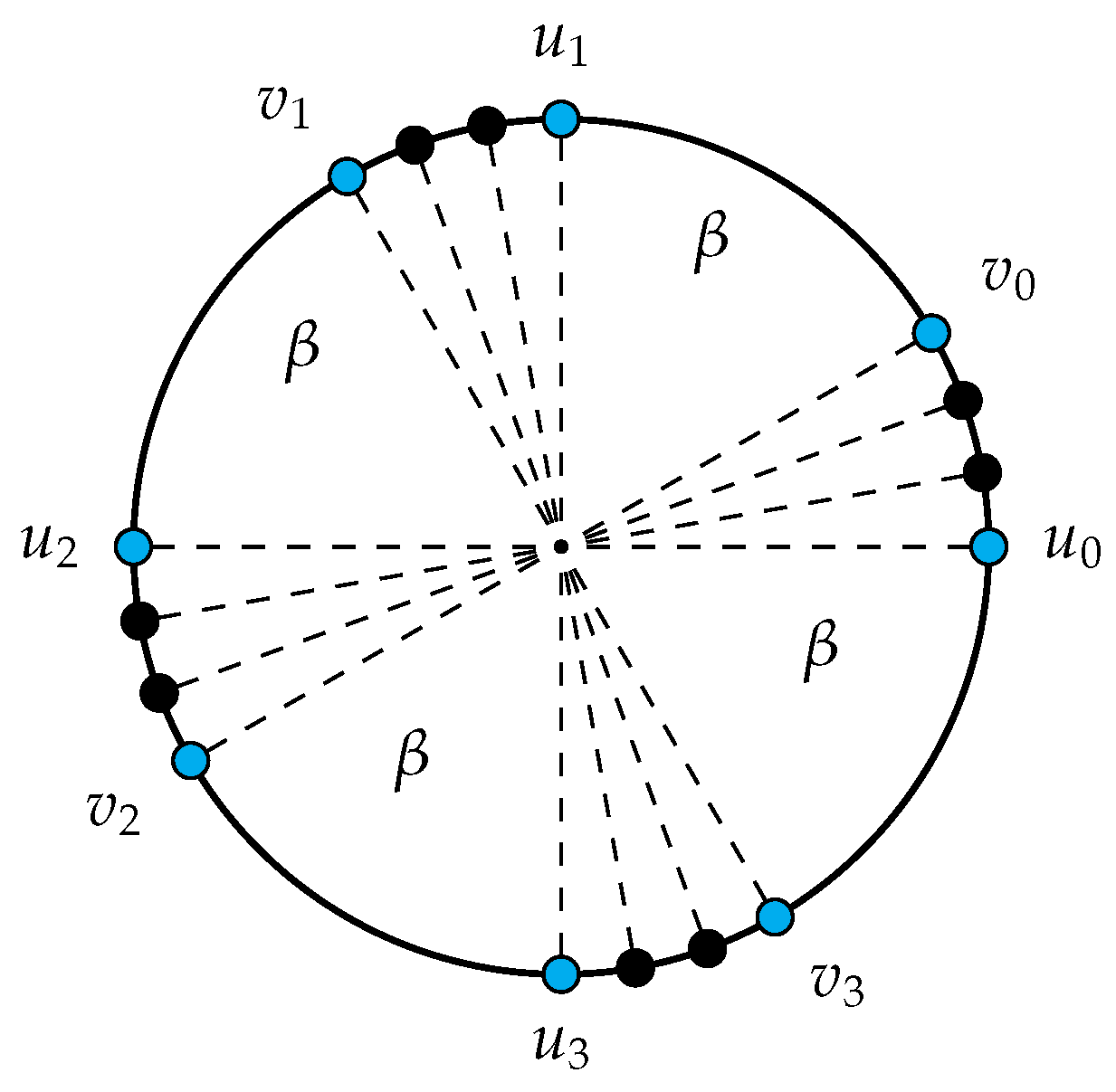
• Theinternal axisof ρ is the symmetry axis passing in the middle point of the arc $\stackrel{⌢}{u_i{v}_i}$;
• Theexternal axesof ρ is the symmetry axes passing in the middle point of the arc ${\stackrel{⌢}{u_{i}v}}_{(i-1) mod k}$ or ${\stackrel{⌢}{v_{i}u}}_{(i+1) mod k}$.

Indeed, for odd k, the same axis is both internal and external, for different pairs of placeholders. It is important to note that no robot lies on these axes, otherwise it would be the case of one main class of symmetry.

Each rotational sector contains $q=\frac{n}{k}$ robots and $u_i\widehat{O}{u}_{(i+1) mod k}=\frac{2\pi }{k}$ (obviously, $v_i\widehat{O}{v}_{(i+1) mod k}=\frac{2\pi }{k}$). The internal and external axes of the placeholders divide the SEC into $2k$slices, each with the same number of robots.

In this cycle, each robot r acts as follows:

• Look–Compute: r spots the two main classes of robots from which the same minimal angle-string starts, and the k placeholder pairs. Then r spots the placeholder pair $(u,v)$ it is closest to, the internal axis l and external axes $h,h^{\prime }$ with respect to $(u,v)$, and hence the slice is lying on (for example, the slice cut by h and l). It computes the two pivots positions p (in its slice) and $p^{\prime }$ (in the opposite slice with respect to h) such that p and $p^{\prime }$ are symmetrical to h, and $p\widehat{O}{p}^{\prime }$ measures the base angle $\frac{2\pi }{n}$. Then it computes the point a in its slice which will form the base angle with p.
• Move: If r is in the placeholder position, then it does not move and sets its color as placeholder. If r is the nearest robot to some points p or a within the same slice (unambiguously chosen with respect to the axis of symmetry in case of equidistance), then it sets its color as pivot or angle, and it heads to the proper position without colliding. Otherwise, r does nothing.

Figure 12 and Figure 13 display the configurations described above.

During this round, each slice does not change the number of robots and the axes passing in the middle of the pivots are maintained: hence, they continue to be equally distributed within the slices.

5.3. Cycle 2: Rappelling down on the Safe Diameters or Safe Chords

Let $C_2$ be the configuration at this point, where all robots lie on the SEC. $C_2$ presents one, two, or more regular tuples which split the SEC into sectors of equal amplitude and define the safe diameters or safe chords through the positions of pivots and angle robots. In this cycle, the other robots safely rappel down on their safe segment, according to the following strategies, which are distinguished according to the number and type of regular tuples:

One or two regular 3-tuples, or 4-tuples. In this case, $C_2$ derives from an initial case of asymmetry, symmetry with one axis, and rotational symmetry with two sectors. Let d be the main diameter, which is uniquely determined by the presence of one or two opposite regular tuples, say $\tau$ and possibly ${\tau }^{\prime }$: d is the diameter passing through the middle point of the arc covered by $\tau$. Let $d^{\prime }$ and $d^{\prime \prime }$ be their safe diameters.

In this cycle, each robot r performs the following:

• Look–Compute: If r is pivot or angle, it does nothing. Otherwise, r computes the safe diameters $d^{\prime }$ and $d^{\prime \prime }$, its target vertex position t on its half-SEC, and the point $t_{\perp }$, which is the projection of t on the safe diameter nearest to r.
• Move: r sets its color as internal and travels to $t_{\perp }$.

Three or more regular 3-tuples. Here, $C_2$ derives from an initial case of rotational symmetry with just one main class of symmetry. In this cycle, each robot r performs the following:

• Look–Compute: If r is pivot or angle, it does nothing. Otherwise, r computes the nearest safe chord c, its target vertex position t on its sector, and the point $t_{\perp }$, which is the projection of t on c.
• Move: r sets its color as internal and travels to $t_{\perp }$.

Three or more regular 4-tuples. Here, the case with $k\ge 3$ regular 4-tuples is considered. The configuration $C_2$ derives from an initial case of rotational symmetry with two main classes of symmetry. Let $(a_{(j-1) mod k}^{\prime },p_{(j-1) mod k}^{\prime },p_j,a_j)$ and $(a_j^{\prime },p_j^{\prime },p_{(j+1) mod k},a_{(j+1) mod k})$ be two adjacent regular 4-tuples which delimit the sector j, for each $j\in \{0,\cdots ,k-1\}$. The chord $\overline{g_j{g}_j^{\prime }}$ is defined as the safe symmetry chord of the sector j (see Figure 13), where the following applies:

• $g_j$ is the middle point on the SEC between $p_{(j-1) mod k}^{\prime }$ and $p_j$;
• $g_j^{\prime }$ is the middle point on the SEC between $p_j^{\prime }$ and $p_{(j+1) mod k}$.

In this cycle, each robot r performs the following:

• Look–Compute: if r is neither a pivot nor an angle, then it computes the safe symmetry chord $\overline{g{g}^{\prime }}$ of its sector. Then it computes $t_{\perp }$, which is the projection of its target vertex t on $\overline{g{g}^{\prime }}$.
• Move: if r is neither a pivot nor an angle, then it sets its color as internal and moves to its $t_{\perp }$. Otherwise r does nothing.

The algorithm yields safe robot movements, as stated in the following:

Lemma 2.

The movements in Cycle 2 of robots towards safe diameters and (symmetry) chords yields collision-free trajectories.

Proof. 

Each robot lies either on the half-SEC or on the arc of a rotational symmetry containing its future target vertex. Clearly, this guarantees that it does not have to cross its safe diameter or safe (symmetry) chord. So, collisions may only occur within each sector/half-disk. However, the algorithm avoids collisions at all, as it is now going to be explained. Let d be a safe (symmetry) chord or a safe diameter, and consider the convex arc c cut off by d. Consider now the set of h robots laying on c. During their look–compute phase, these robots compute their own destination on the basis of their position within robot displacement on c. For instance, let r and s be two robots on c. The robot r looks at the robot displacement on c and realizes it is the i-th robot starting from its closest endpoint of d. The robot s instead realizes it is the j-th robot starting from the same endpoint (without loss of generality). Let $t_i$ and $t_j$ be the destination points of r and s, respectively. Indeed, if $i<j$, then $t_i$ must be closer than $t_j$ to the endpoint, otherwise the opposite holds. Starting from a common endpoint, let $(t_1,\cdots ,t_h)$ be an ordering on the destination points of the robots on c, which induces a corresponding ordering $(t_{1_{\perp }},\cdots ,t_{h_{\perp }})$ on the projection points on d. This ensures collision-free trajectories.

To help intuition, Figure 14 depicts rappelling down on a safe diameter. It is not hard to see that no problem occurs whenever different robots start enumeration along c from different safe diameter endpoints.  □

5.4. Cycle 3: Reaching the SEC

At the end of the previous round, each robot which is neither pivot nor angle colored lies on a safe diameter or on a safe (symmetry) chord. The algorithmic strategy was to move the robot to a position where enough information from the system configuration is available to compute its final destination on the SEC. So, in this cycle, each robot r performs the following:

• Look–Compute: If r is pivot or angle colored, it does nothing. Otherwise, r is within the SEC on a safe (symmetry) chord or a safe diameter, and sees at least three robots on the SEC which are pivot or angle colored. Thus, r can reconstruct the SEC. So, r computes: the SEC upon which it has to travel, the safe (symmetry) chord or safe diameter it currently lies on, its destination arc H, and the projection point t of r on H.
• Move: r sets its color as sec and travels to t.

At the end of this round, the final regular n-gon is attained.

5.5. Pseudo-Code

The pseudo-code of the fsynch algorithm is presented in Algorithm 1.

Algorithm 1fsynch algorithm.

Input:  A valid configuration $C_0$ of the swarm $\mathcal{R}$ of n robots 1: Preliminary Steps: 2:   $C_1\leftarrow \mathtt{Complete}\mathtt{Visibility}\mathrm{on}{C}_0$ by [39]; 3:   $C_H\leftarrow \mathcal{R}\mathrm{on}\mathrm{the}\mathrm{SEC}\mathrm{of}{C}_1;$ 4:   if $C_H$ is a perfect convex hull then 5:     $C_R\leftarrow \mathrm{Regular}\mathrm{Polygon}\mathrm{by}$ [42]; 6:     return $C_R$; 7:   end if 8: Cycle 1: 9:   switch $C_H$ do 10:    case asymmetry 11:      unambiguously fix the main diameter splitting $\mathcal{R}$ in two halves; 12:      if Even n then 13:        set pivot and angles according to Figure 4; 14:      else 15:        set pivot and angles according to Figure 5; 16:      end if 17:     case symmetry with exactly one axis 18:        unambiguously fix the main diameter; 19:        switch $C_H$ do 20:          case odd n 21:            set pivot and angles according to Figure 6; 22:          case even n ∧ two robots on the axis 23:            set pivots and angles according to Figure 7; 24:          case even n ∧ no robots on the axis 25:            set pivots and angles according to Figure 8; 26:     case rotational symmetry 27:        if$\exists !$ main class of symmetry then 28:            $P\leftarrow \mathrm{the}\mathrm{unique}\mathrm{main}\mathrm{class}\mathrm{of}\mathrm{symmetry};$ 29:            make robots in P set their light as pivot; 30:            set the regular 3-tuples as in Figure 9, or Figure 10; 31:        else 32:            $P_u,P_v\leftarrow \mathrm{the}2\mathrm{main}\mathrm{classes}\mathrm{of}\mathrm{symmetry};$ 33:            make robots in $P_u\cup P_v$ set their light as placeholder; 34:            set regular 4-tuples as in Figure 12 or Figure 13; 35:        end if 36:   $C_2\leftarrow \mathrm{Output}\mathrm{of}\mathrm{Cycle}1;$ 37: Cycle 2: 38:   $I\leftarrow \mathrm{robots}\mathrm{not}\mathrm{forming}\mathrm{the}\mathrm{regular}\mathrm{tuples};$ 39:   if $C_2$ has 3 or more regular tuples then 40:     spot the safe (symmetry) chords; 41:     make robots in I move onto safe (symmetry) chords, setting their light as internal; 42:   else 43:     spot the safe diameters; 44:     make robots in I move onto safe diameters, setting their light as internal; 45:   end if 46:   $C_3\leftarrow \mathrm{Output}\mathrm{of}\mathrm{Cycle}2;$ 47: Cycle 3: 48:   $I\leftarrow \mathrm{internal}\mathrm{robots};$ 49:   make robots in I reach their destination on the SEC, setting their light as sec; 50:   $C_R\leftarrow \mathrm{Output}\mathrm{of}\mathrm{Cycle}3;$ 51:   return $C_R$; Output:  $C_R$ forming a regular n-gon.

6. The Algorithm for the Semi-Synchronous Mode

This section introduces and explains an algorithm for solving the UCF problem in the ssynch mode, pointing out the differences with the fsynch algorithm presented in the previous section. Let ${\mathit{C}}_{\mathit{H}}$ be the configuration where all the n robots sit on their SEC with the same color. Again, the dynamic of the algorithm depends on the symmetry degree of ${\mathit{C}}_{\mathit{H}}$.

One of the main differences with respect to the fsynch algorithm is the need for an initial epoch where some initial information about the original configuration (symmetry degree, symmetry axis position) must be encoded by robot positions and colors. In particular, in this epoch, just some pivots and the placeholders will be set. In fact, pivots and placeholders (note that placeholders are needed when pivots have to reach their final destination) fix the safe segments and the sectors where all other robots must travel. Moreover, all pivots will assume a specific color $pivotx$ where x is the suffix encoding the initial symmetry degree. Due to the ssynch dynamic, this extra epoch ensures subsets of robots follow the proper path of the algorithm, determined by the initial configuration.

Asymmetry. For this case, the strategy used in the fsynch mode is adapted to achieve the regular n-gon within the ssynch mode. In the first epoch, one or two pivots must be set, at the endpoints of the main diameter d (which is chosen with the same strategy as in the fsynch mode). If n is odd, the robot on d colors itself as pivot. If n is even, two pivots will be placed on the endpoints of d, with two different colors pivot and pivot_down, to fix the upper and lower part of the SEC. Notice that the asymmetrical configuration allows robots to agree on these two directions.

In the second epoch, the regular tuples are set, but now more angle robots in each half-SEC are required. These longer tuples will allow robots on the SEC to compute the base angle and the safe diameters where they have to rappel down. In fact, internal robots can hide the pivots on the main diameter from the remaining robots on the SEC, preventing the computation of their target positions on the safe diameters. So, for the odd case, robots complete the regular 3-tuple (angle, pivot, angle) around the pivot, whereas they set the regular 4-tuple (angle, angle, angle, angle) on the opposite side of d (centered on it). For the even case, robots complete the regular 3-tuple (angle, pivot, angle) around the upper pivot, and the regular 5-tuple (angle, angle, pivot_down, angle, angle) on the lower side of the SEC (centered on d). Notice that, in this epoch, no more than three robots per half-SEC move to angle positions, so that Theorem 2 can be still applied.

In the third epoch, the remaining robots (i.e., not belonging to any regular tuples) update their color to internal and move to their safe diameter, following the same strategy as in the fsynch mode. Possibly, if an activated robot sits on a vertex of the target n-gon and it is neither a pivot nor an angle robot, it is assumed to color itself as sec and stay still. At the beginning of the fourth epoch, all robots are on their own safe diameter, except those on the SEC with light color pivot, pivot_down angle, sec. Each internal robot sees at least three lighted robots on the SEC. So, it computes its target vertex on the SEC and reaches it by traveling perpendicularly to the main diameter.

Symmetry with exactly one axis. In this case, pivot lights pivot_s1, pivot_s2, and pivot_s3 are set depending on the odd or even number of robots and on the number of robots (zero, one, or two) laying on the symmetry axis at the beginning of this epoch. Precisely, case a—pivot_s1 is used to light the pivots in a configuration with an odd number of robots and one robot on the symmetry axis, case b—pivot_s2 is used for an even number of robots and no robots on the symmetry axis, and case c—pivot_s3 is used for an even number of robots and two robots on the symmetry axis.

As in the fsynch mode, robots can agree on an upper and a lower part of the main diameter, and so of the SEC, by considering the half-SEC angle-strings.

As stated before, more angle robots in each half-SEC must be fixed, so that at least three robots on the SEC are always visible to the robots which have to travel towards the safe diameters. Note that only pivots on the axis can be hidden from the robots on the SEC, whereas pivot_s2 and angle robots are always visible to them.

So, in this first epoch, for cases a and c, the robots on the symmetry axis immediately assume the color pivot_s1 and pivot_s3, respectively, and stay still. For case b, just two robots are elected such that they are symmetrical to the axis, one for each half-SEC, and set their lights with the color placeholder. To elect the placeholders, the closest robot (per each half-SEC) to the upper endpoint of the main diameter can be chosen. The two placeholders fix the initial axis of symmetry (in fact, given two points on a circle there exists just one symmetry axis dividing them) which is necessary in the second epoch where the pivots set themselves properly.

Now, the second epoch comes: two regular tuples centered around the two opposite endpoints of the main diameter are set, by moving some robots on the n-gon vertices. Placeholders stay still.

So, in case a, a regular 3-tuple (angle, pivot_s1, angle) is formed in the upper part of the SEC, and a regular 4-tuple (angle, angle, angle, angle) in the lower part. For case b, a regular 4-tuple (angle, pivot_s2, pivot_s2, angle) is formed in the upper part of the SEC (by moving both angles and pivots), and a regular 2-tuple (angle, angle) in the lower part. For case c, a regular 3-tuple (angle, pivot_s3, angle) is formed in the upper part of the SEC, and a regular 5-tuple (angle, angle, pivot_s3, angle, angle) in the lower part. It is important to note that in all these cases, no more than three robots per half-SEC move to reach their final destinations. Hence, by Theorem 2, no collisions exist.

In the third epoch, as in the fsynch mode, robots not forming the regular tuples can set safe diameters and move onto them on the orthogonal projections of the n-gon vertices, updating their color as internal. It is worth mentioning that during this epoch, in all three cases a, b, and c at least three pivot or angle robots are always visible, so that the SEC can be safely reconstructed.

At this point, in the fourth epoch, internal robots return to the SEC by leaving perpendicularly from safe diameters.

Rotational symmetry. This case presents four different sub-cases which are dealt with distinctly. In particular, specific colors for the pivots pivot_r1, pivot_r2, pivot_r3, and pivot_r4 will be adopted to signal the initial geometric pattern along the whole computation. A first strategy discriminant is given by the existence of a unique main class of symmetry or two main classes of symmetry.

One main class of symmetry. In the first epoch, only those robots which will act as pivots light them with a specific color to store needed information about the initial rotational pattern.

Let k be the number of rotational symmetry sectors. For $k>2$, the following epochs basically take place as in the fsynch mode. During the second epoch, k regular 3-tuples (angle, pivot_r1, angle) are set; in the third epoch, robots drop down to the safe chords; in the fourth epoch, all internal robots return to the SEC at polygon vertex positions.

For $k=2$, the first epoch is used to properly color the two pivots, elected as in the fsynch mode. A peculiar approach is now explained for the next three epochs which deflects from the usual strategy in the setting of the safe diameters. Let w be the angle-string between the two pivots. Two cases can occur: (i)$w=w^R$ and (ii)$w\ne w^R$.

For $w=w^R$ both sectors can be divided into two halves having the same number of robots. In this pattern, the robots at the endpoints of the main diameter d color themselves as pivot_r2 (first epoch). Moreover, the angle robots will complete the regular 3-tuples around the endpoints of d, as usual (second epoch). Being a palindrome, w does not allow robots to set an upper endpoint of d. For this reason, a different strategy is needed to guarantee robots can see at least three robots on the SEC, and to move at most three robots per sector to set the regular tuples (i.e., apply Theorem 2). Hence, the diameter perpendicular to d is elected as the new main diameter $d^{\prime }$. If some robots are lying on $d^{\prime }$, they are in their final position, w being a palindrome. Otherwise, $d^{\prime }$ splits two opposite polygon edges. The algorithm continues by setting the safe diameters parallel to $d^{\prime }$ and following the strategy for the asymmetry case (i.e., by making robots rappel down on the new safe diameters in the third epoch and by making them go back to the SEC in the fourth epoch).

In case (ii)$w\ne w^R$, the strategy for the (i) case can be properly adapted. A regular 3-tuple (angle, pivot_r3, angle) is set at each endpoint of the main diameter d (first and second epoch). Let $d^{\prime }$ be the perpendicular diameter to d. Note that also $d^{\prime }$ (like d) splits the SEC into two half-SECs with the same number of robots. By counting themselves, robots can understand if the endpoints of $d^{\prime }$ are vertices of the target n-gon. As a consequence, at most one robot per half-SEC must move from or to the related endpoint of $d^{\prime }$, according to the position of the vertices. These movements can be achieved during the second epoch, together with the angle robots. This, in turn, assures Theorem 2 can be properly applied. Now, the third and fourth epoch follow as the case (i).

Two main classes of symmetry. In the first epoch, each activated robot checks if it is a placeholder and, if so, it sets its light as placeholder, and no robot moves.

In the second epoch, each activated robot sees all the placeholders have been set, so it is time to move robots on the SEC to set the pivots (with the color pivot_r4) and angles. Each robot can spot its own slice (as in the fsynch algorithm). If the positions for pivot_r4 or angle of the slice are not occupied yet, one or two robots belonging to the slice can be selected unambiguously to move safely in those positions and complete the regular 4-tuple (angle, pivot_r4, pivot_r4, angle) for the whole sector. The other robots do nothing.

In the third epoch, each activated robot, which is neither pivot_r4 nor angle, acts like this: it spots its sector and the safe diameter (two sectors case) or the safe symmetry chord (more than two sectors case), it computes its index within the robots on the sector (by counting robots on the SEC and on the safe segments) and the projection of its target position on the safe segment. It rappels down on this projection, changing its color in internal.

In the fourth epoch, each activated robot with internal color spots the SEC and its sector, it sets its color as sec, and it travels towards the SEC perpendicularly to the safe segment.

7. The Algorithm for the Asynchronous Mode

In the asynch mode, severe issues may arise whenever robots are activated while other robots are moving to their destinations. In fact, robot snapshots may not be sufficient to reconstruct some fundamental aspects of the system (e.g., SEC, main diameters, safe diameters and chords), crucial for their correct motion. This is basically due to the fact that (i) moving robots can be obstructed by other robots, (ii) moving robots can obstruct other robots, and (iii) a static snapshot does not reveal the motion of the robots. For (i), the algorithm guarantees obstructed moving robots cause neither collisions nor ambiguous snapshots. For (ii) and (iii), new light colors of type moving are lighted up as soon as a robot starts moving. Specifically, let r be a robot that must set its light with c as color (note that c can be equal to the current color of the robot) and reach a new position q according to the ssynch algorithm. In the asynch strategy, r set its color as moving_c before starting moving (at the beginning of the move phase). Once on q, r stops itself and so completes its cycle (still remaining with the color moving_c). At the next activation, r simply updates its color from moving_c to c. If a robot $r^{\prime }$ sees at least a moving-colored robot and $r^{\prime }$ is not lighted with a moving color, $r^{\prime }$ skips its turn and does nothing. This technique allows an asynchronous swarm to simulate a ssynch scheme. Therefore, the ssynch algorithm can be adapted through the following features, depending on the phases of the algorithm, to solve the UCF problem in the asynch mode:

• In the first phase, pivots and angles (after having set placeholders if necessary) must be set, according to the same precedence logic as in the ssynch mode. More precisely, if an activated robot r figures out that regular tuples are incomplete and it does not see moving robots (i.e., robots with some moving light colors), r establishes whether or not it has to become a pivot or angle robot. In the affirmative, if r already lies on a pivot or angle position, r assumes the proper color as in the ssynch mode; otherwise, r updates its color as moving_pivot_down, moving_pivot_s2, moving_pivot_r4 or moving_angle (note that these colors are intended for the only pivots and angle robots which have to move) depending on its final destination, and r moves there. Once re-activated, a robot with the color moving_x simply changes its color into x$\in \{$pivot_down, pivot_s2, pivot_r4, angle}, and stands still. Otherwise, if the robot does not have to reach a pivot or angle position, or it sees some robots with color light of type moving, then it stays still.
• The second phase starts after the regular tuple setting. Robots enter the SEC on diameters and chords only if they see no other robot with the color moving_internal. Activated robots that sit on n-gon vertices and are neither pivots nor angles, assume the color sec and stay still. When entering the SEC, a robot assumes the color moving_internal. Once re-activated, a moving_internal colored robot simply switches its color into internal and stays still.
• In the third phase, the internal robots go back to the SEC traveling perpendicularly with respect to the safe segment they lie on. An internal robot r starts to move only if it sees only robots with lights on (with colors pivot, pivot_down, pivot_r1, pivot_r2, pivot_r3, pivot_r4, pivot_s1, pivot_s2, pivot_s3, angle, sec, internal). If this is the case, r determines its n-gon vertex position and moves there while assuming the color moving_sec. Otherwise, it stays still. This strategy guarantees the internal robot to correctly compute the SEC, the safe segment where it lies, and so the target n-gon. Once on the SEC, r will turn its color from moving_sec to sec.

8. Algorithms Analysis

The presented algorithms solve the UCF problem in the fsynch, ssynch, and asynch synchronization modes.

Table 1. Phases of the algorithms to solve UCF for the different modes, according to the initial configuration symmetry (asymmetry as, symmetry with one axis sy, rotational symmetry rs).

Algorithm Phases Each phase is fulfilled synchronously, in one round	fsynch
PHASE 1: Regular tuples Pivots and angle robots form the regular tuples	Who? Robots elected as pivots or angle robots What? They set their colors as pivot or angle and form the regular tuples around the endpoints of: the main diameter (as, sy, rs with 2 sectors) the safe chords (rs with more than 2 sectors)
PHASE 2: Towards safe segments Robots (not forming a regular tuple) rappel down on safe diameters or safe chords	Who? Robots not forming a regular tuple What? They set their colors as internal and rappel down on safe diameters or safe chords
PHASE 3: Reaching the SEC The internal robots reach their target vertex traveling perpendicularly to their safe segment	Who? The internal robots What? They travel perpendicularly to their safe segment towards the SEC
Algorithm Phases Each phase is fulfilled synchronously, in groups, in one epoch	ssynch
PHASE 1: Configuration fixing Pivots and placeholders fix the original configuration and the safe segments	Who? Robots elected as pivots or placeholders What? They set their colors properly according to the role and the configuration
PHASE 2: Regular tuple completion Angle robots move to complete the “long” regular tuples	Who? Robots elected as angle robots What? They set their color as angle and move to complete the regular tuples
PHASE 3: Towards safe segments Robots (not forming a regular tuple) rappel down on safe diameters or safe chords	Who? Robots not forming a regular tuple What? They set their colors as internal and rappel down on safe diameters or safe chords. In a specific case of rs, the safe diameters are perpendicular to the original main diameter
PHASE 4: Reaching the SEC The internal robots reach their target vertex traveling perpendicularly to their safe segment	Who? The internal robots What? They travel perpendicularly to their safe segment towards the SEC
Algorithm Phases Each phase is fulfilled asynchronously, in $\mathcal{O}\left(n\right)$ epochs in the worst case	asynch
Same phases as inssynch	Same strategy as in ssynch but using color moving_ to synchronize robot movements

summarizes their main steps and strategies.

It is evident that the three algorithms are deterministic: in fact, there are neither nondeterministic choices nor probabilistic actions. Starting from a valid initial configuration ${\mathit{C}}_0$, the computation generated by the execution of the algorithms terminates in a configuration where all the n robots in the swarm form a regular n-gon. No deadlock may occur, since at any instant there is at least one robot that can execute a cycle. The algorithms are clearly distributed since every robot executes the same deterministic algorithm on the basis of its own current snapshot. Moreover, no central agent leads and coordinates the robot swarm.

The fsynch and ssynch algorithms take full advantage of the parallelism in the system. In particular, by restricting to the original part (i.e., from configuration $C_H$), (i) concurrent movements do not create collisions, and (ii) obstructed visibility does not cause delays or deadlocks: each robot on the safe diameter, or (symmetry) chord sees at least three robots on the SEC with lights on. Such a parallel speed-up cannot be guaranteed for the asynch algorithm, which in the worst case can take an amount of time linear in n.

Concerning the running time, the Complete Visibility is achieved in $\mathcal{O}\left(1\right)$ time by [39] (fsynch and ssynch) and [40] (asynch). The other two preliminary steps (moving robots on the SEC and the perfect convex hull case solution) require one round (epoch) each for the fsynch (ssynch and asynch) mode. Next, the algorithm for the fsynch and ssynch modes uses three rounds and four epochs, respectively, in the original part. Instead, the asynch original part requires a $\mathcal{O}\left(n\right)$ number of epochs in the worst case.

Concerning the number of colors, a constant number of colors is used to solve Complete Visibility in all the modes [39,40]. For the other two preliminary steps, no mode uses additional light colors. For the original parts, five colors (pivot, angle, internal, placeholder, sec) are used by the fsynch algorithm, thirteen colors (pivot, pivot_{down, s1, s2, s3, r1, r2, r3, r4}, placeholder, angle, internal, sec) are used for the ssynch algorithm, and nineteen colors (pivot, pivot_{down, s1, s2, s3, r1, r2, r3, r4}, moving_{angle, pivot_down, pivot_s2, pivot_r4, internal, sec}, placeholder, angle, internal, sec) are used for the asynch algorithm.

9. Conclusions and Research Outlooks

This paper presents three algorithms which solve the UCF problem for opaque luminous robot swarms. The first algorithm solves the problem for fsynch swarms of robots, by using a constant number of look–compute–move cycles as well as a constant number of colors. In particular, compared to the previous result in [26], here the number of cycles is reduced from six to three. In addition, the other two algorithms solve UCF for the ssynch and asynch modes. For the former mode, an algorithm featuring a constant number of epochs is proposed; for the latter one, a linear amount of epochs is required in the worst case. In both modes, a constant number of colors is used.

Several directions for future research may be explored. E.g., the constant number of colors in the presented solutions is obtained by summing the constant number of colors needed to solve Complete Visibility [39,40] in the preliminary phase, plus the constant number of colors required by the rest of the original approaches in this paper. A better integration between these two phases would certainly lower the number of colors. Indeed, it would be interesting to establish the minimal number of colors needed to solve the UCF problem in the different synchronization modes. More generally, concerning the actual relevance of using lights to solve UCF, one may easily notice that a solution without light would imply a solution without light for Complete Visibility as well. To the best of our knowledge, this latter task is still to be investigated.

It is evident that theasynch algorithm derives from a proper adaptation of the ssynch algorithm, where robots exploit colors as “traffic lights” to set precedence in the movements and simulate an ssynch scheme. A similar approach is used in [21] in Theorem 3.1, where the authors construct an asynch simulator for any ssynch algorithm, thus proving that, assuming the presence of lights, the computational power of the ssynch model is equal to the computational power of the asynch model. However, the result in [21] considers a swarm model which is different from the model studied here: in fact, such robots are transparent, guaranteeing complete visibility to the swarm. An interesting and remarkable future work would be to investigate the computational relation between the presented model in the ssynch and in the asynch modes.

Another line of research is the study and analysis of solutions of the UCF problem for other models of robot swarms. For instance, it might be worth investigating the realistic case of fat opaque robots. In [13], a solution is proposed for fat transparent robots. A first attempt can be performed by combining results and technique in [13] with the approach presented in this paper. Robots under non-rigid systems can be also investigated.

Moreover, it may be interesting to pinpoint connections with Formal Language Theory. In the literature, and in the present paper as well, some interesting formal language aspects show up and might deserve further and more systematic investigations. For instance, as observed, recognizing certain types of symmetries in the robot swarm displacement reduces to verifying certain properties enjoyed by angle-strings. This is equivalent to accepting certain languages, such as the palindrome language, mirror language, copy language, etc.

Therefore, well-established results on the hardness of language acceptance can carry over to distributed system investigation, stating the possibility to solve certain problems or not, or the minimal amount of computational resources agents must possess to correctly operate. In particular, considering the realm of luminous robots, the communication system provided by a constant number of colors is easily seen to be modeled by a finite-state automaton. This observation might suggest, e.g., that minimizing the number of colors can be related to minimizing the number of states in finite-state automata. More generally, finite-state automata can be examined by so many points of view: descriptional complexity [43,44,45,46,47], studying the size (number of states) of automata, descriptive complexity [48], studying automaton representation by logic frameworks, and quantum computing [49,50,51], studying the impact of the quantum paradigm on finite-state machine size reduction. All these and other viewpoints might bring interesting insights and new tools and research problems in distributed system investigation.