Convergence Check Phase-Field Scheme for Modelling of Brittle and Ductile Fractures
Abstract
:1. Introduction
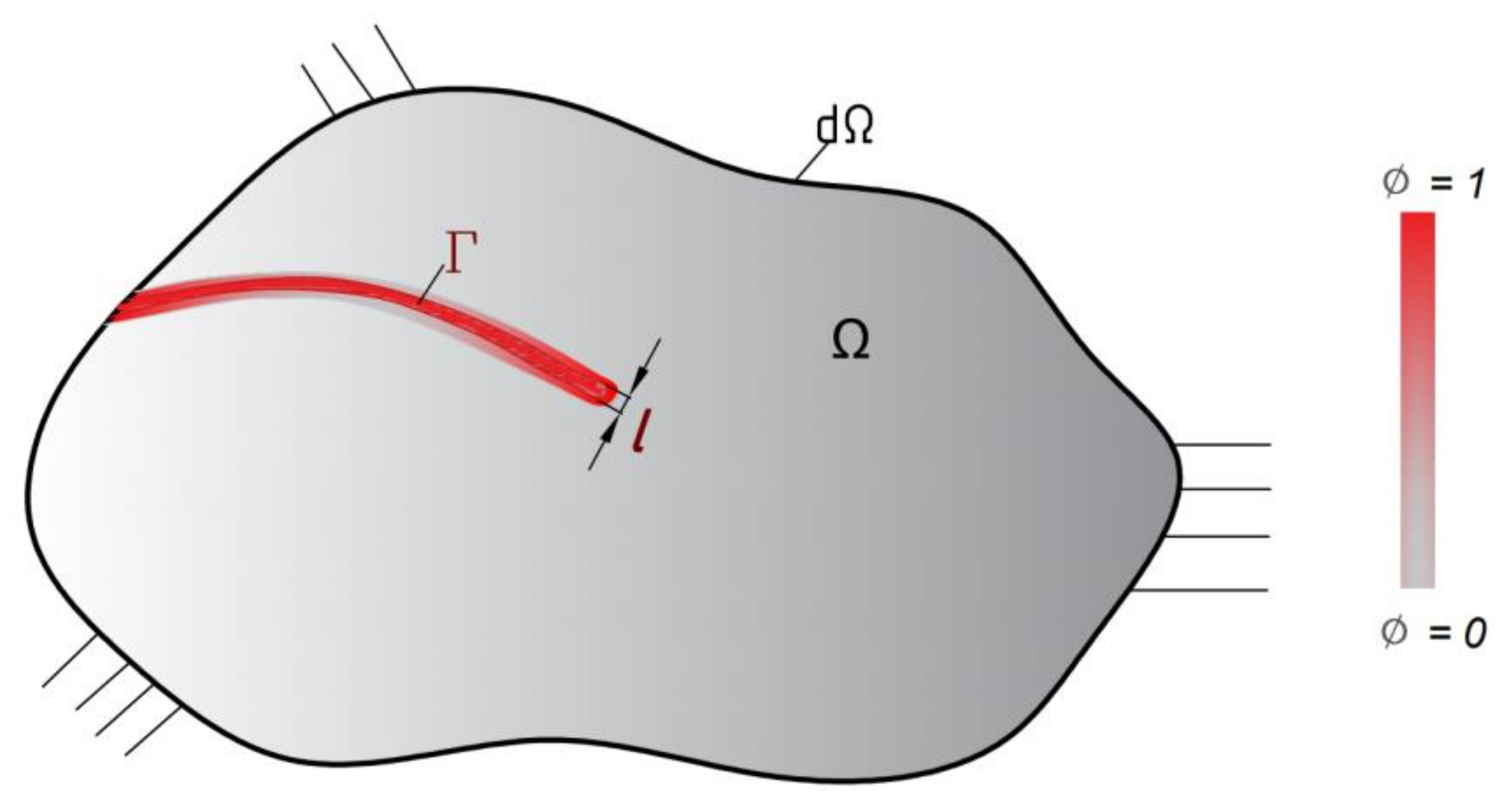
2. Phase-Field Method
2.1. Extension of Phase-Field Method to Fatigue
3. Numerical Implementation into Finite Element Method
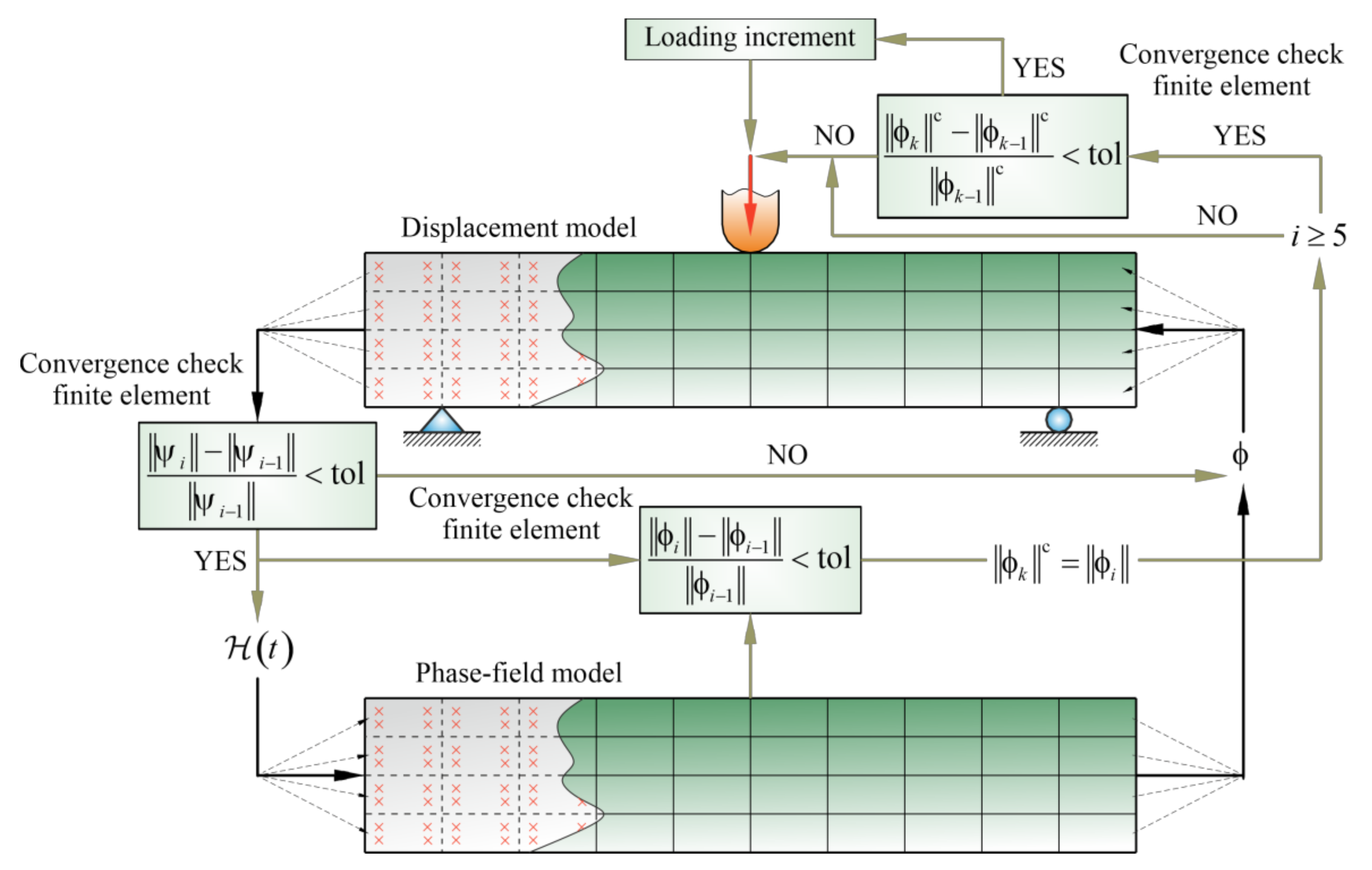
4. Convergence Check Phase-Field Algorithm
Cycle-Skipping Technique
5. Numerical Examples
5.1. Brittle Fractures
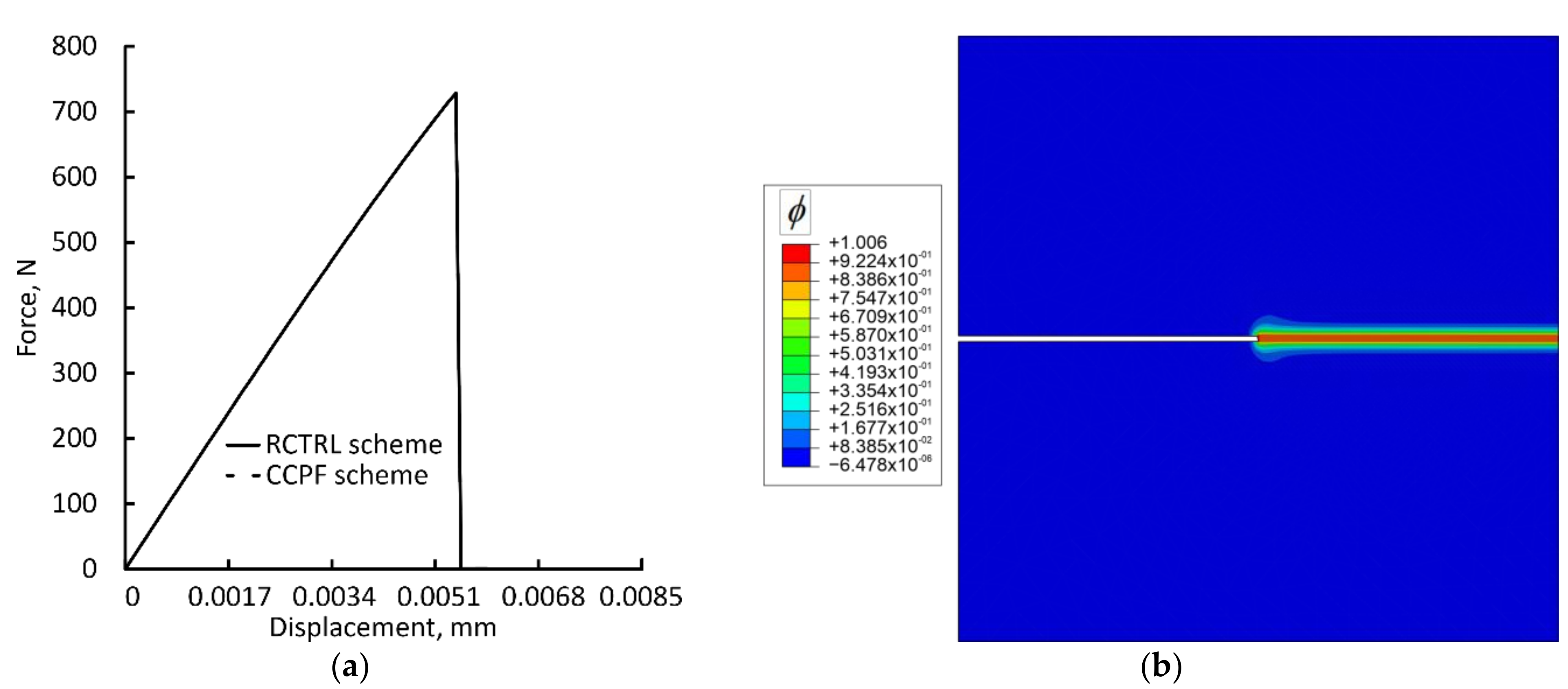
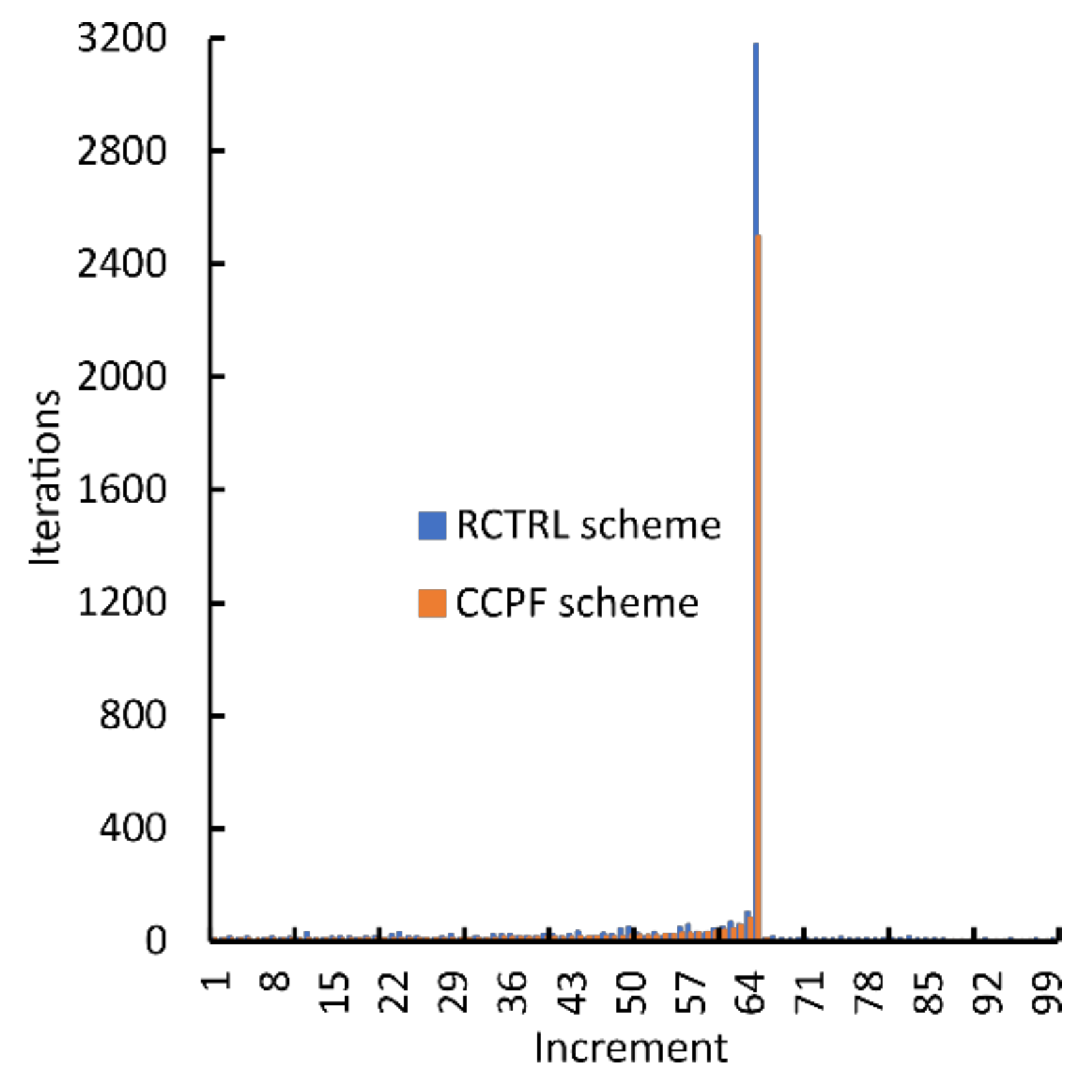
5.1.1. Single-Edge Notched Tensile Test
5.1.2. Single-Edge Notched Shear Test
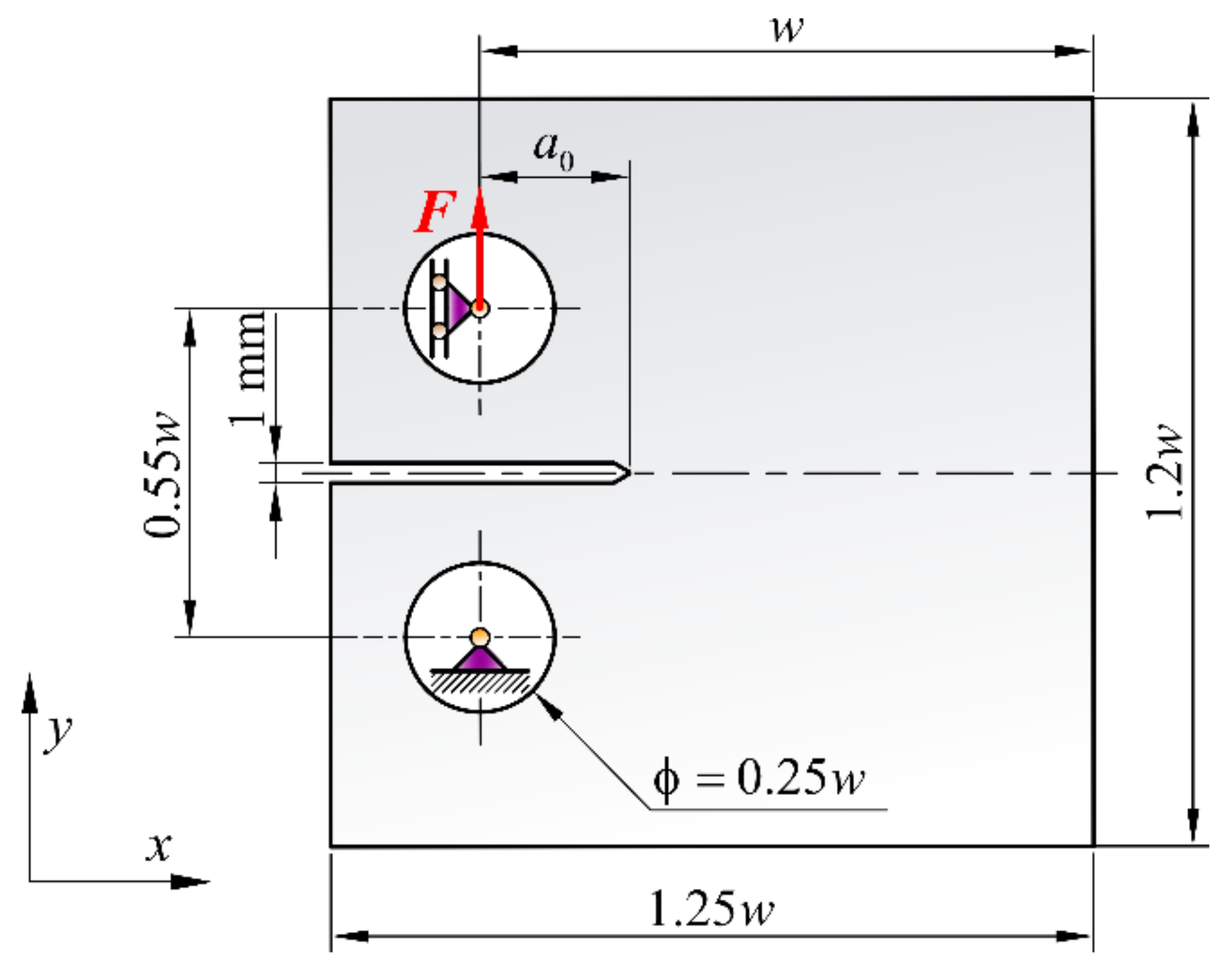
5.1.3. Asymmetric Three-Point Bending Test
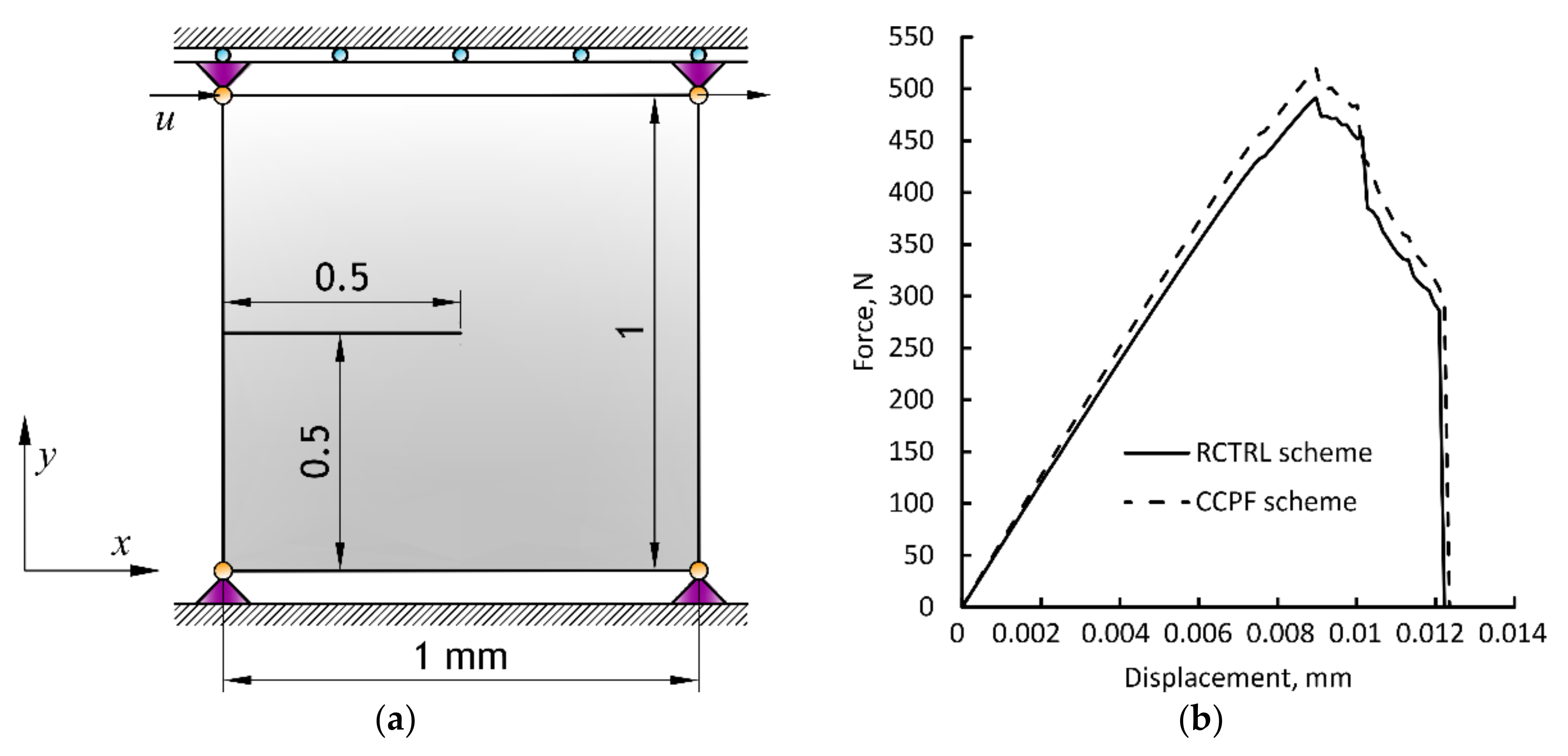
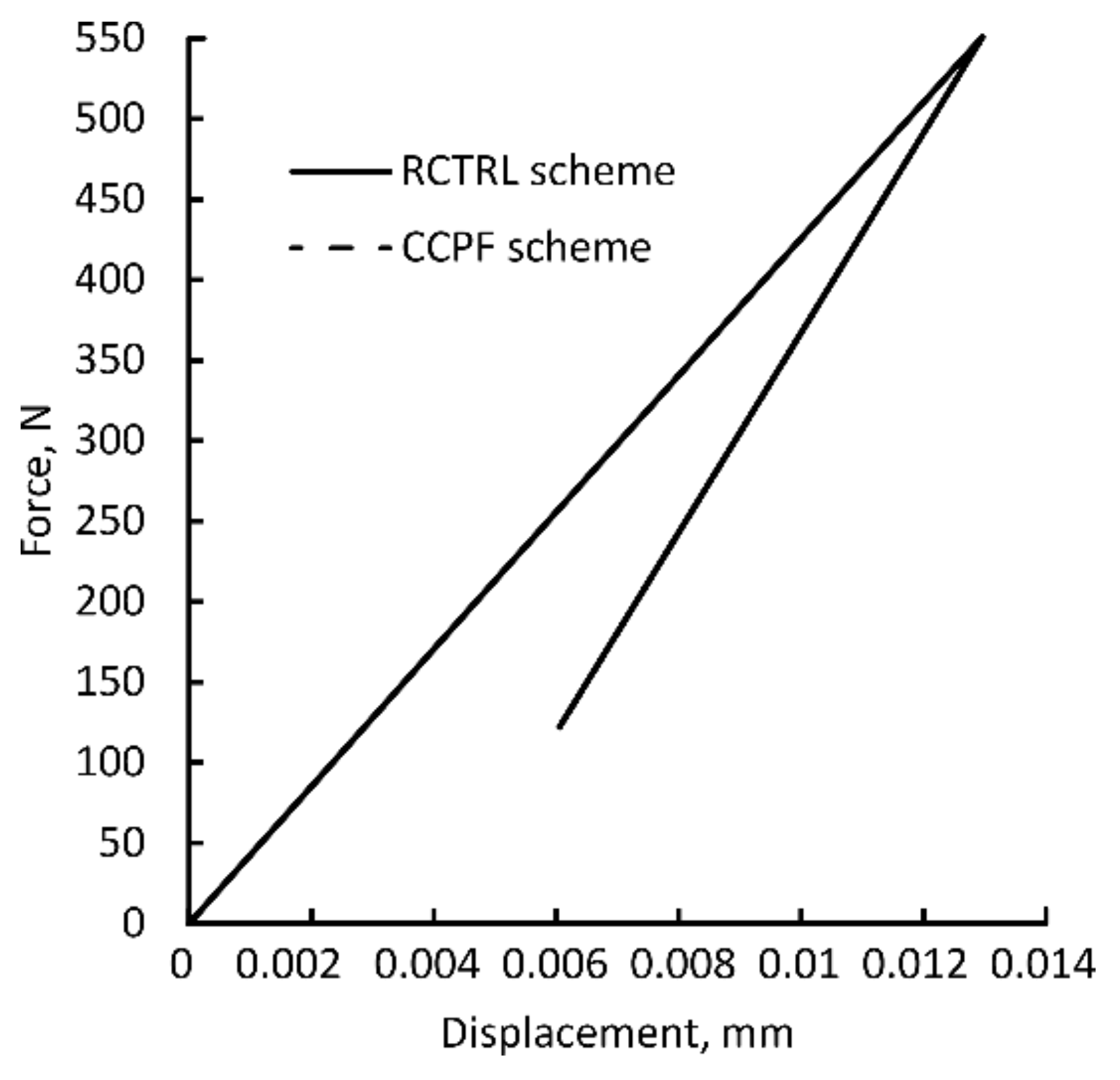
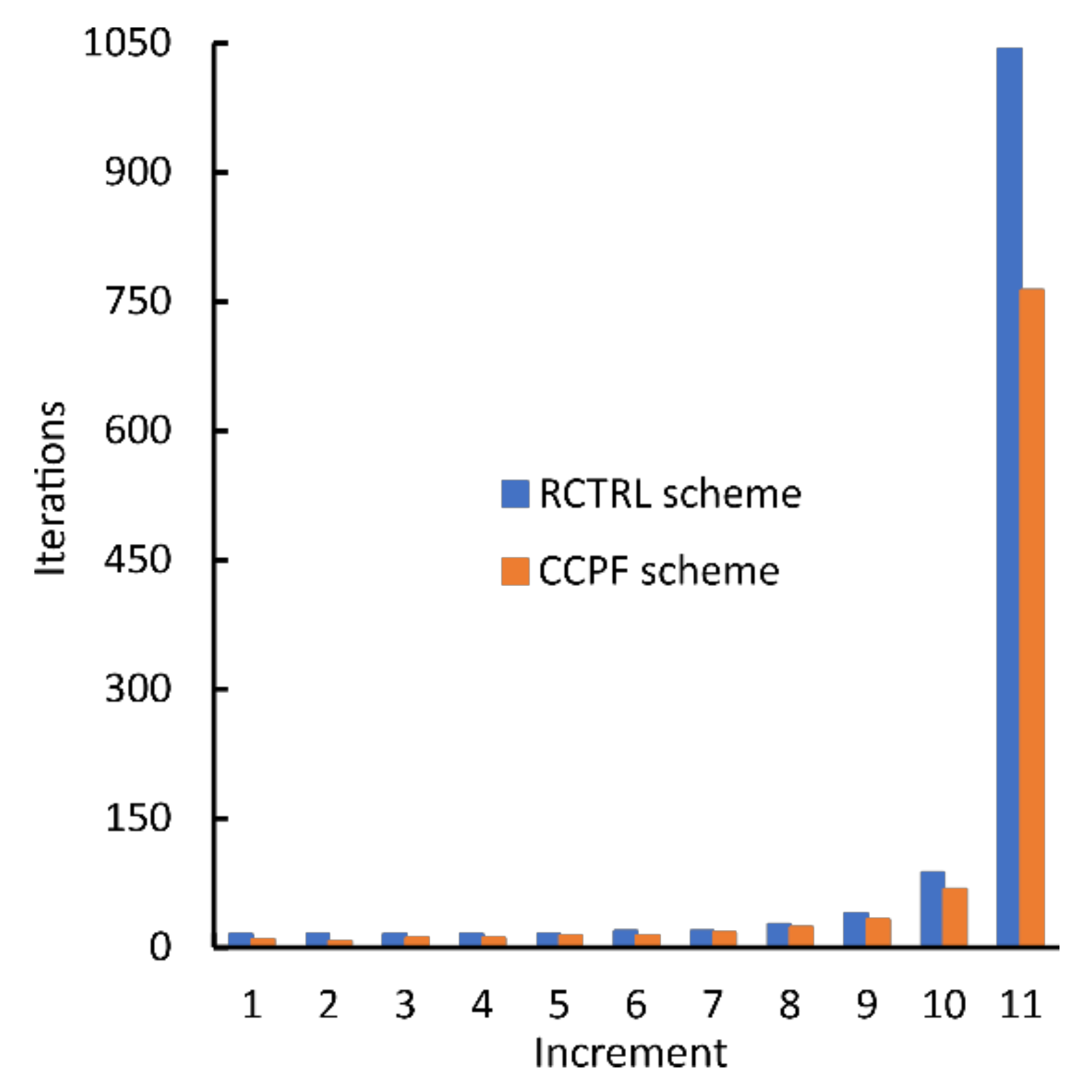
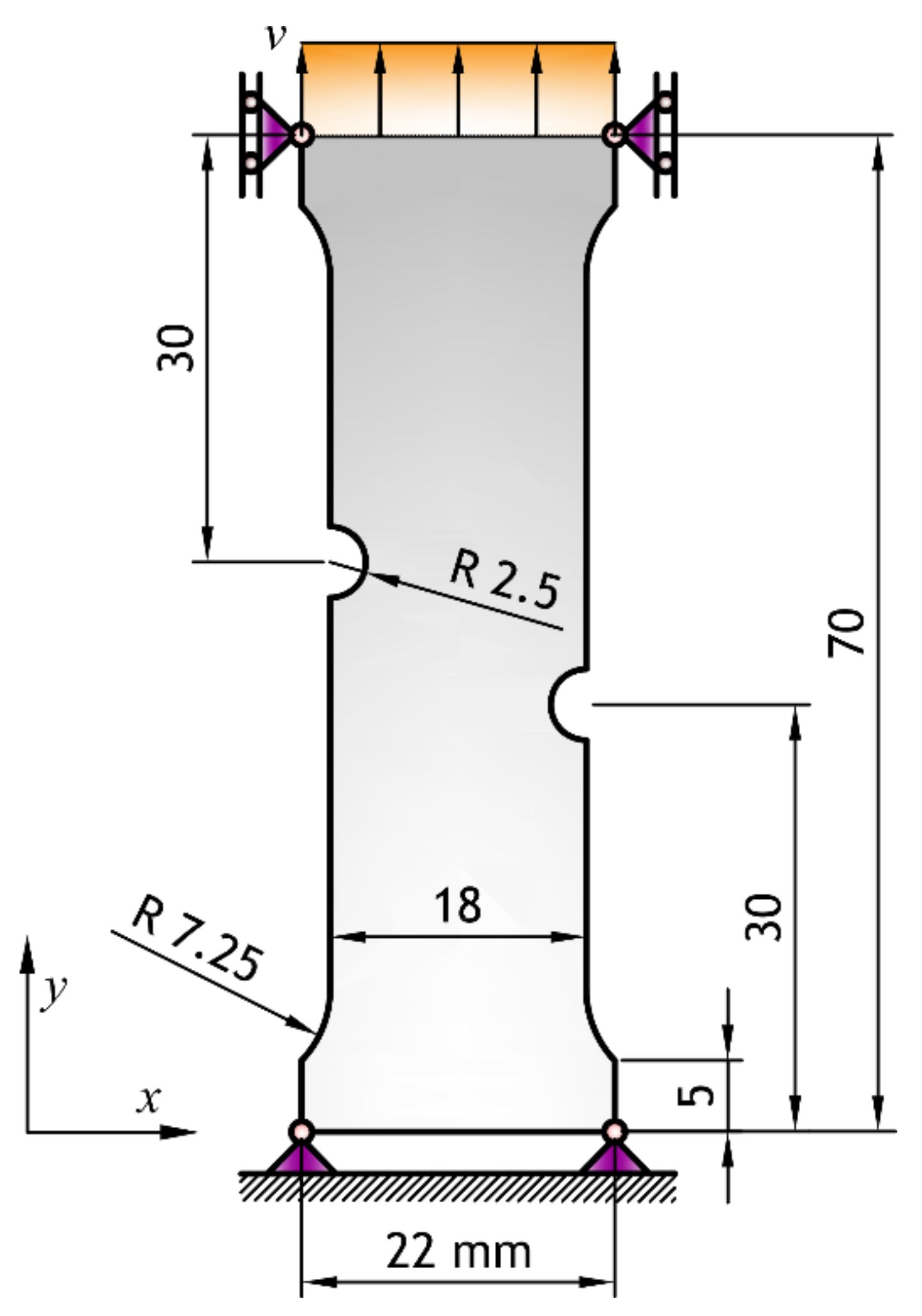
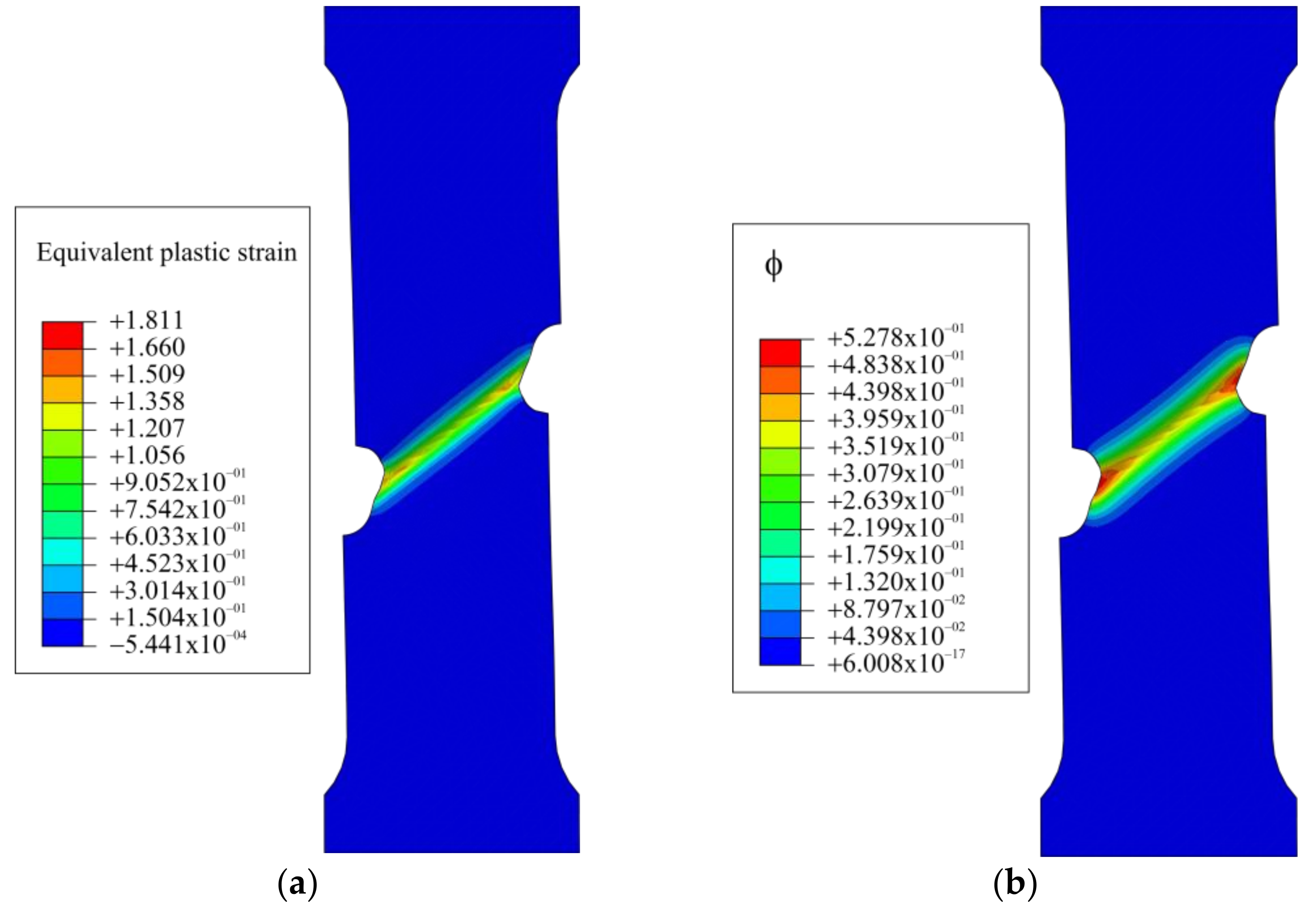
5.2. Ductile Fractures
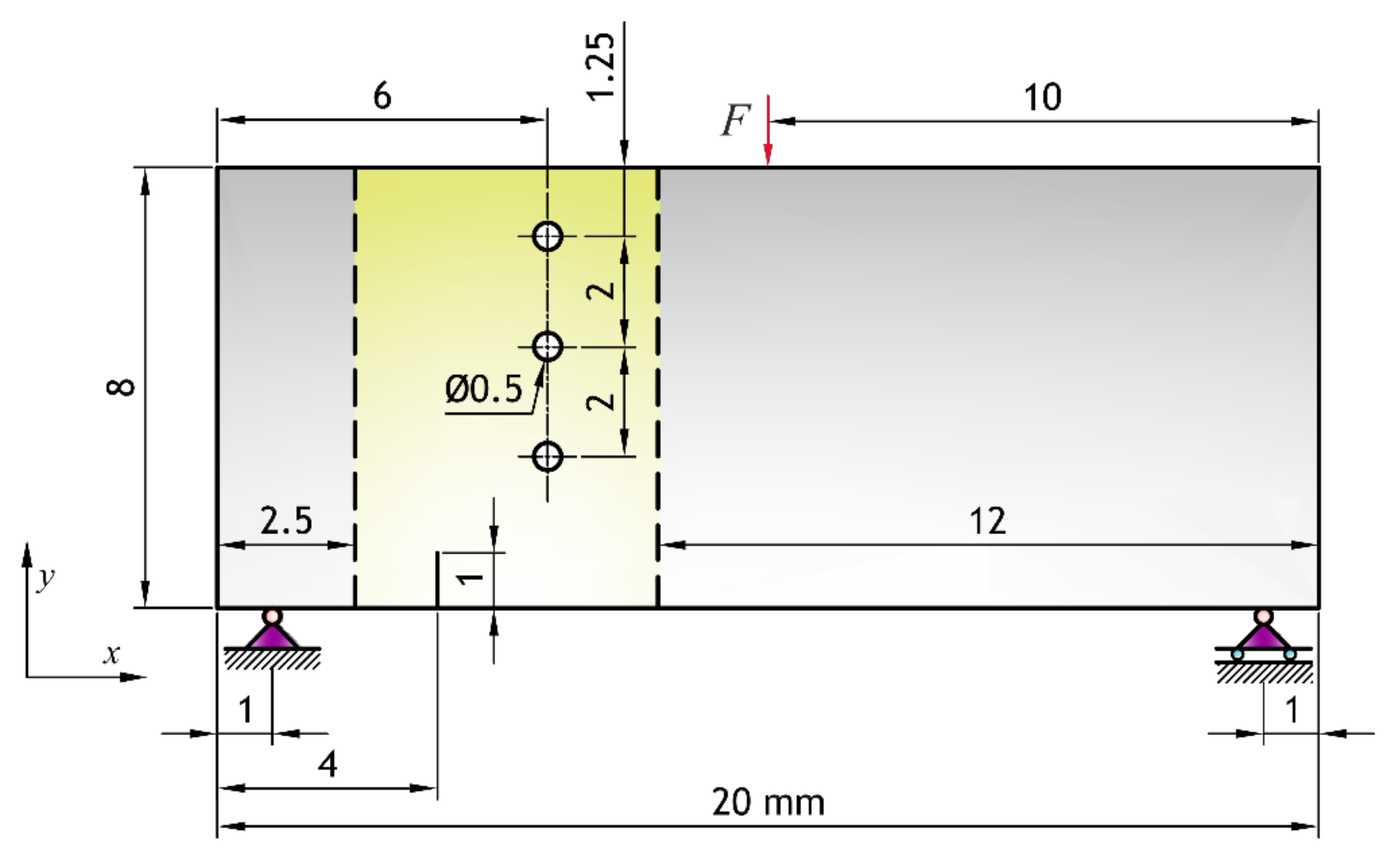
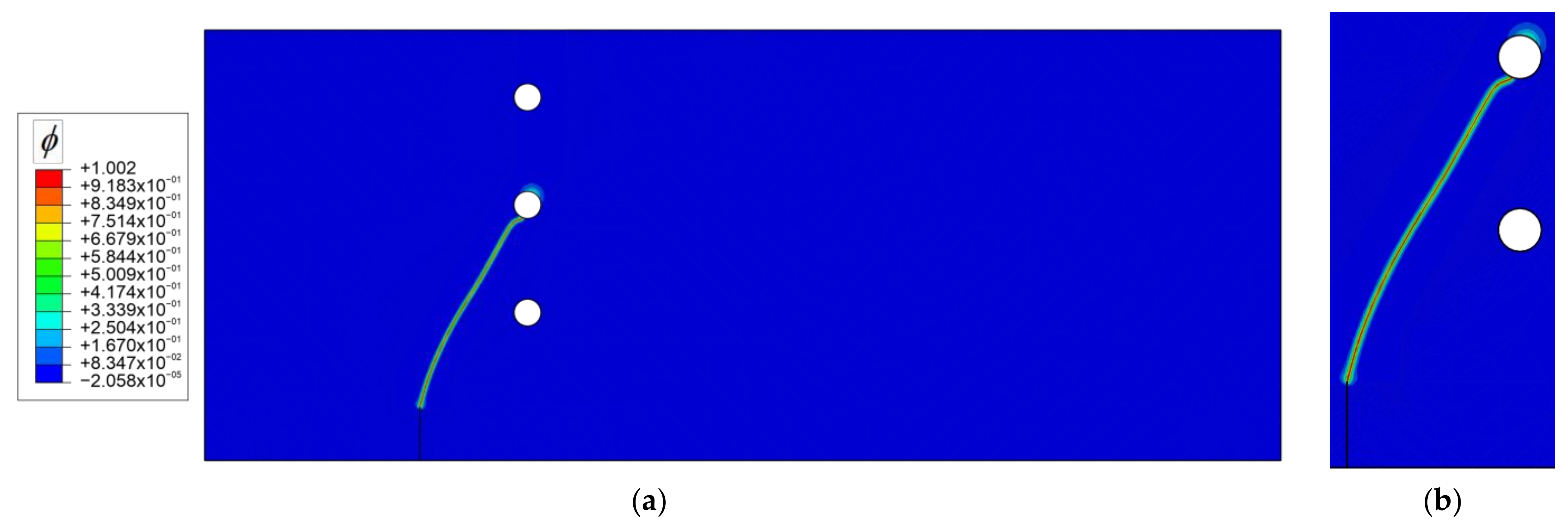
5.3. Low Cyclic Fatigue
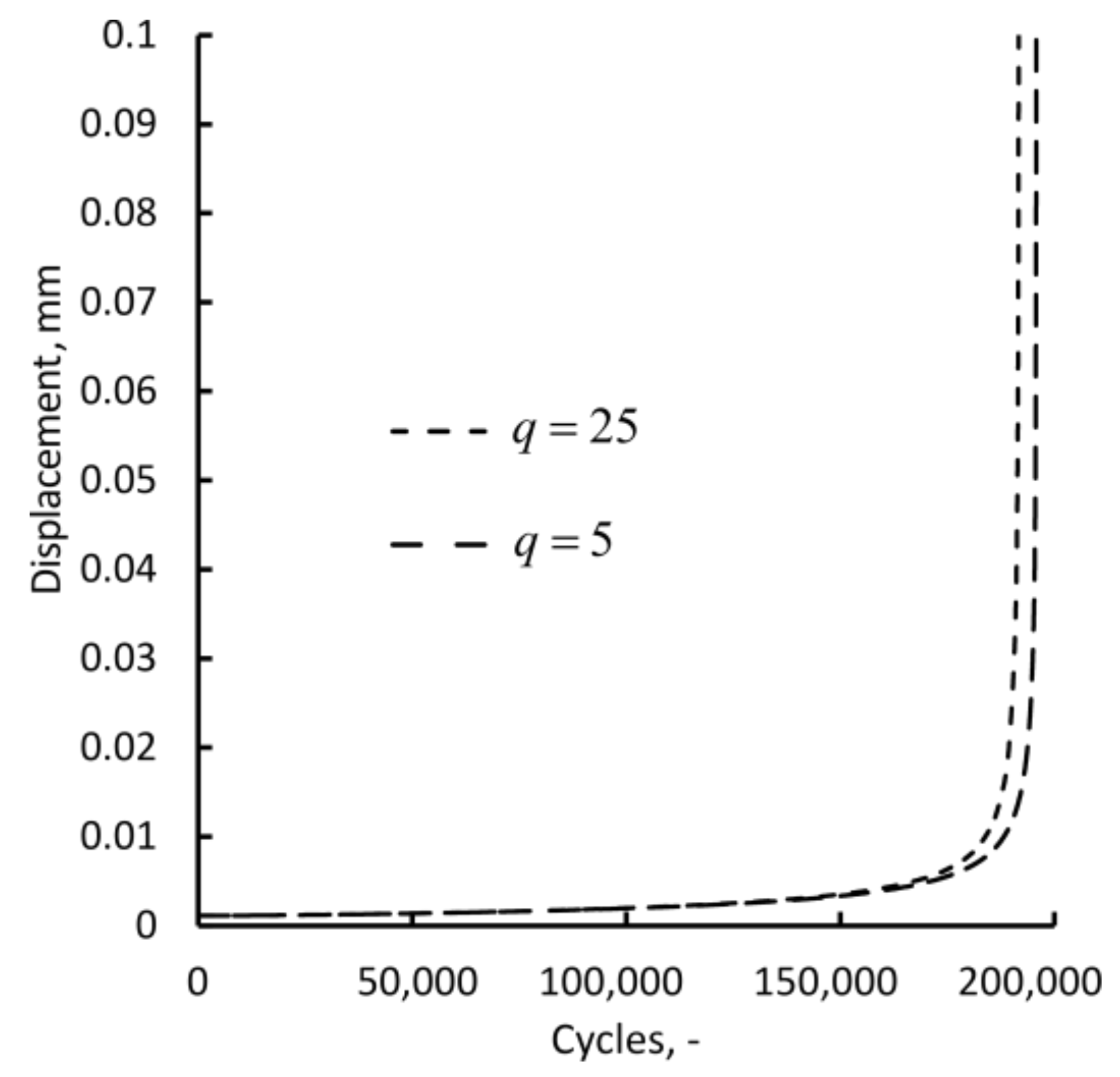
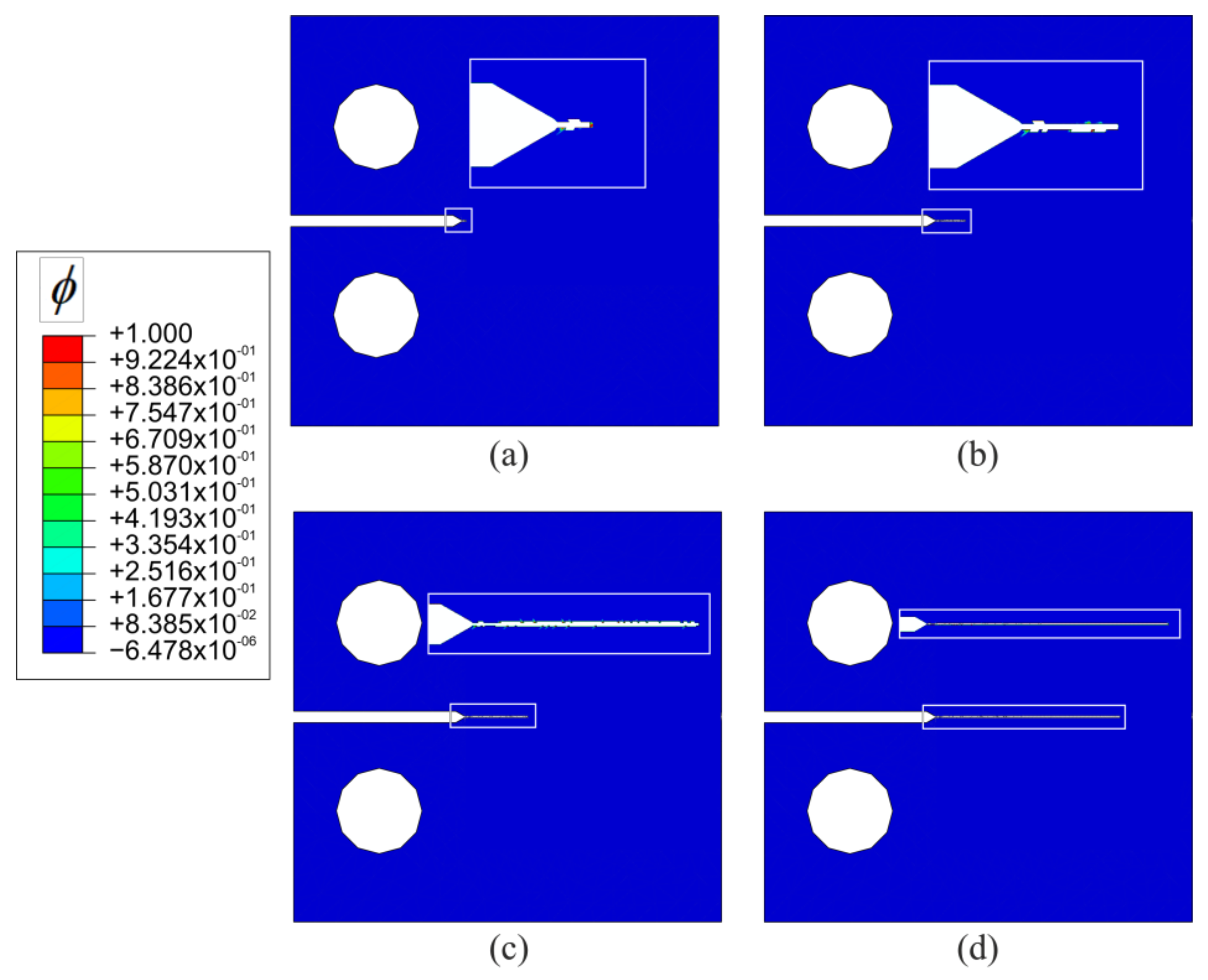
5.4. High Cyclic Fatigue
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | saturation exponent |
| prescribed body force vector | |
| u | |
| spatial derivative matrix corresponding to ϕ | |
| C | tangent material matrix |
| kinematic hardening modulus | |
| driving state function | |
| E | Young’s modulus |
| F | force |
| external force vector corresponding to v | |
| internal force vector corresponding to v | |
| external force vector corresponding to ϕ | |
| internal force vector corresponding to ϕ | |
| fatigue degradation function | |
| degradation function | |
| Griffith’s critical energy release rate | |
| H | heaviside function |
| stiffness matrix corresponding to u | |
| stiffness matrix corresponding to ϕ | |
| l | length scale parameter |
| n | normal vector |
| shape function matrices corresponding to u | |
| shape function matrices corresponding to | |
| q | fidelity parameter |
| saturation coefficient | |
| R | load ratio |
| residual vector corresponding to u | |
| residual vector corresponding to | |
| prescribed surface force vector | |
| tol | user-imposed tolerance |
| u | displacement field |
| v | vector of nodal displacements |
| external work | |
| internal work | |
| Greek | |
| α | back stress tensor |
| γ | crack density function |
| decrease rate of kinematic hardening | |
| crack surface | |
| elasticity matrix | |
| strain tensor | |
| equivalent plastic strain | |
| Láme constants | |
| Poisson ratio | |
| phase-field parameter | |
| history field | |
| energy density accumulation variable | |
| material-dependent fatigue parameter | |
| specific fracture energy | |
| elastic strain energy density | |
| positive or negative part of the elastic strain energy density | |
| plastic strain energy density | |
| free energy functional of the body | |
| body’s stored elastic deformation energy | |
| fracture induced dissipated energy | |
| σ | Cauchy stress tensor |
| initial yield stress | |
| n-dimensional body | |
| Sub/superscripts | |
| i | |
| k | iteration number |
| n | increment number |
| Abbreviations | |
| CCFE | convergence check finite element |
| CCPF | convergence check phase-field |
| CZM | cohesive zone model |
| DOF | degrees of freedom |
| EFG | element free Galerkin |
| FE | finite element |
| FEM | finite element method |
| FPZ | fracture processing zone |
| HCF | high cycle fatigue |
| LCF | low cycle fatigue |
| nFE | user-controlled number of cycles |
| NLGEOM | nonlinear geometry |
| UEL | abaqus user subroutine to define a finite element |
| RCTRL | residual control |
| UEXTERNALDB | abaqus user subroutine to manage user-defined external databases and calculate model-independent history information |
| UMAT | abaqus user subroutine to define a material’s mechanical behaviour |
| X-FEM | extended finite element method |
References
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H. Cohesive Zone Models: A Critical Review of Traction-Separation Relationships Across Fracture Surfaces. Appl. Mech. Rev. 2011, 64, 20. [Google Scholar] [CrossRef]
- Chandra, N.; Li, H.; Shet, C.; Ghonem, H. Some issues in the application of cohesive zone models for metal-ceramic interfaces. Int. J. Solids Struct. 2002, 39, 2827–2855. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, J.; Gomez, G.V.; Planas, J. The cohesive zone model: Advantages, limitations and challenges. Eng. Fract. Mech. 2002, 69, 137–163. [Google Scholar] [CrossRef]
- Tradegard, A.; Nilsson, F.; Ostlund, S. FEM-remeshing technique applied to crack growth problems. Comput. Methods Appl. Mech. Eng. 1998, 160, 115–131. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; Saouma, V. Numerical Modeling of Discrete Crack Propagation in Reinforced and Plain Concrete; Springer: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Dolbow, J.; Moes, N.; Belytschko, T. Discontinuous enrichment in finite elements with a partition of unity method. Finite Elem. Anal. Des. 2000, 36, 235–260. [Google Scholar] [CrossRef]
- Moes, N.; Gravouil, A.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets—Part I: Mechanical model. Int. J. Numer. Methods Eng. 2002, 53, 2549–2568. [Google Scholar] [CrossRef]
- De Borst, R. Damage, Material Instabilities, and Failure. In Encyclopedia of Computational Mechanics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Aifantis, E.C. On the role of gradients in the localization of deformation and fracture. Int. J. Eng. Sci. 1992, 30, 1279–1299. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Belytschko, T.B. Wave-propagation in a strain-softening bar—Exact solution. J. Eng. Mech.-Asce 1985, 111, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Bazant, Z.P.; Pijaudiercabot, G. Nonlocal continuum damage, localization instability and convergence. J. Appl. Mech.-Trans. Asme 1988, 55, 287–293. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; de Borst, R.; Brekelmans, W.A.M.; de Vree, J.H.P. Gradient enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Eng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- Hakim, V.; Karma, A. Laws of crack motion and phase-field models of fracture. J. Mech. Phys. Solids 2008, 57, 342–368. [Google Scholar] [CrossRef] [Green Version]
- Griffith, A.A.; Taylor, G.I.V.I. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1921, 221, 163–198. [Google Scholar] [CrossRef] [Green Version]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Molnar, G.; Gravouil, A.; Molnár, G. 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef] [Green Version]
- Soghrati, S.; Xiao, F.; Nagarajan, A. A conforming to interface structured adaptive mesh refinement technique for modeling fracture problems. Comput. Mech. 2017, 59, 667–684. [Google Scholar] [CrossRef]
- Heister, T.; Wheeler, M.F.; Wick, T. A primal-dual active set method and predictor-corrector mesh adaptivity for computing fracture propagation using a phase-field approach. Comput. Methods Appl. Mech. Eng. 2015, 290, 466–495. [Google Scholar] [CrossRef] [Green Version]
- Nagaraja, S.; Elhaddad, M.; Ambati, M.; Kollmannsberger, S.; De Lorenzis, L.; Rank, E. Phase-field modeling of brittle fracture with multi-level hp-FEM and the finite cell method. Comput. Mech. 2019, 63, 1283–1300. [Google Scholar] [CrossRef] [Green Version]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Gerasimov, T. Numerical Implementation of Phase-Field Models of Brittle Fracture BT. In Modeling in Engineering Using Innovative Numerical Methods for Solids and Fluids; De Lorenzis, L., Düster, A., Eds.; CISM International Centre for Mechanical Sciences, Springer International Publishing: Cham, Switzerland, 2020; Volume 599, pp. 75–101. [Google Scholar] [CrossRef]
- Seleš, K.; Lesičar, T.; Tonković, Z.; Sorić, J. A residual control staggered solution scheme for the phase-field modeling of brittle fracture. Eng. Fract. Mech. 2019, 205, 370–386. [Google Scholar] [CrossRef]
- Aldakheel, F.; Schreiber, C.; Müller, R.; Wriggers, P. Phase-Field Modeling of Fatigue Crack Propagation in Brittle Materials. In Current Trends and Open Problems in Computational Mechanics; Springer Nature: Cham, Switzerland, 2022; p. 15. [Google Scholar]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. A ductile phase-field model based on degrading the fracture toughness: Theory and implementation at small strain. Comput. Methods Appl. Mech. Eng. 2020, 366, 113068. [Google Scholar] [CrossRef]
- Levitas, V.I.; Warren, J.A. Phase field approach with anisotropic interface energy and interface stresses: Large strain formulation. J. Mech. Phys. Solids 2016, 91, 94–125. [Google Scholar] [CrossRef] [Green Version]
- Tan, W.; Martínez-Pañeda, E. Phase field predictions of microscopic fracture and R-curve behaviour of fibre-reinforced composites. Compos. Sci. Technol. 2021, 202, 108539. [Google Scholar] [CrossRef]
- Mandal, T.K.; Gupta, A.; Nguyen, V.P.; Chowdhury, R.; de Vaucorbeil, A. A length scale insensitive phase field model for brittle fracture of hyperelastic solids. Eng. Fract. Mech. 2020, 236, 107196. [Google Scholar] [CrossRef]
- Abdollahi, A.; Arias, I. Phase-field modeling of crack propagation in piezoelectric and ferroelectric materials with different electromechanical crack conditions. J. Mech. Phys. Solids 2012, 60, 2100–2126. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.Y.; Nguyen, V.P.; Nguyen, C.T.; Sutula, D.; Sinaie, S.; Bordas, S.P.A. Phase-field modeling of fracture. Adv. Appl. Mech. 2020, 53, 1–183. [Google Scholar] [CrossRef]
- Hosseini, Z.S.; Dadfarnia, M.; Somerday, B.P.; Sofronis, P.; Ritchie, R.O. On the Theoretical Modeling of Fatigue Crack Growth. J. Mech. Phys. Solids 2018, 121, 341–362. [Google Scholar] [CrossRef]
- Branco, R.; Antunes, F.V.; Costa, J.D. A review on 3D-FE adaptive remeshing techniques for crack growth modelling. Eng. Fract. Mech. 2015, 141, 170–195. [Google Scholar] [CrossRef]
- Boldrini, J.L.; de Moraes, E.A.B.; Chiarelli, L.R.; Fumes, F.G.; Bittencourt, M.L. A non-isothermal thermodynamically consistent phase field framework for structural damage and fatigue. Comput. Methods Appl. Mech. Eng. 2016, 312, 395–427. [Google Scholar] [CrossRef]
- Amendola, G.; Fabrizio, M.; Golden, J.M. Thermomechanics of damage and fatigue by a phase field model. J. Therm. Stress. 2016, 39, 487–499. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. Damage and fatigue described by a fractional derivative model. J. Comput. Phys. 2015, 293, 400–408. [Google Scholar] [CrossRef]
- Schreiber, C.; Kuhn, C.; Müller, R.; Zohdi, T. A phase field modeling approach of cyclic fatigue crack growth. Int. J. Fract. 2020, 225, 89–100. [Google Scholar] [CrossRef]
- Carrara, P.; Ambati, M.; Alessi, R.; de Lorenzis, L. A framework to model the fatigue behavior of brittle materials based on a variational phase-field approach. Comput. Methods Appl. Mech. Eng. 2020, 361, 29. [Google Scholar] [CrossRef]
- Alessi, R.; Vidoli, S.; de Lorenzis, L. A phenomenological approach to fatigue with a variational phase-field model: The one-dimensional case. Eng. Fract. Mech. 2018, 190, 53–73. [Google Scholar] [CrossRef]
- Seiler, M.; Linse, T.; Hantschke, P.; Kastner, M. An efficient phase-field model for fatigue fracture in ductile materials. Eng. Fract. Mech. 2020, 224, 15. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.M.; Baxevanis, T. A phase-field model for low-cycle fatigue of brittle materials. Int. J. Fatigue 2021, 150, 106297. [Google Scholar] [CrossRef]
- Golahmar, A.; Kristensen, P.K.; Niordson, C.F.; Martínez-Pañeda, E. A phase field model for hydrogen-assisted fatigue. Int. J. Fatigue 2022, 154, 106521. [Google Scholar] [CrossRef]
- Ulloa, J.; Wambacq, J.; Alessi, R.; Degrande, G.; François, S. Phase-field modeling of fatigue coupled to cyclic plasticity in an energetic formulation. Comput. Methods Appl. Mech. Eng. 2021, 373, 113473. [Google Scholar] [CrossRef]
- Seleš, K.; Aldakheel, F.; Tonković, Z.; Sorić, J.; Wriggers, P. A general phase-field model for fatigue failure in brittle and ductile solids. Comput. Mech. 2021, 67, 1431–1452. [Google Scholar] [CrossRef]
- Haveroth, G.A.; Vale, M.G.; Bittencourt, M.L.; Boldrini, J.L. A non-isothermal thermodynamically consistent phase field model for damage, fracture, and fatigue evolutions in elasto-plastic materials. Comput. Methods Appl. Mech. Eng. 2020, 364, 112962. [Google Scholar] [CrossRef]
- Khalil, Z.; Elghazouli, A.Y.; Martínez-Pañeda, E. A generalised phase field model for fatigue crack growth in elastic–plastic solids with an efficient monolithic solver. Comput. Methods Appl. Mech. Eng. 2022, 388, 114286. [Google Scholar] [CrossRef]
- Gerasimov, T.; De Lorenzis, L. A line search assisted monolithic approach for phase-field computing of brittle fracture. Comput. Methods Appl. Mech. Eng. 2016, 312, 276–303. [Google Scholar] [CrossRef]
- Wick, T. Modified Newton methods for solving fully monolithic phase-field quasi-static brittle fracture propagation. Comput. Methods Appl. Mech. Eng. 2017, 325, 577–611. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. The Variational Approach to Fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Duda, F.P.; Ciarbonetti, Á.A.; Sánchez, P.J.; Huespe, A.E. A phase-field/gradient damage model for brittle fracture in elastic–plastic solids. Int. J. Plast. 2015, 65, 269–296. [Google Scholar] [CrossRef] [Green Version]
- Farrell, P.E.; Maurini, C. Linear and nonlinear solvers for variational phase-field models of brittle fracture. arXiv 2015, arXiv:1511.08463. [Google Scholar] [CrossRef] [Green Version]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Van Dijk, N.P.; Espadas-Escalante, J.J.; Isaksson, P. Strain energy density decompositions in phase-field fracture theories for orthotropy and anisotropy. Int. J. Solids Struct. 2020, 196–197, 140–153. [Google Scholar] [CrossRef]
- Alessi, R.; Ambati, M.; Gerasimov, T.; Vidoli, S.; De Lorenzis, L. Comparison of Phase-Field Models of Fracture Coupled with Plasticity. In Advances in Computational Plasticity: A Book in Honour of D. Roger J. Owen; Oñate, E., Peric, D., de Souza Neto, E., Chiumenti, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–21. [Google Scholar] [CrossRef]
- Miehe, C.; Schaenzel, L.-M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Kristensen, K.K.; Niordson, F.N.; Martinez-Paneda, E. An assessment of phase field fracture: Crack initiation and growth. Philos. Trans. R. Soc. A 2021, 379, 20210021. [Google Scholar] [CrossRef] [PubMed]
- Cojocaru, D.; Karlsson, A.M. A simple numerical method of cycle jumps for cyclically loaded structures. Int. J. Fatigue 2006, 28, 1677–1689. [Google Scholar] [CrossRef] [Green Version]
- Ingraffea, A.R.; Grigoriu, M. Probabilistic Fracture Mechanics: A Validation of Predictive Capability; Cornell University: New York, NY, USA, 1990. [Google Scholar]
- Čanžar, P.; Tonković, Z.; Bakić, A.; Kodvanj, J. Experimental and Numerical Modelling of Fatigue Behaviour of Nodular Cast Iron. Key Eng. Mater. 2012, 488–489, 182–185. [Google Scholar]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lesičar, T.; Polančec, T.; Tonković, Z. Convergence Check Phase-Field Scheme for Modelling of Brittle and Ductile Fractures. Appl. Sci. 2023, 13, 7776. https://doi.org/10.3390/app13137776
Lesičar T, Polančec T, Tonković Z. Convergence Check Phase-Field Scheme for Modelling of Brittle and Ductile Fractures. Applied Sciences. 2023; 13(13):7776. https://doi.org/10.3390/app13137776
Chicago/Turabian StyleLesičar, Tomislav, Tomislav Polančec, and Zdenko Tonković. 2023. "Convergence Check Phase-Field Scheme for Modelling of Brittle and Ductile Fractures" Applied Sciences 13, no. 13: 7776. https://doi.org/10.3390/app13137776
APA StyleLesičar, T., Polančec, T., & Tonković, Z. (2023). Convergence Check Phase-Field Scheme for Modelling of Brittle and Ductile Fractures. Applied Sciences, 13(13), 7776. https://doi.org/10.3390/app13137776





